„Nawet w dziecięcych 

zabawach są rzeczy, które 

zainteresowałyby 

największego matematyka.”

Gottfried Wilhelm von Leibniz

LICZBY NA OSI LICZBOWEJ.

Oś  liczbowa  to  najprostszy  sposób  na 
dokładne  podanie  położenia  przedmiotu, 
który może poruszać się tylko po linii prostej, 
jest to także najprostszy sposób na graficzne 
przedstawienie  miejsca,  które  dana  liczba 
zajmuje wśród innych.

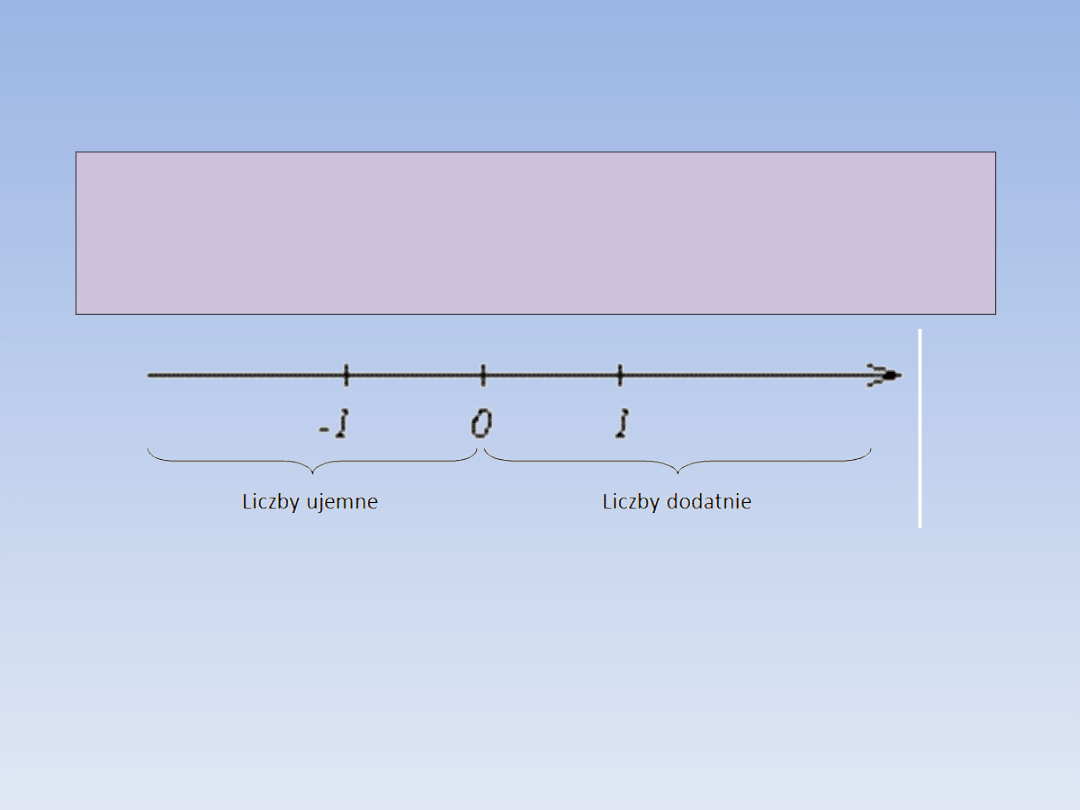
OŚ LICZBOWA.

Oś liczbowa to prosta z zaznaczonym 

zwrotem, punktem zerowym (0) oraz 

ustaloną jednostką.

Punkt początkowy 0 dzieli oś liczbową na 
dwie części:
- dodatnią – na prawo od zera, znajdują się 
tu wszystkie liczby większe od 0 a więc 
dodatnie
- ujemną – na lewo od 0, znajdują się tu 
wszystkie liczby mniejsze od 0 a więc 
ujemne

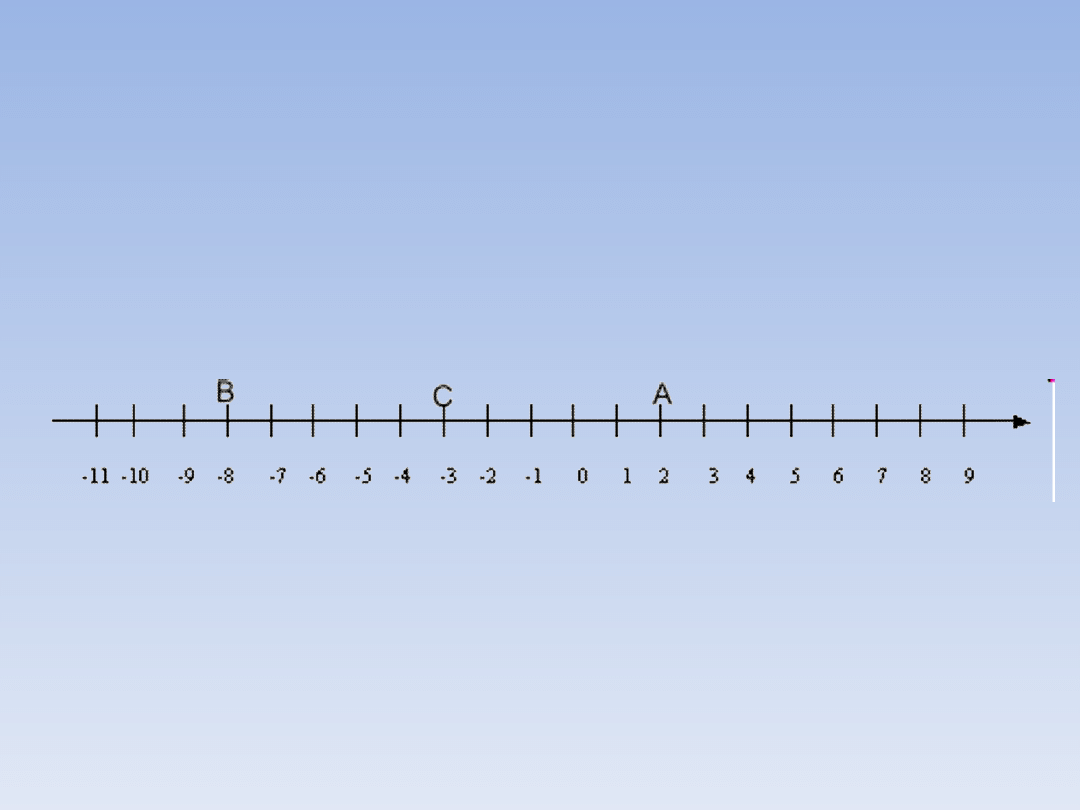
WSPÓŁRZĘDNA PUNKTU 

NA OSI.

Liczbę 

odpowiadającą 

pewnemu 

punktowi 

zaznaczonemu  na  osi  liczbowej  nazywamy 
współrzędną tego punktu.
Przykład:

Punkt A ma współrzędną 2 

(co można zapisać jako A = 2)

.

Punkt B ma współrzędną -8 

(co można zapisać jako B = -8)

.

Punkt C ma współrzędną -3 

(co można zapisać jako C = -3).

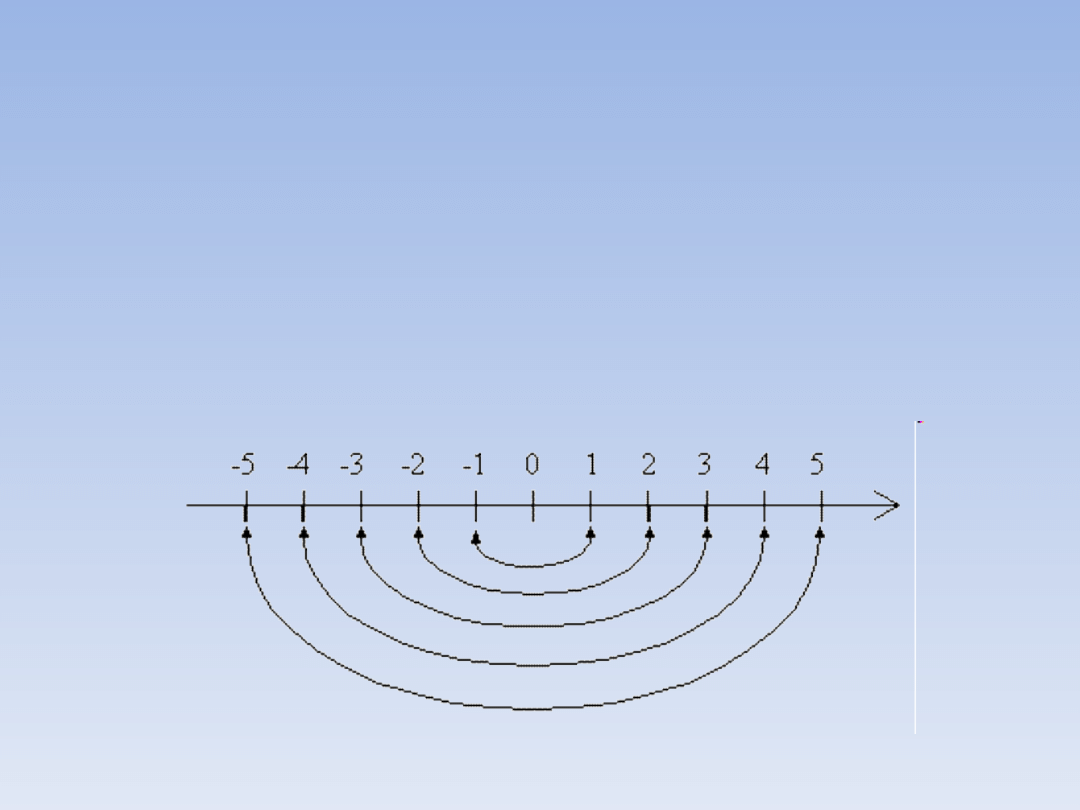
LICZBY PRZECIWNE NA OSI.

Pary liczb przeciwnych to na przykład: 1 i -1, 
5 i -5, 100 i -100 itp. 
Na  osi  liczbowej  liczby  przeciwne  są 
jednakowo oddalone od zera.

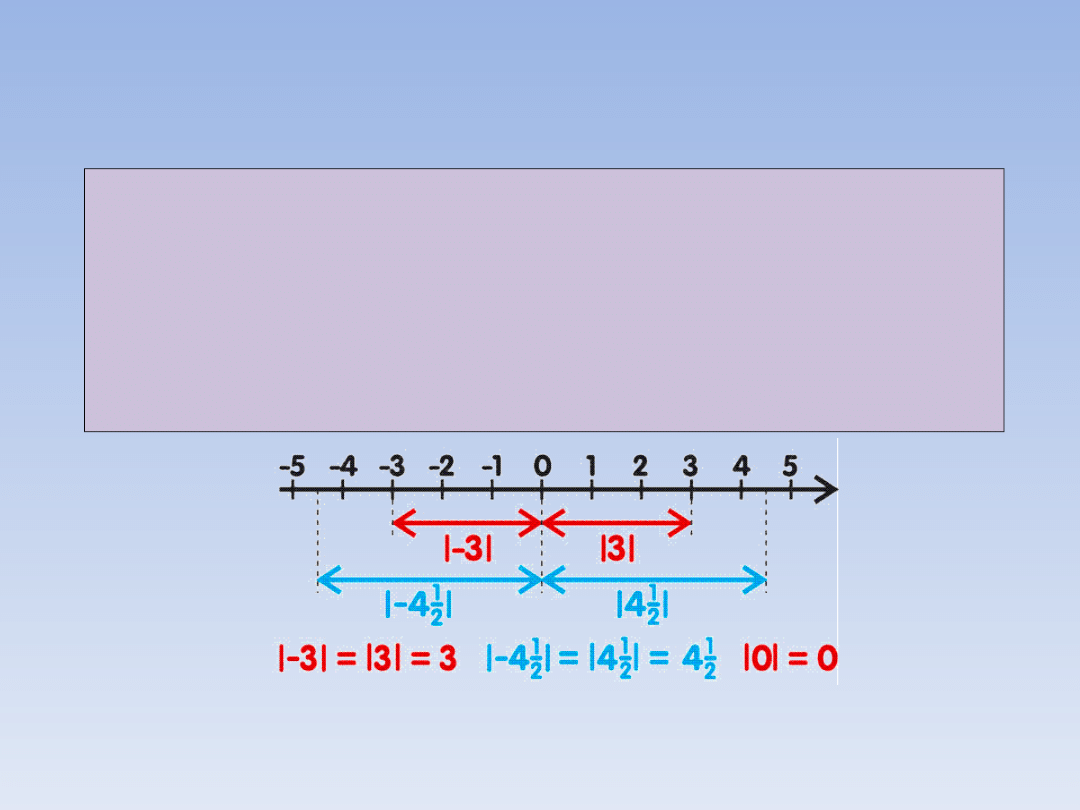
WARTOŚĆ BEZWZGLĘDNA 

LICZBY.

Wartością bezwzględną liczby a 

nazywamy odległość na osi liczbowej tej 

liczby od zera.

Wartość bezwzględna liczby a oznaczamy 

symbolem |a|.

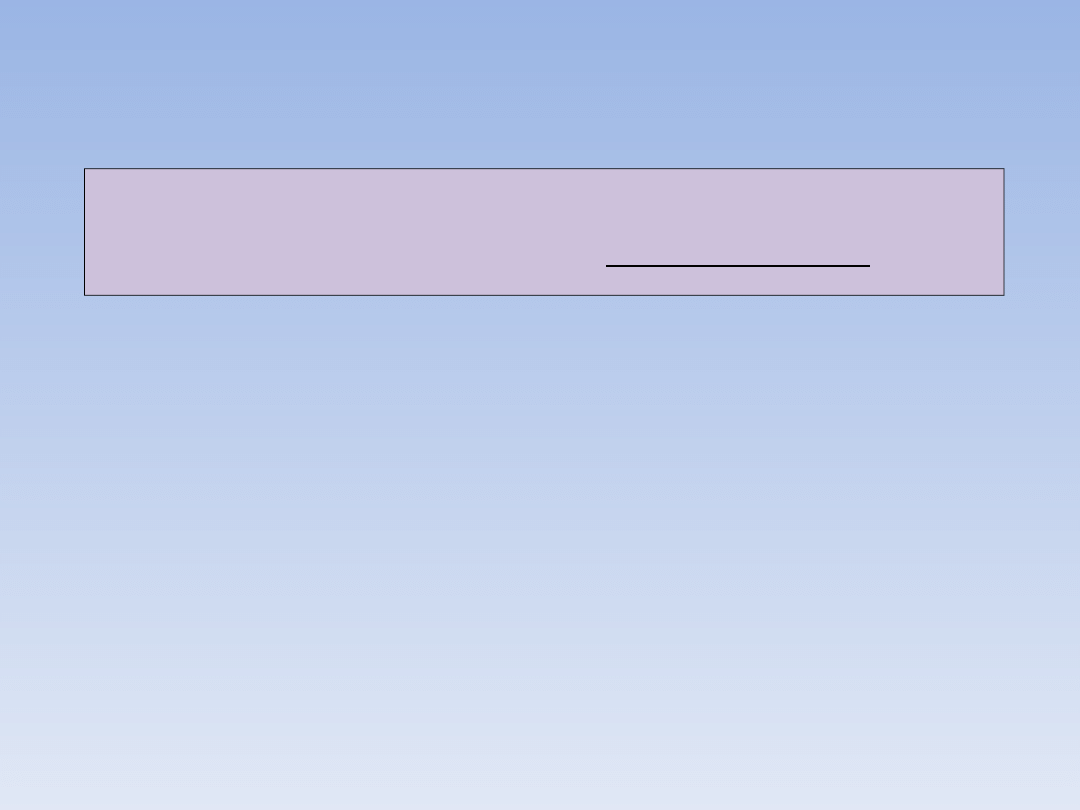
WARTOŚĆ 

BEZWZGLĘDNA LICZBY.

Wartością  bezwzględną  liczby  dodatniej  jest 
ta sama liczba dodatnia.
Wartością bezwzględną liczby 0 jest 0.
Wartością  bezwzględną  liczby  ujemnej  jest 
liczba do niej przeciwna.

Wartość bezwzględna dowolnej liczby 

jest zawszę liczbą nieujemną.

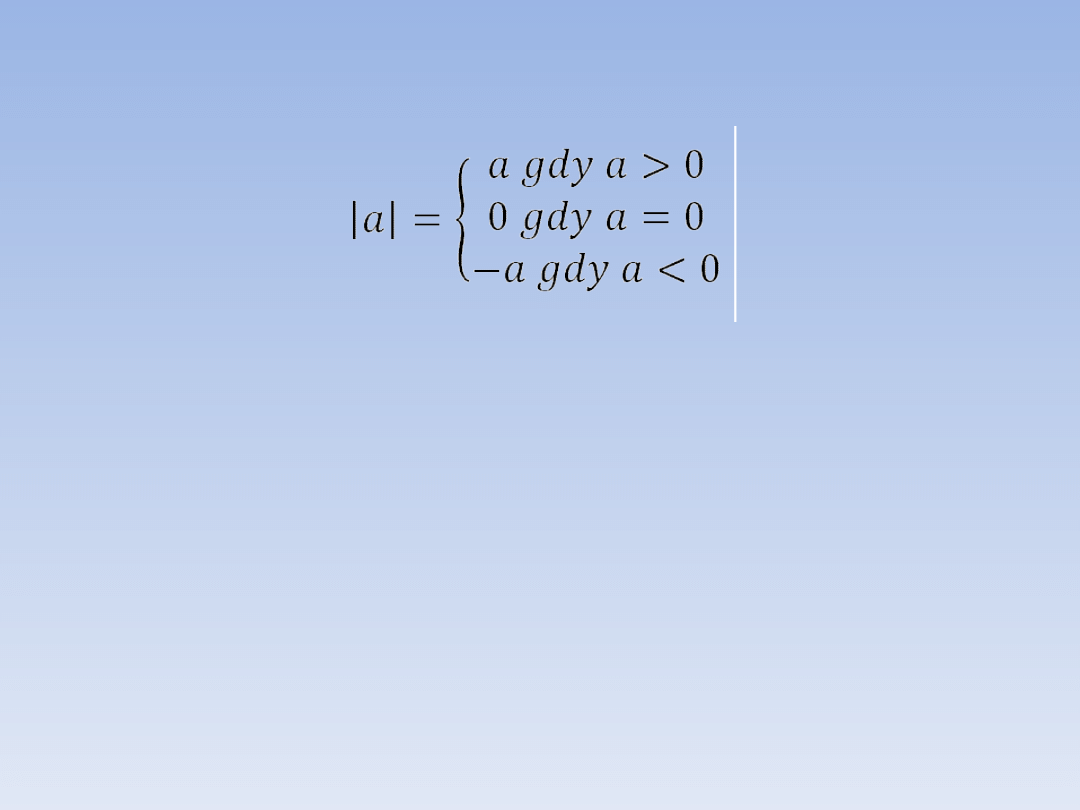
WARTOŚĆ 

BEZWZGLĘDNA LICZBY.

Przykłady:
|12| = 12
|-124| = 124
|0| = 0
|-3,5| = 3,5
|1,75| = 1,75
|-0,25| = 0,25

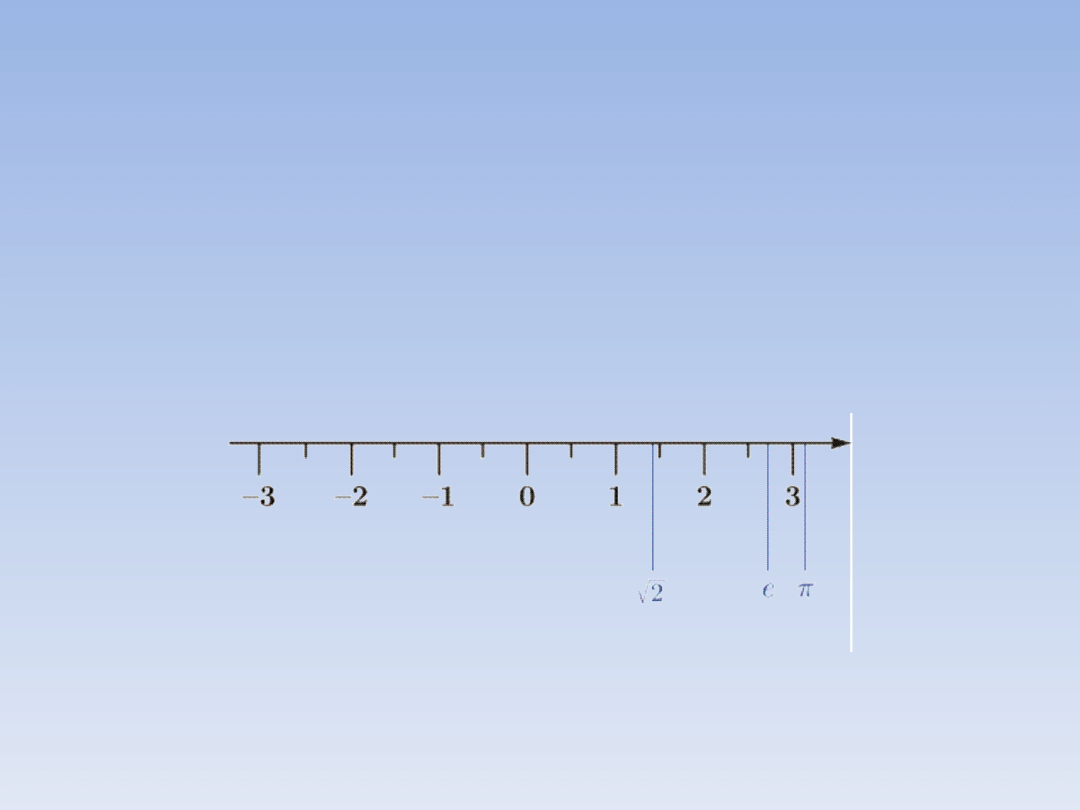
LICZBY WYMIERNE I 

NIEWYMIERNE.

Liczba  wymierna  to  taka,  którą  da  się  łatwo 
zmierzyć i zaznaczyć na osi liczbowej (każda, 
którą  da  się  zapisać  w  postaci  ułamka 
zwykłego). Liczby niewymierne są  trudne  do 
zaznaczenia  na  osi  liczbowej  i  możemy 
podać  jedynie  przybliżone  miejsce  ich 
położenia.

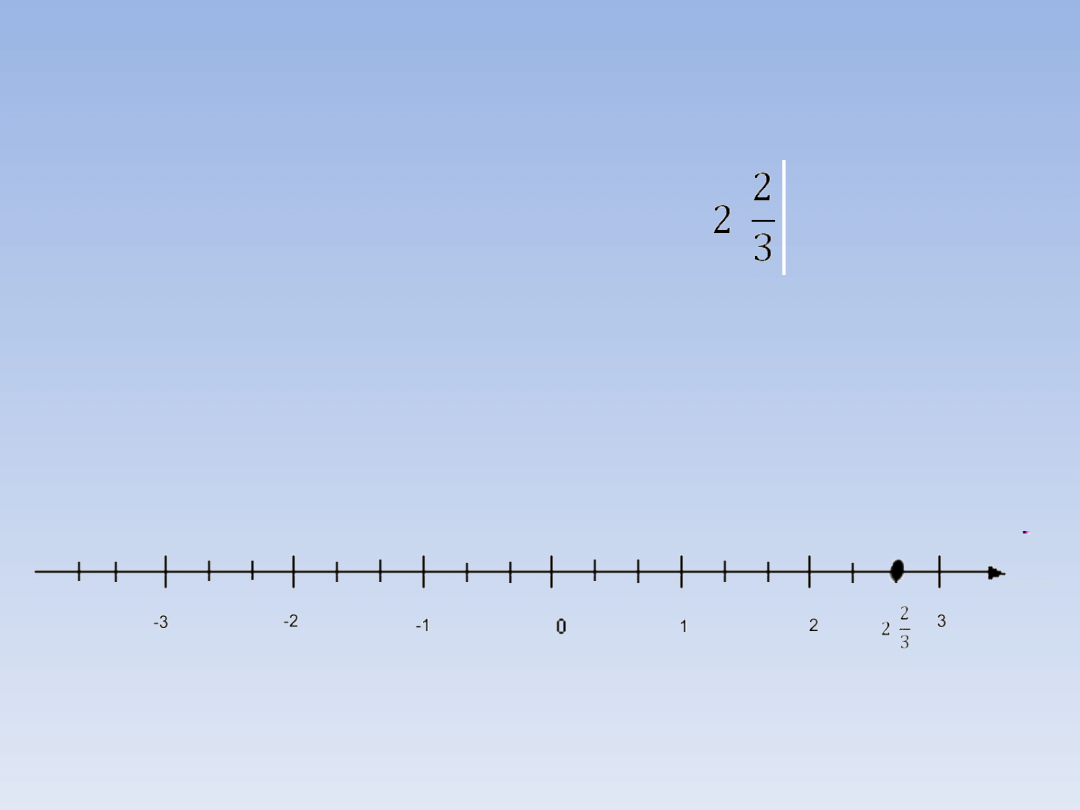
JAK ZAZNACZAĆ LICZBY 

WYMIERNE NA OSI 

LICZBOWEJ?

Na przykład: zaznacz na osi liczbowej           .

Aby  zaznaczyć  na  osi  tę  liczbę  przestrzeń 
między  jednostkami  dzielimy  na  3  równe 
części  a  następnie  zaznaczamy  2  pełne 
jednostki i 2 części z trzech mniejszych:

PRZYKŁADOWE ZADANIA.

Zadanie 1.
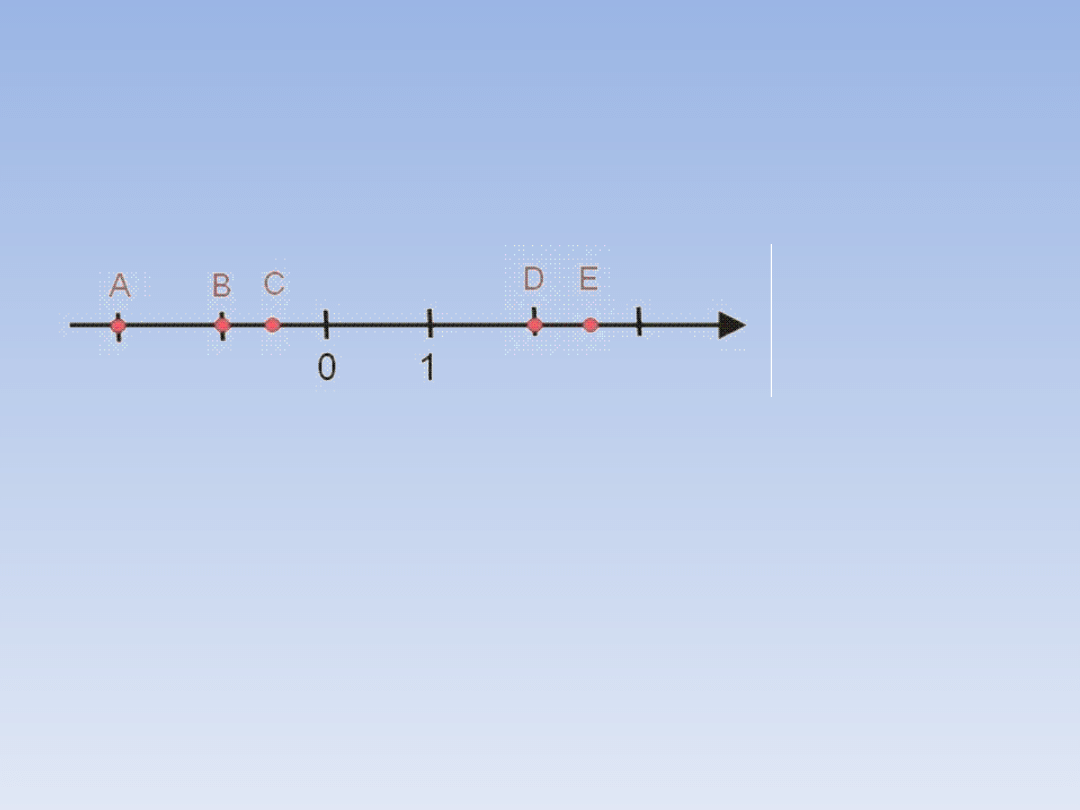
Odczytaj z osi współrzędne punktów.

Punkt  A  oddalony  jest  o  dwie  jednostki  w  lewo 
więc:
A = -2
B = -1
Punkt C leży w połowie jednostki więc:
C = -0,5
D = 2
E = 2,5

PRZYKŁADOWE ZADANIA.

Zadanie 2.
Wymień  liczby  całkowite,  których  odległość 
od zera jest mniejsza od 3.

Zaznaczmy  na  osi  liczbowej  liczby,  których 
odległość od zera jest równa 3, a więc liczby 
3 i -3:

Liczby  całkowite,  których  odległość  od  zera 
jest  mniejsza  od  3  to  wszystkie  całkowite 
pomiędzy zaznaczonymi, a więc: -2, -1, 0, 1, 
2.

PRZYKŁADOWE ZADANIA.

Zadanie 3.
Zaznacz  na  osi  liczbowej  liczby  spełniające 
warunek 
|x| = 3.

Zgodnie  z  definicją  wartości  bezwzględnej 
warunek 
|x|  =  3  oznacza,  że  odległość  liczby  x  od 
zera  ma  być  równa  3,  a  więc  liczby  o  które 
nam chodzi to 3 i -3:

PRZYKŁADOWE ZADANIA.

Zadanie 4.
Zaznacz  na  osi  liczbowej  liczby  spełniające 
warunek 
|x| < 3.

Tak  jak  w  zadaniu  2  warunek  |x|  =  3 
oznacza,  że  odległość  liczby  x  od  zera  ma 
być  równa  3,  a  więc  warunek  |x|  <  3 
oznacza, że odległość tych liczb od zera ma 
być  mniejsza  niż  3,  są  to  więc  wszystkie 
liczby  pomiędzy  3  i  -3,  bez  3  i  -3,  a 
zaznaczamy to tak:

PRZYKŁADOWE ZADANIA.

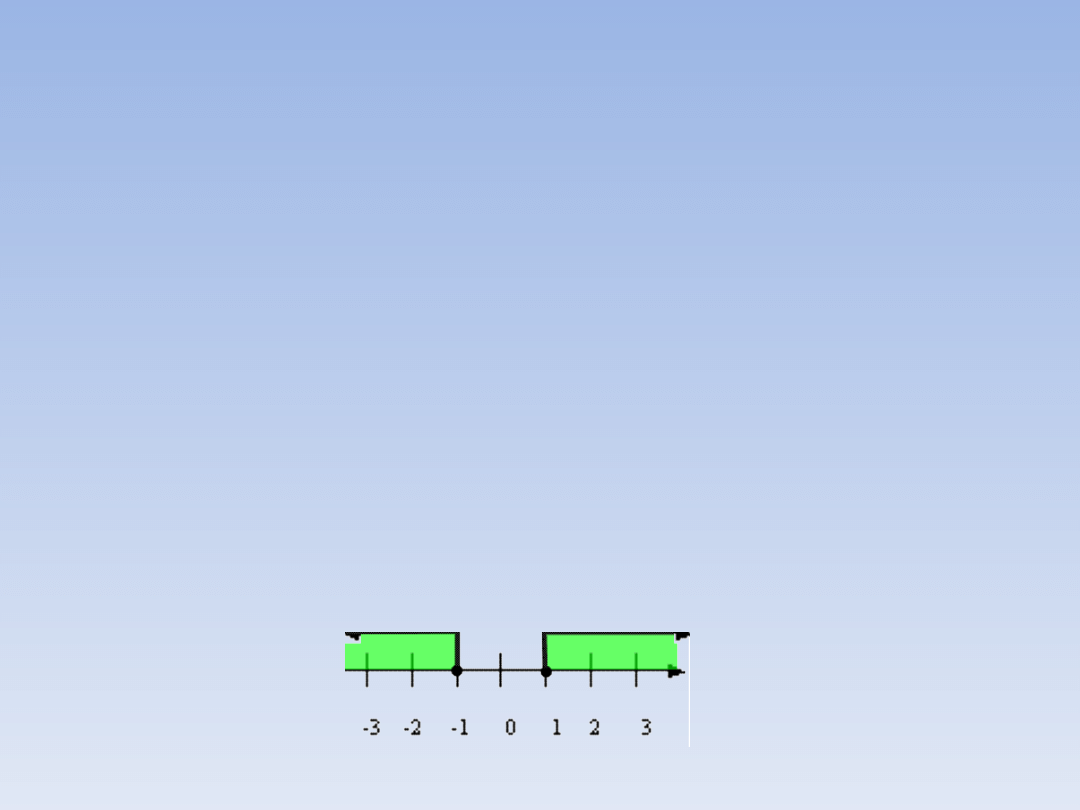
Zadanie 5.
Zaznacz  na  osi  liczbowej  liczby  spełniające 
warunek 
|x| ≥ 1.

Warunek |x| = 1 oznacza, że odległość liczby 
x od zera ma być równa 1, a więc warunek |
x|  ≥  1  oznacza,  że  odległość  tych  liczb  od 
zera  ma  być  większa  bądź  równa  1,  są  to 
więc  wszystkie  liczby  większe  od  1  i 
mniejsze  od  -1  wraz  z  1  i  -1,  a  zaznaczamy 
to tak:

PRZYKŁADOWE ZADANIA.

Zadanie 6.
Wykonaj obliczenia:
|-5 – 4| = |-9| = 9

|0 – 2,5| = |-2,5| = 2,5

|6| + |-6| = 6 + 6 = 12

|4 + (-4)| = |0| = 0

|-5 · 3| = |-15| = 15

|-2,5| · (-4) = 2,5 · (-4) = -10

PRZYKŁADOWE ZADANIA.

Zadanie 7.
Znajdź brakującą liczbę:
|x| + 2 = 6
Rozwiązanie równania x + 2 = 6 jest oczywiste: 
x = 4. Wartość bezwzględna sprawia, że 4 
dostaniemy zarówno kiedy x = 4 jak i x = -4 i 
to są właśnie brakujące liczby.
|3 + y| = 8
Rozwiązanie y = 5 nasuwa się samo, ale 
pamiętajmy, że wynik będzie prawidłowy, także 
kiedy pod wartością bezwzględną otrzymamy 
-8, czyli kiedy y = -11. Brakujące liczby to: y = 
5 oraz y = -11