1

Wyznaczenie punktów o zaprojektowanych pozycjach względem

osi konstrukcyjnych obiektu

Tyczenie

Bez obserwacji
nadliczbowych

lokalizacyjne

szczegółowe

jednoetapowe

dwuetapowe

wielokrotne

Z obserwacjami
nadliczbowymi

Bez obserwacji
nadliczbowych

Z obserwacjami
nadliczbowymi

Wyznaczenie punktów o zaprojektowanych pozycjach względem

osnowy realizacyjnej

lub też

2

Metody tyczenia (1)



d

A

B

P

P





d

b

A

B



d

A

B

P

A

B

punkt osnowy realizacyjnej

punkt
tyczony

odłożone w terenie
obliczone wartości
obserwacji

baza
tyczenia

P’

domiarów prostokątnych

biegunowa

przedłużenia kierunku

3

Metody tyczenia (2)

A

B

P’

P

P’

A

B

P

II.

P’

w

2

w

1

W

1

W

2

a

IV.

I.

W

1

W

2

st. tach.

P

zero limbusa

a

III.

4

Zalecenia

powinien być spełniony warunek, że l < d

d

l

P

B

A



P

A

B

d

domiar

d

powinien być jak najkrótszy

A

B

P

d

przedłużenie

d

nie powinno przekraczać 1/3

długości bazy tyczenia

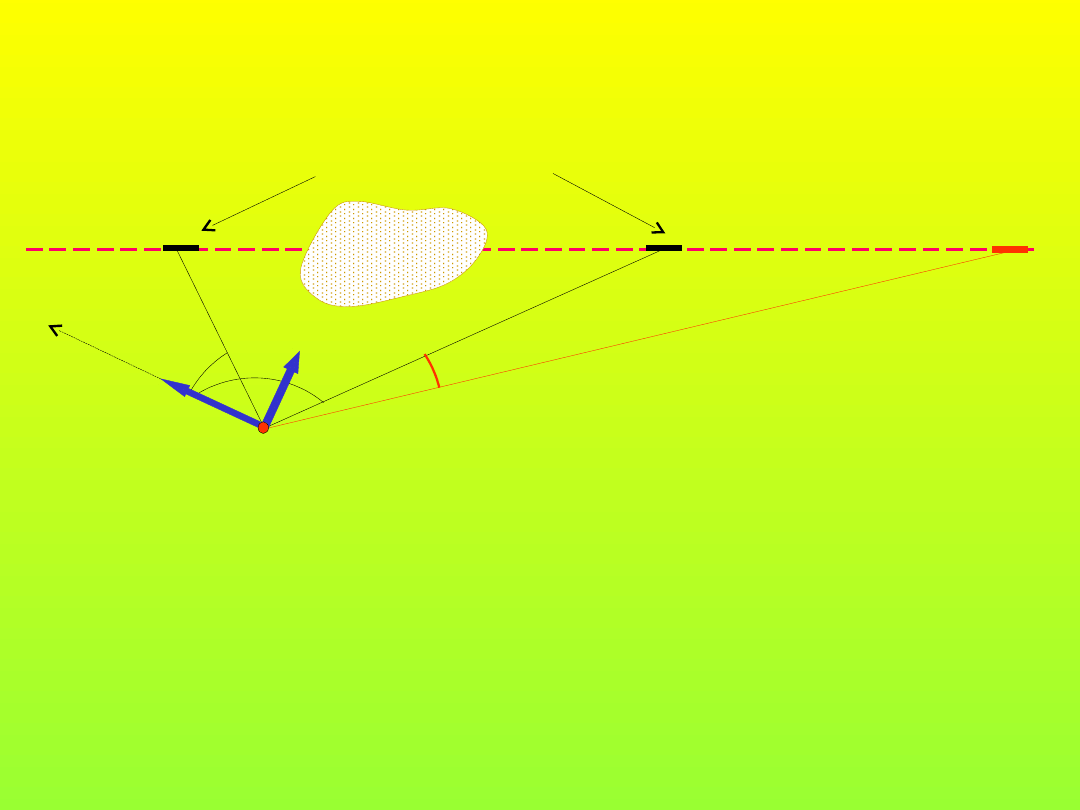
5

Tyczenie linii prostej

ZER

O LIM

BUS

A

WSKAŹNIKI OSIOWE

T

X

L

W

1

W

2

d

1

d

2

Y

L

k

1

k

2

W

3

D

Zadnie: wytyczyć wskaźnik W

3

na linii W

1

,W

2

w odległości D od W

2

.

1.Na podstawie pomierzonych kier. k

i

i długości d

i

obliczamy współrzędne punktów W

1

i W

2

w lokalnym układzie wsp. X

L

Y

L.

2.Dla znanej odległości D obliczamy współrzędne wskaźnika W

3

.

3.Obliczamy k

3

i d

3

k

3

d

3

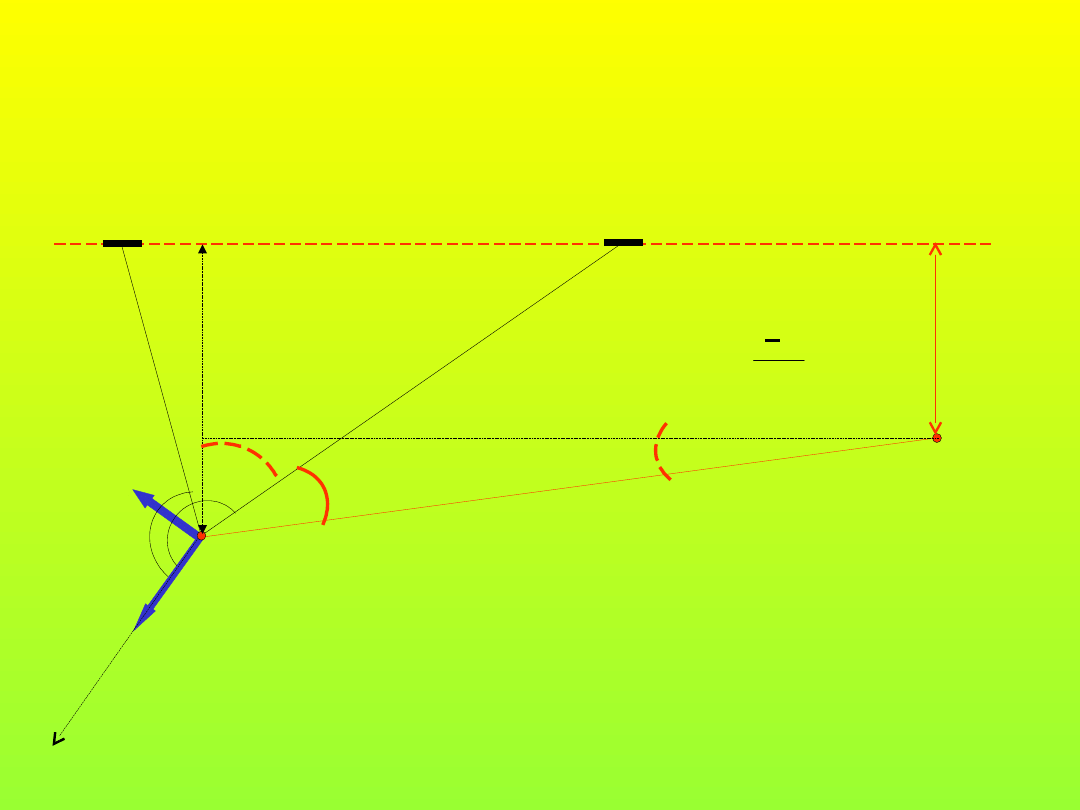
6

Y

L

k

1

Tyczenie linii równoległej

W

1

W

2

ZE

RO

L

IM

BU

SA

X

L

d

P

T

k

2

k

P

=90--

d

1

d

2

d

P

Zadanie: wytyczyć punkt P w odległości d od linii W

1

W

2

1.dla ustalonej wartości k

P

obliczamy d

P

2.dla ustalonej wartości d

P

obliczamy k

P

Wyznaczając w ten sposób dwa punkty uzyskujemy linię równoległą



l



a

d

l

=

ε

sin

7

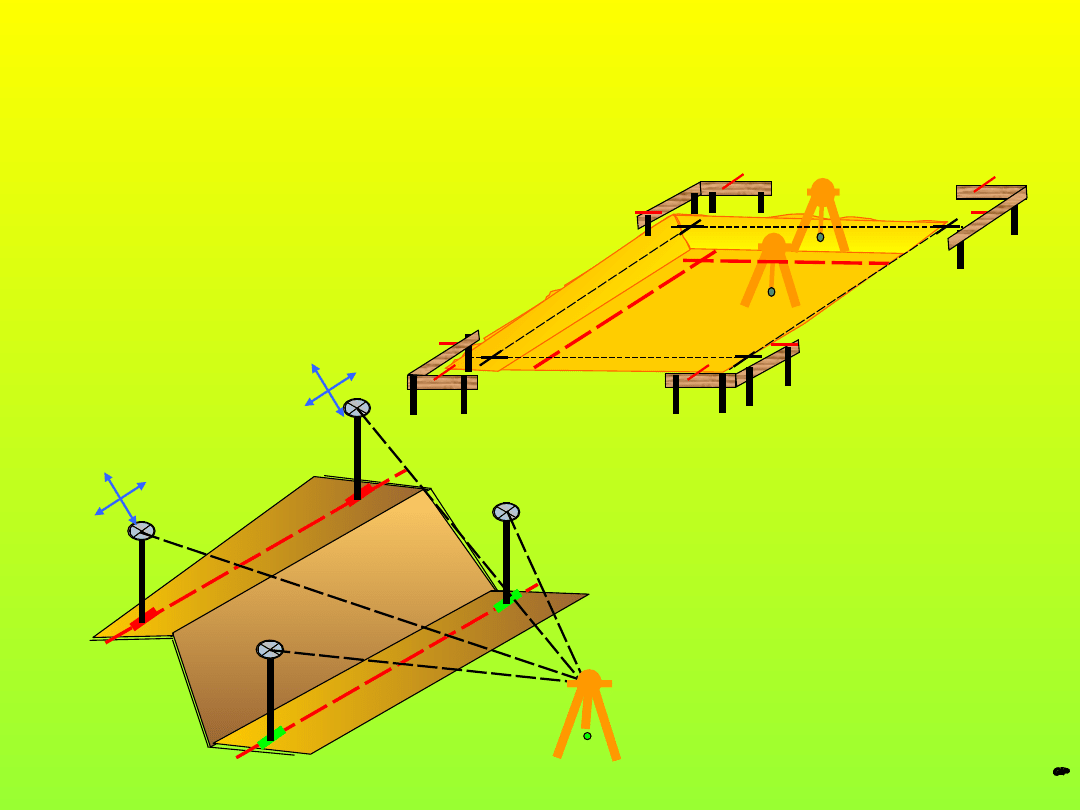
Tyczenie

(przykład)

P

W

1

W

2

W

3

W

4

8

dl = l -
l

pr

d =  



pr.

Tyczenie dwuetapowe

’

l’

A

B

P

d

dl

’ l’

-wstępnie odłożone obserwacje
-przybliżona pozycja punktu
-poprawki tyczenia
-projektowana pozycja punktu
-obserwacje pomierzone z zaprojek-
towaną dokładnością

P’

d d

lP



l

l’

’

P

P’

P’

A

B

X

Y

dx

dy



a



b

l

b

l

a

Bez obserwacji nadliczbowych

Z obserwacjami nadliczbowymi

dx= x

w

-

x

pr

dy= y

w

-

y

pr

-P’ wyznaczone na podstawie

’ i l’

-

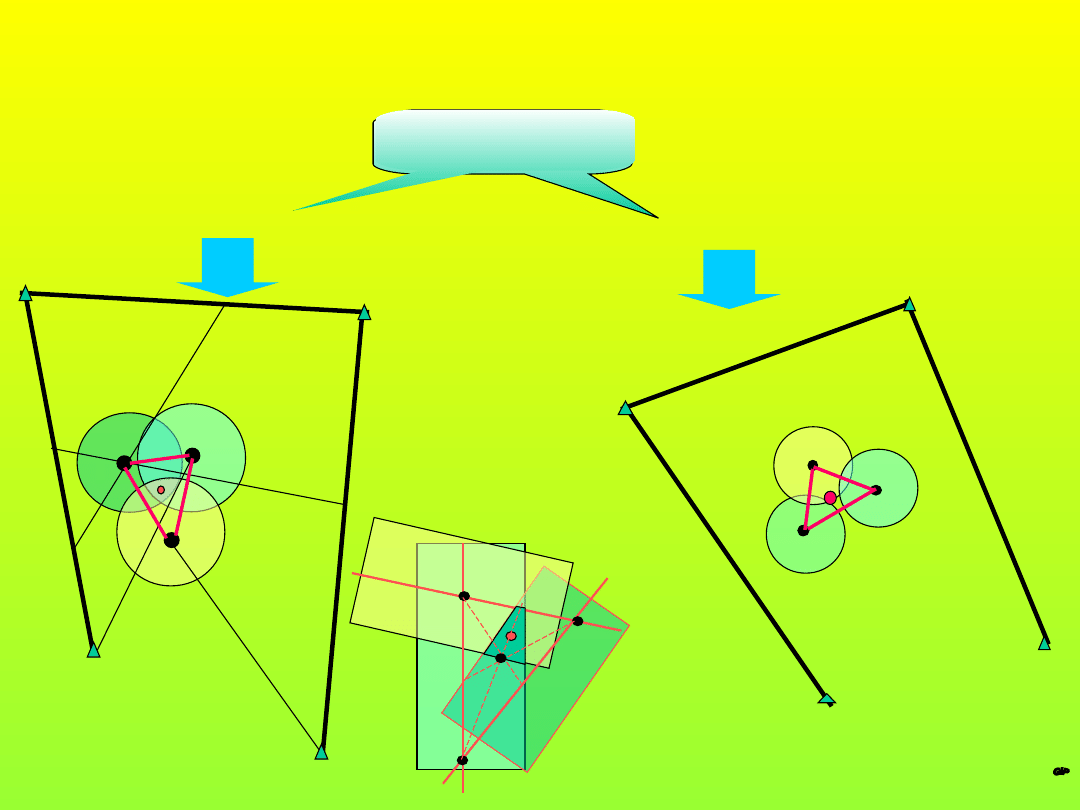
9

Tyczenie wielokrotne

A

B

C

D

P’

P’’

P’’’

P

P’

P’’

P’’’

P

A

D

B

C

ROZWIĄZANIE

poprawne

niepoprawne

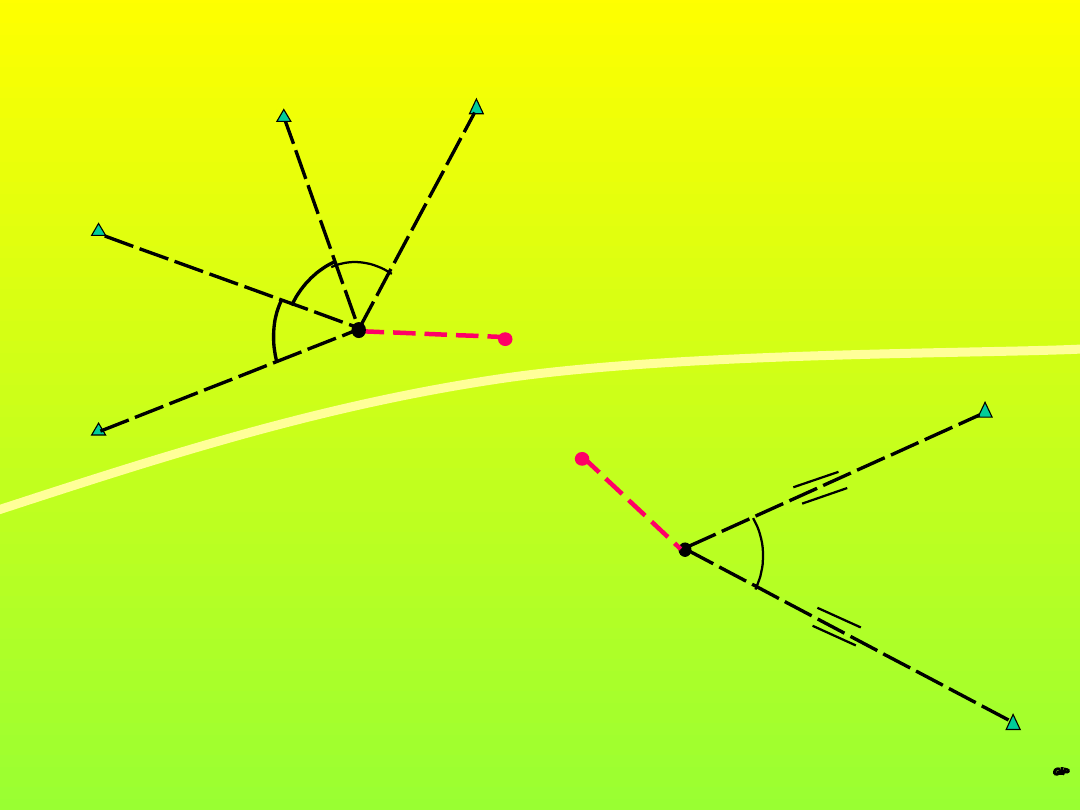
10

A

A

B

C

P’



2



1

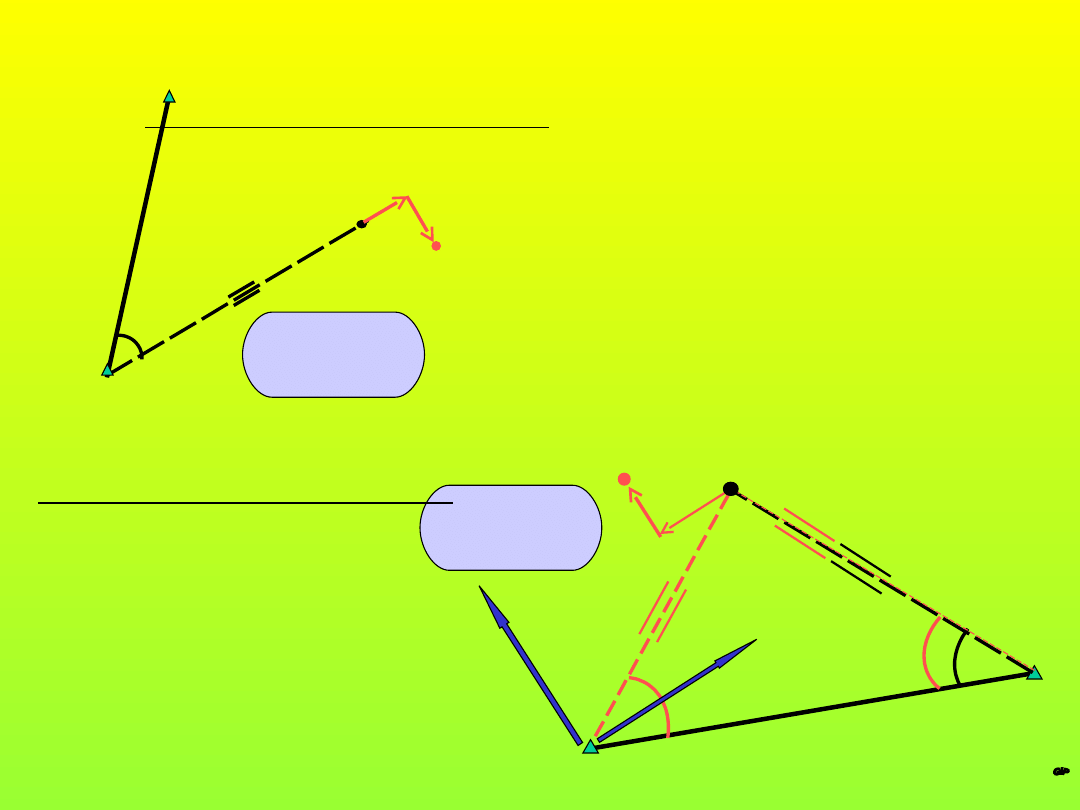
Trzy punkty bazy tyczenia pozwalają na
wyznaczenie punktu P’ w sposób jednoznaczny

Tyczenie z obserwacjami

nadliczbowymi

D



3

Dopiero czwarty punkt pozwala na wykonanie
wcięcia wstecz z jedną obserwacją nadliczbową

A

B

P’

l

A

l

B



Dwa punkty bazy tyczenia pozwalają
na wyznaczenie punktu P’ z jedną
obserwacją nadliczbową.

P

P

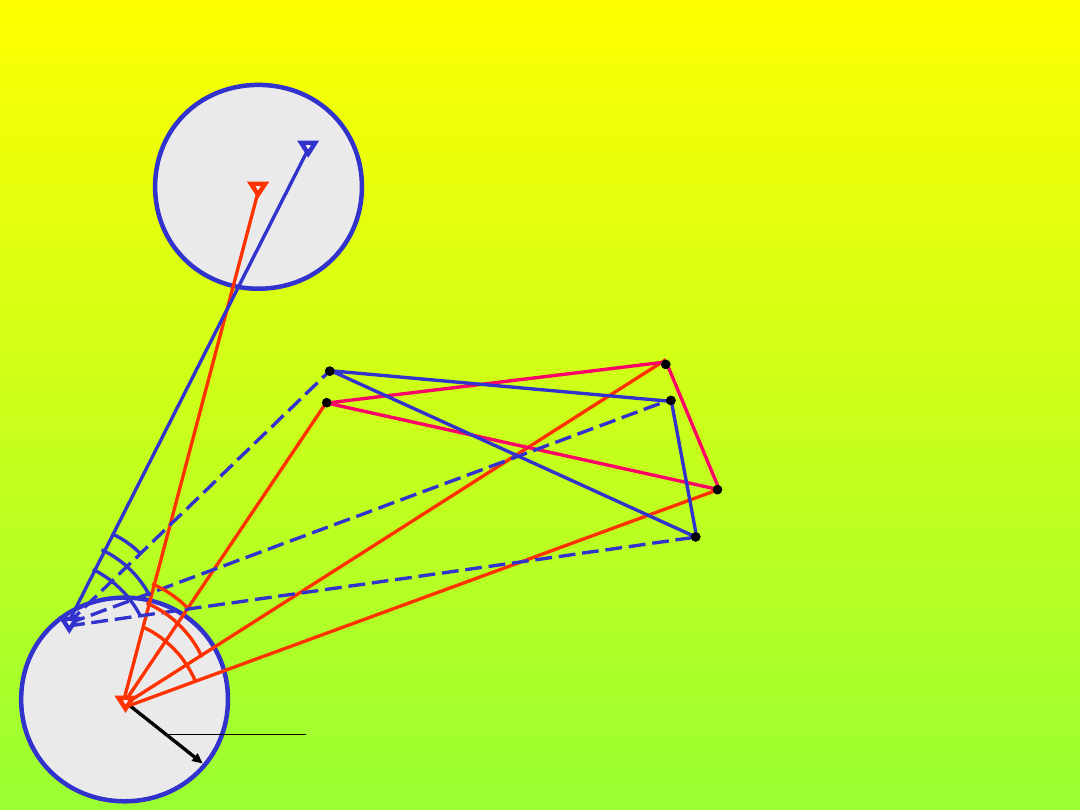
11

Baza tyczenia A,B-(1)

m

p

1

2

3

3

2

1

A

p

A

R

B

R





d

d

B

p

Tyczenie obiektu z jednego

stanowiska

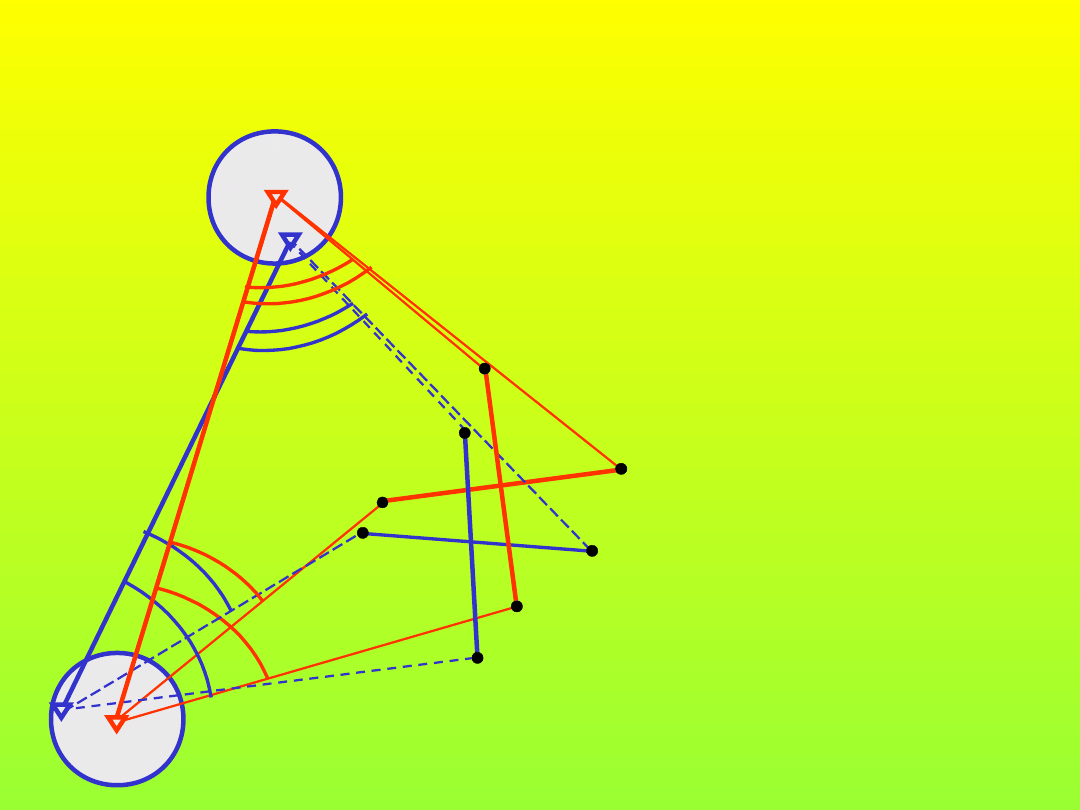
12

Baza tyczenia A,B-(2)

1

2

3

4

1

2

3

4

A

p

B

R

A

R

B

p

Tyczenie obiektu z różnych

stanowisk

13

Dokładność tyczenia

Tyczone są z reguły

punkty

, których położenie jest określone względem,

a) osnowy realizacyjnej- tyczenie lokalizacyjne,
b) siatki konstrukcyjnej lub osnowy budowlano- montażowej- tyczenie szczegółowe.

JEST TO OGÓLNA ZASADA, KTÓRA W PRAKTYCE MOŻE BYĆ

REALIZOWANA W RÓŻNYCH WARIANTACH

WYMAGANA DOKŁADNOŚĆ TYCZENIA OKREŚLONA
-W PROJEKCIE
-PREPISY BRANŻOWE,

-PRZEZ WYKONAWCĘ OBIEKTU,
W RZADKICH PRZYPADKACH DOTYCZY DOKŁADNOŚCI WYTYCZENIA
PUNKTÓW WZGLĘDEM OSNOWY (szczególnie w przypadku tyczenia
szczegółowych punktów obiektu).

14

Dokładność tyczenia (1)

P

X

Y

A

B

mx= Fx ( ; m ; ml ; l)

=……..
my= Fy ( ; m ; ml ; l)

=……..

m

ml

Przy założeniu że punkty bazy
tyczenia są bezbłędne

B

A

m

m

ml

ml

P

X

Y

mx ; my –obliczone na podstawie
wyrównania

m

p

2

= mx

2

+ my

2

m

p

2

= mx

2

+ my

2

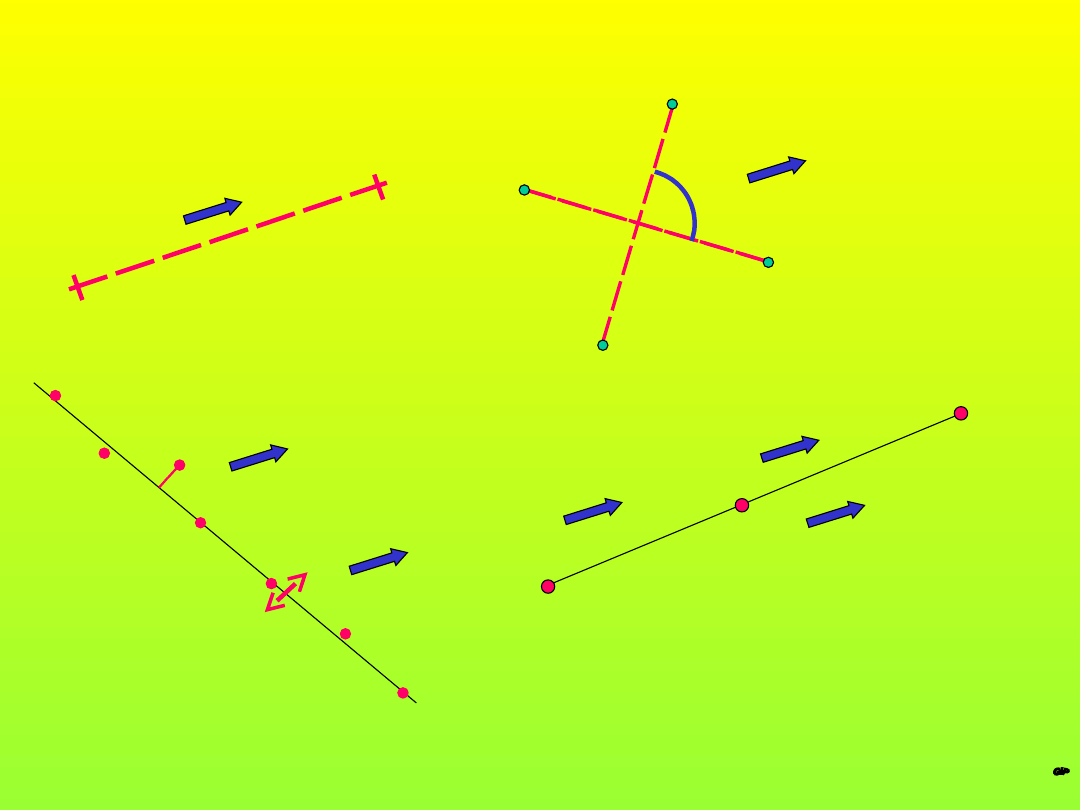
15

Dokładność tyczenia (2)

l

m

l

Oś a

Oś b



m



d

m

d

d

m

d

d

m

d

l

m

l

l

m

l

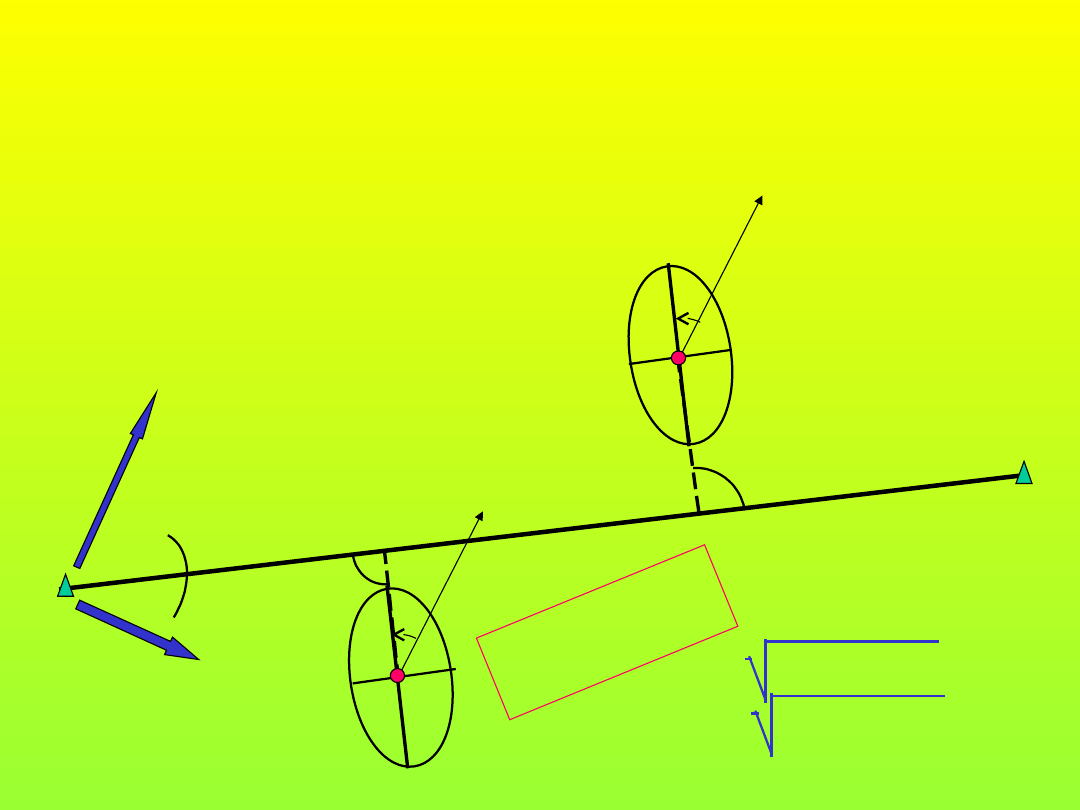
16

Dokładność tyczenia met. domiarów

prostokątnych

Y

X

A

B

A

2

B

2



1

A

i

= m

2

+ md

2

B

i

= m

2

+ mb

2



i

= Az

AB

-180

o

P

2

m

p

2

= A

2

+ B

2



1

X

X

P

1

B

1

A

1







m- dokładność wtyczenia w linię

m- dokładność odłożenia kąta prostego

md- dokładność odłożenia domiaru

mb- dokładność odłożenia bieżącej

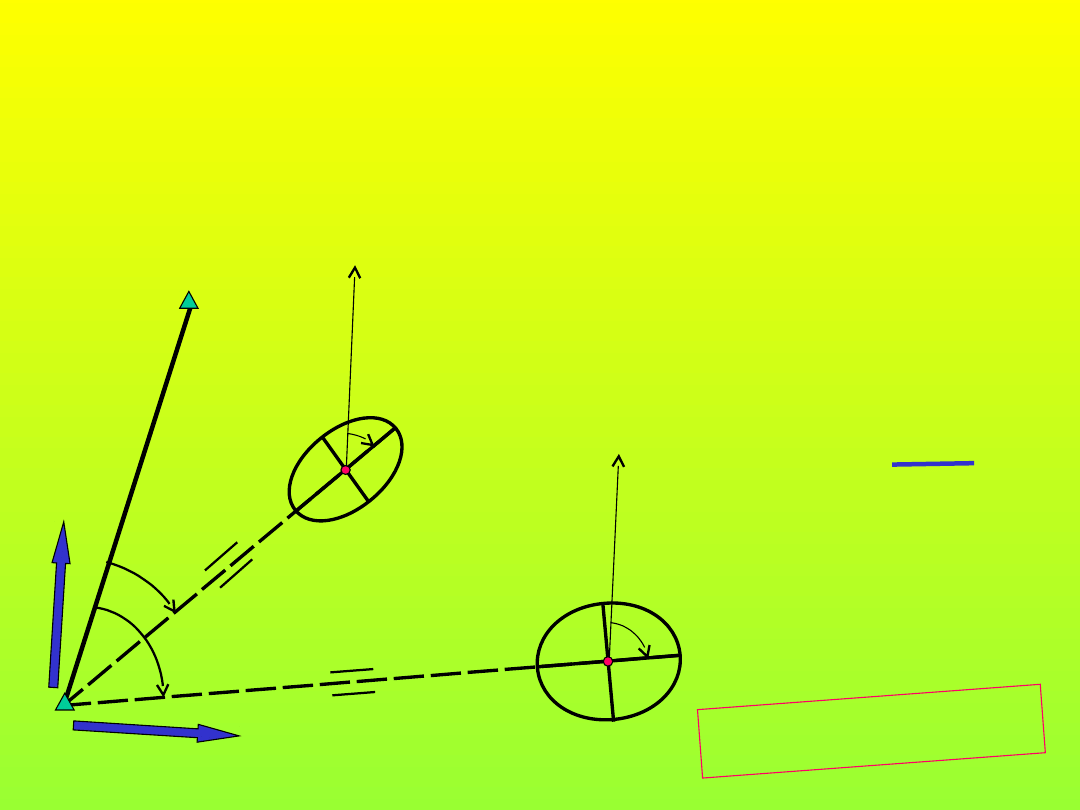
17



i

= Az

AB

+

i

A

i

= ml

i

B

i

= m

i

=

Dokładność tyczenia met.

biegunową

B

A

1

A

2

B

2

B

1



1



2

A

1

2

l1

l2

X

Y

X

P

1

P

2

m

p

2

= A

2

+ B

2

l

i



m

i

m- dokładność odłożenia kąta

ml- dokładność odłożenia długości

18

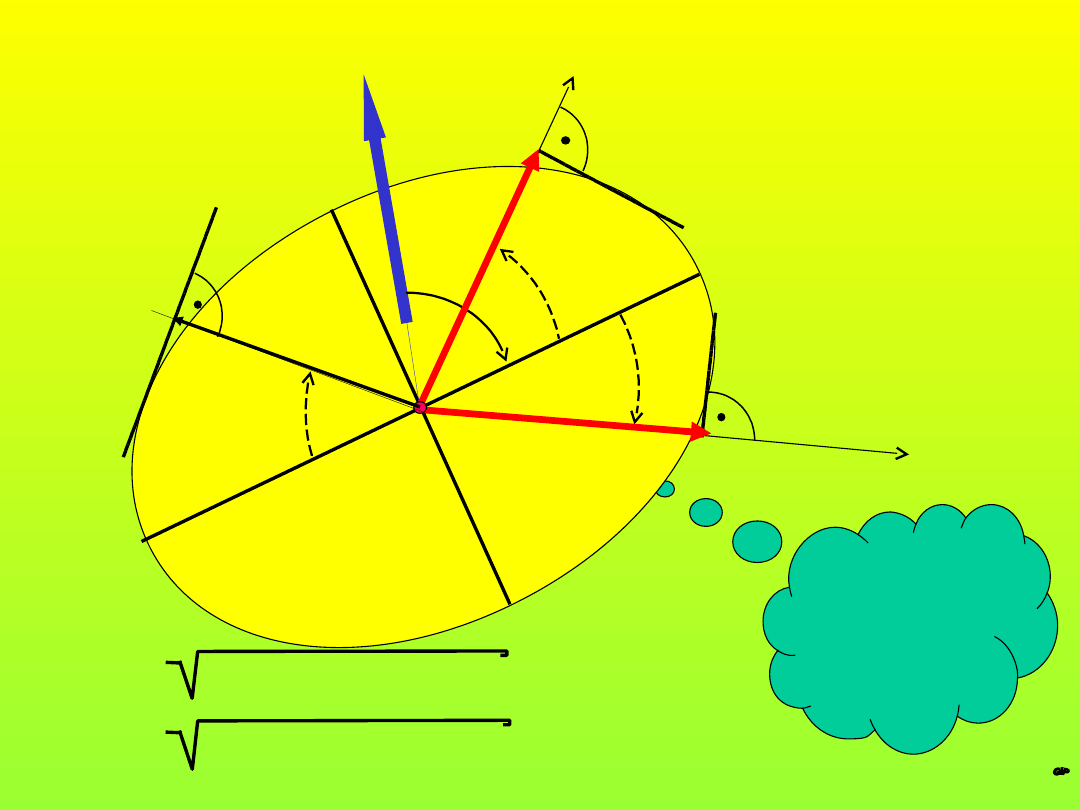
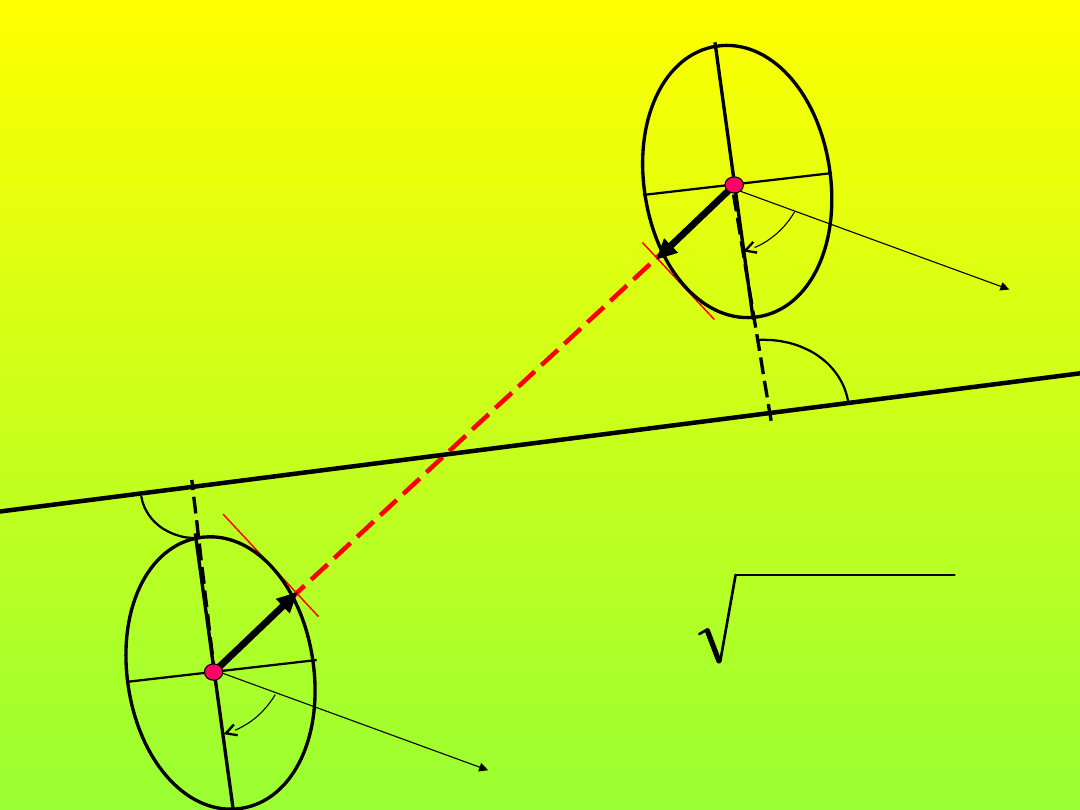
Dokładność tyczenia

b

m

a

= A

2

cos

2



a

+ B

2

sin

2



a

m

b

= A

2

cos

2



b

+ B

2

sin

2



b

Czy ta właściwość
jest istotna?
Co z niej może
wynikać?

(właściwości elipsy
błędu średniego)

X

A

B



a

m

a

m

b



b



a

P

m

c

c

19

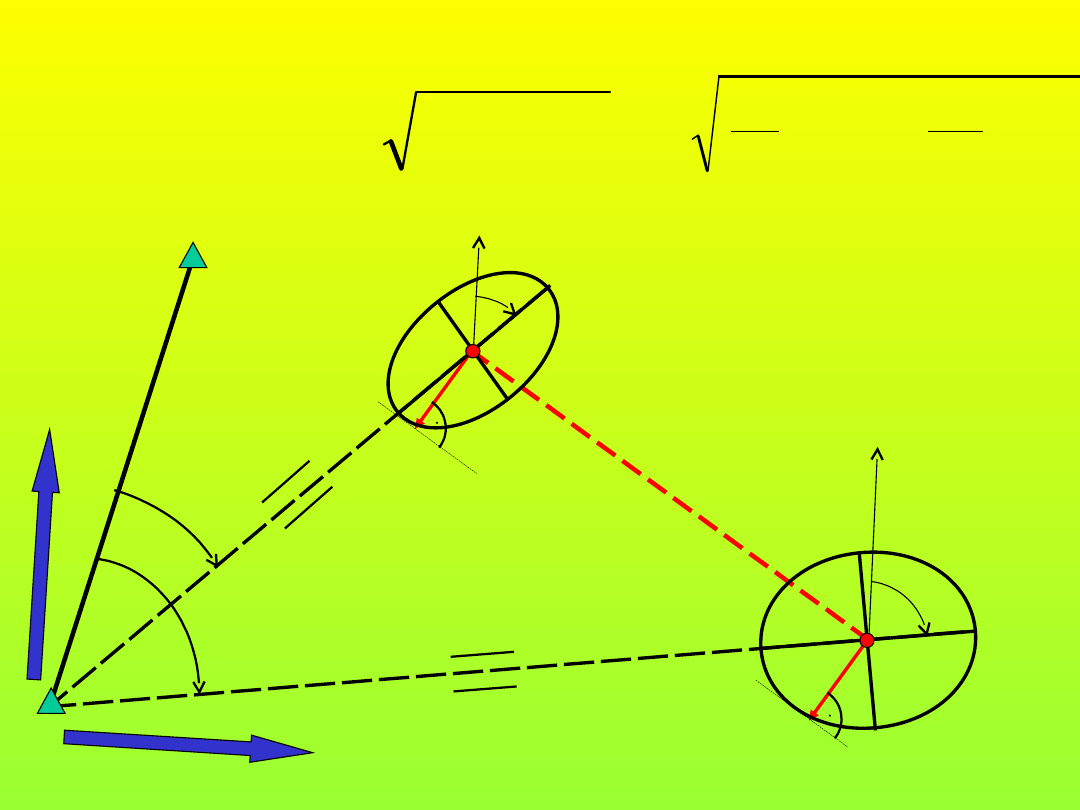
Dokładność tyczenia met. domiarów

prostokątnych

A

2

B

2



2

P

2



1

X

X

P

1

B

1

A

1





m

d

=

?

m

1

m

2

2

2

2

1

m

m

m

d





d

20

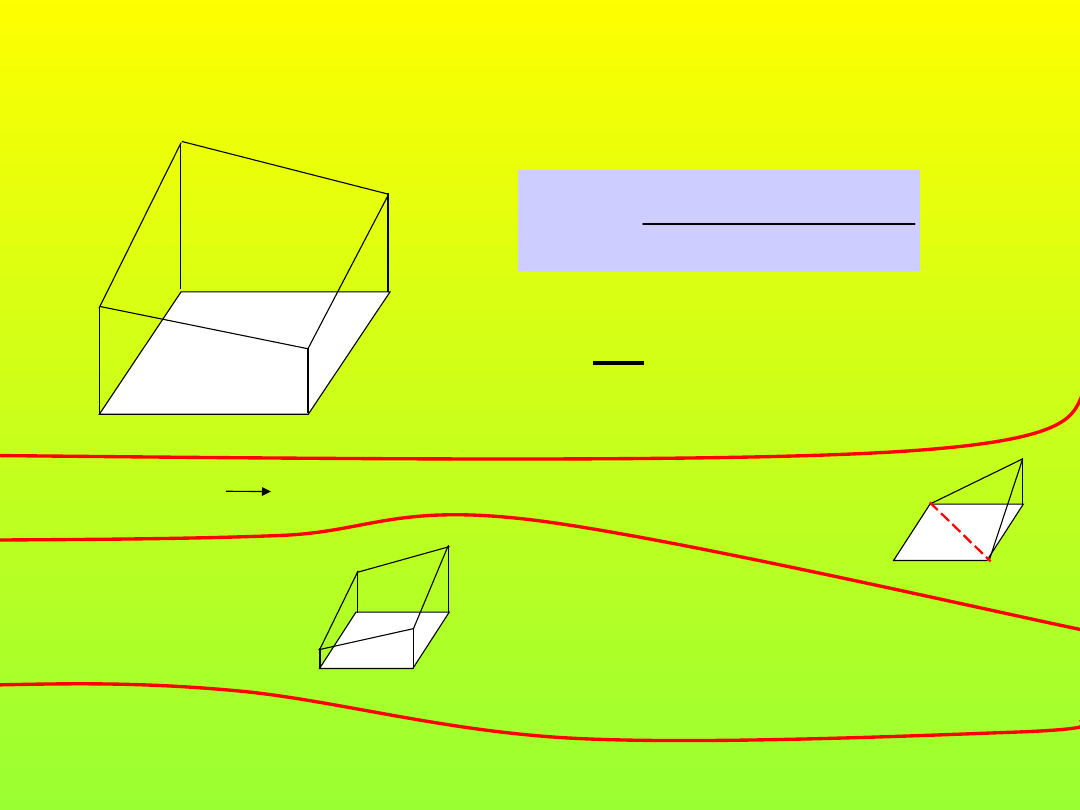
Dokładność wytyczenia kierunku

B

A

1

A

2

B

2

B

1



1



2

A

m

1

m



2

ml

1

ml

2

X

Y

X

P

1

P

2

m

2

m

1

m

k =

?

2

2

2

1

m

m

m

k





X

( ) ( )

2

d

2

m

2

d

1

m

ρ

+

ρ

=

d

21

OBLICZENIA OBJĘTOŚCI

2

3

4

a

b

1

H

o

4

h

+

h

+

h

+

h

ab

=

V

4

3

2

1

?

V = (2h

1

+h

2

+2h

3

+h

4

)

ab
6

?

1.)

1.) V= 100*(1+3+3+5)/4=300m

3

h

1

=h

2

=h

3

=0 ;

h

4

=8

1.)

V= 100*8/6 = 133,3m

3

;

V=100*8/4=200m

3

2

3

4

a

b

1

h

1

=1;h

2

=3;h

3

=3;h

4

=5

2

3

4

a

b

1

2.) V= 100*(1+6+6+5)/6=300m

3

DLACZEGO TAK?

2.)

2.)

22

PRZYKŁAD 2

2

3

4

a

b

1

H

o

Z jaką dokładnością należy pomierzyć wysokości
punktów 1, 2, 3, 4, aby błąd objętości bryły nie
przekroczył wartości dopuszczalnej V=5m

3

a=b=10m

m

V

=V/3 =

1,7m

3

P

1

P

2

V

1

= P

1

*h

1

śr

V

2

= P

2

*h

2

śr

ab
6

V = (2h

1

+h

2

+2h

3

+h

4

)

V= V

1

+ V

2

;

h

V

m

P

P

m

3

+

=

2

2

2

1

1.7m

3

*1,7 50

2

+50

2

= 0,04m

m

h

=

2

2

1

+

3

=

P

P

m

m

v

h

2

23

a

a=10m; b=5m;

V=10m

3

m

h

=0,036m

V=5%

h

1

=1m;h

2

=3m;h

3

=3m;h

4

=5m

V=300m

3 ;

V = 5% = 15m

3

a=10; b=10;

m

v

= 5m

3

m

h

= 0.054m

h

1

=0.1m;h

2

=0.3m;

h

3

=0.3m;h

4

=0.5m

V=30m

3 ;

V = 5% = 1.5m

3

m

v

= 0.5m

3

;

m

h

= 0,005m

h

1

=0.02m;h

2

=0.02m;

h

3

=0.02m;h

4

=0.02m

V= 2m

3 ;

V = 5%= 0.1 m

3

m

v

=0.033m

3

;

m

h

= 0,0004m= 0,4mm

b

m

v

* 3

P *
n

m

h

=

P

n = 40 ; P = 25m

2

; m

v

=3,3m

3

24

Tyczenie lokalizacyjne

OGÓLNIE PRZYJMUJE SIĘ, ŻE POWINNO SPEŁNIAĆ NAST. WARUNKI:

-tyczenie lokalizacyjne ma wskazać położenie obiektu budowlanego
w
terenie względem innych obiektów,
-tyczenie lokalizacyjne wykonujemy w oparciu o punkty osnowy
realizacyjnej
dowiązanej do państwowej osnowy geodezyjnej,
-tyczeniu podlegają główne punkty osiowe obiektu budowlanego
(uzgodnione
z projektantem lub wykonawcą obiektu,
-dokładność tyczenia z reguły nie mniejsza jak 10 cm. w stosunku
do osnowy
realizacyjnej,
-szkic tyczenia jako potwierdzenie wykonania tyczenia jest
przekazywany
wykonawcy
-geodeta dokonuje wpis w dzienniku budowy potwierdzający
wykonanie
tyczenia.

ALE, PRAWIE KAŻDY Z TYCH PUNKTÓW MOŻE BYĆ DYSKUSYJNY
I W SZCZEGÓŁACH RÓŻNIE ROZWIĄZYWANY

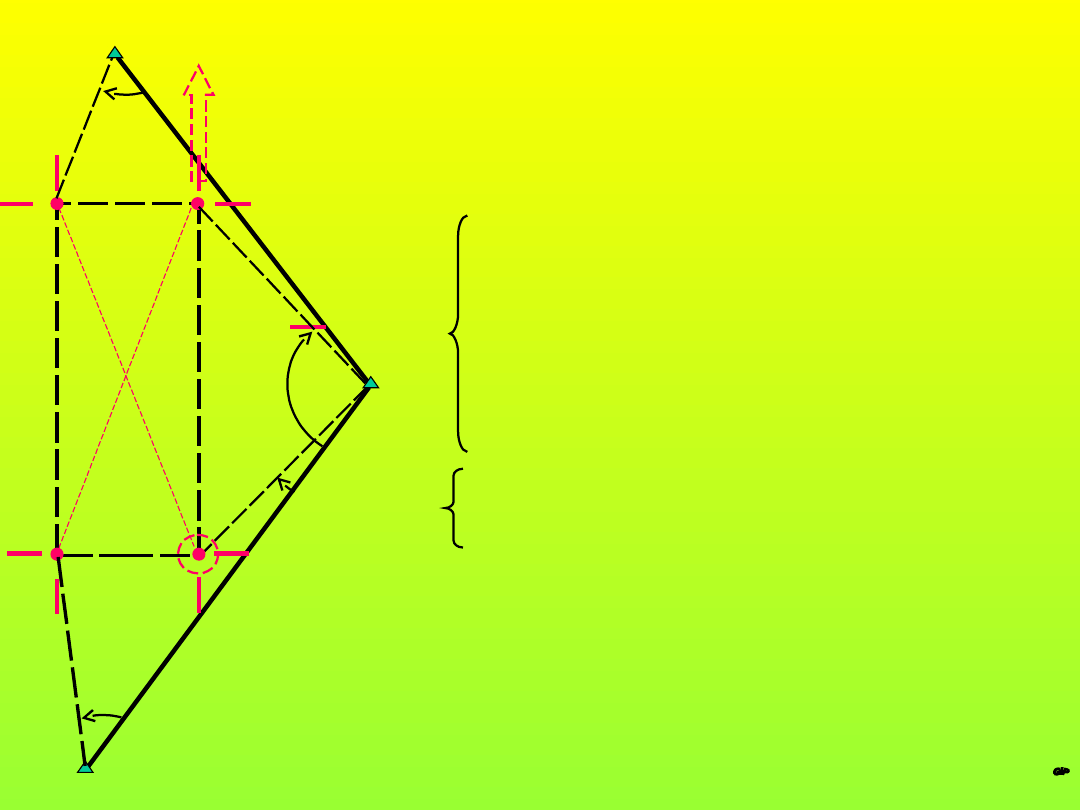
25

Tyczenie lokalizacyjne (1)

ZADANIE.
Wytyczyć A,B,C,D główne punkty osiowe obiektu

-tyczenie lokalizacyjne tych punktów w oparciu o
osnowę realizacyjną (dokł. 10 cm)
-przyjmujemy tylko punk np.: C jako wyznaczony
ostatecznie i kierunek na p-kt B
-mierzymy kontrolnie obserwacje zaprojektowane
w konstrukcji A, B, C, D z dokładnością
wynikającą z projektu (przeważnie z obserwacjami
nadliczbowymi),
-obliczamy poprawki tyczenia dla punktów A, B, D,
-poprawiamy położenie tych punktów
-wykonujemy ostateczny pomiar kontrolny

A

B

C

D

P1

P2

P3

I

e

ta

p

II

e

ta

p

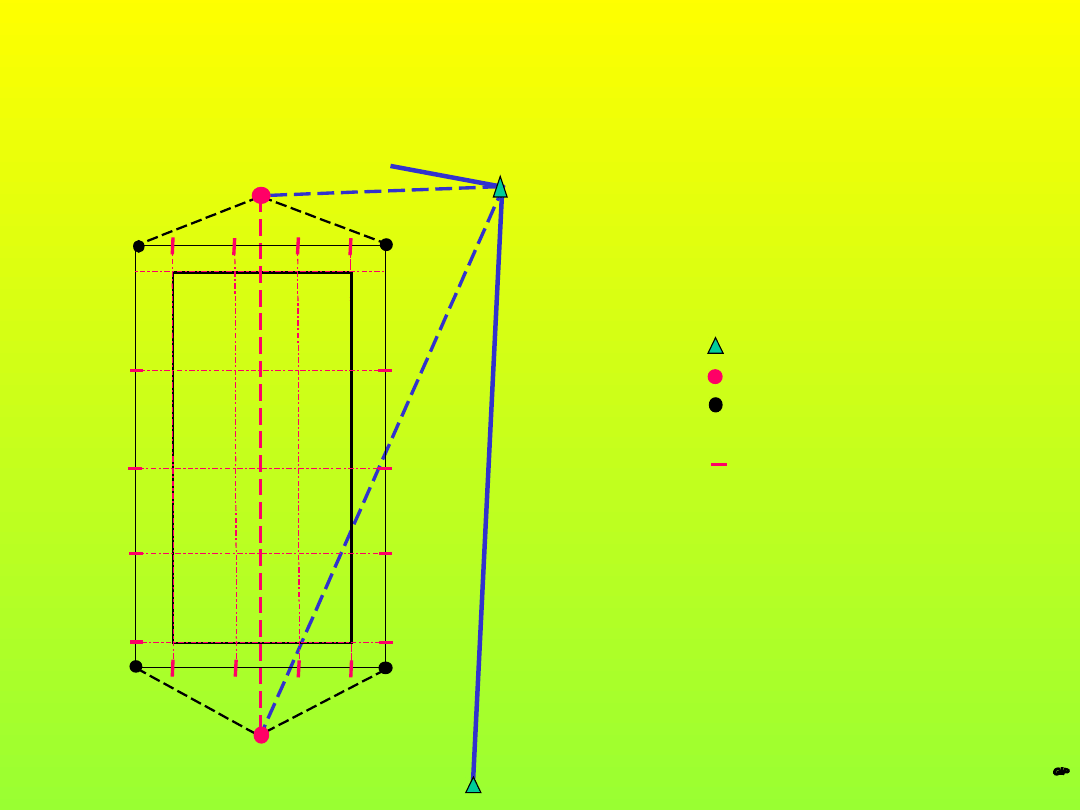
26

Osnowa budowlano-montażowa

(2)

-punkt osnowy realizacyjnej
-punkt głównej osi obiektu
-punkt osnowy budowlano-
montażowej
-wskaźnik osiowy (punkt
osnowy budowlano- mont.

27

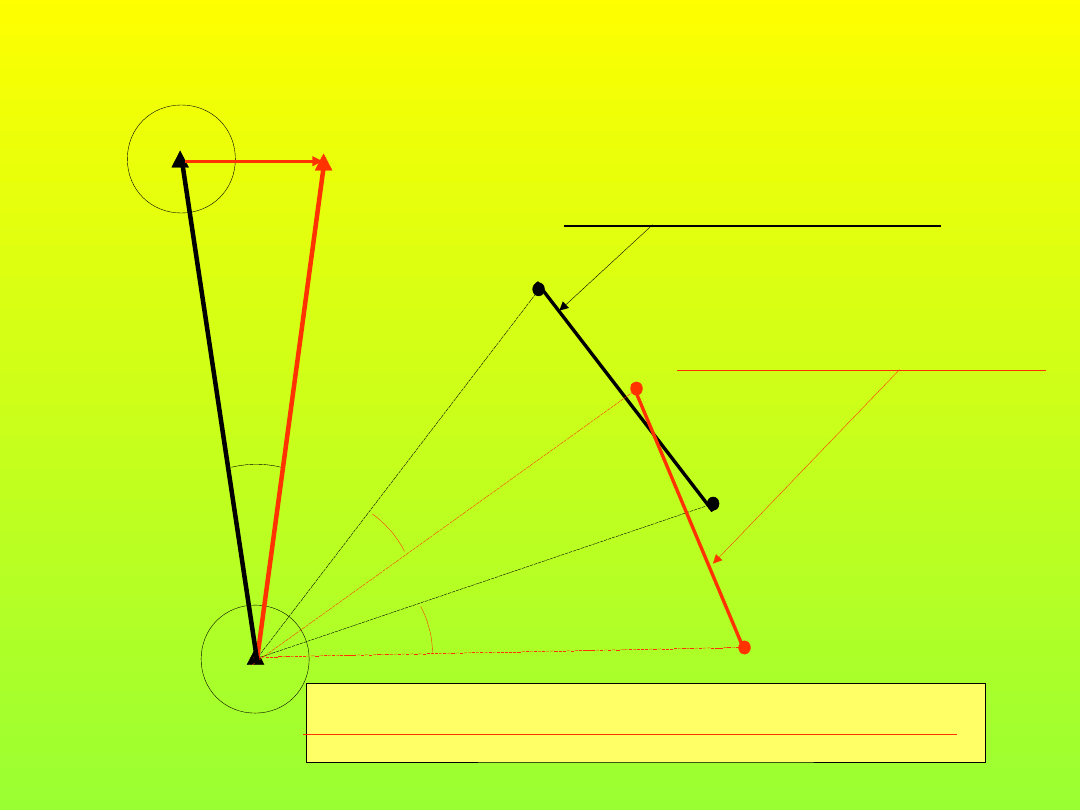
Tyczenie lokalizacyjne -

szczegółowe

ε

ε

ε

A

B

d

ε

Lokalizacja zrealizowana

Lokalizacja projektowana

Lokalizacja się zmienia – kształt obiektu nie

d

d

1

1

2

2

A

28

Tyczenie lokalizacyjne -

szczegółowe

ε



2

ε

A

B

d

ε

d

d

C

1=

1

2

2



1

l

2

l

1

Tyczenie z dwóch różnych punktów ( B i C). Położenie punktu A obarczone jest
błędem

grubym.

Lokalizacja projektowana

Lokalizacja zrealizowana

WYNIK POMIARU KONTROLNEGO d=

d

-d może świadczyć

o błędach tyczenia

Zmienił się kształt i położenie obiektu (położenie punktu 2 jest nieprawidłowe)

29

P o m i a r y K o n t r o l n e

1.Kontrola tyczenia

-jest to ocena poprawności postępowania
geodezyjnego
-nie musi dotyczyć elementów realizowanej
konstrukcji
-nie interesuje wykonawcy obiektu
(wewnętrzna sprawa geodety)

2.Kontrola kształtu
konstrukcji

-ocena zgodności kształtu zrealizowanego z
projektowanym
-opis kształtu zrealizowanego
-opis kształtu na moment wykonywania pomiaru
(na określonym
etapie realizacji lub po zakończeniu budowy)

3.Kontrola przemieszczeń
i odkształceń budowli

-

przemieszczenie się obiektu, lub jego

fragmentu
w okresie czasu od momentu t

0

(pomiar

wyjściowy)
do momentu t

1

(pomiar aktualny)