KOREKCJA ZNIEKSZTAŁCEŃ

KOREKCJA ZNIEKSZTAŁCEŃ

GEOMETRYCZNYCH OBRAZÓW

GEOMETRYCZNYCH OBRAZÓW

CYFROWYCH

CYFROWYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Urządzenia umieszczone na satelitach dostarczają danych, które w swojej surowej

postaci mogą być obarczone usterkami i brakami.

Zdjęcia wykonane z satelity Landsat cechuje brak przesunięć obrazów punktów

spowodowanych rzeźbą.

Jednak zdjęcia te mają wiele innych zniekształceń geometrycznych, które muszą być

skorygowane, jeśli mają mieć one cechy kartometryczne.

Zniekształcenia geometryczne cyfrowych obrazów satelitarnych powstają w wyniku:

-

ruchu obrotowego Ziemi w czasie pozyskiwania obrazów

-

zbyt dużego pola widzenia niektórych skanerów

-

krzywizny Ziemi

-

niedoskonałości konstrukcji skanerów

-

zmian wysokości i orientacji platformy przenoszącej skaner oraz zmian jego prędkości

-

zniekształceń panoramicznych

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Przedmiotem korekcji geometrycznej obrazów skanerowych jest takie

przetworzenie obrazu, aby przedstawiał on teren w przyjętym
odwzorowaniu

i określonej skali.

Proces korekcji przebiega w dwóch etapach:

1.

Znajdujemy zależność funkcyjną, która uzależnia obraz oryginalny od
hipotetycznego obrazu przetworzonego.

2.

Sporządza się nowy – skorygowany obraz.

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Korekcję obrazów skanerowych przeprowadza się metodami analitycznymi
i analogowymi.

Analityczne metody korekcji dzielone są na dwie grupy:

•

Metody parametryczne

•

Metody nieparametryczne (interpolacyjne)

Metody parametryczne
Wykorzystują warunek kolinearności. Polegają one na określaniu

elementów orientacji zewnętrznej urządzenia skanerowego.
W czasie korekcji oblicza się również pewną liczbę parametrów
dodatkowych umożliwiających poprawę orientacji wewnętrznej urządzenia
skanerowego.

Takie parametry orientacji zewnętrznej i wewnętrznej pozwalają na

geometrycznie poprawne przetworzenie obrazu cyfrowego.

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Metody nieparametryczne ( o charakterze interpolacyjnym) z

pominięciem parametrów orientacji, polegają na wzajemnym

przyporządkowaniu zespołu punktów lub fragmentu obrazu skanerowego

znanym punktom lub powierzchni układu terenowego.

Określa się funkcje zależności pomiędzy współrzędnymi X,Y w przestrzeni

przedmiotu (terenu) i współrzędnymi x,y (lub wierszem i kolumną) w

przestrzeni obrazu oraz zakłada się przekształcenie jednej przestrzeni w

drugą.

W przekształceniu tym pomijane jest źródło poszczególnych dystorsji, a

uwzględniany jest ich sumaryczny wpływ poprzez wykorzystanie punktów

dostosowania obrazu i mapy.

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Najlepszą korekcję można uzyskać, stosując kombinację obydwu metod:
w pierwszym etapie stosując metodę parametryczną ( z wykorzystaniem
przybliżonych parametrów lotu), a następnie do końcowej korekcji
stosując metodę nieparametryczną.

Przedstawione metody służą do uzyskania poprawionego obrazu w postaci
cyfrowej.

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

W procesie obliczania nowego skorygowanego położenia pikseli każdemu polu

(oczku siatki) w przyjętym odwzorowaniu kartograficznym przypisuje się

wartości obliczone z wzoru:

X = f

1

(x,y)

Y = f

2

(x,y)

gdzie:
x,y – współrzędne zdjęcia (kolumna, wiersz)
X,Y – współrzędne kartograficzne
f

1

, f

2

- zależności transformacyjne

Te wartości stają się teraz adresami pikseli w nowym zbiorze obrazowym.
Tym nowym adresom pikseli przyporządkowuje się następnie wartość liczbową

(jaskrawość) piksela.

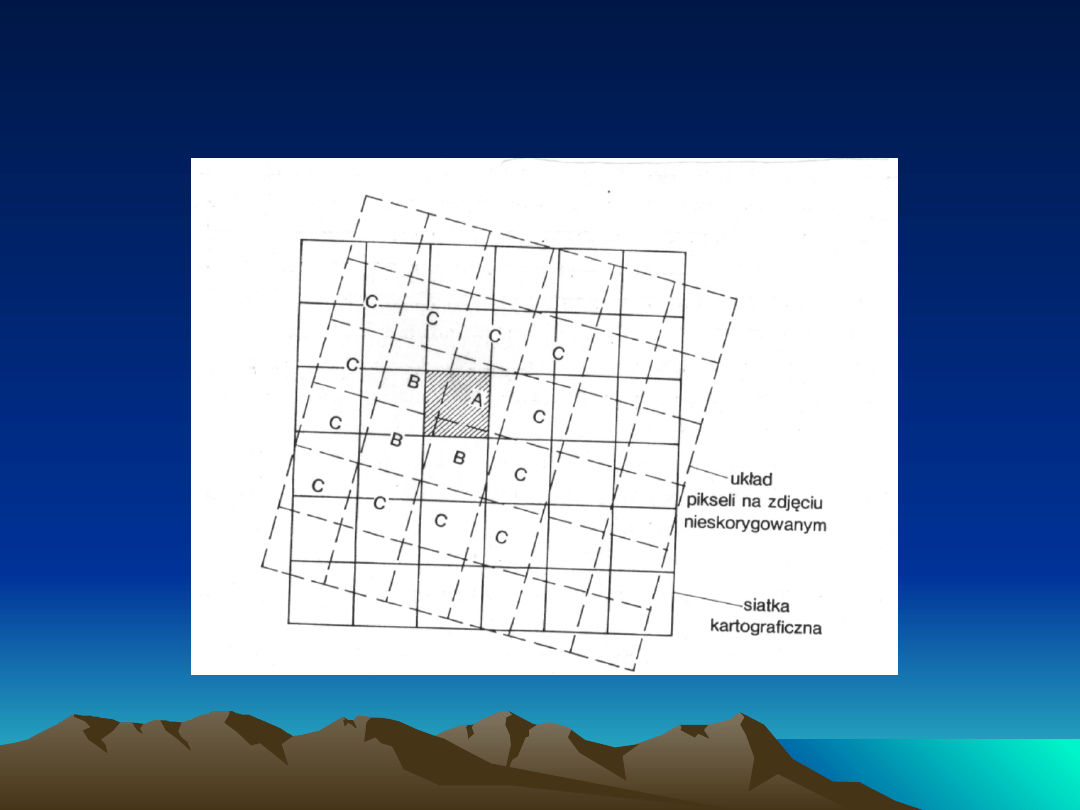
Pojawia się poważny problem jaką wartość liczbową przypisać pikselom pod

nowym ich adresem w geometrycznie skorygowanym obrazie ( ze względu na

przesunięcie równolegle lub prostopadłe siatki kartograficznej wg. układu

pikseli na zdjęciu).

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

Oczko siatki kartograficznej oznaczonej szrafem pokrywa nie jeden, ale

częściowo aż cztery piksele geometryczne nieskorygowanego zdjęcia.
Najprostszym rozwiązaniem byłoby:

•

wykorzystanie piksela w największej części pokrywającego oczko nowego
układu , nie biorąc pod uwagę, że geometrycznie jest on nieco przesunięty
i wpisać w nowy układ wartość liczbową (jaskrawość) tego właśnie piksela.
To rozwiązanie jest często stosowane (najszybsze i nie zmienia wartości
liczbowej nowego piksela). Mankamentem tego przetworzenia jest fakt, że
piksele są przesunięte względem siebie, aż o połowę ich wielkości co
sprawia, że obraz nie jest powiązany.

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

KOREKCJA ZNIEKSZTAŁCEŃ GEOMETRYCZNYCH

OBRAZÓW CYFROWYCH

OBRAZÓW CYFROWYCH

•

Doskonalszą metodą z punktu widzenia jakości nowego zdjęcia, jest
metoda interpolacji dwuliniowej. Do nadania nowemu pikselowi wartości
liczbowej wykorzystuje się w niej jaskrawość czterech pikseli
pokrywających dane oczko siatki kartograficznej (oznaczone A,B,B,B) i
oblicza średnią arytmetyczną. Obliczona jaskrawość przypisuje się
pikselowi w nowym zbiorze obrazowym. Otrzymane w ten sposób nowe,
geometrycznie skorygowane zdjęcie jest wyraźniejsze (kontury obiektów są
bardziej ostre), ale jest obarczone mankamentem. Wartości liczbowe
nowych pikseli są całkowicie sztuczne i nie odpowiadają jaskrawości
realnych obiektów występujących na obrazowanym terenie.

ĆWICZENIE

ĆWICZENIE

W module Edit, w typach plików wskazujemy opcję „Correspondence file”

(zbiór referencyjny).

Formuła pliku tekstowego

4 - Ilość punktów kontrolnych
współrzędne: x , y X,Y (każdą współrzędną oddzielamy
spacją)
x,y – z obrazu satelitarnego
X,Y – z mapy

- W jednym wierszu znajdują się dwie pary współrzędnych dla
konkretnego punktu

Po wprowadzeniu współrzędnych dla 4 punktów wychodzimy z
programu Edit przez F2 (wyjście i zapisanie pliku tekstowego)

ĆWICZENIE

ĆWICZENIE

Uruchamiamy moduł Resample (Spatial management), pozwoli on w

czasie rektyfikacji na transformację geometryczną obrazu do nowego

układu współrzędnych i przyporządkowanie nowych wartości

jaskrawości pikselom (resampling), konieczne wskutek zmiany układu

pikseli.

1.

W pole „ Correspondence file” wprowadzamy punkty

2.

W polu „reference units” (jednostka miary) wybieramy obcej km

Pozostawiamy bez zmian:

1.

Opcje „reference system” (system odniesienia)

2.

„Unit distance” (długość jednostkowa)

3.

Background value (wartość tła)

4.

Resampling type (metoda przyporządkowania pikselom nowych wartości

jaskrawości)

5.

Mapping function (rząd transformacji)

ĆWICZENIE

ĆWICZENIE

Wprowadzamy wartości współrzędnych X,Y min; X,Y max odczytane z mapy,
Wprowadzamy ilość kolumn w zasięgu regionu – 533
Wprowadzamy ilość wierszy w zasięgu regionu – 333

•

Jako wynik klasyfikacji zdjęcia satelitarnego, należy użyć metody
najbliższego sąsiada, nie zmienia ona wartości pochodzących z mapy
wejściowej.

ĆWICZENIE

ĆWICZENIE

Po wprowadzeniu danych uzyskujemy:

-

błędy położenia punktów kontrolnych ( z możliwością usunięcia punktu z
największym błędem – są to błędy powstałe w czasie odczytywania
współrzędnych)

-

średni błąd położenia [total RMS error]. Błąd ten nie powinien przekraczać
wartości jednego piksela, w naszym przypadku akceptujemy błąd sięgający
nawet 5 pikseli),

-

współczynniki transformacji.

Po wykonaniu obliczeń przez system, ponownie wchodzimy do modułu

Display, który umożliwia wizualizacje obrazu.

KOREKCJA ZNIEKSZTAŁCEŃ

KOREKCJA ZNIEKSZTAŁCEŃ

GEOMETRYCZNYCH OBRAZÓW

GEOMETRYCZNYCH OBRAZÓW

CYFROWYCH

CYFROWYCH

Moduł Resample pozwolił na zdefiniowanie układu współrzędnych

tworzonego obrazu za pomocą wybieranych opcji. Określając minimalne i
maksymalne współrzędne x i y, zdefiniowano obszar, jaki ma zostać
wycięty z obrazu satelitarnego w jednostkach współrzędnych nowego
układu. Ponieważ obraz satelitarny nie musi wypełniać całego zadanego
minimalnymi i maksymalnymi współrzędnymi x i y obszaru, puste miejsce
jest wartościami określonymi w opcji „Background” (najczęściej jest to 0).