Przekładnie obiegowe

Przekładnie, w których oś chociażby jednego koła zębatego jest ruchoma
względem obudowy, noszą nazwę przekładni obiegowych lub
planetarnych. Przekładnie obiegowe wykazują pewne cechy wspólne z
przekładniami zwykłymi o ustalonym położeniu osi kół, ale też mają wiele
cech odmiennych. W niektórych przypadkach te odmienne cechy
stanowią na tyle istotne zalety, że skłaniają konstruktora do stosowania
przekładni obiegowych. Do cech wspólnych można zaliczyć:

1) współosiowość wału czynnego i biernego:

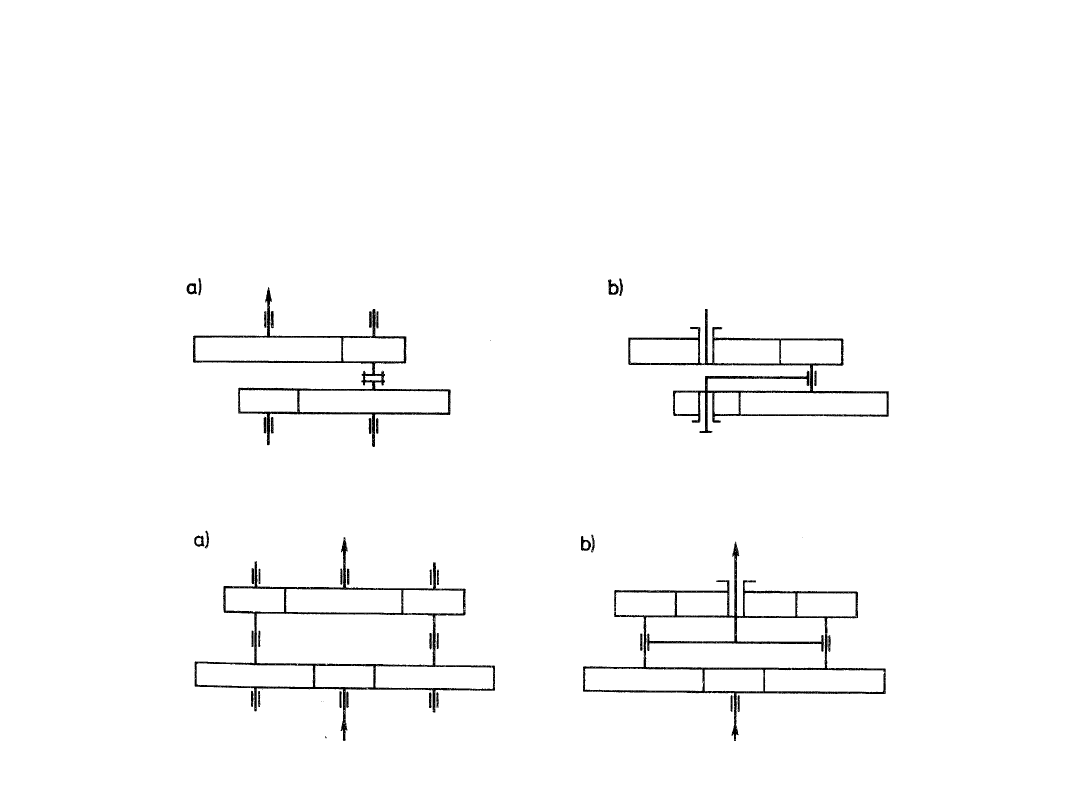
Przekładnia dwustopniowa: a) o stałym położeniu osi kół i o współosiowych
wałach, b) o zmiennym położeniu osi jednej pary kół łożyskowanych w
jarzmie

2) wielodrożność przepływu mocy:

Przekładnia dwudrożna: a) o stałym położeniu osi kół, b) o zmiennym

położeniu osi kół ułożyskowanych w ruchomym jarzmie

Wymienione cechy występują zawsze w przekładniach obiegowych,
natomiast rzadko spotykamy je w zwykłych przekładniach o stałych
osiach. Wielodrożność przepływu mocy powoduje istotne zmiany
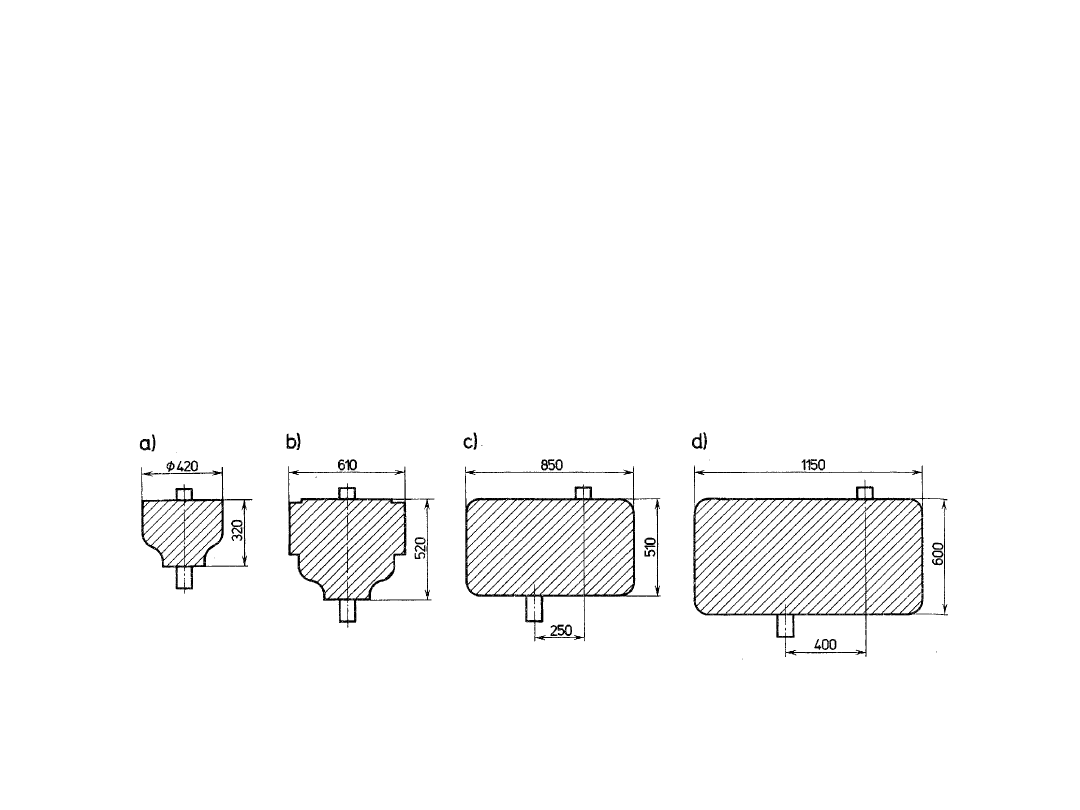
gabarytów i mas przekładni. Na rysunku przedstawiono w jednakowej
skali cztery przekładnie przeznaczone do przenoszenia mocy 750 kW przy
prędkości obrotowej 24000/3000 obr/min. Przekładnia obiegowa (a) w
specjalnym wykonaniu ma masę 87 kg, natomiast w standardowym
wykonaniu, oferowanym w zwykłych katalogach (b), ma masę około 370
kg. Zwykła przekładnia szeregowa (c), wykonana ze stali do nawęglania,
ma masę około 570 kg, natomiast w przypadku zastosowania stali do
ulepszania cieplnego (d) ma masę 1400 kg. Odpowiednio do
powiększonej masy powiększone są jej gabaryty, wobec czego przy
ustalonych prędkościach obrotowych pracuje ze znacznie zwiększonymi
prędkościami obwodowymi.

Wpływ rodzaju przekładni zębatej na jej masę i gabaryty: a) przekładnia

obiegowa w

 

specjalnym wykonaniu, b) przekładnia obiegowa w normalnym

wykonaniu, c)

 

przekładnia walcowa o stałych osiach i zębach utwardzanych,

d) przekładnia walcowa o stałych osiach i zębach ulepszanych cieplnie

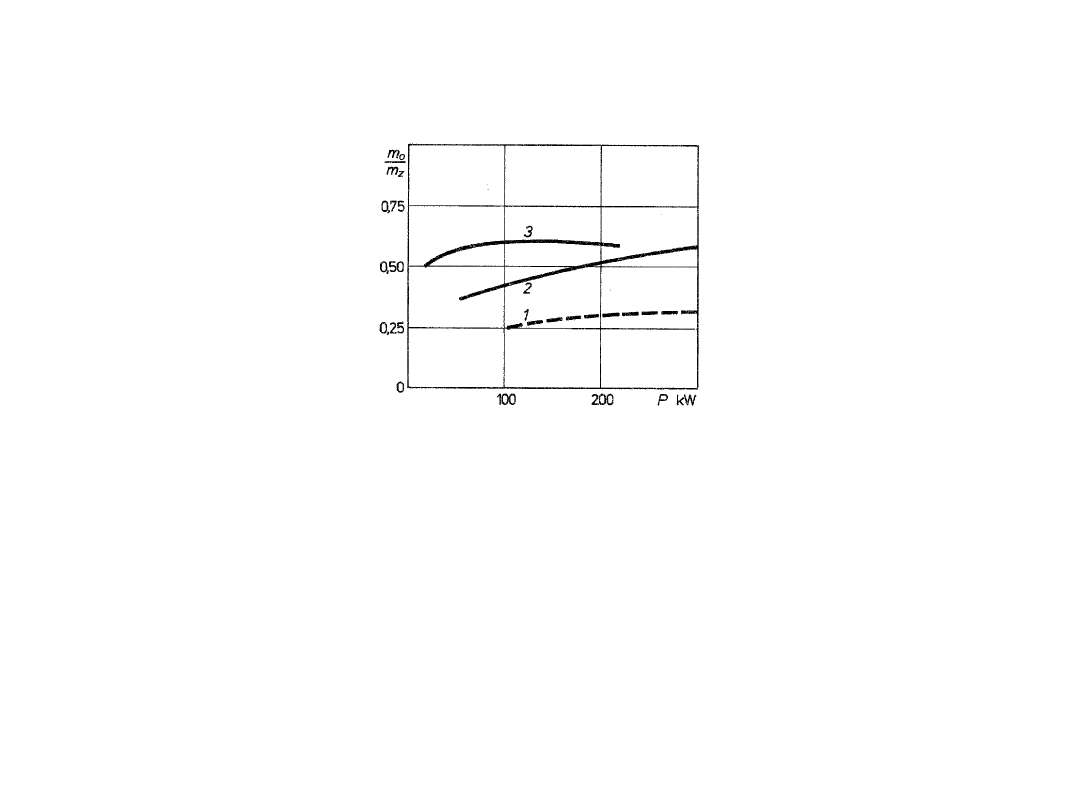
Na rysunku przedstawiono wartość stosunku masy przekładni obiegowej
m

o

do masy przekładni zwykłej m

z

w zależności od przenoszonej mocy.

Wartości określono dla przekładni o prędkości obrotowej na wejściu n =
1000 obr/min.

Stosunek masy przekładni obiegowej m

o

do masy przekładni zwykłej m

z

w

zależności od przenoszonej mocy

Przekładnia obiegowa wykonana była ze stali utwardzanych, z wyjątkiem
koła wewnętrznie uzębionego, wykonanego ze stali ulepszanej cieplnie.
Zwykłe przekładnie wykonane były też ze stali ulepszanych. Linia 1
dotyczy przekładni o przełożeniu i = 5 z łożyskami ślizgowymi, linia 2
dotyczy analogicznych przekładni z łożyskami tocznymi. Linia 3 dotyczy
przekładni dwustopniowych o przełożeniu i = 10 wyposażonych w łożyska
toczne. Wraz ze zmniejszaniem się masy przekładni obiegowej w
stosunku do zwykłej, zmniejszeniu ulegają masy i masowe momenty
bezwładności elementów wirujących, co jest korzystną cechą przekładni
w przypadku częstych rozruchów.

Przekładnie obiegowe mają wiele cech nie spotykanych w zwykłych
przekładniach o stałych osiach. Są one niekiedy tak istotne dla
konstruktora, że nie widzi on możliwości zastąpienia przekładni
obiegowych zwykłymi przekładniami. Między innymi przekładnie
obiegowe mają zwykle większą liczbę stopni swobody, co umożliwia:

•

sumowanie momentów i mocy pochodzących z kilku napędów

(przekładnie

sumujące),

•

rozdział momentów i mocy na kilka odbiorników (przekładnie

różnicowe).

Istnieje też prosty sposób na zmianę przełożenia przekładni obiegowej,
wystarczy spowodować zahamowanie jednego jej elementu, natomiast w
zwykłej przekładni konieczne jest stosowanie synchronizatorów podczas
przełączania kół zębatych.

Przez sprzężenie dwóch przekładni obiegowych lub przekładni obiegowej
z przekładnią bezstopniową uzyskuje się możliwość dużo większej zmiany
przełożenia niż dwustopniowej przekładni o stałych osiach.

Przekładnie obiegowe stały się konkurencyjne wobec zwykłych przekładni
nawet w tych przypadkach, gdy konstrukcyjnie ograniczymy ich liczbę
stopni swobody do jednego, a więc, gdy zastosujemy jeden napęd i jeden
odbiornik mocy. Przekładnie obiegowe mają mniejsze gabaryty i masy, a
także ich sprawność jest większa. Pomimo zwykle wyższych kosztów
wytwarzania, znajdują one szerokie zastosowanie szczególnie tam, gdzie
istotną rolę odgrywają zarówno małe gabaryty jak i masy.

Podstawowe określenia

Analiza pracy przekładni obiegowej wymaga wprowadzenia pojęć i
określeń rzadko lub w ogóle nie stosowanych w przypadkach zwykłych
przekładni o stałych osiach kół. Konieczne jest też uściślenie definicji
niektórych pojęć stosowanych w przypadkach zwykłych przekładni. Tak na
przykład w zwykłych przekładniach przez przełożenie rozumie się
najczęściej stosunek bezwzględnych wartości prędkości obrotowych, nie
zwraca się zwykle uwagi na ich kierunki. W przekładniach obiegowych
konieczne jest rozróżnienie kierunków. Musimy zatem uwzględniać znak
przy liczbie zębów. I tak, dla podstawowych cech geometrycznych kół
zębatych:

•

koła zewnętrznie uzębione mają liczbę zębów dodatnią,

•

koła wewnętrznie uzębione mają liczbę zębów ujemną,

•

współczynnik przesunięcia zarysu (zęby korygowane) jest

dodatni, gdy

narzędzie odsuwane jest od materiału, bez

względu na to, czy jest to koło

zewnętrznie czy wewnętrznie

uzębione,

•

współczynnik przesunięcia zarysu (zęby korygowane) jest ujemny,

gdy

narzędzie wsuwane jest w głąb materiału, bez względu na

rodzaj

zazębienia.

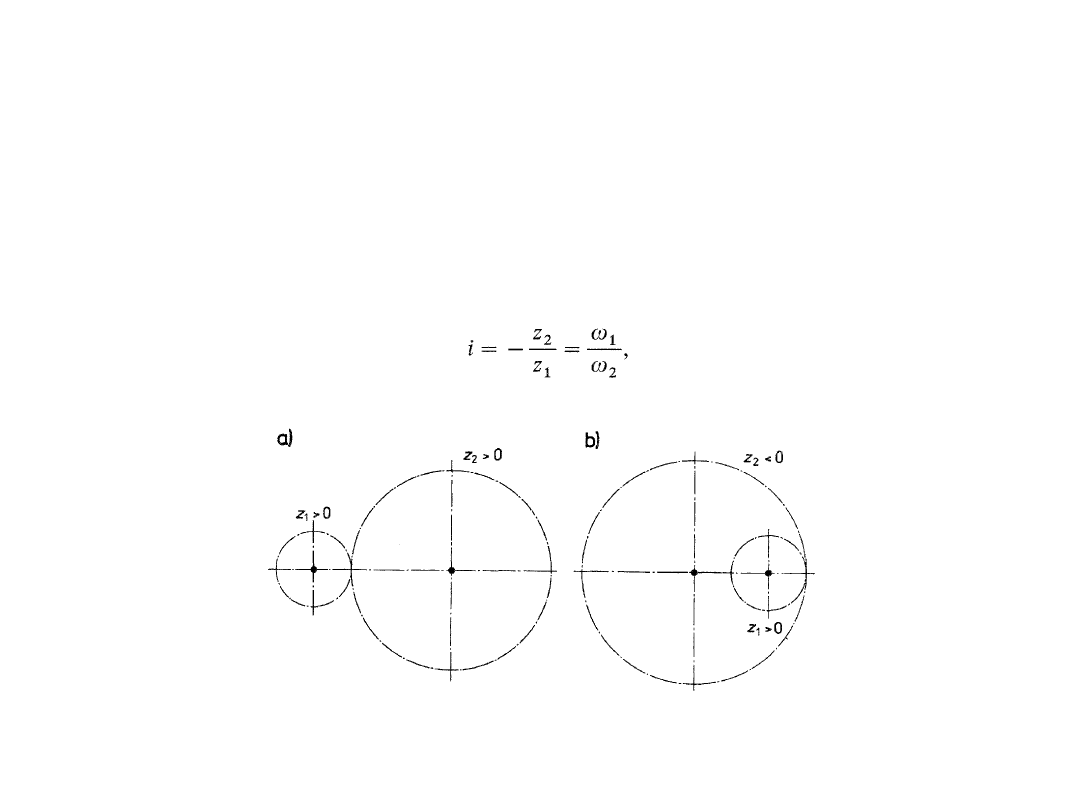
Zarówno w kołach zewnętrznie uzębionych, jak i w kołach wewnętrznie
uzębionych moduł zęba jest zawsze dodatni. Po uwzględnieniu znaku
liczby zębów:

•

średnice kół zewnętrznie uzębionych są dodatnie, a kół

wewnętrznie

uzębionych są ujemne

•

odległość osi kół zewnętrznie uzębionych (a) jest dodatnia, a

odległość osi

kół o wewnętrznym zazębieniu (b) jest ujemna.

Dla tak przyjętych oznaczeń przełożenie jednej pary kół wyraża się
zależnością:

gdzie

 jest prędkością kątową.

Przekładnia: a) o zazębieniu zewnętrznym, b) o zazębieniu wewnętrznym

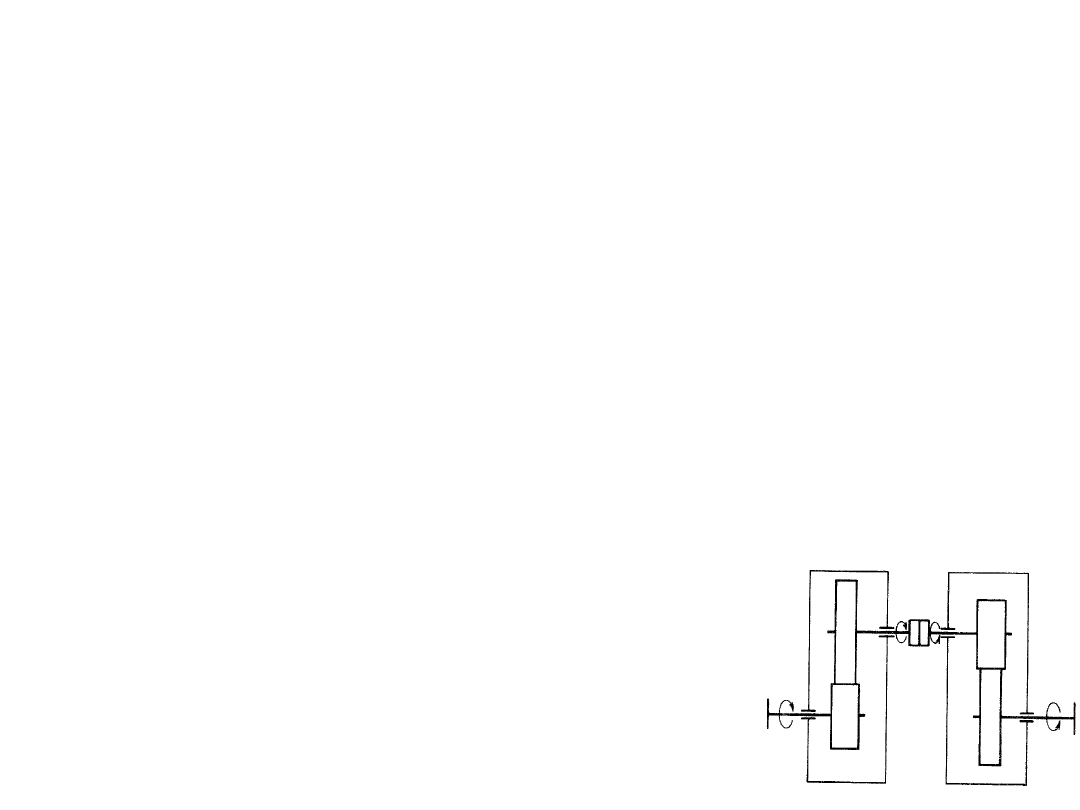
W przypadku zazębienia zewnętrznego przełożenie jest liczbą ujemną, co

oznacza, że koła obracają się w przeciwnych kierunkach, natomiast w
przypadku zazębienia wewnętrznego przełożenie jest dodatnie, ponieważ
koła obracają się w zgodnych kierunkach, przy czym jest rzeczą obojętną,
który kierunek uznany zostanie za dodatni, a który za ujemny; o znaku
przełożenia decyduje ich zgodność lub niezgodność. Istotną rzeczą jest
natomiast, aby w rozpatrywanej przekładni wszystkie prędkości kół
obracających się w zgodnym kierunku miały ten sam znak.

Znaki momentów obrotowych są następujące:

• na wałku (kole) napędzającym przekładnię moment obrotowy ma

znak zgodny ze znakiem prędkości kątowej, zatem ich iloczyn
określający moc doprowadzoną do przekładni ma znak dodatni bez
względu na kierunek obrotów,

• na wałku roboczym (hamowanym przez maszynę roboczą) moment

obrotowy ma znak przeciwny do znaku prędkości obrotowej, a więc
moc ma zawsze znak ujemny jako moc odprowadzana.

W przypadku przekładni dwustopniowej, sprzęgło
pomiędzy stopniami obciążone jest z jednej strony
momentem dodatnim, a z drugiej strony momentem
ujemnym lub ogólnie momentami o różnych znakach,
ponieważ jedna połówka sprzęgła należy do wału
zdawczego, a druga do wału napędzającego
przekładnię.

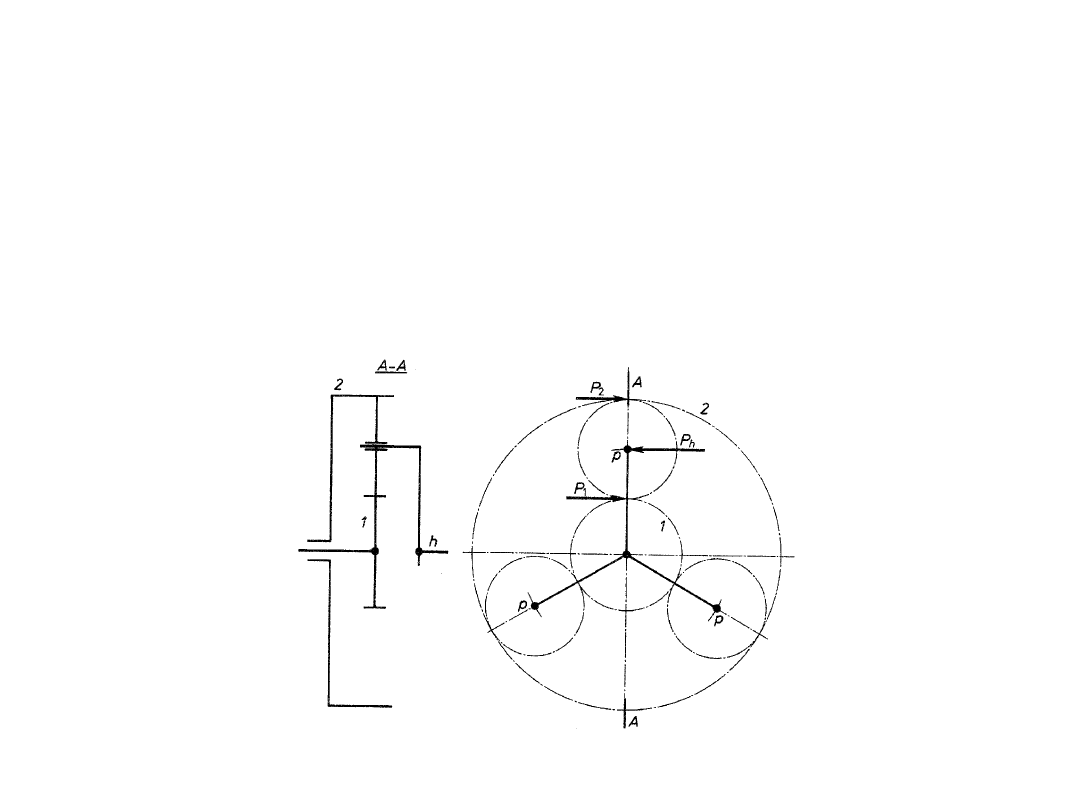
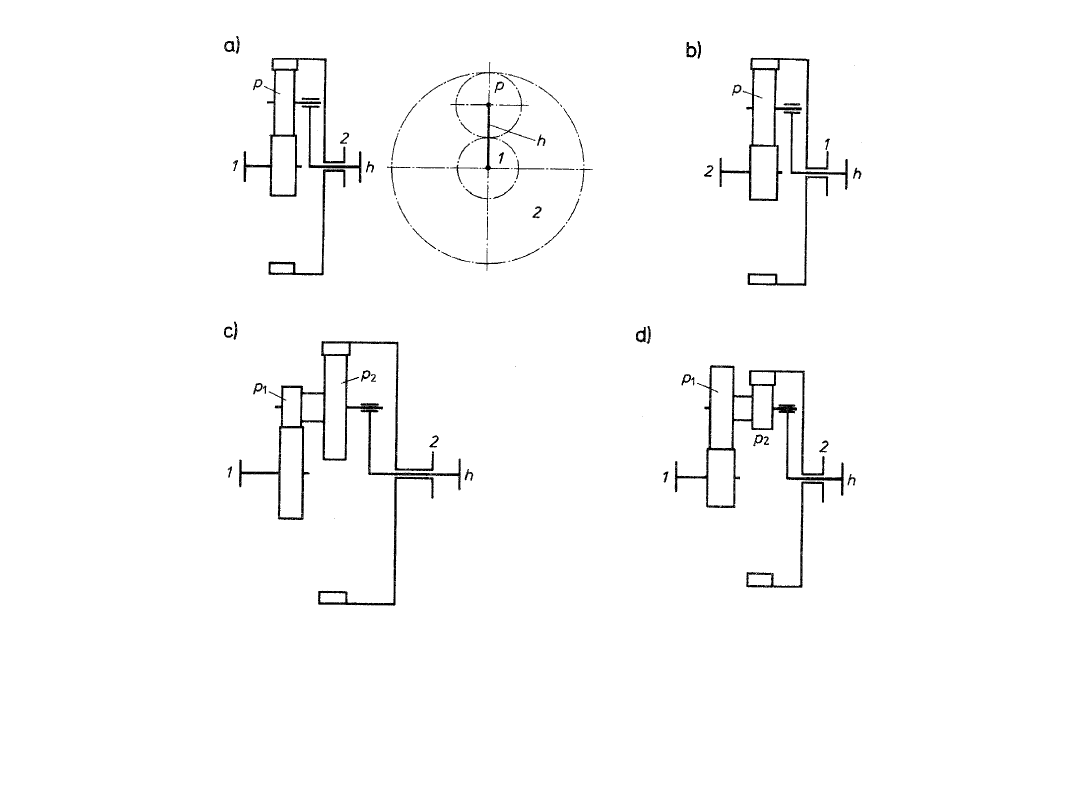
Na rysunku przedstawiono prostą przekładnię obiegową złożoną z
następujących elementów:

•

koła centralnego 1 osadzonego na wale 1,

•

koła centralnego 2 osadzonego na wale 2,

•

jarzma kół obiegowych osadzonego na wale h,

•

trzech kół obiegowych (satelitów) p, ułożyskowanych w jarzmie h
i równomiernie rozmieszczonych na obwodzie, sprzęgających koło

1 z kołem 2.

Schemat prostej przekładni obiegowej

Przekładnia ta może pracować w następujących wariantach:

1. Gdy jarzmo i wał h są nieruchome, tj. na stałe związane z

obudową przekładni, przekładnia pracuje w układzie trójdrożnym.
Ponieważ osie wszystkich kół związane są z obudową i nie
wykonują

wzajemnych

ruchów,

przekładnia

nie

spełnia

podstawowego warunku przekładni obiegowej. Jest więc zwykłą
trójdrożną przekładnią z wewnętrznym zazębieniem. Cechuje się
ona współosiowością wałów 1 i 2, rozdziałem przepływu mocy i
zwartą budową.

2. Gdy jarzmo i wał h są ruchome, tj. gdy osie kół obiegowych

przemieszczają się razem z jarzmem, przekładnia pracuje jako
przekładnia obiegowa bez względu na stan kół lub wałów 1 i 2.
Koła obiegowe p wykonują złożony ruch, obracają się bowiem
względem własnych osi i są unoszone wraz z jarzmem, dokonując
dodatkowego obrotu względem osi 1 i 2. Przekładnia ta ma dwa
stopnie swobody, co oznacza, że dla jednoznacznego określenia
ruchu poszczególnych elementów trzeba założyć stan dwóch
wałów.

Gdyby na przykład przyjąć, że wał 2 jest nieruchomy (n

2

= O), to dopiero

po założeniu prędkości obrotowej n

1

wału 1 można by wyznaczyć

prędkość obrotową wału h lub prędkości kątowe kół obiegowych.

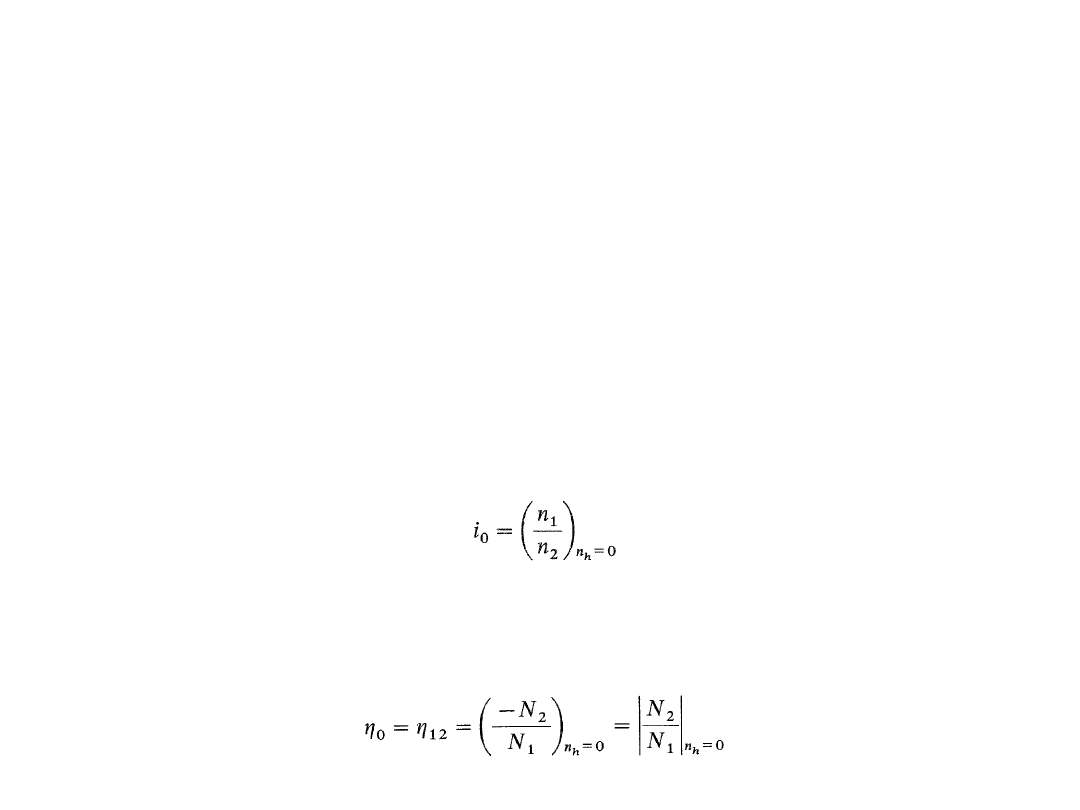
2. Sprawność bazowa będąca stosunkiem mocy wyjściowej N

2

ze znakiem

ujemnym do mocy wejściowej N

i

lub wartością bezwzględną tego

stosunku, przy nieruchomym jarzmie (n

h

= 0).

W schematach kinematycznych nie ma potrzeby rysowania wszystkich kół
obiegowych, zwykle rozpatruje się tylko przekrój A-A, na którym
przedstawia się wymiary tylko jednego koła obiegowego. Dopiero w
obliczeniach geometrycznych i wytrzymałościowych uwzględnia się liczbę
i

położenie

kół

obiegowych.

Pomimo

tego,

że

podstawową

charakterystyczną cechą przekładni obiegowej jest ruchome jarzmo kół
obiegowych, w obliczeniach analitycznych stosuje się wielkości określone
w przypadku nieruchomego jarzma. Ten szczególny przypadek oznaczany
będzie indeksem 0, a w ten sposób określone wielkości nazywane będą
wielkościami bazowymi. W dalszych rozważaniach przydatne będą dwie
wielkości bazowe:

1. Przełożenie bazowe określające stosunek prędkości obrotowych wałów
n

1

, n

2

przy nieruchomym jarzmie (n

h

= 0):

Bardzo istotną cechą przekładni obiegowych jest znak i

0

, określający

kierunek obrotów kół centralnych w przypadku nieruchomego jarzma (n

h

= 0). Jeżeli kierunki obrotów obu kół centralnych są jednakowe, to
zgodnie z poprzednio przyjętymi ustaleniami przełożenie bazowe jest
dodatnie (i

0

> 0), natomiast gdy kierunki są przeciwne, przełożenie

bazowe jest ujemne (i

0

< 0).

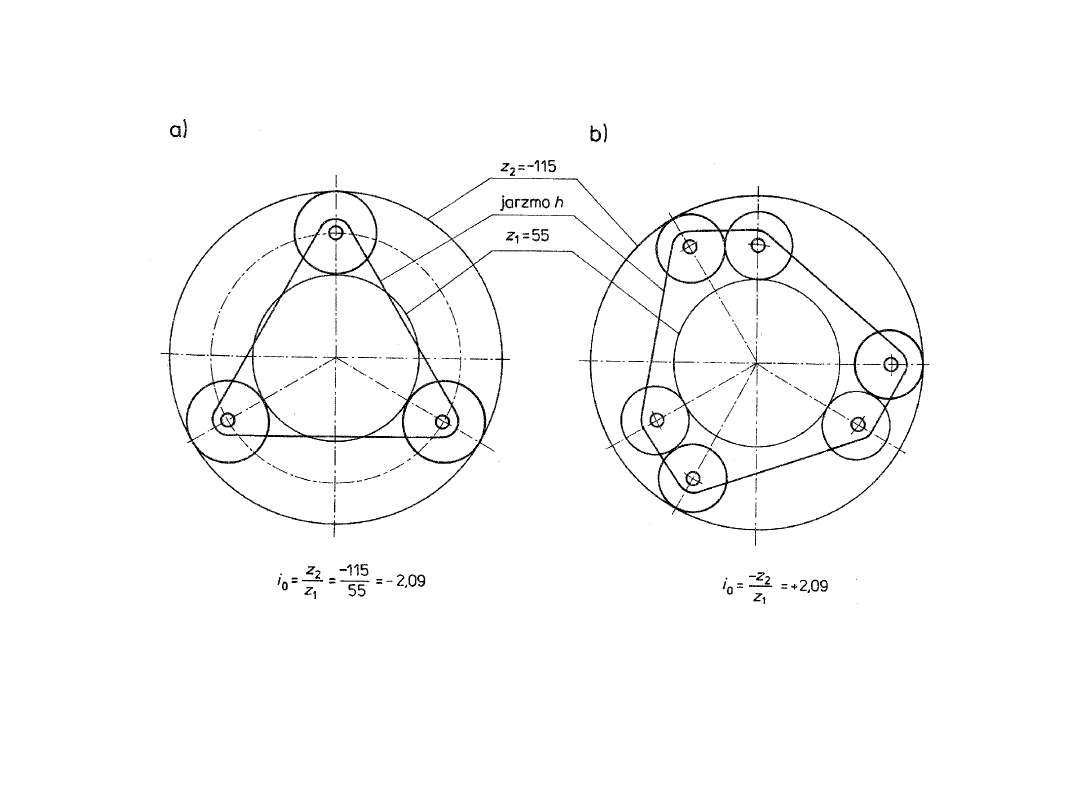
Schematy przekładni obiegowych o dodatniej wartości bazowego przełożenia

(i

0

> 0). Przełożenie osiąga następujące wartości ekstremalne: a) i

0max

= 13,2,

b) i

0max

= 0,076, c) i

0max

= 4,55

Schematy przekładni obiegowych o ujemnej wartości bazowego przełożenia (i

0

 0). Ekstremalne wartości przełożenia wynoszą: a) i

0

od -1,2 do -11,3, b) i

0

od -0,09 do -0,83, c) i

0

od -0,22 do -11,3, d) i

0

od -11,3 do -23,3

Schematy przekładni obiegowych o tej samej wartości bezwzględnej

przełożenia bazowego i

0

, lecz o różnych znakach: a) przekładnia z

pojedynczymi kołami obiegowymi (i

0

< 0), b) przekładnia z dwoma kołami

obiegowymi (i

0

> 0)

Metoda analityczna wyznaczania prędkości obrotowych

elementów przekładni

W metodzie analitycznej zaproponowanej przez Willisa rozpatruje się
przypadek, w którym obserwator porusza się wraz z jarzmem i określa
liczby obrotów kół względem jarzma. Dla takiego obserwatora osie kół są
w stałym względem niego i jarzma położeniu, wobec tego przekładnię
uważamy za zwykłą o stałych osiach, Oznaczając bezwzględne prędkości
obrotowe (mierzone względem stałego układu, np. obudowy) symbolami
n

1

, n

2

oraz n

h

, prędkości obrotowe względem jarzma (obserwatora)

określamy jako (n

1

- n

h

) oraz (n

2

-n

h

), zatem przełożenie bazowe wynosi:

Symbolu i używa się do oznaczania przełożenia w przypadku, gdy jeden
wał jest unieruchomiony; wtedy znak i

12

oznacza przełożenie pomiędzy

wałem 1 i 2 przy zatrzymanym jarzmie h, natomiast znak i

1h

oznacza

przełożenie pomiędzy wałem 1 i jarzmem h przy nieruchomym wale 2.
Zawsze indeksy u dołu symbolu i oznaczać będą dwa wały ruchome
przekładni obiegowej. Oznaczenie trzeciego wału unieruchomionego jest
pomijane.

W przypadku gdy wszystkie trzy wały są ruchome, przełożenie oznacza
się literą j z odpowiednimi indeksami u dołu.

Z równania:

możemy wyznaczyć przełożenia dla różnych kombinacji obrotów, między
innymi w następujących szczególnych przypadkach:

1. W przypadku zahamowania jarzma (n

h

= 0) otrzymujemy:

2. Jeżeli n

2

= 0, otrzymujemy:

3. Jeżeli n

1

= 0, to:

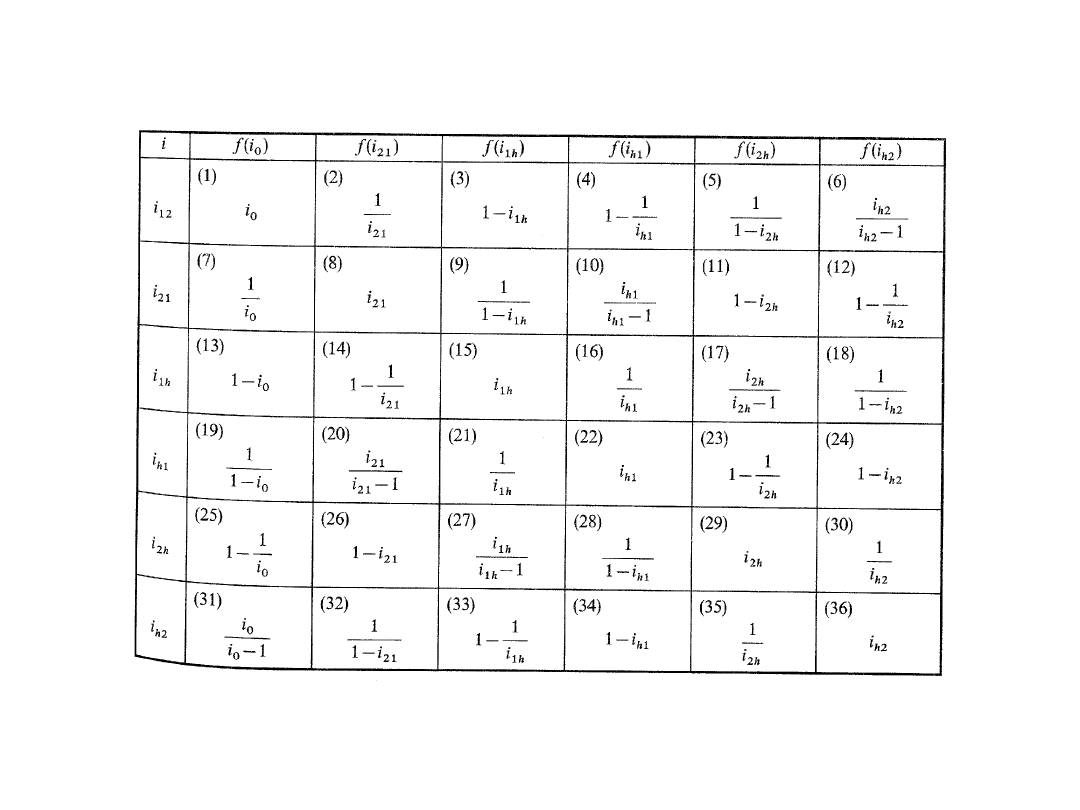
Zależności pomiędzy różnego rodzaju przełożeniami przekładni o dwóch

wałach

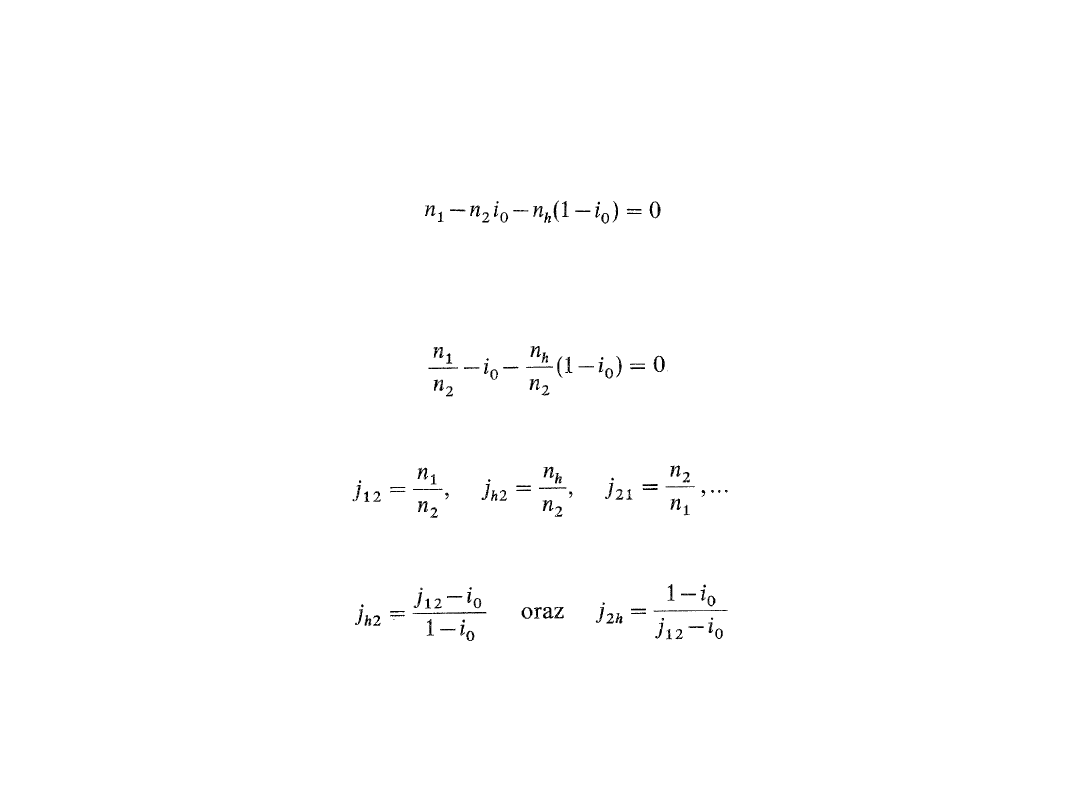
W przypadku gdy wszystkie wały są ruchome, muszą być ustalone dwie
prędkości obrotowe, np. n

1

oraz n

2

, umożliwia to wyznaczenie, trzeciej

wielkości, np. n

h

. Zwykle równanie:

sprowadzamy do bezwymiarowej postaci, tj. do związku pomiędzy
przełożeniami, będącymi stosunkami prędkości obrotowych
poszczególnych wałów przekładni:

Podstawiając do powyższego równania przyjęte oznaczenia:

Otrzymujemy między innymi:

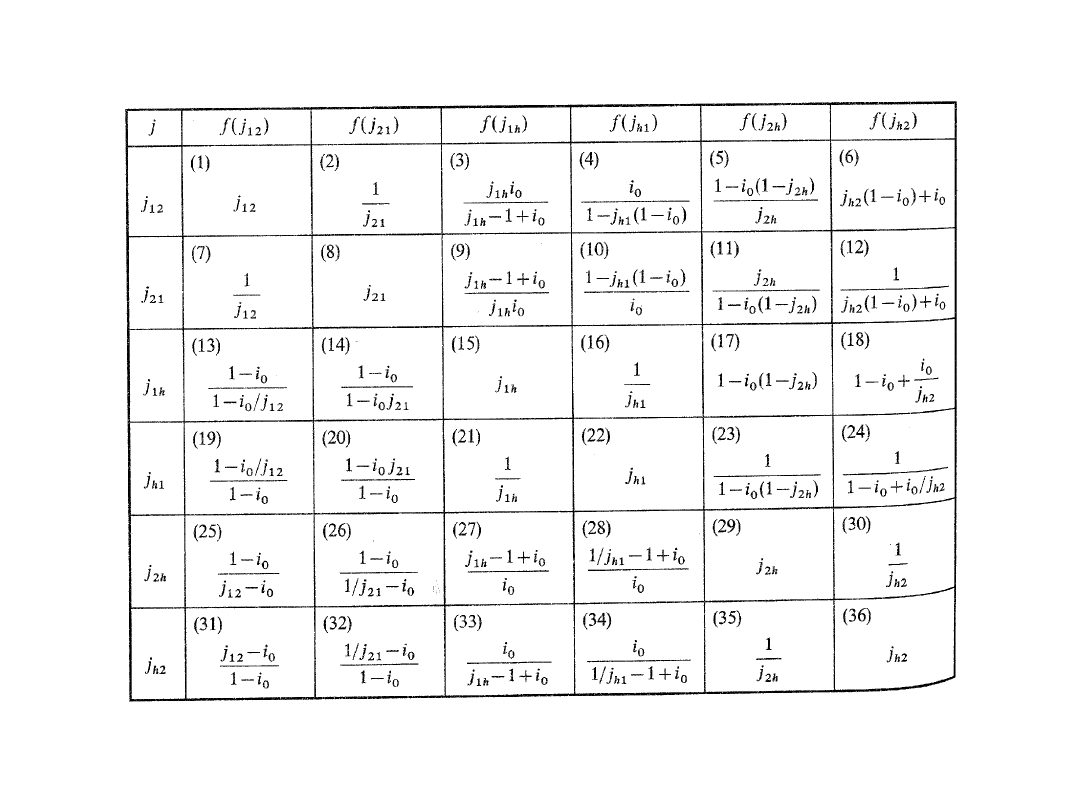
Związki pomiędzy przełożeniami j

xy

Obliczanie momentów

Zgodnie z warunkami równowagi suma momentów działających na trzy
wały przekładni musi spełniać równanie

M

1

+M

2

+M

h

= 0

Z równania tego wynika, że jeden wał obciążony jest momentem o
przeciwnym znaku niż dwa pozostałe wały. Wał ten nazywa się wałem
sumującym, ponieważ obciążony jest momentem równym bezwzględnej
wartości sumy pozostałych dwóch momentów.

W przekładni o bazowym przełożeniu ujemnym (i

0

< 0) sumaryczny

moment występuje zawsze na wale jarzma, co łatwo zauważyć, jeżeli
przyjmie się dwie siły międzyzębne na obwodzie koła obiegowego,
których wypadkowa działająca na oś koła obiegowego, a tym samym na
jarzmo, wytwarza moment sumaryczny. Oznacza to jednocześnie, że wały
kół centralnych są wałami różnicowymi.

W przekładni o bazowym przełożeniu dodatnim (i

0

> 0) wał jarzma jest

zawsze wałem różnicowym, natomiast wał koła centralnego o mniejszej
prędkości, obrotowej, tj. większym momencie obrotowym, jest wałem
sumującym. Wynika stąd, że o umiejscowieniu wału sumującego decyduje
przełożenie bazowe. W przypadku gdy jest ono większe od 1, większy
moment występuje na wale zdawczym, który jest wałem sumującym.

Znaki momentów określa się następująco: moment, który działa na wał w
kierunku zgodnym z dodatnim kierunkiem prędkości obrotowych, ma znak
dodatni, natomiast gdy moment działa w przeciwną stronę, ma on znak
ujemny.

Zależności pomiędzy momentami obrotowymi z uwzględnieniem strat
tarcia wyznaczamy przy nieruchomym jarzmie, a więc tak jak dla
przekładni bazowej. Gdy silnik napędowy połączony jest z wałem 1, wtedy
moc oddaną wyrażamy zależnością:

Gdy natomiast silnik napędza wał 2, wówczas zachodzi zależność:

gdzie



12

oraz



21

określają sprawność przekładni przy założonym kierunku

przepływu mocy. Powyższe równania możemy sprowadzić do wspólnej
postaci

przy czym wykładnik potęgowy w = ±1, w zależności od kierunku
przepływu mocy. Znak wykładnika w można wyznaczyć z zależności

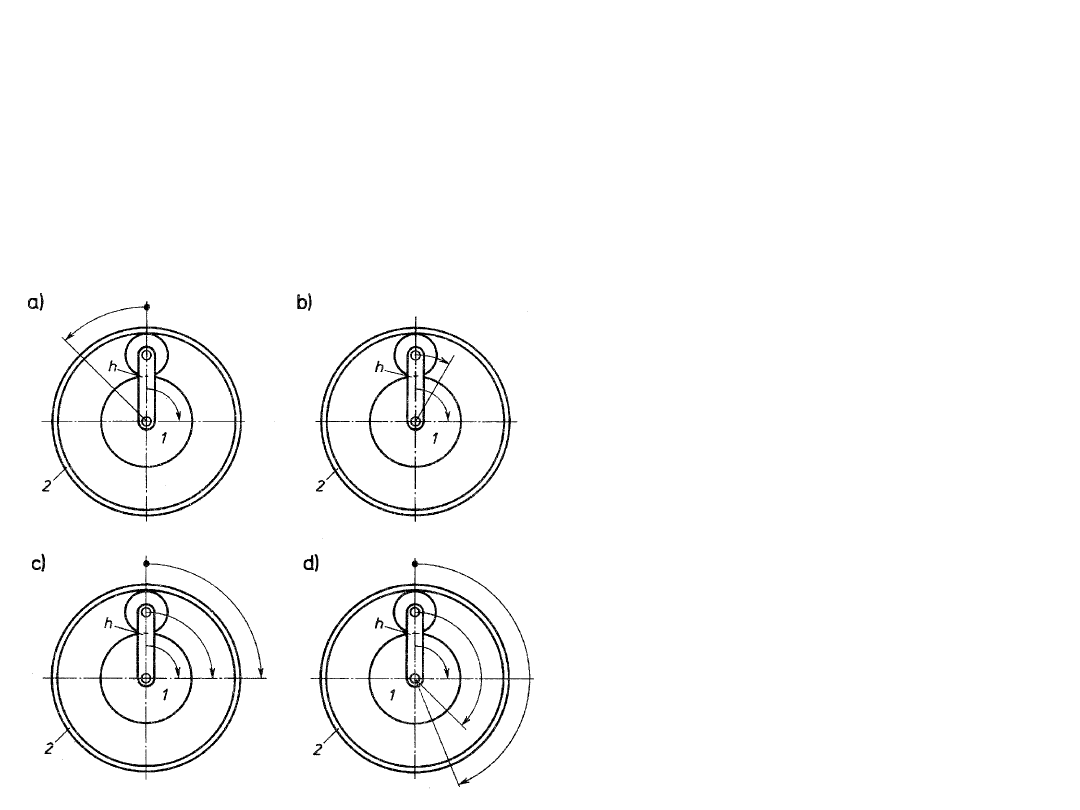
Obliczanie mocy

W przekładniach obiegowych rozróżnia się kilka rodzajów mocy. Nie
występują one jednocześnie we wszystkich przypadkach konstrukcyjnych
i kinematycznych, dlatego omawiane będą kolejno, w trakcie opisu
każdego rodzaju przekładni.

Na rysunku przedstawiono przekładnię 2K-H z ujemnym przełożeniem
bazowym w czterech sytuacjach ruchowych.

Przekładnia typu 2K-H w czterech

sytuacjach ruchowych:

a) unieruchomione jarzmo (n

h

= 0),

b) unieruchomione koło wewnętrznie

uzębione (n

2

= 0),

c) zrównanie prędkości wszystkich

elementów przekładni -działanie

sprzęgła zębatego,

d) ruchome trzy wały -prędkość

obrotowa jarzma jest większa od

prędkości obrotowej wału 1

1. W przypadku nieruchomego jarzma (n

h

= 0) (a) przekładnia działa jak

zwykła przekładnia o stałych osiach kół. Moc doprowadzona do koła 1 jest
przenoszona poprzez zazębienie na koło pośredniczące, a stąd na koło
wewnętrznie uzębione 2. Ten sposób przenoszenia mocy oznaczany
będzie indeksem z (zazębienie).

2. W przypadku nieruchomego koła 2 (b) ruch koła 1 wywołuje
przemieszczanie się w tym samym kierunku jarzma h, co oznacza, że
maleje względna prędkość koła 1 względem jarzma h. W stosunku do
przypadku 1 zmniejsza się więc moc przenoszona przez zazębienie,
natomiast pojawia się inny sposób przenoszenia mocy. Odpowiada on
przenoszeniu mocy za pomocą sprzęgła zębatego, w którym zęby nie
zmieniają swojego wzajemnego położenia. Moc tę określa się mianem
mocy sprzężenia lub unoszenia. Zachodzi więc zależność

N = N

z

+N

s

gdzie N jest całkowitą mocą przenoszoną przez przekładnię, N

z

- częścią

przenoszoną przez zazębienie, N

s

- częścią przenoszoną przez sprzężenie

(unoszenie), przy czym

N

z1

= M

1

(n

1

-n

h

) > 0,

N

s1

= M

1

n

h

> 0.

Oba rodzaje mocy mają znak dodatni, albowiem kierunek działania
momentu pokrywa się z kierunkiem względnej prędkości.

3. Przy założeniu ruchomych wszystkich trzech wałów przekładni (c) może
wystąpić szczególny przypadek zrównania się prędkości obrotowych
wszystkich wałów. Wtedy zęby nie wykonują wzajemnych ruchów, lecz
cała przekładnia zachowuje się jak sprzęgło zębate, przenosząc moc
wyłącznie przez sprzężenie, tzn.

N=N

s

=M

1

n

h

,

N

z1

=0.

4. Przy założeniu ruchomych trzech wałów (d) może zaistnieć przypadek,
w którym prędkość obrotowa jarzma jest większa od prędkości obrotowej
wału 1. Wtedy, zgodnie z poprzednim tokiem rozumowania, moc
przenoszenia przez zazębienie będzie ujemna, podczas gdy moc
sprzężenia pozostanie nadal dodatnia, tzn.

N

z1

= M

1

(n

1

-n

h

) < 0,

Ns = M

1

n

h

> 0,

przy czym nadal obowiązuje ogólna zależność:

N

1

= N

z1

+N

s

= M

1

n

1

-M

1

n

h

+M

1

n

h

= M

1

n

1

.

Sprawność

Straty mocy w przekładniach obiegowych składają się z następujących
strat:

1) w zazębieniu,

2) w łożyskach,

3) na pokonanie oporów hydraulicznych związanych z mieszaniem
i rozbryzgiwaniem oleju przekładniowego.

Straty w zazębieniu dają się stosunkowo najłatwiej określić, chociażby z
uwagi na wielką liczbę doświadczeń w tej dziedzinie. Z dostateczną dla
praktyki dokładnością można ocenić straty w łożyskach, zwłaszcza
tocznych. Najtrudniej natomiast jest ocenić straty na mieszanie i
rozbryzgiwanie oleju z powodu bardzo dużej liczby wariantów
konstrukcyjnych elementów przekładni, zarówno ruchomych jak i stałych.
Dodatkową trudność sprawia to, że straty na mieszanie i rozbryzgiwanie
praktycznie nie zależą od przenoszonej mocy, a głównie od prędkości
obrotowej, która w przekładni przemysłowej najczęściej jest stała. Z tego
względu sprawność uwzględniająca straty hydrauliczne jest nieliniową
funkcją obciążenia.

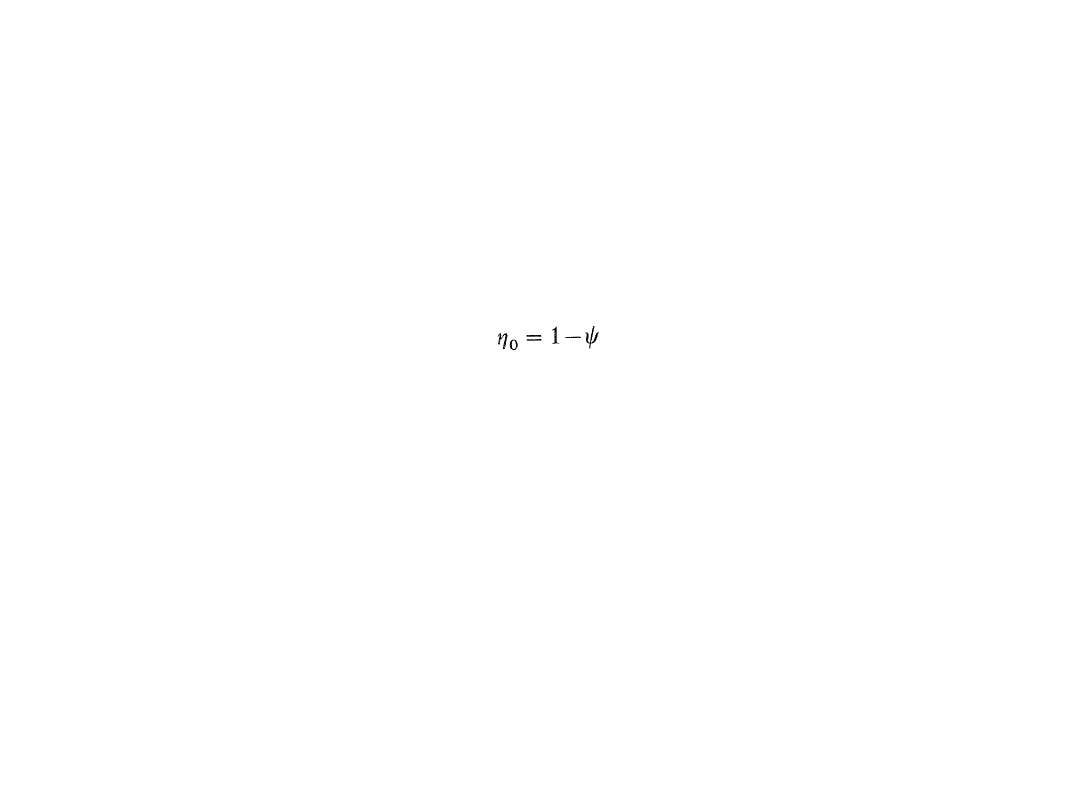
Wyznaczanie strat w zazębieniu i łożyskowaniu kół prostej

przekładni obiegowej

Dla prostej przekładni obiegowej o dwóch wałach i przełożeniu bazowym
i

o

ujemnym oraz przy założeniu nieruchomego jarzma, sprawność bazowa



0

wyraża się wzorem:

gdzie

 -współczynnik strat w przekładni.

Współczynnik ten jest sumą strat w zazębieniach, strat w łożyskach i strat
spowodowanych

rozbryzgiwaniem

i

mieszaniem

oleju.

Straty

spowodowane rozbryzgiwaniem i mieszaniem oleju przy małych
prędkościach obrotowych są małe w stosunku do pozostałych i rosną wraz
ze wzrostem prędkości obrotowej. Pomijając wyżej wymienione straty,
współczynnik strat obliczamy ze wzoru:

= 

z

+





gdzie



z

-współczynnik strat w zazębieniu,





-współczynnik strat w

łożyskach.

Dobór podstawowych cech przekładni obiegowej

Większość parametrów charakteryzujących przekładnie zębate, w tym
także przekładnie obiegowe, można sprowadzić do bezwymiarowej
postaci. Do parametrów tych należą stosunki jednoimiennych wielkości,
takie jak np. stosunki średnic, przełożenia, liczby zębów, stosunek
szerokości koła do jego średnicy, współczynniki przesunięcia zarysu itd.
Wielkości te mogą być z łatwością przenoszone z jednej konstrukcji na
drugą bez względu na skalę zmian wielkości wymiarowanych, np. bez
względu na moduł zęba, średnicę koła czy odległość między osiami.
Należy więc wzorować się na sprawdzonych konstrukcjach, wprowadzając
ewentualnie

nieznaczne

zmiany

wartości

bezwymiarowych

współczynników i obliczając tylko jeden charakterystyczny wymiar, np.
moduł lub średnicę, co wobec przyjętych wstępnie proporcji ustala
wymiary pozostałych elementów.

Nie wszystkie parametry można ustalić jednocześnie na samym początku
projektowania. Niektóre wybiera się dopiero na podstawie wstępnych
wyników obliczeń. Jednak dla przejrzystości omówimy wszystkie
parametry wybieralne, bez względu na kolejność ich wyboru.

Dobór liczby zębów w kołach

W przekładniach obiegowych oprócz warunków spotykanych w zwykłych
przekładniach zębatych występują dodatkowo zależności wynikające z ich
specyfiki. W zwykłej przekładni liczbę zębów w zębniku dobiera się
najczęściej ze względów wytrzymałościowych, przy czym dolna granica
wynika z warunku uniknięcia podcinania stopy zęba. Przez zastosowanie
dodatniej korekcji zazębienia i odpowiedniego kąta pochylenia linii zęba
można ogólnie przyjętą wartość graniczną z'

min

= 14 zębów wydatnie

zmniejszyć. Nie zawsze jednak najmniejsza liczba zębów jest wartością
optymalną. Obecnie omówimy warunki geometryczne, których spełnienie
jest konieczne, a następnie podamy kryteria wyboru optymalnej liczby
zębów.

W zwykłej przekładni dwustopniowej o wałach współosiowych zachodzi
potrzeba uzyskania jednakowych odległości osi na obu stopniach (to
samo zjawisko występuje w przekładniach wielodrożnych, a także w
skrzynkach biegów). Nie stwarza to jednak większych trudności
obliczeniowych wobec możliwości zastosowania na obu stopniach różnych
szerokości kół, modułów, kątów pochylenia linii zębów, a także
współczynników przesunięcia zarysu.

W przekładniach obiegowych nawet jednostopniowych muszą być
spełnione następujące wymagania:

-liczba zębów w kołach powinna być bliska optymalnej, tj. zapewniającej
odpowiedni stosunek współczynników bezpieczeństwa na złamanie i
naciski,

-spełniony musi być warunek współosiowości poszczególnych par kół,
wiążący w pewien określony sposób liczbę zębów i kąty przyporu,

-koła obiegowe nie mogą dotykać się obwodami, co ogranicza ich
maksymalną średnicę, a tym samym i ekstremalną wartość przełożenia,

-montaż musi umożliwiać usytuowanie koła centralnego pomiędzy kołami
obiegowymi o ustalonym już wzajemnym położeniu, warunek ten
wyznacza związek pomiędzy liczbą zębów a liczbą kół obiegowych.

Dodatkowo wskazany jest taki wybór liczby zębów, aby zapewnić
optymalne warunki dynamiczne związane z chwilą wejścia w przypór
poszczególnych par zębów.

Sposób postępowania przy poszukiwaniu związków pomiędzy liczbami
zębów przedstawiony będzie na przykładzie przekładni 2K-H o ujemnej
wartości przełożenia bazowego.

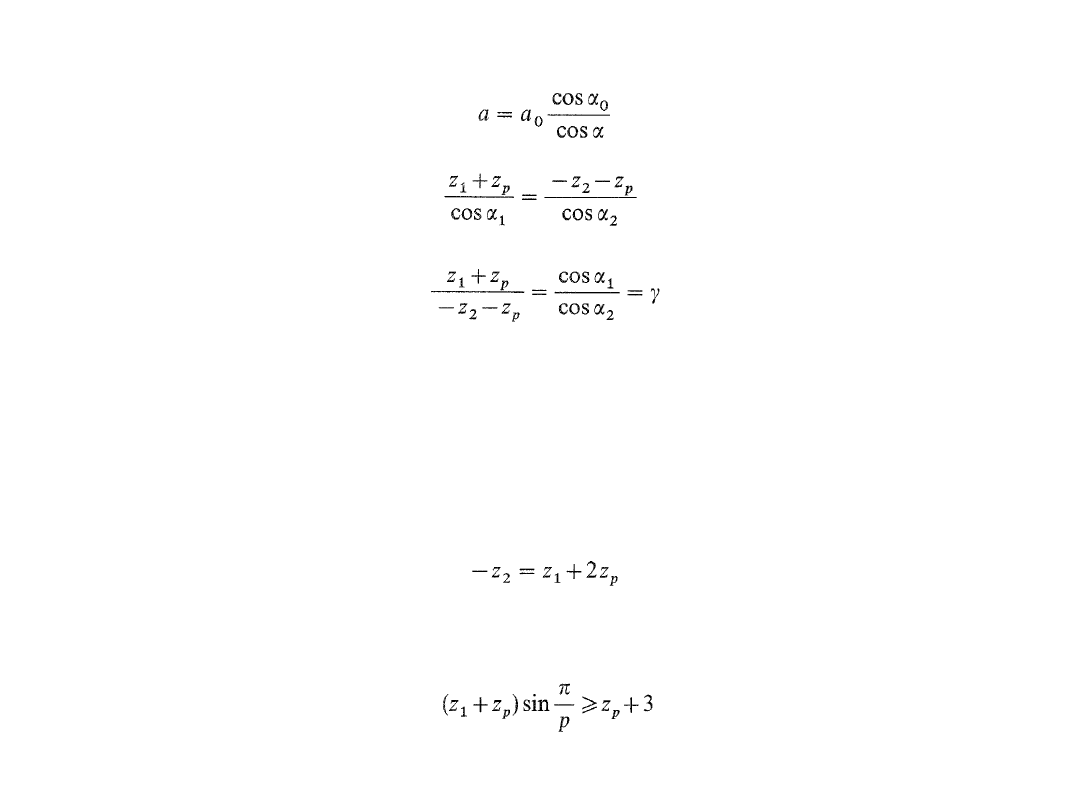
Warunek współosiowości sprowadza się, po wykorzystaniu znanej
zależności:

do następującej postaci:

lub jej równoważnej:

gdzie a - rzeczywista odległość osi, a

0

- zerowa odległość osi, z

1

- liczba

zębów w kole centralnym 1, z

2

- liczba zębów w kole wewnętrznie

uzębionym (z

2

< 0), z

p

-liczba zębów w kole obiegowym,



1

-kąt przyporu

na średnicy tocznej kół z

1

, z

p

,



2

-kąt przyporu na średnicy tocznej kół z

2

,

z

p

,



o

-nominalna wartość kąta przyporu.

W szczególnym przypadku, gdy



1

=



2

(zęby niekorygowane), powyższe

wzory sprowadzają się do postaci

Warunek sąsiedztwa kół obiegowych, przy założeniu minimalnej
odległości pomiędzy obwodami kół równej modułowi m, dany jest
zależnością:

gdzie p – liczba kół obiegowych.

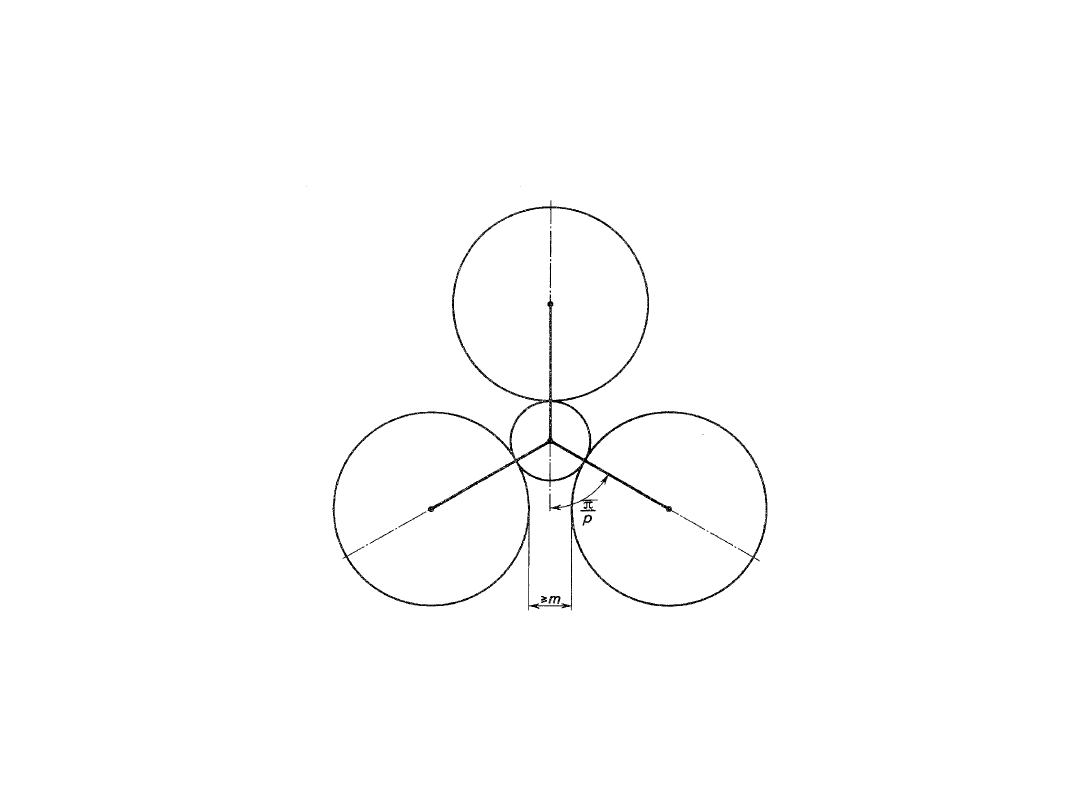
Szkic do wyznaczenia warunku sąsiedztwa kół obiegowych w przekładni o

trzech kołach obiegowych

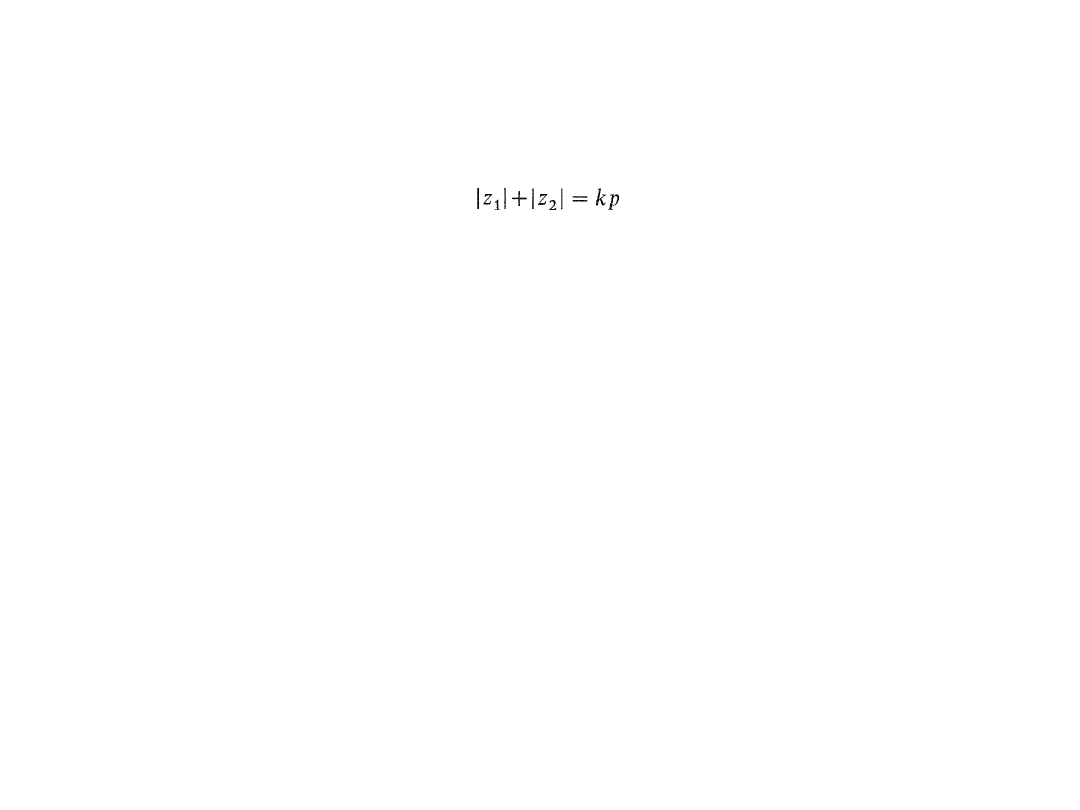
Warunkiem montażu kół przy założeniu równomiernego rozmieszczenia
kół obiegowych na obwodzie jest spełnienie następującego równania:

gdzie k jest dowolną liczbą całkowitą.

Oznacza to, że warunek montażu jest zrealizowany, gdy suma
bezwzględnych wartości liczb zębów kół centralnych przekładni jest bez
reszty podzielna przez liczbę kół obiegowych.

Zazwyczaj przystępując do obliczeń zakłada się wstępnie następujące
wartości:

• liczbę kół obiegowych p,

• liczbę zębów w kole centralnym z

1

• pożądaną wartość przełożenia bazowego i

0

; w omawianym przykładzie

jest to wartość ujemna.

Dla tych założeń został opracowany algorytm i program wyznaczania
liczby zębów kół prostej przekładni obiegowej uwzględniający
rozpatrywane poprzednio wymagania.