Ewolucja modelu atomu

Twórcą atomistycznej teorii budowy materii był Demokryt z
Abdery, filozof grecki (przełom V i IV w. p.n.e.). Według Demokryta
atom to elementarna, niepodzielna cząstka materii („atomos” –
niepodzielny).

Swoją teorię opisał w dziele: "O małym porządku świata".

Model ten częściowo zmodyfikowany i rozszerzony w tzw. model
kinetyczno-molekularnej budowy materii wyjaśniał prawa gazowe
(m. in. Prawo Boyle’a i Mariotte’a, a także inne prawa gazowe
odkryte w XVII w).
Model ten przetrwał do XIX w.

"Nie istnieje nic oprócz atomów i

przestrzeni,

wszystko inne jest opinią"

- Demokryt z Abdery

Demokryt z Abdery (460 - 370 p.n.e.)

Joseph John Thompson badając przepływ prądu w rurze częściowo
opróżnionej z powietrza stwierdził, że atom musi mieć strukturę
złożoną, bo obojętne atomy gazu stają się w rurze (w polu
elektrycznym) nośnikami ładunku. Stąd wniosek, że atom dzieli się
na część naładowaną dodatnio (jon dodatni) i część naładowaną
ujemnie (elektron).

J.J. Thomson w 1896 r. odkrył elektron i zmierzył stosunek e/m dla
elektronu. Wyniki badań prowadziły do modyfikacji modelu atomu
jako cząstki niepodzielnej. Według Thomsona atom to kula ładunku
dodatniego, w której jak rodzynki w cieście rozmieszczone są
elektrony. Fizycy nazwali ten model „rodzynkowym”.

Joseph John Thompson

(1856-1940)

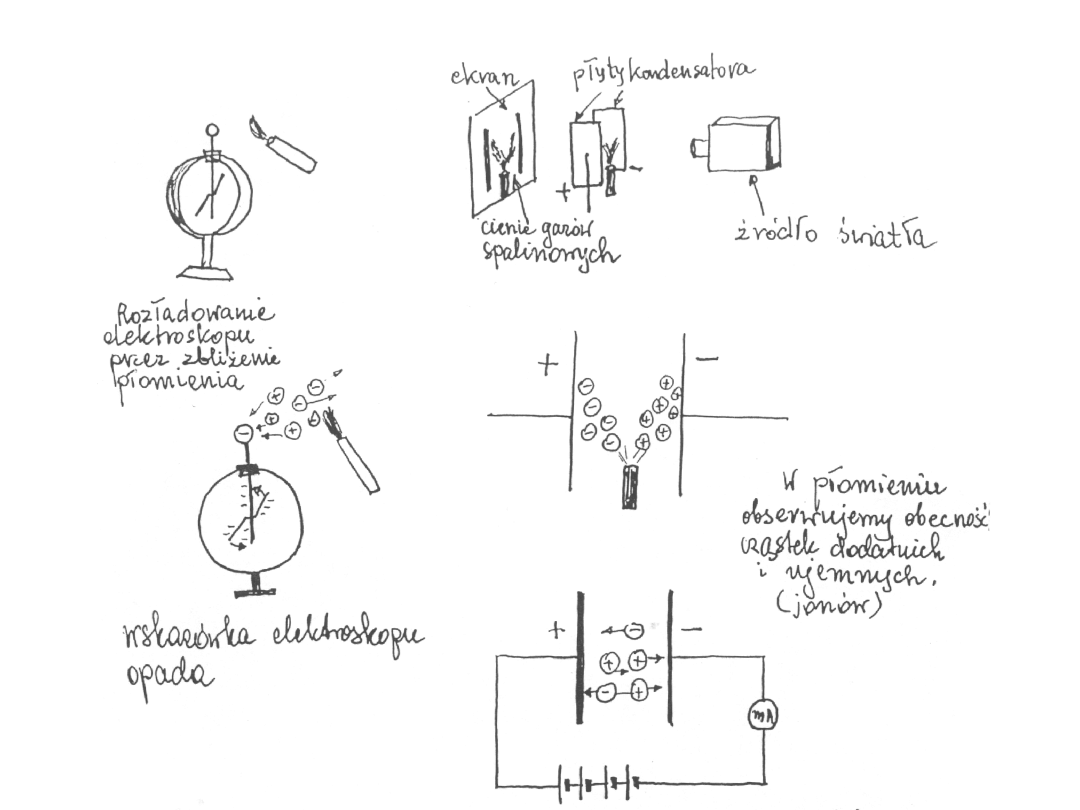
Prądy niesamoistne

Jeśli w obszarze między płytkami pojawi się czynnik jonizujący w obwodzie
płynie prąd. Po usunięciu czynnika jonizującego prąd przestaje płynąć. Prąd
ten nazywamy prądem niesamoistnym.
Można spowodować jonizację przy zderzeniach atomów neutralnych ze sobą
ogrzewając gaz do wysokiej temperatury.

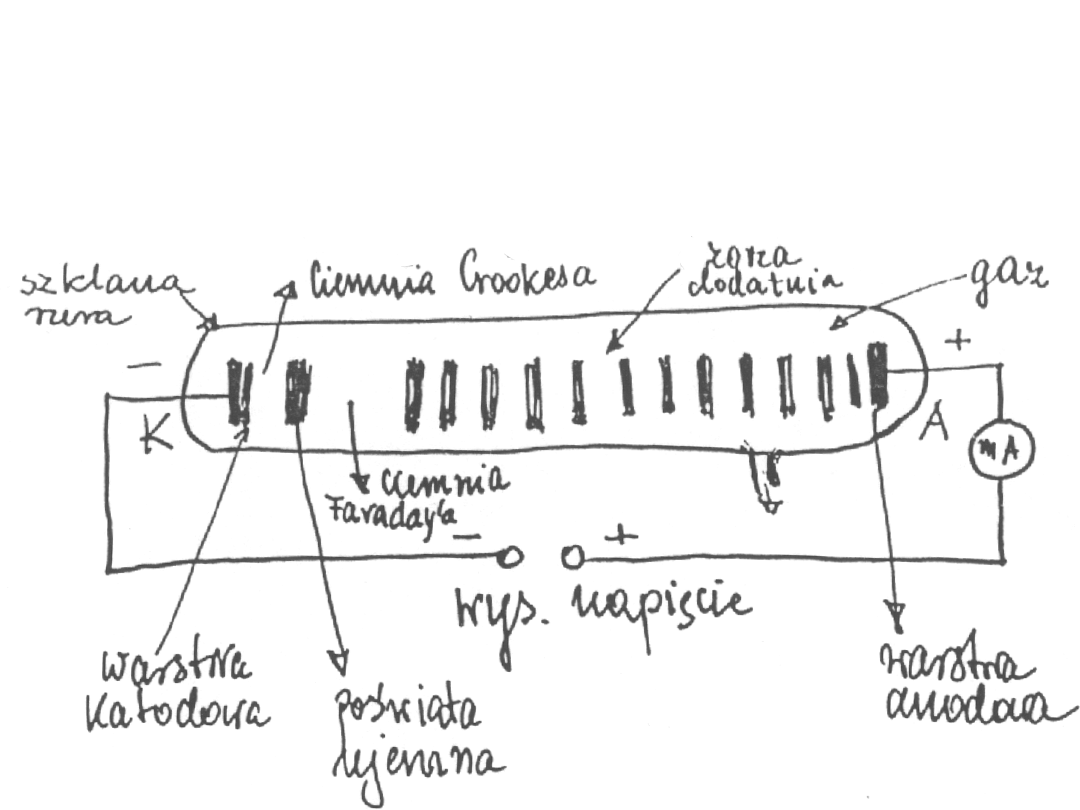
Prąd elektryczny w gazach rozrzedzonych

Przy ciśnieniu ok. 0,01 mm Hg świecenie gazu znika. Pojawia się świecenie
rury szklanej, naprzeciwko katody, seledynowym światłem.

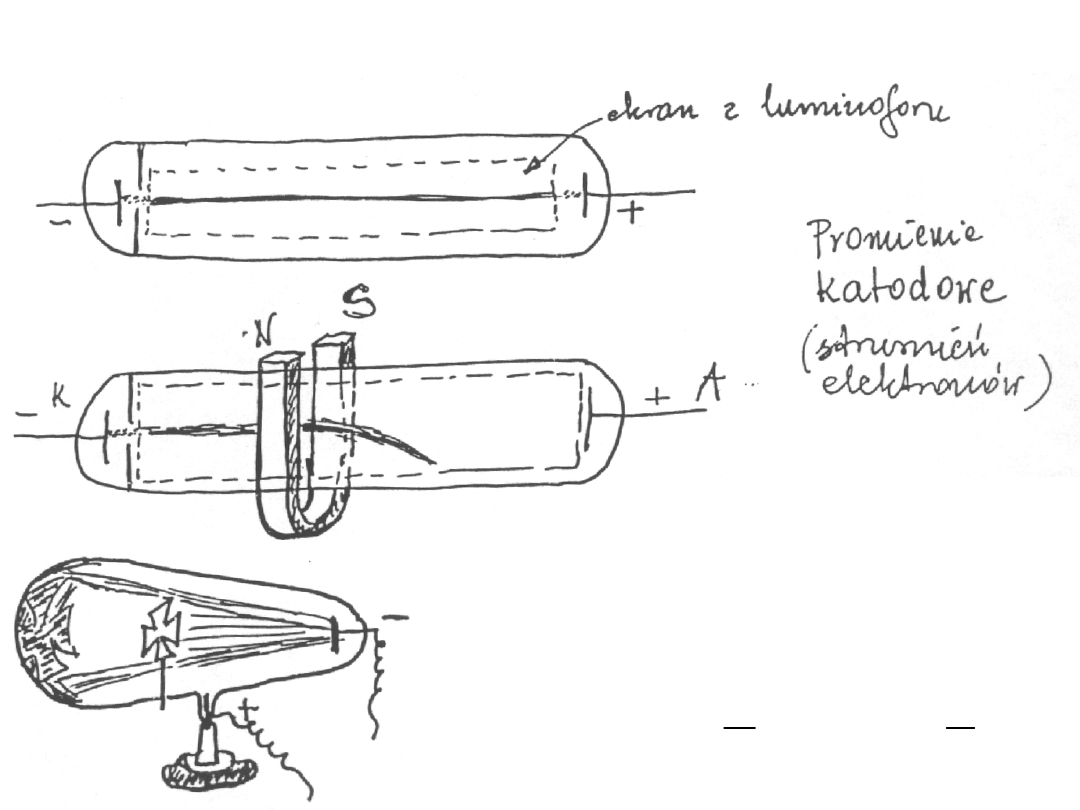
Thomson odkrył, że promienie katodowe
to strumienie bardzo lekkich cząstek o
ładunku ujemnym. Odchylając strumień
tych cząstek w polu elektrycznym i
magnetycznym wyznaczył stosunek e/m.

8

C

1,759 10

g

e

m

=

�

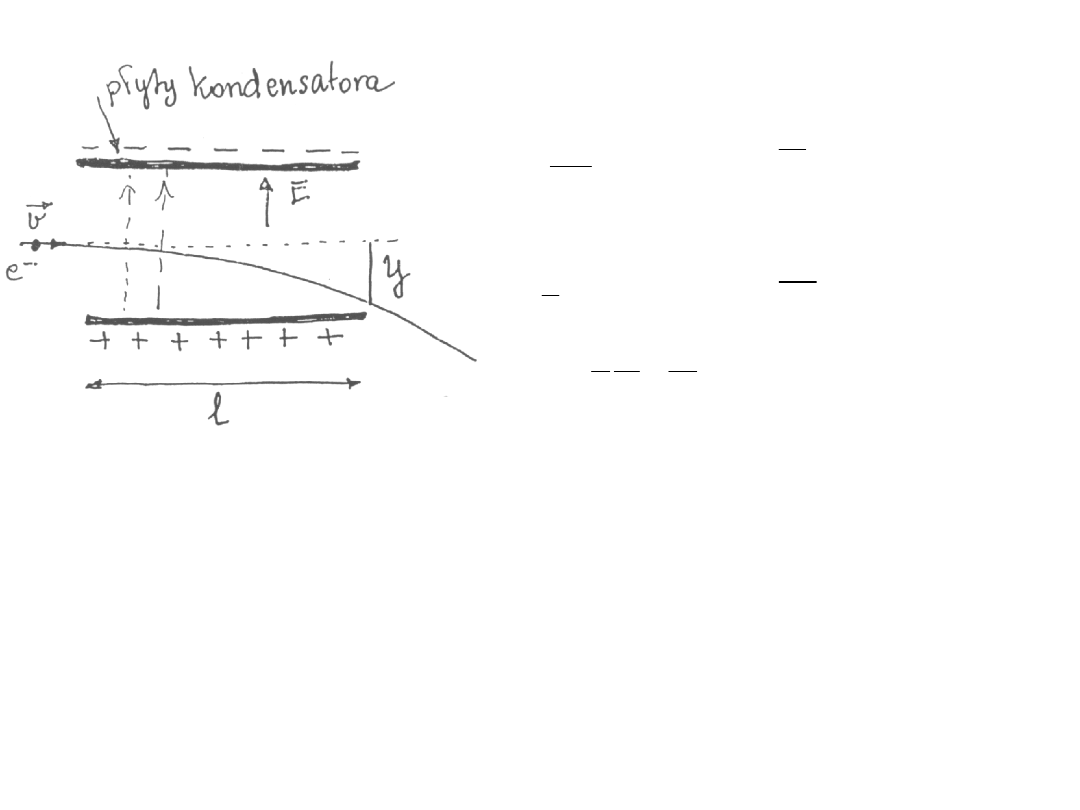
Wyznaczanie e/m dla elektronu przez Thomsona

Odchylenie elektronu w polu elektrycznym

2

2

at

y

l vt

l

t

v

=

=

=

F

a

m

F eE

eE

a

m

=

=

=

2

2

1

2

e l

y

E

m v

=

(*)

gdzie:

m  masa cząstki

(elektronu)

e ładunek cząstki
v prędkość cząstki
E natężenie pola

elektrycznego

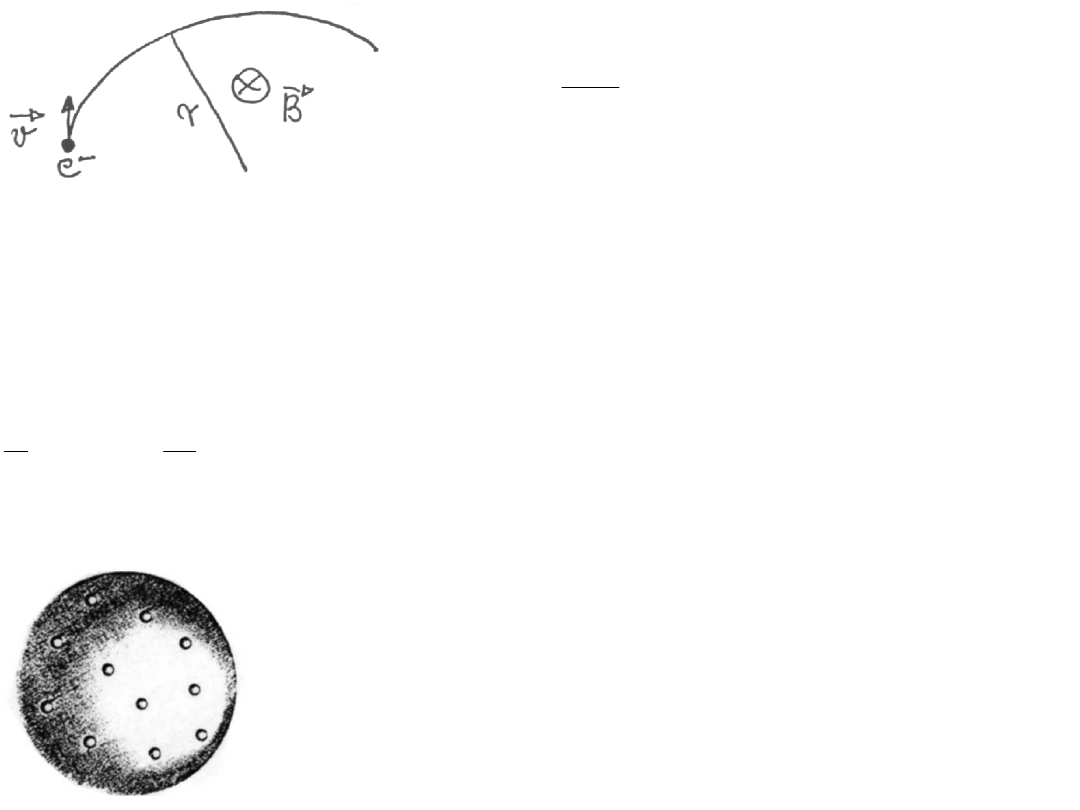
Odchylenie elektronu w polu magnetycznym

2

mv

evB

r

=

(**)

Z równań (*) i (**) można było wyznaczyć v i e/m.

Thomson stwierdził, że te czątki (elektrony) muszą być elementami atomów.
Termin „elektron” w odniesieniu do tych cząstek pojawił się później.

11

C

1,76 10

kg

e

m

=

�

Model atomu wg Thomsona

Atom na zewnątrz jest elektrycznie obojętny.

W 1911 r. Ernest Rutherford (fizyk brytyjski, pochodzący z Nowej
Zelandii) wraz ze współpracownikami Marsdenem i Geigerem badali
rozpraszanie cząstek  (jąder helu ) przy przechodzeniu przez

cienkie (kilka m) folie złota. Wyniki badań wykazały, że niektóre

cząstki  przechodzą przez folie bez zmiany kierunku, ale są takie,

które ulegają rozproszeniu – niektóre nawet pod bardzo dużymi
kątami.

4

2

He

Tak duże kąty rozpraszania wskazywały na to, że ładunek dodatni nie
może być w atomie rozłożony równomiernie. Z obliczeń wynikało, że
prawie cała masa i ładunek dodatni skupione są w bardzo małym
obszarze (o rozmiarach 10

-15

m), a elektrony, jak planety w układzie

słonecznym krążą wokół jądra. Model nazwano modelem
„planetarnym”. Promień toru elektronu jest rzędu 10

-10

m. A więc, jeśli

jądro wyobrazimy sobie jako kulkę o promieniu 1 m, to elektron
krążyłby wokół tej kulki po torze o promieniu 100 km. Atom zatem jest
bardzo „ażurowy”. Jeśli cząsteczka  przebiega blisko jądra to jej tor

ulega dużemu odchyleniu, a jeśli daleko to tor odchyla się wcale lub
słabo.

Ernest Rutherford

(1871-1937)

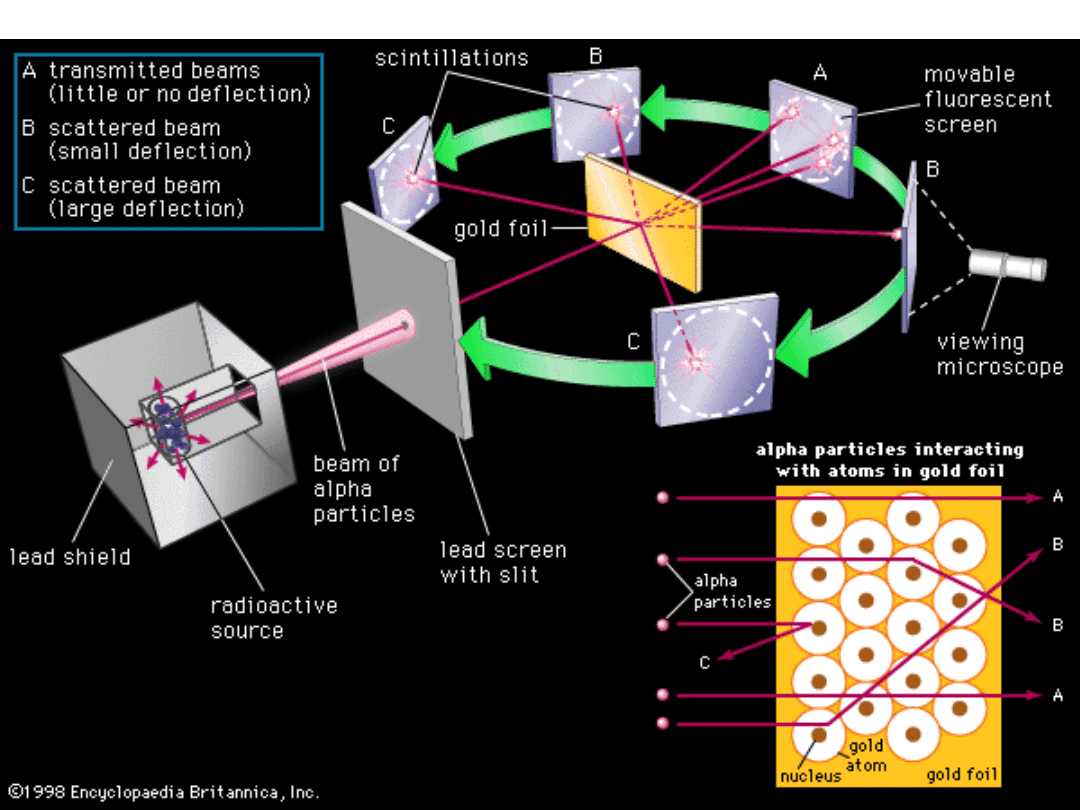
Doświadczenie Rutherforda

Pomiary wykonywali Geiger i Marsden.

150

135

120

105

60

45

15

10

5

Kąt odchylenia

Eksperymentalna liczba

Zliczeń cząstek odchylonych

33

43

52

69

477

1435

120570

502570

8289000

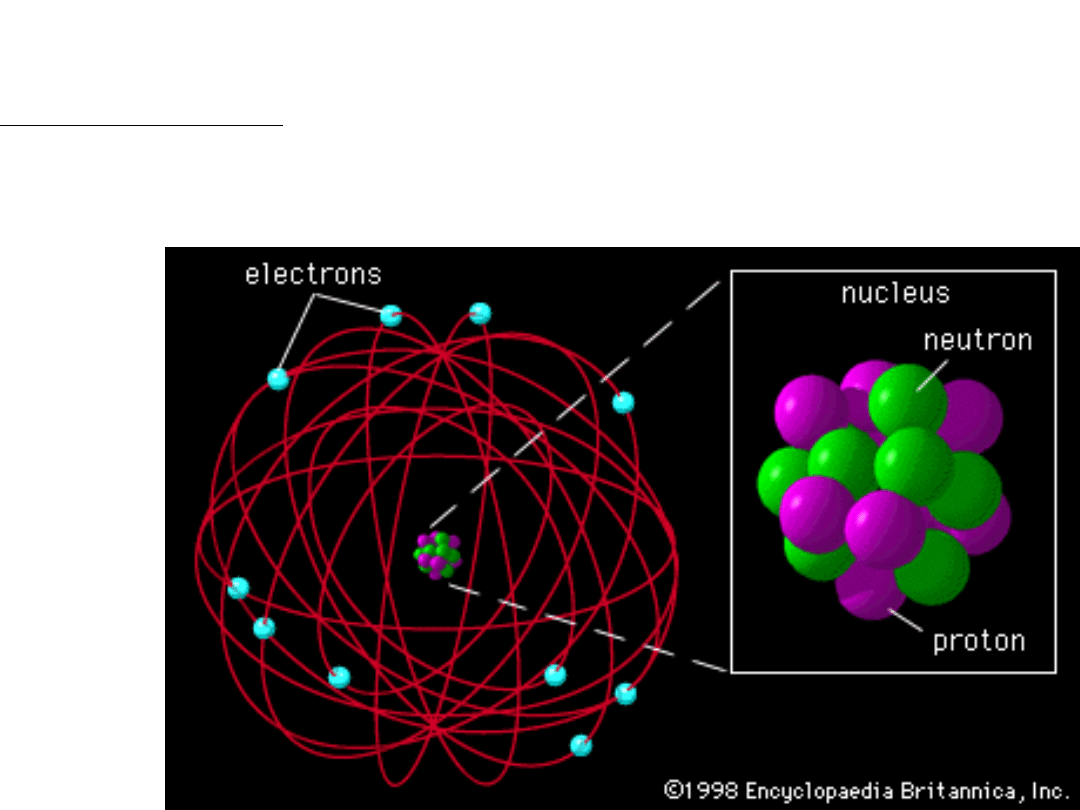
Model Thomsona nie wyjaśniał wyników eksperymentu Rutherforda. Nie
można było wyjaśnić odchyleń cząstek  pod tak dużymi kątami.

Hipoteza Rutherforda

Cały dodatni ładunek atomu rozmieszczony jest w jego jądrze i zajmuje
objętość bardzo małą w porównaniu do objętości całego atomu.

Przy takim założeniu otrzymał Rutherford następujący wynik:

Liczba cząstek  (

dN

dW

) rozproszonych w jednostkowy kąt bryłowy w jednostce
czasu wyraża się wzorem:

2

4

0

2

2

1

4

4

sin

dN

e Ze

n

d

j

pe e

�

�

�

= �

�

W

�

�

gdzie:

n – gęstość strumienia cząstek 

 – energia cząstki 

Z – liczba atomowa

Dla określonej substancji ropraszającej, określonej energii cząstki  oraz

określonej gęstości strumienia n iloczyn

4

sin

2

dN

d

j

W

powinien być stały.

Wyniki te zostały potwierdzone przez Geigera i Marsdena

(od 10

o

do 150

o

).

o

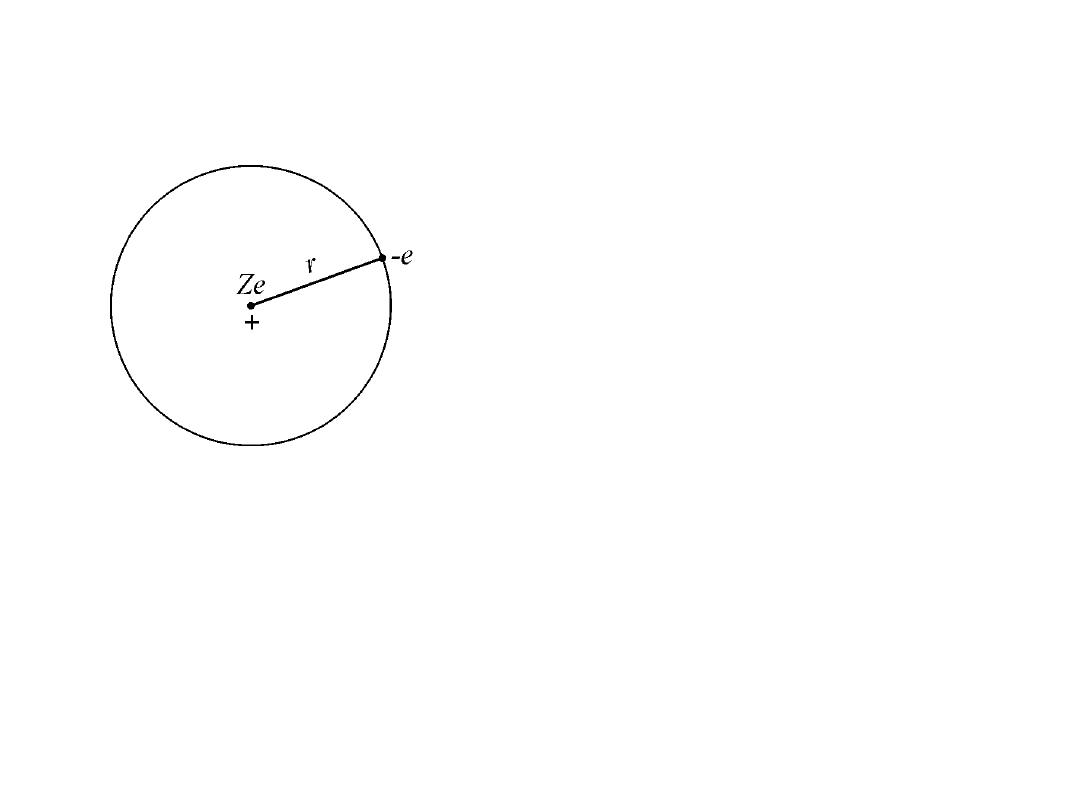
Model jądrowy atomu wg. Rutherforda

Prawie cała masa atomu i cały jego ładunek dodatni skoncentrowane są w
obszarze o rozmiarach 10

-15

m w tzw. jądrze atomu. Wokół jądra krąży

elektron o ładunku ujemnym.

8

10

15

10 cm 10 m (1A)

10 m

1

j

r

R

Z

-

-

-

=

=

o

:

:

~

~

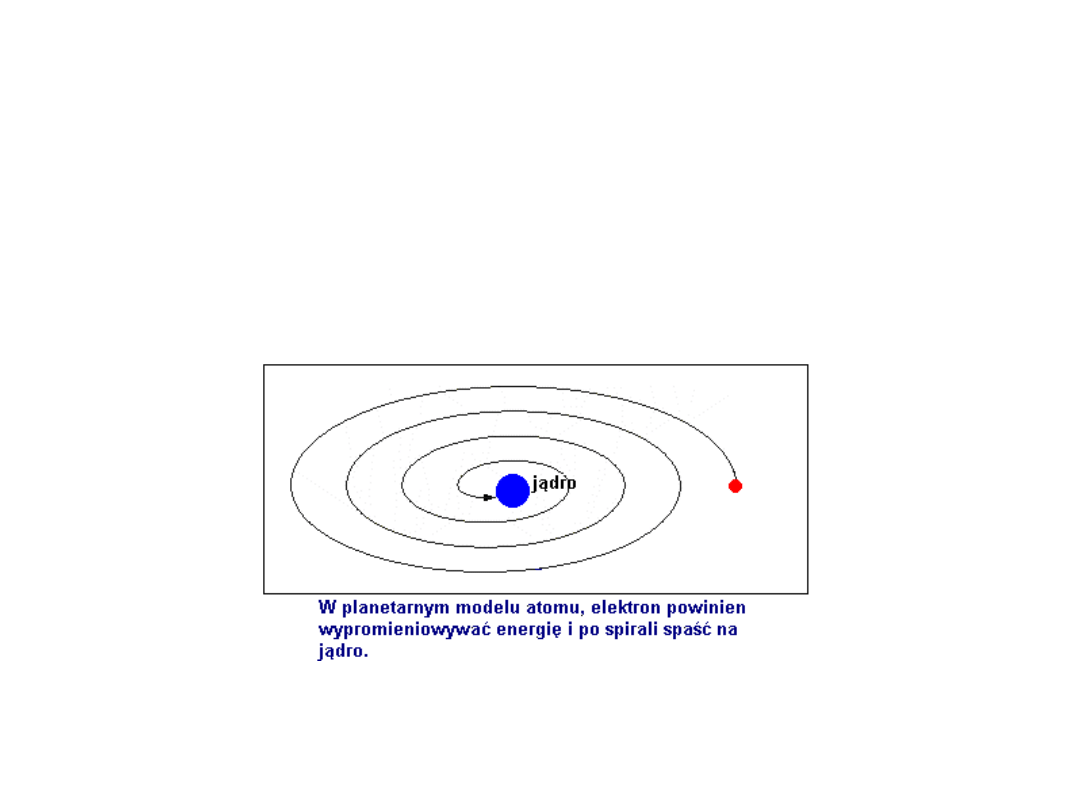
Pojawia się jednak kolejny problem. Krążenie elektronu wokół jądra
powinno być związane z emisją energii, a elektron powinien spadać
na jądro. Stąd wniosek – atom byłby układem nietrwałym.
Tymczasem atomy są układami trwałymi.

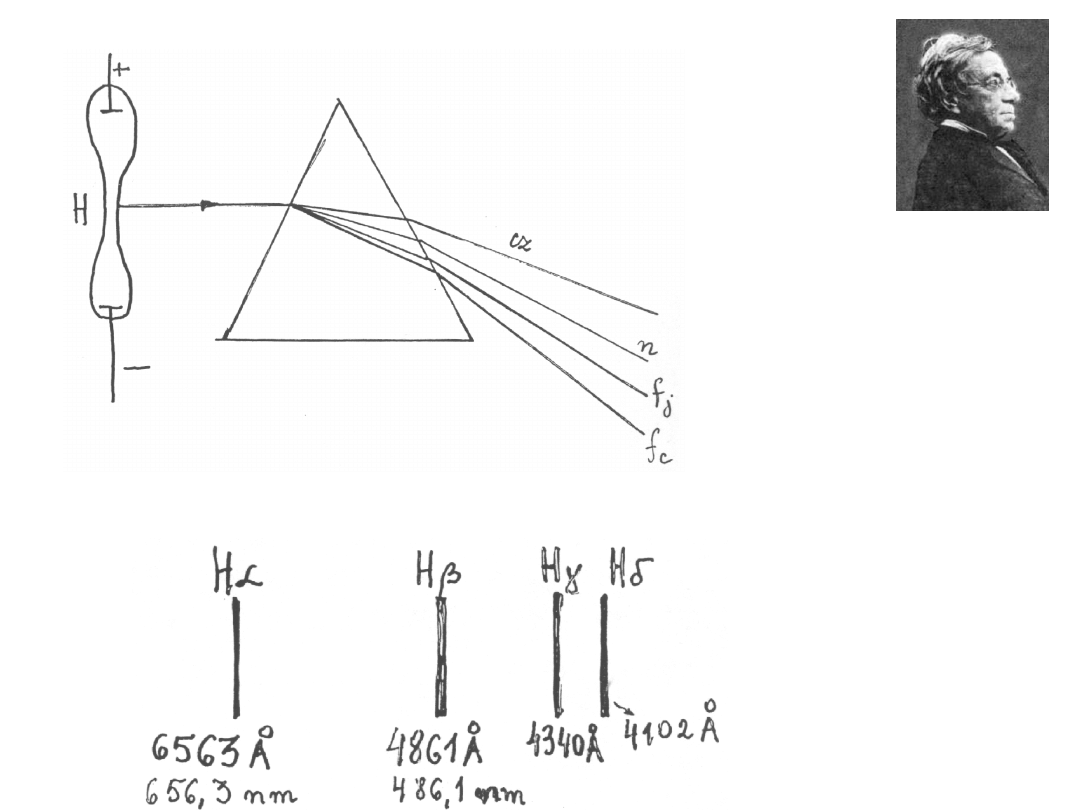
Doświadczenie Balmera

J. Balmer (fizyk szwajcarski) zmierzył długość fali w widmie liniowym wodoru.

Johann Jakob
Balmer

(1825 – 1898)

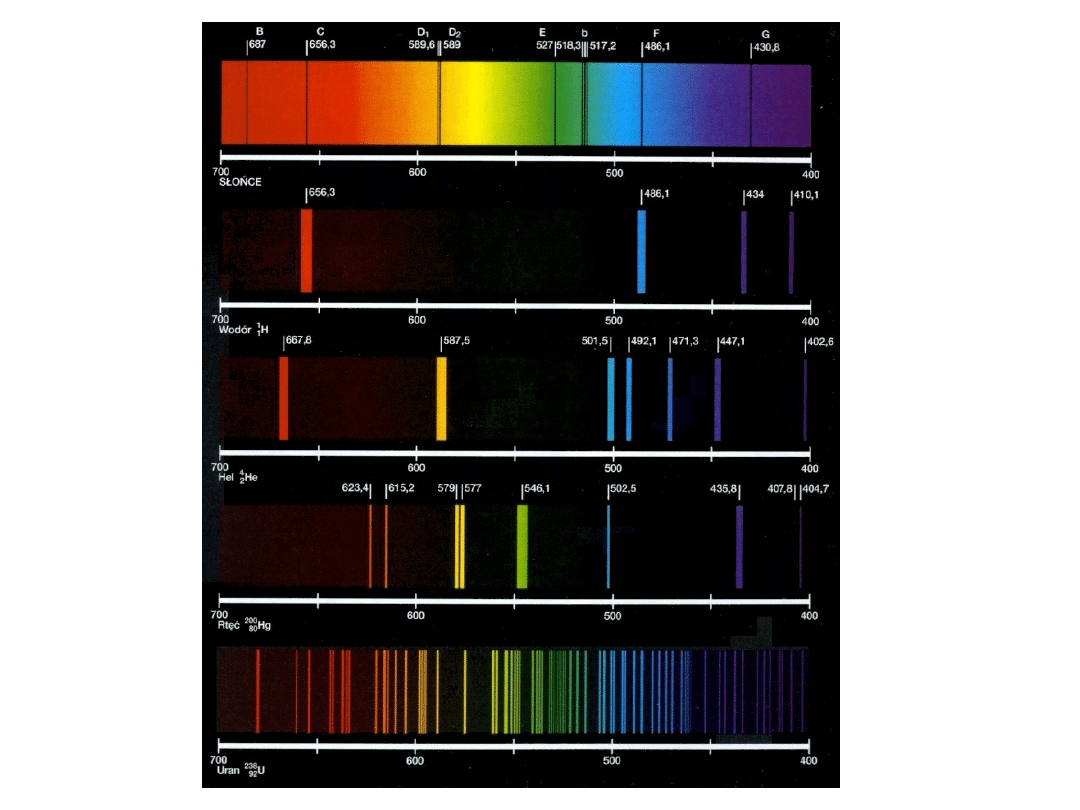
Balmer obliczył, że można te długości fal przedstawić prostym wzorem:

2

2

'

[A]

4

n

R

n

l =

-

o

gdzie:

'

R

 wielkość stała = 3645,6

A

o

n – kolejne liczby całkowite

Wnioski ze wzoru:
1.Widać, że musi być spełniony warunek n  3. Zatem seria przedstawiona

tym wzorem nie może zawierać fal o długościach większych od wartości
otrzymanej dla n = 3 ( = 6563 )

A

o

2.Istnieje najmniejsza, graniczna długość fali określona warunkiem

n��

,

'

R

l �

min

3645,6 A

l

=

o

Jest to tak zwana granica serii.

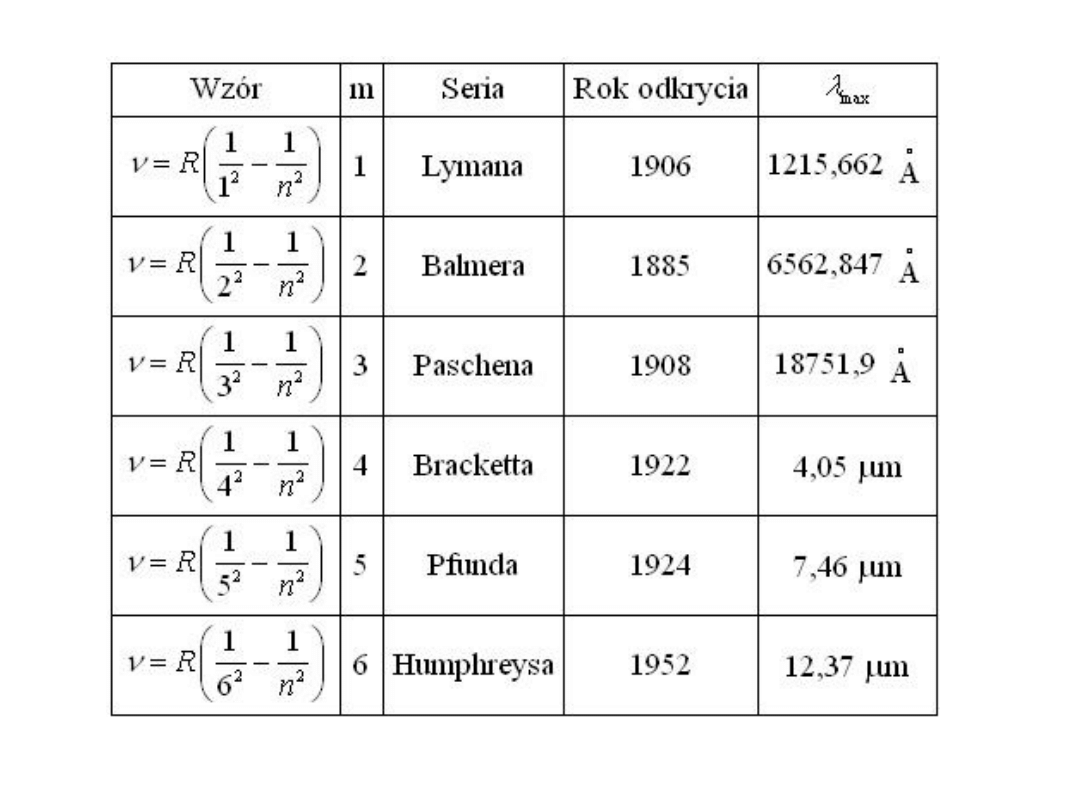
Wzór J. Rydberga:

2

2

1

1

R

m

n

n

�

�

=

-

�

�

�

�

n > m

gdzie:

R – stała Rydberga

Niels Bohr, fizyk duński, w 1913 r. dokonał kolejnej modyfikacji modelu
planetarnego budowy atomu.

Elektrony krążą wokół jądra po pewnych ściśle określonych (tzw.
dozwolonych) orbitach nie promieniując przy tym energii
elektromagnetycznej. W każdym stanie stacjonarnym układ jądro-
elektron ma określoną energię. Pod wpływem czynników zewnętrznych
elektron może przejść na dalszą od jądra orbitę. Wtedy atom jest w
stanie wzbudzonym (o wyższej energii). Jest to stan nietrwały i po czasie
10

-8

s atom wraca do stanu podstawowego (o niższej energii).

Niels Henrik David Bohr

(1885 – 1962)

n

m

hn e e

= -

gdzie:



n

– energia atomu w wyższym stanie energetycznym



m

– energia atomu w niższym stanie energetycznym

Model atomu ulegał dalszym modyfikacjom. Niektóre zjawiska
tłumaczy on w wystarczającym stopniu i w tych przypadkach jest do
dziś stosowany.

Model Bohra stanowił ważny krok (chociaż nie ostatni !) w rozwoju
poglądów na budowę materii.

W czasie takiego przejścia emitowana jest energia kwantu promieniowania:

Model atomu wodoru wg. Bohra

Postulaty Bohra:

1. W układzie atomowym istnieje pewna liczba stanów, w których nie
dochodzi do emisji promieniowania energii, nawet jeśli cząstki poruszają się
względem siebie, a zgodnie z zasadami elektrodynamiki klasycznej
należałoby się spodziewać takiej emisji.
Tego rodzaju stany nazwano stanami „stacjonarnymi”.

2. Każdej emisji lub absorpcji energii promieniowania odpowiada przejście
elektronu pomiędzy dwoma stanami stacjonarnymi. Promieniowanie
emitowane podczas takiego przejścia jest jednorodne, a jego częstość
określana jest zależnością:

2

1

hn e e

= -

gdzie h jest stałą Plancka, a



1

i



2

odpowiadają energiom układu o obu

stanach stacjonarnych.
3. Równowaga dynamiczna układu w stanach stacjonarnych podlega zwykłym
prawom mechaniki. Prawa te nie stosują się do przejść z jednego stanu do
drugiego.
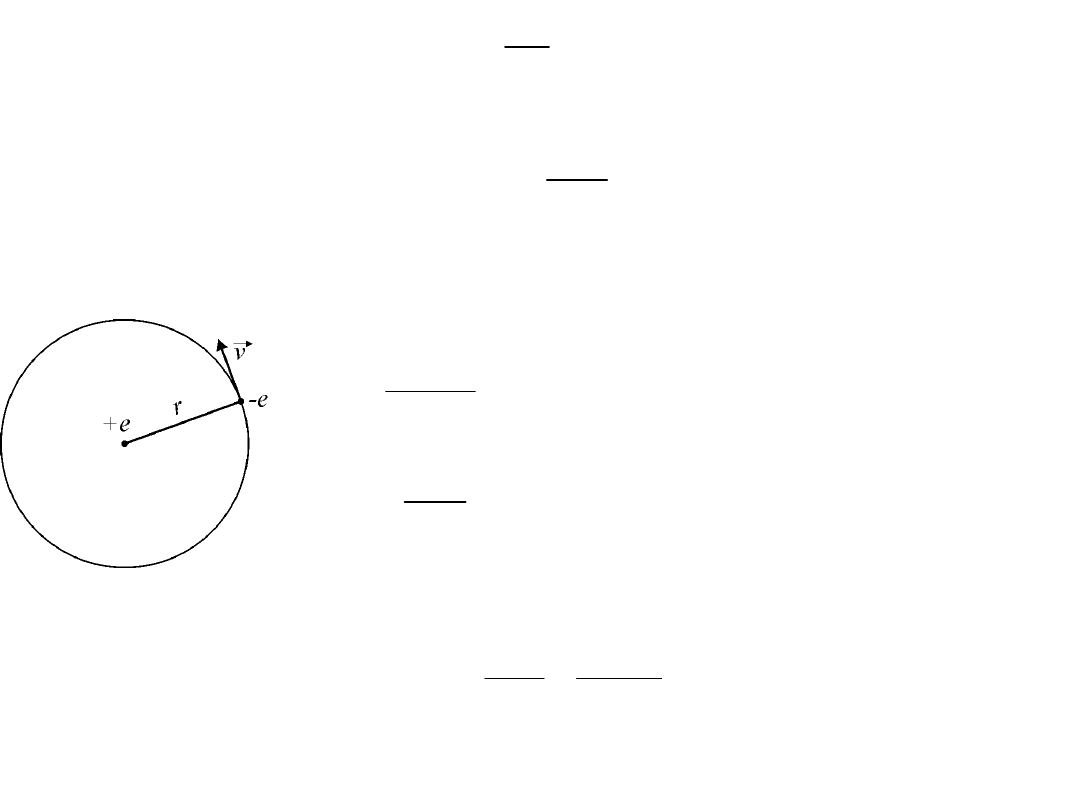
Warunek kwantowy Bohra
W dowolnym układzie atomowym lub cząsteczkowym, składującym się z
dodatniego jądra i elektronów, w którym jądra znajdują się względem siebie
w spoczynku, natomiast elektrony poruszają się po orbitach kołowych,
moment pędu każdego elektronu względem środka jego orbity jest równy
h/2 w „normalnym” stanie układu, to znaczy w stanie, w którym całkowita

jego energia jest minimalna

1

2

h

mvr

p

=

=h

2

n

nh

mvr

p

=

Model atomu wodoru wg. Bohra

2

e

d

mv

F

r

=

2

2

0

4

c

e

F

r

pe

=

siła dośrodkowa

siła kulombowskiego
oddziaływania między
jądrem i elektronem

Siła F

c

pełni rolę siły dośrodkowej.

2

2

2

0

4

e

mv

e

r

r

pe

=

Obliczamy promień toru elektronu:

2

2

0

4

e

e

r

mv

pe

=

(*)

Z warunku kwantowego:

2

nh

mvr

p

=

obliczamy

v

.

2

nh

v

mr

p

=

(**)

Wstawiamy do równania (*) i otrzymujemy:

2

2

0

2

e

h

r

n

e m

e

p

=

�

(***)

r ~ n

2

dla n = 1, r

1

= 0,53

.

10

-10

m

Obliczamy całkowitą energię układu atomowego w n-tym stanie stacjonarnym.

k

p

e e e

= +

gdzie:



k

– energia kinetyczna elektronu



p

– energia potencjalna układu jądro-elektron

2

2

2

0

2

4

e

mv

e

r

e

pe

-

=

+

(****)

2

2

2

0

4

2

e

mv

e

r

r

r

pe

=

�

2

2

0

2

8

e

k

mv

e

r

e

pe

=

=

Wstawiając do wzoru (****) otrzymujemy:

2

2

2

0

0

0

8

4

4

e

e

e

r

r

r

e

pe

pe

pe

=

-

=-

Ale

2

2

0

2

e

h

r

n

e m

e

p

=

�

4

2 2 2

0

8

e

e m

n h

e

e

=-

4

2 2

2

0

1

8

e

e m

h n

e

e

=-

�

1

2

13,6 eV

3,39 eV

e
e

=-

=-

Dla n   r  , ale

ε

 0

Dla n=1

8

Z drugiego postulatu Bohra:

2

1

hn e e

= -

4

4

2 2 2

2 2 2

0

0

8

2

8

1

e

e

e m

e m

h

h

h

n

e

e

�

�

=-

- -

�

�

�

�

4

2 2

2

2

0

1

1

8

1

2

e

e m

h

h

n

e

�

�

=

-

�

�

�

�

{

4

2 3

2

2

0

1

1

8

1

2

e

R

e m

h

n

e

�

�

=

-

�

�

�

�

- wniosek z modelu

2

2

1

1

R

m

n

n

�

�

=

-

�

�

�

�

- wniosek z eksperymentu

Różnica pomiędzy wartością R obliczoną ze wzoru i wyznaczoną
doświadczalnie jest mniejsza od 0,1%.
Wniosek z modelu Bohra zgodny jest z równaniem Rydberga wynikającym z
eksperymentu.

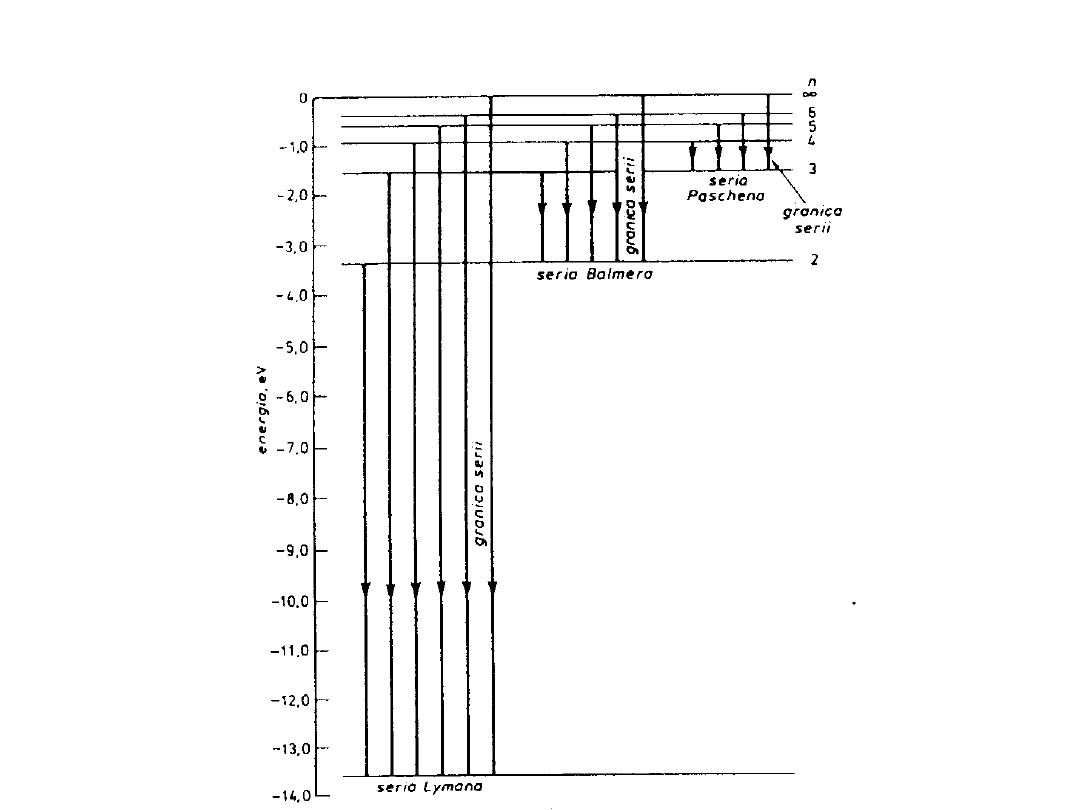
Skwantowane poziomy energetyczne atomu wodoru.

Doświadczenie Francka-Hertza (1914)

1.Doświadczenie Francka-Hertza, wyniki
eksperymentu, wnioski z doświadczenia.

2.Wyjaśnienie wyników doświadczeń na podstawie modelu
skwantowanych poziomów energetycznych.

James Franck (

1882-1964

) i Gustav Hertz (

1887-1975

)

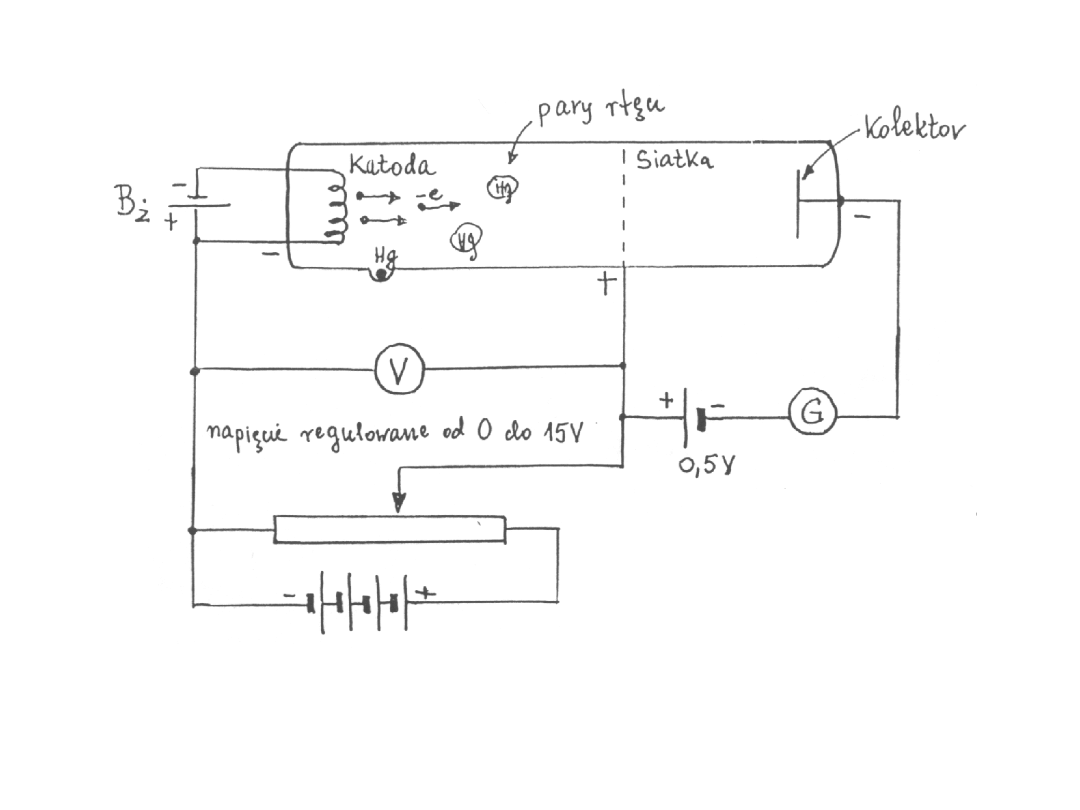
Schemat połączeń

Między katodą i siatką jest pole elektryczne przyśpieszające
elektrony. Między siatką i kolektorem występuje pole elektryczne
hamujące.

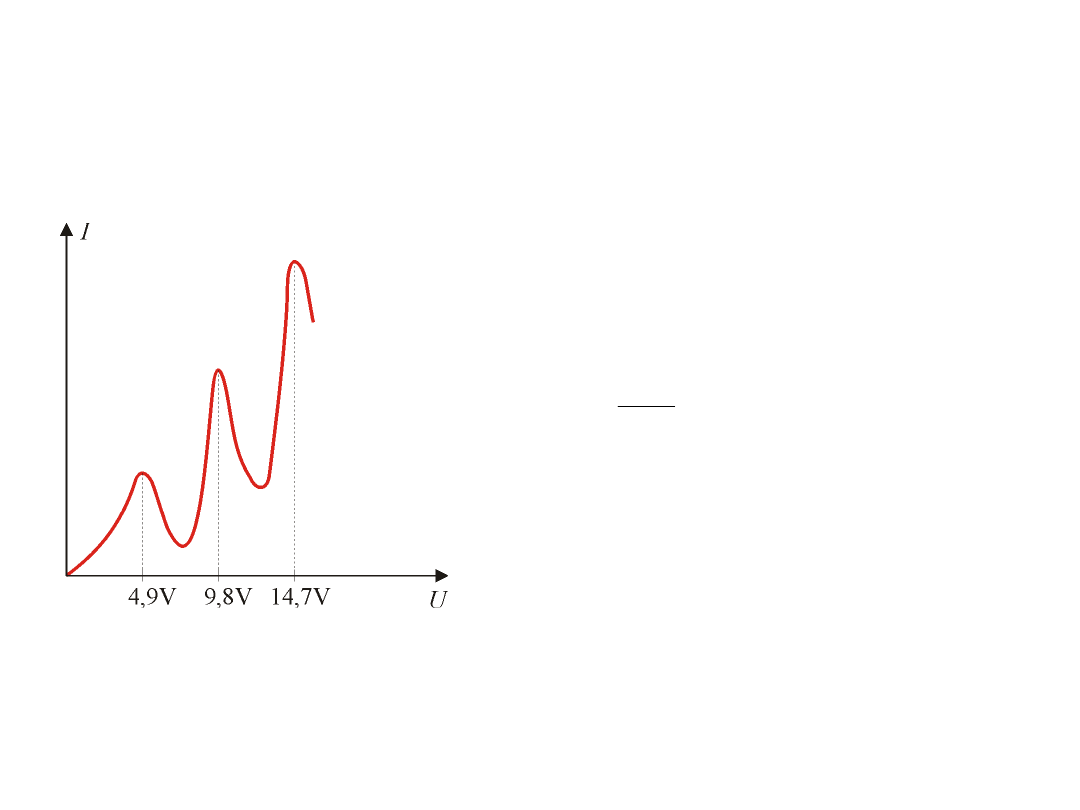
Elektrony poruszając się w polu
elektrycznym między katodą i siatką
uzyskują energię kinetyczną:

2

2

mv

eU

=

1914 r. James Franck, Gustav Hertz

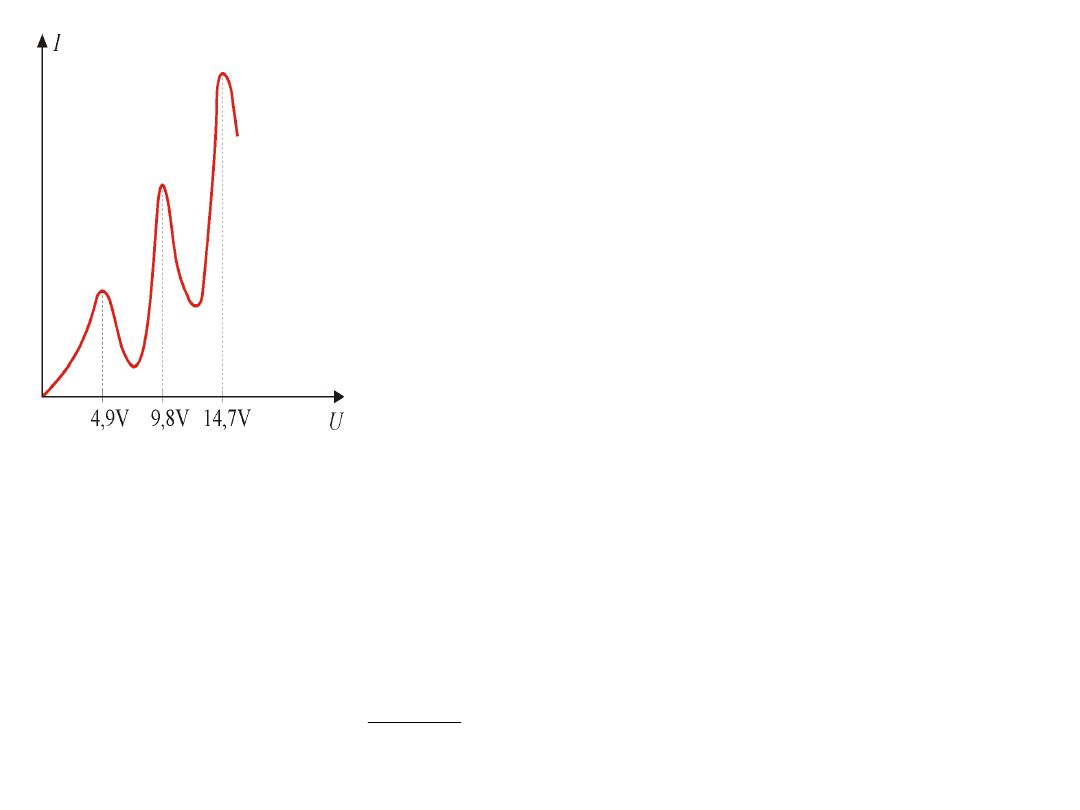
Eksperymenty Francka i Hertza wykonane w rok
po ogłoszeniu postulatów Bohra stanowiły
dowód istnienia skwantowanych poziomów
energetycznych w atomach.
W zakresie napięcia od 0 – 4,9 eV zderzenia
elektronów z atomami rtęci są sprężyste
(zachodzą prawie bez strat energii
elektronów).Przy energii 4,9 eV (napięciu 4,9 V)
pojawiają się zderzenia niesprężyste. Elektron
przekazuje atomom rtęci całą swoją energię.
Przy napięciu 9,8 V elektron na drodze między
K – S doznaje dwukrotnie zderzeń
niesprężystych.

Energia 4,9 eV jest najmniejszą, jaka może być pochłonięta przez atom
rtęci. Zatem pierwszy poziom atomu Hg powinien mieć energię o 4,9 eV
większą niż stan podstawowy. Powrót ze stanu wzbudzonego do
podstawowego wiąże się z emisją kwantu, także o energii 4,9 eV, co
odpowiada długości fali ok. 253,6 nm. Obserwacje potwierdziły
występowanie linii widmowej o tej długości.

 = 253,6 nm

4,9 eV

hc

l =

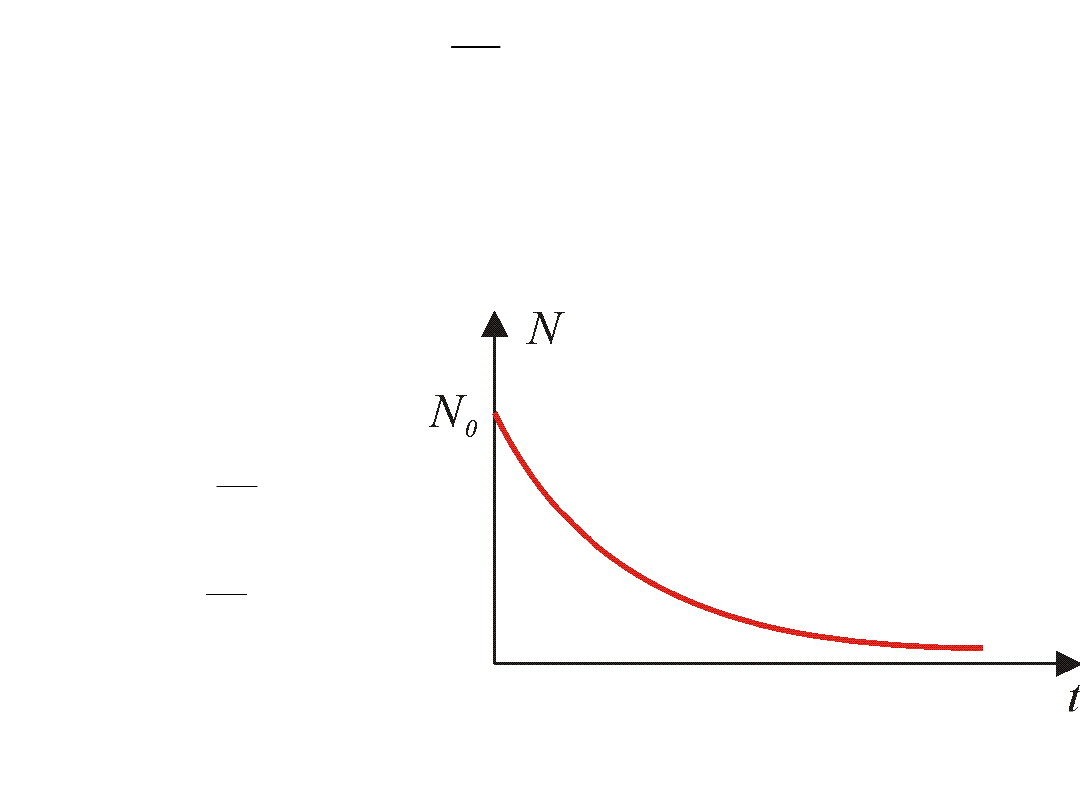
Emisja spontaniczna

Przejście atomów ze stanu wzbudzonego do stanu podstawowego z
emisją fotonu opisuje prawo statystyczne.

Niech w chwili t liczba atomów w stanie wzbudzonym wynosi N.

Oznaczymy:

-dN – ubytek atomów w stanie wzbudzonym
N – aktualna liczba w stanie wzbudzonym
dt – czas, w którym ubyło dN atomów

Możemy zapisać:

dN ANdt

-

=

gdzie:

A – współczynnik proporcjonalności

dN N dt

-

�

:

~

dN

Adt

N

=-

Całkując stronami otrzymujemy:

lnN

At C

=-

+

C wyznaczamy z warunków początkowych – jeśli t = 0, to N = N

0

 lnN

0

= C

Zatem

0

0

0

0

ln

ln

ln

ln

ln

At

N

At

N

N

N

At

N

At

N

N

e

N

-

=-

+

-

=-

=-

=

0

At

N N e

-

=

�

Liczba atomów w stanie wzbudzonym maleje wykładniczo.

Wzbudzanie atomów i cząsteczek

Sposoby wzbudzania atomów i cząsteczek:

1.wzbudzanie optyczne
2.wzbudzanie termiczne
3.wzbudzanie elektryczne
4.wzbudzanie chemiczne

*

2

2

*

1

2

2

A

A

A

A

h

mv

mv

e

n e

e

e

+ =

+

= +

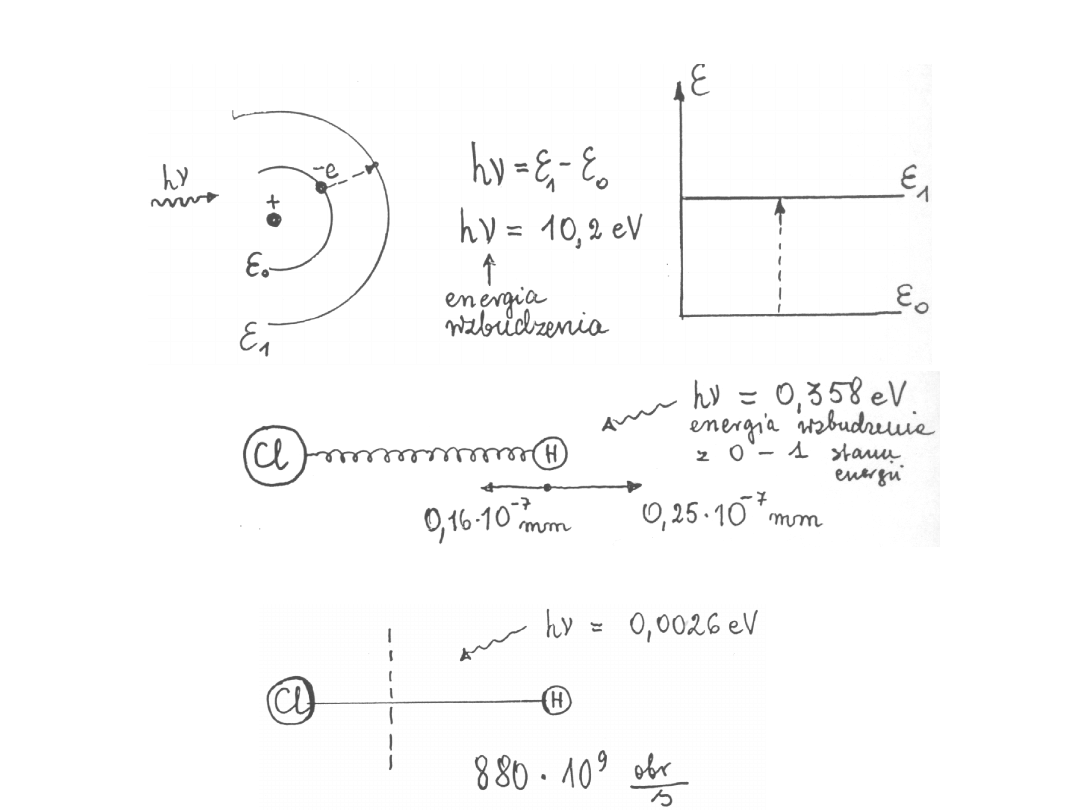
Rodzaje wzbudzeń:

1.

2.Oscylacje

3.Rotacje

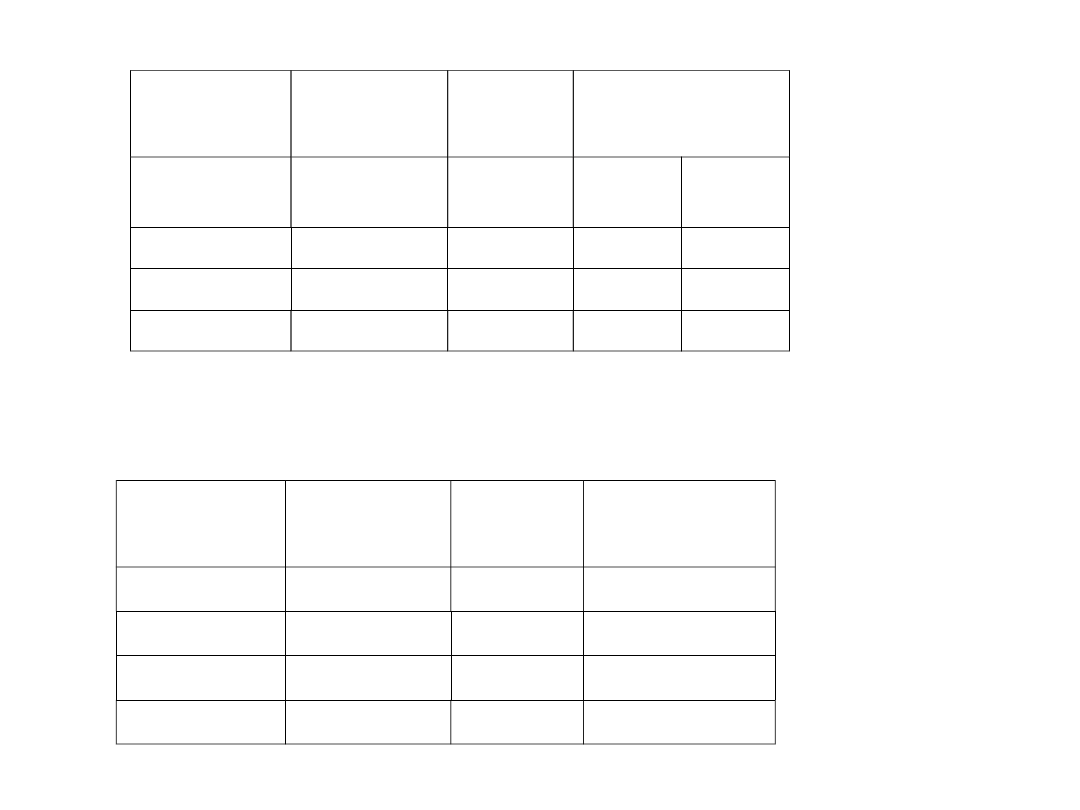
Oscylacje

Zmiana

stanu

Niezbędny

kwant

energii

Osiągnięt

y

stan

Amplitudy

w 10

-7

mm

0

0,15

0,10

0 – 1

0,358 eV

1

0,25

0,16

1 – 2

0,345 eV

2

0,33

0,20

2 – 3

0,333 eV

3

0,39

0,23

Rotacje

Zmiana stanu

Niezbędny

kwant energii

Osiągnięt

y

stan

Liczba obrotów

w czasie 10

9

/s

0 – 1

0,0026 eV

1

880

1 – 2

0,0051 eV

2

1520

2 – 3

0,0077 eV

3

2150

3 – 4

0,0103 eV

4

2770

Pierwiastek

Energia wzbudzania

Energia jonizacji

H

10,2 eV

13,6 eV

He

19,8 eV

24,6 eV

Hg

0

4,9 eV

10,4 eV

Na

0

2,1 eV

0

5,1 eV

K

0

1,6 eV

0

4,3 eV

Cs

0

1,5 eV

0

3,9 eV

Pb

0

1,2 eV

0

7,4 eV

Diamagnetyzm

Zastosowanie modelu Bohra do wyjaśnienia zjawiska diamagnetyzmu.

Moment magnetyczny prądu kołowego związanego z ruchem elektronu
względem jądra przedstawia wzór:

2

[A m ]

m

p

I S

= �

�

gdzie:

I – natężenie prądu
S – powierzchnia objęta orbitą elektronu

Ale

2

e

I

T

S

r

p

=

=

e – ładunek

elektronu

T – okres

obiegu

r – promień

orbity

Stąd:

2

2

2

2

m

m

e

p

r

T

r

T

v

ev

p

r

r

p

p

p

p

=

=

=

2

m

evr

p =

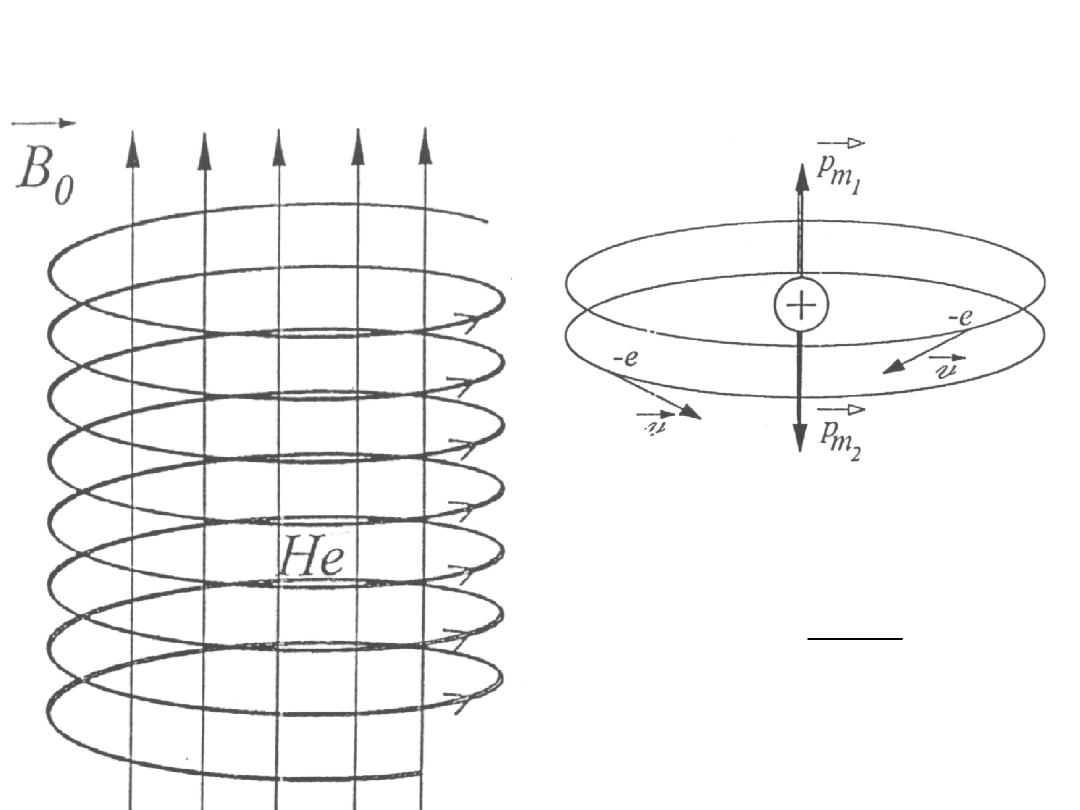
Diamagnetyzm He

2

m

evr

p =

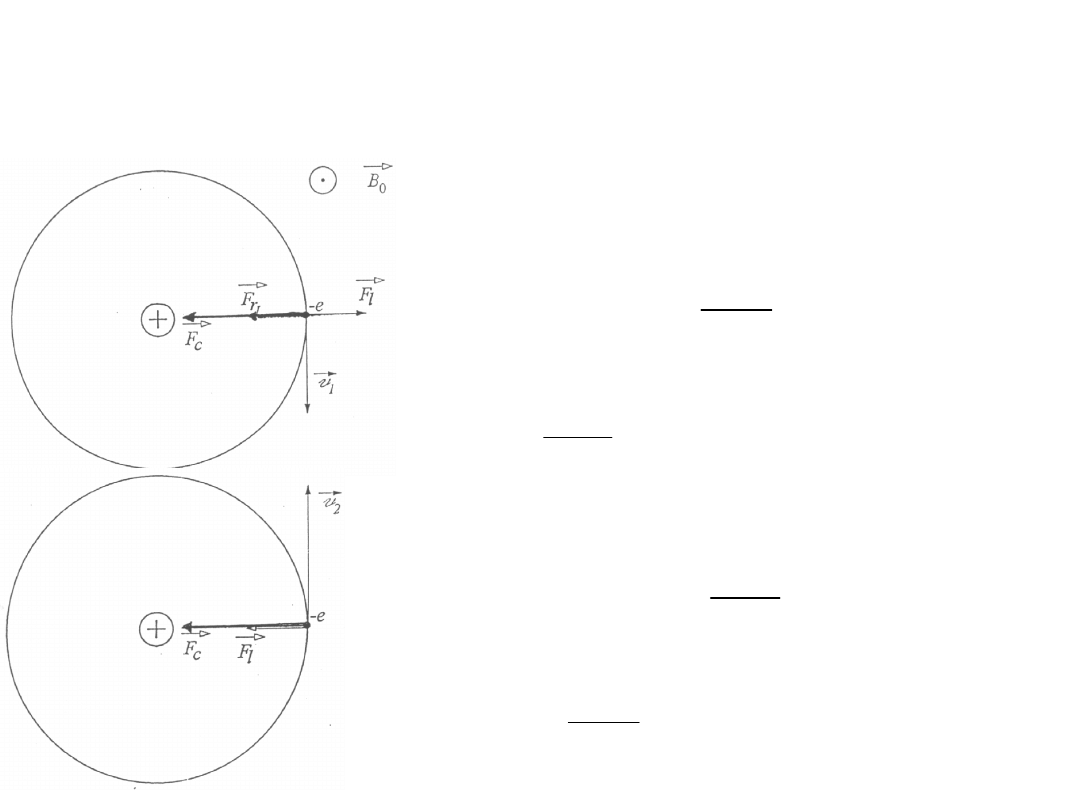
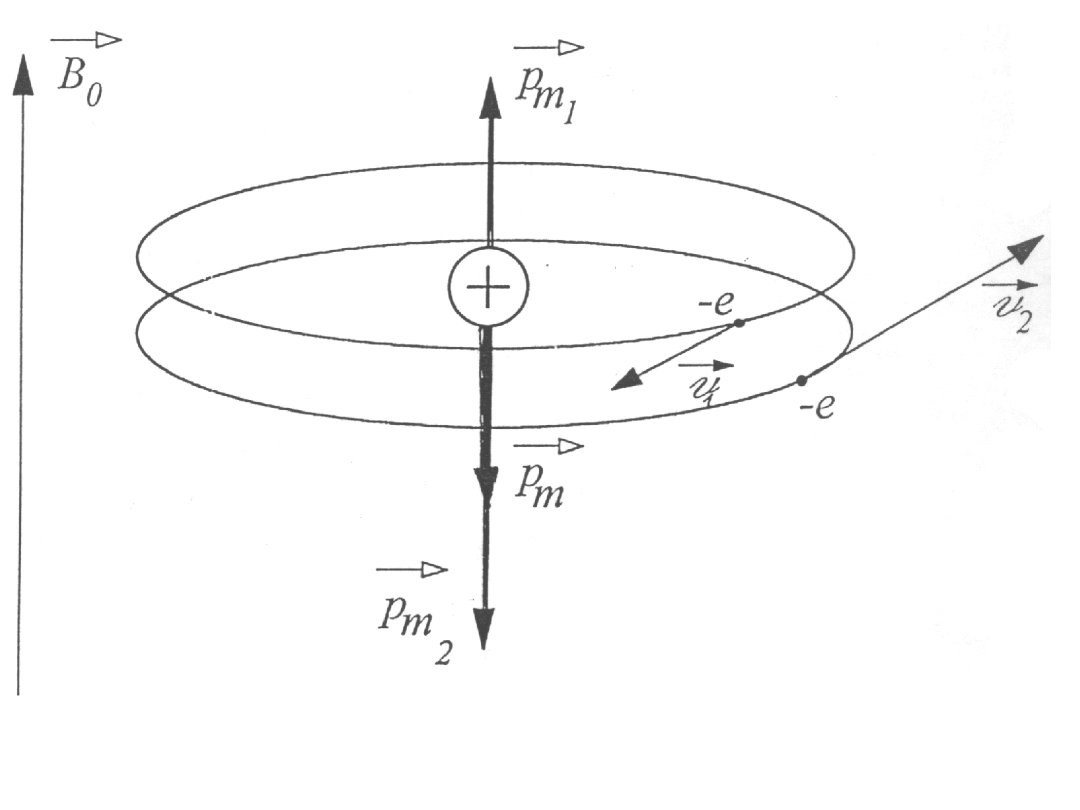
Zgodnie z modelem Bohra w atomie He elektrony krążą wokół jądra po

orbitach o tym samym promieniu i tej samej wartości prędkości, ale w

przeciwne strony.

Zatem

1

2

0

m

m

m

p

p

p

=

-

=

2

1

1

2

I

r

c

l

I

mv

F

F F

r

evr

p

= -

=

=

2

2

2

2

II

r

c

l

I

mv

F

F F

r

ev r

p I

= + =

=

Siły

I

r

F

i

II

r

F

równe są różnicy (I) lub sumie (II) sił: kulombowskiej F

c

i

Lorentza F

l

, które pełnią rolę sił dośrodkowych.

2

1

2

1

m

m

v

v

p

p

>

>

2

1

2

m

m

m

m

p

p

p

M n p

M

H

c

=

-

= �

= �

r

r

r

r

2 2

0

2 2

0

2

2

e r n

M

H

m

e r n

m

m

m

c

=-

=-

r

r

9

1,2 10

He

c

-

=-

�

z modelu teoretycznego

9

2,25 10

He

c

-

=-

�

z eksperymentu

Obliczamy p

m

2

2

1

1 0

2

0

2

2

2

2 0

2

0

2

4

2

4

I

II

r

c

l

r

c

l

e

mv

F

F F

evB

r

r

e

mv

F

F F

ev B

r

r

pe

pe

= -

=

-

=

= + =

+

=

Widać, że

2

1

v

v

>

Stronami otrzymujemy:

2

2

2

2

2

1

2 0

1 0

2

2

0

0

0

2

1

2

2

4

4

(

)

e

e

mv

mv

ev B

evB

r

r

r

r

eB v v

pe

pe

+

-

+

=

-

+

2

1

(

)

m

v v

r

=

+

2

1

0

2

1

(

)

v v

eB r

v v

m

-

-

=

Ale

2

1

2

1

2

2

(

)

2

m

m

ev r evr

p

er

p

v v

=

-

=

-

Podstawiamy

0

0

0

2 2

0

;

2

2

m

m

er eB r

p

B

H

m

e r

H

p

m

m

m

=

=

=

r

r

2 2

0

2

m

e r

H

p

m

m

=-

r

r

„-” bo zwroty

m

p

r

i

H

r

są przeciwne

2 2

0

2

m

e r n

M np

H

m

m

=

=-

r

r

r