1

1

ELEKTROTECHNIKA  II

WYKŁAD I

        

prof. dr hab. inż. T. Niedziela

 

 

2

2

Literatura

1. Bolkowski S.: Elektrotechnika.  Wydawnictwo 
Szkolne i Pedagogiczne Spółka Akcyjna, 
Warszawa 1993.
2. Bolkowski S.: Elektrotechnika teoretyczna, Tom 
1, Teoria obwodów elektrycznych. Wydawnictwo 
Naukowo – Techniczne, Warszawa 1986.
3. Goźlińska E. Maszyny elektryczne. 
Wydawnictwo Szkolne i Pedagogiczne Spółka 
Akcyjna, Warszawa 1995r.
4. Lucyk C. Zasady energoelektryki. Oficyna 
Wydawnicza Politechniki Warszawskiej, 
Warszawa 2000.
5. Lucyk C. Elektrotechnika podstawowa, 
Warszawa 2006. – 

http://www.it.pw.edu.pl/

-

clucyk 

 

 

3

 

 

4

• Sygnałem 

 nazywamy funkcję, 

opisującą wielkość fizyczną, którą 
może być napięciem lub prądem 
elektrycznym.

 

 

5

Sygnały elektryczne dzielimy na:

 Ciągłe w czasie

  jednokierunkowe

 stałe
 zmienne

 Dyskretne w czasie

 nieokresowe
 okresowe (periodyczne)

 przemienne

 sinusoidalne
 niesinusoidalne

 tętniące

 

 

6

Co to jest sygnał 

jednokierunkowy?

Sygnałem jednokierunkowym 

nazywany taki sygnał, którego zwrot 
nie ulega zmianie w funkcji czasu

Kolejny slajd przedstawia przykłady 

sygnałów jednokierunkowych.

 

 

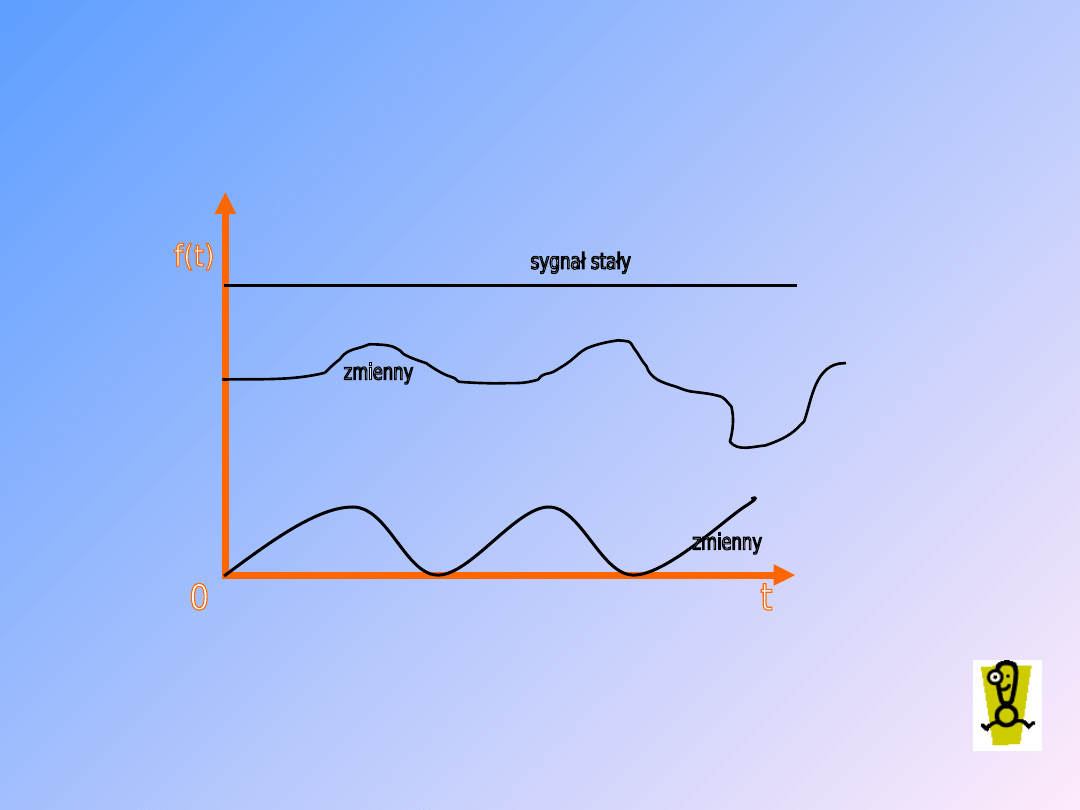
7

Przykład sygnałów 

jednokierunkowych

 

 

8

Co to jest sygnał zmienny?

Sygnałem zmiennym

 nazywamy taki sygnał, 

dla którego w funkcji czasu ulega zmianie 

jego wartość liczbowa przy niezmiennym 

zwrocie, zmienia się zwrot przy niezmiennej 

wartości liczbowej lub ulega zmianie 

zarówno zwrot jak i wartość liczbowa

Kolejne slajdy przedstawiają przykłady 

wykresów sygnałów zmiennych opisanych w 

definicji.

 

 

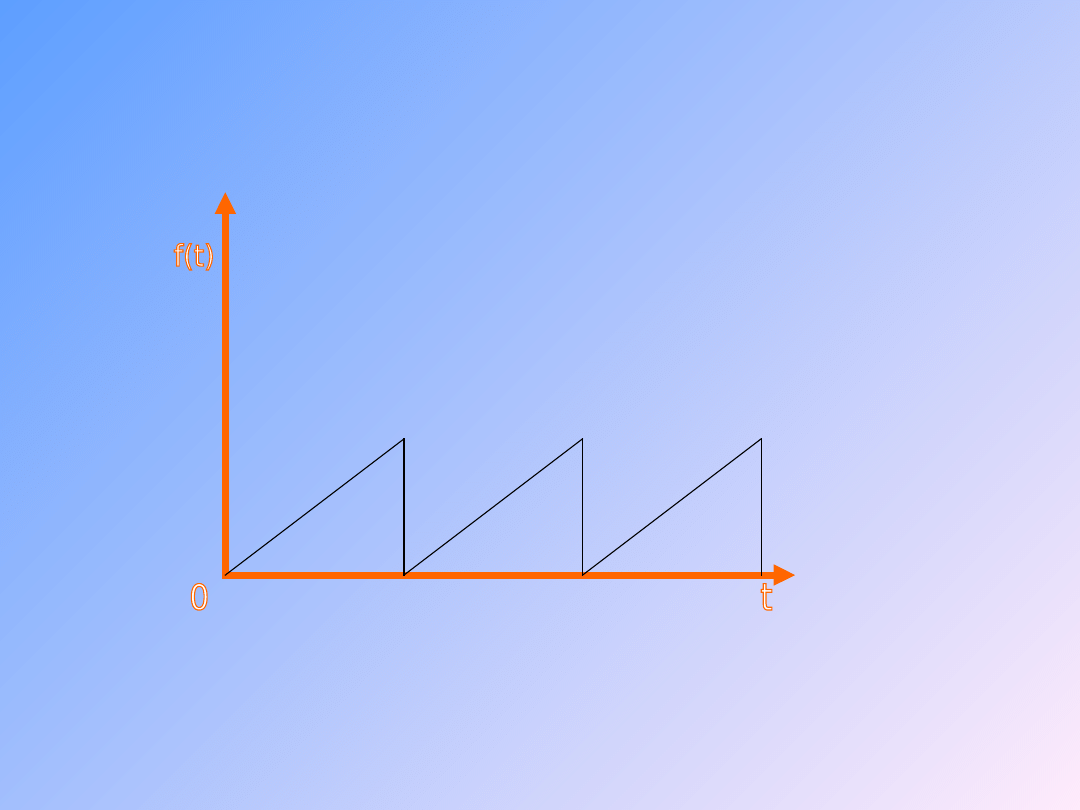
9

Przykłady sygnałów 

zmiennych

Zmiana wartości liczbowej przy stałym zwrocie

 

 

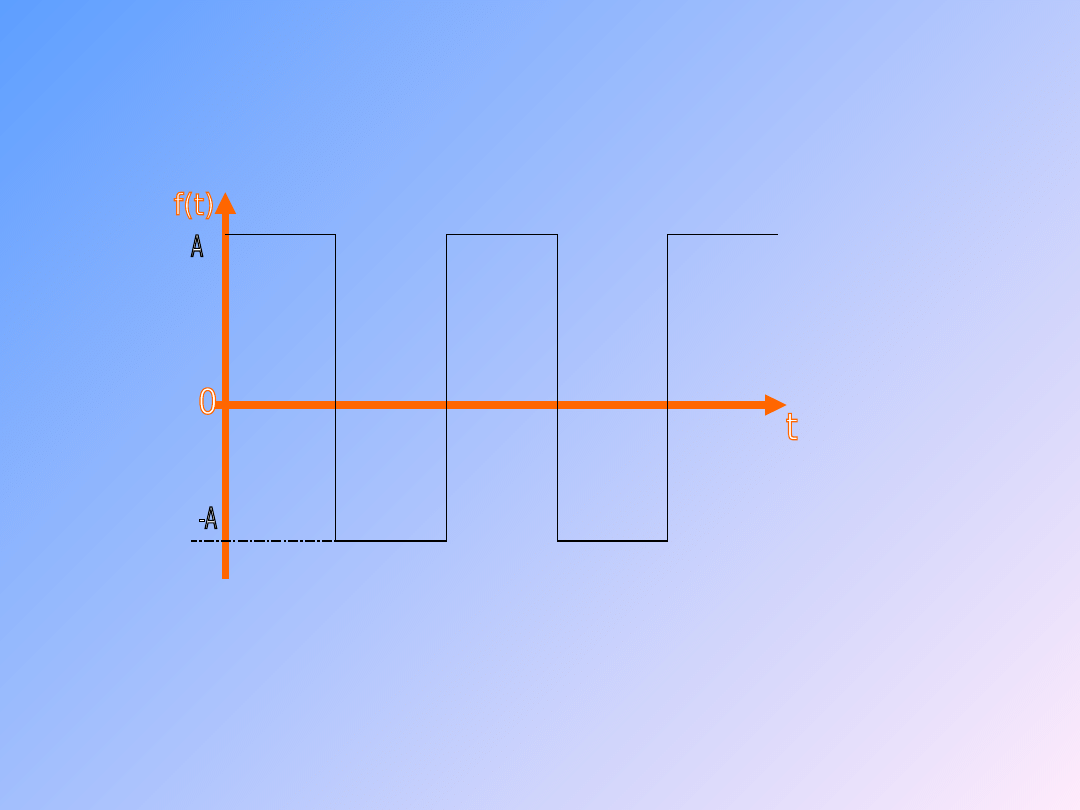
10

Przykłady sygnałów 

zmiennych

Zmiana zwrotu przy niezmiennej wartości liczbowej 

 

 

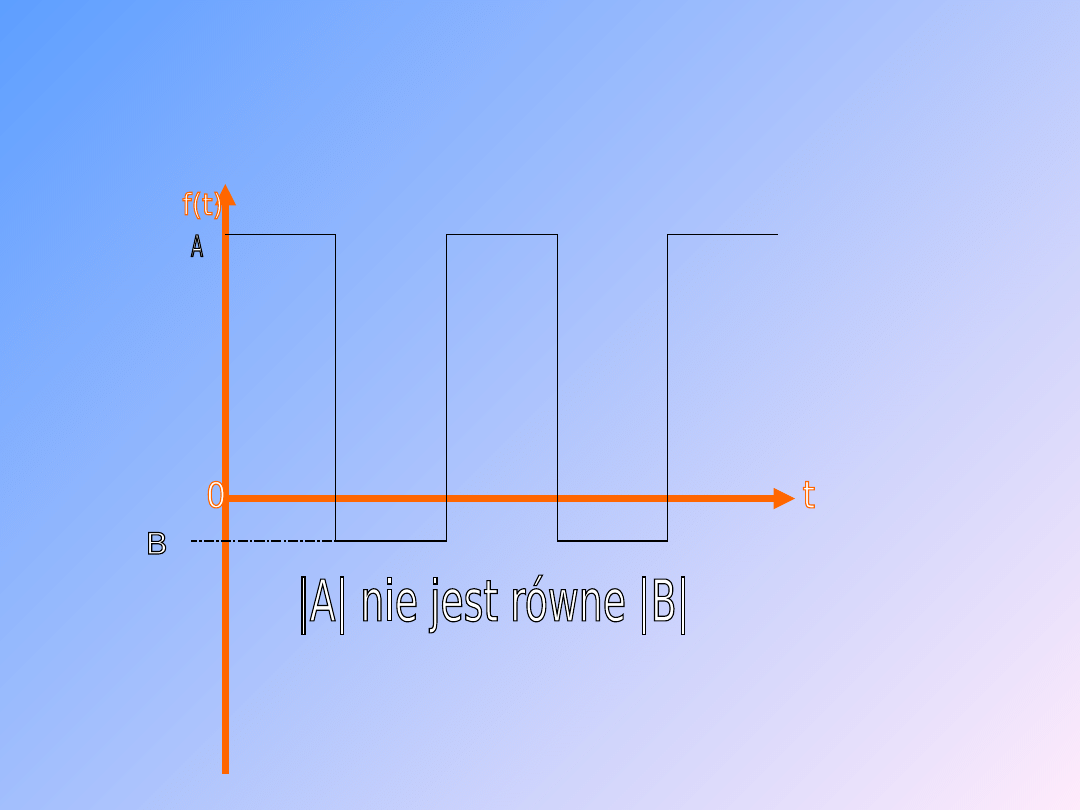
11

Przykłady sygnałów 

zmiennych

Zmiana zwrotu i wartości liczbowej

 

 

12

Co to jest sygnał okresowy?

Sygnał nazywamy okresowym 

lub 

periodycznym

, jeśli powtarza się on w równych 

odstępach czasu (tak zwanych okresach ).

- Okres 

jest to najmniejszy przedział czasu w 

którym sygnał się powtarza. (oznacza się go 

literą 

T

 )

- Zaś 

częstotliwość

 to odwrotność okresu czyli 

f=1/T

 i mierzona jest w hercach (1 Hz) 

 

 

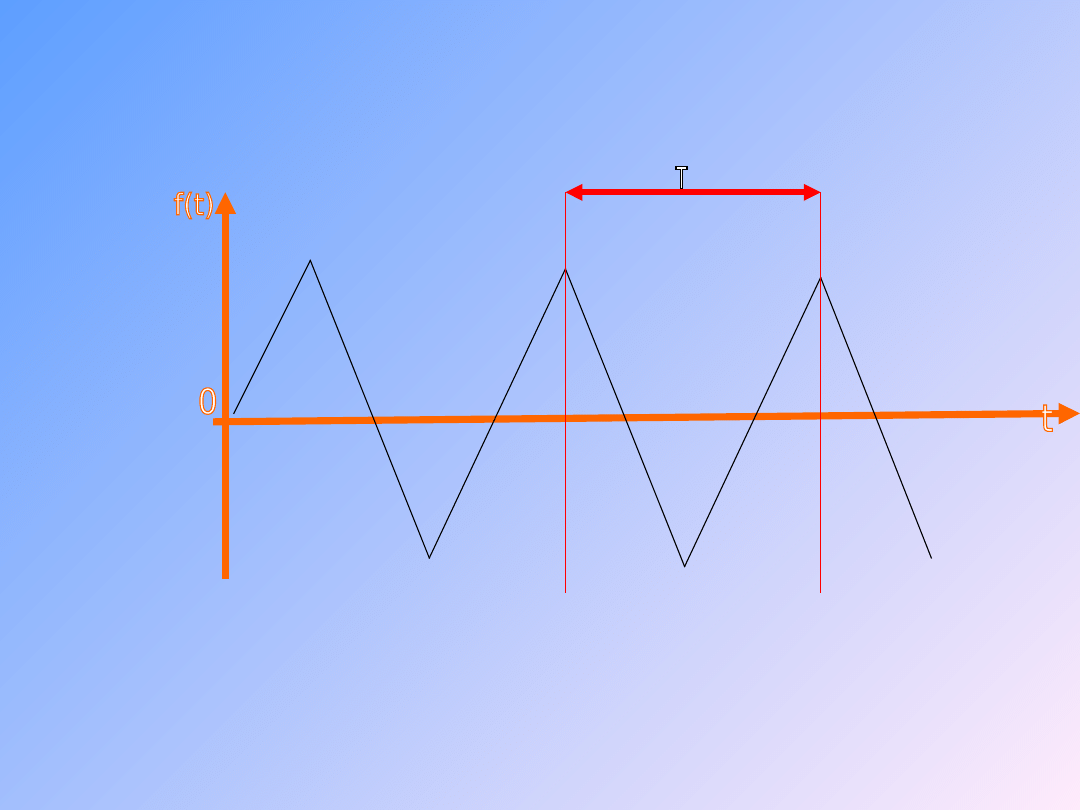
13

Przykład sygnału 

periodycznego

 

 

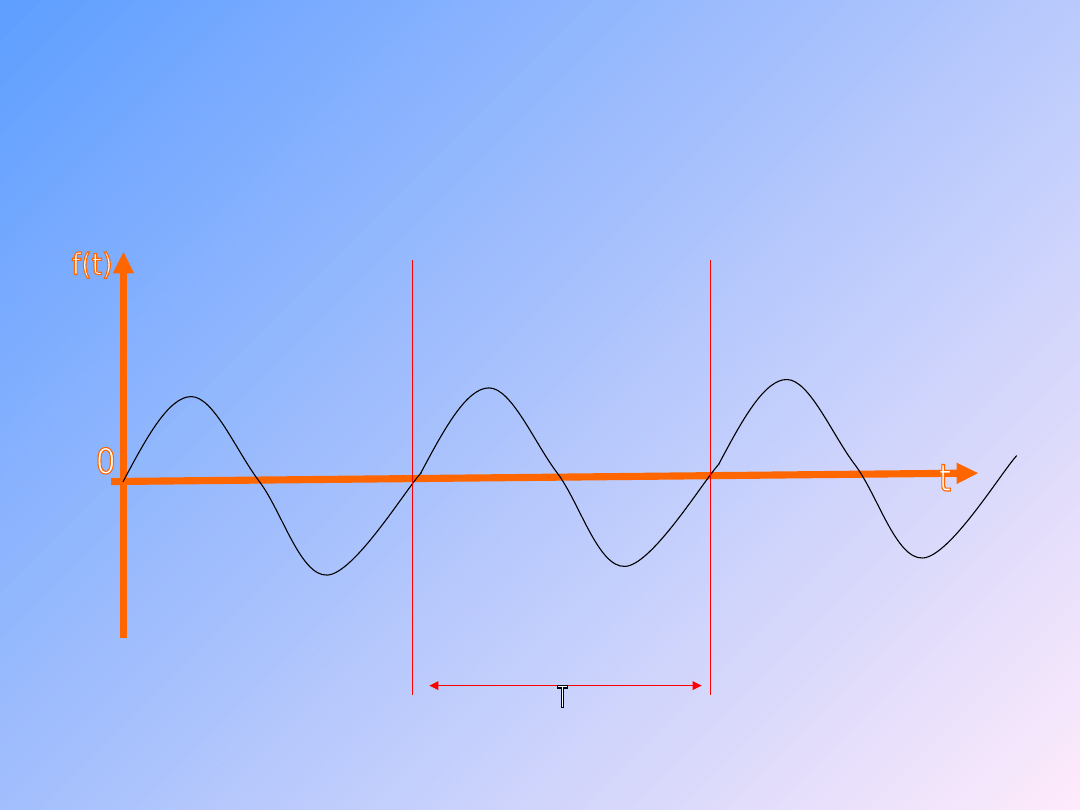
14

Przykład sygnału 

periodycznego sinusoidalnego

 

 

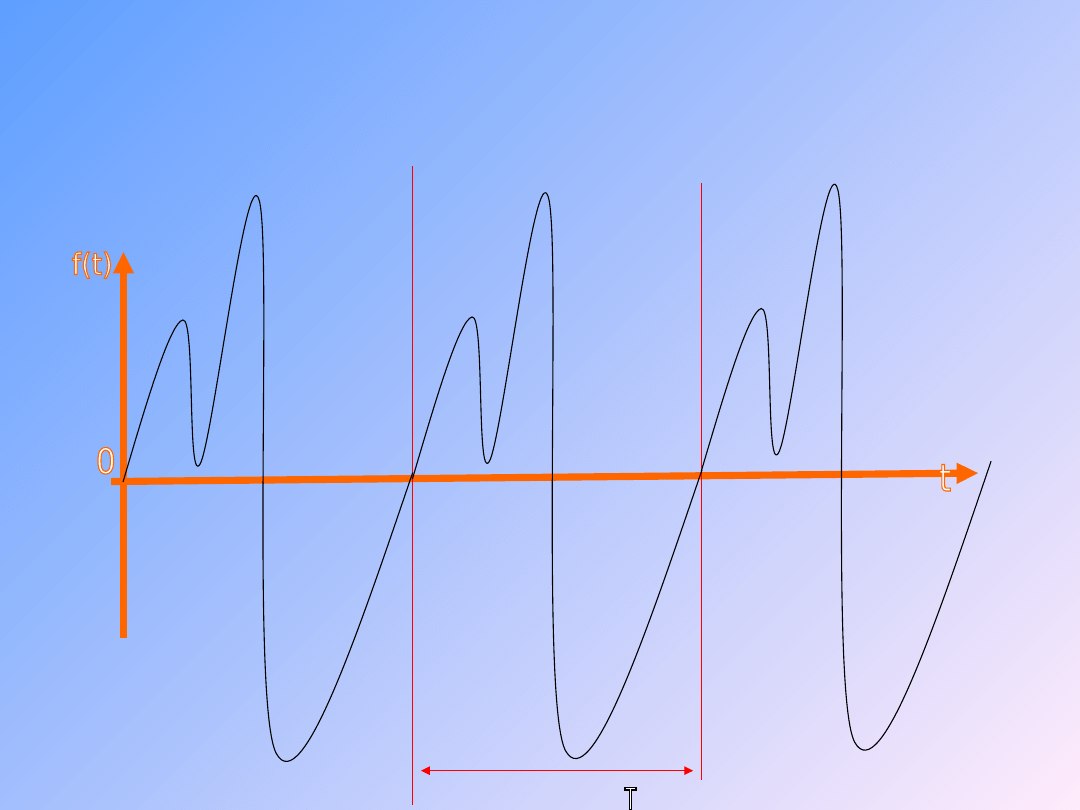
15

Przykład sygnału 

periodycznego 

niesinusoidalnego 

(przemienny)

-

+

∫

(t)dt=0

0

T

 

 

16

A co to znaczy że sygnał jest 

przemienny?

• Sygnał okresowy nazywamy 

przemiennym 

gdy pole powierzchni ograniczonej przebiegiem 

sygnału w ciągu okresu T jest równe zeru:

• Czyli pole „ponad” osią t jest równe polu „pod” 

osią t w obszarze okresu  sygnału. Co widać 

było na poprzednim  slajdzie

• Jeśli sygnał nie jest sygnałem przemiennym to 

jest 

sygnałem tętniącym

, bo nie spełnia 

równania

∫(t)dt=0

0

T

∫

(t)dt=0

0

T

 

 

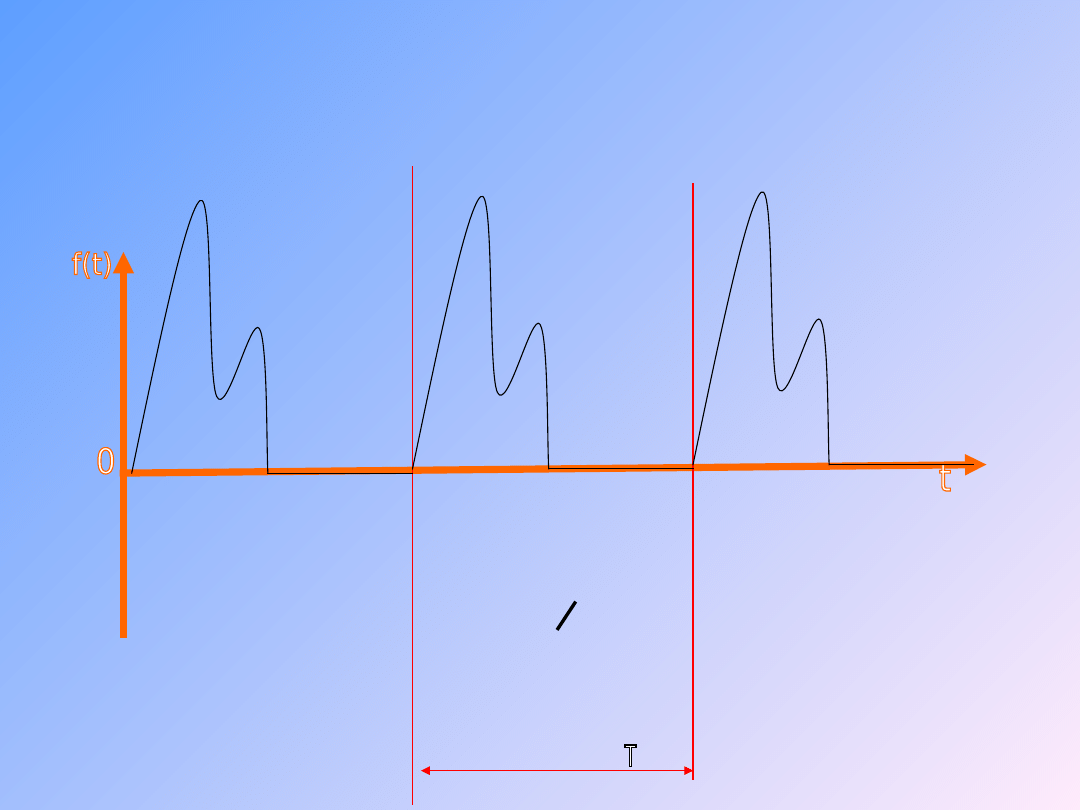
17

Przykład sygnału 

periodycznego tętniącego

∫(t)dt = 0

0

T

 

 

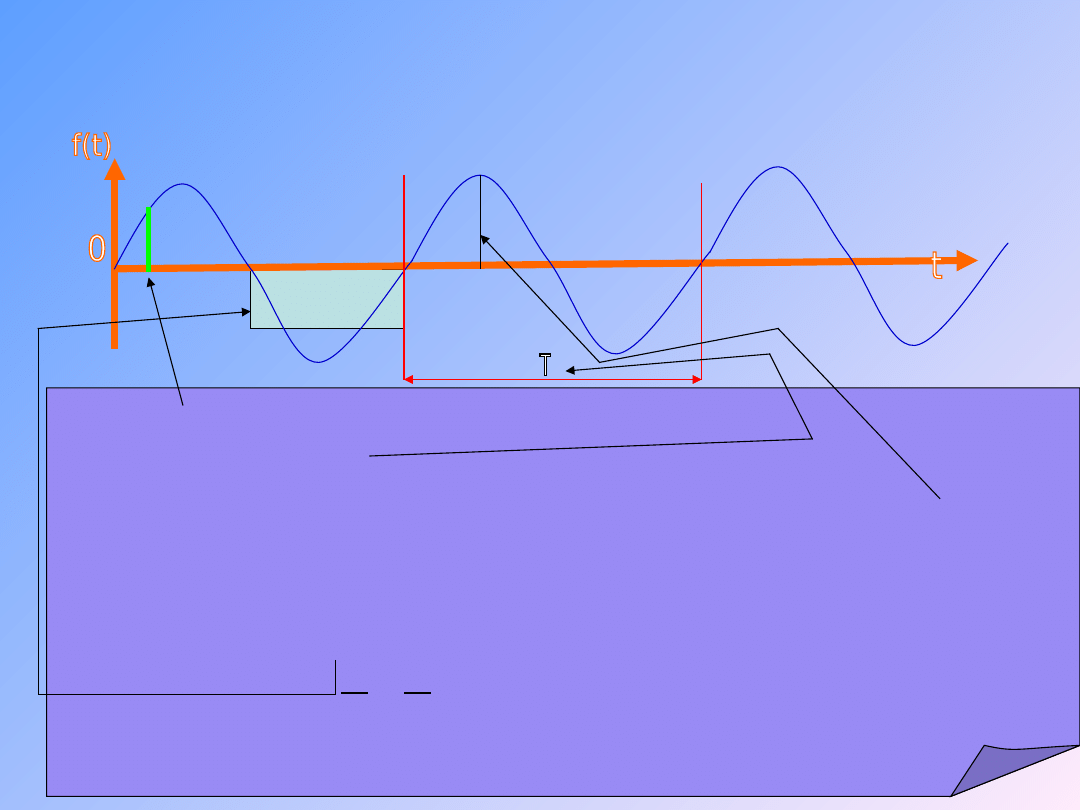
18

Wielkości charakteryzujące 

sygnały okresowe 

x(t) – 

wartość chwilowa

 czyli, taka która występuje w danej chwili

T – 

okres funkcji okresowej

.

F

m

 – 

wartość szczytowa sygnału

 jest to największa wartość chwilowa, 

jaką sygnał osiągnął w danym przedziale  (jeśli sygnałem tym jest np. 
y=sin(x) a badamy obszar okresu T to wartość szczytowa będzie wynosiła 
1 )

I

śr

 – 

wartość średnią półokresową sygnału okresowego

 o okresie T 

nazywamy średnią arytmetyczną  obliczaną dla połowy okresu. 
Interpretacja graficzna została zaznaczona na rysunku:

                                        

F

śr, p 

= f(t ) = 2/T

∫

f(t)dt  - wartości średniej 

okresowej

Występuje też pojęcie 

wartości średniej okresowej (

 

F

ś, c 

= f(t ) = 

1/T

∫

f(t)dt)

 które jest analogiczne do definicji wartości średniej 

półokresowej.  

T/2

0

 

 

19

Wartość skuteczną sygnału okresowego

 

o okresie T nazywamy pierwiastek 

kwadratowy z wartości średniej kwadratu 

sygnału obliczonej dla jednego okresu T

F=   1/T∫f (t)dt

Wartość skuteczną prądu sinusoidalnego

 można rozumieć  jako 

wartość prądu stałego która wytworzy taką samą ilość ciepła na 

rezystorze co prąd sinusoidalny na tym samym rezystorze w tym 

samym czasie.  

2

t

0

 

 

t

f

dt

t

f

T

F

T

2

0

2

1







 

 

20

• Współczynnik szczytu

 

sygnału okresowego 

nazywamy stosunek wartości 
szczytowej do jego wartości 
skutecznej.

• Współczynnik kształtu

   

sygnału okresowego 

nazywamy stosunek wartości 
skutecznej sygnału do jego 
wartości średniej.

 

 

21

 

Współczynnikiem szczytu

 

k

sz

 

sygnału 

okresowego nazywamy stosunek wartości 
maksymalnej F

m

 (szczytowej)  sygnału do jego 

wartości skutecznej F.

        

np:

 

Współczynnikiem kształtu

 

k

k

 

sygnału 

okresowego nazywamy stosunek wartości 
skutecznej sygnału F do jego wartości średniej .

np:

 

 

F

m

F

sz

k 

U

u

u

sz

k

I

i

i

sz

k

max

,

max

,





 

t

f

F

k

k 

)

(

,

t

i

I

i

k

k



 

 

22

 

Wartością średnią całookresową 

sygnału 

okresowego o okresie T nazywamy średnią 
arytmetyczną tego sygnału obliczoną dla 
jednego okresu T.

 

 





T

dt

t

f

T

t

f

0

1

 

 

23

Sygnał w postaci 

wykładniczej

• Rysunek przedstawia wektor wirujący na 

płaszczyźnie zespolonej

• e    -  operator obrotu
• I

m

 – moduł wektora

Re

Im

ω

ωt

T=0

I

m

e

jωt

jωt

Warto zwrócić uwagę 
na to iż każdy sygnał 
może być wyrażony w 
postaci sumy funkcji 
wykładniczych

I(t)=I

m

 cos ωt +j I

m

 sin ωt 

Część 

rzeczywi

sta

Część 

urojona

 

 

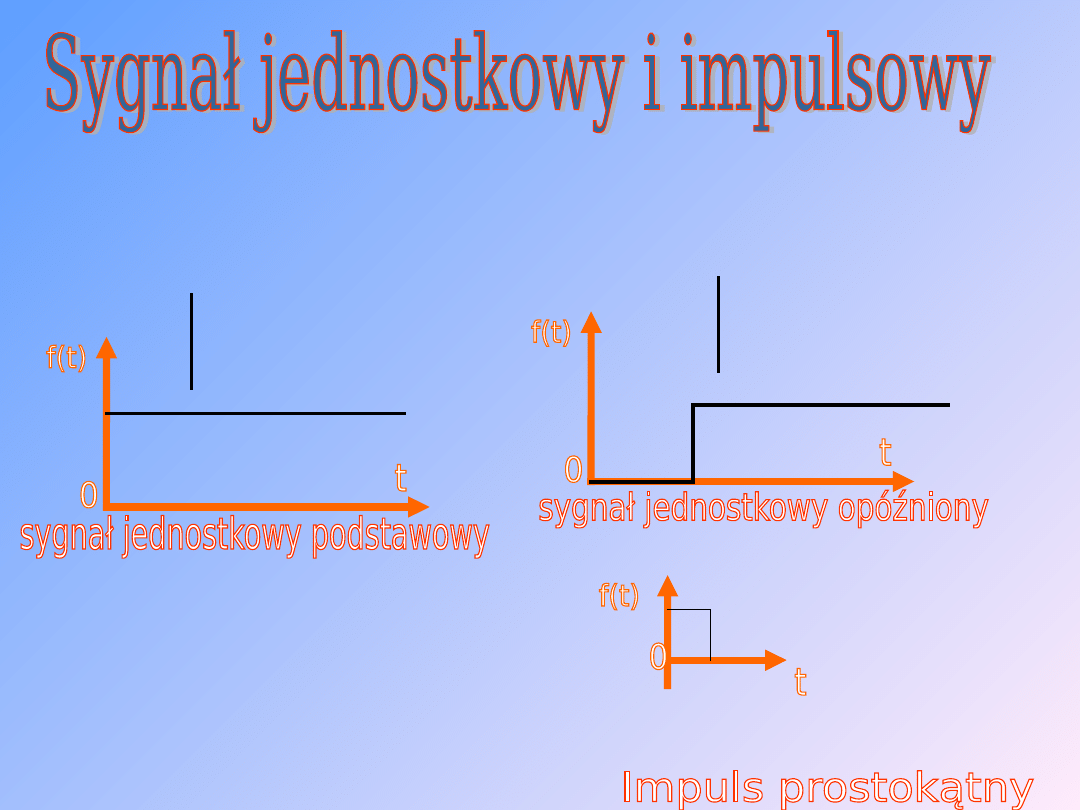
24

• Funkcję jednostkową

, zwaną też funkcją skoku 

jednostkowego, oznacza się zwykle poprzez: ε(t) 

lub 1(t) i określa następująco:

ε(t)= 0 dla t < 0

1 dla t > 0

ε(t)

ε(t-α)

α

ε(t- α)=

0 dla t < 0
1 dla t > 0

Jeśli zaś mamy do czynienia ze 
zjawiskami o bardzo krótkim czasie 
trwania i o znacznej intensywności 
wówczas mówimy o

 

impulsie

  

danej wielkości. Charakter impulsu 
może mieć zarówno napięcie jak i 
prąd. 

α

 

 

25

Podsumowanie

 

 

26

1. 

Wartością chwilową sygnału

 

nazywamy 

wartość, jaką przyjmuje sygnał w danej chwili 
(np. f(t), i(t), u(t)).

2. 

Wartością średnią całookresową 

sygnału 

okresowego o okresie T nazywamy średnią 
arytmetyczną tego sygnału obliczoną dla 
jednego okresu T.

3.

Wartością skuteczną 

sygnału okresowego o 

okresie T nazywamy pierwiastek kwadratowy z 
wartości średniej kwadratu sygnału obliczonej 
dla jednego okresu T.

4. 

Wartością wyprostowaną

 

nazywamy średnią z 

modułu sygnału.

 

 





T

dt

t

f

T

t

f

0

1

 

 

t

f

dt

t

f

T

F

T

2

0

2

1







 





T

dt

t

f

T

F

0

1

 

 

27

5. 

Współczynnikiem szczytu

 

sygnału okresowego 

nazywamy stosunek wartości maksymalnej 
(szczytowej)  sygnału do jego wartości 
skutecznej F.

        

np:

6. 

Współczynnikiem kształtu

 

sygnału 

okresowego nazywamy stosunek wartości 
skutecznej sygnału F do jego wartości średniej .

np:

 

 

F

m

F

sz

k 

U

u

u

sz

k

I

i

i

sz

k

max

,

max

,





 

t

f

F

k

k 

)

(

,

t

i

I

i

k

k



 

 

28

Współczynniki szczytu oraz kształtu prądu 

i napięcia sinusoidalnego

gdzie: 

i,

 

u,

 - faza początkowa odpowiednio 

prądu i napięcia.

Wartości skuteczne: 
Wartości wyprostowane: 

 Stąd:

Współczynniki szczytu, oraz współczynnik kształtu

)

sin(

)

(

)

sin(

2

)

sin(

)

(

u

t

m

U

t

u

i

t

I

i

t

m

I

t

i































2

,

2

m

U

U

m

I

I





m

U

U

m

I

śr

I

I





2

,

2







2

2

2

2

)

(sin

2

2

max

)

(sin





















m

I

m

I

I

I

k

k

m

I

m

I

I

i

sz

k

 

 

29

DZIĘKUJĘ ZA UWAGĘ