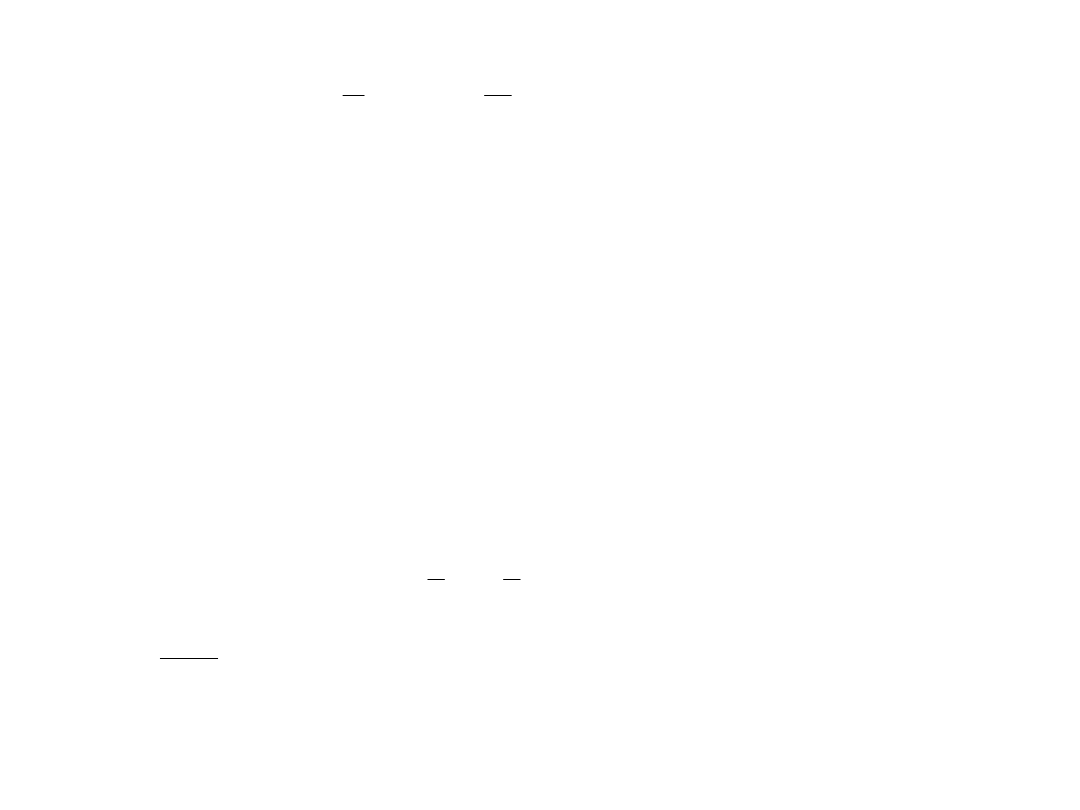
Pierwszy wyraz w tym wyrażeniu przedstawia potencjał Ziemi
kulistej, natomiast główny efekt pochodzący od spłaszczenia Ziemi
wyraża tzw. druga harmoniczna tj. drugi wyraz powyższego
rozwinięcia (dla ). Współczynnik drugiej harmonicznej jest
związany ze spłaszczeniem Ziemi zależnością
Biorąc wzór na potencjał grawitacyjny
2
sin
1
n
n
n
e
n
P
r
a
J
r
V
gdzie:
sin
n
P
- wielomiany Legendre’a stopnia
n
e
a
- promień równikowy Ziemi
- szerokość geocentryczna
0
n
n
C
J
2
n
2
J
- współczynniki w rozwinięciu potencjału w szereg funkcji sferycznych
q
J
2
1
3
2
2
gdzie:
1
3
2
e
a
q
- prędkość kątowa obrotu Ziemi
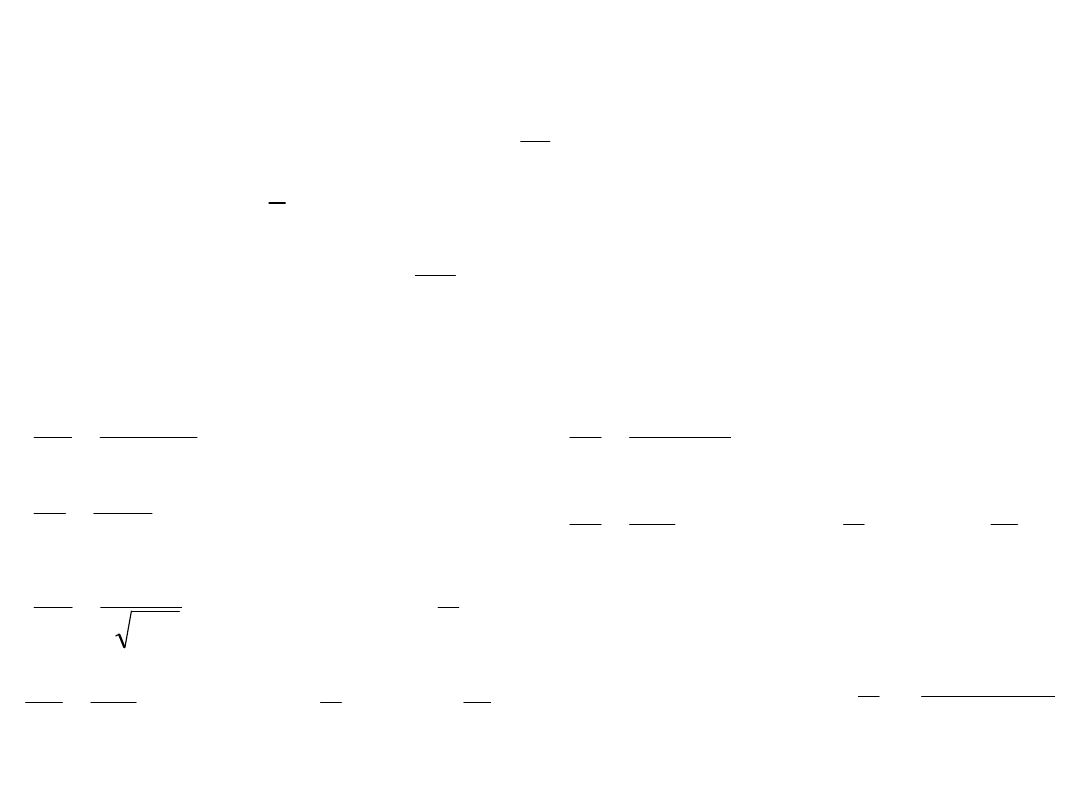
Jeśli w rozwinięciu potencjału uwzględnimy jedynie wyrazy do
, a potencjał Ziemi kulistej oznaczymy przez , to potencjał
zakłócający ruch satelity w naszym przypadku wyniesie
V
2
n
0
V
sin
2
3
2
2
0
P
r
a
J
V
V
V
e
II
Ponieważ
1
sin
3
2
1
sin
2
2
P
or
az
u
isin
sin
sin
więc:
1
sin
sin
3
2
2
2
3
2
2
u
i
r
a
J
V
e
Do obliczenia perturbacji elementów orbity spowodowanych
potencjałem zakłócającym wykorzystamy wzory:
V
W
i
p
u
G
r
du
d
sin
sin
3
W
p
u
G
r
du
di
cos
3
S
G
r
du
dp
3
2
S
p
er
S
p
r
R
e
G
r
du
de
cos
1
sin
2
uW
i
p
er
S
p
r
e
R
e
G
r
du
d
sin
cot
sin
1
cos
2
NS
r
p
R
N
e
p
e
G
r
du
dt
p
cos
sin
3
4
gdzie:
0
3
2
cos
1
cos
2
e
d
r
p
N
Najpierw jednak musimy wyznaczyć występujące w tych wzorach rzuty siły perturbacyjnej
W
S
R ,
,
1
sin
sin
3
2
3
2
2
4
2
2
i
u
r
a
J
r
V
R
e
i
u
r
a
J
u
V
S
e
2
4
2
2
sin
2
sin
2
3
2
1
i
u
r
a
J
i
V
u
r
W
e
2
sin
sin
2
3
sin
1
4
2
2
oznaczając:
2
2
2
3
e
a
J
s
mamy:
1
sin
sin
3
2
2
4
i
u
r
s
R
i
u
r
s
S
2
4
sin
2
sin
i
u
r
s
W
2
sin
sin
4
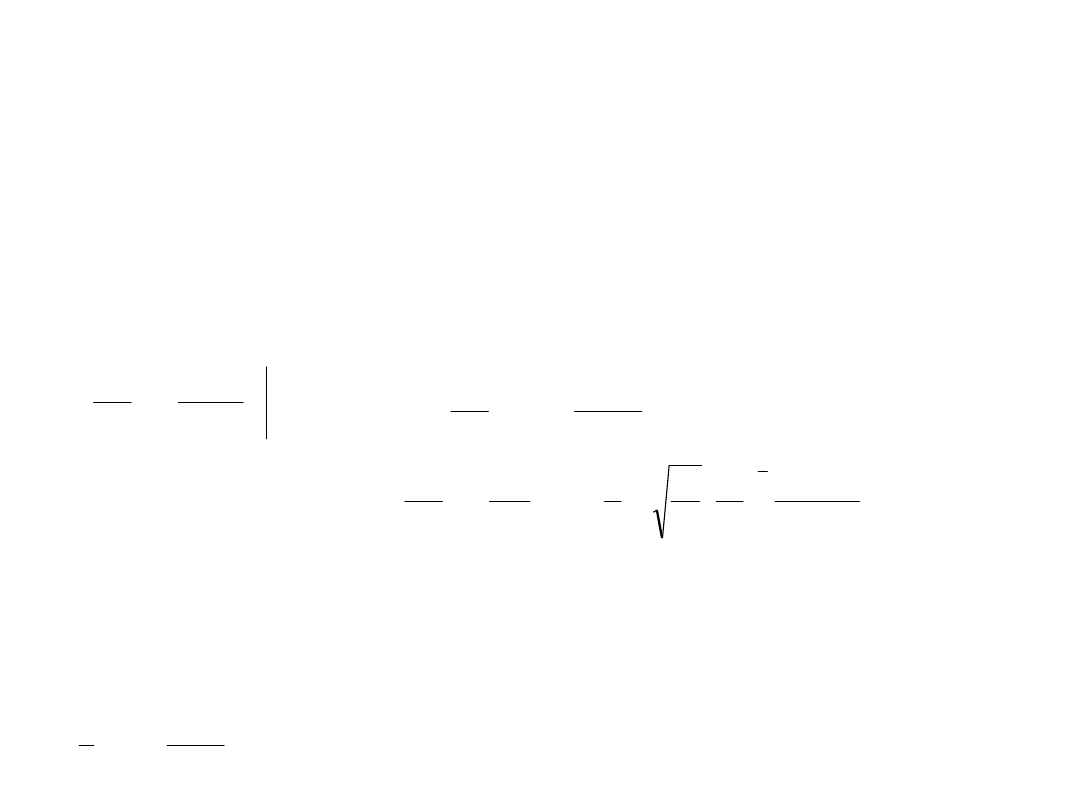
Analizując przytoczone wzory zauważamy, że niekulistość Ziemi
powoduje głównie dwa rodzaje istotnych perturbacji o charakterze
wiekowym, a mianowicie perturbację wiekową długości węzła
wstępującego (linii węzłów) i perturbację wiekową argumentu
perigeum (linii apsyd). Występują również pewne perturbacje
wiekowe obiegu satelity. Spłaszczenie Ziemi wywołuje więc znaczne
zmiany położenia płaszczyzny orbity w przestrzeni i położenia orbity
w jej płaszczyźnie, natomiast kształt i rozmiary orbity pozostają
praktycznie nie zmienione.
Perturbacja węzła wstępującego orbity uwidacznia się w precesji
płaszczyzny orbity, czyli obrocie płaszczyzny orbity względem osi
Ziemi w kierunku przeciwnym do ruchu satelity. Wynikiem tego
zjawiska jest ustawiczne przesuwanie się po równiku węzła
wstępującego orbity w kierunku przeciwnym do ruchu satelity.
Prędkość zmiany można obliczyć ze wzoru
0
2
cos
2
u
u
u
p
i
s
dt
d
czyli
obrót
i
p
a
J
dt
d
e
1
/
cos
180
3
2
2
2
lub
średnią
dobę
e
i
a
a
a
J
dt
d
e
e
1
/
1
cos
3
4
86400
180
2
2
2
7
3
2
gdzie:
e
a
- promień równikowy Ziemi
a
- duża półoś orbity satelity
i
- kąt nachylenia orbity do równika
Występująca we wzorze wielkość jest stałą, zależną od
spłaszczenia, rozmiaru, masy i prędkości kątowej obrotu Ziemi i
wynosi
2
J
6
3
2
2
10
8
,
1082
2
3
1
e
a
J
- spłaszczenie Ziemi
- prędkość kątowa obrotu Ziemi
Podstawiając
2
3
5
/
10
986
,
3
sek
km
km
a
e
6378
6
2
10
8
,
1082
J
otrzymamy:
średnią
dobę
i
e
a
a
e
1
/
cos
1
97
,
9
2
2
2
7
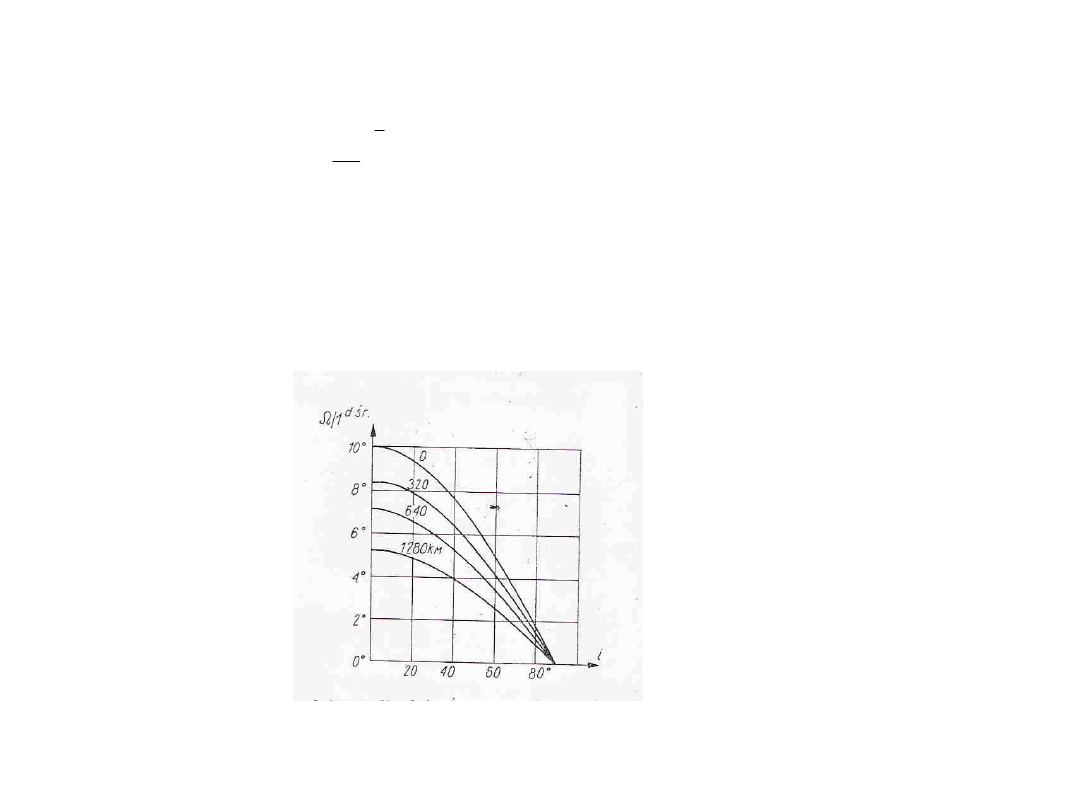
Ze wzoru tego wynika, że obrót linii węzłów następuje tym
szybciej, im kąt nachylenia orbity do równika jest mniejszy. Dla
satelitów biegunowych zjawisko precesji płaszczyzny
orbity praktycznie nie występuje. Dla satelitów o małym kącie
nachylenia orbity (prawie równikowych) przemieszczenie się węzła
wstępującego odbywa się bardzo szybko i dla satelitów
poruszających się na wysokości około 300 km prędkość obrotu
linii węzłów może wynosić blisko .
)
90
(
i
dobę
1
/
5
,
8
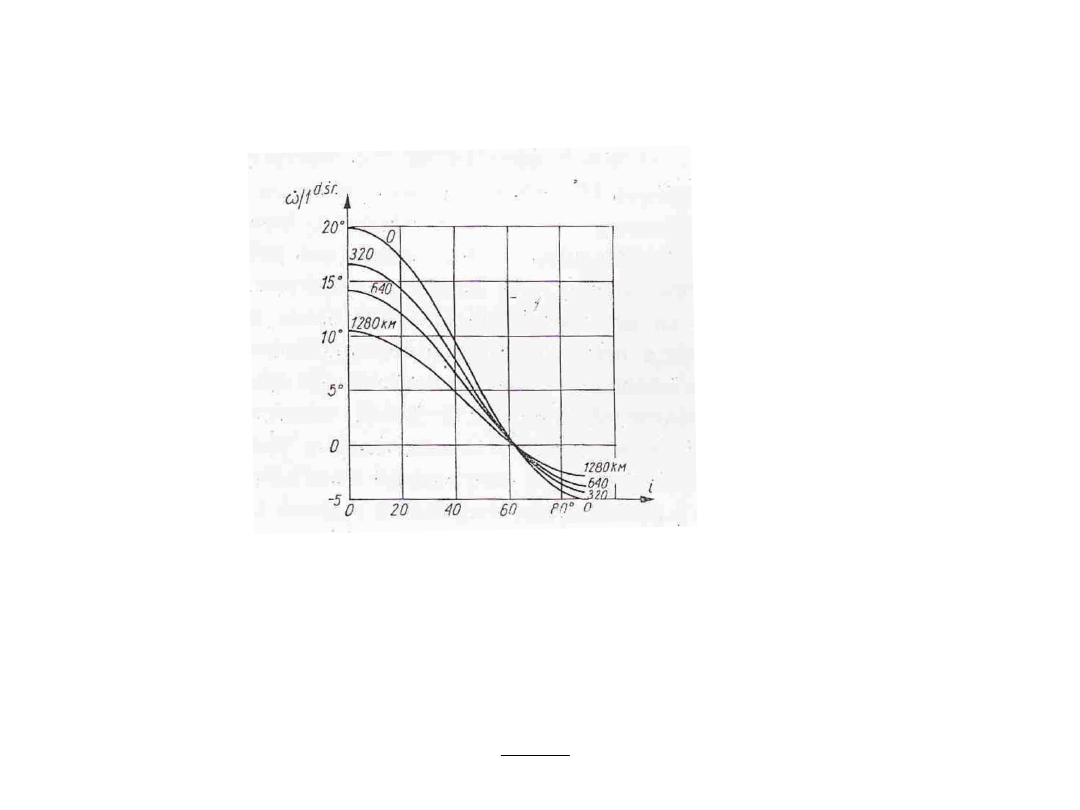
Wykres zależności prędkości obrotu linii węzła od kąta
nachylenia orbity i dla różnych średnich odległości satelity.
Drugim rodzajem perturbacji orbit SSZ, wywołanym przez
niekulistość Ziemi, jest obrót orbity SSZ w jej płaszczyźnie. Duża
oś orbity obraca się w płaszczyźnie orbity, czego faktem jest
ciągłe przemieszczanie się punktu perigeum.
Prędkość obrotu linii apsyd, tzn. prędkość wzrastania
argumentu perigeum, można wyznaczyć ze wzoru:
0
2
1
cos
5
2
1
2
2
u
u
u
p
s
i
dt
d
obrót
i
p
a
J
dt
d
e
1
/
1
cos
5
180
2
3
2
2
2
2
lub
średnią
dobę
e
i
a
a
a
J
dt
d
e
e
1
/
1
1
cos
5
4
3
86400
180
2
2
2
2
7
3
2
Po wstawieniu znanych wartości otrzymujemy:
średnią
dobę
i
e
a
a
e
1
/
1
cos
5
1
98
,
4
2
2
2
2
7
Ze wzoru tego wynika: 0
dla
'
34
116
'
26
63
5
1
cos
2
1
i
i
i
dla
2
1
i
i
i
będzie
0
co oznacza, że
przemieszczenie satelity
odbywa się w kierunku
ruchu satelity
dla
2
1
i
i
i
0
będzie
ruch perigeum jest
przeciwny do ruchu
satelity
dla
'
34
116
'
26
63
i
i
„wartości krytyczne” – ruch perigeum nie występuje
Maksymalna wartość prędkości obrotu linii apsyd przypada dla
i wynosi np. dla średniej wysokości satelity 300 km około
. Dla przypada maksimum ujemnej wartości prędkości
linii apsyd, wynoszące dla wysokości satelity 300 km około
0
i
dobę
1
/
17
90
i
dobę
1
/
5
,
4
Zależność między prędkością obrotu linii apsyd i katem
nachylenia orbity do równika dla różnych średnich wysokości
satelity.
Z analizy wzorów wynika, że kąt nachylenia orbity i , parametr p
oraz mimośród orbity e nie doznają w pierwszym przybliżeniu
perturbacji wiekowych. Podczas jednego obiegu satelity nachylenie
orbity i doznaje dwóch pełnych wahań w amplitudzie
i
p
s
A
i
2
sin
4
2
Perturbacje spowodowane oporem atmosfery.
Opór atmosfery jest jednym z najsilniej działających zakłóceń ruchu
niskich satelitów i objawia się tym silniej im satelita porusza się
niżej.
- siła oporu atmosfery
m
D
v
v
m
D
D
Na podstawie tego wzoru można stwierdzić, że prędkość obiegu
satelity poruszającego się po prawie kołowej orbicie na skutek
oporu atmosfery zwiększa się, zaś przyspieszenie satelity jest
równe sile oporu powietrza przypadającemu na jednostkę masy
satelity. Z wzoru tego wypływa jeszcze jeden wniosek, a mianowicie,
że z dwóch satelitów poruszających się na tej samej wysokości ten
będzie poruszał się szybciej, na który działa działa większa siła
oporu powietrza. Jest to tzw. „paradoks” ruchu satelity.
v
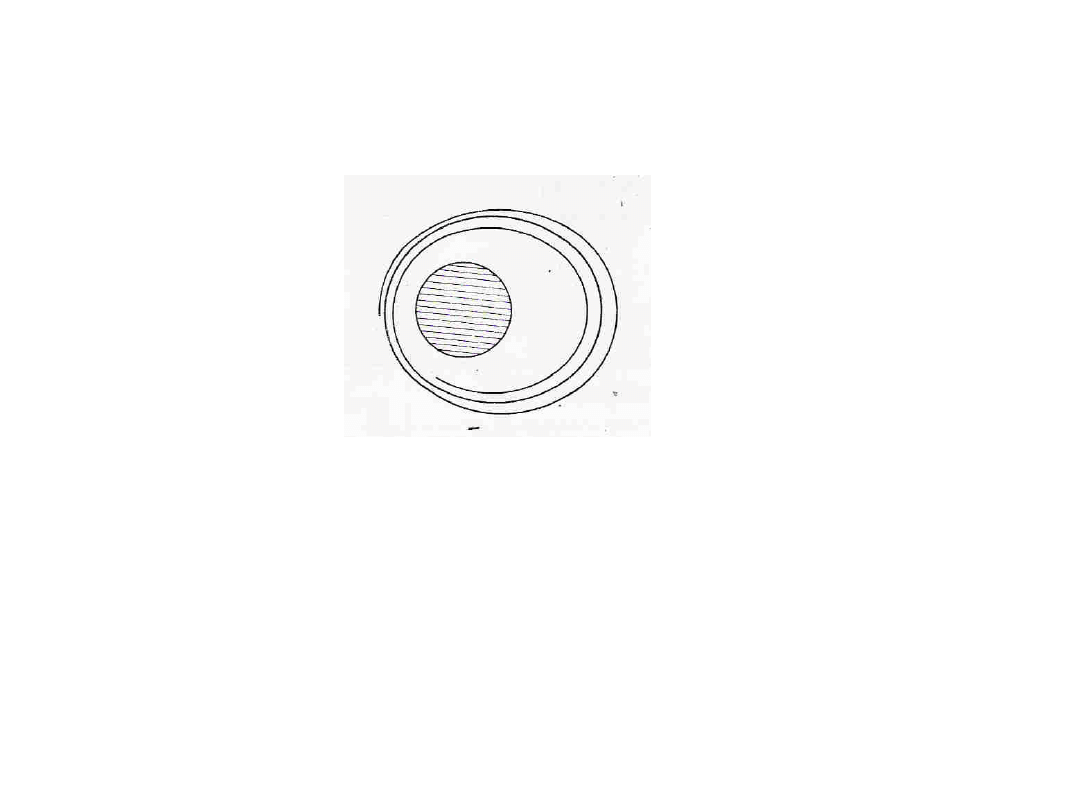
Na satelitę poruszającego się po orbicie eliptycznej opór powietrza
działa głównie na odcinku orbity położonej najbliżej Ziemi, tj. w
okolicy perigeum. Pod działaniem oporu atmosfery następuje tu
niewielkie wyhamowanie prędkości ruchu satelity i zmniejszenie
wysokości perigeum. Jednak niewielkie nawet zmniejszenie
wysokości perigeum powoduje znacznie większe zmniejszenie
wysokości apogeum.
Pod wpływem działania oporu atmosfery wysokość apogeum satelity
zmniejsza się więc znacznie szybciej wysokość perigeum. Zmieniają
się zatem ustawicznie kształt i rozmiar orbity eliptycznej. Następują
ciągłe zmiany półosi a i mimośrodu e, w wyniku których orbita
eliptyczna co do formy zbliża się ustawicznie do orbity kołowej.
Okres obiegu satelity wokół Ziemi ulega tez zmianie zmniejszając się
stopniowo do wartości 87 minut, co odpowiada krytycznej wysokości
około 150 km, przy której następuje spalenie satelity.
Zmiana kształtu orbity
eliptycznej pod wpływem
oporu powietrza
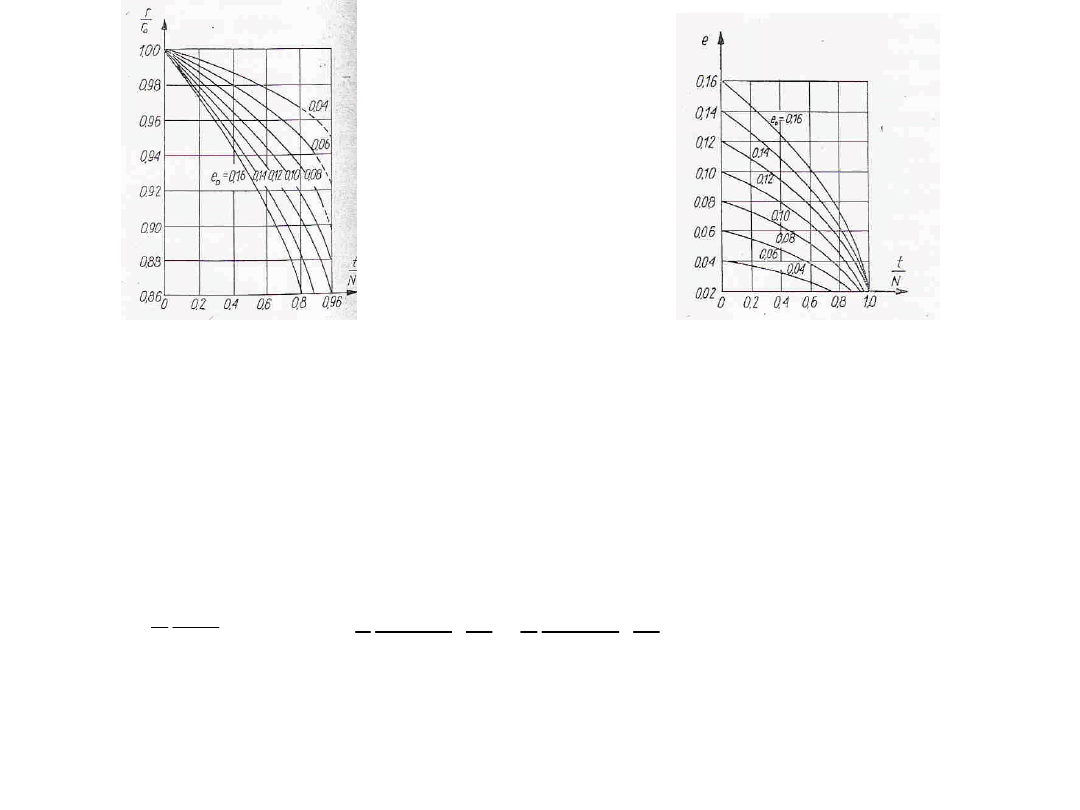
Wykres zmian okresu obiegu
satelity w czasie, spowodowanych
działaniem oporu atmosfery
Wykres zmian mimośrodu orbity
w czasie, spowodowany
działaniem oporu atmosfery.
Z powyższych wykresów widać, że zmiany okresu obiegu i zmiany
mimośrodu są na początku „życia” satelity niewielkie, jednak
prędkość tych zmian stopniowo wzrasta w miarę wchodzenia
satelity w gęstsze warstwy atmosfery.
Okres życia satelity N można określić w przybliżeniu (z
dokładnością 10%) na podstawie jednego z poniższych wzorów
x
T
e
N
0
0
4
3
x
T
h
h
h
h
x
T
a
h
h
N
p
a
p
a
p
a
0
0
4
3
8
3
lub
gdzie
0
0
,e
T
- oznaczają odpowiednio początkowy okres obiegu SSZ
i początkowy mimośród jego orbity
x
- zmiana okresu T na dobę
Perturbacje spowodowane ciśnieniem światła słonecznego
Wpływ ciśnienia światła słonecznego staje się zauważalny dla
satelitów poruszających się na znacznych wysokościach i to dla
takich satelitów, dla których stosunek powierzchni przekroju
poprzecznego S do masy m jest większy od 25 cm
2
/g
Ciśnienie światła słonecznego powoduje wiekowe i długookresowe
zmiany kształtu orbity, tzn. zmianę mimośrodu e oraz w związku z
tym zmianę (zmniejszenie) wysokości perigeum, a także niewielkie
zmiany w elementach określających położenie orbity w przestrzeni.
Nie doznaje perturbacji duża półoś orbity a.
Pod wpływem działania światła słonecznego satelita doznaje
przyspieszenia, okreslanego zwykle wzorem.
cos
1
2
0
k
c
S
q
f
gdzie
m
S
q
- stosunek powierzchni satelity S do jego masy m
- stała słoneczna charakteryzująca
intensywność promieniowania
słonecznego w rejonie orbity ziemskiej
- prędkość
światła
- współczynnik charakteryzujący sposób odbicia i
pochłaniania światła przez powierzchnię satelity (np.
pełne pochłanianie światła k=0, pełne odbicie lustrzane
k=1, odbicie dyfuzyjne k≈1,44)
- stosunek odległości r Ziemi od Słońca do odległości satelity od Słońca
- kąt padania promieni słonecznych na powierzchnię satelity
1
2
0
min
04
,
0
94
,
1
cm
cal
S
c
k
r
Perturbacje spowodowane wpływami Księżyca i Słońca
Wpływy perturbacji Księżyca i Słońca na orbity niskich satelitów są
bardzo małe i wzrastają wraz ze wzrostem odległości orbity od
powierzchni Ziemi. Nieuwzględnianie tych wpływów powoduje błąd
położenia satelity poruszającego się na wysokości tysięcy
km, wynoszący kilkaset metrów, zaś dla orbit o wysokości około 40
000 km błąd ten wynosi już kilkadziesiąt kilometrów.
4
3
h
km
f
max
f
max
f
max
g
f
max
g
f
max
G
f
g max
g
10
-6
m sek
-2
0
2 000
10 000
20 000
50 000
100 000
0,50
0,66
1,3
2,1
4,4
8,3
1,1
1,4
2,8
4,5
9,8
18,0
5,1· 10
-8
1,2· 10
-7
8,6· 10
-7
3,6· 10
-6
3,5· 10
-5
2,4· 10
-4
1,1 · 10
-
7
2,5 · 10
-
7
1,9 · 10
-
6
7,9 · 10
-
6
7,7 · 10
-
5
5,2 · 10
-
4
3,4 · 10
-
3
1,9 · 10
-
3
5,1 · 10
-
4
2,0 · 10
-
4
4,3 · 10
-
5
1,2 · 10
-
5
6,0 · 10
-
5
3,5 · 10
-
5
9,1 · 10
-
6
3,5 · 10
-
6
7,8 · 10
-
7
2,2 · 10
-
7
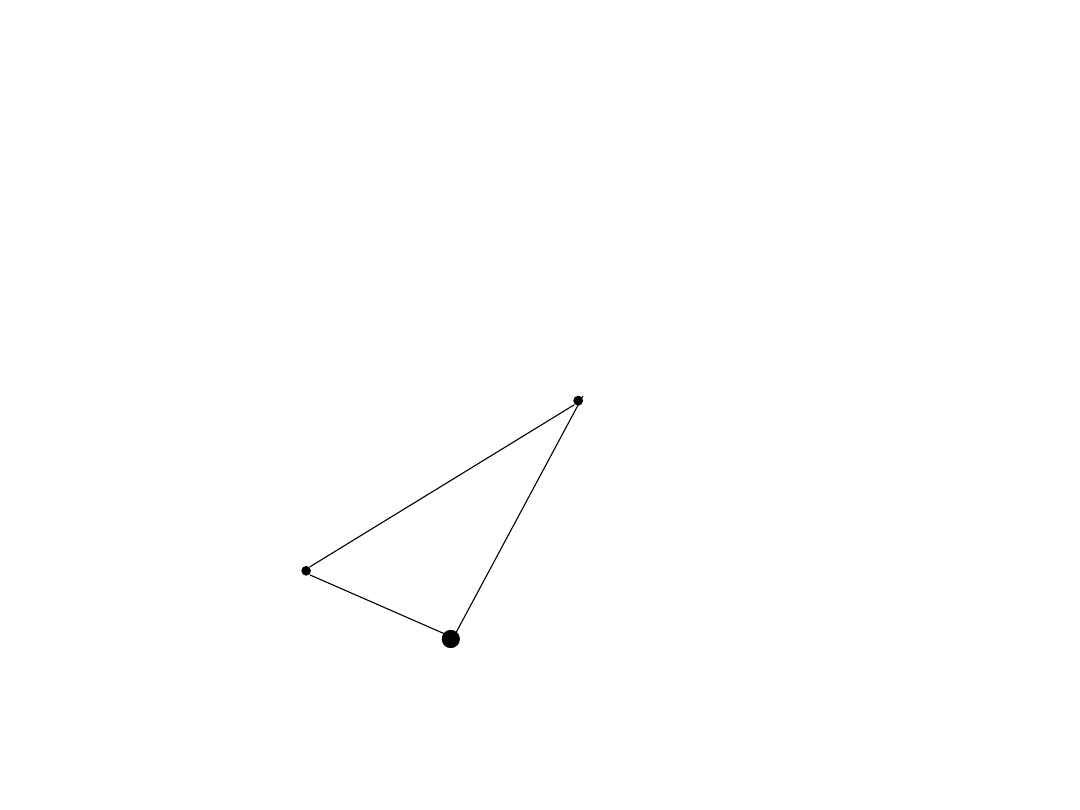
Przyjmijmy układ współrzędnych, którego początek umieścimy
w środku mas Ziemi Z. Masę Ziemi oznaczmy przez M.
Współrzędne Księżyca K i satelity S w tym układzie niech będą
odpowiednio x
, y
, z
oraz x, y, z. Masa Księzyca niech będzie
równa m
, natomiast masę satelity jako znikomo mała w
porównaniu z masami Ziemi i Księżyca zaniedbamy. Odległość
satelity i Księżyca od Ziemi niech wynosi r i r’, odległośc zaś
satelity od Księżyca oznaczmy przez
r’
r
S(x,y,
z)
K(x
,y
,z
,m
)
Z(M)
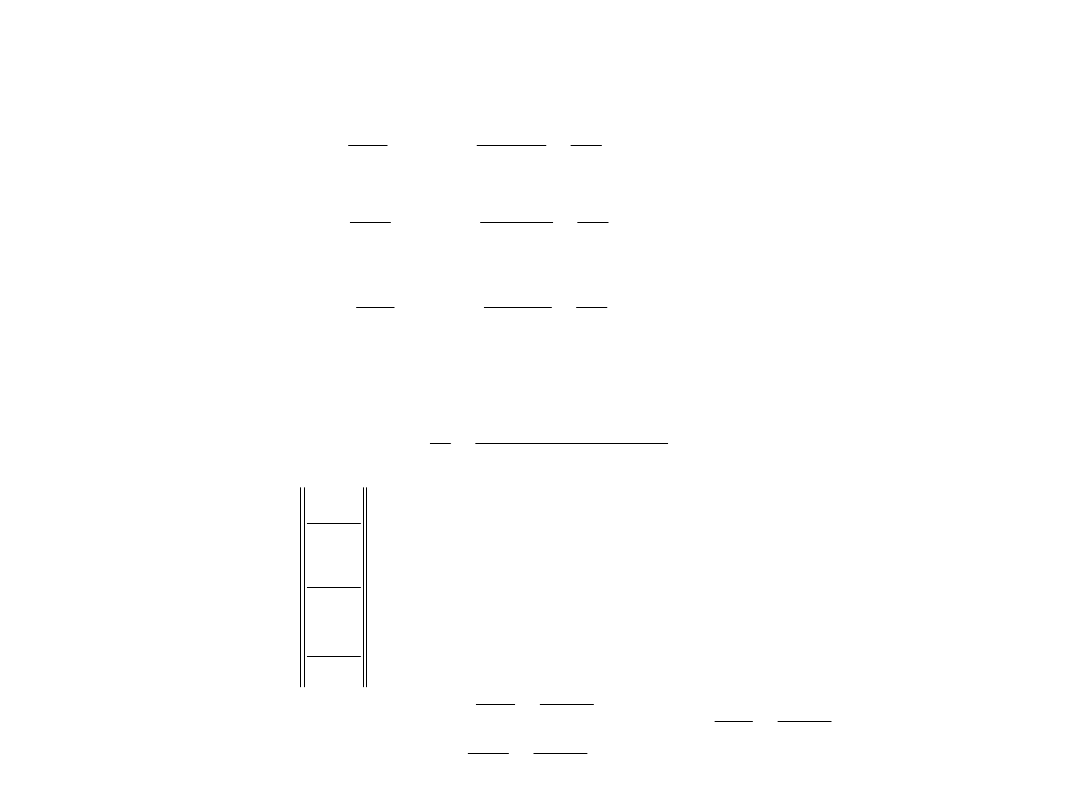
Ruch satelity w takim przypadku można przedstawić za pomocą
następującego układu równań różniczkowych
3
3
3
'
r
x
x
x
Gm
r
x
x
3
3
3
'
r
y
y
y
Gm
r
y
y
3
3
3
'
r
z
z
z
Gm
r
z
z
Jeśli przez R
oznaczymy funkcję perturbacyjna określoną wyrażeniem:
3
'
1
r
zz
yy
xx
Gm
R
Czyli gdy:
z
R
y
R
x
R
R
grad
to ruch satelity możemy przedstawić w postaci:
x
R
r
x
x
3
y
R
r
y
y
3
z
R
r
z
z
3
Wstawiając do równań Lagrange’a i całkując otrzymamy:
0
2
sin
sin
1
4
15
2
2
1
2
i
e
fe
e
2
2
2
2
1
2
sin
5
1
cos
1
2
3
e
e
i
e
f
2
sin
2
sin
1
8
15
2
1
2
2
i
e
fe
i
2
2
2
2
2
1
2
sin
5
2
1
sin
cos
5
1
2
3
e
i
e
f
2
sin
sin
1
4
15
2
2
1
2
i
e
fae
h
p
gdzie:
3
0
1
a
f
,
GM
0
1
- odnosi się do Ziemi
- odnosi się do ciała wywołującego zakłócenie
- odległość satelity od ciała zakłócającego
Duża półoś orbity a nie doznaje żadnych wiekowych ani
długotrwałych zakłóceń, zmiany zaś wszystkich pozostałych
elementów są proporcjonalne do a
3
. Największe wiekowe
zakłócenia występują dla elementów i , pozostałe elementy
doznają zmian długookresowych. Należy jeszcze zaznaczyć, że
wpływy Księżyca i Słońca na niektóre elementy orbity wzrastają
wraz ze wzrostem mimośrodu orbity.
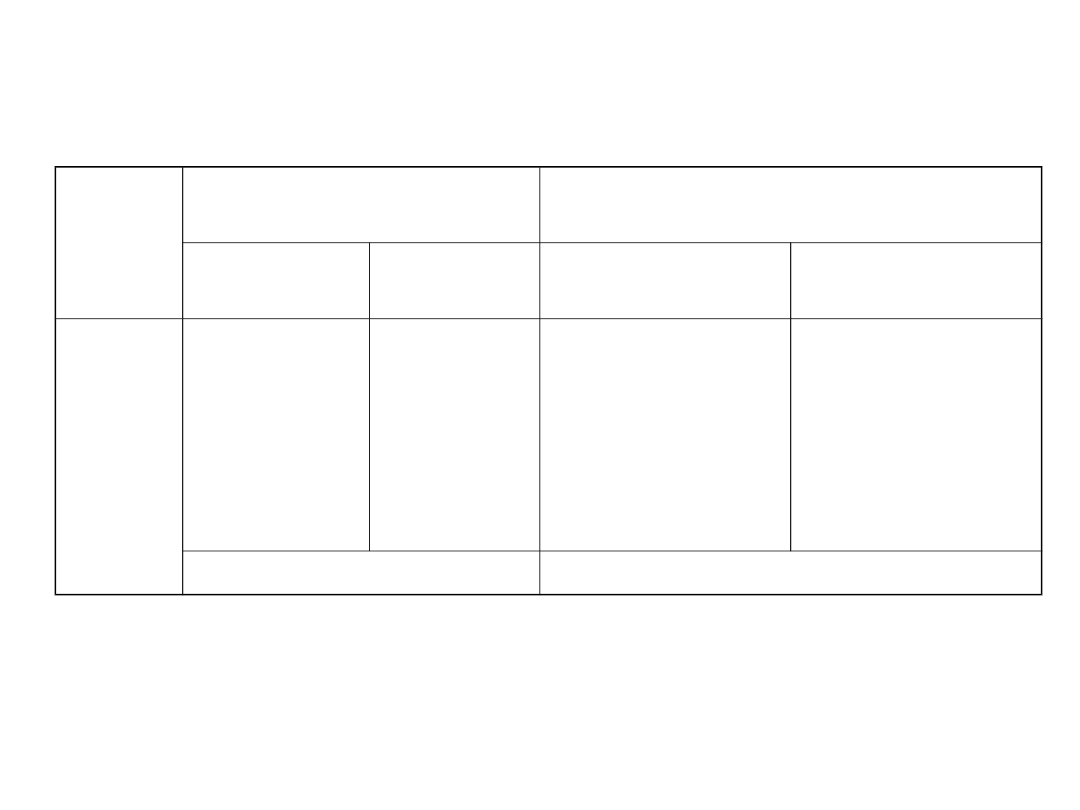
Zestawienie wpływu Księżyca i Słońca na elementy orbity, dla której a = 7350 i e = 0,1
Eleme
nt
Zmiana na 1 obieg
satelity
Zmiana na 1 obieg ciała
zakłócającego
Wpływ
Wpływ
Wpływ
Wpływ
i
e
h
p
< 0,17”
< 0,29”
< 0,17”
< 2· 10
-7
< 1,5m
< 0,08”
< 0,14”
< 0,08”
< 0,93·
10
-7
< 0,06 m
< 34”
< 2’
< 0,43”
< 0,41· 10
-4
< 0,3 m
< 3,2’
< 11,3’
< 2,4”
< 2,31· 10
-4
< 1,7 km
łączny wpływ < 2,1 m łączny wpływ na 1 rok < 5,1 km
Document Outline