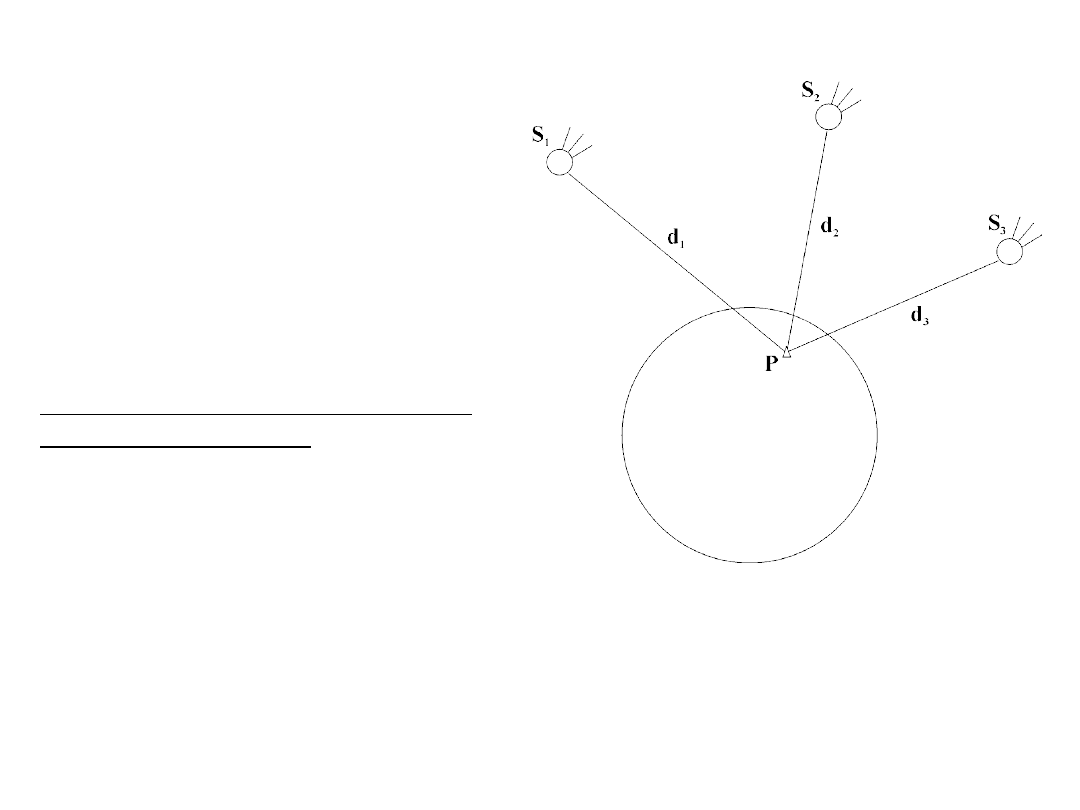
Wyznaczenie pozycji z obserwacji sztucznych satelitów Ziemi

1. Z pomiarów odległości do satelity

d

1

, d

2

, d

3

– pomierzone

odległości do satelitów,
na ogół każda w innym
momencie, przypadek
trudniejszy będzie
omówiony później

W przypadku pomiaru w tym
samym momencie (n.p. do
kilku satelitów) ma to n.p.
miejsce w przypadku
technologii GPS . Rozwiązanie
polega na obliczeniu
przestrzennego wcięcia
liniowego.

Równania układamy w tym układzie współrzędnych, w którym
znamy położenie satelity (układzie niebieskim ICRF)

X

i

ITRF

,

Y

i

ITRF

, Z

i

ITRF

– współrzędne i-tego satelity w układzie ICRF

x

ICRF

, y

ICRF

, Z

ICRF

– współrzędne punktu P w układzie ICRF

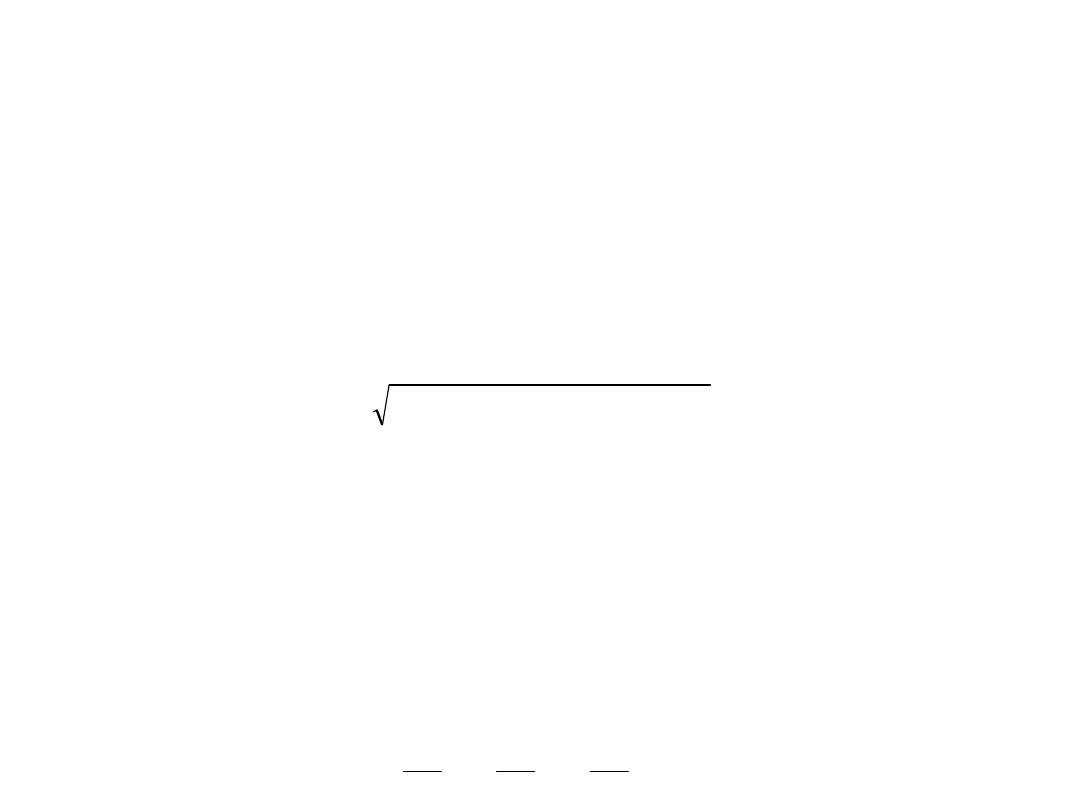
Równania dla kul przyjmują postać



 

 





 

 





 

 



2

3

2

3

2

3

2

3

2

2

2

2

2

2

2

2

2

1

2

1

2

1

2

1

d

z

Z

y

Y

x

X

d

z

Z

y

Y

x

X

d

z

Z

y

Y

x

X

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF





































W tym układzie będą trzy niewiadome x

ICRF

, y

ICRF

, z

ICRF

– wyznaczane

współrzędne punktu w układzie ICRF.

Tych jednoczesnych pomiarów może być więcej niż 3. W tym przypadku:



 

 



2

2

2

z

Z

y

Y

x

X

d

i

i

i

i













(1)

Napiszemy równanie obserwacyjne w metodzie pośredniczącej:





dz

dxdy

dd

d

v

d

i

obl

i

i

obs

i

,







gdzie:

i

v

obs

i

d

obl

i

d

dz

z

d

dy

y

d

dx

x

d

dd

i

i

i

i



















- poprawka do pomierzonej i-tej odległości

- zaobserwowana odległość do satelity

- obliczona przy pomocy wzoru (1) wartość odległości,

gdzie podstawiamy przybliżone wartości współrzędnych
wyznaczanego punktu x

przybl

, y

przybl

, z

przybl

Równanie obserwacyjne przy założeniu bezbłędnej orbity przyjmie postać

 

 



i

l

obs

i

obl

i

i

i

i

i

d

d

dz

z

d

dy

y

d

dx

x

d

v























gdzie: d

x

, d

y

, d

z

– poszukiwane niewiadome (poprawki do

przybliżonych współrzędnych punktu wyznaczanego)





























i

i

i

i

i

i

c

dz

d

b

dy

d

a

dx

d

Współczynniki przy niewiadomych uzyskujemy różniczkując (1)

obs

i

obl

i

i

d

d

l





wyraz wolny w równaniu poprawek

podstawiając otrzymamy:

i

i

i

i

i

l

dz

c

dy

b

dx

a

v









albo w postaci krakowianowej

l

a

x

v



 























dz

dy

dx

x



























n

n

n

c

b

a

c

b

a

c

b

a

...

...

...

2

2

2

1

1

1

a



























n

l

l

l

...

2

1

l

gdzie:

v – krakowian poprawki do obserwacji
x – krakowian niewiadomych
τ – krakowian jednostkowy
l – krakowian wyrazów wolnych

następnie układamy krakowianowy układ równań normalnychla

xa

2



rozwiązując otrzymamy:

 

 

1





2

a

la

x

Lub w zapisie macierzowym

równanie obserwacyjne:

L

AX

V





gdzie:























dz

dy

dx

X



























n

n

n

c

b

a

c

b

a

c

b

a

...

...

...

2

2

2

1

1

1

A



























n

l

l

l

...

2

1

L

dla obserwacji niejednakowo dokładnych, używając macierzy wag:























n

P

P

P

1

...

1

B

P





2

0

σ

 

x

cov



B

n

n

σ

PV

V

T



2

0

ˆ

gdzie:

2

0

ˆ

σ

- estymator współczynnika wariancji

n

n

- liczba stopni swobody (obserwacji nadliczbowych)

Równania normalne mają postać:

0

PL

A

PA

A

T

T





niewiadome i ich charakterystyki dokładności





PL

A

PA

A

X

T

T

1

ˆ







n

n

σ

PV

V

T



2

0

ˆ

 





1

2
0

cov





PA

A

T

x



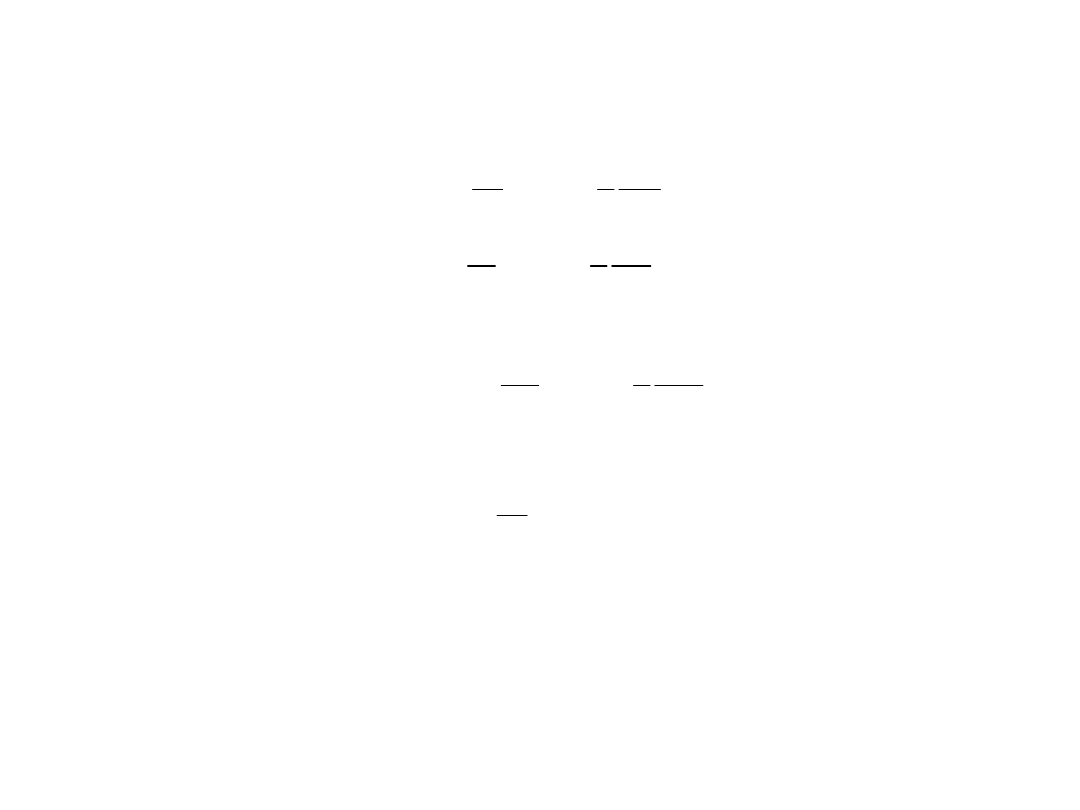
Schemat obliczeń

Dane: a, e, i , , , t

p

– parametry orbity oskulacyjnej na moment

obserwacji t obliczamy na przykład następująco dla każdego z
powyższych elementów:

















 









...

2

1

..........

..........

..........

..........

..........

..........

...

2

1

...

2

1

2

0

2

2

0

0

2

0

2

2

0

0

2

0

2

2

0

0





























































t

t

t

t

t

t

t

t

t

t

t

t

t

e

t

t

t

e

e

e

t

t

t

a

t

t

t

a

a

a

p

p

p

p

lub też n.p. dla elementu a:











t

t

dt

t

a

a

a

0

0

gdzie:

a

0

, e

0

, t

0

, 

0

, 

0

, (t

p

)

0

– wartości średnich elementów

orbity na moment t

0

Mając dane parametry orbity oskulacyjnej obliczamy X

i

ICRF

, Y

i

ICRF

,

Z

i

ICRF

na moment wykonania obserwacji

i dalej według schematu

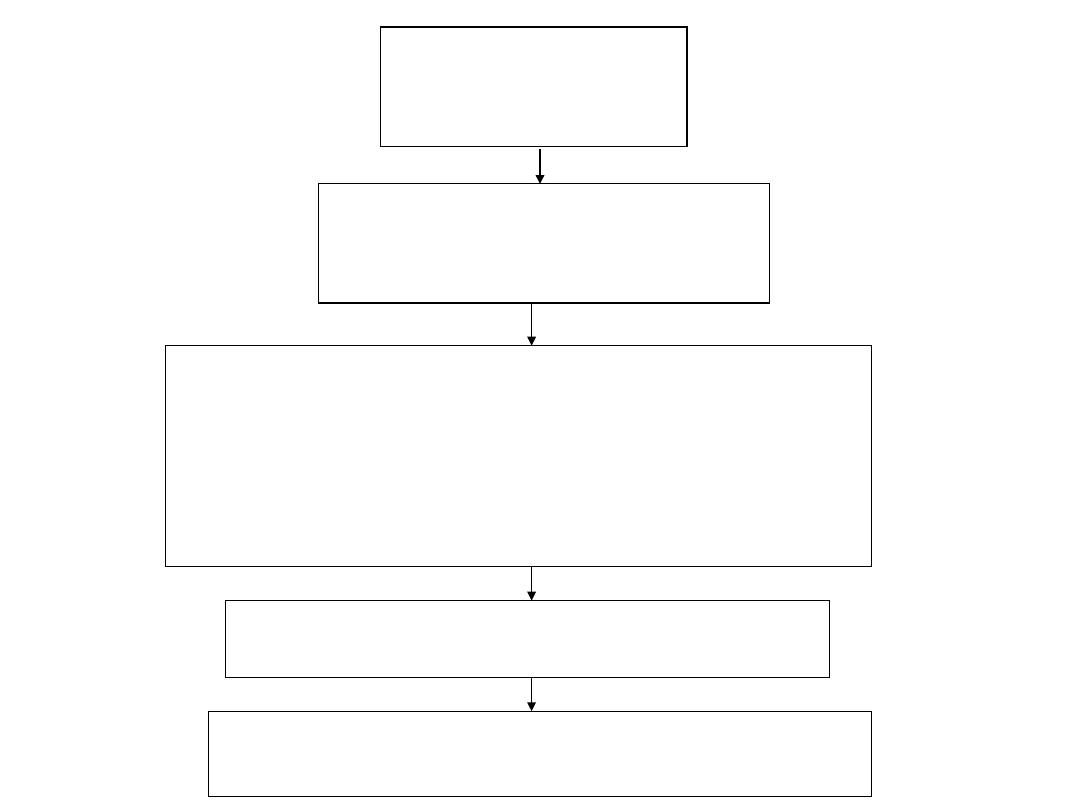
Dane początkowe

a

0

, e

0

, t

0

, 

0

, 

0

, (t

p

)

0

na moment t

0

Obliczenie parametrów

orbity oskulacyjnej na

moment obserwacji t

a, e, i, , , t

p

Obliczenie współrzędnych „n” satelitów w
układzie ICRF

ICRF

n

ICRF

n

ICRF

n

ICRF

ICRF

ICRF

ICRF

ICRF

ICRF

Z

Y

X

Z

Y

X

Z

Y

X

,

,

.......

..........

..........

,

,

,

,

2

2

2

1

1

1

Ułożenie i rozwiązanie równań
obserwacyjnych – obliczenie pozycji
punktu w układzie ICRF

Transformacja współrzędnych punktu do układu ITRF
(precesja, nutacja, ruch bieguna, kąt ERA)

Podobnie można wyznaczyć pozycję punktu z niejednoczesnych
obserwacji odległości do satelitów, w tym przypadku jednak
będziemy posługiwali się pozycją satelity w układzie ziemskim
ITRF.

Schemat obliczeń będzie następujący dla i-tego satelity w momencie obserwacji

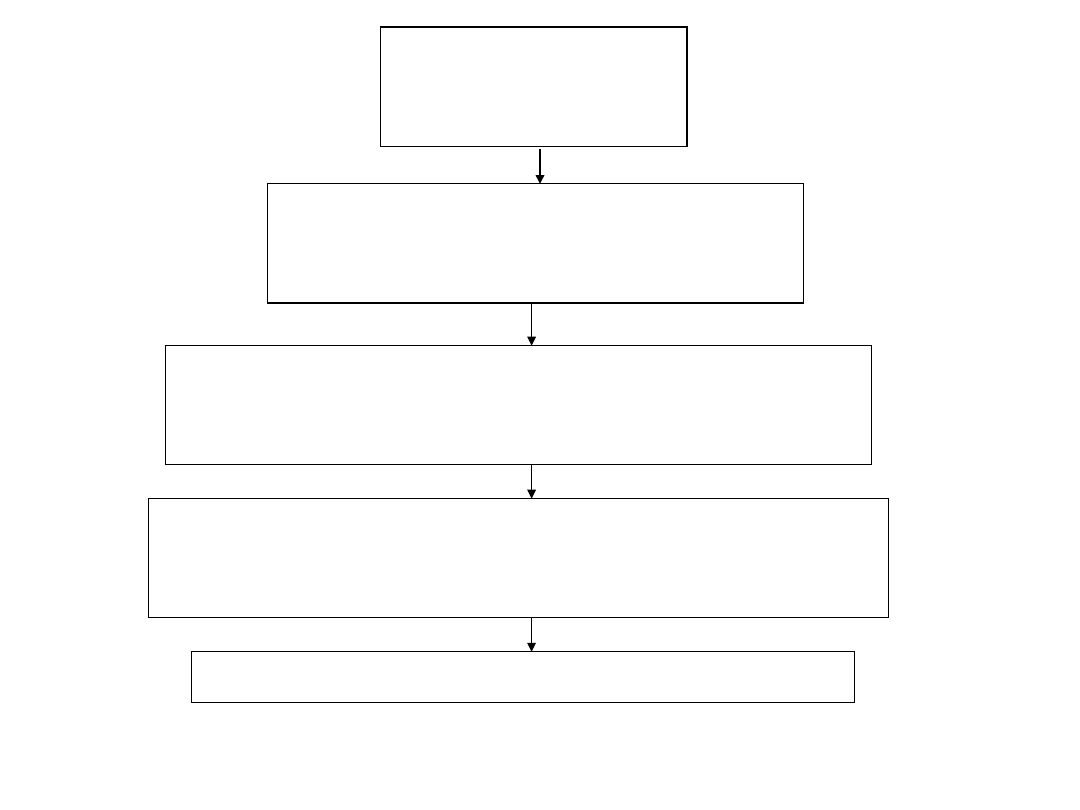
Dane początkowe

na moment t

0

a

0

, e

0

, t

0

, 

0

, 

0

, (t

p

)

0

Obliczenie parametrów orbity

oskulacyjnej na moment

obserwacji i-tego satelity t

i

a, e, i, , , t

p

Obliczenie współrzędnych i-tego satelity w

momencie czasu t

i

w układzie ICRF

ICRF

i

ICRF

i

ICRF

i

Z

Y

X

,

,

TRANSFORMACJA współrzędnych i-tego

satelity w momencie , do układu ITRF

obliczenie X

i

ITRF

, Y

i

ITRF

, Z

i

ITRF

Transformacja o precesję, nutację, ruch

bieguna i kąt ERA

Ułożenie równań obserwacyjnych w układzie ITRF

Podobnie układy równań obserwacyjnych dla kolejnych obserwacji i=1,2,3 ....
Rozwiązujemy metodą najmniejszych kwadratów.

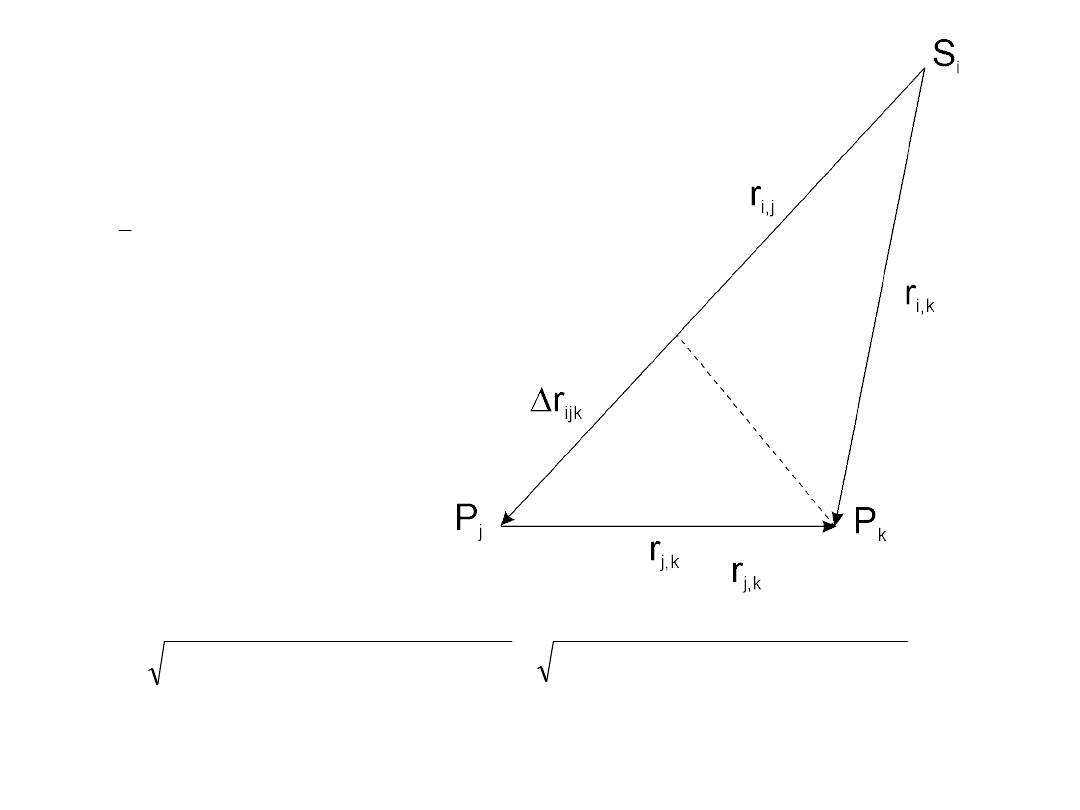
2. Wyznaczenie pozycji z pomiarów różnych długości

























































kj

kj

kj

j

k

j

k

j

k

z

y

x

z

z

y

y

x

x

jk

r

ijk

r

- pewna różnica odległości



 

 





 

 



2

2

2

2

2

2

k

i

k

i

k

i

j

i

j

i

j

i

ijk

z

Z

y

Y

x

X

z

Z

y

Y

x

X

r



























Równanie obserwacji

ijk

obl

ijk

ijk

pom

ijk

r

d

r

v

r

















kj

kj

kj

ijk

ijk

dz

dy

dx

r

d

r

d

,

,







pom

ijk

obl

ijk

kj

kj

ijk

kj

kj

ijk

kj

kj

ijk

ijk

r

z

d

z

d

r

y

d

y

d

r

x

d

x

d

r

v













































Równanie obserwacyjne przyjmie postać

ijk

kj

ijk

kj

ijk

kj

ijk

ijk

l

y

d

C

y

d

B

x

d

A

v















Rozwiązując układ równań obserwacyjnych metoda najmniejszych
kwadratów uzyskamy wyrównane wartości przyrostów
współrzędnych i ich charakterystyki dokładności