Płaskie zginanie belek

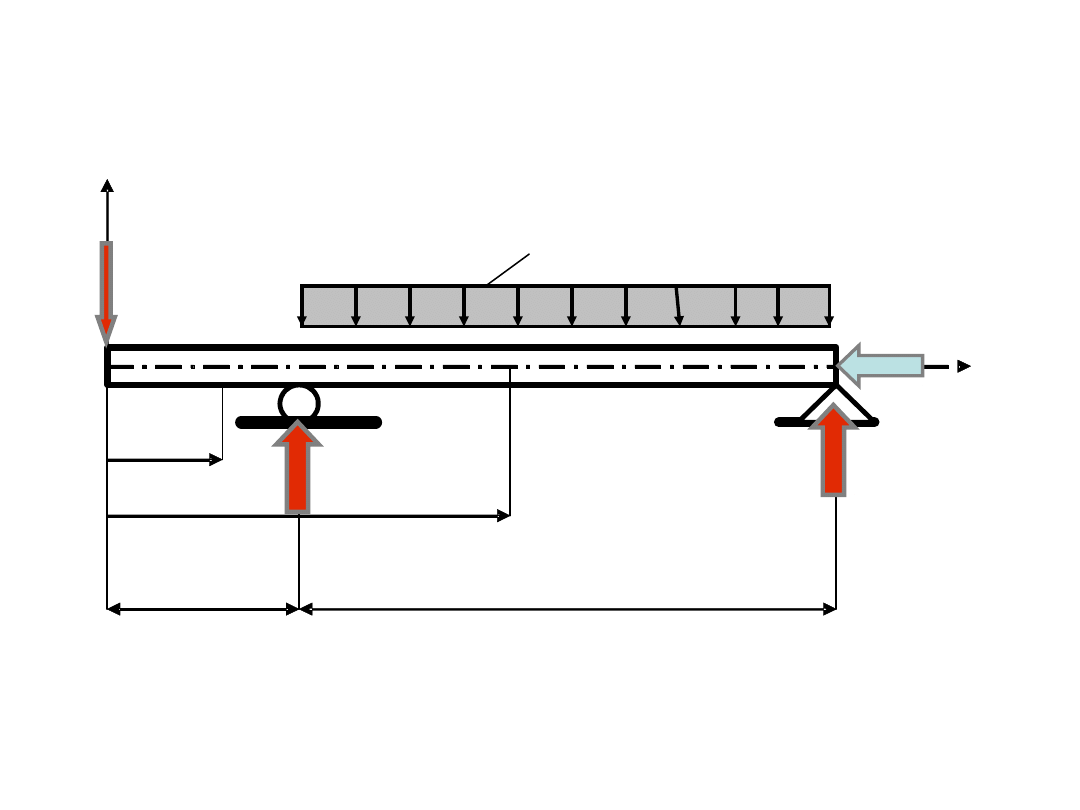
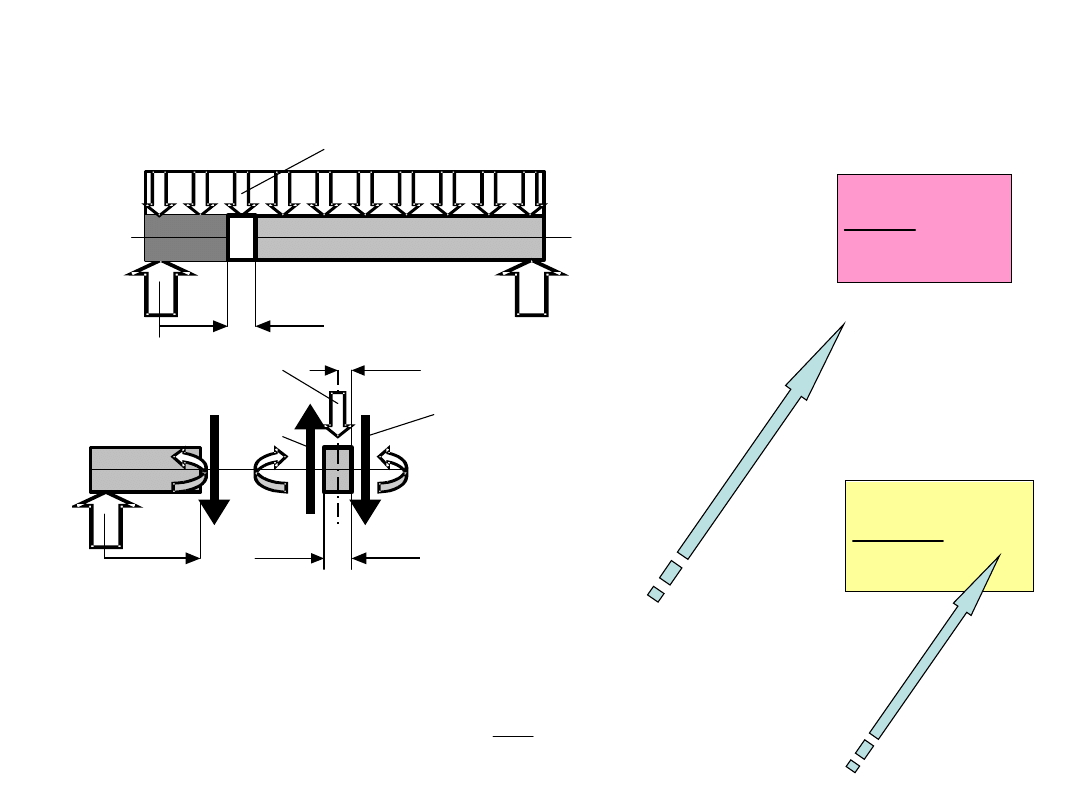
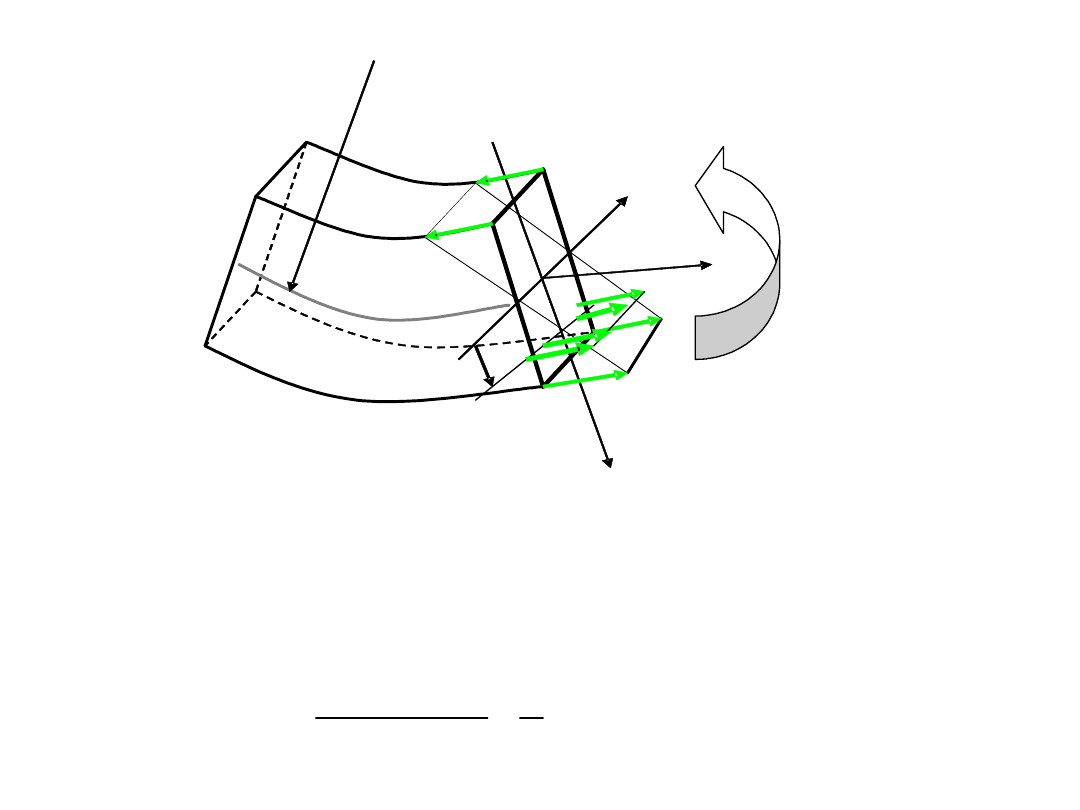
Podpory przegubowo – przesuwne oraz podpory przegubowe

( nieprzesuwne ) mostu na rzece Warcie w Konopnicy

Podpory przegubowo – przesuwne oraz podpory przegubowe

( nieprzesuwne ) mostu na rzece Warcie w Konopnicy

Podpory przegubowo – przesuwne

Podpory przegubowe – nieprzesuwne

R

BY

R

A

P=ql

x

2 l

q [kN/m ]

l/2

R

BX

y

x

1

x

2

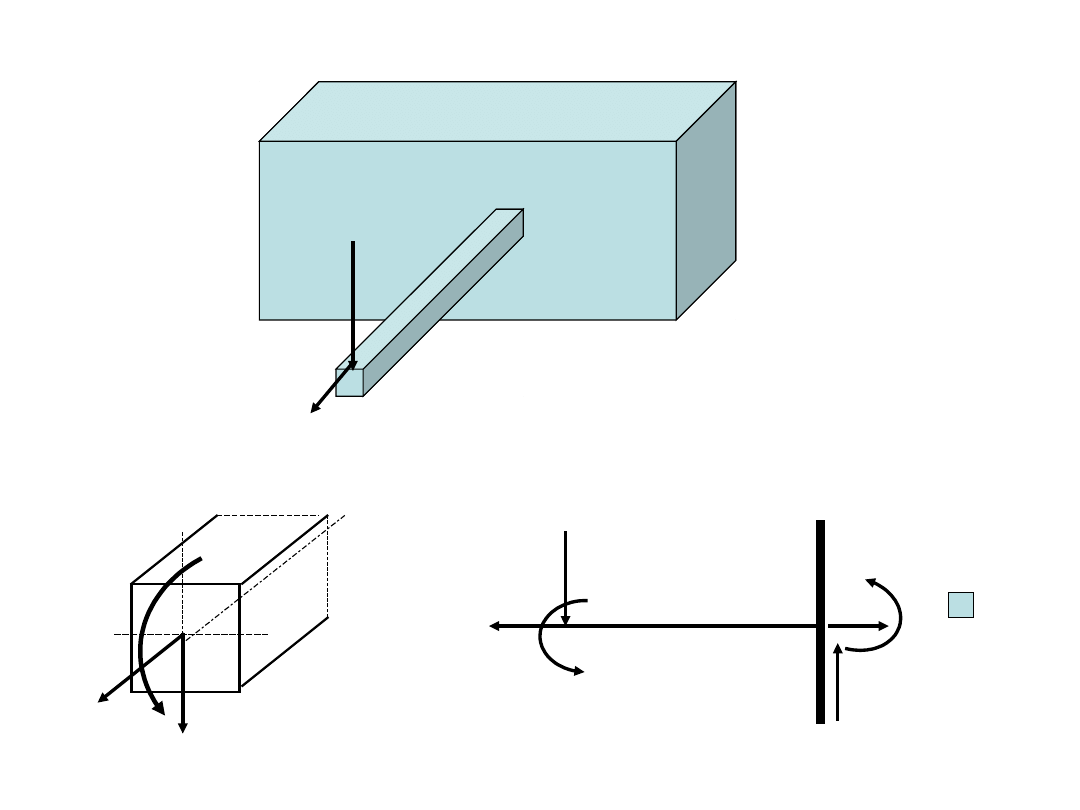
P

Q

P

Q

M

M

u

M

P

Q

R

y

R

x

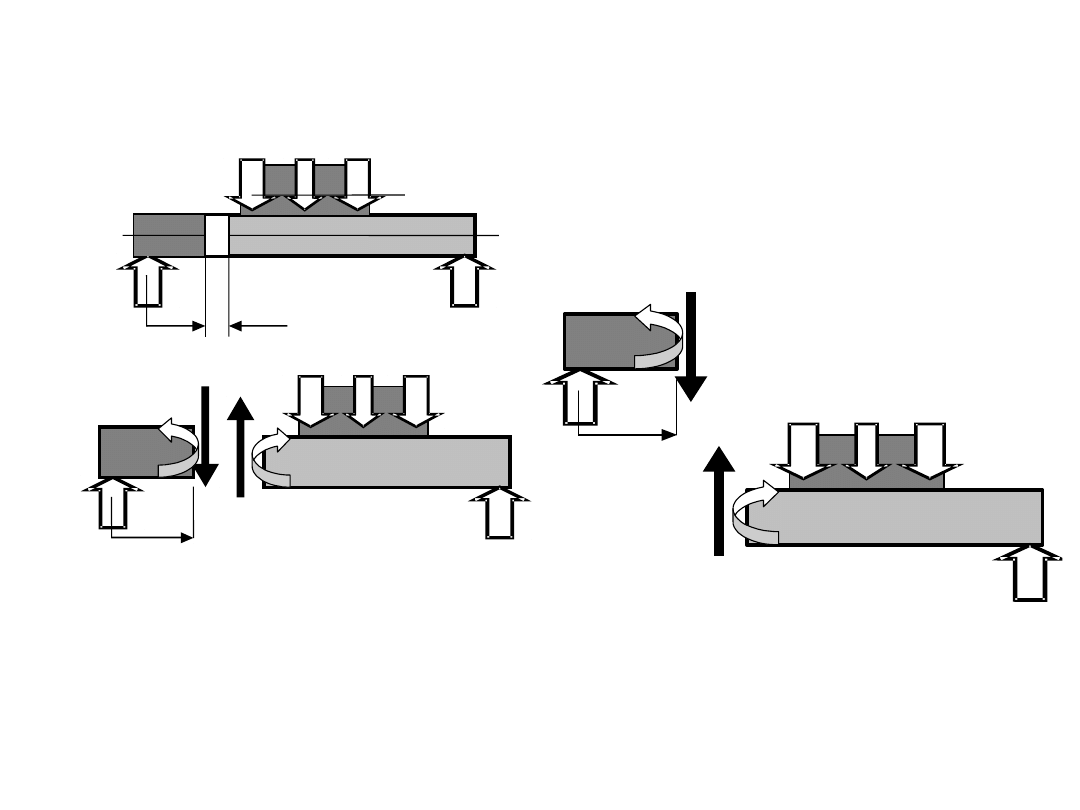
Siły wewnętrzne w belkach zginanych

Siły wewnętrzne w belkach zginanych

dx

x

x

T

x

+dT

x

T

x

M

g

R

1

M

g

+dM

g

R

2

P

i

x

T

x

T

x

M

g

M

g

R

1

T

x

= R

M

g

= Rx

R

2

1

2

dx

x

dx

T

x

+dT

x

T

x

M

gx

R

1

M

g

+dM

gx

R

2

P

1

T

x

P

2

x

R

1

a)

T

x

T

x

 0 (+)

T

x

dodatnia siła tnąca

M

gx

M

gx

M

gx

 0 (+)

dodatni moment gnący

b)

dx

dx

Konwencja (umowa) dotycząca znaku siły tnącej i momentu gnącego

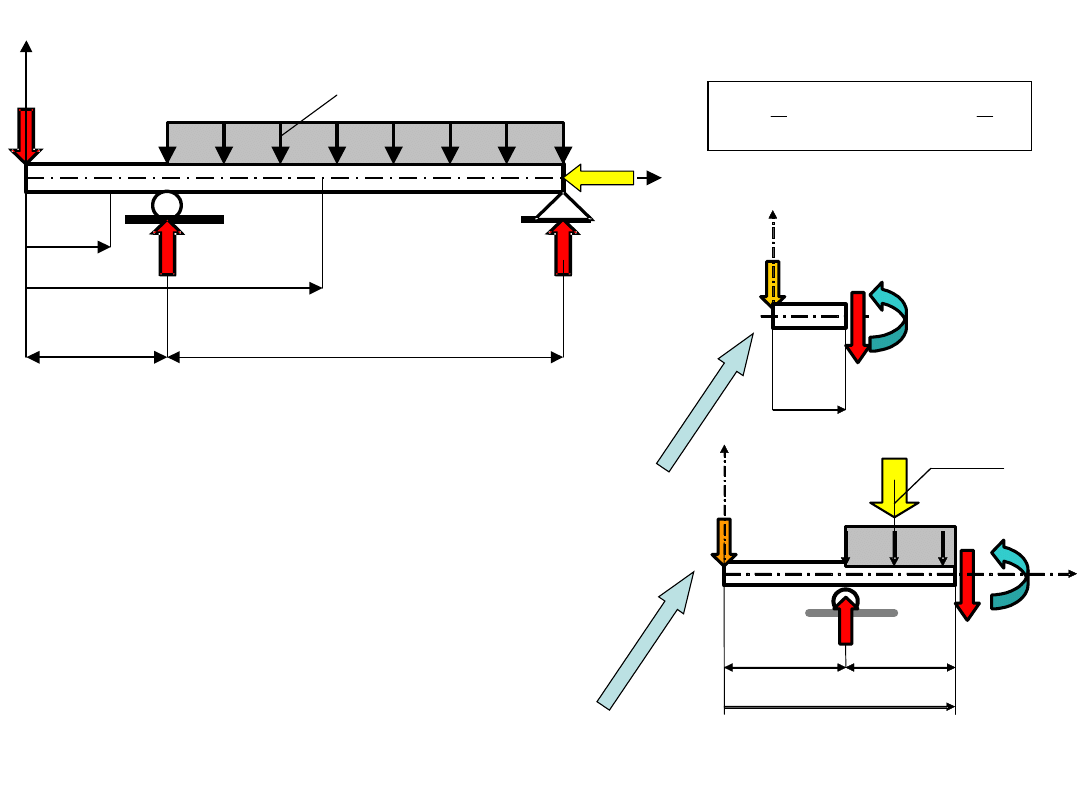
Definicja siły tnącej – siła tnąca T w dowolnym przekroju równa się sumie wartości sił
składowych obciążeń i reakcji w kierunku poprzecznym do osi belki, działających na część
belki oddzieloną tym przekrojem.

Definicja momentu gnącego – moment gnący M

gx

w dowolnym przekroju równy jest sumie

momentów względem środka tego przekroju wszystkich sił działających na część belki oddzieloną
Tym przekrojem.

dx

x

x

T

x

+dT

x

T

x

M

g

R

1

M

g

+dM

g

R

2

q = q(x)

dx

T

x

M

g

qdx

dx/2

R

1

0

dx

q

)

dT

T

(

T

F

X

x

x

iy















q

dx

dT

X





0

)

dM

M

(

2

dx

dx

q

M

dx

T

M

gx

gx

gx

X

i





















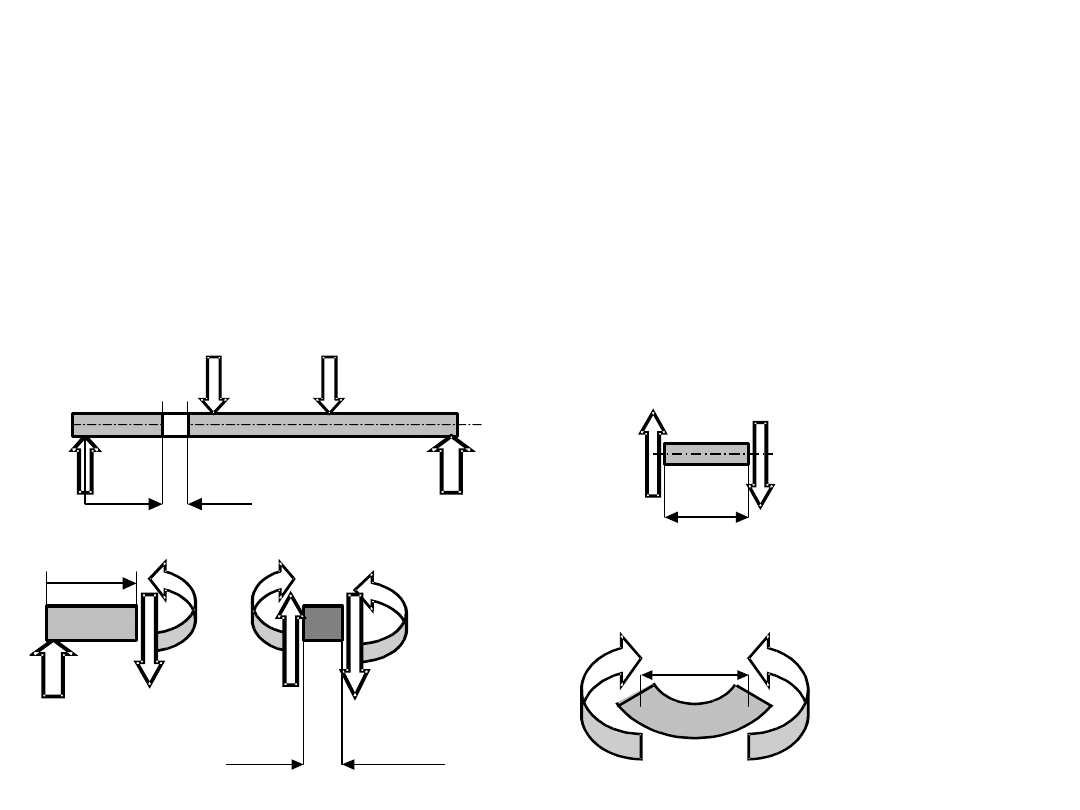
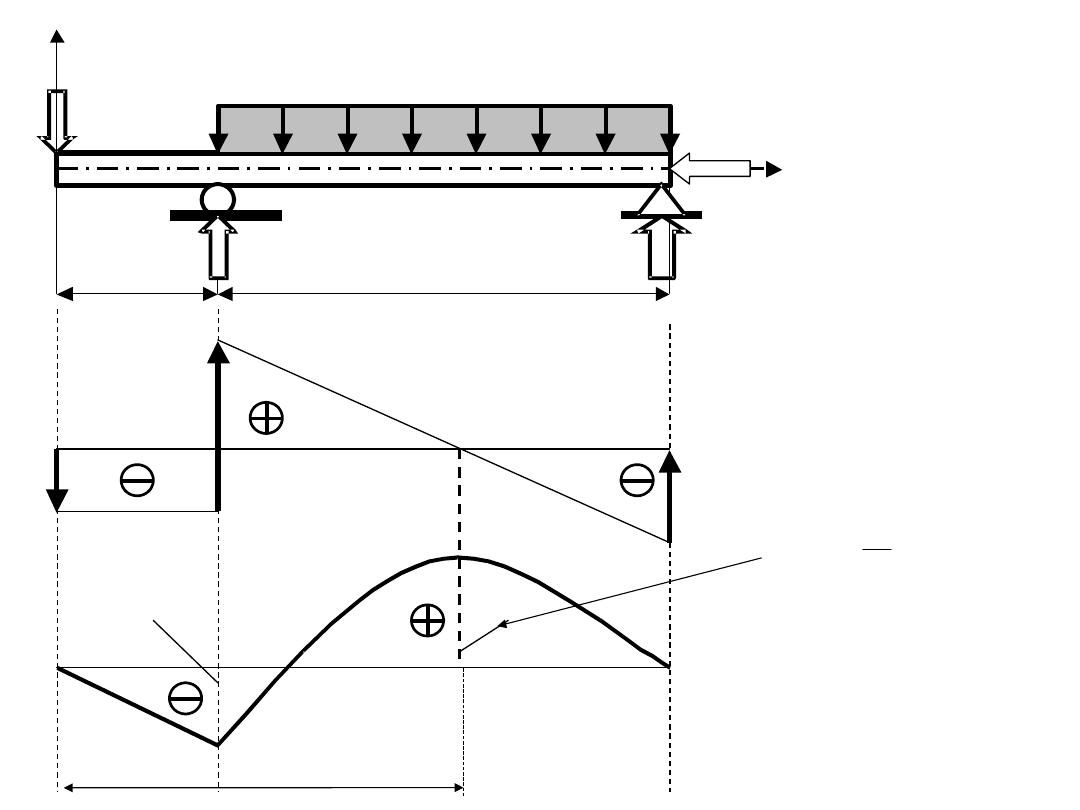
Zależność pomiędzy siłą tnącą a momentem gnącym

X

gx

T

dx

dM



R

BY

R

A

P=ql

x

2 l

q [kN/m ]

l/2

R

BX

y

x

1

x

2

M

gx

2

R

A

P=ql

x

x

2

- l/2

q (x

2

-l/2)

l/2

T

X2

y

x

2

P=ql

y

M

gx1

T

X1

x

1

;

ql

4

3

R

;

ql

4

9

R

B

A





;

2

/

ql

)

2

/

l

(

M

;

0

)

0

(

M

;

qlx

M

;

ql

T

2

/

l

x

0

2

g

g

1

gx

x

1

1

1



















;

0

)

2

/

l

5

(

M

;

2

/

ql

)

2

/

l

(

M

;

2

/

)

2

/

l

x

(

q

)

2

/

l

x

(

R

qlx

M

4

/

ql

3

)

2

/

l

5

(

T

;

4

/

ql

5

)

2

/

l

(

T

);

2

/

l

x

(

q

R

ql

T

2

/

l

5

x

2

/

l

g

2

g

2

2

2

A

2

gx

2

A

x

2

1

2







































R

BY

R

A

P=ql

x

2 l

q [“a” kN/m ]

l/2

R

BX

y

P

R

A

R

BY

T

x

M

gx

-Pl

M

gmaz

7l /
4

2

max

g

ql

32

9

M



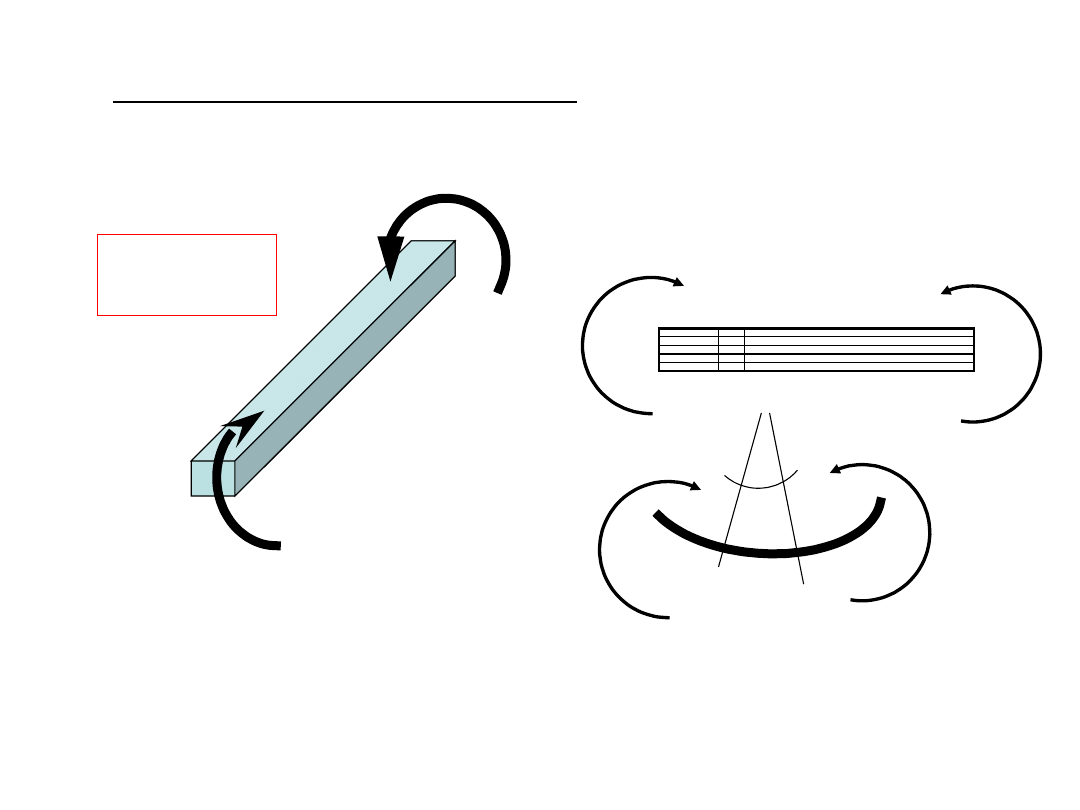
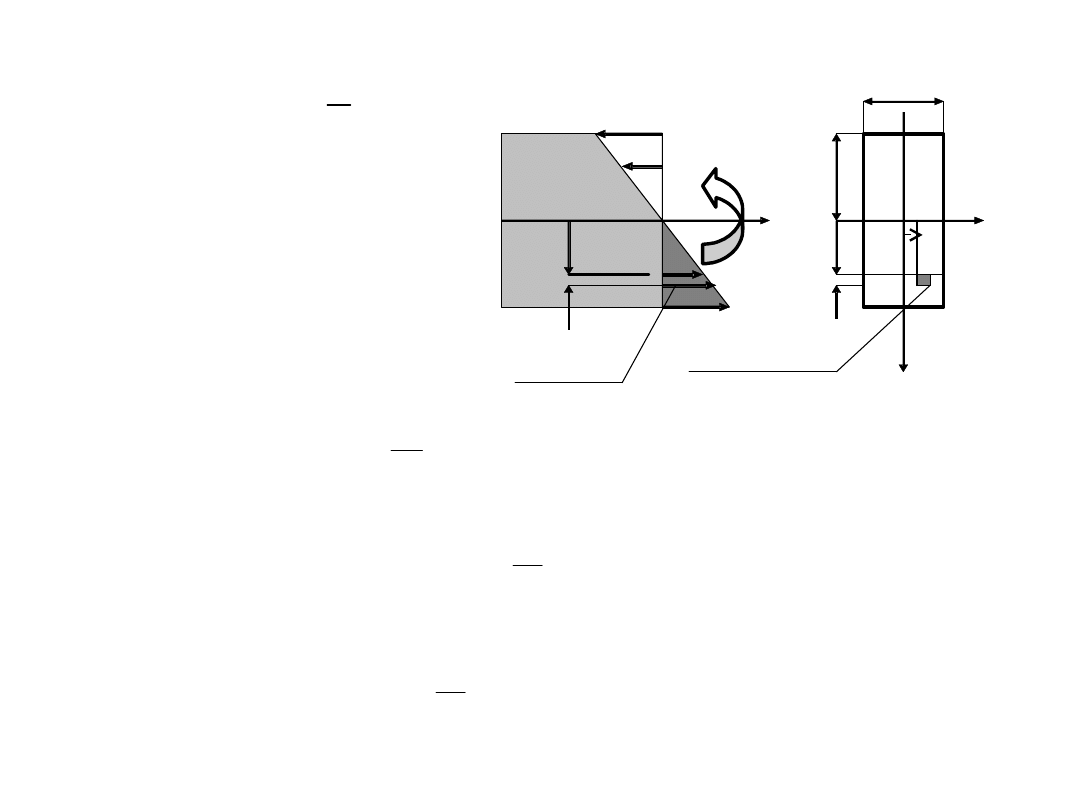
Naprężenia przy czystym zginaniu

M

g

M

g

T=0
M

g

=const.

Założenia:

-Przekroje poprzeczne pozostają płaskie,
- Warstwy nie oddziałują na siebie wzajemnie,

-Warstwy poddane są jedynie rozciąganiu bądź ściskaniu (jednokierunkowy stan
naprężenia).



x

z

y

y



M

g





 - promień krzywizny warstwy obojętnej

)

(

)

(

y

E

y

x

x









;

)

(

)

(













y

y

y

x









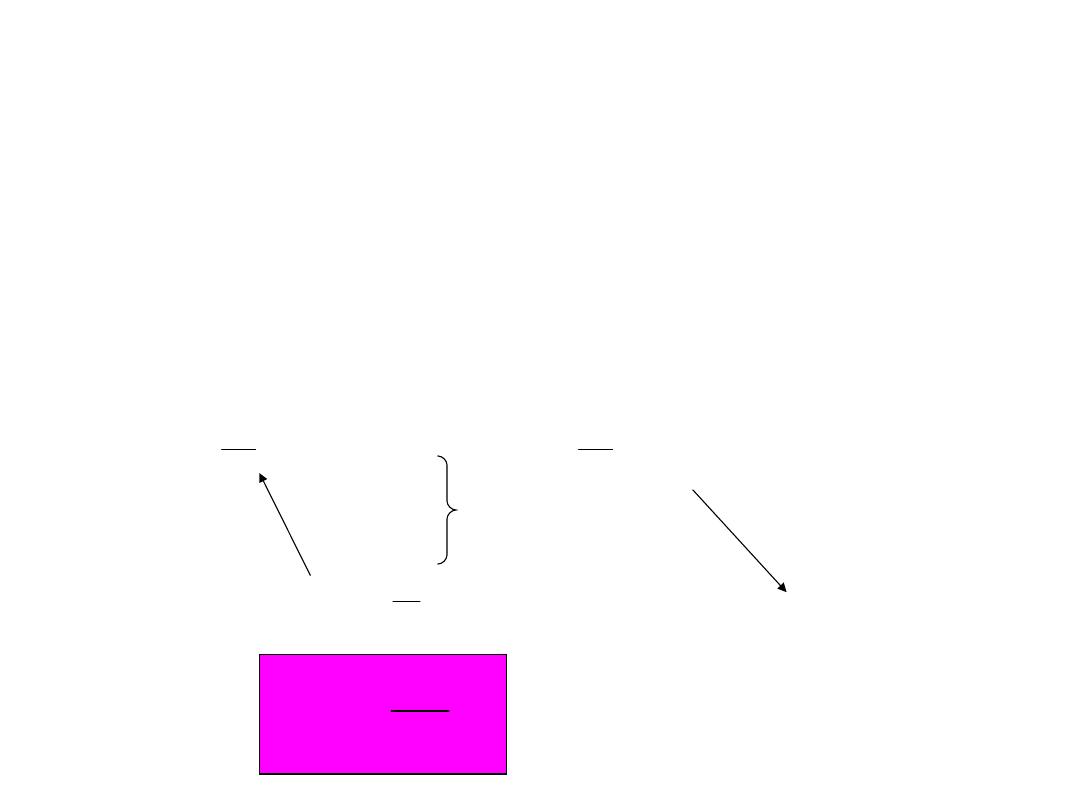
Wydłużenie warstwy odległej o y od warstwy obojętnej

)

(

)

(

)

(

y

y

y

x

z

y

















;

)

(





y

E

y

x





z

y

y

y

x

dy

dA

M

g



x

=E

b

h/2















A

A

x

ix

0

ydA

1

0

dA

F





Warstwa obojętna zawiera środek

ciężkości

przekroju poprzecznego (Oz=Oz

c

)

Warunki równowagi



















A

g

2

A

g

x

iz

M

dA

y

E

;

0

M

dA

y

M























A

A

x

iy

;

0

ydA

z

E

;

0

dA

z

M





E=const., =const.

;

I

ydA

z

;

I

dA

y

A

z

y

A

z

2

C

C

C











Moment bezwładności przekroju
poprzecznego względem osi z

c

Moment bezwładności przekroju
poprzecznegowzględem układu
osi y

c

z

c

Wprowadzając oznaczenia

Mamy:

;

0

I

E

;

M

I

E

C

C

C

z

y

g

z









;

0

I

C

C

z

y



;

)

(





y

E

y

x





;

)

(

y

I

M

y

C

z

g

x







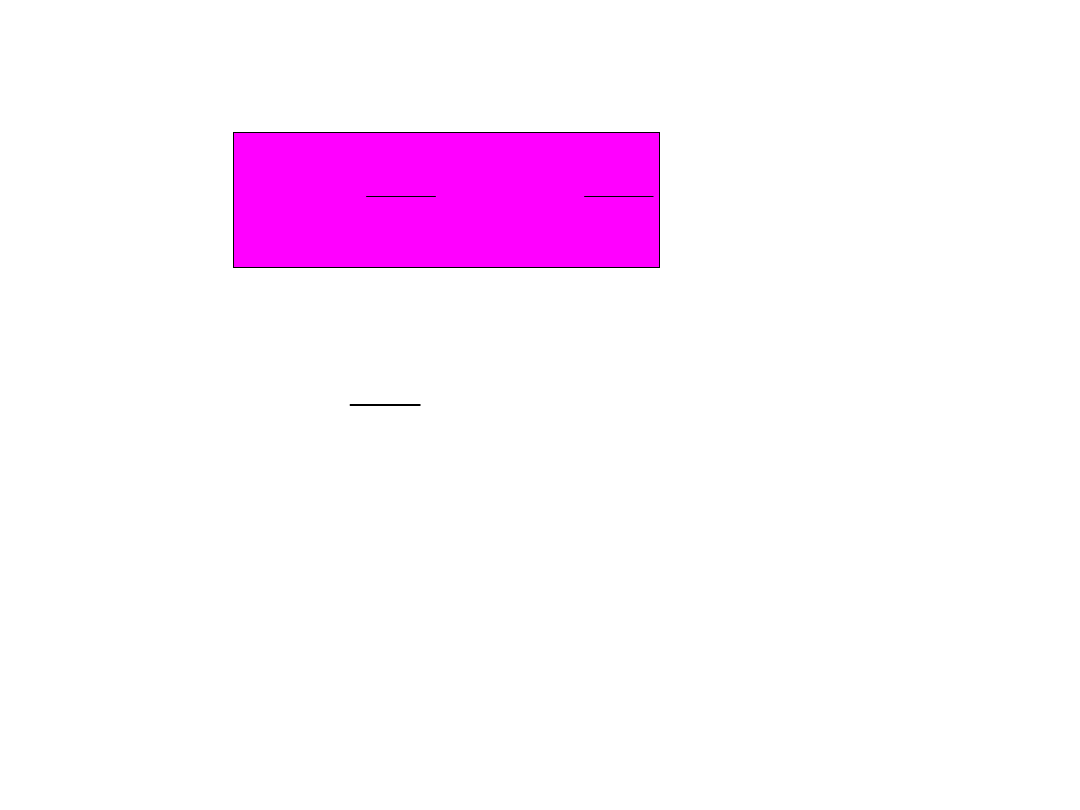
z

g

max

z

g

max

W

M

y

J

M

C









max

y

J

W

zc

z



Wskaźnik przekroju

2

2

2

/

3

2

2

2

dx

w

d

dx

dw

1

dx

w

d

1









































z

g

J

M

E





z

g

2

2

EJ

M

dx

w

d





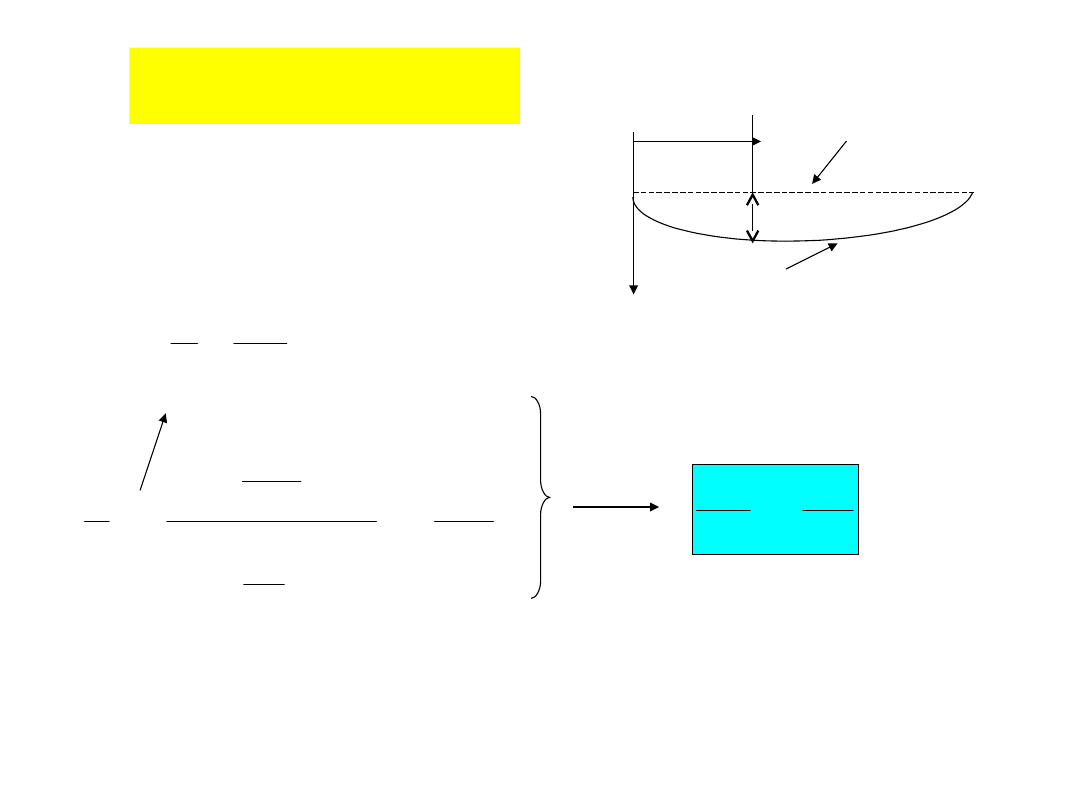
w – przemieszczenie warstwy obojętnej

Równanie różniczkowe linii
ugięcia

w

x

w(x)

nieodkształcona warstwa
obojętna

Warstwa obojętna
po odkształceniu

Warunki brzegowe

max

y

J

W

zc

z

