
Opracował: Romuald
Redzicki
MECHANIKA
MECHANIKA
Wykład Nr 3
DYNAMIKA
Temat
Dynamika punktu materialnego
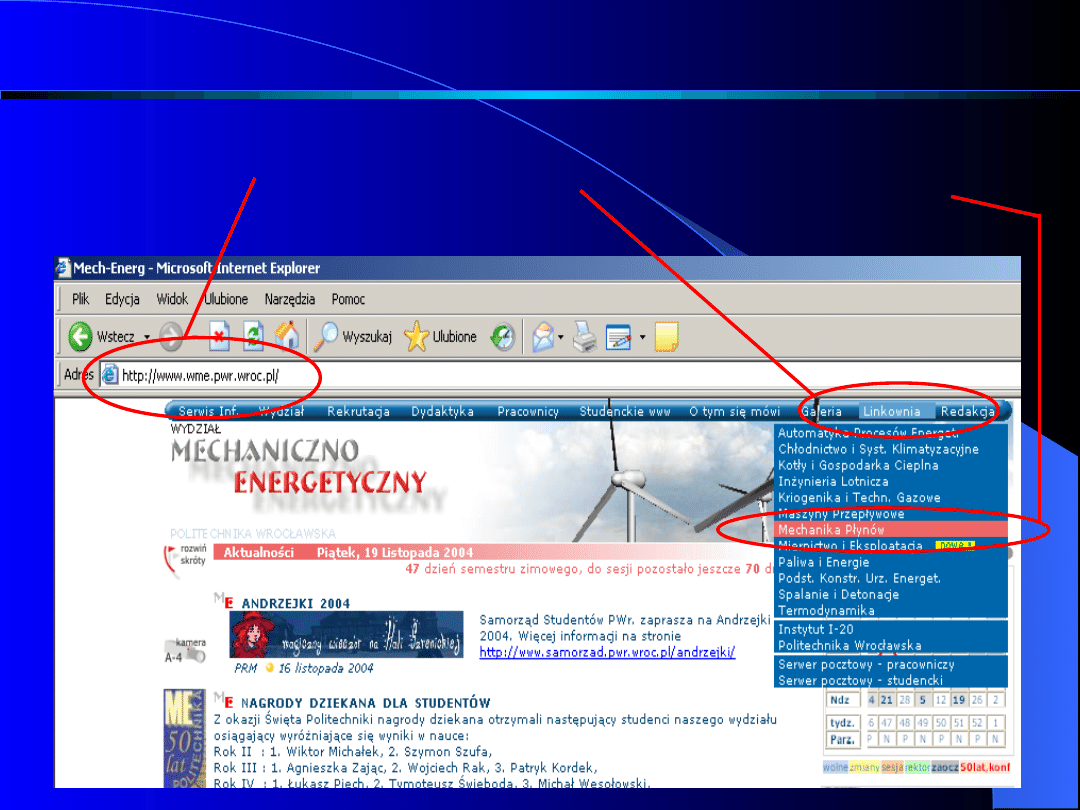
Jak znaleźć wykłady na stronie www
Jak znaleźć wykłady na stronie www
www.wme.pwr.wroc.pl
Rys. 1
Linkown
ia
Mechani
a Płynów
Ruch bezwzględny jest rezultatem
złożenia ruchu względnego i unoszenia.
DZIAŁALNOŚĆ
DYDAKTYCZNA
Jak znaleźć wykłady na stronie www
Jak znaleźć wykłady na stronie www

Dynamika punktu materialnego
Dynamika punktu materialnego
DYNAMIKA
jest
działem
mechaniki
opisującym ruch układu materialnego pod
wpływem sił działających na ten układ.
Oparta jest na zasadach sformułowanych
przez Newtona w traktacie
Philosophiae naturalia principia mathematica
(1687
r.).
Prawa te stały się podstawą rozwoju
mechaniki.
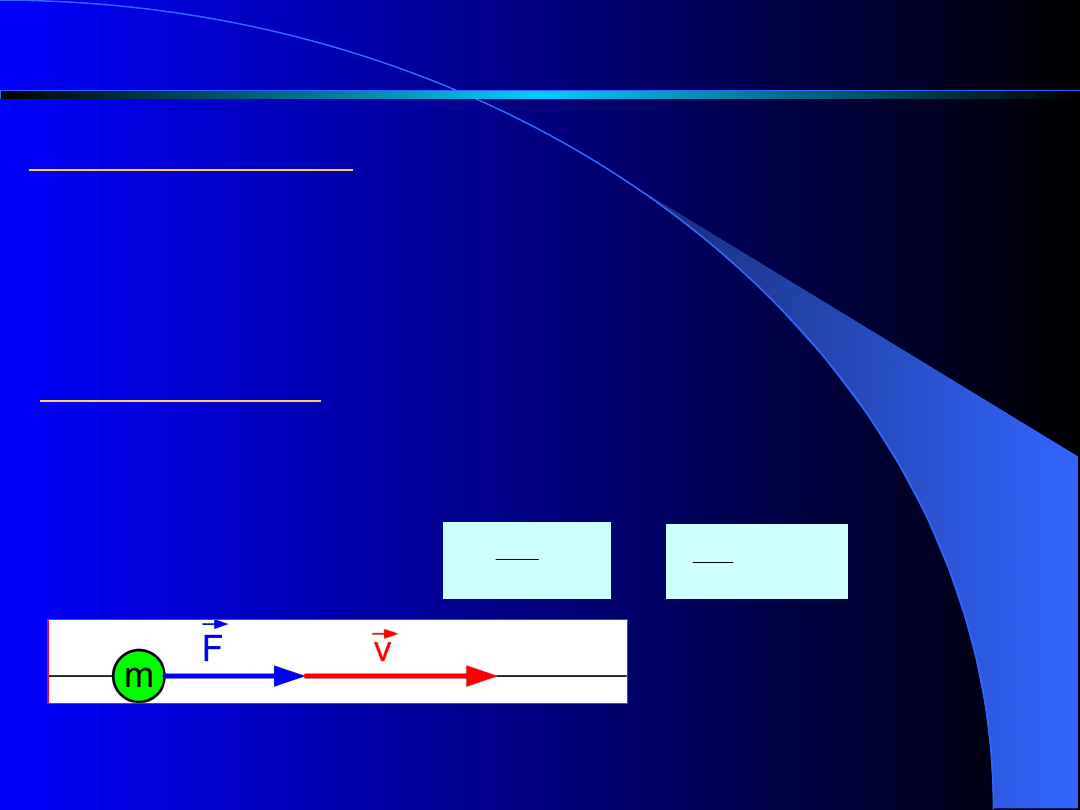
Zasada pierwsza.
Punkt materialny, na który nie działają żadne siły lub
działają siły wzajemnie równoważące się, pozostaje
względem układu odniesienia w spoczynku lub ruchu
jednostajnym prostoliniowym.
Zasady dynamiki klasycznej Newtona
Zasady dynamiki klasycznej Newtona
Zasada druga.
Zmiana ilości ruchu (pędu) jest proporcjonalna
względem siły działającej i ma kierunek prostej, wzdłuż
której ta siła działa.
)
v
(m
dt
d
F
F
a
m
dt
v
d
m
Rys. 1
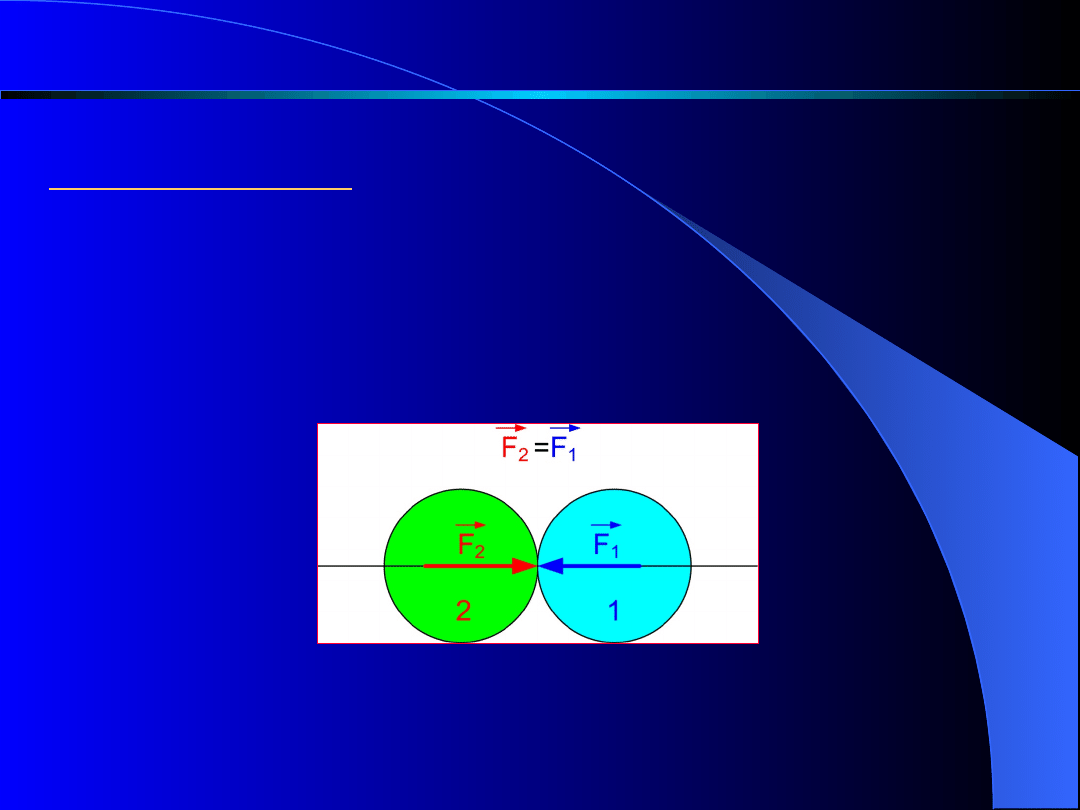
Zasada trzecia.
Każdemu
działaniu
towarzyszy
równe,
lecz
przeciwnie zwrócone oddziaływanie, czyli wzajemne
oddziaływania dwóch ciał są zawsze równe i
skierowane przeciwnie.
Zasady dynamiki klasycznej Newtona
Zasady dynamiki klasycznej Newtona
Rys. 2
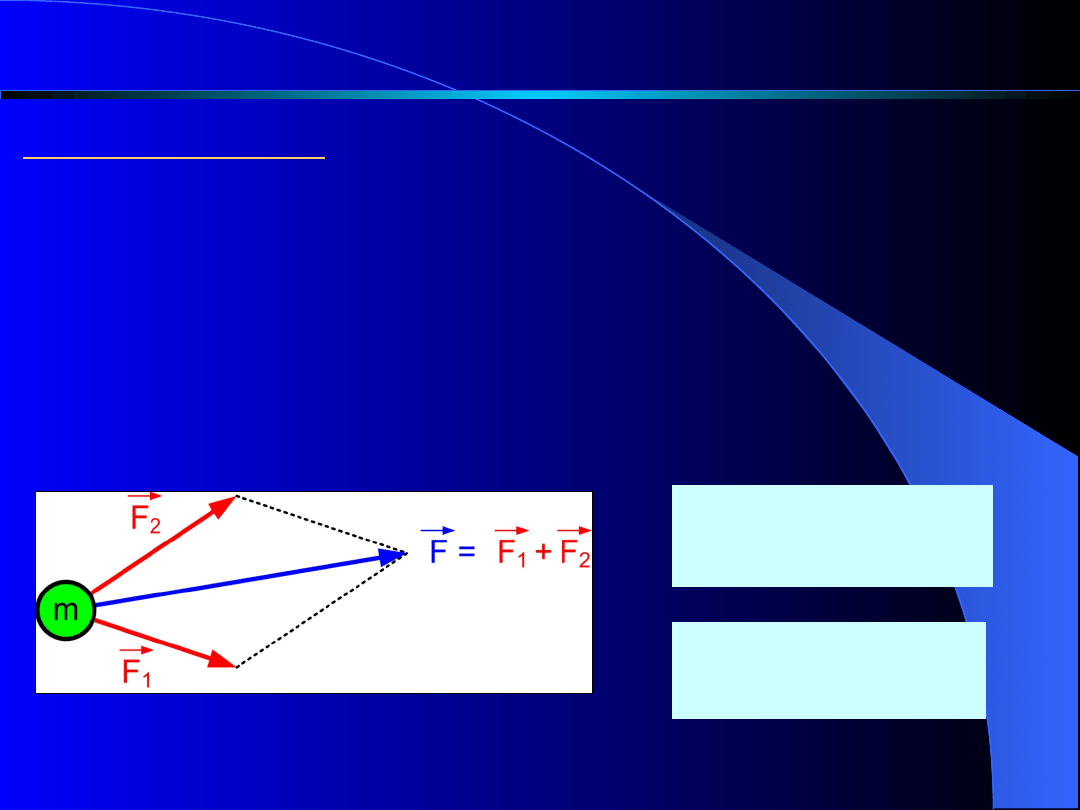
Zasada czwarta.
Jeśli na punkt materialny o masie
m
działa jednocześnie
kilka sił, to punkt uzyskuje przyspieszenie równe sumie
geometrycznej przyspieszeń, jakie uzyskałby w wyniku
niezależnego działania każdej z sił.
Zasadę czwartą nazwano
prawem superpozycji.
Zasady dynamiki klasycznej Newtona
Zasady dynamiki klasycznej Newtona
Rys. 3
n
i 1
...
n
F
n
2
1
F
F
F
n
i 1
...
n
a
n
2
1
a
a
a
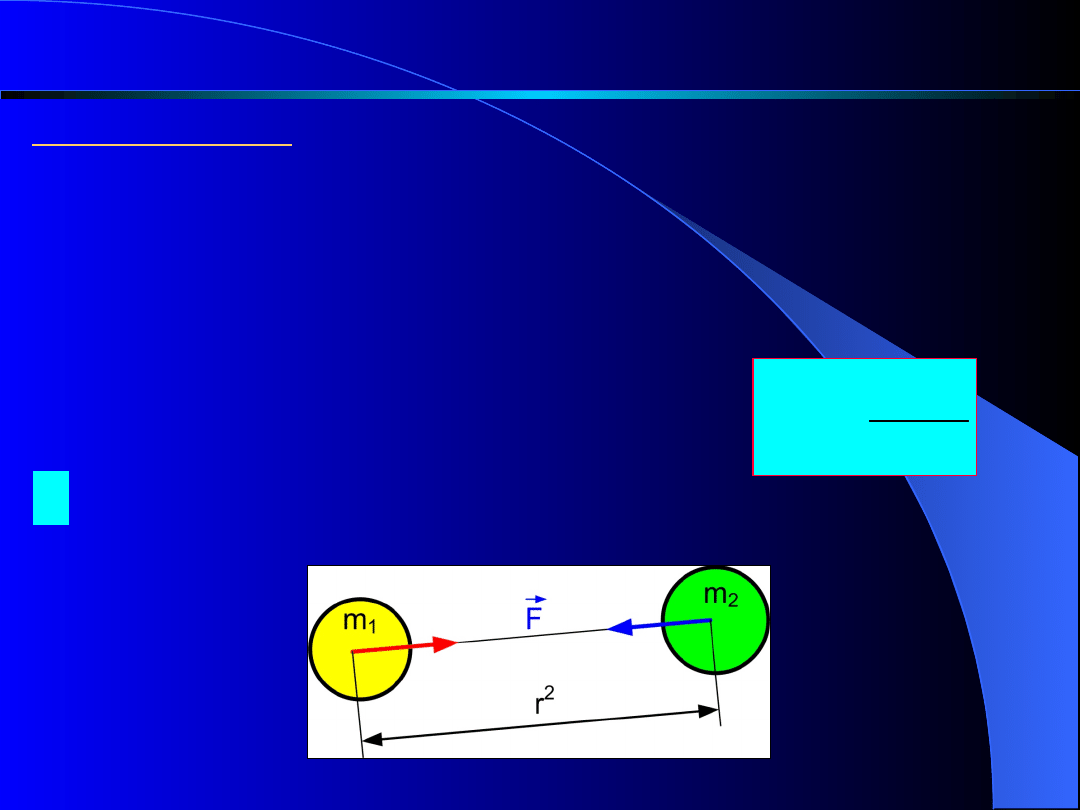
Zasada piąta.
Każde dwa punkty materialne przyciągają się
wzajemnie z siłą wprost proporcjonalną do iloczynu
mas (
m
1
, m
2
) i odwrotnie proporcjonalnie do kwadratu
odległości
r
między nimi. Kierunek siły leży na prostej
łączącej te punkty.
Prawo to nazywamy
prawem grawitacji.
2
2
1
r
m
m
k
F
-
stała
grawitacji
k
Rys. 4
Zasady dynamiki klasycznej Newtona
Zasady dynamiki klasycznej Newtona
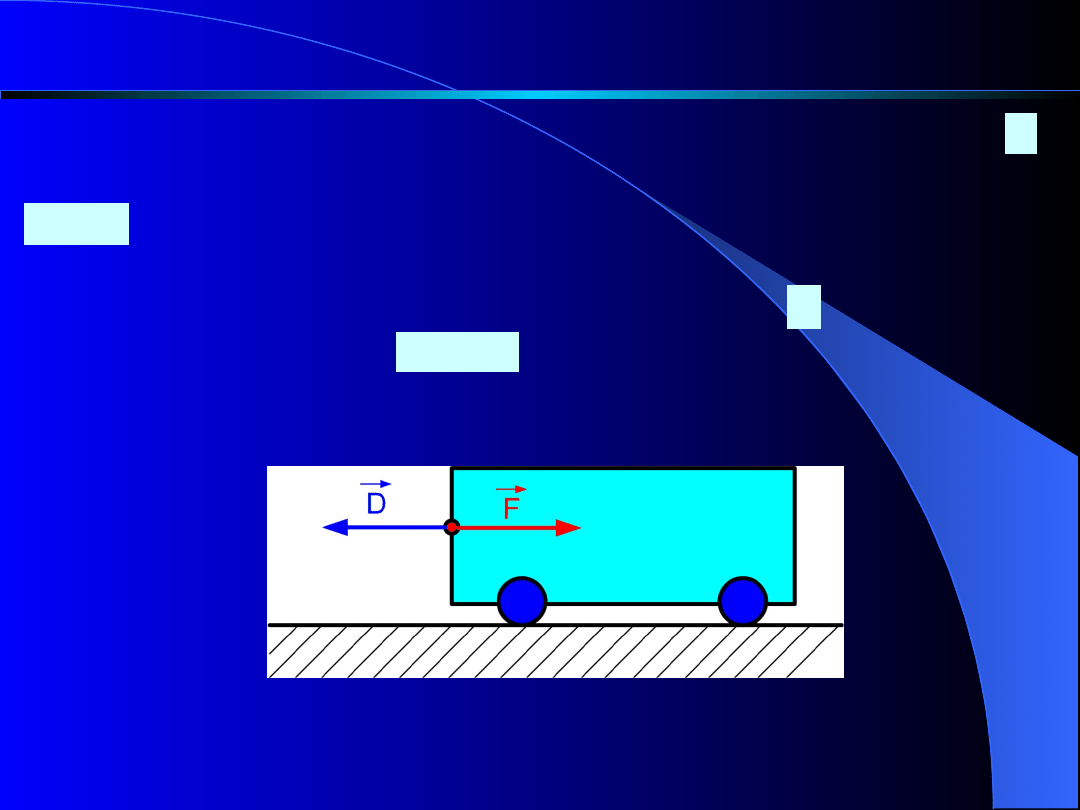
Wyobraźmy sobie, że pchając wózek nadajemy mu
przyspieszenie . Do wózka przyłożyliśmy siłę
pochodzącą od naszych mięśni równą
,
,
gdzie m-masa wózka (pomijamy tarcie wózka przy
toczeniu). Jednocześnie zgodnie z zasadą akcji i reakcji
do naszych rąk przyłożona jest siła pochodząca od
działania wózka, równa sile , lecz zwrócona przeciwnie,
czyli siła . Siłę tę będziemy nazywali siłą
bezwładności lub siłą d’Alemberta
(rys. 5).
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
a
a
m
F
F
a
m
D
Rys. 5
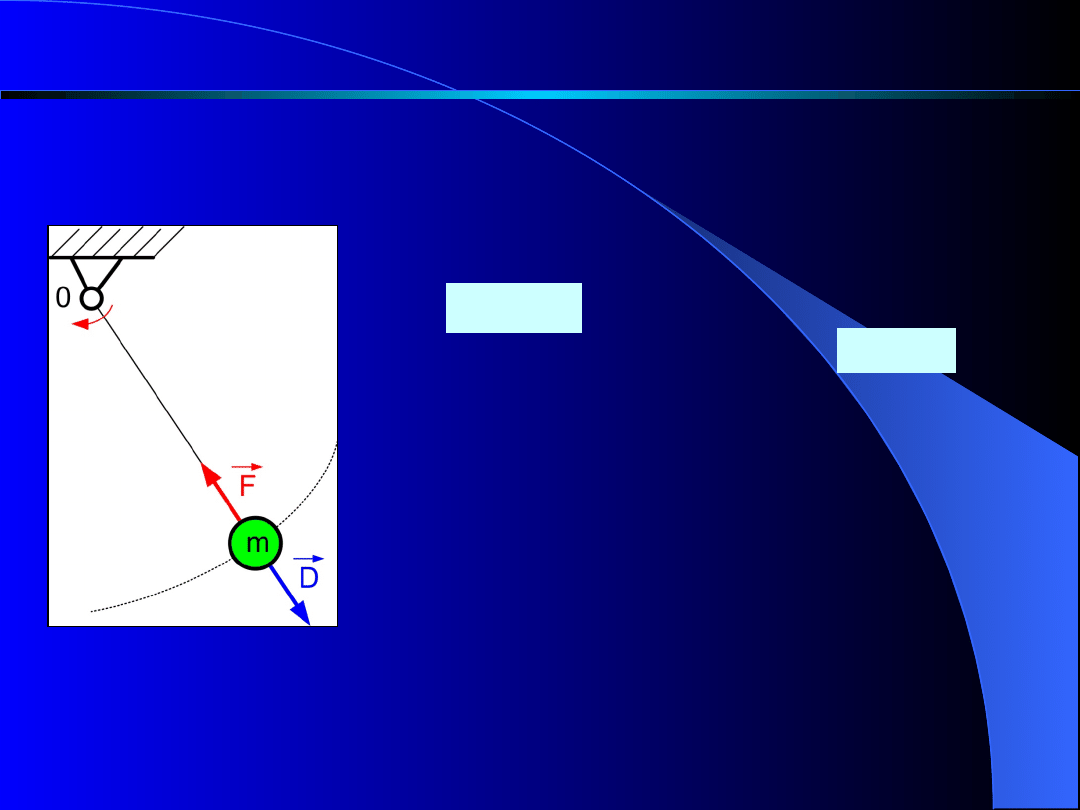
Podobnie ciężarek o masie m
obracany na nici wokół punktu 0
poddany jest działaniu siły
działającej do środka 0. Nić
natomiast jest rozciągana siłą
. Jest to siła bezwładności.
Nazywamy
ją
czasem
siłą
odśrodkową (rys. 6).
Rys. 6
n
a
m
F
n
a
m
D
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
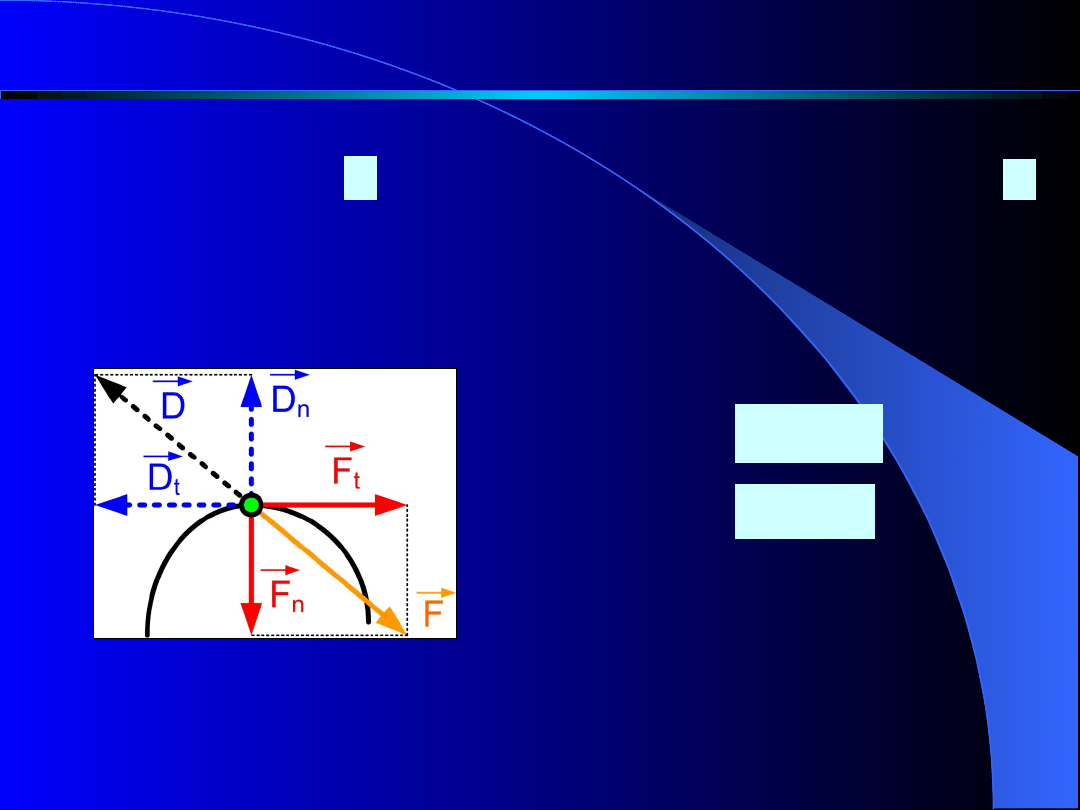
Niech po dowolnym torze porusza się punkt materialny
o masie m. Na punkt ten działa siła nadając, mu
przyspieszenia całkowitego . Siłę F oraz
przyspieszenie a rozłożymy na kierunek styczny i
normalny do toru, otrzymamy (rys. 7)
F
a
siła styczna
-
siła
normalna -
t
t
a
m
F
n
n
a
m
F
Rys. 7
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
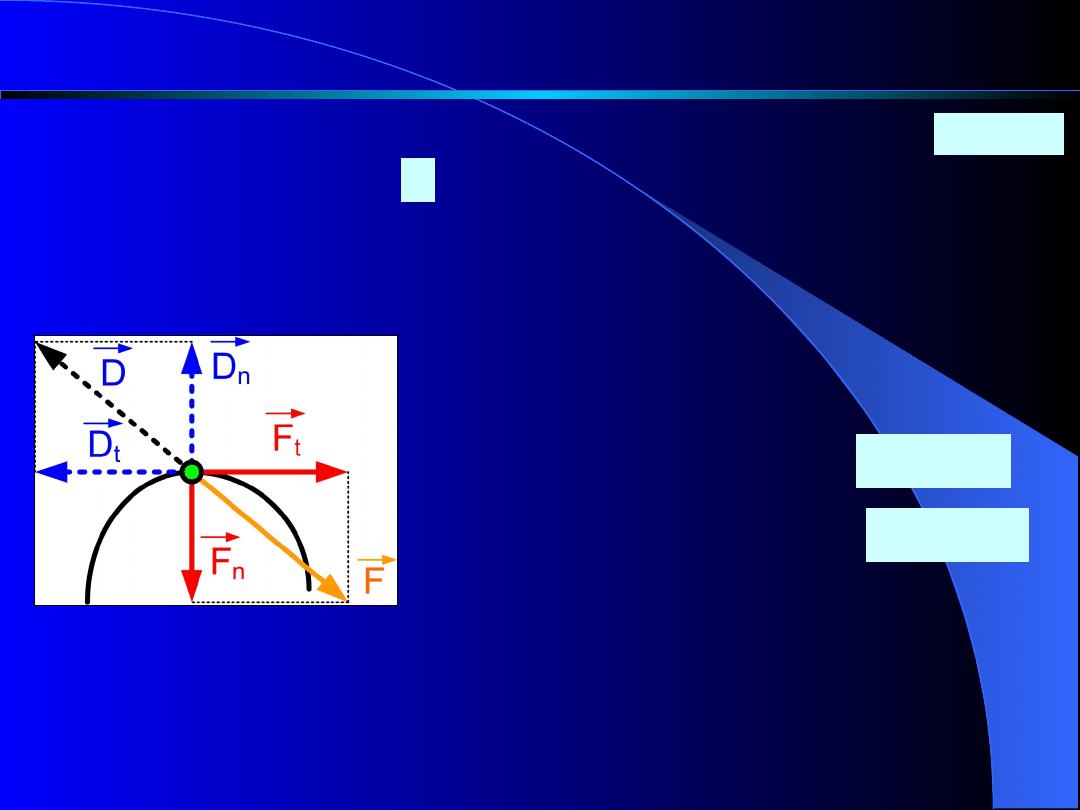
Poruszającemu
się
punktowi
przypiszemy
siłę
bezwładności , równą co do modułu sile ,
lecz zwróconą przeciwnie. Siłę tę możemy również
rozłożyć na kierunek styczny i normalny do toru.
Otrzymamy wtedy tzw. styczną i normalną siłę
bezwładności. Będzie mianowicie
Rys. 7
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
a
m
D
F
styczna
siła
bezwładności -
normalna
siła
bezwładności -
t
t
a
m
D
n
n
a
m
D

Siła bezwładności jest równa
iloczynowi masy przez
przyspieszenie ruchu. Jej kierunek
jest taki jak kierunek przyspieszenia
ruchu, jej zwrot zaś jest zawsze
przeciwny niż zwrot przyspieszenia
.
Siła bezwładności jest równa zeru wtedy, gdy
w ruchu nie występuje przyspieszenie. W
szczególności, styczna siła bezwładności nie
występuje w ruchu jednostajnym punktu,
normalna siła bezwładności jest równa zeru w
ruchu prostoliniowym.
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta

W rzeczywistości siła bezwładności nie jest przyłożona
do poruszającego się punktu, jest dla tego punktu siłą
pomyślaną. Przyjęcie tej siły prowadzi do bardzo
dogodnej
metody
rozwiązywania
zagadnień
dynamicznych. Przeprowadzone rozumowanie jest
treścią zasady d'Alemberta, która w odniesieniu do
swobodnego punktu materialnego będzie brzmiała, jak
następuje:
Przyjmiemy, że po dowolnym torze porusza się punkt
materialny na skutek działania nań sił
nadających mu przyspieszenia całkowitego . Jeżeli
do punktu materialnego oprócz sił czynnych
przyłożymy jeszcze siłę bezwładności ,
otrzymany układ sił będzie w równowadze.
n
2
1
F
F
F
,....,
,
a
a
m
D
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta

W ruchu swobodnego punktu
materialnego układ sił czynnych
równoważy się z pomyślaną siłą
bezwładności.
Możemy ją przedstawić za pomocą wzoru, który jest
konsekwencją równania
czyli
a
m
F
0
)
(
a
m
i
F
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta

W ruchu punktu nieswobodnego
siły czynne i reakcje więzów
równoważą się z pomyślaną silą
bezwładności.
W przypadku ruchu punktu nieswobodnego oprócz sił
czynnych , na punkt taki działają reakcje więzów
. Wprowadzając pomyślaną siłę bezwładności ,
zasadę
d'Alemberta
dla
punktu
nieswobodnego
stwierdzamy:
i
F
i
R
)
( a
m
0
)
(
a
m
i
i
R
F
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
Tak więc wprowadzając do zagadnień dynamiki siłę
bezwładności sprowadzamy je do zagadnień statyki.
Metodę tę nazywamy metodą kinetostatyki.
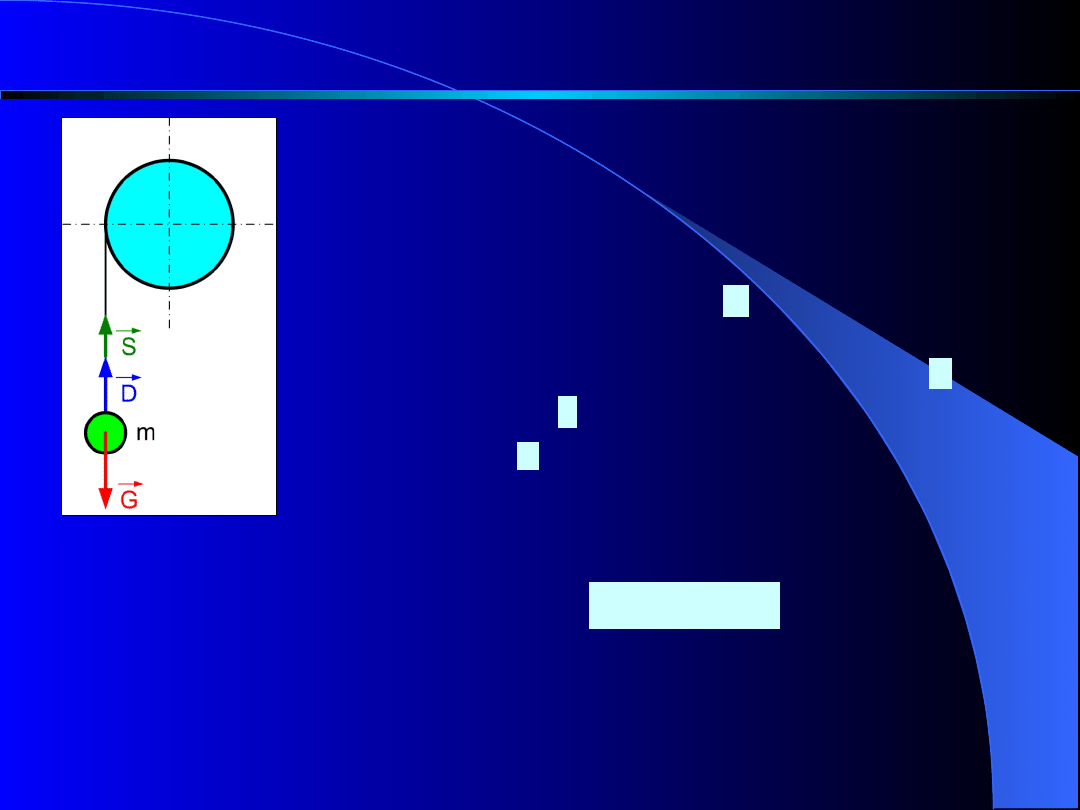
Dla przykładu rozpatrzmy ruch
masy m zawieszonej na końcu liny
rozwijającej się z bębna (rys. 8).
Załóżmy,
że
przyspieszenie
opadającej masy wynosi .
Na
rozważaną
masę
działa
siła
ciężkości i siła napięcia w linie .
Wprowadzając
pomyślaną
siłę
bezwładności , zwróconą przeciw
przyspieszeniu, stosujemy warunek
równowagi (warunek rzutów na oś
liny):
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
Rys. 8
a
G
S
D
0
D
G
-
S

Rys. 8
Siła bezwładności. Zasada D’Alemberta
Siła bezwładności. Zasada D’Alemberta
0
D
G
-
S
0
a
m
g
m
S
)
a
-
g
m(
S
a
g
czyli
stąd
W przypadku swobodnego spadku masy , siła
napięcia będzie równa zeru. Przy jednostajnym ruchu
masy siła w linie będzie równa sile ciężkości.

Punkt materialny o masie m porusza się pod wpływem sił
. Zgodnie z podstawowym równaniem dynamiki
możemy napisać
ale , zakładając więc, że masa punktu jest stała,
napiszemy
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY
Wektor nazywamy
pędem
lub
ilością ruchu
punktu materialnego. Jest to wektor o module m razy
większym od modułu wektora prędkości, mający
kierunek i zwrot taki jak wektor prędkości.
n
2
1
F
F
F
,....,
,
i
F
a
m
dt
v
d
a
i
F
)
v
(m
dt
d
v
m
p

W układzie kartezjańskim wektor pędu przedstawimy w
następujący sposób:
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY
k
z
m
j
y
m
i
x
m
p
Jednostką pędu w układzie SI
1 kgm/s = 1
Ns.
Uwzględniając wprowadzone pojęcie pędu, równanie
(1.5) możemy przedstawić w postaci
(1.6)
i
F
p
(1.7)
Równanie to przedstawia drugą zasadę Newtona,
wyrażoną poprzednio za pomocą wzoru . Jest to
sformułowanie ogólne, słuszne również w mechanice
relatywistycznej. W przypadku szczególnym, przy
założeniu m = const, równanie to prowadzi do
równania .
a
m
F
a
m
F

W przypadku gdy na punkt nie działają siły lub siły
działające równoważą się, czyli , równanie (1.7)
przyjmie postać
0
i
F
.
const
p
Widzimy więc, że drugą zasadę Newtona możemy napisać
w następujący sposób:
Pochodna pędu punktu materialnego względem
czasu jest równa sumie sił działających na dany
punkt.
(1.8
)
Wniosek powyższy, obowiązujący również w mechanice
relatywistycznej, gdzie masa jest zmienna, jest treścią
zasady zachowania pędu punktu materialnego.
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY

Pęd punktu materialnego jest wektorem stałym,
jeżeli suma geometryczna sil działających na punkt
materialny jest równa zeru.
Równanie (1.5) przepiszemy w postaci
)
v
d(m
dt
F
(1.9
)
gdzie
i
F
F
Wektor nazywamy elementarnym impulsem
siły. Jest to
wektor o kierunku i zwrocie takim jak wypadkowa sił
działających .
Równanie (1.9) możemy opisać następująco:
Impuls elementarny siły działającej na punkt
materialny jest równy przyrostowi elementarnemu
pędu tego punktu.
d
dt
F
F
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY

Całkując obustronnie równanie (1.9)
otrzymamy
)
(
1
2
t
t
mv
mv
F
2
1
lub
,oznaczając
dt
2
1
t
t
F
-impuls całkowity siły F w przedziale
czasu t
2
-t
1
,
otrzymamy
1
2
p
p
(1.10)
Przyrost pędu masy poruszającego się punktu jest
równy impulsowi całkowitemu sił działających.
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY

Stwierdzamy więc, że dla zmiany pędu masy niezbędny
jest określony czas działania siły. Siły działające
nieskończenie krótko lub, praktycznie biorąc, mające
bardzo
krótki
czas
działania
nazywamy
siłami
chwilowymi
(działanie nogi gracza na piłkę, siły przy
uderzeniu kul bilardowych) w odróżnieniu od
sił ciągłych
,
do której zaliczamy np. siłę ciężkości.
Równanie (1.10) podaje nam dogodny sposób określania
impulsu sił. Stosujemy je często w przypadku działania sił
chwilowych.
Z równania tego wynika, że zmiana wektora pędu
będzie tym intensywniejsza, im większa będzie siła
oraz
im
mniejsza
będzie
masa
m
i
pęd
początkowy .
F
1
p
PĘD MASY. IMPULS SIŁY
PĘD MASY. IMPULS SIŁY

KRĘT PUNKTU MATERIALNEGO
KRĘT PUNKTU MATERIALNEGO
Po dowolnym torze porusza się punkt o masie m, z
prędkością . Pęd tego punktu jest wektorem o
takim samym kierunku i zwrocie jak wektor . Obierzmy
dowolny punkt 0 jako początek układu stałego x, y, z i
połączmy go z poruszającym się punktem promieniem-
wektorem
.
V
v
m
p
v
r
Krętem
poruszającego
się
punktu
materialnego
względem obranego bieguna 0 nazywamy wektor równy
iloczynowi wektorowemu promienia
,
przez pęd
poruszającego się punktu.
Kręt jest więc momentem pędu
(momentem ilości ruchu) względem obranego bieguna.
r
p
v
m
r
p
mom
K
o
o

Jeżeli przez obrany biegun 0 przeprowadzimy dowolną oś
i zrzutujemy na nią wektor krętu , to otrzymamy kręt
poruszającego się punktu względem tej osi. W
szczególności, względem osi współrzędnych x, y, z kręt
ma następujące składowe:
o
K
)
y
z
-
z
m(y
K
x
)
z
x
-
x
m(z
K
y
)
x
y
-
y
m(x
K
z
,
,
gdzie x, y, z - współrzędne poruszającego się punktu
materialnego. Zróżniczkujemy względem czasu
równanie (1.11)
czyl
i
)
v
(m
dt
d
r
v
m
dt
dr
dt
K
d
o
a
m
r
v
m
v
K
o
KRĘT PUNKTU MATERIALNEGO
KRĘT PUNKTU MATERIALNEGO

ale iloczyn wektorowy wektorów równoległych ,
natomiast iloczyn przedstawia moment sił
działających na poruszający się punkt materialny
względem obranego bieguna 0. Tak więc
0
v
m
v
a
m
r
(1.13
)
o
o
M
K
Pochodna wektora krętu względem czasu jest równa
momentowi głównemu wszystkich sil działających na
dany punkt materialny.
Z równania (1.13) wynika, że
jeżeli moment sil
działających na poruszający się punkt materialny jest
względem jakiegoś bieguna
równy zeru ( ), to kręt poruszającego się
punktu względem tego bieguna jest wektorem
stałym.
0
o
M
KRĘT PUNKTU MATERIALNEGO
KRĘT PUNKTU MATERIALNEGO
Fakt ten stanowi
zasadę zachowania krętu
dla punktu
materialnego. Płaszczyznę prostopadłą do wektora krętu
nazywamy płaszczyzną niezmienną. W układzie SI
jednostką krętu jest 1 Nms.

DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO
Równanie to, przedstawiające związek między masą,
przyspieszeniem i siłą, nazywamy dynamicznym
równaniem ruchu. Powyższy związek podany jest w
postaci wektorowej. Uwzględniając znane zależności
k
j
i
x
y
x
F
F
F
F
ora
z
k
j
i
z
y
x
a
Dynamiczne równanie ruchu w postaci wektorowej
można zastąpić trzema równaniami analitycznymi:
x
m
F
x
y
m
F
y
z
m
F
z
,
,
Napiszmy jeszcze raz równanie przedstawiające drugą
zasadę dynamiki.
a
m
F

Przy analizie ruchu punktu stosuje się w mechanice
oprócz układu kartezjańskiego również inne układy
ortogonalne. Równania ruchu w tych układach
otrzymamy uwzględniając znane z kinematyki wzory
przedstawiające przyspieszenia w tych układach.
Tak
na
przykład
w
biegunowym
układzie
współrzędnych
dynamiczne równania ruchu maja
postać:
,
r
2
F
)
r
-
r
m(
F
)
(r
dt
d
r
m
2
W
układzie współrzędnych walcowych
, równania te
będą wyglądały następująco:
r
2
F
)
r
-
r
m(
F
)
(r
dt
d
r
m
2
z
F
z
m
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO

W kinematyce podaliśmy składowe przyspieszenia w
naturalnym układzie współrzędnych. Opierając się na
tych składowych napiszemy dynamiczne równania ruchu
w
naturalnym układzie współrzędnych
,
t
F
dt
dv
m
n
2
F
r
v
m
0
b
b
F
ma
,
Wreszcie podamy jeszcze dynamiczne równania ruchu we
współrzędnych kulistych
:
r
2
2
2
F
)
sin
r
-
r
-
r
m(
F
r
-
)
2
(r
dt
d
r
m
cos
sin
2
2
F
)
sin
(r
dt
d
sin
r
m
2
2
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO

Rozwiązanie równań dynamicznych sprowadza się do
dwóch zagadnień zwanych niekiedy
dwoma
zadaniami
dynamiki
.
1. Zadanie pierwsze
polega na tym, że mamy
parametryczne równania toru, po którym porusza się
punkt materialny, czyli mamy określone równania
,
)
(t
x
x
)
(t
y
y
)
(t
z
z
,
Chcemy natomiast wyznaczyć siłę , pod której
wpływem porusza się punkt materialny Zadanie to
rozwiązuje się w prosty sposób. Różniczkując dwukrotnie
względem czasu równania parametryczne, określamy
składowe
przyspieszenia,
podstawiając
je
do
dynamicznych równań ruchu znajdujemy szukane
składowe siły działającej, a więc i wektor siły.
F
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO

2. Bardziej złożone jest drugie zadanie dynamiki
.
Polega ono na wyznaczeniu (przy danej masie i sile)
przyspieszenia, prędkości i toru poruszającego się
punktu.
W zadaniu tym musimy mieć określoną siłę
działającą.
Możemy
tu
rozróżnić
następujące
przypadki.
a) Siła jest wektorem stałym, np. siła ciężkości,
tarcie,
b) Siła jest funkcją czasu, np. siła odśrodkowa
wahadła,
c) Siła zależy od położenia, np. siła sprężystości, siła
ciężkości przy uwzględnieniu dużego obszaru,
d) Siła zależy od prędkości poruszającego się punktu,
np. opór powietrza.
W najogólniejszym przypadku równania ruchu w
współrzędnych kartezjańskich b miały postać
)
,
,
,
,
,
,
(
t
z
y
x
z
y
x
F
x
m
x
)
,
,
,
,
,
,
(
t
z
y
x
z
y
x
F
y
m
y
)
,
,
,
,
,
,
(
t
z
y
x
z
y
x
F
z
m
z
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO

Całka ogólna tych równań (o ile istnieje) ma postać
trzech równań zawierających sześć stałych całkowania.
Różniczkując te równania i uwzględniając warunki
początkowe dla t=0
,
o
x
x
o
x
x
,
o
y
y
o
y
y
o
z
z
o
z
z
,
określimy parametryczne
równania toru
)
,
,
,
,
,
,
(
1
t
z
y
x
z
y
x
f
x
o
o
o
o
o
o
)
,
,
,
,
,
,
(
2
t
z
y
x
z
y
x
f
y
o
o
o
o
o
o
)
,
,
,
,
,
,
(
3
t
z
y
x
z
y
x
f
z
o
o
o
o
o
o
Ten układ równań określa ruch punktu, na który działają
znane siły i który w chwili początkowej zajmował
określone
położenie
i
miał
określoną
prędkość
początkową.
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
DYNAMICZNE RÓWNANIA RUCHU PUNKTU
MATERIALNEGO
MATERIALNEGO

CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU
Określenie siły na podstawie parametrycznych
równań toru.
Masa m = 4 kg porusza się po torze
określonym parametrycznymi równaniami
6
2t
4t
2
3
x
m,
4
t
3
y
2
,
m.
Określić działająca siłę.
Różniczkujemy dwukrotnie względem czasu i znajdujemy
składowe przyspieszenia
2
,
4
24
s
m
t
x
2
,
6
s
m
y
Podstawiając je do równań ruchu znajdujemy
szukaną siłę
N
16
96t
x
m
F
x
N
24
y
m
F
y
lub w postaci
wektorowej
j
24
i
16)
96t
F
(

Ruch pod wpływem siły
.
W tym przypadku
równanie dynamiczne ma postać
0
F
, czyli
0
a
m
0
r
Po scałkowaniu i przyjęciu, że w chwili t = 0
, otrzymamy
o
o
v
r
o
o
v
r
Całkując drugi raz i uwzględniając, że dla t = 0
, otrzymamy
o
r
r
o
o
r
v
r
t
Dochodzimy w ten sposób do znanych równań ruchu
jednostajnego i prostoliniowego.
CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU

Po dwukrotnym scałkowaniu i przyjęciu warunków
początkowych:
dla t = 0 oraz dla będzie
Ruch pod wpływem siły stałej .
Napiszemy
równanie ruchu w postaci
const
F
F
r
m
1
o
o
v
r
o
r
r
o
o
r
v
F
m
r
t
t
2
1
CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU
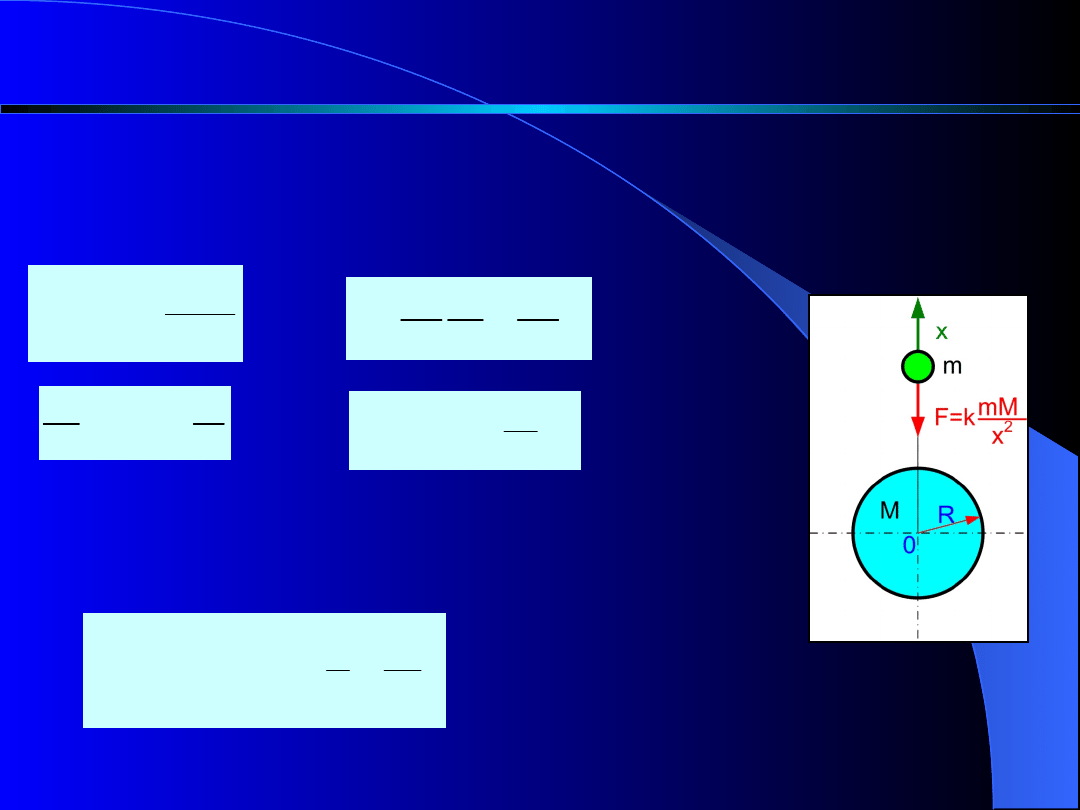
Ruch pod wpływem siły, która jest funkcją
położenia.
Jako przykład rozpatrzmy ruch punktu materialnego o
masie m wystrzelonego z planety o masie M (rys. 9).
Równanie ruchu ma postać
2
x
mM
k
x
m
ale
v
d
v
v
x
d
dt
dx
dx
d
x
CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU
2
1
x
kM
x
d
v
d
v
x
x
kM
d
d
v
v
2
1
lu
b
Po całkowaniu otrzymujemy
równanie
o
x
x
kM
1
1
2
2
o
2
v
v
Rys. 9

Obliczymy, na jaką wysokość H wzniesie się punkt
materialny wyrzucony z planety o promieniu R, jeżeli
nadano mu prędkość początkową v
o
. Podstawimy więc v
= 0, x = H, x
o
= R otrzymamy
R
H
kM
1
1
2
2
o
v
lub po
przekształceniu
R
kM
kMR
H
2
o
v
2
2
Zastanówmy się, z jaką prędkością należy wyrzucić
punkt materialny z planety, aby na nią nie wrócił,
czyli aby stał się satelitą planety.
Prędkość tę, zwaną prędkością ucieczki v
∞
,
otrzymamy, podstawiając do wzoru v
o
= v
∞
oraz H =
∞. Na prędkość ucieczki otrzymamy wyrażenie
R
kM
2
v
CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU

Na powierzchni Ziemi siła grawitacji ma
wartość
mg
R
mM
2
Prędkość ucieczki dla Ziemi będzie
gR
2
v
Przyjmując w szczególności R = 6340 km oraz g = 9,81
m/s
2
otrzymamy
v
∞
≈ 11,8 km/s ≈ 42 500 km/h.
Jest to prędkość, jaką należy nadać ciału, aby stało się
ono satelitą Ziemi.
CAŁKOWANIE RÓWNAŃ RUCHU
CAŁKOWANIE RÓWNAŃ RUCHU

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch postępowy
– układ ruchomy wykonuje ruch postępowy
Względem układu stałego ruch punktu jest określony
równaniem
i
b
m
F
a
u
w
b
a
a
a
W układzie ruchomym ruch określony jest więc
równaniem
u
i
w
m
m
a
F
a
oraz
u
u
ma
D
w którym nazywamy siłą bezwładności
unoszenia. Jest ona równa iloczynowi masy punktu przez
przyspieszenie unoszenia i jest zwrócona przeciwnie niż
.
u
a
(17)

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch postępowy
– układ ruchomy wykonuje ruch postępowy
Równanie ruchu przyjmuje następującą postać:
u
i
w
m
D
F
a
Względem ruchomego układu odniesienia wykonującego
ruch postępowy punkt materialny porusza się tak, jakby
działała na niego, oprócz sił danych, jeszcze pomyślana
siła bezwładności unoszenia.
Zasada względności mechaniki klasycznej:
Za pomocą żadnych zjawisk mechanicznych nie możemy
wykazać
istnienia prostoliniowego, jednostajnego ruchu
postępowego układu
odniesienia.
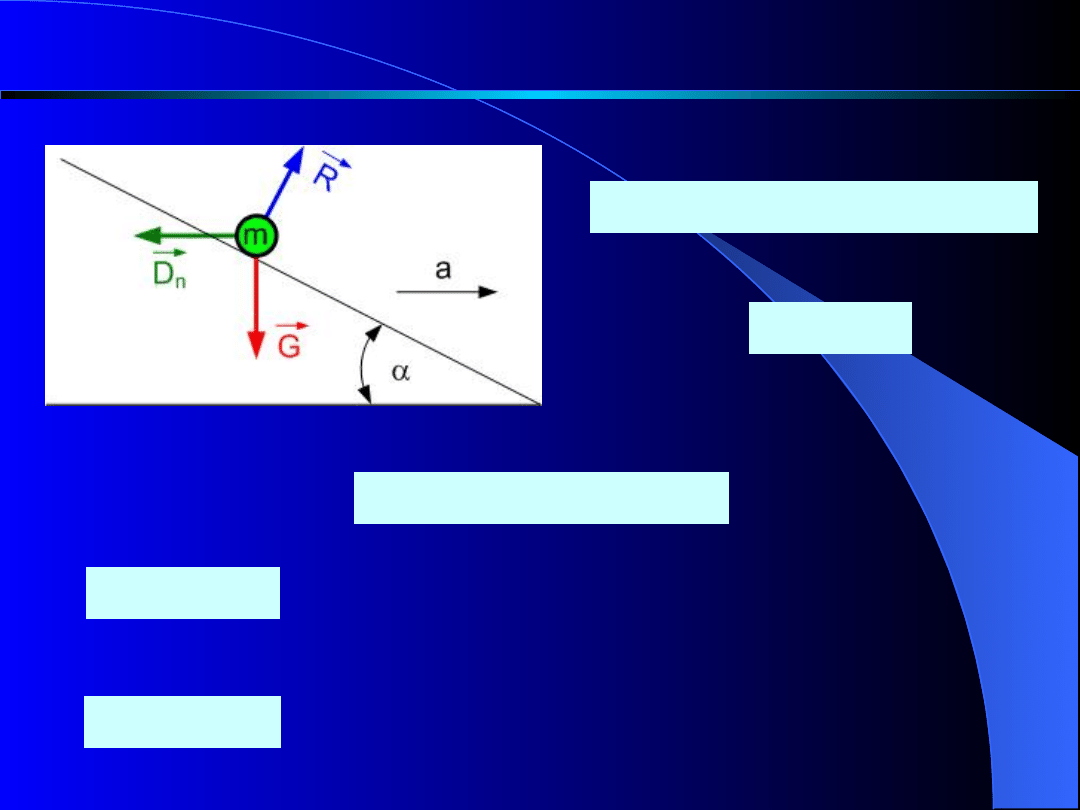
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch postępowy
– układ ruchomy wykonuje ruch postępowy
Rys. 8
cos
sin
u
D
mg
x
m
u
u
ma
D
cos
sin
u
a
g
x
Ostatecznie:
Dla punkt materialny będzie poruszał się
w dół. W przeciwnym przypadku punkt będzie poruszał
się do góry.
Gdy , punkt pozostanie w spoczynku lub w
ruchu jednostajnym prostoliniowym (względem ruchomej
płaszczyzny).
tg
g
a
u
tg
g
a
u

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch obrotowy
– układ ruchomy wykonuje ruch obrotowy
W układzie stałym równanie ruchu będzie następujące:
i
b
m
F
a
c
u
w
b
a
a
a
a
oraz
Równanie ruchu w układzie ruchomym przyjmie postać:
c
u
i
w
m
m
m
a
a
F
a
– siła bezwładności unoszenia,
– siła bezwładności unoszenia Coriolisa.
u
u
ma
D
c
c
ma
D
(18)

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch obrotowy
– układ ruchomy wykonuje ruch obrotowy
c
u
i
w
m
D
D
F
a
Względem ruchomego układu odniesienia wykonującego
ruch obrotowy punkt materialny porusza się tak jakby
działała na niego, oprócz sil danych, jeszcze pomyślana
siła bezwładności unoszenia i pomyślana siła
bezwładności Coriolisa.
W ruchu obrotowym przyspieszenie całkowite jest sumą
geometryczną przyspieszenia obrotowego i doosiowego,
czyli
d
o
u
a
a
a
c
d
o
i
w
m
D
D
D
F
a
w związku z tym
(19)
(20)

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch obrotowy
– układ ruchomy wykonuje ruch obrotowy
– obrotowa (styczna) siła bezwładności,
– poosiowa (normalna) siła bezwładności,
o
o
ma
D
d
d
ma
D
przy czym
mh
D
o
2
mh
D
d
ω
,
v
sin
2
w
w
c
mv
D
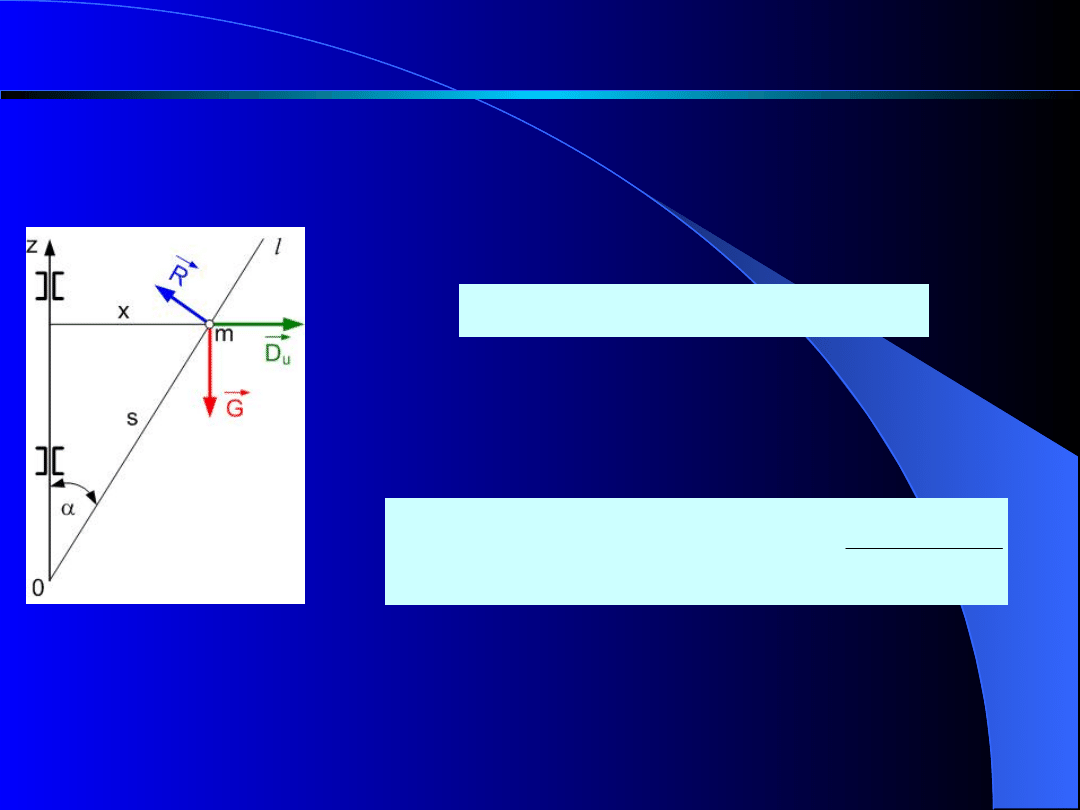
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch obrotowy
– układ ruchomy wykonuje ruch obrotowy
Rys. 9
Ruch punktu wzdłuż prostej l opisuje
równanie
sin
cos
u
D
mg
s
m
2
2
sin
sin
sin
cos
g
e
B
e
A
s
t
t
Rozwiązaniem ogólnym będzie
wyrażenie

RUCH WZGLĘDNY PUNKTU MATERIALNEGO
RUCH WZGLĘDNY PUNKTU MATERIALNEGO
– układ ruchomy wykonuje ruch obrotowy
– układ ruchomy wykonuje ruch obrotowy
W wielu zagadnieniach praktycznych za układ
odniesienia przyjmujemy Ziemię. W ogólności jest to
układ nieinercjalny. Jednak z wystarczająco dobrym
przybliżeniem Ziemię możemy uważać za układ
inercjalny, o ile tylko będziemy rozpatrywać ruch w
przedziałach czasu krótkich w porównaniu z okresem
ruchu postępowego i obrotowego Ziemi. Szczególnie
niewielką rolę odgrywa, przy występujących w praktyce
prędkościach, siła Coriolisa.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
Wyszukiwarka
Podobne podstrony:
W3 Dynamika pktu materialnego ruch wzgledny
zestaw 5 dynamika punktu materi Nieznany
05 dynamika punktu materialnego II
04 Dynamika punktu materialnego I
8 Dynamika 1 Dynamika punktu materialnego
04 dynamika punktu materialnego
4 Dynamika punktu materialnego, Fizjoterapia i Rehabilitacja, AWF MGR Fizjoterapia, Biomechanika AWF
Dynamika pasywa, materiały liceum i studia, WSZiB Kraków, Finanse przedsiębiorstw, IV semestr
dynamika pkt materialnego
DYNAMIKA PUNKTU MATERIALNEGO W JEDNYM WYMIARZE
8 Dynamika 1, Dynamika punktu materialnego
Podstawowe pojęcia fizykochemiczne i podział materiałów ze względu
Dynamika punktu materialnego
Dynamika punktu materialnego w jednym wymiarze 1A
3 Dynamika punktu materialnego Nieznany (2)
04 Dynamika punktu materialneg Nieznany (2)
więcej podobnych podstron