SYSTEMS OF LINEAR EQUATIONS II
Lecture 7
In this lecture we shall consider the Kronecker-Capelli Theorem, which
allows us to determine whether a system of equations has a solution
and if it does, whether it is unique.

m
n
mn
m
m
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
.
a
a
a
a
A
mn
m
n
1
1
11
m
mn
m
n
b
a
a
b
a
a
B
|
A
1
1
1
11
Kronecker – Capelli Theorem
The system of m linear equations in n unknowns possesses a solution (it
is said to be consistent) if and only if the coefficient matrix A and the
augmented matrix A|B have the same rank.
rank A = rank A|B = r.
(i) If the rank of both of the matrices r is equal to the number of
unknowns n
rank A = rank A|B = r = n,
then the solution is unique.
(ii) If the rank of both of the matrices r is smaller than the
number of unknowns n,
rank A = rank A|B = r < n,
then (n – r) of the unknowns may be assigned any values, the
other r unknowns are uniquely determined from the system.
This system has infinitely many solutions, because its
solutions depend on (n – r) parameters.
(iii) If the rank r of the coefficient matrix is smaller than the rank
of the augmented matrix
rank A < rank A|B,
then the system does not have a solution, it is said to be
inconsistent.
Let rank(A) = r. Then there can be at least one nonsingular r x r
matrix M made from A .
The equations corresponding with the rows of M are called the
basic equations, the other equations are the side equations.
The unknowns corresponding with the columns of M are called
the basic unknowns, the other columns are the side
unknowns.

Illustration of Kronecker-Capelli Theorem using
Gaussian Elimination.

0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
2
0
0
2
1
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
2
0
2
2
1
0
0
0
0
0
1
1
0
0
0
1
1
1
0
0
1
3
2
2
1
2
2
2
0
0
3
3
0
0
0
0
0
0
0
0
1
3
2
2
1
3
5
4
2
1
6
12
6
6
3
2
6
4
4
2
1
3
2
2
1
Gaussian Elimination gives
3
6
2
1
x
x
x
x
5
4
2
1
12
6
6
3
6
4
4
2
3
2
2
1
4
3
2
1
The reduced row echelon form of A
means that rank A = rank A|B = 3, there are 4 unknowns so one of them will be
the parameter.
1
x
0
x
p
x
2
p
2
x
0
0
1
x
0
x
2
p
2
x
4
3
2
1
4
3
1
Let
x
2
= p
- parameter
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
2
0
0
2
1
•If we cross out the second column
the ranks: rank A = rank A|B do not change, so
x
2
can be the parameter.
•If we cross out the second column
the ranks: rank A = rank A|B do not change, so
x
1
can be the parameter.
Let
x
1
= p
- parameter
1
x
0
x
1
2
p
x
p
x
0
0
1
x
0
x
2
x
2
p
4
3
2
1
4
3
2


Other Examples
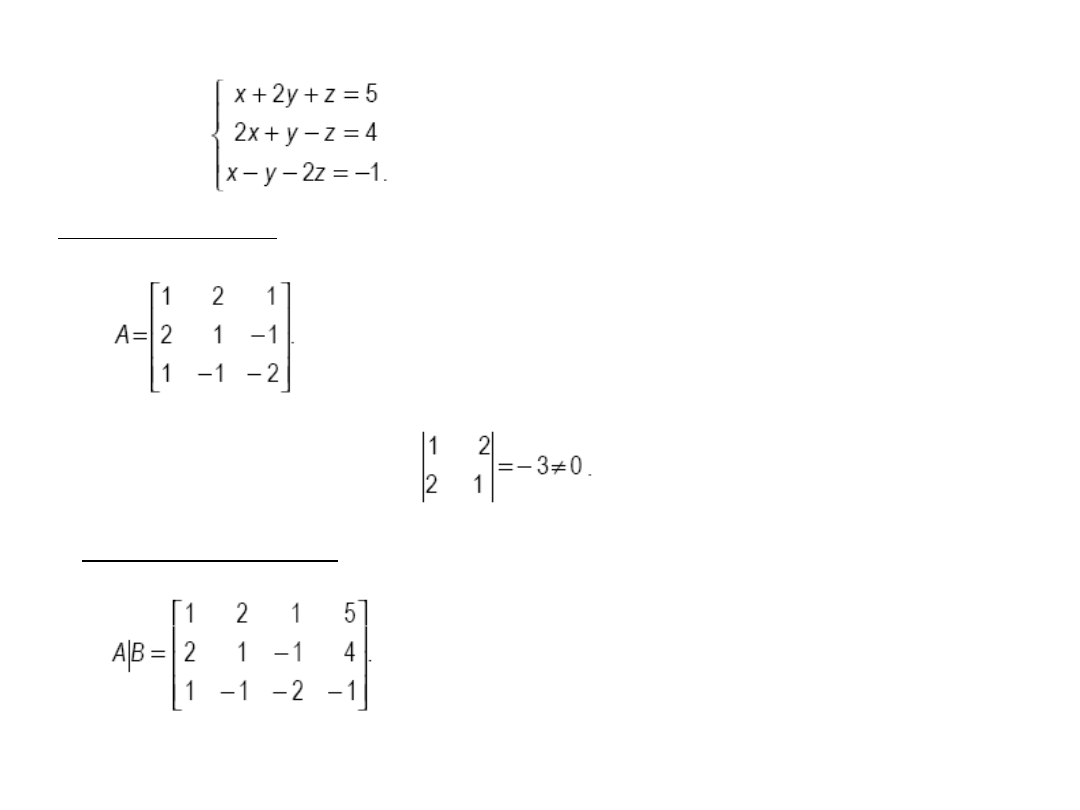
Example
det A =0, because the third row is equal to the
difference
between the second and the first row ( R2 = (R2
–R1) )
Rank A = 2 because
1. The rank of A
2. The rank of A|B
0
0
0
0
6
3
3
0
5
1
2
1
6
3
3
0
6
3
3
0
5
1
2
1
So rank A|B = 2
The system is consistent because rank A = rank A|B =2
The number of unknowns is 3, thus there is (3 - 2 =1) 1 parameter,
there is an infinite number of solutions.
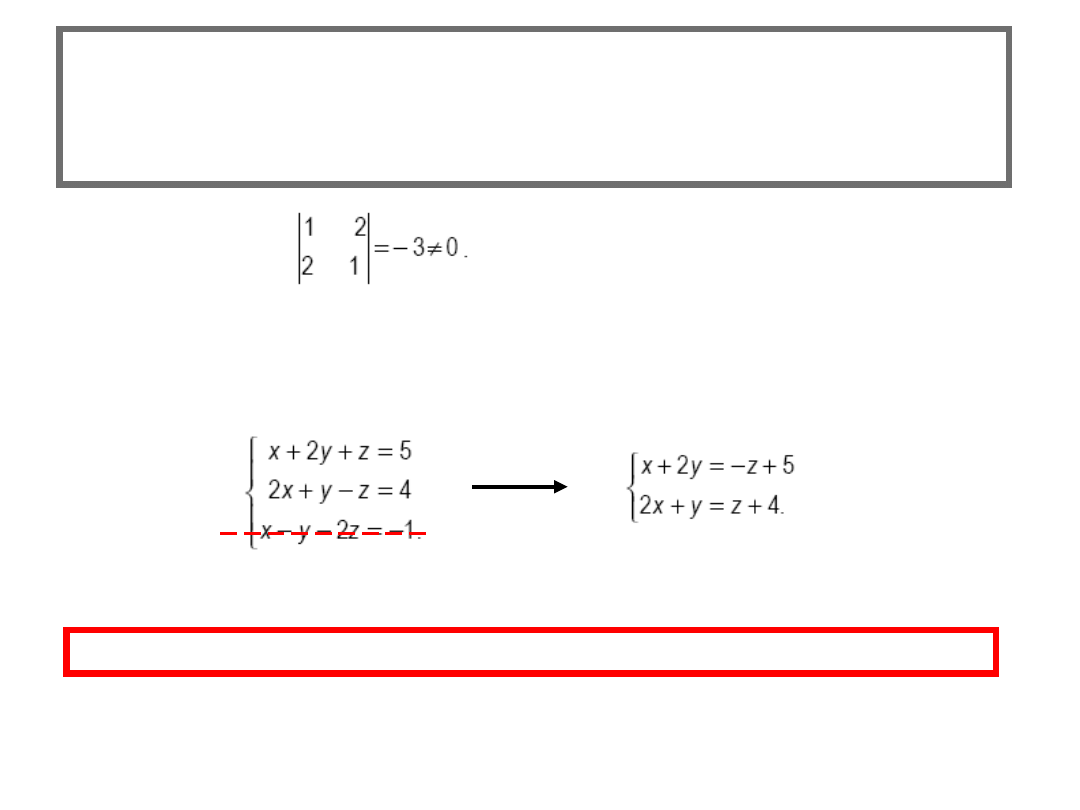
How do we choose the parameter (the side unknown)?
It has to be in the column which if removed does not change the ranks.
It is either the third or second unknown,
y = p
or
z = p
.
We choose the third one
z = p
and place it on the Right Hand
Side of the equations.
Now we can
1) either continue the Gaussian Elimination procedure:
0
0
0
0
2
1
1
0
1
1
0
1
0
0
0
0
2
1
1
0
5
1
2
1
0
0
0
0
6
3
3
0
5
1
2
1
R
z
2
z
y
1
z
x
so
R
p
,
p
z
2
p
y
1
p
x
or
2) or we can reduce the original system to a 'smaller' one
A* x* = B* for which rank A* = rank A*|
B*.
because
let
1
2
2
1
A*
4
z
5
z
B*
this means that we cross out the last equation and use
z = p
as a parameter:
This system can be solved using methods for nonsingular systems.

a) the inverse matrix method
4
p
5
p
y
x
1
2
2
1
A*
4
p
5
p
)
(
y
x
1
*
A
b) the Cramers Rule
4
p
2
5
p
1
Det
Det
1
y
1
4
p
2
5
p
Det
Det
1
x
*
A
*
A

TASK
Find the relationship between the number of solutions and the
value of the parameter p.
p
p
p
A
3
2
2
3
p
p
p
p
p
B
A
2
3
2
2
2
3
|
det A = p
2
- 3p - 4= (p - 4)(p + 1)
p
y
p
x
p
y
p
px
2
)
3
(
2
2
)
2
3
(
1) det A = 0 iff p= -1 or p = 4
If p ≠ 4, and p ≠ -1 then det A ≠ 0,
thus rank A = 2, also rank A|B = 2, so there is one
solution.
2) For p = 4:
7
2
14
4
4
3
2
2
4
3
4
A
2
2
2
1
1
1
1
2
1
3
2
1
2
2
1
3
1
)
(
)
(
B
|
A
3) For p= -1:
2
2
1
1
1
3
2
2
1
3
1
)
(
A
8
7
2
6
14
4
4
2
4
3
2
4
2
2
4
3
4
B
|
A
p
p
p
p
p
B
|
A
2
3
2
2
2
3
Rank A = 1 and rank A|B = 2 so there are no solutions
Rank A = 1, rank A|B = 1, there is an infinite number of solutions,
dependent on one parameter.
Answer:
For p \in R \ { 4, -1} the system has a unique solution,
for p = 4 it is inconsistent – there are no solutions
for p = -1 there is an infinite number of solutions

Definition
A system of equations is called homogeneous when all the constants
are equal to zero, otherwise the system is called non homogeneous.
From the fact that a non-singular system has a unique solution we
conclude:
the obvious zero solution is the only solution of a homogeneous
system when it is non-singular.
0
x
a
x
a
x
a
0
x
a
x
a
x
a
0
x
a
x
a
x
a
n
mn
2
2
m
1
1
m
n
n
2
2
22
1
21
n
n
1
2
12
1
11

The necessary condition for a homogeneous
system to have a non zero solution is that, it IS
singular, i.e
det A = 0.
Document Outline
- SYSTEMS OF LINEAR EQUATIONS II
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
Wyszukiwarka
Podobne podstrony:
L 6 Systems of linear equations I
Barret et al Templates For The Solution Of Linear Systems Building Blocks For Iterative Methods [s
Phase Linear 200 II
THE USUI SYSTEM OF REIKI
The?ginning of World War II German Invasion of Poland
ts - zadania, Egzamin poprawkowy z Teorii Systemów (test otwarty) 22 II 2005, Egzamin pisemny z Teor
Luhmann - Teoria system w spo ecznych, Socjologia II
Hamilton W R On quaternions, or on a new system of imaginaries in algebra (1850, reprint, 2000)(92s)
Modeling complex systems of systems with Phantom System Models
więcej podobnych podstron