ANALIZA 

DYNAMICZNA 

MANIPULATORÓW 

JAKO 

MECHANIZMÓW 

PRZESTRZENNYCH

 

 

Chwilowy stan przestrzennego ruchu ogniwa i określają:

  wektor prędkości kątowej członu

 wektor prędkości liniowej





 T

Oiz

Oiy

Oix

Oiz

Oiy

Oix

Oi

v

v

v

v

v

v

v































 T

iz

iy

ix

iz

iy

ix

i

ω

ω

ω

ω

ω

ω

ω



























 

 





 T

Si

Si

Si

Si

Si

Si

Si

z

y

x

z

y

x

r



























punktu O

i

, w którym przyjęto początek układu współrzędnych

x

i

   y

i

   z

i

związanego z członem i

Jeśli ponadto dane są

• masa ogniwa

m

i

• wektor położenia środka masy

względem układuOx

i

y

i

z

i

 

 

• macierz tensora bezwładności członu

 

[J]

Oi,

to można wyznaczyć wektory pędu i momentu pędu – krętu 
członu względem punktu O

i

 wg następujących zależności

)

r

ω

v

(

m

p

Si

i

Oi

i

i















(równanie wektorowe pędu)

)

v

r

(

m

ω

H

Oi

Si

i

i

Oi

Oi













[J]

(równanie wektorowe krętu)

 

 

Jeśli osie układu

x

i

   y

i 

  z

i

pokrywają się z osiami symetrii ogniwa, to macierz tensora
bezwładności























2

2

2

0

0

0

0

0

0

[J]

iz

iy

ix

i

Oi

k

k

k

m

 

 

Wypadkową siłę i wypadkowy moment sił bezwładności 
względem   punktu  O

i

  wyznacza   się  według  równań 

dynamiki   Newtona,  które   można  zapisać  w  postaci 
wektorowej

i

i

i

i

p

ω

p

F















(równanie wektorowe sił)

i

Oi

Oi

i

Oi

Oi

p

v

H

ω

H

M























(równanie wektorowe momentów sił)

 

 

iz

iy

iy

iz

ix

ix

p

p

p

F









 



ix

iz

iz

ix

iy

iy

p

p

p

F









 



iy

ix

ix

iy

iz

iz

p

p

p

F









 



(równania skalarowe sił)

lub w postaci skalarowej

 

 

iy

Oiz

iz

Oiy

Oiz

iy

Oiy

iz

Oix

Oix

p

v

p

v

H

ω

H

ω

H

M









 

iz

Oix

ix

Oiz

Oix

iz

Oiz

ix

Oiy

Oiy

p

v

p

v

H

ω

H

ω

H

M









 

ix

Oiy

iy

Oix

Oiy

ix

Oix

iy

Oiz

Oiz

p

v

p

v

H

ω

H

ω

H

M









 

(równania skalarowe momentów sił)

Równania  wektorowe  i  skalarowe  pędów  oraz 
wektorowe         i skalarowe sił i momentów sił opisują 

dynamikę ruchu członu manipulatora robota

w   układzie   współrzędnych   związanych   z   tym   członem
w punkcie  O

i

  i  przy  czym  położenie  punktu O

i

 i orientację 

układu   x

i

 y

i 

z

i 

  można   przyjąć  tak,  aby  uwzględnić  więzy

nałożone na ogniwo i

 

 

Współrzędne wektora prędkości punktu O

i

 w układzie x

i

 y

i

 z

i

 

związanym z ogniwem i można wyznaczyć ze wzoru

i

Oi

iO

iO

i

Oi

)

r

(

T

T

)

v

(







1





gdzie:

i

iO

...A

A

A

T

2

1



E

T

T

iO

iO





 1





 T

i

Oi

)

r

(

1

0

0

0

1

0

0

0































 

 

Współrzędne  wektora  prędkości  kątowej  członu  w 
układzie x

i

 y

i

 z

i  

można wyznaczyć z zależności

i

iO

i

i

ω

T

)

ω

(





1





1

1

2

1

32

2

1

21

1

1



















i,i

i

i

ω

...A

A

A

...

...

ω

A

A

ω

A

ω

ω











 

 

 

 

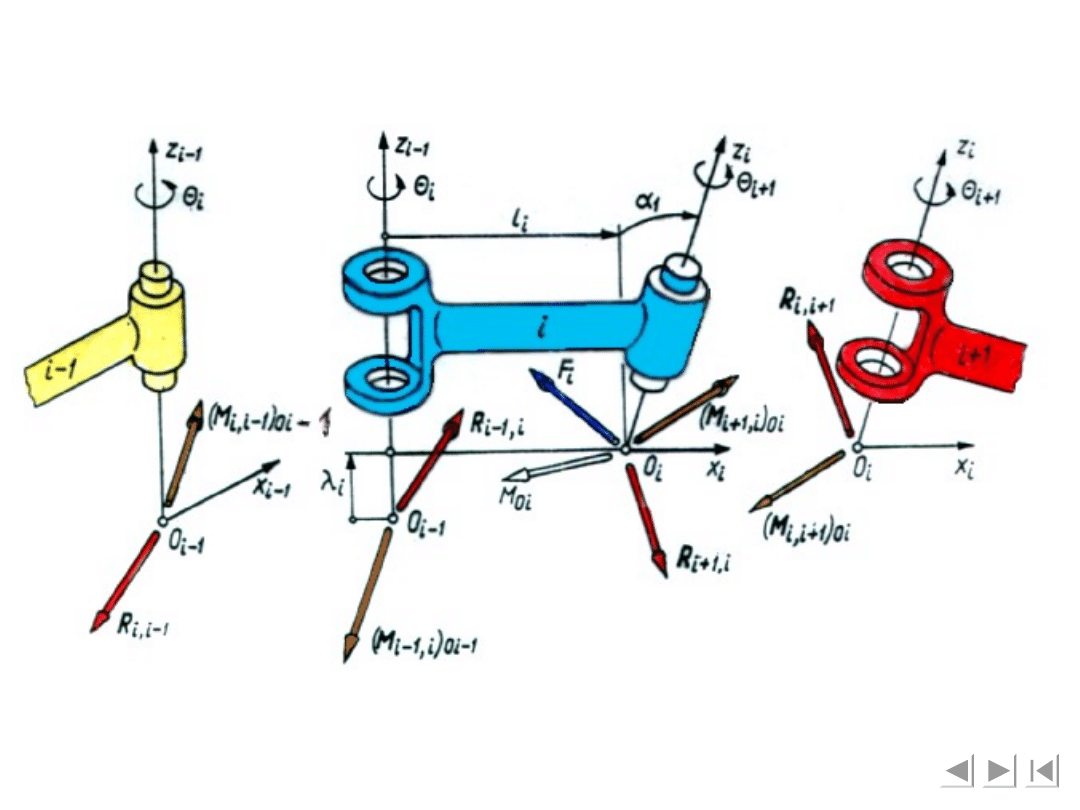
Na rysunku przedstawiono schemat rozkładu sił  działających
na  ogniwo  i  oraz  sił  i  momentów  sił oddziaływania ogniw  
w parach obrotowych. Przyjęto oznaczenia (***)

,i

i

R

1





 - wektor siły oddziaływania ogniwa i - 1 na ogniwo i





1

1





Oi

,i

i

M



- wektor  momentu  sił  oddziaływania ogniwa     
  i – 1 na ogniwo i względem punktu O

i-1

,i

i

R

1





- wektor siły oddziaływania ogniwa i + 1 na ogniwo i





Oi

,i

i

M

1





- wektor   momentu   sił  oddziaływania  ogniwa
 i + 1 na ogniwo i

i

F



- wektor siły wypadkowej

Oi

M



- wektor      wypadkowego     momentu     względem
  punktu O

i

 sił działających na ogniwo i

 

 

Równania  równowagi  dynamicznej  ogniwa  i  w 
układzie  odniesienia  związanym  z  tym  ogniwem 
przy  uwzględnieniu  ogólnego  równania  dynamiki 
wynikającego z zasady d’Alemberta są następujące:

• w odniesieniu do sił

0

A

1

1

1













,i

i

i

,i

i

i

R

F

R







• w odniesieniu do momentów sił









 

0

A

A

A

1

1

1

1

1

1

1

1





























,i

i

i

i

Oi

i

Oi

,i

i

Oi

Oi

,i

i

i

R

r

M

M

M











 

 

W  przypadku  gdy  para  łącząca  ogniwa  i  –  1  z  i  jest 
parą obrotową, wtedy składowa momentu





z

,i)

i

M

1





skierowana  wzdłuż  osi  pary  jest  równa  momentowi 
napędowemu lub momentowi oporu ruchu.

 

 

W przypadku pary przesuwnej składowa reakcji

,i,z

i

R

1





skierowana  wzdłuż  osi  przesuwu  jest  równa  sile 
napędowej lub sile oporu przesuwu w tej parze.

Gdy  dane  są  wymiary  schematu  kinematycznego 
mechanizmu, 

rozkłady 

mas 

ogniw 

oraz 

przemieszczenie, prędkość i przyspieszenie ogniwa 
napędowego,  wtedy          z  równań  równowagi 
dynamicznej  można  wyznaczyć  siły      i  momenty 
reakcji  w  parach  kinematycznych  oraz  siłę 
względnie  moment  napędowy  zapewniający  ruch 
mechanizmu  manipulatora  robota  z  żądaną 
prędkością,  wyrównoważyć  robota  statycznie  i 
dynamicznie.