DYNAMIKA

MANIPULATORÓW I

ROBOTÓW

PRZYKŁAD

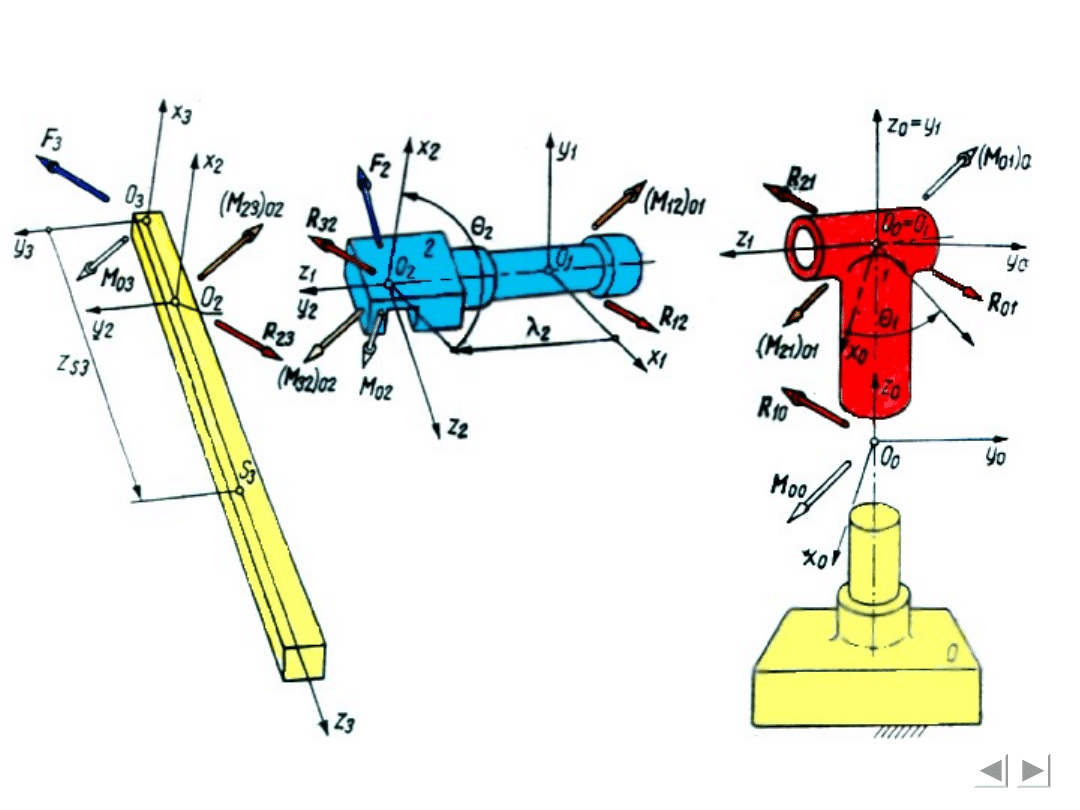
W przypadku manipulatora stanfordzkiego z
przykładu dotyczącego jego kinematyki dane są:

- położenia środków mas ogniw





T

S

S

y

r

1

0

0

1

1











T

S

S

y

r

1

0

0

2

2











T

S

S

z

r

1

0

0

3

3





przy czym znak „minus” przed y

S1

i y

S2

wynikają

z usytuowania środków mas S

1

i S

2

po

ujemnej stronie osi y

1

i y

2

Macierze tensorów bezwładności są zdefiniowane
przez wartości

 























2

2

2

0

0

0

0

0

0

J

iz

iy

ix

i

Oi

k

k

k

m

gdzie:

i

ij

ij

m

J

k 

2

,

x,y,z

j 

czyl
i

k

1x

, k

1y

, k

1z

k

2x

, k

2y

, k

2z

k

3x

, k

3y

, k

3z

ponieważ osie układów współrzędnych są głównymi
centralnymi osiami bezwładności (PYTANIE: CO TO
ZNACZY?)

Rozwiązanie problemu zaczyna się od wyznaczenia
współrzędnych wektorów prędkości zgodnie z wzorem

 

i

iO

i

i

ω

ω





1

T





 

 

i

Oi

iO

iO

i

Oi

r

v







T

T

1





czyli

- w przypadku
ogniwa 1

 

0

1

1



O

v

 



















































































0

0

0

0

0

0

1

0

0

0

0

0

cos

sin

0

1

0

0

0

0

sin

cos

A

1

1

1

1

1

1

1

1

1

1

θ

θ

θ

θ

θ

θ

ω

ω

i







0

1



p



























0

0

0

1

2

1

1

1

θ

k

m

H

y

O





0

1



F





























0

0

0

1

2

1

1

1

θ

k

m

M

y

O





- w przypadku ogniwa 2

 





























1

0

0

0

T

T

20

1

20

2

2





O

v

gdzie
:





































1

0

0

0

0

cos

0

0

cos

sin

sin

cos

cos

sin

sin

sin

cos

sin

cos

cos

A

A

T

2

1

2

2

1

1

2

1

1

2

2

1

1

2

1

2

1

20

θ

θ

λ

θ

θ

θ

θ

θ

θ

λ

θ

θ

θ

θ

θ

































1

0

0

0

0

cos

sin

sin

sin

cos

0

cos

sin

0

sin

cos

sin

cos

cos

T

2

2

1

2

1

2

1

1

2

2

1

2

1

1

20

θ

θ

θ

θ

θ

λ

θ

θ

θ

θ

θ

θ

θ

stąd

 































1

sin

0

cos

2

1

2

2

1

2

2

2

θ

θ

λ

θ

θ

λ

v

O







 

2

1

20

2

2

T ω

ω







gdzie:

 























































































































0

cos

sin

0

0

0

1

0

0

0

0

0

1

0

0

cos

0

sin

0

sin

0

cos

0

0

0

A

1

1

2

1

2

2

1

1

1

1

1

1

1

1

1

2

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

θ

ω

ω

ω

















 

































0

cos

sin

2

1

2

2

1

2

2

θ

θ

θ

θ

θ

ω









skąd

Współrzędne wektorów

2

p



i

2

O

H



względem układu

współrzędnych

x

2

, y

2

, z

2

wyznacza się z równań skalarowych pędów, czyli





2

1

2

2

2

2

cosθ

θ

y

λ

m

p

S

x







0

2



y

p





2

1

2

2

2

2

sinθ

θ

y

λ

m

p

S

z







oraz równań skalarowych krętów, jako





2

1

2

2

2

2

2

2

sinθ

θ

λ

y

k

m

H

S

x

x

O







Współrzędne wektorów i w układzie
współrzędnych





2

1

2

2

2

2

2

2

cosθ

θ

λ

y

k

m

H

S

z

z

O









2

F



2

O

M



x

2

, y

2

, z

2

wyznacza się z równań skalarowych sił, jako





2

1

2

2

2

2

cosθ

θ

y

λ

m

F

S

x













 

2

1

2

2

2

2

θ

y

λ

m

F

S

y















2

1

2

2

2

2

sinθ

θ

y

λ

m

F

S

z









2

2

2

2

2





y

y

O

k

m

H



oraz z równań skalarowych momentów sił





































2

2

1

2

2

2

2

2

2

2

1

2

2

2

2

2

2

cos

sin

θ

θ

θ

k

k

k

θ

θ

λ

y

k

m

M

z

y

x

S

x

x

O















2

2

2

1

2

2

2

2

2

2

2

2

2

cos

sin

θ

θ

θ

k

k

θ

k

m

M

x

z

y

y

O

















































2

2

1

2

2

2

2

2

2

2

1

2

2

2

2

2

2

sin

cos

θ

θ

θ

k

k

k

θ

θ

λ

y

k

m

M

x

y

z

S

z

z

O







- w przypadku ogniwa 3 wyznaczono kolejno

wektory prędkości

 





























1

0

0

0

T

T

30

1

30

3

3





O

v

gdzie:













































































































0

cos

sin

sin

sin

sin

cos

cos

0

sin

cos

sin

sin

cos

cos

cos

sin

sin

1

0

0

0

T

2

3

2

1

3

1

1

2

2

1

3

1

1

2

2

2

3

2

1

2

2

1

1

3

2

1

2

2

1

1

3

30

03

θ

λ

θ

θ

λ

θ

θ

λ

θ

θ

λ

θ

θ

λ

θ

θ

λ

θ

θ

θ

θ

θ

θ

λ

θ

θ

θ

θ

θ

θ

λ

v



























































1

0

0

0

cos

sin

sin

sin

cos

0

cos

sin

0

sin

cos

sin

cos

cos

T

3

2

2

1

2

1

2

1

1

2

2

1

2

1

1

30

λ

θ

θ

θ

θ

θ

λ

θ

θ

θ

θ

θ

θ

θ

stąd

 





































0

sin

sin

cos

2

1

2

3

2

1

3

2

1

2

2

3

3

3

θ

θ

λ

λ

θ

θ

λ

θ

θ

λ

θ

λ

v

O













   

2

2

3

3

ω

ω







ponieważ ogniwa 2 i 3 są połączone parą
przesuwną, która nie daje względnej prędkości
kątowej

Współrzędne wektorów

3

p



i

3

O

H



względem układu

współrzędnych

x

3

, y

3

, z

3

wyznacza się z równań skalarowych pędów, czyli









2

1

2

2

3

3

3

3

cosθ

θ

λ

θ

y

λ

m

p

S

x



 









2

1

3

3

3

3

sinθ

θ

z

λ

m

p

S

y













2

1

2

3

3

3

sin













m

p

z

oraz z równań skalarowych krętów, jako





2

1

3

3

2

3

3

3

sinθ

θ

λ

z

k

m

H

S

x

x

O











2

1

2

3

2

3

3

2

3

3

3

cosθ

θ

λ

z

θ

λ

z

k

m

H

S

S

y

y

O



 









2

1

2

3

3

3

cosθ

θ

k

m

H

z

x

O







Współrzędne wektorów

3

F



i

3

O

M



współrzędnych

w układzie

x

3

, y

3

, z

3

wyznacza się z równań skalarowych sił, jako





































2

3

2

1

2

2

2

2

1

2

3

3

3

3

2

cos

cos

sin

θ

λ

θ

θ

λ

θ

θ

θ

θ

z

λ

m

F

S

x

















































2

1

3

2

1

2

2

2

1

2

3

3

3

3

sin

2

cos

2

θ

θ

λ

θ

λ

θ

θ

θ

θ

z

λ

m

F

S

y



















































3

2

1

2

2

2

1

2

2

3

3

3

3

sin

sin

λ

θ

θ

λ

θ

θ

θ

z

λ

m

F

S

x









oraz z równań skalarowych momentów sił, jako

























































2

1

3

3

2

1

2

3

3

2

2

1

2

3

2

3

2

3

2

1

3

3

2

3

3

3

sin

2

cos

sin

θ

θ

λ

z

θ

λ

z

λ

θ

θ

θ

k

k

k

θ

θ

λ

z

k

m

M

S

S

z

y

x

S

x

x

O





















2

2

1

2

3

2

3

2

3

2

1

2

3

3

3

sin

cos

















z

y

x

y

z

O

k

k

k

k

m

M











































































2

1

3

2

2

2

1

3

2

2

3

3

3

2

2

2

1

3

3

2

3

2

3

3

3

2

3

3

3

cos

sin

2

2

cos

sin

















































S

S

S

z

x

S

y

y

O

z

z

z

k

k

z

k

m

M

Równanie równowagi dynamicznej ogniwa 3
zapisane zgodnie z postulatem d’Alemberta w
układzie współrzędnych

x

3

, y

3

, z

3

0

A

3

23

1

3







F

R





 

 

0

A

A

A

23

1

3

3

3

1

3

3

2

23

1

3















R

r

M

M

O

O

O









gdzie:

 





T

O

λ

λ

r

1

0

0

1

0

0

A

3

3

3

3

1

3





































stąd

R

23x2

=

-F

3x

R

23y2

= -F

3y

R

23z2

= -F

3z

y

x

x

F

λ

M

M

3

3

03

2

23







x

y

y

F

λ

M

M

3

3

03

2

23







z

z

M

M

03

2

23





Równania równowagi dynamicznej ogniwa 2
zapisane zgodnie z postulatem d’Alamberta w
układzie współrzędnych

x

2

, y

2

, z

2

0

A

32

2

12

1

2









R

F

R







 

 

 

0

A

A

A

12

1

2

2

2

1

2

2

32

2

1

12

1

2



















R

r

M

M

M

O

O

O

O











gdzie:

3

23

32

F

R

R













 





T

O

λ

λ

r

1

0

0

1

0

0

A

2

2

2

2

1

2





































stąd









2

3

2

2

3

2

1

12

cos

sin

θ

F

F

θ

F

F

R

z

z

x

x

y



















2

3

2

2

3

2

1

12

sin

cos

θ

F

F

θ

F

F

R

z

z

x

x

x















x

x

x

F

F

R

3

2

1

12









 

 



































































3

2

2

02

23

02

2

01

12

1

0

0

A

F

F

λ

M

M

M











Z trzech składowych momentu oddziaływania
ogniwa 1 na ogniwo 2 najbardziej interesującą
jest składowa wzdłuż osi z

1

równa momentowi

napędowemu w parze obrotowej 0(obrotowej)-12.

















2

3

2

2

03

02

2

3

2

2

3

3

03

02

1

12

sin

cos











x

x

z

z

z

z

y

x

x

x

F

F

M

M

F

F

F

M

M

M







































2

3

2

2

03

02

2

3

2

2

3

3

03

02

1

12

cos

sin

θ

F

F

λ

M

M

θ

F

F

λ

F

λ

M

M

M

x

x

z

z

z

z

y

x

x

y























x

z

z

z

F

λ

M

M

M

3

3

03

02

1

12









Równania równowagi dynamicznej ogniwa 1
zapisane zgodnie z postulatem d’ Alemberta w
układzie współrzędnych

x

1

, y

1

, z

1

są następujące

0

A

21

1

01

1

1









R

F

R







 

 

 

0

A

A

A

01

1

1

1

1

1

1

1

21

1

01

1

1

















R

r

M

M

M

O

O

O

O











gdzie:

12

21

R

R









0

1



F



 

0

A

1

01

1

1





r

stąd

12

1

01

A R

R







 

 





01

12

01

1

0

01

A

M

M

M













Zatem

1

1

12

1

1

12

0

01

sin

cos

θ

R

θ

R

R

z

x

x





1

1

12

1

1

12

0

01

cos

sin

θ

R

θ

R

R

z

x

y





1

12

0

01

y

z

R

R



1

1

12

1

1

12

0

01

sin

cos

θ

M

θ

M

M

z

x

x





1

1

12

1

1

12

0

01

cos

sin

θ

M

θ

M

M

z

x

y





1

12

1

01

0

01

y

y

z

M

M

M





Moment napędowy w parze obrotowej łączącej
ogniwo 1 z podstawą (ostoją) 0 można
wyznaczyć z wzorów powyżej na momenty z
uwzględnieniem równań momenty w
odniesieniu do ogniw 1 i 2, czyli













2

3

2

2

03

02

2

3

2

2

3

3

03

02

01

1

cos

sin

θ

F

F

λ

M

M

θ

F

F

λ

F

λ

M

M

M

M

x

x

z

z

z

z

y

x

x

y

zO

O







































Podsumowanie

Siły

i

momenty

napędowe

w

parach

kinematycznych manipulatora są wywoływane
przez skokowe silniki elektryczne, sterowane
przez układ z czujnikami potencjometrycznymi
wskazującymi przemieszczenie i czujnikami
indukcyjnymi wskazującymi prędkość ruchu
złożonym członów tworzących pary. Znając
wartości sił i momentów napędowych w parach
kinematycznych określa się możliwości w zakresie
prędkości i przyspieszeń ruchu
chwytaka, gdy dane są parametry silników oraz
łączna masa chwytaka i obiektu.

Analityczna metoda badania dynamiki

mechanizmów przestrzennych daje możliwość
rozwiązania zadania w postaci jawnych zależności
funkcyjnych sił i momentów oddziaływania ogniw
w parach kinematycznych od parametrów
rozkładu mas członów i wielkości kinematycznych.
Zależności te można zaprogramować do obliczeń
na PC w celu różnych położeń manipulatora
robota, przy czym jako dane wprowadza się
przemieszczenia, prędkości i
przyspieszenia w parach kinematycznych oraz
rozkłady mas ogniw. W przypadku, gdy związana z
chwytakiem masa obiektu zmienia parametry
rozkładu jego masy, wtedy do obliczeń trzeba
wprowadzić odpowiednio zmienione dane.

Wyrażenia

na

siły

i

momenty

sił

bezwładności ogniw zawierają dwie grupy
składników. Pierwsza grupa z parametrami
k

ij

przedstawia efekt rozkładu mas członów

względem ich osi symetrii. Druga – efekt
przesunięcia środka masy względem początku
układu odniesienia.

Przykład liczbowy

Parametry rozkładu mas członów przyjęto

według

danych

liczbowych

w

przypadku

manipulatora stanfordzkiego, które zestawiono w
tablicy.

Nr

ogniw

a

Mas

a w

kg

x

Si

w

m

y

Si

w

m

z

Si

w m

m

i

k

2

i

x

w

kgm

2

m

i

k

2

i

y

w

kgm

2

m

i

k

2

i

z

w

kgm

2

1

9.29

0 0.017

5

0.1105 0.276 0.255 0.071

2

5.01

0 0.105

4

0

0.108 0.018 0.100

3

4.25

0

0

0.6447 2.510 2.510 0.006

Ponadto dana jest długość

λ

2

= 0.152 m

Analizę dynamiki manipulatora ograniczono do
jednego położenia, w którym dane są

:

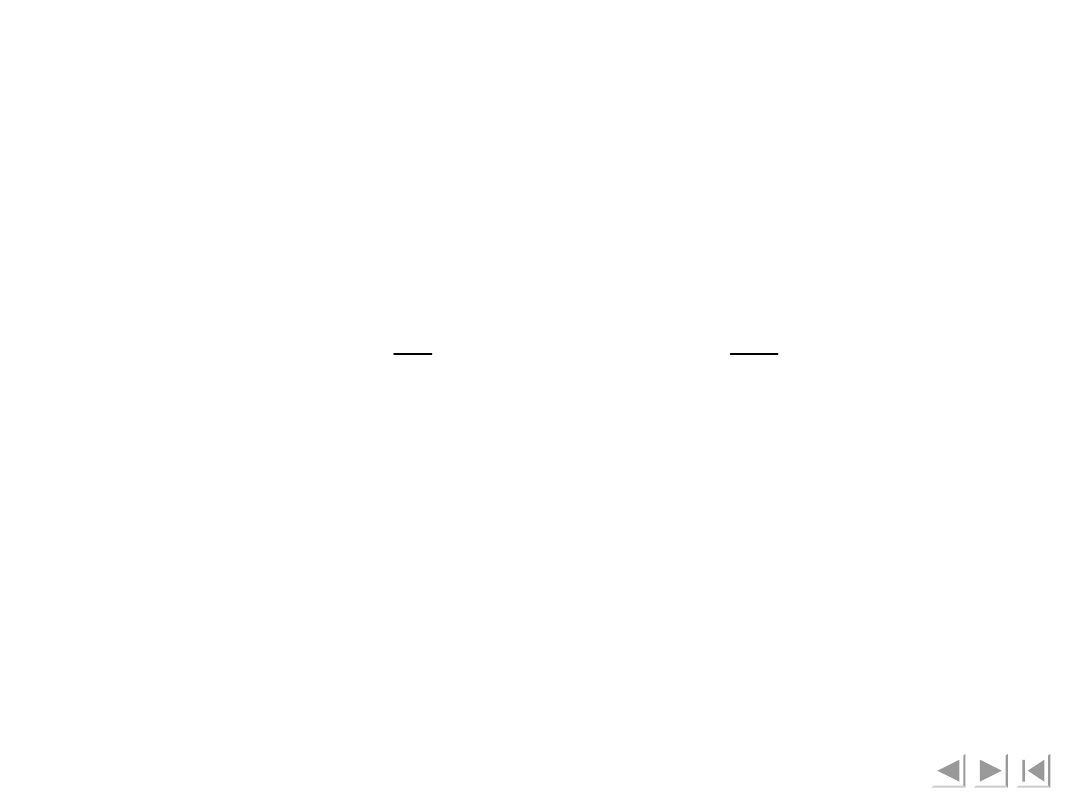
0

1



θ



90

2





θ

m

.

λ

508

0

3



1

2

1

6

1







s

.

θ

θ





2

2

1

5







s

θ

θ





s

m

.

λ

1

0

3





2

3

0

1

s

m

.

λ 



Rozwiązanie

problemu

badania

dynamiki

manipulatora robota stanfordzkiego rozpoczęto od
obliczenia składowych sił i momentów sił
działających na poszczególne
ogniwa. Podstawiając dane liczbowe do wyrażeń
na siły i momenty otrzymano następujące wyniki:

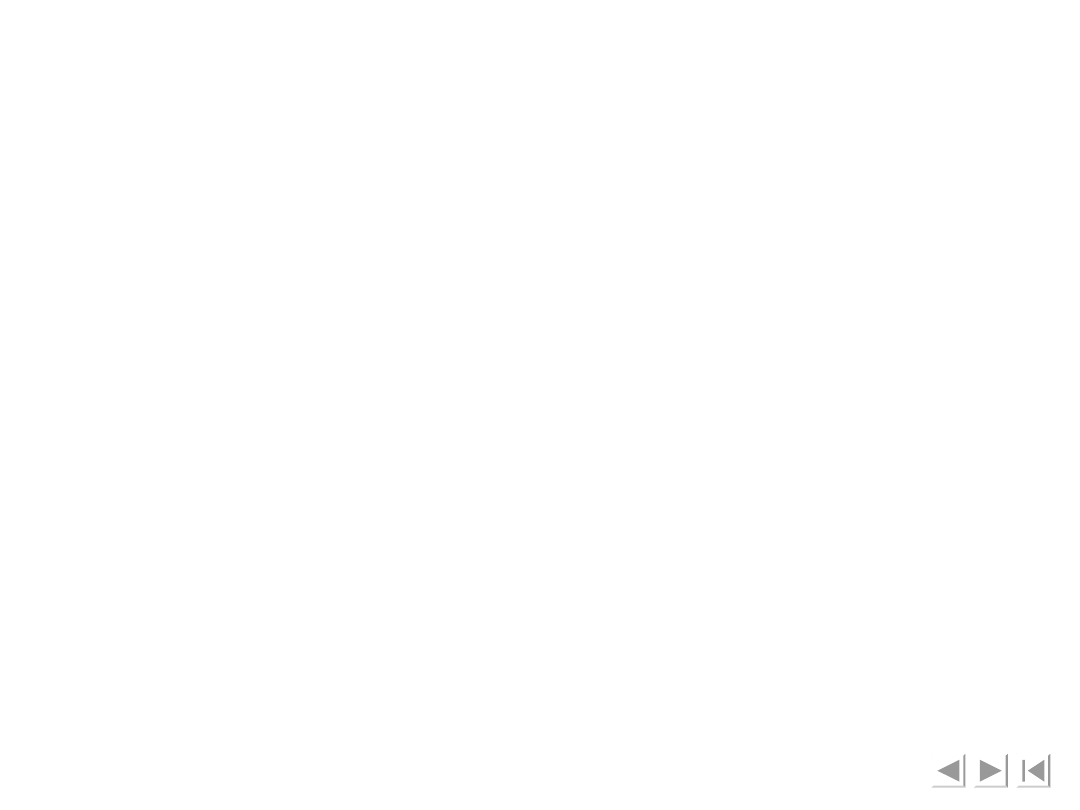
Nm

.

M

z

275

1

01


0

2



x

F

N

.

F

y

119

0

2





N

.

F

z

233

0

2





Nm

.

M

x

1385

0

02





Nm

.

M

y

5400

0

02



Nm

.

M

z

0256

0

02





N

.

F

x

855

28

3



N

.

F

y

789

24

3





N

.

F

z

020

1

3



Nm

.

M

x

6219

19

03





Nm

.

M

y

3970

19

03



Nm

.

M

z

0154

0

03





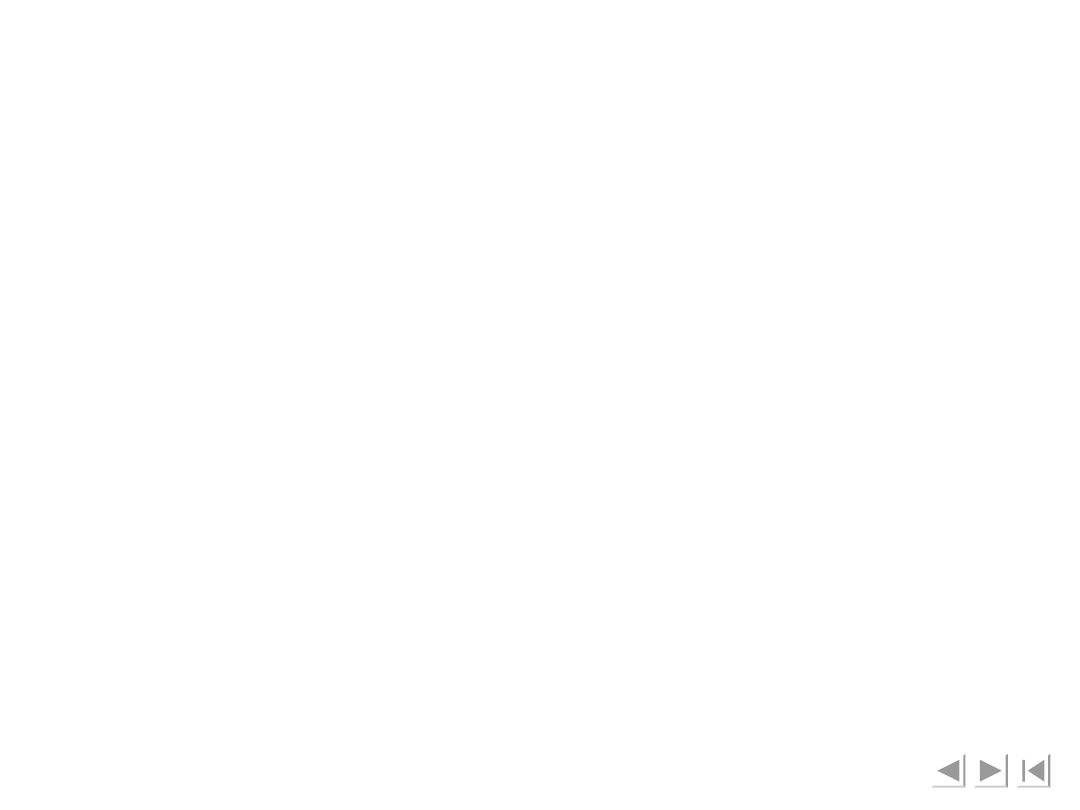
Wartości sił i momentów oddziaływania ogniw w
parach kinematycznych po podstawieniu danych
liczbowych są następujące

N

.

R

x

855

25

2

23



N

.

R

y

789

24

2

23



N

.

R

z

020

1

2

23





Nm

.

M

x

1247

32

2

23



Nm

.

M

y

2627

6

2

23





Nm

.

M

z

0154

0

2

23



N

.

R

x

787

0

1

12



N

.

R

y

855

25

1

12



N

.

R

z

908

24

1

12



Nm

.

M

x

971

3

1

12





Nm

.

M

y

2336

32

1

12



Nm

.

M

z

1753

13

1

12



Nm

.

M

z

5086

33

0

01



Uwagi końcowe

Podana wyżej metoda macierzowa dynamiki

manipulatora robota stanfordzkiego dotyczy tak
zwanego zagadnienia prostego, czyli wyznaczenia
sił i momentów sił w parach kinematycznych.

Rozwiązania zadania odwrotnego to znaczy

wyznaczanie

przemieszczeń

w

parach

kinematycznych odpowiadających żądanym siłom
i momentom jest bardziej skomplikowane i
sprowadza się do rozwiązania zadania na
położenia

odpowiedniego

mechanizmu

przestrzennego manipulatora robota (por. zadanie
na położenia)