
KINEMATYKA
MANIPULATORÓW I
ROBOTÓW
PRZYKŁAD
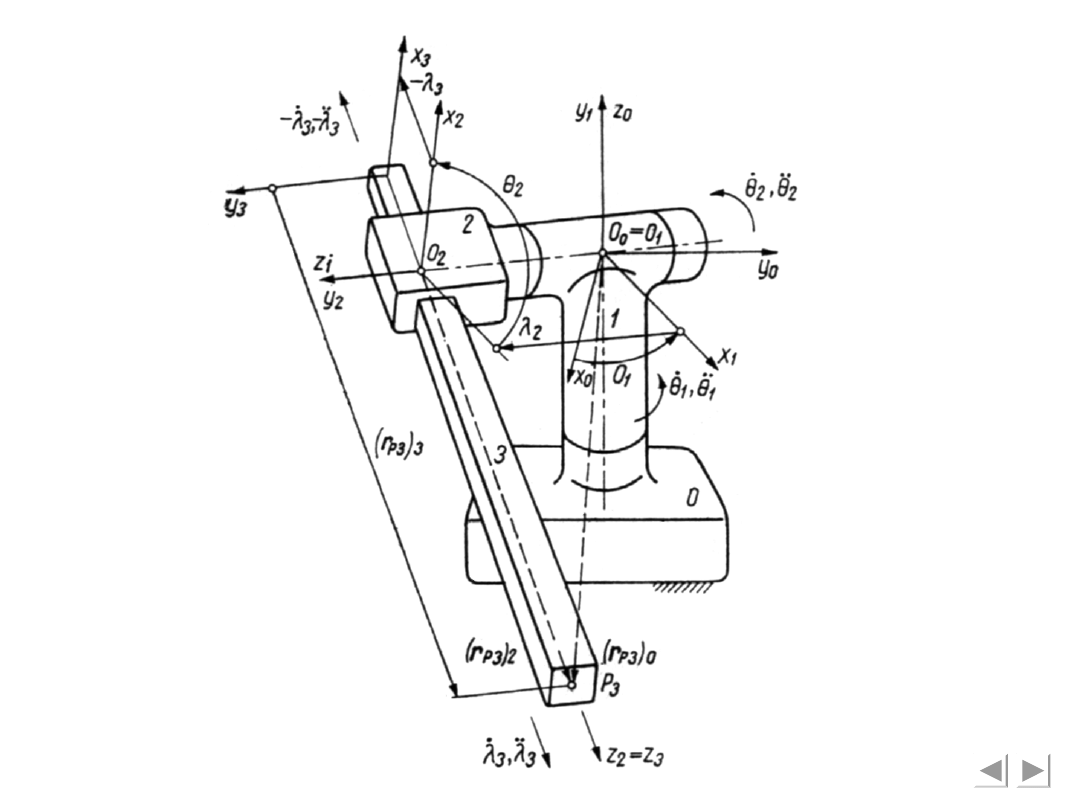

Manipulator robota stanfordzkiego przedstawiony
na rysunku ma dwie pary obrotowe i jedną
przesuwną (OOP). Dane są wymiary i parametry
ogniw:
(rys. ***)
α
1
= 90°, l
1
= 0, α
2
= 90°, l
2
= 0,
λ
1
= 0, λ
2
= 0.05m,
oraz wartości przemieszczeń:
θ
1
= 0°, θ
2
= - 90°, λ
3
= -0.2m,
prędkości:
s
m
.
λ
,
s
.
θ
θ
6
1
6
1
3
1
2
1
i przyspieszeń:
2
3
2
2
1
0
1
5
s
m
.
λ
,
s
θ
θ
w ruchu względnym członów.

Wyznaczyć prędkość przyspieszenie punktu P
3
należącego do ogniwa 3, którego położenie w
układzie współrzędnych tego ogniwa wyznacza
wektor
SPOSÓB
1
T
p
.
.
r
1
6
0
0
0
1
6
0
0
0
3
3
Rozwiązanie zadania rozpoczyna się od obliczenia
macierzy przekształceń według wzoru

1
0
0
0
cos
sin
0
sin
sin
cos
cos
cos
sin
cos
sin
sin
cos
sin
cos
A
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
λ
α
α
θ
l
α
θ
α
θ
θ
θ
l
α
θ
α
θ
θ
w przypadku gdy i = 1, 2, 3
Po podstawieniu danych liczbowych otrzymuje się
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
A
1
1
0
0
0
05
0
0
1
0
0
0
0
1
0
1
0
0
A
2
.

1
0
0
0
2
0
1
0
0
0
0
1
0
0
0
0
1
A
3
.
Wektory
położenia
punktu
P
3
w
układach
współrzędnych ogniw 2, 1 i 0, czyli podstawy oblicza
się według
1
4
0
0
0
1
6
0
0
0
1
0
0
0
2
0
1
0
0
0
0
1
0
0
0
0
1
A
3
3
3
2
3
.
.
.
r
r
p
p
(wzorów na r)
czyli

1
05
0
0
4
0
1
4
0
0
0
1
0
0
0
05
0
0
1
0
0
0
0
1
0
1
0
0
A
2
3
2
1
3
.
.
.
.
r
r
p
p
1
0
05
0
4
0
1
05
0
0
4
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
A
1
3
1
0
3
.
.
.
.
r
r
p
p

Uwzględniając wzory
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
j
θ
θ
Q
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
j
θ
θ
Q
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
2
2
j
j
j
θ
θ
Q

natomiast w przypadku pary przesuwnej
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
λ
Q
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
j
j
λ
Q
0
2
j
Q
a zatem
0
0
0
0
0
0
0
0
0
0
0
6
1
0
0
6
1
0
2
1
.
.
Q
Q

0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
3
.
Q
0
0
0
0
0
0
0
0
0
0
56
2
5
0
0
5
56
2
2
1
1
.
.
Q
Q
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
2
3
3
.
Q
Q
2
1
1
2
2
2
Q
Q
Q
Q

wektory prędkości punktu P
3
wyznacza się zgodnie
ze wzorami na prędkości – (wzory na v)1 –
czyli
0
1
0
0
0
1
4
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
2
3
3
2
3
.
.
.
r
Q
v
p
p

0
0
64
0
1
0
0
1
0
0
0
1
0
0
0
05
0
0
1
0
0
0
0
1
0
1
0
0
1
05
0
0
4
0
0
0
0
0
0
0
0
0
0
0
0
6
1
0
0
6
1
0
A
2
3
2
1
3
2
1
3
.
.
.
.
.
.
.
.
v
r
Q
v
p
p
p

0
64
0
64
0
02
0
0
0
64
0
1
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
1
0
05
0
4
0
0
0
0
0
0
0
0
0
0
0
0
6
1
0
0
6
1
0
A
1
3
1
0
3
1
0
3
3
.
.
.
.
.
.
.
.
.
v
r
Q
v
v
p
p
p
p
s
m
.
.
.
.
v
p
905
0
64
0
64
0
02
0
2
2
2
3

natomiast wektory przyspieszeń punktu P
3
wyznacza
się
zgodnie
ze
wzorami
na
przyspieszenia
(wzory na a)1
czyli
0
1
0
0
0
1
4
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
2
3
2
3
3
2
3
.
.
.
r
Q
Q
a
p
p

0
0
32
2
024
0
0
1
0
0
0
0
0
0
0
05
0
0
1
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
2
3
0
0
2
3
0
0
0
1
0
0
0
0
0
0
05
0
0
1
0
0
0
0
1
0
1
0
0
1
05
0
0
4
0
0
0
0
0
0
0
0
0
0
0
56
2
5
0
0
5
56
2
A
2
A
2
3
2
2
1
3
2
1
3
2
2
2
1
3
.
.
.
.
.
.
.
.
.
.
.
.
v
Q
a
r
Q
Q
a
p
p
p
p
0
32
2
192
2
298
1
0
0
64
0
1
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
2
3
0
0
2
3
0
0
0
32
2
024
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
1
0
05
0
4
0
0
0
0
0
0
0
0
0
0
0
56
2
5
0
0
5
56
2
A
2
A
1
3
1
1
1
3
1
0
3
2
1
1
0
3
3
.
.
.
.
.
.
.
.
.
.
.
.
.
v
Q
a
r
Q
Q
a
a
p
p
p
p
p
2
2
2
2
3
446
3
32
2
192
2
298
1
s
m
.
.
.
.
a
p

Wektory prędkości kątowej ogniw wyznacza
się ze (wzorów na prędkość kątową)
jako
0
6
1
6
1
0
0
6
1
0
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
6
1
0
0
A
1
2
1
1
3
2
.
.
.
.
ω
ω
ω
ω

wektory przyspieszenia kątowego ogniw wyznacza
się ze (wzorów na przyspieszenia kątowe) jako
0
5
5
56
2
0
5
0
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
6
1
0
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
6
1
0
0
6
1
0
0
5
0
0
A
A
1
2
1
1
2
1
1
1
3
2
.
.
.
.
ε
ω
Q
ε
ε
ε

Sposób 2
Współrzędne wektorów
- prędkości
3
P
v
3
P
a
- przyspieszenia punktu P
3
można również wyznaczyć w inny sposób.
Współrzędne wektora
0
3
P
r
- położenia punktu P
3
rozpatruje się jako funkcje złożone zmiennych
θ
1
(t), θ
2
(t), λ
3
(t)

Pierwsze
pochodne
współrzędnych
wektora
położenia
względem
czasu
są
równe
współrzędnym wektora prędkości, a drugie
pochodne wektora przyspieszenia
ze wzoru
i
pi
i
pi
r
...
r
A
A
A
2
1
0
wyznacza się
3
3
3
2
1
0
3
A
A
A
p
P
r
r

1
0
0
0
0
0
1
0
0
cos
0
sin
0
sin
0
cos
A
1
1
1
1
1
θ
θ
θ
θ
1
0
0
0
0
1
0
0
cos
0
sin
0
sin
0
cos
A
2
2
2
2
2
2
λ
θ
θ
θ
θ
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
A
3
3
λ
Mnożąc poszczególne macierze począwszy od
prawej strony otrzymuje się

1
0
0
0
cos
cos
0
sin
cos
sin
sin
sin
sin
cos
cos
sin
sin
sin
cos
sin
cos
sin
cos
cos
A
A
A
2
3
2
2
1
2
2
1
3
2
1
1
2
1
1
2
2
1
3
2
1
1
2
1
3
2
1
30
θ
λ
θ
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
T
Podstawiając powyższą zależność do równania
3
3
3
2
1
0
3
A
A
A
p
P
r
r
i wykonując mnożenie macierzy przez wektor
T
P
P
P
z
z
r
1
0
0
1
0
0
3
3
3
3

1
cos
cos
sin
sin
sin
sin
cos
2
3
3
1
2
2
1
3
3
1
2
2
1
3
3
0
3
θ
λ
z
θ
λ
θ
θ
λ
z
θ
λ
θ
θ
λ
z
r
P
P
P
P
otrzymuje się
Podstawiając wartości liczbowe do powyższej
zależności otrzymuje się wynik identyczny jak
poprzednio, czyli
1
0
05
0
4
0
0
3
.
.
r
P

Pierwsze pochodne współrzędnych wektora
0
3
P
r
są równe współrzędnym wektora prędkości
0
3
3
P
P
v
v
1
1
2
2
1
3
2
1
2
2
1
1
3
3
3
cos
sin
cos
cos
cos
sin
sin
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
θ
λ
z
v
P
x
P
1
1
2
2
1
3
2
1
2
2
1
1
3
3
3
sin
sin
sin
cos
sin
sin
cos
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
θ
λ
z
v
P
y
P
2
3
2
2
3
3
3
cos
sin
θ
λ
θ
θ
λ
z
v
P
z
P
Po podstawieniu wartości kątów
0
1
θ
90
2
θ
oraz wartości prędkości
1
2
1
6
1
s
.
θ
θ
s
m
.
λ
1
0
3
s
m
.
λ
θ
λ
v
x
P
02
0
3
1
2
3
s
m
.
θ
λ
z
v
P
y
P
64
0
1
3
3
3
s
m
.
θ
λ
z
v
P
z
P
64
0
2
3
3
3

czyli wynik zgodny z otrzymanym poprzednio innym
sposobem
Pochodne względem czasu współrzędnych wektora
prędkości są równe współrzędnym wektora
przyspieszenia
1
2
1
1
1
2
2
1
3
2
1
2
2
1
1
3
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
1
1
3
3
3
sin
cos
sin
cos
cos
cos
sin
sin
2
sin
cos
cos
sin
2
sin
cos
cos
cos
sin
sin
θ
θ
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
θ
λ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
λ
z
a
P
x
P

2
3
2
2
3
2
2
2
2
2
3
3
3
cos
sin
2
cos
sin
θ
λ
θ
θ
λ
θ
θ
θ
θ
λ
z
a
P
z
P
1
2
1
1
1
2
2
1
3
2
1
2
2
1
1
3
2
1
2
2
2
1
2
2
1
2
1
2
1
2
1
2
1
1
3
3
3
cos
sin
sin
sin
cos
sin
sin
cos
2
sin
sin
cos
sin
cos
cos
2
sin
sin
sin
cos
θ
θ
θ
θ
λ
θ
θ
λ
θ
θ
θ
θ
θ
θ
λ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
λ
z
a
P
y
P
Po podstawieniu danych liczbowych do wzorów
na współrzędne przyspieszeń obliczone
powyżej otrzymuje się
2
1
2
3
2
2
2
1
3
3
3
298
1
s
m
.
θ
λ
λ
θ
θ
λ
z
a
P
x
P
2
2
3
2
3
3
3
32
2
2
s
m
.
θ
λ
θ
λ
z
a
P
z
P
2
2
1
2
1
3
1
3
3
3
192
2
2
s
m
.
θ
λ
θ
λ
θ
λ
z
a
P
y
P

PODSUMOWANIE
W
rozwiązaniu
zadania
z
przedstawionego
przykładu
pokazano
zastosowanie
dwóch
sposobów
obliczeń
współrzędnych
wektora
położenia, prędkości i
przyspieszenia punktu, leżącego na ogniwie
ruchomym.
Pierwszy sposób oparty na wzorach rekurencyjnych
(wzory na r)
(wzory na v)
(wzory na a)
przy wykorzystaniu operatorów różniczkowania
(wzory na Q)
jest bardziej przydatny do obliczeń na PC

Drugi
sposób
wymaga
pracochłonnego
różniczkowania
analitycznego
jest
bardziej
przydatny w przypadku manipulatorów o małej
liczbie członów; jego zaletą jest mniejsza liczba
operacji algebraicznych aniżeli w przypadku
pierwszym.
Uwaga:
Przy
wyznaczaniu
przemieszczeń
liniowych i kątowych trzeba najpierw
zdefiniować zwroty odpowiednich wektorów; zwrot
przemieszczenia uważa się za dodatni, jeśli obrót
układu i – 1 do układu i odbywa się zgodnie z
regułą śruby prawoskrętnej; zwroty wektorów
prędkości i przyspieszeń przyjmuje się za dodatnie,
jeśli są one zgodne ze zwrotami odpowiednich
przemieszczeń.

Podana wyżej metoda macierzowa kinematyki
manipulatora robota stanfordzkiego dotyczy tak
zwanego zagadnienia prostego, czyli wyznaczania
położeń i orientacji członu roboczego
odpowiadających danym przemieszczeniom w
parach kinematycznych. Rozwiązanie zadania
odwrotnego to znaczy wyznaczenie przemieszczeń
w
parach
kinematycznych
odpowiadających
żądanym położeniom i orientacji ogniwa roboczego.
Wariant
zadania
odwrotnego
jest
bardziej
skomplikowany i sprowadza się do rozwiązania
zadania położenia odpowiedniego mechanizmu
przestrzennego manipulatora robota (por. zadanie
na położenia na początku niniejszego rozdziału).
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
Wyszukiwarka
Podobne podstrony:
04 Analiza kinematyczna manipulatorów robotów metodą macierz
5 Analiza kinematyczna manipulatorów robotów metodą wektorow
9 Dynamika manipulatorów i robotów, przykład
2 Wprowadzenie do kinematyki manipulatorów robotów
Kinematyka manipulatorów robotów
04 Analiza kinematyczna manipulatorów robotów metodą macierz
więcej podobnych podstron