
1
7. Dynamika manipulatora
7.1. Formalizm Lagrange’a
Dynamikę złożonych układów, zawierających podzespoły mechaniczne, można
opisać w stosunkowo prosty sposób za pomocą formalizmu Lagrange’a, bazującego na
zależnościach energetycznych.
Dla manipulatora składającego się z n ogniw połączonych szeregowo, zdefiniujmy
uogólniony wektor położenia
[
]
T
2
1
n
q
q
q
K
=
q
i uogólniony wektor sił działających w złączach,
[
]
T
2
1
n
τ
τ
τ
K
=
τ
przy czym składowa
k
τ
wektora sił odpowiada składowej
k
q wektora położenia. Gdzie
należy zachować takie samo „strzałkowanie” sił i położeń, tzn. dodatnia wartości
k
τ
powinna
powiększać
k
q .
Niech E
kin
i E
pot
oznaczają odpowiednio: energie kinetyczną i energię potencjalną
wszystkich mas układu. Funkcja Lagrange’a jest definiowana jako różnica pomiędzy
całkowitą energią kinetyczną układu a jego całkowitą energią potencjalną
)
(
)
,
(
)
,
(
q
q
q
q
q
pot
kin
E
E
L
−
≡
&
&
(1)
Związki między funkcją Lagrange’a a siłami działającymi w złączach można wyrazić jako
układ n równań skalarnych w postaci
n
k
q
L
q
L
t
k
k
k
≤
≤
=
∂
∂
−
∂
∂
1
,
d
d
τ
&
(2)
nazwanych równaniami Eulera-Lagrange’a. Należy pamiętać, że przy wyznaczaniu
pochodnych cząstkowych zmienne
k
q i
k
q& są traktowanie jako wzajemnie niezależne.
2
Zestaw równań Eulera-Lagrange’a wynika z zasady najmniejszego działania Hamiltona.
W swojej klasycznej postaci zasada ta odnosi się do układu, w którym nie występują siły
niepotencjalne, takie jak siły zewnętrzne czy opory ruchu. Wyprowadzenie równań Eulera-
Lagrange’a, w przypadku występowania przepływu energii z otoczenia do układu,
przedstawiono w [1], dodatek B.
Przykład.
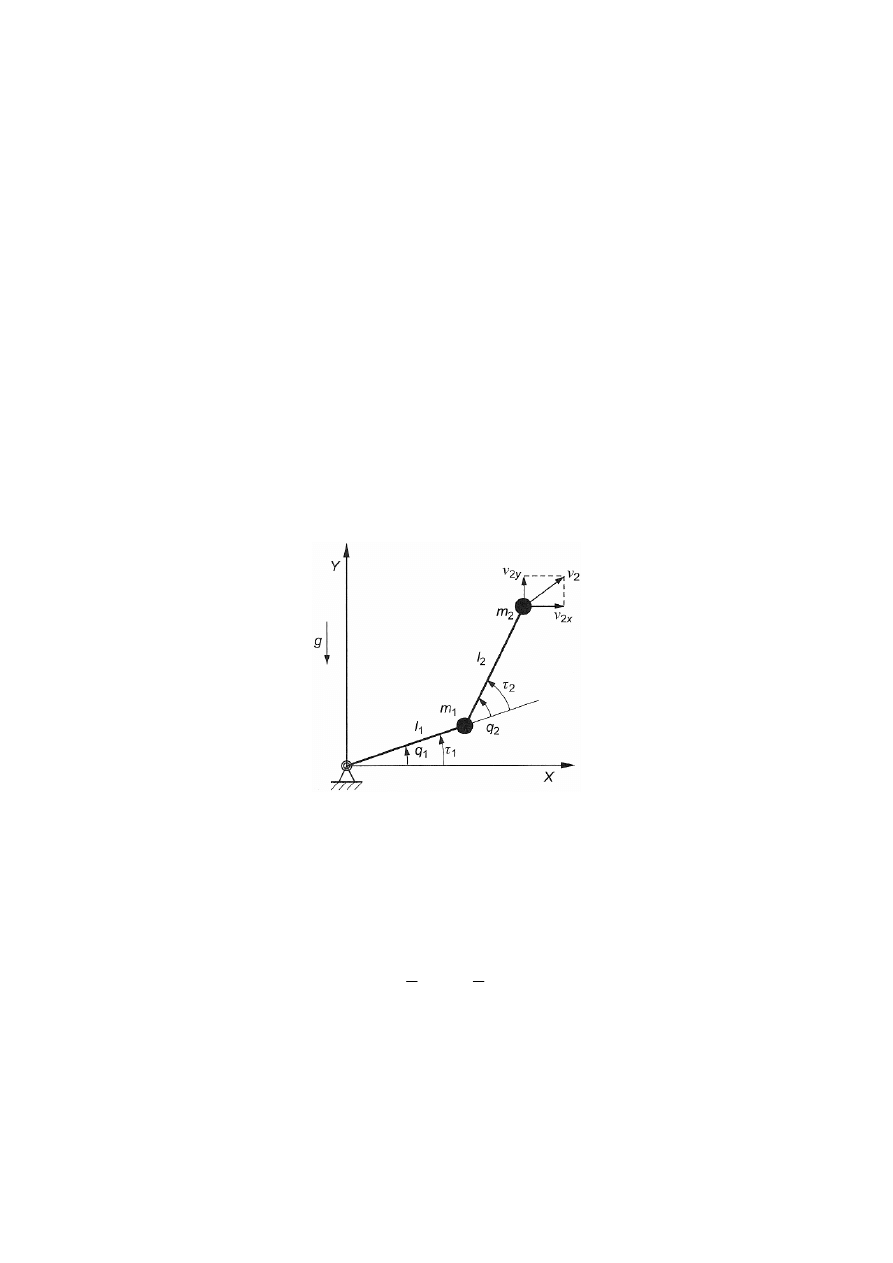
Wyznaczyć równania dynamiki dwuczłonowego manipulatora płaskiego przy użyciu
formalizmu Lagrange’a (rys. 1). Założyć, że masy obu ogniw są reprezentowane przez
punktowe masy m
1
i m
2
umieszczone na końcach sztywnych i nieważkich prętów. Zespoły
napędowe (umieszczone w złączach) generują momenty napędowe
τ
1
i
τ
2
które powodują
przyrosty zmiennych złączowych q
1
i q
2
. Manipulator działa w polu grawitacyjnym o
przyspieszeniu g.
Rys. 1. Model manipulatora płaskiego
Energię kinetyczną i potencjalną masy m
1
można zapisać jako
2
1
2
1
1
2
1
1
1
,
2
1
2
1
q
l
m
v
m
E
kin
&
=
=
)
(
s
1
1
1
1
1
1
,
q
gl
m
gy
m
E
pot
=
=
gdzie: v
1
– prędkość liniowa masy m
1
, y
2
– składowa wektora położenia masy m
1
.

3
Dla masy m
2
postępowanie jest bardziej skomplikowane, ponieważ aby wyznaczyć kwadrat
prędkości liniowej v
2
2
, z którą porusza się masa
2
2
2
2
2
2
2
2
2
2
y
x
v
v
v
y
x
&
&
+
=
+
=
najpierw należy wyznaczyć składowe położenia x
2
i y
2
, a następnie zróżniczkować je
względem czasu, podnieść do kwadratu i zsumować
)
(
s
)
(
)
(
s
)
(
c
)
(
c
2
1
2
1
2
1
1
1
2
2
1
2
1
1
2
q
q
q
q
l
q
q
l
x
q
q
l
q
l
x
+
+
−
−
=
⇒
+
+
=
&
&
&
&
)
(
c
)
(
)
(
c
)
(
s
)
(
s
2
1
2
1
2
1
1
1
2
2
1
2
1
1
2
q
q
q
q
l
q
q
l
y
q
q
l
q
l
y
+
+
+
=
⇒
+
+
=
&
&
&
&
Stąd energię kinetyczną masy m
2
można zapisać jako
(
)
)
2
(
)
(
c
)
(
2
2
1
2
1
2
2
2
1
2
1
2
2
2
2
1
2
1
2
1
2
1
2
1
2
2
2
2
2
,
q
q
q
q
l
q
q
q
q
l
l
q
l
m
v
m
E
kin
&
&
&
&
&
&
&
&
+
+
+
+
+
=
=
Energia potencjalna masy m
2
określona jest wzorem
(
)
)
(
s
)
(
s
2
1
2
1
1
2
2
2
2
,
q
q
l
q
l
g
m
gy
m
E
pot
+
+
=
=
Znając energie potencjalne i kinetyczne obu mas można wyznaczyć funkcję Lagrange’a
=
−
−
+
=
2
,
1
,
2
,
1
,
pot
pot
kin
kin
E
E
E
E
L
+
+
+
+
+
+
+
=
)
2
(
2
1
)
(
c
)
(
2
1
2
1
2
2
2
1
2
1
2
2
2
2
2
1
2
1
2
1
2
2
1
2
1
2
2
1
2
1
1
q
q
q
q
l
m
q
q
q
q
l
l
m
q
l
m
q
l
m
&
&
&
&
&
&
&
&
&
)
(
s
)
(
s
)
(
s
2
1
2
2
1
1
2
1
1
1
q
q
gl
m
q
gl
m
q
gl
m
+
−
−
−
4
Następnie wyznacza się pochodne funkcji Lagrange’a
)
,
,
,
(
2
1
2
1
q
q
q
q
L
&
&
, patrz równanie (2)
)
(
c
)
(
c
)
(
c
2
1
2
2
1
1
2
1
1
1
1
q
q
gl
m
q
gl
m
q
gl
m
q
L
+
−
−
−
=
∂
∂
)
(
c
)
(
)s
(
2
1
2
2
2
2
1
2
1
2
1
2
2
q
q
gl
m
q
q
q
q
l
l
m
q
L
+
−
+
−
=
∂
∂
&
&
&
)
(
)
(
)c
(2
2
1
2
2
2
2
2
1
2
1
2
1
2
2
2
1
2
1
1
1
q
q
l
m
q
q
q
l
l
m
q
l
m
q
l
m
q
L
&
&
&
&
&
&
&
+
+
+
+
+
=
∂
∂
)
(
)
(
c
2
1
2
2
2
2
1
2
1
2
2
q
q
l
m
q
q
l
l
m
q
L
&
&
&
&
+
+
=
∂
∂
)
(
)
(
s
)
(2
)
(
)c
(2
d
d
2
1
2
2
2
2
2
2
1
2
1
2
2
2
1
2
1
2
1
2
2
2
1
2
1
1
1
q
q
l
m
q
q
q
q
l
l
m
q
q
q
l
l
m
q
l
m
q
l
m
q
L
t
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
+
+
+
−
+
+
+
=
∂
∂
)
(
)
(
s
)
(
c
d
d
2
1
2
2
2
2
2
1
2
1
2
2
1
2
1
2
2
q
q
l
m
q
q
q
l
l
m
q
q
l
l
m
q
L
t
&
&
&
&
&
&
&
&
&
+
+
−
=
∂
∂
Wyliczone powyżej pochodne są podstawiane do równań Eulera-Lagrange’a (2), w wyniku
czego otrzymuje się równania dynamiki rozważanego manipulatora. Równania te można
zapisać w postaci następującego równania macierzowo-wektorowego
(
)
(
)
(
)
(
)
(
)
=
+
+
+
+
+
+
−
+
+
+
+
+
+
+
2
1
2
1
2
2
2
1
2
1
1
2
1
1
1
2
2
1
2
1
2
2
2
2
2
1
2
1
2
2
1
2
2
2
2
2
1
2
2
2
2
1
2
2
2
2
2
2
1
2
1
2
2
1
1
)
(
c
)
(
c
)
(
c
)
(
c
)
(
s
)
(
s
2
)
(
c
)
(
c
)
(
c
2
τ
τ
g
q
q
l
m
q
q
l
q
l
m
q
l
m
q
q
l
l
m
q
q
q
q
l
l
m
q
q
l
m
l
q
l
l
m
l
q
l
l
m
l
q
l
l
l
m
l
m
&
&
&
&
&
&
&
&
5
7.2. Energia kinetyczna i potencjalna ogniwa
W rozważanym przykładzie wyprowadzono równania ruchu manipulatora przy
założeniu, że cała masa ogniwa jest skupiona na jego końcu. Przybliżenie to nie zawsze daje
dobre rezultaty. W celu wyznaczenia równań ruchu z równania Eulera-Lagrange’a dla
manipulatora o dowolnej konfiguracji ważne jest aby można było w prosty sposób obliczyć
różnice energii kinetycznej i potencjalnej ogniw (tzn. funkcje Lagrange’a).
Poniżej zostanie wyprowadzone równanie określające energię kinetyczną ruchu
pojedynczego ogniwa, przy założeniu, że jest ono ciałem idealnie sztywnym. Następnie
zostanie wyznaczona energia potencjalna tego ogniwa.
Wielkości związane z ruchem k-tego ogniwa łańcucha kinematycznego, można
rozważać w następujących układach współrzędnych (rys. 2):
•
w nieruchomym związanym z podstawą robota, układ {0}
•
w układzie związanym z tym ogniwem (zgodnie z notacją D-H układ na końcu
ogniwa oznaczony jako {k})
•
w układzie związanym sztywno z ogniwem, którego początek znajduje się w
środku masy ogniwa, układ { k } (osie tego układu są równoległe do odpowiednich
osi układu {k}
•
w układzie {
0
k
} którego początek znajduje się w środku masy ogniwa, a osie są
równoległe do odpowiednich osi układu bazowego.
Rys. 2. Układy współrzędnych k-tego ogniwa

6
Energia kinetyczna elementarnej masy dm
k
ogniwa umieszczonej w punkcie A, której
położenie określone jest przez wektor
0
r
0,A
wynosi
k
A
T
A
k
A
k
A
k
kin
m
m
m
E
d
2
1
d
2
1
d
2
1
d
,
0
0
,
0
0
2
,
0
0
2
,
0
0
,
v
v
v
r
=
=
=
&
(3)
Po scałkowaniu powyższego wyrażenia otrzymuje się wzór na energię kinetyczną
k
m
A
A
k
kin
m
k
kin
m
E
E
k
k
d
2
1
d
,
0
0
T
,
0
0
,
,
∫
∫
=
=
v
v
(4)
Energię kinetyczną można wyrazić także w układzie { k } wówczas
k
m
A
k
A
k
k
kin
m
E
k
d
2
1
,
0
T
,
0
,
∫
=
v
v
(5)
Punkt A ma ustalone położenie w układzie { k }, zatem wektor prędkości tego punktu
względem układu {0}, wyrażony w układzie { k }, zależy od ruchu postępowego i
obrotowego układu { k } względem układu {0}
A
k
k
k
k
k
A
k
k
k
k
k
A
k
S
,
0
,
0
,
0
,
0
,
0
,
0
,
0
)
(
r
ω
v
r
ω
v
v
+
=
×
+
=
(6)
Podstawiając prawą stronę tego równania do wyrażenia na energię kinetyczną po
przekształceniach otrzymuje się
k
k
k
k
k
k
k
k
k
k
kin
m
E
,
0
0
T
0
0
T
,
0
0
,
0
0
T
,
0
0
,
2
1
2
1
ω
R
I
R
ω
v
v
+
=
(7a)
gdzie
k
k
I
jest macierzą bezwładności (inercji) k-tego ogniwa wyrażoną w układzie { k }

7
+
−
−
−
+
−
−
−
+
=
∫
∫
∫
∫
∫
∫
∫
∫
∫
k
k
k
k
k
k
k
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
m
k
A
k
k
A
k
k
k
k
m
y
x
m
z
y
m
z
x
m
z
y
m
x
z
m
y
x
m
z
x
m
y
x
m
z
y
d
)
(
d
d
d
d
)
(
d
d
d
d
)
(
2
,
2
,
,
,
,
,
,
,
2
,
2
,
,
,
,
,
,
,
2
,
2
,
I
(7b)
Energia kinetyczna tego ogniwa składa się z sumy dwóch składników. Pierwszy reprezentuje
energię ruchu postępowego i jest równy energii kinetycznej masy m
k
skupionej w środku
masy ogniwa C
k
. Drugi składnik jest równy energii ruchu obrotowego ogniwa wokół środka
masy. Składnik ten uwzględnia fakt, że rozłożone przestrzennie elementarne masy tworzące
ogniwo poruszają się z innymi prędkościami niż środek masy ogniwa.
Powyższy wzór na energię ogniwa można zapisać także w postaci
k
k
k
k
k
k
k
k
kin
m
E
,
0
0
T
,
0
0
,
0
0
T
,
0
0
,
0
2
1
2
1
ω
I
ω
v
v
+
=
(8a)
gdzie
T
k
k
k
k
k
k
k
k
T
k
k
k
k
R
I
R
R
I
R
I
0
0
0
0
0
=
=
(8b)
Energia potencjalna. Niech
0
g = [
0
g
x
0
g
y
0
g
z
] oznacza wektor grawitacji wyrażony w
układzie {0}. Aby wyznaczyć energię potencjalną k-tego ogniwa najpierw należy wyznaczyć
energię potencjalną elementarnej masy dm
k
, która jest umieszczona w punkcie A tego ogniwa
(położenie tego punktu określa wektor
0
r
0,A
), zatem
k
A
k
k
k
k
k
A
k
pot
m
m
E
)d
(
d
d
,
0
,
0
0
T
0
,
0
0
T
0
,
r
R
p
g
r
g
+
=−
=−
(9)
Po scałkowaniu powyższego wyrażenia i przekształceniach otrzymuje się wzór na energię
potencjalną tego ogniwa
k
k
m
k
pot
k
pot
m
E
E
k
,
0
0
T
0
,
,
d
p
g
−
=
=
∫
(10)
Na wykładzie wyprowadzono wzory na energię kinetyczną i potencjalną ogniwa, tj. (8) i (10),
patrz np. [1] str. 82 – 88.
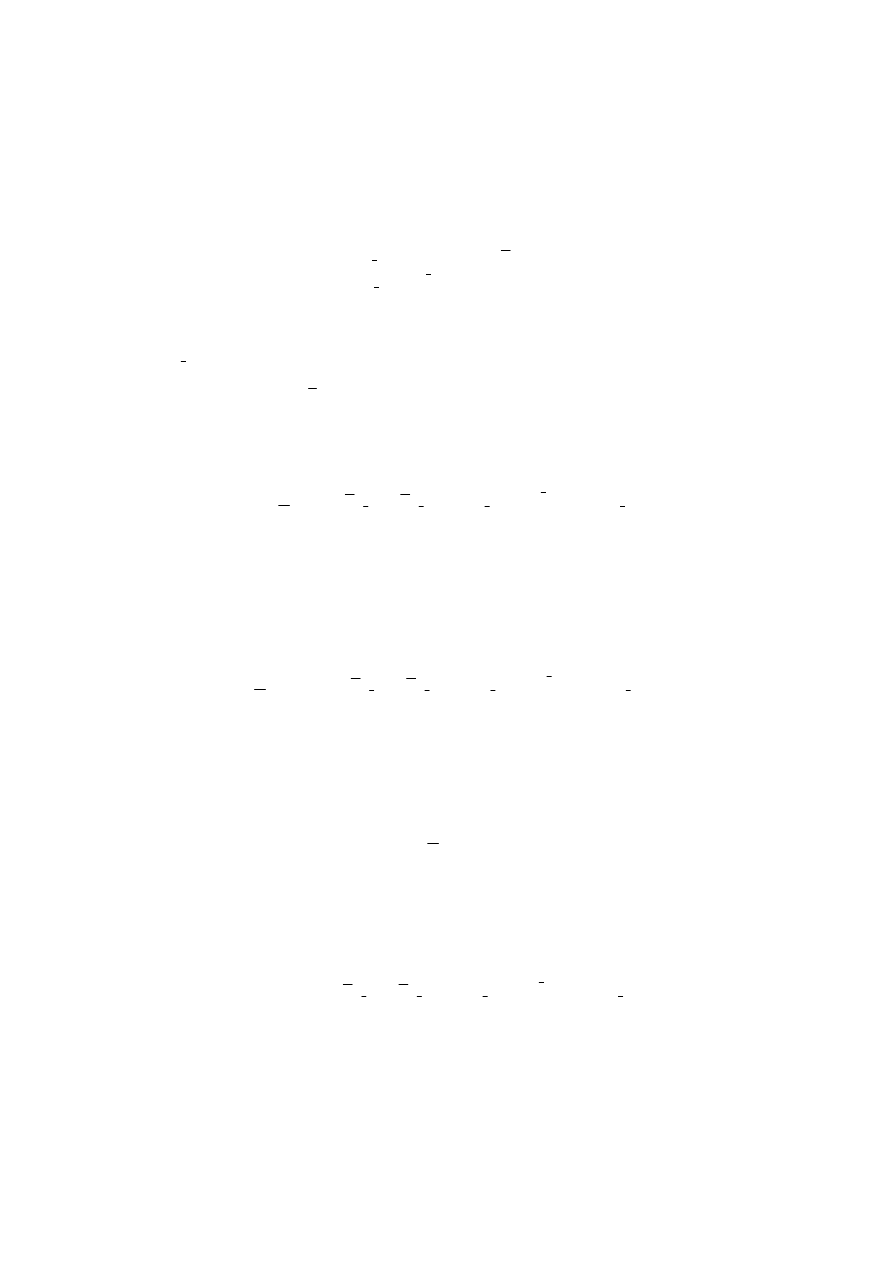
8
7.3. Równania ruchu manipulatora
Uzależniając wzór na energię kinetyczną k-tego ogniwa (8a, 8b) od wektora prędkości
złączowych q& łańcucha kinematycznego (zachodzi bowiem związek
q
q
J
q
J
q
q
J
ω
v
&
)
&
=
=
)
(
)
(
)
(
0
0
,
0
0
,
0
0
,
0
0
k
k
k
gdzie
)
(
,
0
0
q
J
k
jest jakobianem manipulatora wyznaczonym między układem podstawowym
{0} i układem lokalnym {
k } związanym ze środkiem masy k-tego ogniwa), wyrażenie na
energię kinetyczną
k-tego ogniwa można zapisać w postaci
(
)
q
q
J
R
I
R
q
J
q
J
q
J
q
&
)
)
&
)
(
)
(
)
(
)
(
2
1
,
0
0
0
0
T
,
0
0
,
0
0
T
,
0
0
T
,
k
T
k
k
k
k
k
k
k
k
k
kin
m
E
+
=
(11)
Sumując energie kinetyczne wszystkich ogniw manipulatora, otrzymuje się wzór na energię
kinetyczną całego łańcucha kinematycznego
(
)
q
q
J
R
I
R
q
J
q
J
q
J
q
&
)
)
&
+
=
∑
=
n
k
k
T
k
k
k
k
k
k
k
k
kin
m
E
1
,
0
0
0
0
T
,
0
0
,
0
0
T
,
0
0
T
)
(
)
(
)
(
)
(
2
1
(12)
Wzór ten można zapisać w zwartej postaci
q
q
B
q
&
&
)
(
2
1
T
=
kin
E
(13a)
gdzie macierz
(
)
∑
=
+
=
n
k
k
k
k
k
k
k
k
k
k
m
1
,
0
0
T
0
0
T
,
0
0
,
0
0
T
,
0
0
)
(
)
(
)
(
)
(
)
(
q
J
R
I
R
q
J
q
J
q
J
q
B
)
)
(13b)
nazywana jest macierzą
inercji manipulatora.
Całkowitą energię potencjalną manipulatora (patrz równanie (10)) można wyznaczyć z
zależności
9
)
(
1
,
0
0
T
0
q
p
g
∑
=
=−
n
k
k
k
pot
m
E
(14)
Na podstawie powyższych rozważań, funkcję Lagrange’a ogólnego modelu dynamiki
manipulatora można zapisać w postaci
)
(
)
(
2
1
)
,
(
q
q
q
B
q
q
q
pot
T
pot
kin
E
E
E
L
−
=
−
=
&
&
&
(15)
Ogólne równanie dynamiki manipulatora można wyznaczyć korzystając z wektorowej postaci
równań Eulera-Lagrange’a
τ
q
q
q
q
q
q
=
∂
∂
−
∂
∂
T
T
)
(
)
(
d
d
&
&
&
,
L
,
L
t
(16)
Podstawiając (15) do (16) po przekształceniach otrzymuje się ogólną postać równań ruchu
(równań dynamiki) manipulatora o sztywnych ogniwach
τ
q
h
q
q
q,
C
q
q
B
=
+
+
)
(
)
(
)
(
&
&
&
&
(17a)
gdzie:
(
)
T
)
(
2
1
d
)
(
d
)
(
∂
∂
−
=
q
q
B
q
q
B
q
q,
C
&
&
t
,
T
d
d
)
(
=
q
q
h
pot
E
(17b)
Literatura:
[1] Jezierski E.:
Dynamika robotów, Wydawnictwa Naukowo-Techniczne, 2006
[2] Craig J. J.:
Wprowadzenie do robotyki. Mechanika i sterowanie, Wydawnictwa
Naukowo-Techniczne, 1995
[3] Spong M. W., Vidyasagar M.:
Dynamika i sterowanie robotów, Wydawnictwa
Naukowo-Techniczne, 1997
Informacja o prawach autorskich
O ile nie zaznaczono inaczej, rysunki i teksty pochodzą z pierwszej pozycji podanej
w literaturze. Niniejsze opracowanie stanowi pomoc do wykładu „Podstawy Robotyki”.
Wyszukiwarka
Podobne podstrony:
Dynamika manipulatora
tchoń, robotyka1, Dynamika manipulatora
8 Dynamika manipulatora
9 Dynamika manipulatorów i robotów, przykład
6 Analiza dynamiczna manipulatorów robotów jako mechanizmów
1 Kinematyka i dynamika robotów i manipulatorów literatur
obliczenia do robota, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatoró
Kinematyka odwrotna, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów
Notacja Denavita, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów, p
1 Kinematyka i dynamika robotów i manipulatorów literatur
Dynamika1
Techniki wywierania wplywu oparte na dynamice interakcji
więcej podobnych podstron