1

8. Dynamika manipulatora

Masa – wielkość fizyczna charakteryzująca oddziaływanie grawitacyjne i

bezwładność ciała. Bezwładność to zdolność do przeciwstawiania się zmianom prędkości w

ruchu postępowym. Podzielmy myślowo ciało na nieskończoną ilość elementów (punktów

materialnych) i niech

ρ

oznacza gęstość ciała w punkcie, V objętość ciała, wówczas masę

ciała m wyznaczyć można z zależności

(

)

m

z

y

x

z

y

x

V

=

∫

d

d

d

,

,

ρ

(1)

Równanie (1) można zapiać także w następującej postaci

m

v

V

=

∫

d

ρ

(2)

gdzie: dv – elementarna objętość (dv = dxdydz),

ρ

=

ρ

(x, y, z) – jw. funkcja gęstości ciała.

Ś

rodek masy to punkt przyłożenia wypadkowej sił ciężkości działających na ciało.

Ś

rodek masy obiektu ciągłego ma współrzędne (x

c

, y

c

, z

c

) określone jako

∫

∫

∫

=

=

=

V

c

V

c

V

c

v

z

m

z

v

y

m

y

v

x

m

x

d

1

,

d

1

,

d

1

ρ

ρ

ρ

(3)

Równanie (3) można zapiać także w następującej postaci

∫

∫

∫

=

=

=

m

c

m

c

m

c

m

z

m

z

m

y

m

y

m

x

m

x

d

1

,

d

1

,

d

1

(4)

gdzie dm =

ρ

dv opisuje nieskończenie małą masę punktu materialnego o współrzędnych

(x, y, z). Równania (4) zapisane w zwarty sposób ma postać

∫

=

m

c

m

r

m

r

d

1

(5)

2

gdzie: r

c

– wektor opisujący środek masy w trójwymiarowym układzie współrzędnych,

r – wektor opisujący położenie punktu ciała.

Moment bezwładności wielkość fizyczna skalarna charakteryzująca bezwładność

ciała w ruchu obrotowym dookoła danej osi. Matematycznie moment bezwładności względem

osi zdefiniowany jest następująco

(

)

(

)

(

)

∫

∫

∫

+

=

+

=

+

=

m

zz

m

yy

m

xx

m

y

x

I

m

z

x

I

m

z

y

I

d

,

d

,

d

2

2

2

2

2

2

(6)

Moment dewiacji (inaczej iloczyn inercji) – moment bezwładności określony w

prostokątnym układzie współrzędnych wzorami

∫

∫

∫

=

=

=

=

=

=

m

zy

yz

m

zx

xz

m

yz

xy

m

z

y

I

I

m

z

x

I

I

m

y

x

I

I

d

,

d

,

d

(7)

Macierz inercji (inaczej macierz bezwładności lub tensor bezwładności) – macierz

3x3 zawierająca momenty bezwładności i momenty dewiacji, względem prostokątnego

układu współrzędnych, zapisane w postaci





















−

−

−

−

−

−

=

zz

zy

zx

yz

yy

yx

xz

xy

xx

I

I

I

I

I

I

I

I

I

Ι

(8)

Macierz inercji zawiera sześć niezależnych wielkości. Dla danego ciała zależą one od pozycji

i orientacji układu odniesienia ciała. Układ odniesienia można tak dobrać, aby momenty

dewiacji były równe zero. Wówczas osie układu odniesienia nazywane są osiami głównymi, a

odpowiadające im momenty bezwładności – głównymi momentami bezwładności.

Zadanie 1

a)

Znajdź macierz inercji prostopadłościanu o jednorodnej gęstości

ρ

względem układu {0}

pokazanego na rys. 1.

b)

Wyznacz analitycznie środek masy prostopadłościanu z rys. 1.

c)

Znajdź macierz inercji prostopadłościanu z rys. 1 względem układu współrzędnych {1},

powstałego w wyniku przesunięcia układu {0} do punktu środka masy.

3

l

w

h

0

X

0

Y

0

Z

{0}

Rys. 1. Ciało o jednorodnej gęstości

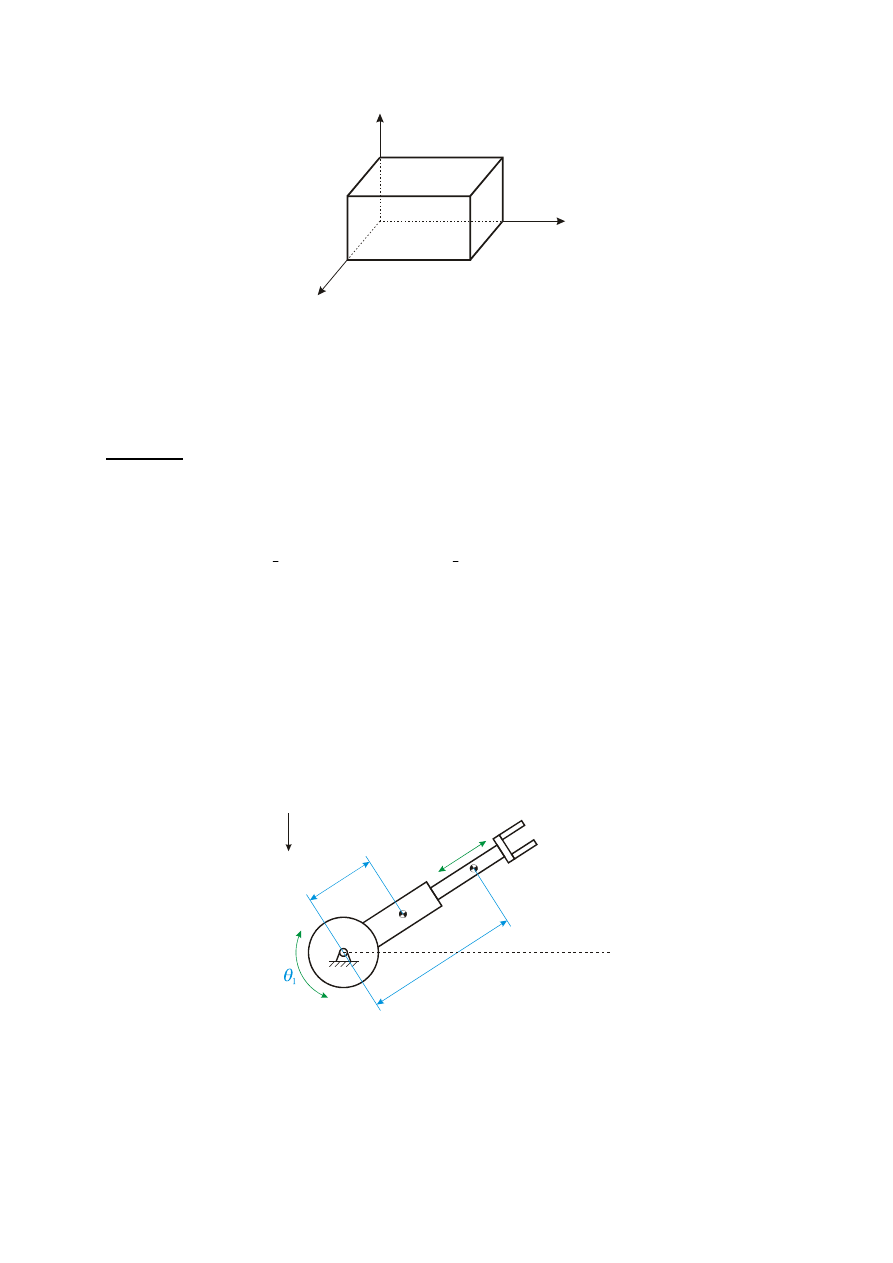
Zadanie 2

Macierze inercji członów manipulatora OP przedstawionego na rys. 2 są następujące





















=

1

1

1

1

1

0

0

0

0

0

0

zz

yy

xx

I

I

I

I

,





















=

2

2

2

2

2

0

0

0

0

0

0

zz

yy

xx

I

I

I

I

a całkowite masy są równe m

1

i m

2

. Środek masy członu 1 jest umieszczony w odległości l

1

od osi pary obrotowej, a środek masy członu 2 jest położony w odległości d

2

od osi pary

obrotowej. Wyznacz równania ruchu tego manipulatora stosując równania Lagrange’a.

E

p

= 0

l

1

d

2

m

1

m

2

g

Rys. 2. Manipulator typu OP

4

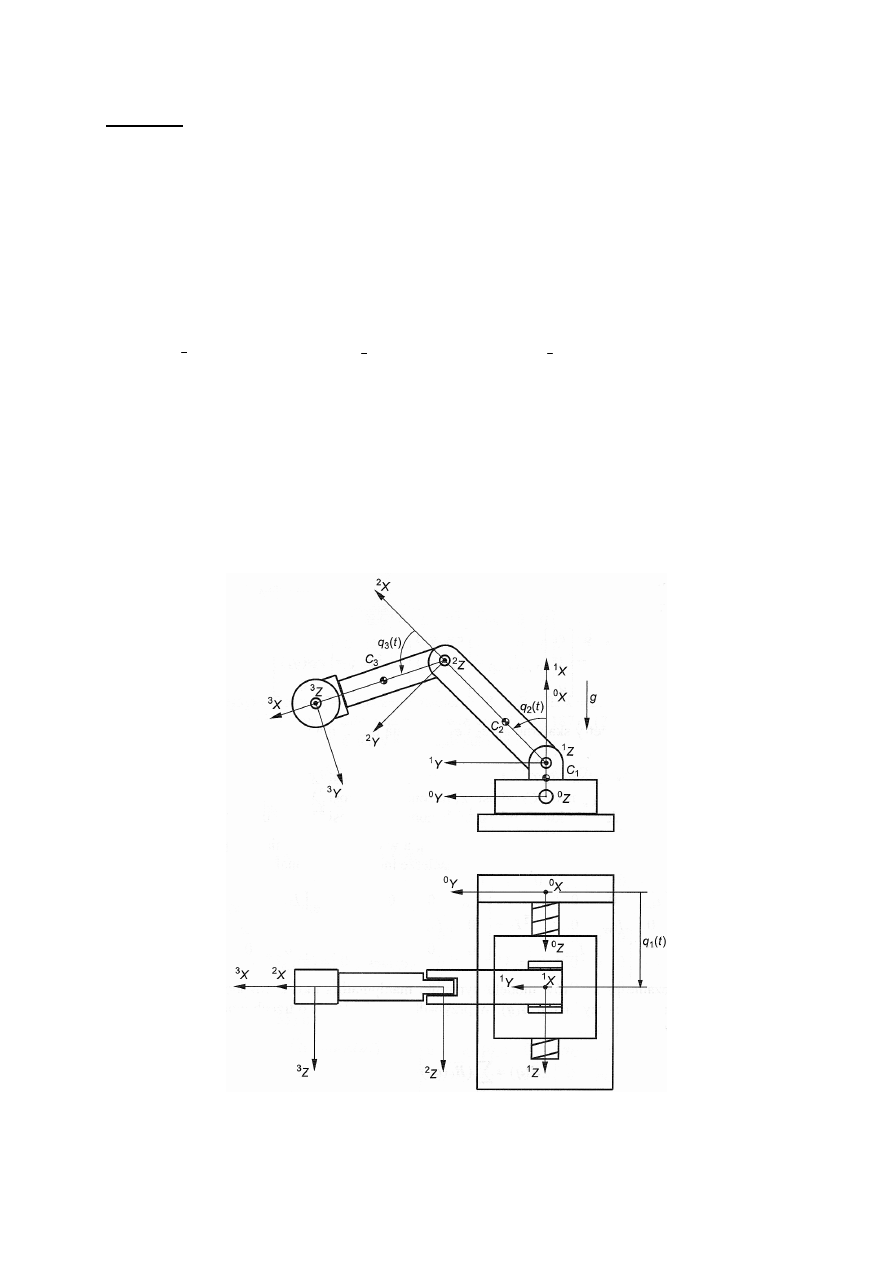
Zadanie 3

Wyznacz równania ruchu manipulatora POO, przedstawionego na rys. 3. Przyjmij, że

wszystkie ogniwa są symetryczne. Długość pierwszego ogniwa, czyli odległość od osi

0

Z do

osi

1

Z, liczona wzdłuż osi

1

X, wynosi a

1

. Długość drugiego ogniwa, czyli odległość od osi

1

Z

do osi

2

Z, liczona wzdłuż osi

2

X, wynosi a

2

. Analogicznie, długość trzeciego ogniwa wynosi

a

3

. Macierze inercji kolejnych ogniw wynoszą





















=

1

1

1

1

1

0

0

0

0

0

0

zz

yy

xx

I

I

I

I

,





















=

2

2

2

2

2

0

0

0

0

0

0

zz

yy

xx

I

I

I

I

,





















=

3

3

3

3

3

0

0

0

0

0

0

zz

yy

xx

I

I

I

I

a ich masy są równe m

1

, m

2

, m

3

. Środki mas kolejnych ogniw umieszczone są w punktach C

1

,

C

2

i C

3

. Odległość punktu C

1

od osi

0

Z liczona wzdłuż osi

1

X wynosi e

1

. Analogicznie

odległości punktów C

2

i C

3

od osi

1

Z i

2

Z wynoszą odpowiednio e

2

i e

3

.

Rys. 3. Manipulator POO

5

Literatura:

[1] Buratowski T.: Podstawy robotyki, AGH Uczelniane Wydawnictwa Naukowo-

Dydaktyczne, 2006

[2] Craig J. J.: Wprowadzenie do robotyki. Mechanika i sterowanie, Wydawnictwa

Naukowo-Techniczne, 1995

[3] Jezierski E.: Dynamika robotów, Wydawnictwa Naukowo-Techniczne, 2006

[4] Spong M. W., Vidyasagar M.: Dynamika i sterowanie robotów, Wydawnictwa

Naukowo-Techniczne, 1997

[5] Wrotny L.T.: Dynamika układów mechanicznych. Repetytorium teoretyczne i zadania,

Oficyna Wydawnicza Politechniki Warszawskiej, 1995

[6] Wrotny L.T.: Kinematyka i dynamika maszyn technologicznych i robotów

przemysłowych

, Oficyna Wydawnicza Politechniki Warszawskiej, 1996

Informacja o prawach autorskich

O ile nie zaznaczono inaczej, rysunki i teksty pochodzą z pozycji podanych w literaturze.

Niniejsze opracowanie stanowi pomoc do laboratorium z Podstaw Robotyki.