22:47 22:47

1

Astronomia obserwacyjna

Astronomia obserwacyjna

Wykład 1

Wykład 1

Orientacja na niebie.

Orientacja na niebie.

Geometria sfery niebieskiej.

Geometria sfery niebieskiej.

Astronomiczne układy współrzędnych sferycznych

Astronomiczne układy współrzędnych sferycznych

22:47 22:47

2

Program wykładu

Wykład:

30 godzin, wtorek, 8:15

Ćwiczenia:

30 godzin, wtorek, 10:15

prowadzenie:

dr Urszula Bąk-Stęślicka

Zaliczenie + egzamin

Program wykładu:

1. Orientacja na niebie. Geometria sfery niebieskiej. Układy

współrzędnych sferycznych używane w astronomii.
Transformacje między układami.

2. Ruch roczny Słońca.
3. Czas i kalendarz.
4. Ruch planet, komet i sztucznych satelitów Ziemi na sferze

niebieskiej.

5. Astrometria, ruchy własne gwiazd. Precesja i nutacja.
6. Instrumenty astronomiczne: konstrukcje teleskopów

optycznych, wady optyczne teleskopów.

7. Teleskopy kosmiczne, radioteleskopy, teleskopy do

obserwacji promieniowania rentgenowskiego i γ.

22:47 22:47

3

Program wykładu – c.d.

Program wykładu (c.d.):

7. Specyfika obserwacji w podczerwieni i ultrafiolecie.
8. Detektory: klisza, fotopowielacz i CCD.
9. Fotometria gwiazd. System UBV Johnsona i uvbyβ

Strömgrena. Ekstynkcja atmosferyczna i międzygwiazdowa.

10. Spektroskopia i spektrografy.
11. Klasyfikacja widmowa gwiazd.
12. Wyznaczanie temperatur efektywnych, średnic kątowych,

prędkości rotacji, prędkości radialnych.

13. Wyznaczanie mas i promieni gwiazd.
14. Wyznaczanie odległości do obiektów astronomicznych.
15. Interferometria optyczna i polarymetria.

Zalecana literatura:

1. J.Mietelski – Astronomia w geografii
2. E.Böhm-Vitense — Stellar Astrophysics
3. M.Harwit — Astronomical Concepts
4. W.A.Hiltner (ed.) — Astronomical Techniques
5. C.R.Kitchin — Astrophysical Techniques
6. M.Kubiak — Gwiazdy i materia międzygwiazdowa

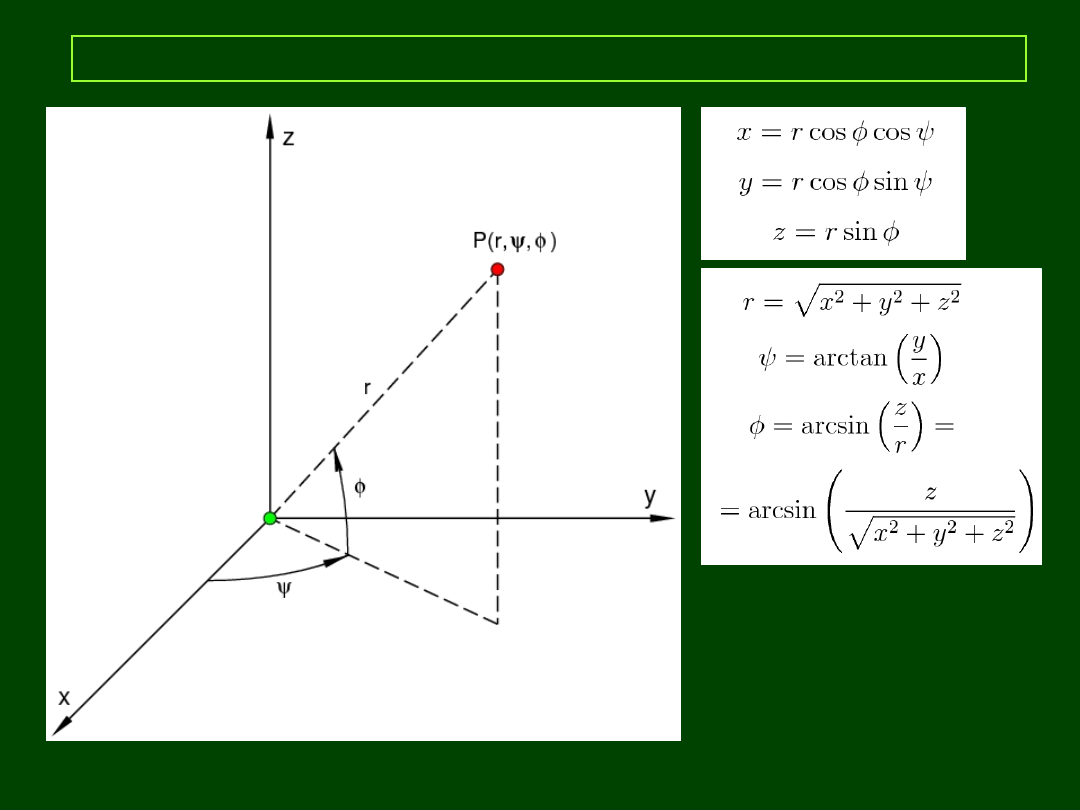
22:47 22:47

4

Elementy astronomii sferycznej

To jest układ

prawoskrętny.

W układzie

lewoskrętnym

osie x i y zamienione są
miejscami.

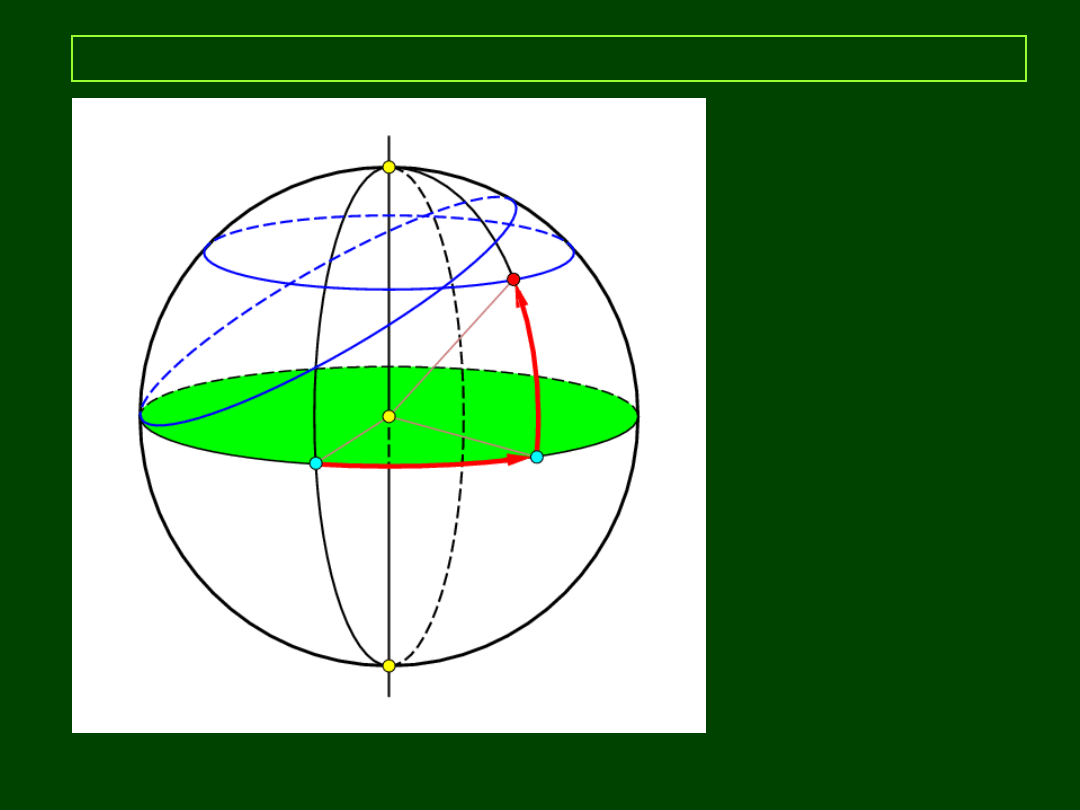
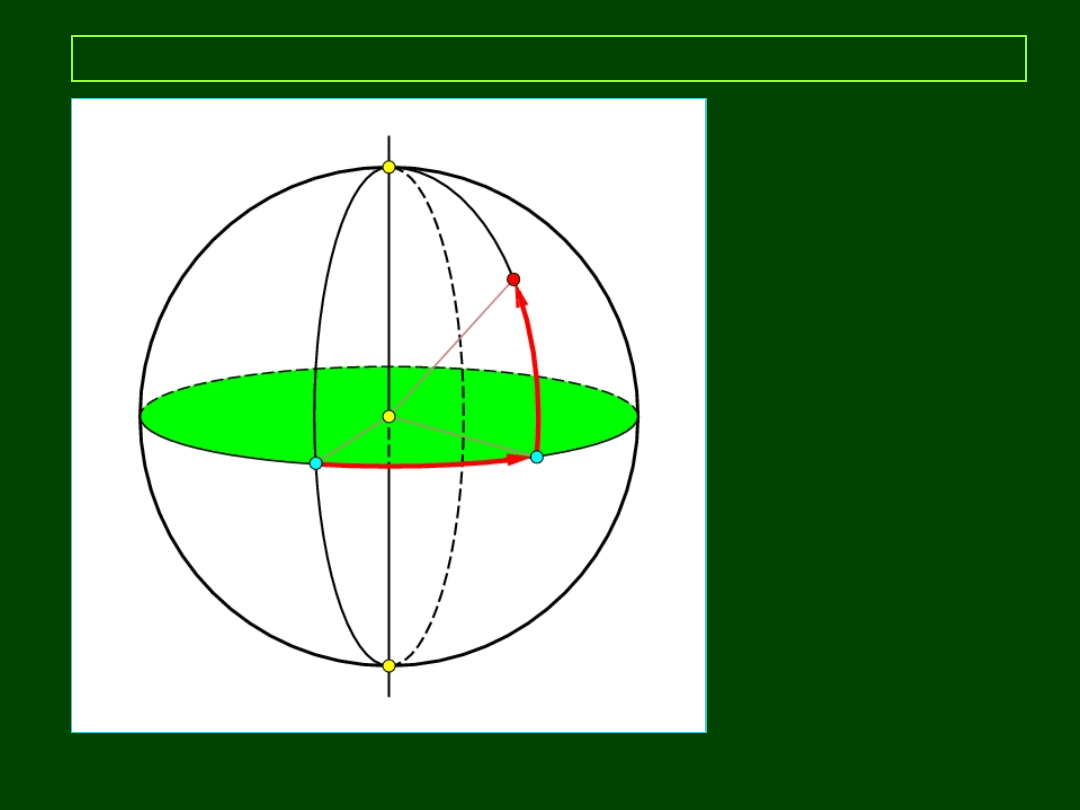
22:47 22:47

5

Elementy astronomii sferycznej

sfera niebieska

płaszczyzna
podstawowa (PP)
Koło podstawowe (KP)

półkole
początkowe (PkP)

2 współrzędne (kąty)

- koło wielkie
- koło małe
- środek układu
współrzędnych (O)

O

22:47 22:47

6

Przykład: współrzędne geograficzne

Pł. podstawowa:

pł. równika ziemskiego

równik

biegun północny (N)

biegun południowy (S)

p

o

ł.

G

re

e

n

w

ic

h

Półkole początkowe:

pł. połudn. Greenwich

Współrzędne:

długość gegraficzna

λ

0-360º, od płd.
Greenwich w kierunku
wschodu,
Tradycyjnie:
0-180º E i 0-180º W

λ

szerokość geogr.

φ

-90º ÷ +90º,
Tradycyjnie:
0-90º N, 0-90º S

φ

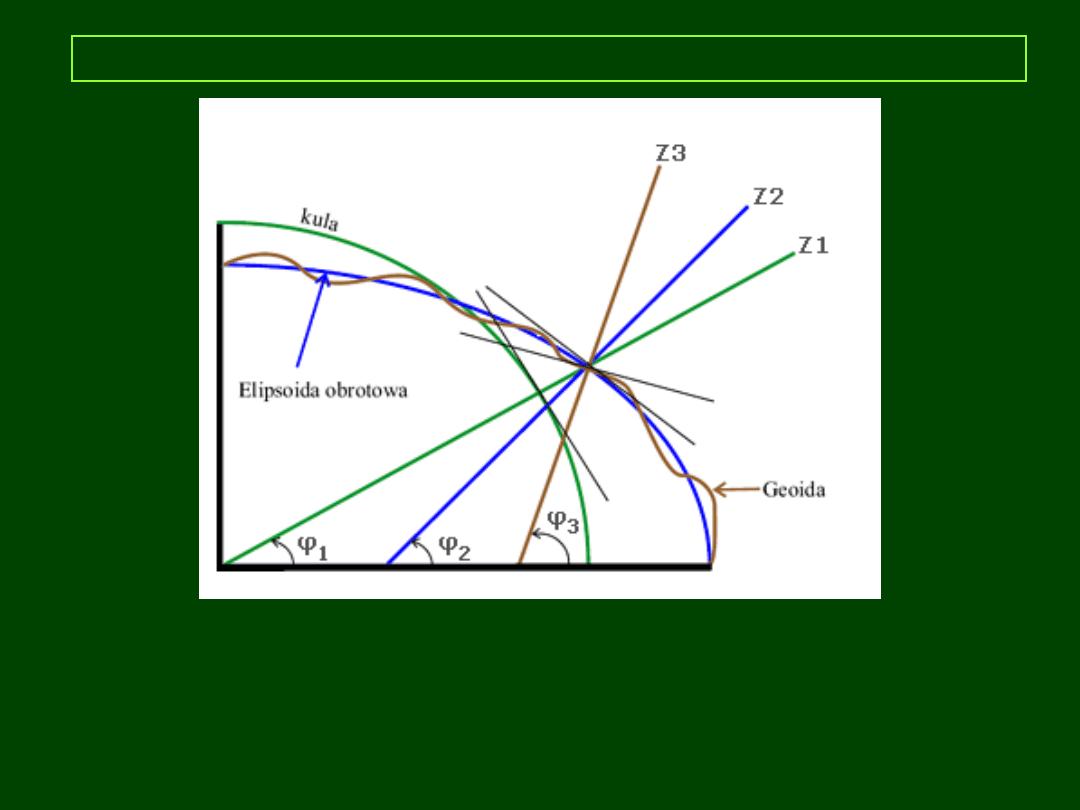
22:47 22:47

7

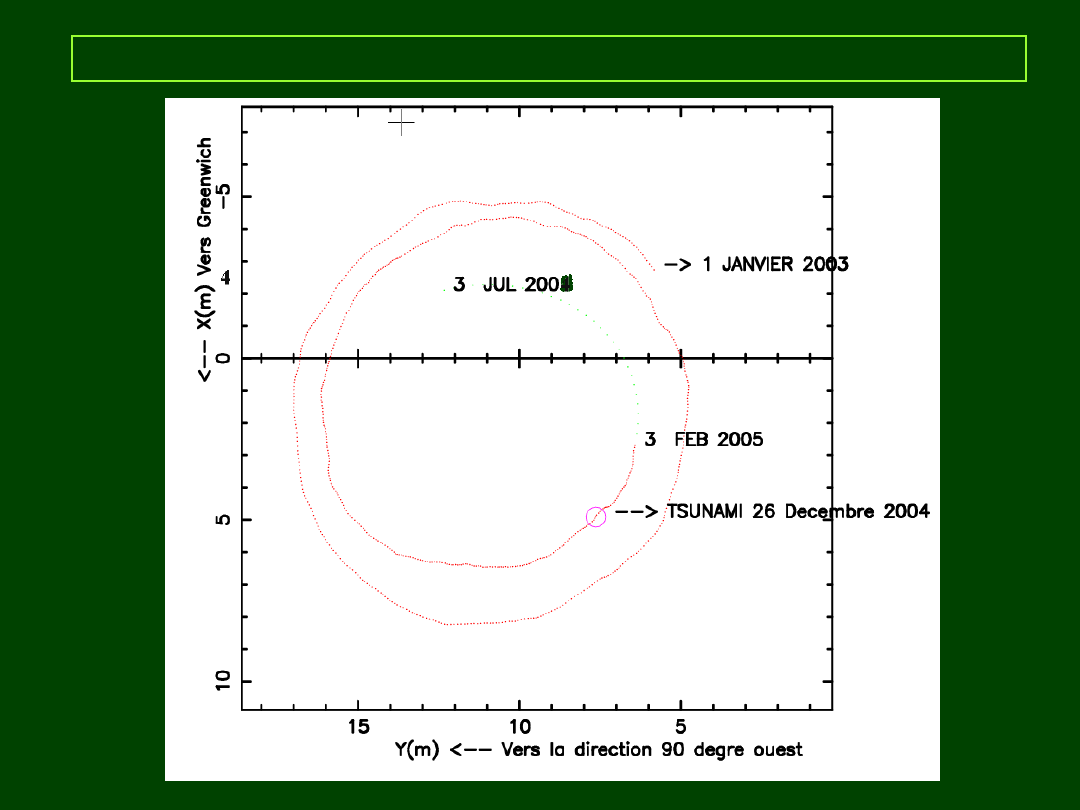
Przykład: współrzędne geograficzne

http://www.nauticalissues.com/astronomy.html

φ

1

– geocentryczna szerokość geograficzna

φ

2

– geodezyjna szerokość geograficzna

φ

3

– astronomiczna szerokość geograficzna

Dla φ ≈ 50º, φ

3

– φ

1

≈ 11’

22:47 22:47

8

Ruchy bieguna Ziemi

22:47 22:47

9

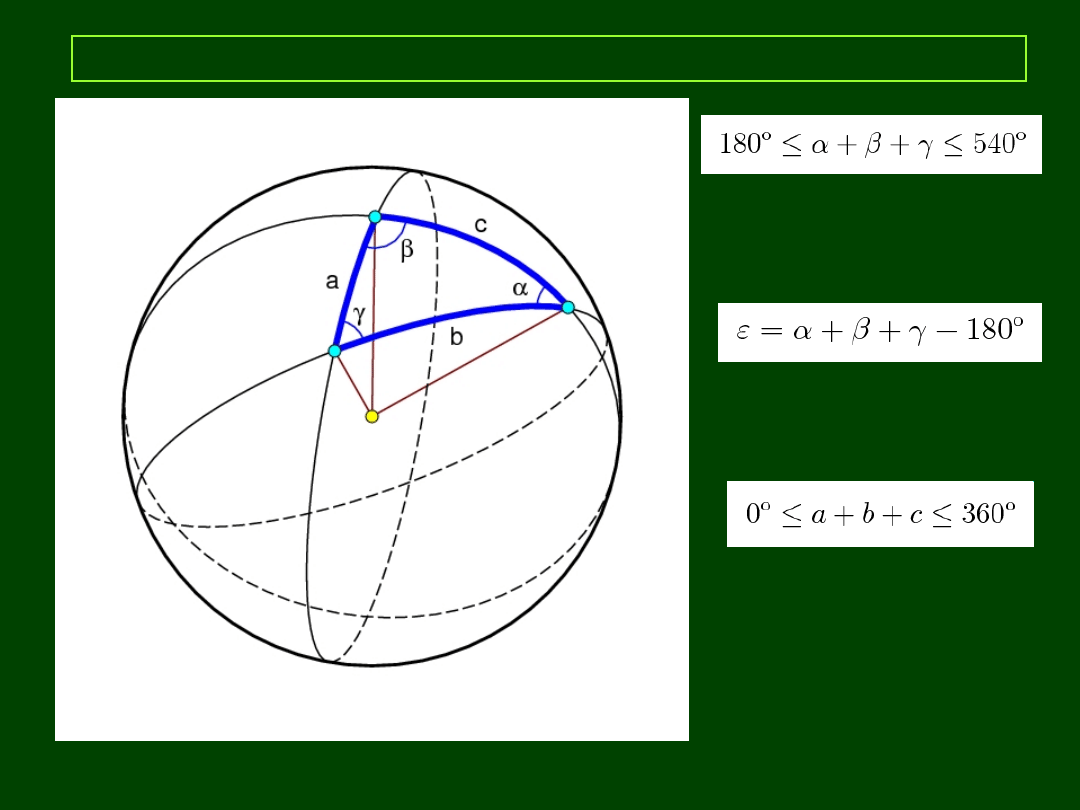
Trójkąt sferyczny

Nadmiar (eksces)

sferyczny ε

22:47 22:47

10

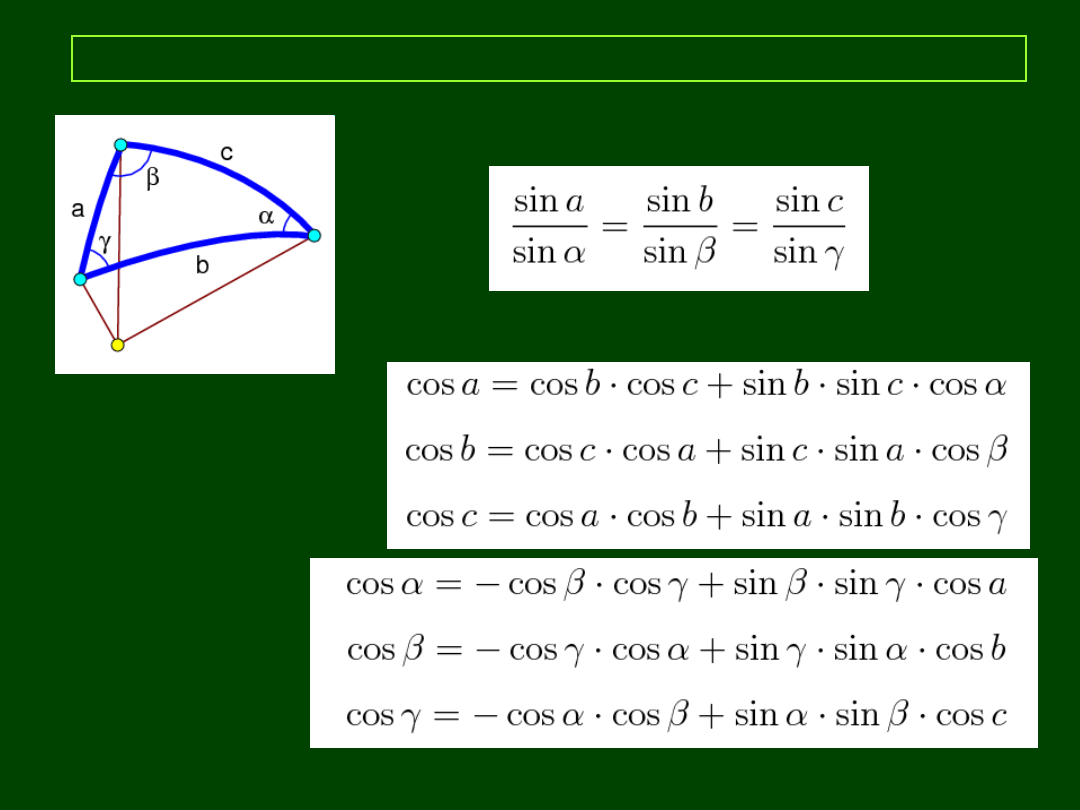
Trójkąt sferyczny

Twierdzenie sinusowe:

Twierdzenie

cosinusowe

boków:

Twierdzenie

cosinusowe

kątów:

22:47 22:47

11

Układy współrzędnych: położenie centrum, płaszczyzny

Topocentryczny:

środek układu współrzędnych (O) na powierzchni

Ziemi.

Geocentryczny:

O w centrum Ziemi.

Selenocentryczny:

O w centrum Księżyca.

Planetocentryczny:

O w centrum planety.

Heliocentryczny:

O w centrum Słońca.

Barocentryczny:

O w centrum masy Układu Słonecznego.

Płaszczyzna horyzontu

(płaszczyzna prostopadła do lokalnego

kierunku pionu, przechodząca przez obserwatora).

Lokalny południk

(płaszczyzna zawierająca wertykał i kierunek osi

obrotu Ziemi).

22:47 22:47

12

Układy współrzędnych: płaszczyzny

Równik niebieski

(płaszczyzna prostopadła do osi obrotu Ziemi,

przechodząca przez jej środek).

Ekliptyka

(średnia płaszczyzna orbity Ziemi wokół Słońca).

Południk planetarny

(płaszczyzna zawierająca oś obrotu planety i

jakiś charakterystyczny szczegół na jej powierzchni).

Równik planetarny

(płaszczyzna prostopadła do osi obrotu planety,

przechodząca przez jej centrum).

Płaszczyzna orbity

(płaszczyzna orbity jakiegoś ciała względem

drugiego, np. planety wokół Słońca lub barycentrum).

Płaszczyzna niezmiennicza (Laplace’a)

(płaszczyzna prostopadła do

kierunku wektora momentu pędu systemu, przechodząca przez
jego środek masy).

Równik galaktyczny

(płaszczyzna definiująca płaszczyznę

Galaktyki).

22:47 22:47

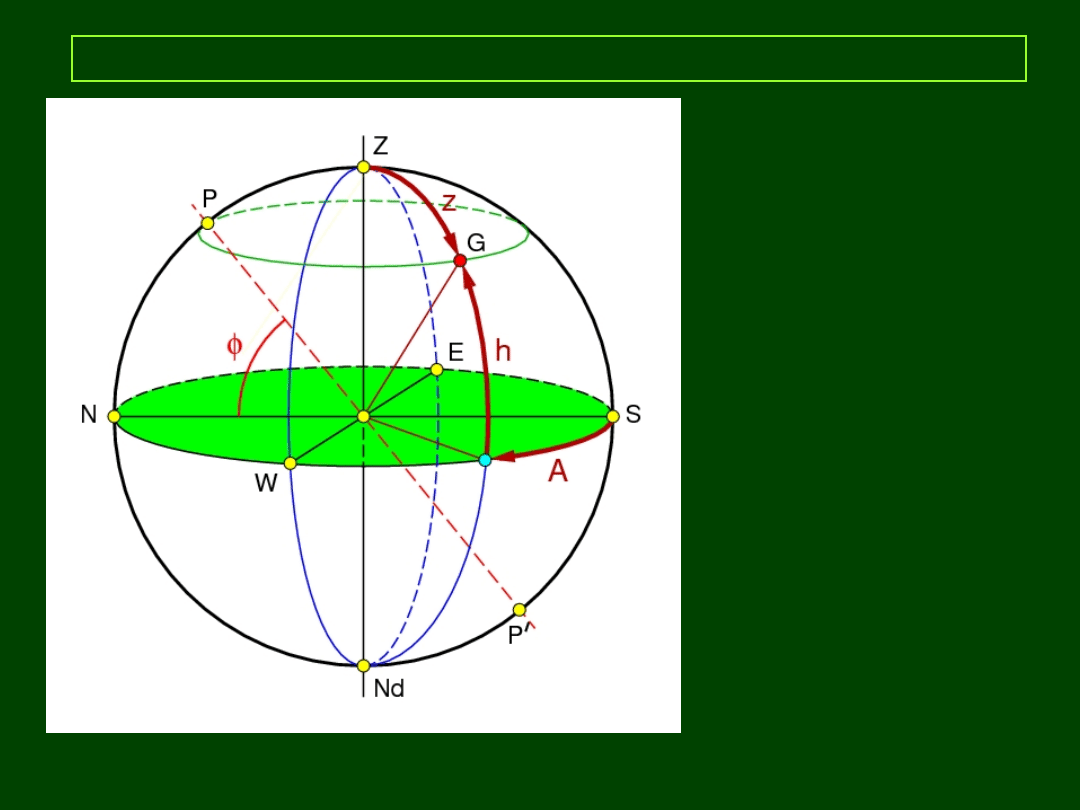
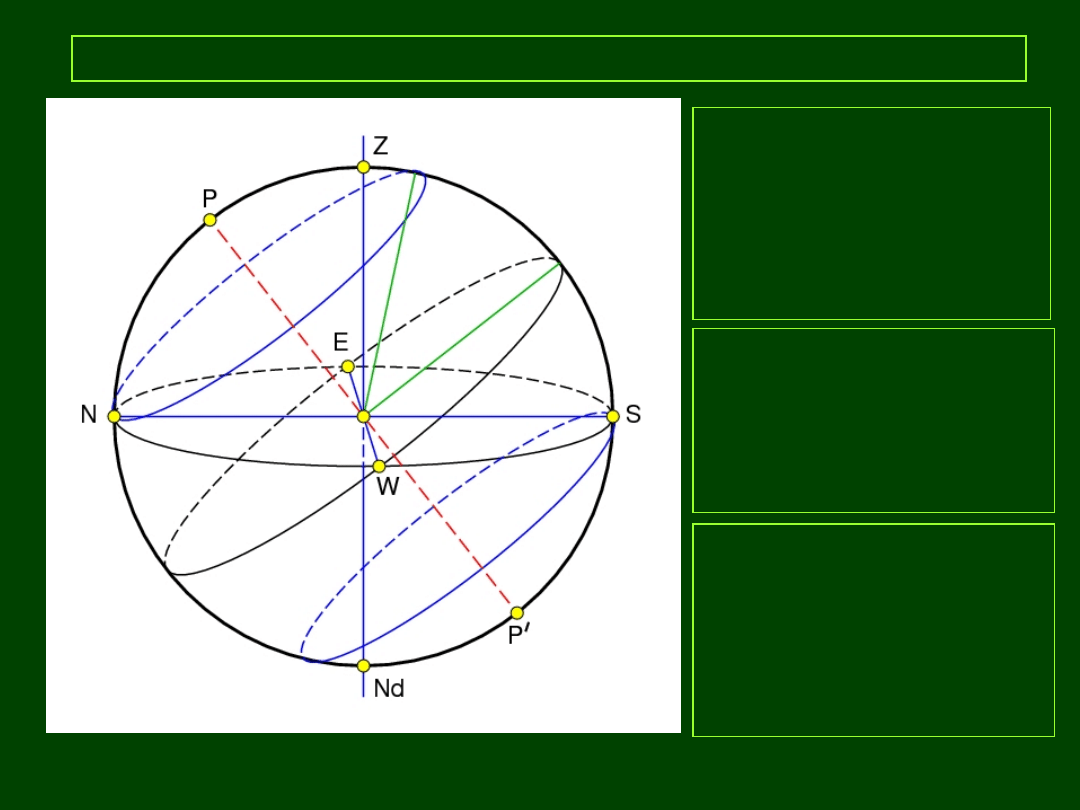
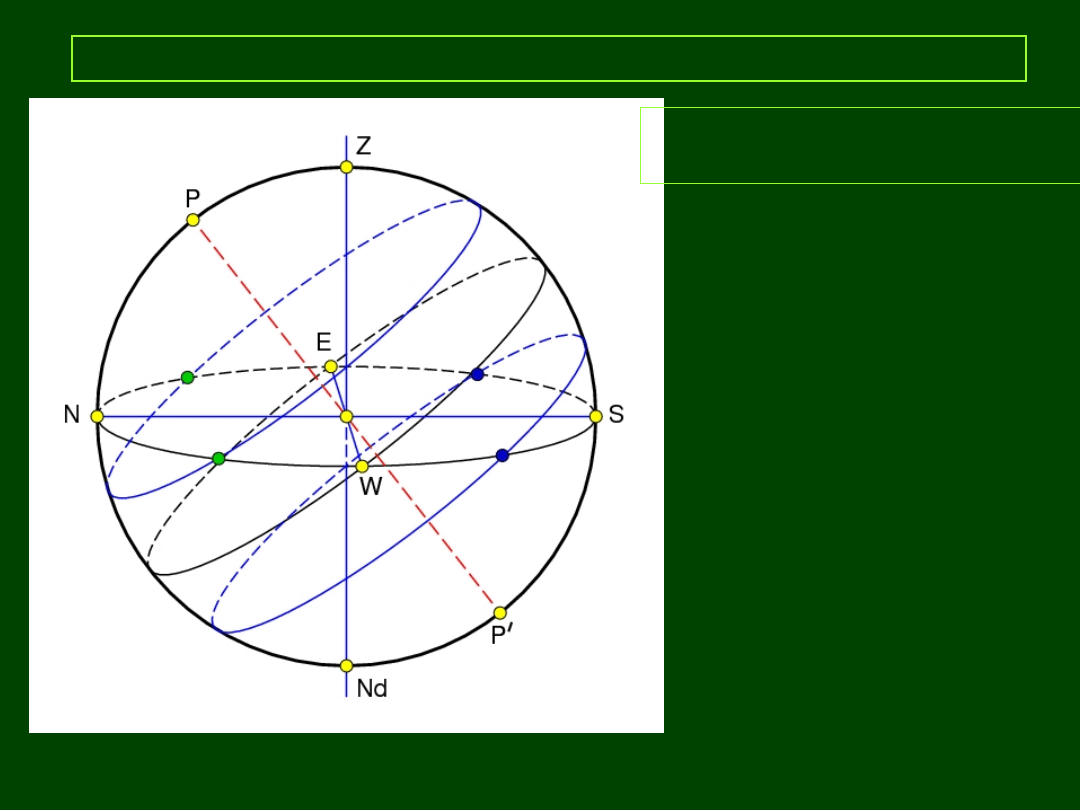
13

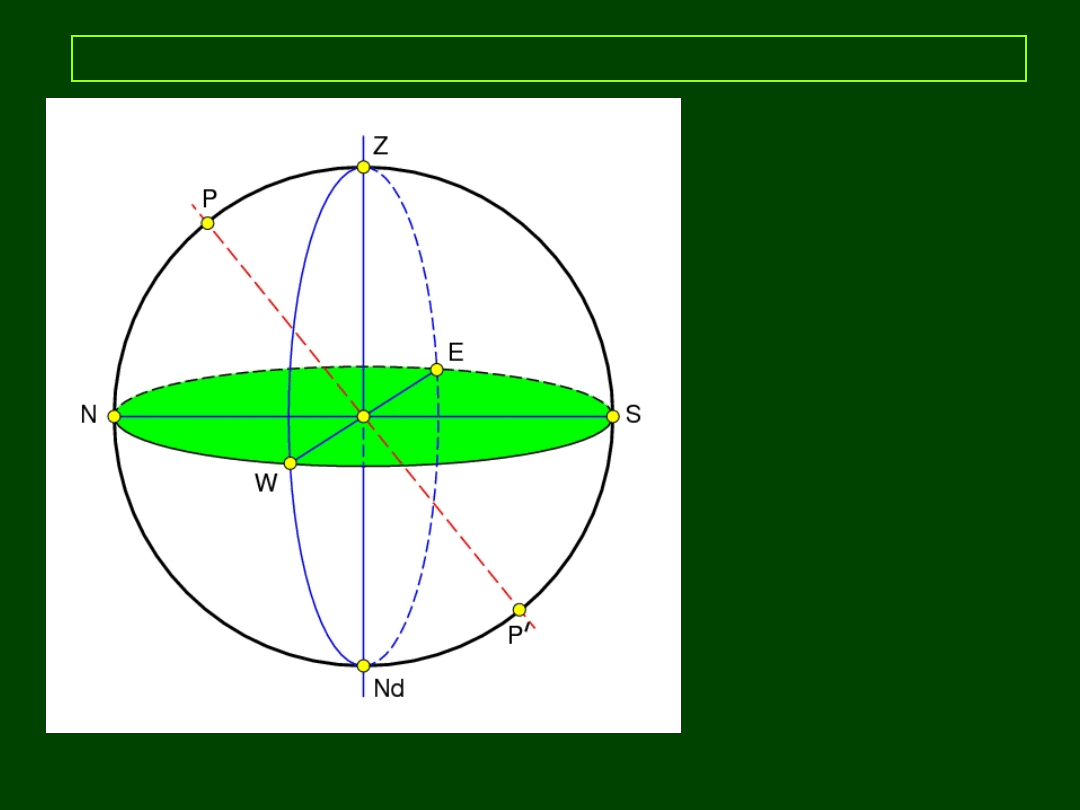
Horyzontalny układ współrzędnych

PP:

pł. horyzontu

KP:

horyzont

O:

obserwator

OG:

kierunek lokalnego

pionu

Z = zenit

Nd = nadir

PkP:

połowa lokalnego

południka przechodząca
przez S

N – kierunek północy
E – kierunek wschodu
S – kierunek południa
W – kierunek zachodu

NSWE: kardynalne punkty

horyzontu

(Z E Nd W):
pierwszy wertykał

(P Z S P’ Nd N): lokalny południk astronomiczny

22:47 22:47

14

Horyzontalny układ współrzędnych

φ – szerokość geogr.

A – azymut

Kąt dwuścienny między
wertykałem przechodzącym
przez punkt S a wertykałem
przechodzącym przez obiekt G,
mierzony po horyzoncie
w kierunku zachodu (W).
Zakres:

0 – 360º

h – wysokość

Kąt pomiędzy płaszczyzną
horyzontu a kierunkiem na
obiekt.
Zakres: od

-90º

(poniżej

horyzontu) do

+90º

(powyżej

horyzontu).

Uwaga: w geodezji i kartografii
azymut mierzy się od N
w kierunku E.

A

G

= A - 180º

z – odległość zenitalna,

z = 90º - h (0-180º)

almukantarat

22:47 22:47

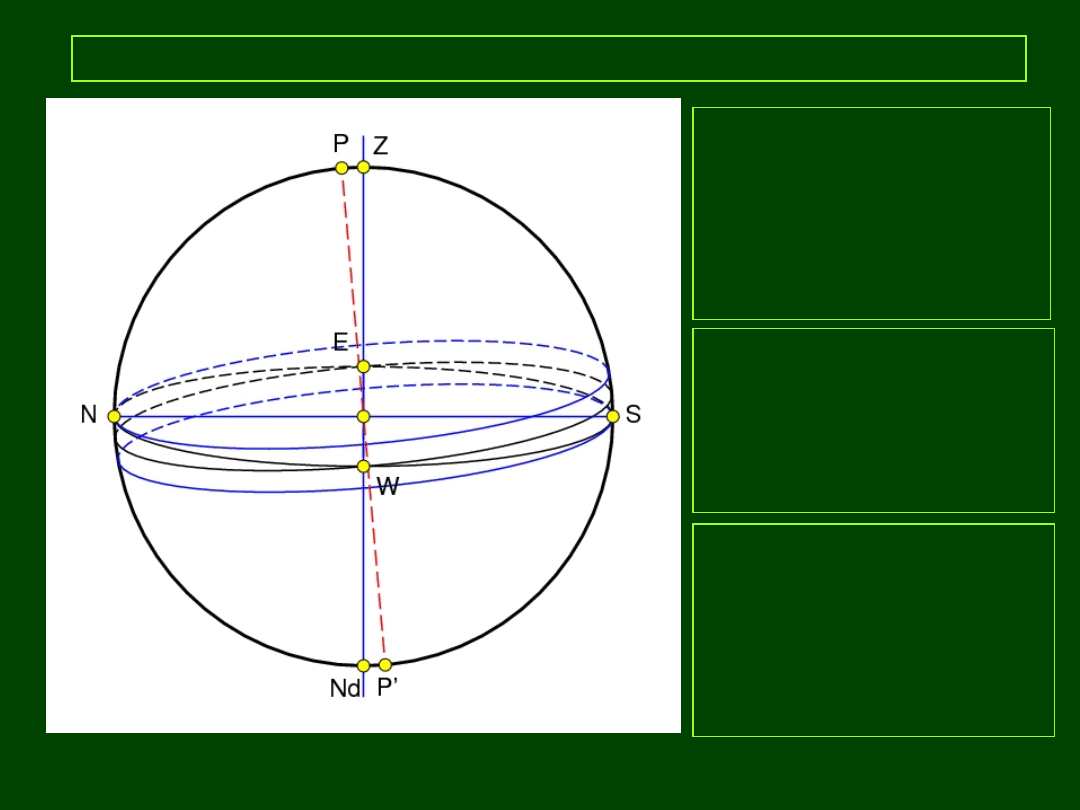
15

Horyzontalny układ współrzędnych

φ = 90º

φ = 52º

φ = 25º

φ = 0º

φ = -30º

równik

o

ś

o

b

ro

tu

22:47 22:47

16

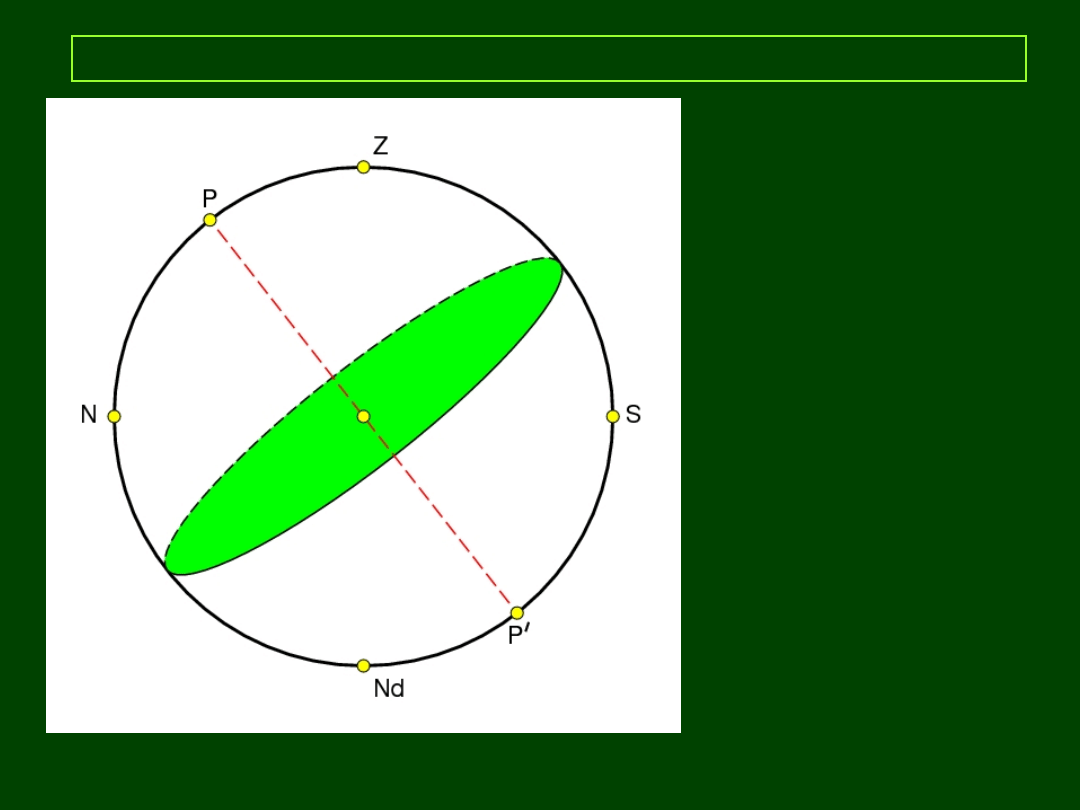
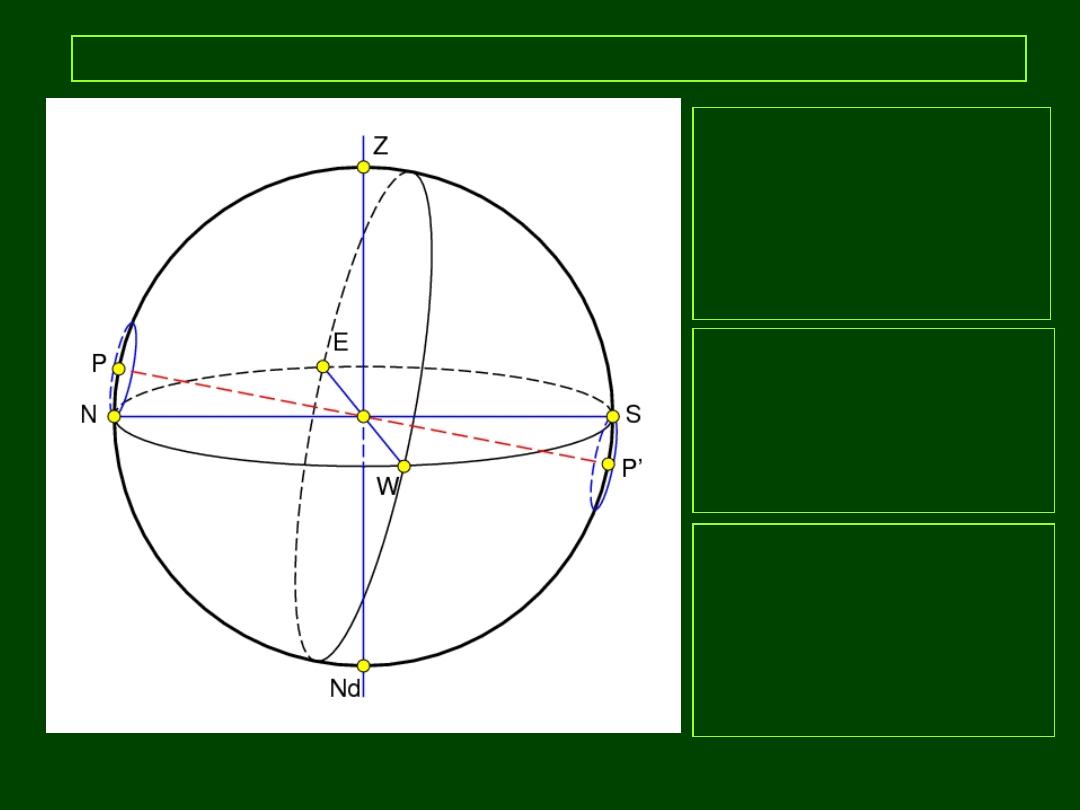
Układ równikowy I (godzinny)

PP:

pł. równika nieb.

KP:

równik niebieski

O:

obserwator

OG:

oś świata

P – północny biegun świata
P’ – połudn. biegun świata

PkP:

połowa lokalnego

południka przechodząca
przez Z

22:47 22:47

17

Układ równikowy I (godzinny)

t – kąt godzinny

Kąt dwuścienny między
półkolem początkowym
południka a półkolem
godzinnym przechodzącym
przez obiekt G, mierzony po
równiku niebieskim w kierunku
w kierunku dziennego ruchu
sfery niebieskiej.
Zakres:

0 – 24

h

lub 0 – 360º

1

h

= 15º

δ – deklinacja

Kąt pomiędzy płaszczyzną
równika niebieskiego
a kierunkiem na obiekt G.
Zakres: od

-90º

do

+90º

.

δ < 0º oznacza obiekty na

południowej części nieba,

δ > 0º - obiekty na

półkuli

północnej.

Północna odległość biegunowa, n

n = 90º - δ

S’

22:47 22:47

18

Związki między współrzędnymi (UH i URI)

Ogólny związek pomiędzy współrzędnymi dwu układów prostokątnych
w 3 wymiarach:

Np. dla prawoskrętnego układu współrzędnych
i obrotu wokół osi x o kąt β:

UH

URI

Oś x

OS

OS’

Oś y

OW

OW

Oś z

OZ

OP

Przejście od UH do URI:

ujemny obrót o kąt
90º - φ wokół osi y

22:47 22:47

19

Związki między współrzędnymi (UH i URI)

czyli:

Dla takiej transformacji mamy:

22:47 22:47

20

Związki między współrzędnymi (UH i URI)

Rozpisując równanie macierzowe dostajemy:

Dzieląc równanie 2 przez 1 dostajemy wyrażenie na

tan t

:

Kąt godzinny

t

wyznaczamy jednoznacznie biorąc pod uwagę znak

licznika i mianownika w tym wyrażeniu.
Deklinację

δ

wyznaczamy jednoznacznie z równania 3.

22:47 22:47

21

Związki między współrzędnymi (UH i URI)

Azymut

A

wyznaczamy jednoznacznie biorąc pod uwagę znak

licznika i mianownika w tym wyrażeniu.
Wysokość

h

wyznaczamy jednoznacznie z równania 3.

W podobny sposób dostajemy wyrażenia na transformację odwrotną:

Dzieląc równanie 2 przez 1 dostajemy wyrażenie na

tan A

:

22:47 22:47

22

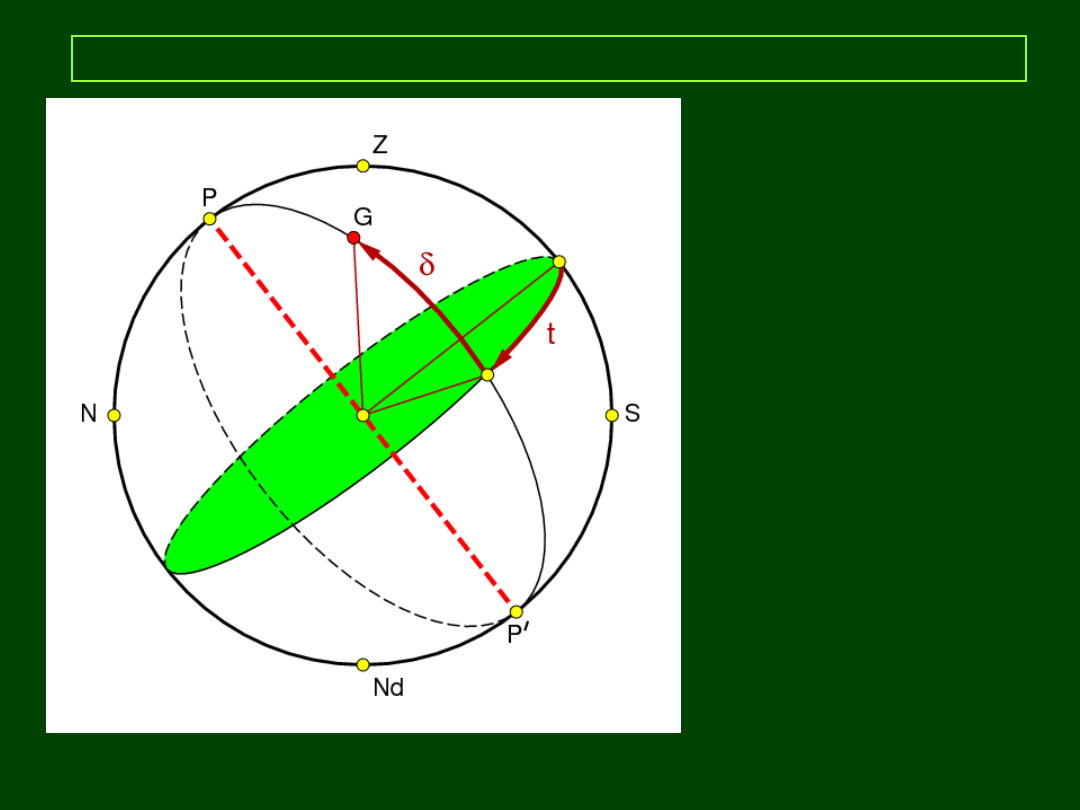
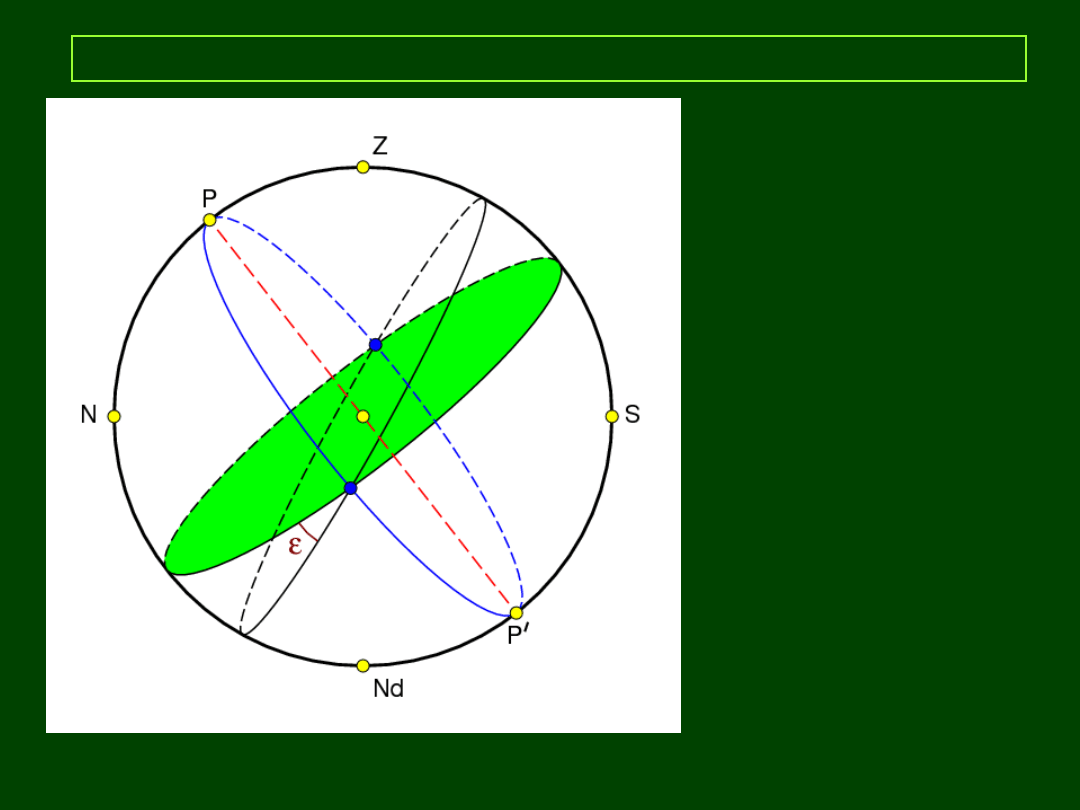
Układ równikowy II (równonocny)

PP:

pł. równika nieb.

KP:

równik niebieski

O:

obserwator

OG:

oś świata

P – północny biegun świata
P’ – połudn. biegun świata

PkP:

półkole godzinne

przechodzące przez

punkt równonocy
wiosennej

(punkt

Barana)





ε – kąt pomiędzy

płaszczyzną równika
i ekliptyki

ε ≈ 23,5 º

22:47 22:47

23

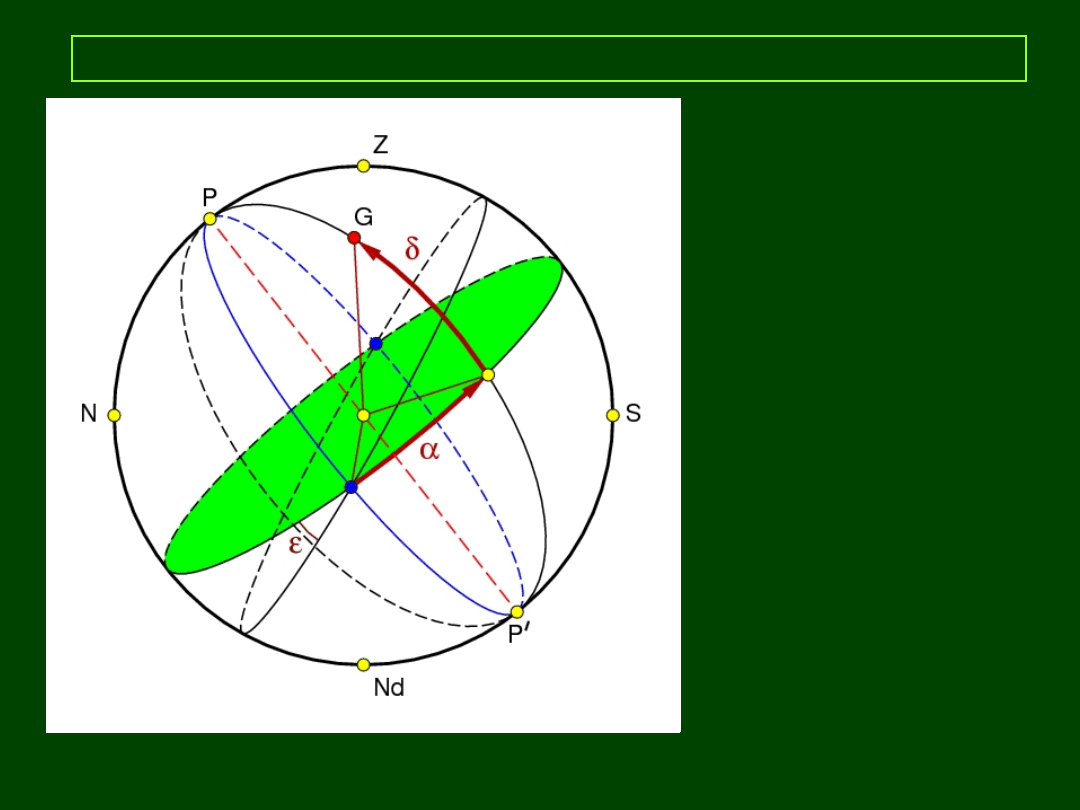
Układ równikowy II (równonocny)







δ – deklinacja

Kąt pomiędzy płaszczyzną
równika niebieskiego
a kierunkiem na obiekt G.
Zakres: od

-90º

do

+90º

.

δ < 0º oznacza obiekty na

południowej części nieba,

δ > 0º - obiekty na

półkuli

północnej.

α – rektascensja

Kąt pomiędzy płaszczyzną
Półkola godzinnego
Przechodzącego przez punkt
Barana a płaszczyzną półkola
Godzinnego przechodzącego
Przez obiekt.
Zakres: od

0

h

do

24

h

.

Współrzędne (α,δ)
zmieniają się bardzo
wolno w czasie:
używane są na mapach
nieba i w katalogach

22:47 22:47

24

Północny biegun świata

Źródło: Carte du Ciel

22:47 22:47

25

Południowy biegun świata

Źródło: Carte du Ciel

22:47 22:47

26

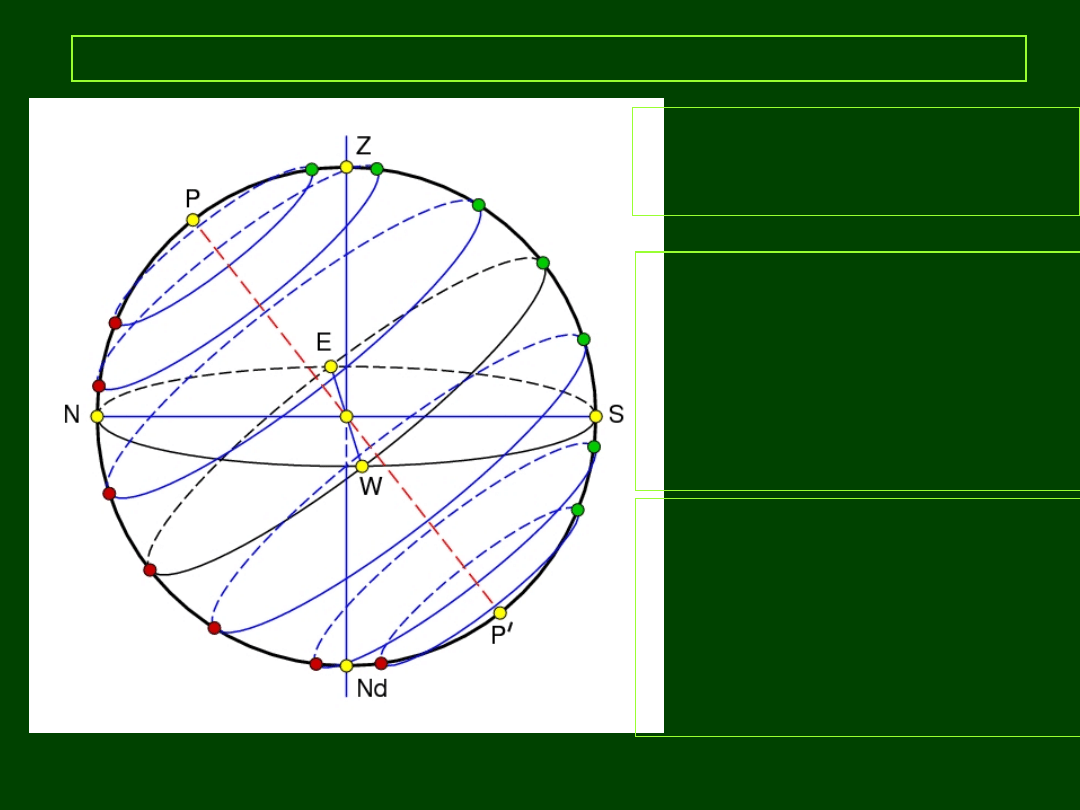
Wschody i zachody

Obiekty nigdy nie

zachodzące

(okołobiegunowe)

δ ≥ 90º - φ

(dla półkuli N)

δ ≤ -90º - φ

(dla półkuli S)

Obiekty wschodzące

i zachodzące

90º - φ ≥ δ ≥ φ - 90º

(dla półkuli N)

-90º - φ ≤ δ ≤ 90º + φ

(dla półkuli S)

Obiekty nigdy

nie wschodzące

(niewidoczne)

δ ≤ φ - 90º

(dla półkuli N)

δ ≥ 90º + φ

(dla półkuli S)

φ = 52º

22:47 22:47

27

Wschody i zachody: blisko bieguna północnego

Obiekty nigdy nie

zachodzące

(okołobiegunowe)

δ ≥ 90º - φ

δ ≥ +5º

Obiekty wschodzące

i zachodzące

90º - φ ≥ δ ≥ φ - 90º

+5º ≥ δ ≥ -5º

Obiekty nigdy

nie wschodzące

(niewidoczne)

δ ≤ φ - 90º

δ ≤ -5º

φ = 85º

22:47 22:47

28

Wschody i zachody: blisko równika

Obiekty nigdy nie

zachodzące

(okołobiegunowe)

δ ≥ 90º - φ

δ ≥ +79º

Obiekty wschodzące

i zachodzące

90º - φ ≥ δ ≥ φ - 90º

+79º ≥ δ ≥ -79º

Obiekty nigdy

nie wschodzące

(niewidoczne)

δ ≤ φ - 90º

δ ≤ -79º

φ = 11º

22:47 22:47

29

Ruch gwiazd na niebie

Wiedeń (φ = +48°)

Andy, Ojos del Salado

(φ = -27°)

22:47 22:47

30

Ruch gwiazd na niebie

Okolice równika (Kenia)

Mudgee (Australia)

22:47 22:47

31

Wschody i zachody: górowanie i dołowanie

φ = 52º

Dla górowań i dołowań:

A = 0º lub 180º

t = 0 lub 12h

Wysokość górowań:

- północnego (na Pn od Z)

h

gPn

= φ + 90º - δ

- południowego (na Pd od Z)

h

gPd

= 90º - φ + δ

Wysokość dołowań:

- północnego (na Pn od Nd)

h

dPn

= φ - 90º + δ

- południowego (na Pd od Nd)

h

dPd

= -90º - φ - δ

22:47 22:47

32

Wschody i zachody: azymut i kąt godzinny

φ = 52º

Ze wzorów transformacyjnych
możemy łatwo dostać, że dla
wschodu i zachodu

t

w,z

= arccos(- tan δ tan φ)

oraz

A

w,z

= arccos(- sin δ / cos φ)

Sytuacja taka, że

|- tan δ tan φ| > 1

albo

|- sin δ / cos φ| > 1

oznacza oczywiście, że
zjawisko wschodu/zachodu

nie ma miejsca

: obiekt jest

niewidoczny lub
okołobiegunowy.

Dla wschodu i zachodu:

h = 0º