dr Jolanta Gadawska

Cel bieżący

(krótkoterminowy)

Maksymalizacja zysku

Realizacja tych celów wymaga

podjęcia przedsięwzięć

inwestycyjnych zapewniających

rozwój podmiotu.

Cel
strategiczny
(długotermino
wy)

Wzrost
wartości
przedsiębiorst
wa

Muszą opierać się na obiektywnych

kryteriach wyboru. Muszą
uwzględniać :



nadwyżkę efektów nad nakładami,



czynniki pozaekonomiczne,



ryzyko (nie uzyskania efektów lub
przekroczenia dochodów),



czas w jakim uzyska się planowane
efekty,



inflację.

Proste

(statyczne)

Oparte na relacjach

między nakładami,

efektami a czasem.

Nie uwzględniają

zmian wartości

pieniądza w czasie,

ryzyka i inflacji.

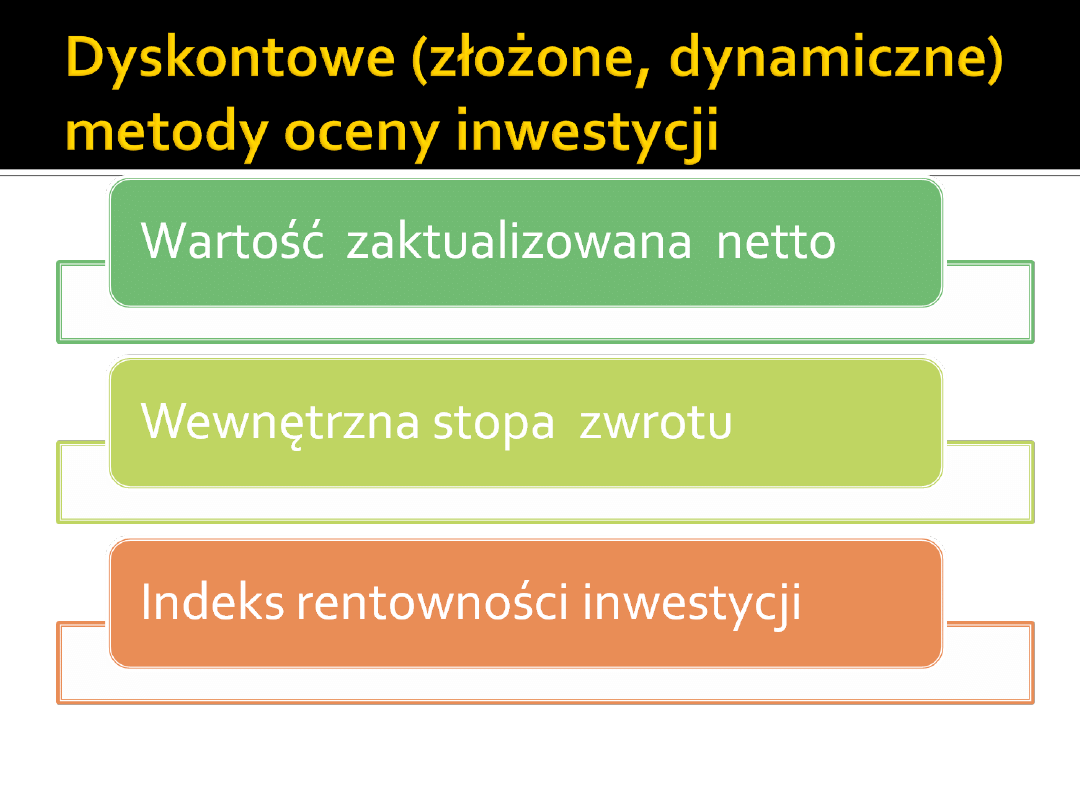
Złożone

(dynamiczne)

Oparte na stopie

procentowej

(dyskontowej).

Uwzględniają zmianę

wartości pieniądza

w czasie, ryzyko i

inflację.

Przeciętna stopa zwrotu z inwestycji z całego

cyklu życia przedsięwzięcia. Liczy się ją na

podstawie zysków lub przepływów

pieniężnych (cash flow) generowanych przez

aktywa związane z realizacją danej

inwestycji.

∑ Zn/n

KSZ= Co ; ∑Zn- suma zysków netto,

Co – kapitał finansujący

początkowe wydatki

Podstawia się przeciętne zyski i nakłady inwestycyjne

Wybieramy przedsięwzięcie o najwyższej stopie.

jest wskaźnikiem prezentującym średni
księgowy zysk w stosunku do poniesionej
inwestycji. Jest wiec to średnioroczny zysk
netto (suma zysków netto podzielona przez
liczbę lat funkcjonowania projektu) generowany
przez projekt podzielony przez średnioroczną
inwestycję rozumianą jako suma wartości
początkowej i końcowej księgowej wartości
netto inwestycji (czyli po uwzględnieniu
amortyzacji) podzielony przez dwa.

zysk netto +amortyzacja

Prosta stopa zwrotu całkowity nakład

inwest.

Stopa zwrotu informuje jaka część nakładu stanowi roczny

dochód.

Dzięki temu wskaźnikowi można dokonać oceny możliwości

finansowych przedsiębiorstwa przyjęcia wybranej inwestycji.

Stopę zwrotu można wykorzystać we wstępnej ocenie

konkurencyjnych projektów.

=

Jest to odwrotność prostej stopy zwrotu.

OZ = 1/stopa zwrotu

OZ= Co/CFn

CFn – skumulowane przepływy pieniężne lub

nadwyżka finansowa (amortyzacja +zysk

netto);

Informuje wciągu ilu lat inwestor pokryje

poniesione wydatki wygenerowanymi

zyskami.

Rok w którym poniesione nakłady

(wydatki) zostaną zrównoważone
przez nadwyżki będzie zamykał
okres, w którym nastąpi zwrot
początkowych wydatków.

ROI = średni roczny zysk/ Co

lub
ROI = zysk netto/wartości aktywów x 100%

lub
ROI = EBIT/Co x 100%

Stopa ta mierzy rentowność

przedsięwzięcia.

• jedynie we wstępnych fazach procesu

przygotowania przedsięwzięć inwestycyjnych, gdy
nie ma jeszcze szczegółowej i rozbudowanej
informacji dotyczącej danego przedsięwzięcia,

• w wypadku przedsięwzięć inwestycyjnych o

stosunkowo krótkim ekonomicznym cyklu życia,
gdy różne rozłożenie w czasie nakładów i efektów
nie wpływa w sposób decydujący na ocenę
opłacalności przedsięwzięcia,

• w wypadku przedsięwzięć inwestycyjnych o

niewielkiej skali, gdy efekty i nakłady są niewielkie
i nie naruszają pozycji rynkowej oraz sytuacji
ekonomiczno – finansowej przedsiębiorstwa
realizującego dane przedsięwzięcie.

Stopą dyskontową jest średni ważony koszt

kapitału, niekiedy oprocentowanie (depozytów lub

kredytów).

Najważniejszy miernik oceny inwestycji

uwzględniający zmianę wartości
pieniądza w czasie. Polega na
sprowadzeniu wszystkich przyszłych
dochodów pieniężnych z inwestycji do ich
aktualnej wartości i odjęciu nakładów
inwestycyjnych.

NPV= ∑CF/(1+r)ⁿ - No

Jeśli NPV >0 projekt należy przyjąć, jest opłacalny;
Jeśli NPV < 0 projekt należy odrzucić

Jeśli mamy inwestycję, która będzie

finansowana kredytem bankowym
należy obliczyć NPV dla stopy kredytu.
Nieujemna wartość NPV oznacza że
daną inwestycję można sfinansować
przy pomocy tego kredytu bez strat dla
właścicieli. Jeśli NPV równe jest zero
oznacza to, że dochód z inwestycji
pozwoli np. jedynie na spłatę kredytu.

Jeśli mamy inwestycję, która będzie

finansowana kredytem bankowym
należy obliczyć NPV dla stopy kredytu.
Nieujemna wartość NPV oznacza że
daną inwestycję można sfinansować
przy pomocy tego kredytu bez strat dla
właścicieli. Jeśli NPV równe jest zero
oznacza to, że dochód z inwestycji
pozwoli np. jedynie na spłatę kredytu.

Miernik IRR wyraża efektywność inwestycji

w formie procentu. Umożliwia

porównanie efektywności inwestycji ze

średnim ważonym kosztem kapitału

zainwestowanego w to przedsięwzięcie.

IRR to graniczna stopa rentowności

inwestycji, to stopa dyskontowa, która

zrównuje zaktualizowaną wartość

przyszłych wpływów z nakładami

inwestycyjnymi. Im wyższe IRR tym

większy dochód inwestycja przynosi.

IRR- jest maksymalną stopą oprocentowania

kredytu, który pozwoli sfinansować projekt

bez straty dla właścicieli

Jest to takie r =IRR, dla którego

∑ CF/(1+IRR)ⁿ = No czyli NPV = 0

jeśli

IRR > WACC (ŚWKK)

ŚWKK – średni ważony koszt kapitału

przedsięwzięcie jest opłacalne

jeśli IRR < WACC

wówczas projekt należy odrzucić

IRR- jest maksymalną stopą oprocentowania

kredytu, który pozwoli sfinansować projekt

bez straty dla właścicieli

Jest to takie r =IRR, dla którego

∑ CF/(1+IRR)ⁿ = No czyli NPV = 0

jeśli

IRR > WACC (ŚWKK)

ŚWKK – średni ważony koszt kapitału

przedsięwzięcie jest opłacalne

jeśli IRR < WACC

wówczas projekt należy odrzucić

Należy znaleźć dwa poziomy stopy d

1

i d

2

dla

których:

d

1

– NPV jest bliskie 0 ale dodatnie, oznaczane

jako PNPV

d

2

– NPV jest bliskie 0 ale ujemne, oznaczane

jako NNPV

IRR = d

1

+ [PNPV(d

2

– d

1

)] / (PNPV + |

NNPV|)

Inwestycja jest opłacalna, jeśli IRR jest większe

lub równe od stopy granicznej, czyli najniższej

stopie rentowności możliwej do

zaakceptowania przez inwestora.

Odzwierciedla stopień zyskowności

zaangażowanego kapitału.

∑CF/(1+r)ⁿ
Zi = No

Jeśli

Zi>1 projekt należy przyjąć,

jeśli

Zi<1 inwestycję należy

odrzucić.

Oparte na systemie oceny kryteriów, mającym

odbicie w priorytetach przedsiębiorstwa, nie

oparte na wartości inwestycji.

Są tu brane pod uwagę efekty jakościowe,

ilościowe, pieniężne i niepieniężne.

Wyróżnić można dwa systemy:



zero-jedynkowy - polega na akceptacji

lub negacji przedsięwzięcia w odniesieniu

do przyjętego kryterium,



wagowy – polega na nadawaniu wag

poszczególnym kryterium, suma wag dla

wszystkich kryteriów powinna wynosić

jeden. Waga jest odbiciem priorytetów

przedsiębiorstwa.

Kierownictwo firmy F rozważa sposób inwestycji

100.000 zł na 4 lata. Projekt A w kolejnych latach
wygeneruje dochody w wysokości 60.000; 20.000;
30.000; 5.000. Projekt B przewiduje otrzymanie
50.000; 50.000; 50.000; 70.000.

Cały czas istnieje możliwość ulokowania tych pieniędzy

w banku na 10%. Wszystkie 3 inwestycje nie są
obarczone ryzykiem.

Lokata na 4 lata (proc. składany)daje 46.410 zł zysku.
NPVa=-100000 +54545+16529+22539+3415=

-2971;

NPVb=-100000 +45455+41322+37566+47811=

72154

Wariant B jest znacznie korzystniejszy niż lokata.

Należy obliczyć IRR dla projektów z poprzedniego

przykładu.

Można ustalić IRR metodą kolejnych przybliżeń.

R NPV

dla projektu B IRR wynosi 38,5%

5% 5312 Na tej podstawie można stwierdzić,
6% 3553 że :
7% 1847 -projekt B jest bardziej rentowny od A
8% 192 -projekt B jest bardziej rentowny
8,12%

0

niż lokata na 10%,

9% -1413-projekt B może być sfinansowany
10% -2971przy pomocy kredytu o opr.10%

-projekt B może być finansowany

nawet przy

wyższej stopie

procentowej

(czyli wyższym

koszcie).

Dwa te same projekty uwzględniające inną stopę

dyskontową różnią się pod względem opłacalności.

Inwestycja będzie kosztowała nas 10.000 i corocznie

(przez 5 lat) możemy liczyć na dochody równe: 1000;
5000; 7000; 3000;1000; Jakie będzie NPV dla stopy
10% i 25%.

a) dla r=10%
DCF (zdyskontowane przepływów)=

=909,1+4132+5259,1+2049+620= 12.970,1

NPV= 12.970,1 – 10.000 = 2.970,1

b) dla r=25%
DCF = 800 + 3.200+3.584+1228,8+327= 9140,5
NPV = 9140,5 – 10.000 = -859,5
Wzrost stopy spowodował, iż inwestycja nie jest opłacalna

Projekt trzyletni kosztuje podmiot 20 000 zł .

Będzie generował dochody 6000; 7000; 8000.

Czy należy przyjąć projekt czy też odrzucić jeśli

koszt kapitału wynosi 9%?

NPV=
=6000/(1,09) + 7000/(1,09)² + 8000/(1,09)³-

20.000=

=18.000 – 20.000 = -2.000
Projekt należy odrzucić gdyż spodziewane

dochody są niższe od wydatku poniesionego
na początku czyli nakładu inwestycyjnego.

Wiedząc, że koszt inwestycji to 14%, nakłady inwestycyjne, które

należy ponieść na początku to 250 000zł. Spodziewamy się
dochodów w pierwszym roku 100 000zł i roku drugim 200.000zł.
Ustal IRR wewnętrzną stopę zwrotu z inwestycji i jej
efektywność.

Przy założeniu, że 1+IRR = z, skróceniu równania kwadratowego

i przemnożeniu przez z² otrzymujemy:

25 z² = 10 z +20; 25z²-10z-20=0
∆= (-10)²-4x25x(-20)=100+2000=2100; √∆=45,8
Z1= 10- 45,8/2x25 = -0,716 odrzucamy;
Z2= 10 + 45,8/2x25=1,116
czyli IRR = z - 1 =1,116 – 1 = 0,116 = 11,6% ; IRR<Kk

(śwkk)

Koszt kapitału jest za wysoki dla tej inwestycji, jest

wyższy od stopy granicznej, dla której nakłady =
zdyskont.doch.