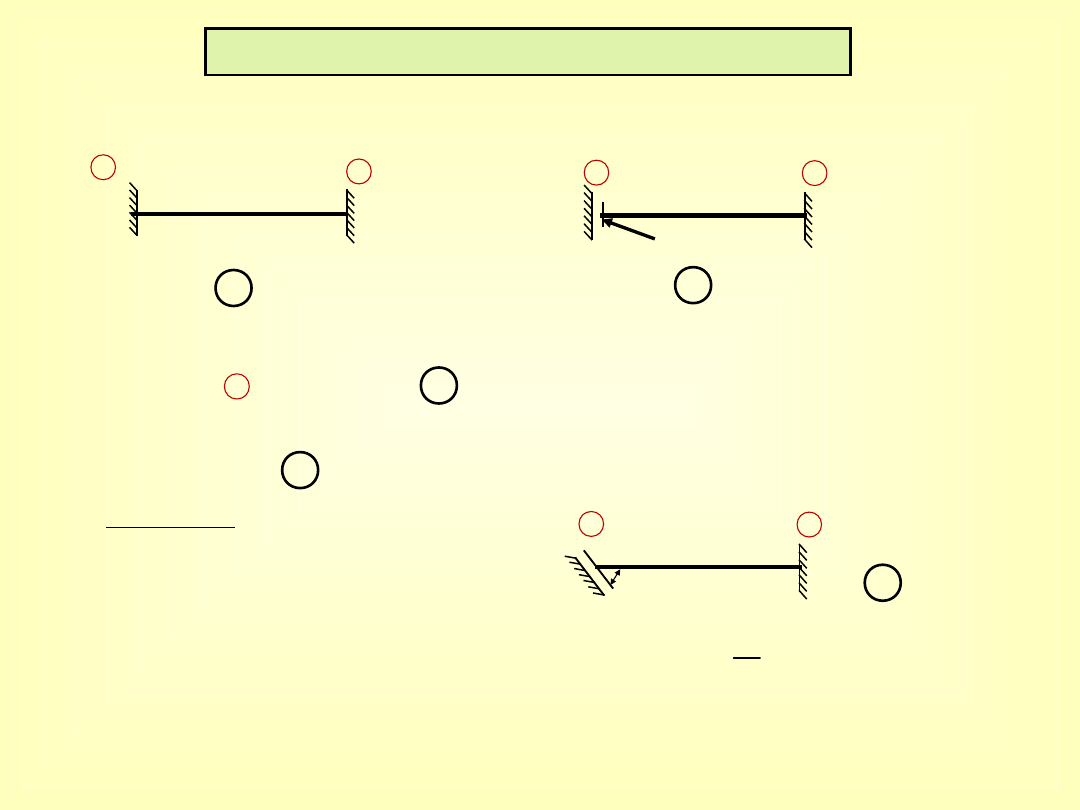
WYBÓR SCHEMATU PODSTAWOWEGO
i
k
k
i
1) Znane są wzory transformacyjne dla prętów:
oraz
A
B
kąt prosty
k
i
C
2
gdy podpora dla przypadku tworzy kąt inny niż 90º
to obowiązują wzory transformacyjne,
jak dla przypadku !
(udowodnić)
B
i
A
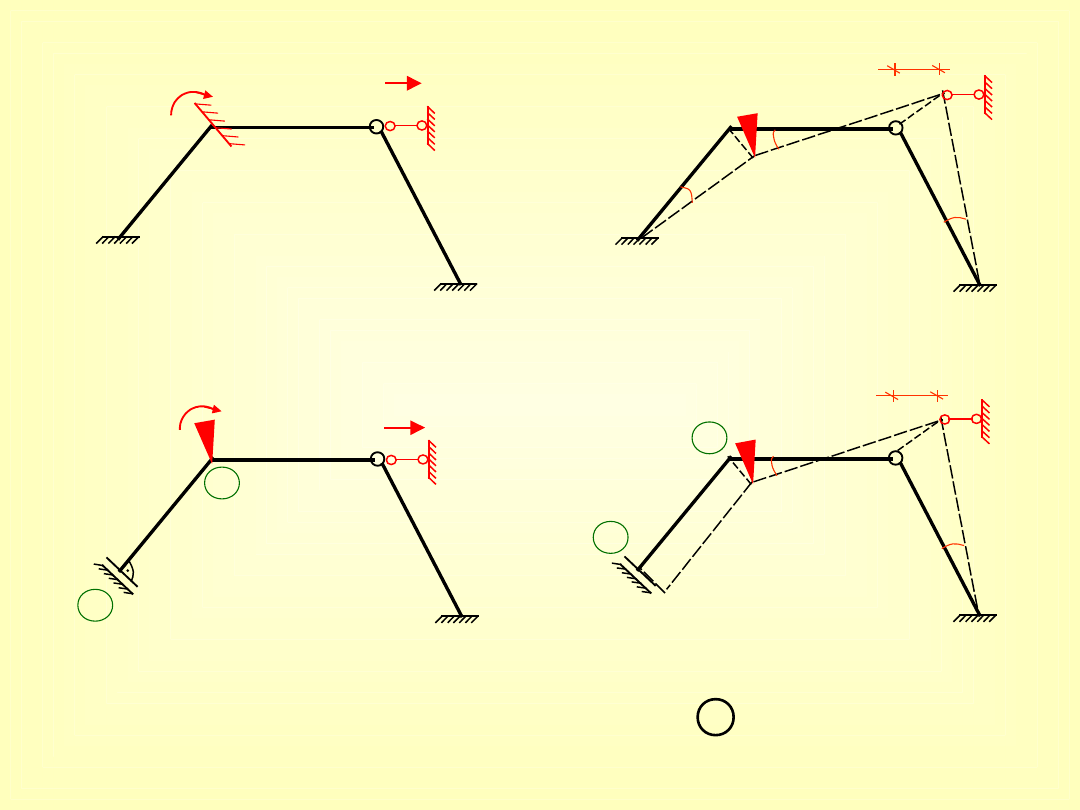
I)
Układ 2x kinematycznie niewyznaczalny
II)
90
2
0
1
3
1
2
1
2
Układ 2x kinematycznie niewyznaczalny
;
0
1
wzory dla (1-2) dla obrotu tak jak dla
schematu
B
1
2
1
3
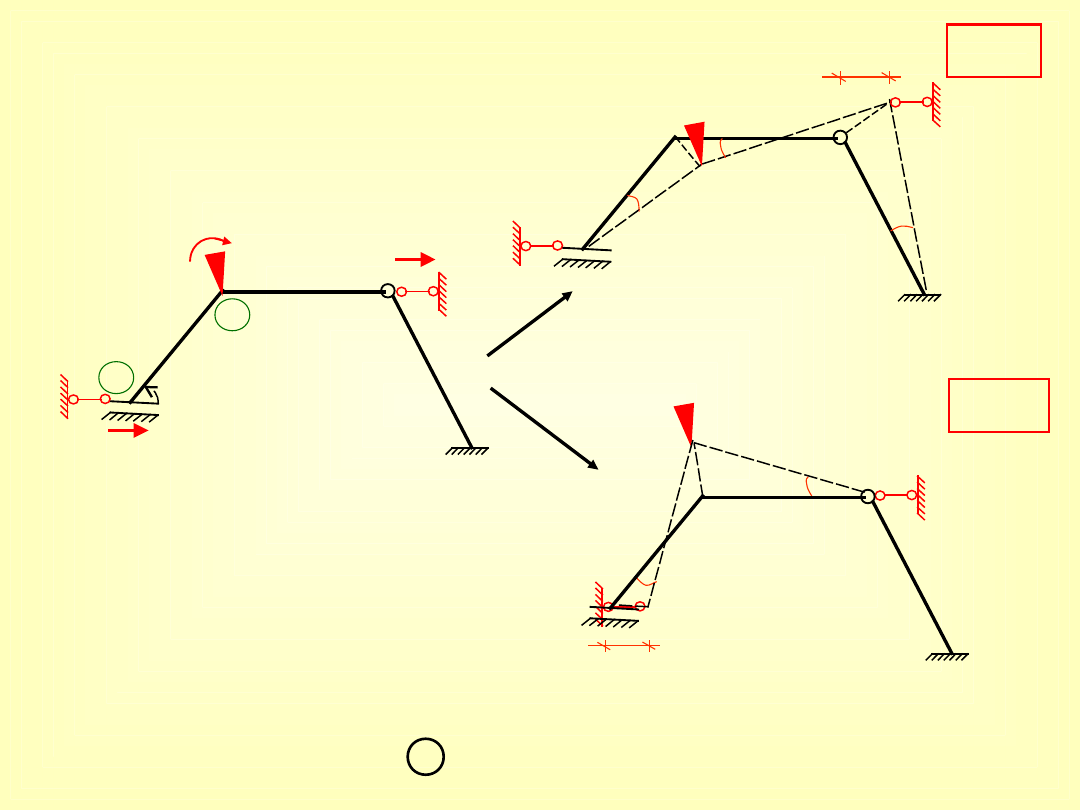
2
2
1
2
2
0
2
3
III)
1
2
1
2
90
1
1
2
1
1
1
3
1
1
1
2
Układ 3x kinematycznie niewyznaczalny
wzory dla (1-2) jak dla schematu
A
2
1
;
;
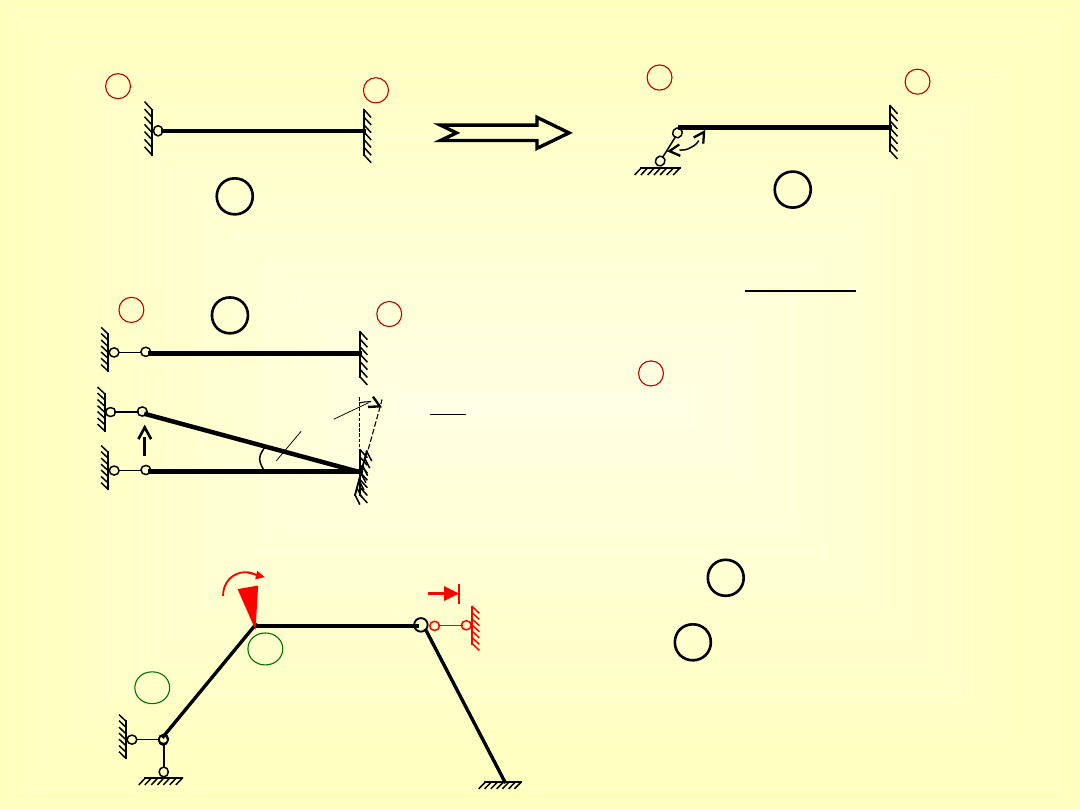
2) Znane są wzory transformacyjne dla pręta:
i
k
i
k
identycznie dla
A’
B’
pod warunkiem, że
180
C’
i
k
Ten pręt zachowuje się jak statycznie
wyznaczalny, tzn. obrót podpory o kąt
nie wywoła momentów zginających w pręcie:
k
k
k
1
2
wzory jak dla postać łańcucha
kinematycznego jak w poprzednim
przypadku
A’
I
układ 2 x kinematycznie
niewyznaczalny
;
I)
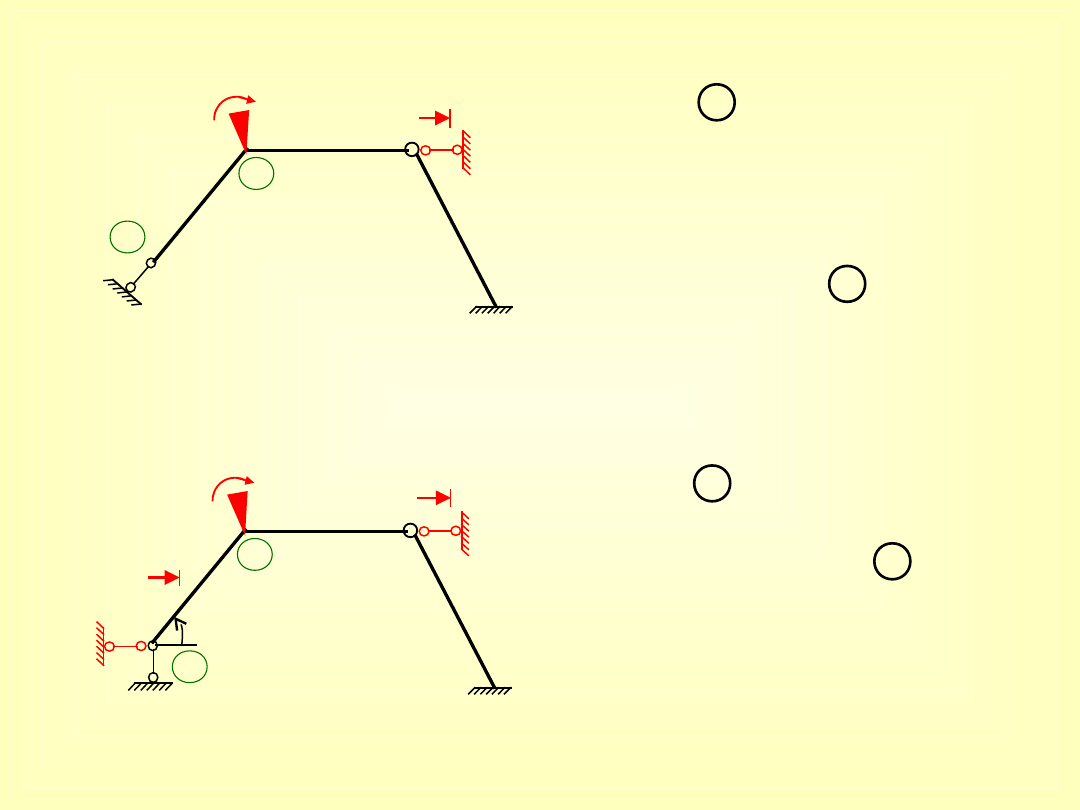
1
2
układ 2 x kinematycznie
niewyznaczalny
;
II)
wzory jak dla tzn. stan
nie wywoła się wewnętrznych w pręcie
(1-2)
C’
1
i
1
Łańcuch kinematyczny jak dla
przypadku poprzedniego
II
1
2
III)
Układ 3x kinematycznie niewyznaczalny
2
1
;
;
180
wzory jak dla
postacie łańcucha kinematycznego (
) jak w poprzednim przypadku
A’
III
2
1
i
dla
1
2
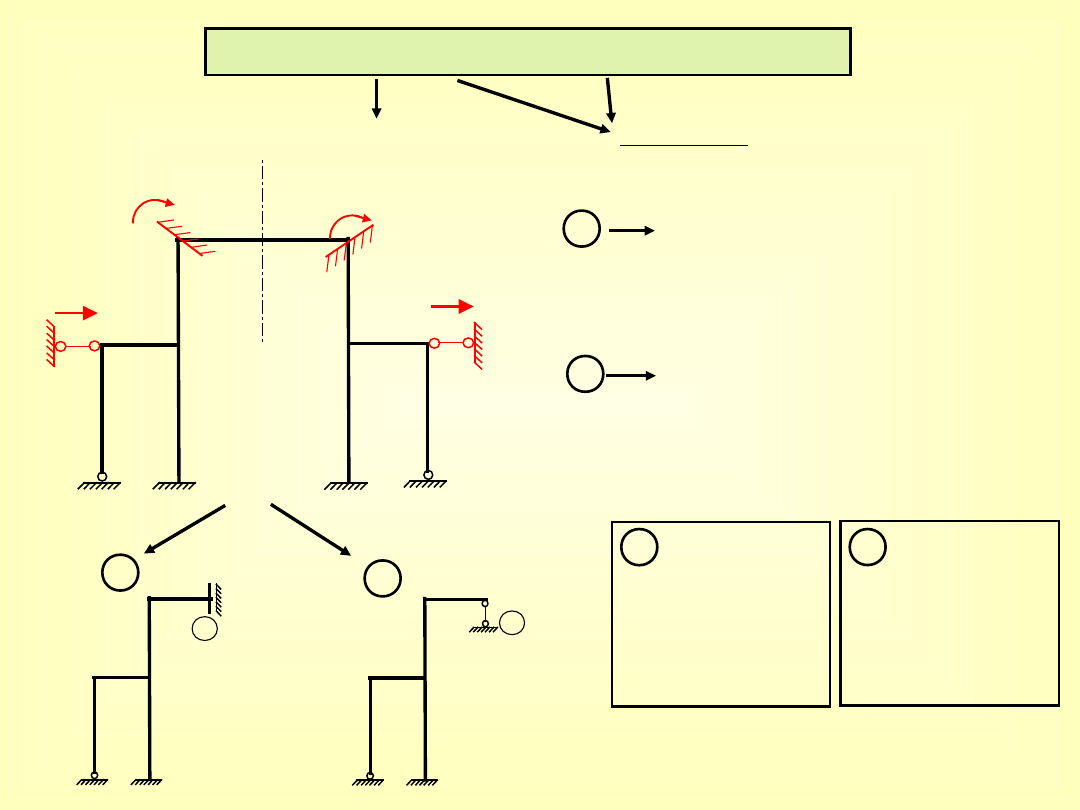
SYMETRIA I ANTYSYMETRIA
oś symetrii
O
geometryczn
a
obciążenie
O
O
S
A
dla obciążenia
symetrycznego
S
2
1
2
1
A
dla obciążenia
antysymetrycznego
2
1
2
1
S
dla
punktu
O
0
v
0
u
0
M
A
dla
punktu
O
0
v
0
u
0
M
1
2
2
1
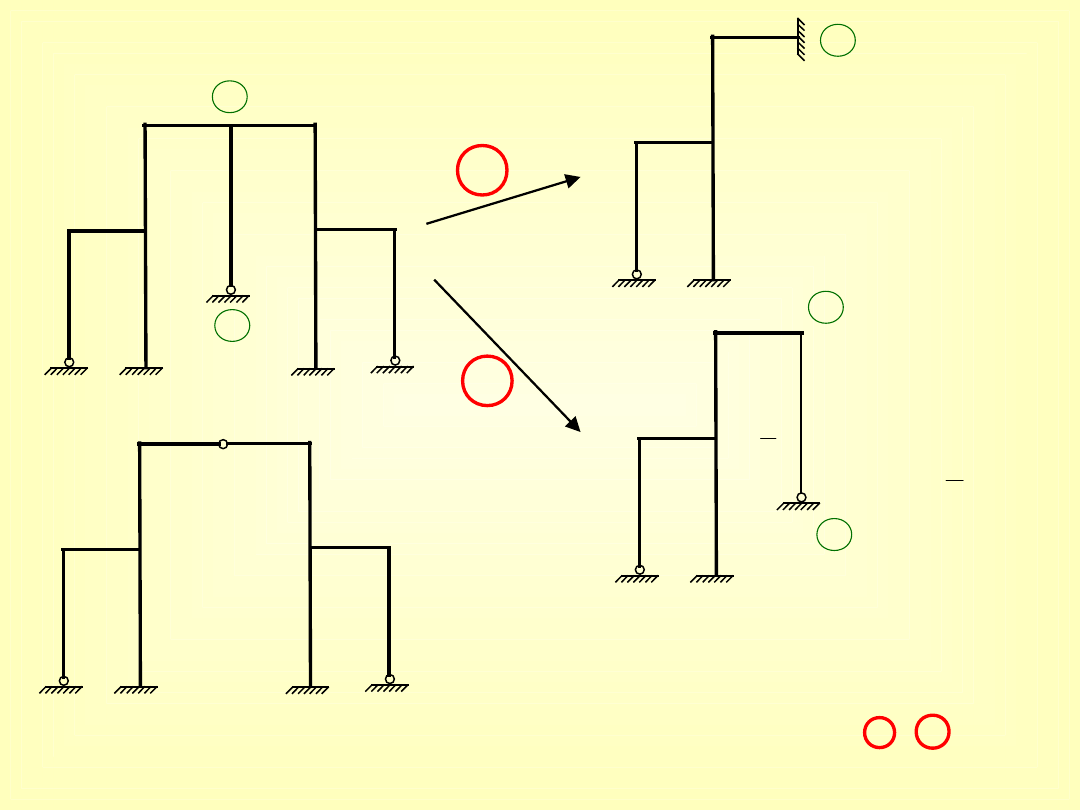
1
2
1
- wykres M
dla pręta 1-
2 jest
zerowy -
u=0
- v=0
- wykres M
dla pręta 1-2
nie jest
zerowy
12
)
A
(
12
J
2
1
J
1
2
J
2
1
pozostałe warunki
przemieszczeniowe pozostają
zgodne z przemieszczeniami
całego układu
3)
S
A
Zadanie domowe: sprowadzić schemat 3) do obliczenia dwóch
schematów i
S A
2)
pręt w osi symetrii
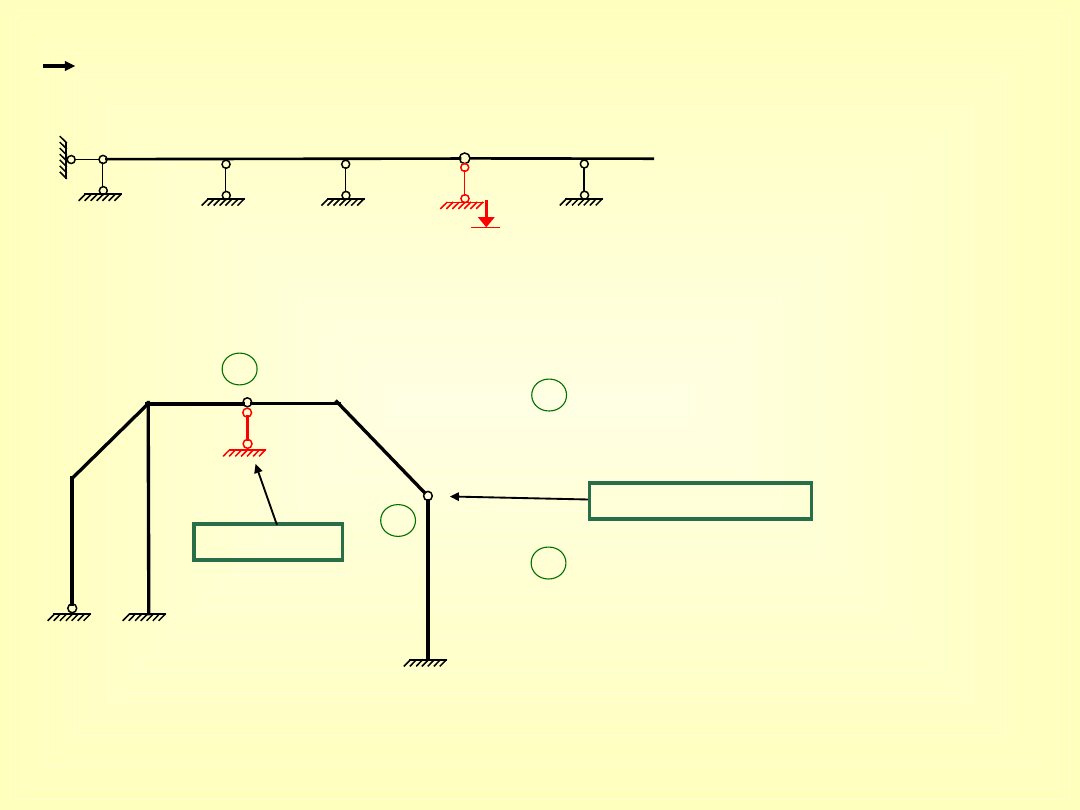
przeguby występujące w prętach prostych
„blokada” do pręta
(podpora liniowa) →
niewiadomy przesuw
A
B
A
przegub łączący pręty
leżące na jednej prostej
B
przegub łączący pręty ,
które nie leżą na jednej
prostej
niekoniecznie
zawsze
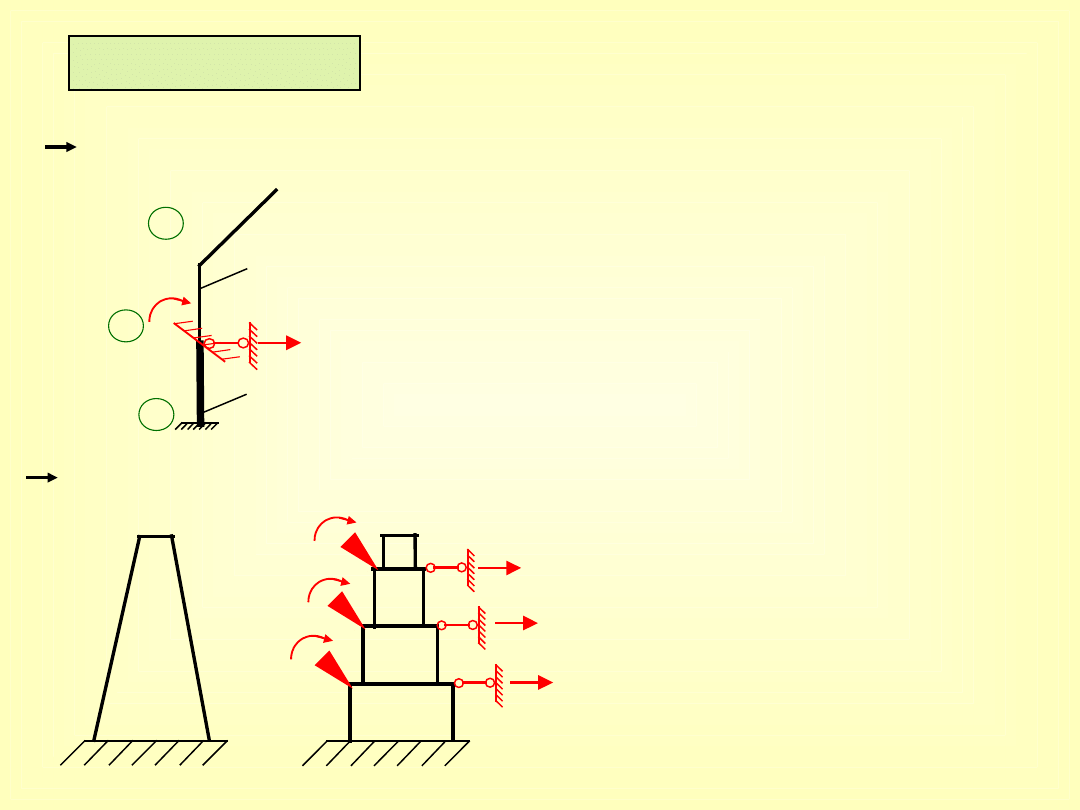
INNE PRZYPADKI
zmienna sztywność pręta na jego długości (skokowa)
1
J
2
J
1
2
C
- pręt dzielimy na 2 odcinki (1-C) i (C-2)
- C staje się dodatkowym węzłem
wewnętrznym
niewiado
ma
- (1-C) i (C-2) leżą na jednej
prostej ; C ma możliwość
przesuwu poziomego
dodatkowa niewiadoma
zmienna sztywność o charakterze ciągłym
1
2
1
3
3
2
model
dodatkowe
dzielimy na skończoną
liczbę odcinków (prętów) o
stałej sztywności (EJ)
niewiadom
e
i
i
oraz
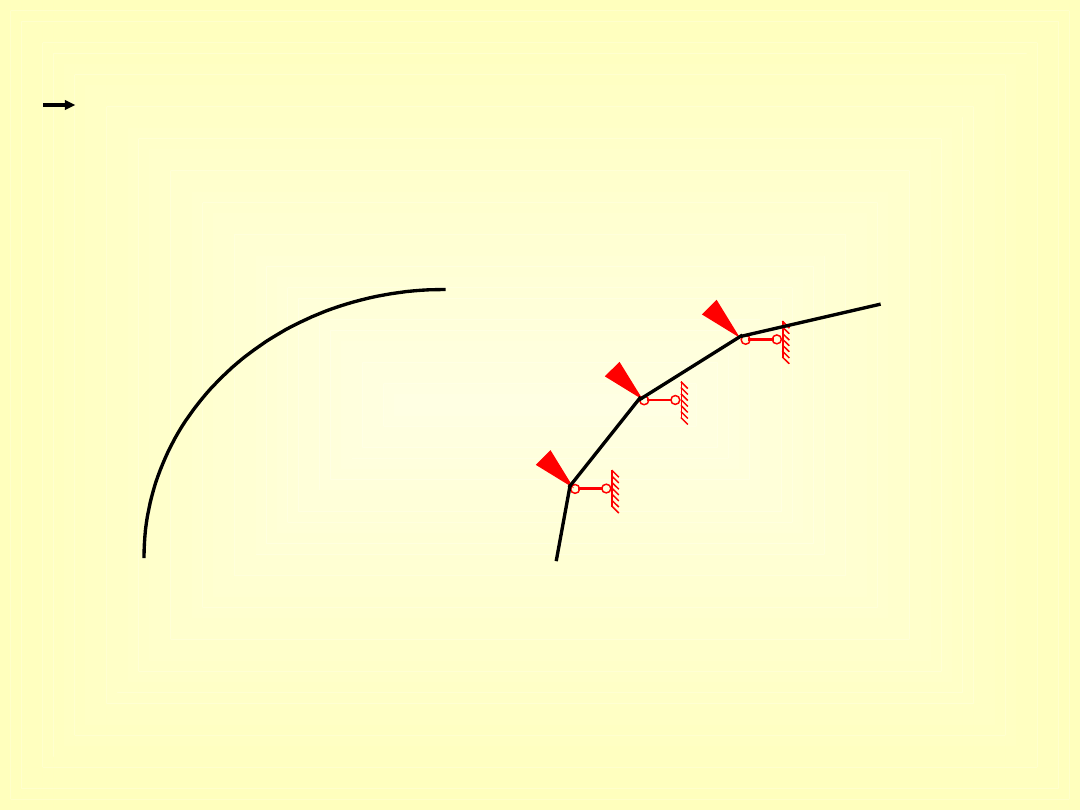
pręty zakrzywione aproksymuje się ciągiem prętów
prostych
kształt zmienia się w
sposób ciągły
rama; ciąg prętów
prostych krzywa
„łamana”
model
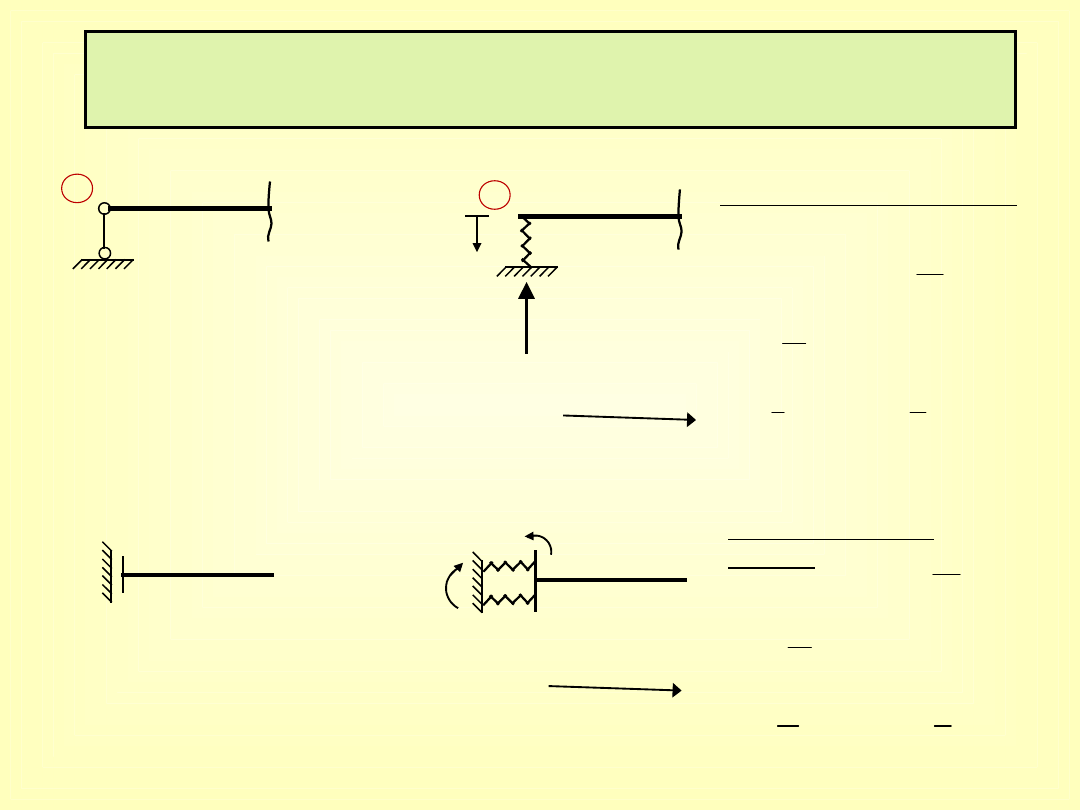
WZORY TRANSFORMACYJNE DLA PRĘTÓW PROSTYCH
O SPRĘŻYSTYCH PODPORACH
i
i
i
v
i
R
podatna podpora liniowa
k
1
f
;
f
1
k
k
v
R
;
f
v
R
k
R
v
;
f
R
v
i
i
i
i
i
i
i
i
liniowa:
f – podatność podpory
k – sztywność
podpory
i
i
M
podatna podpora
kątowa
1
f
;
f
1
M
;
f
M
M
;
f
M
i
i
i
i
i
i
i
i
kątowa:
– sztywność podpory
– podatność podpory
f
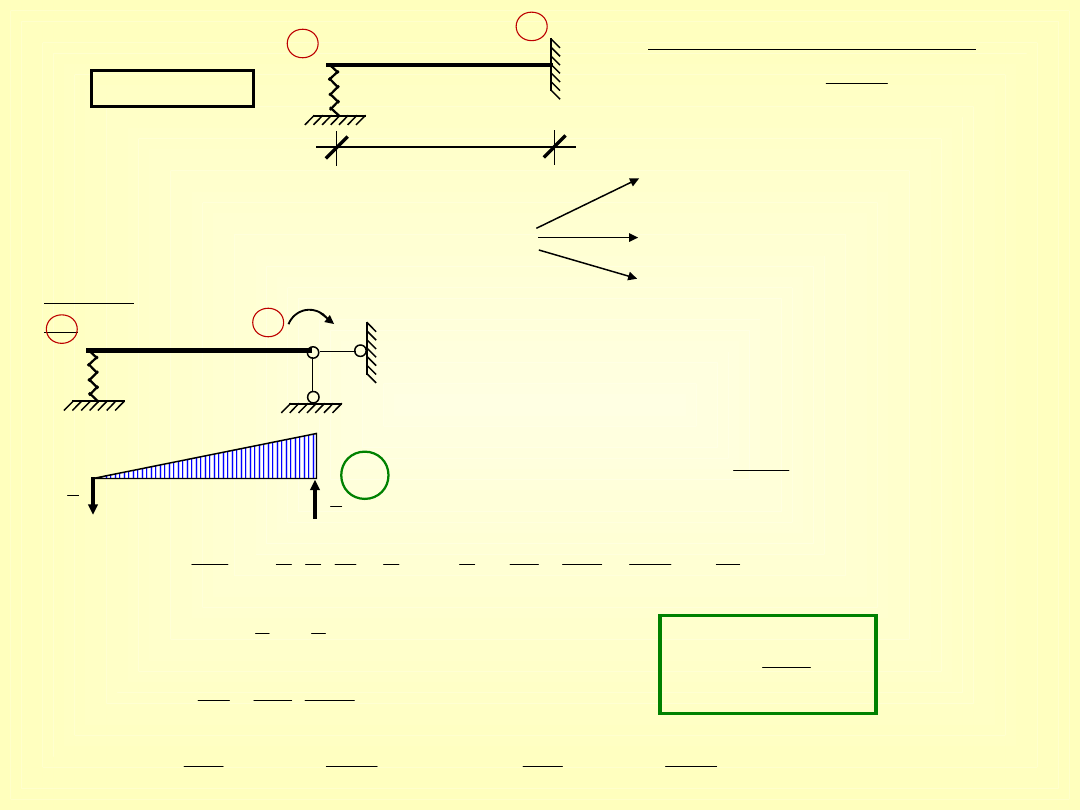
Zadania:
1)
liniowa
i
k
i
L
Wymuszenie kinematyczne
ik
i
k
k
i
k
L
v
v
v
i
v
oraz
rozwiązanie:
równanie różniczkowe
osi odkształconej
metoda sił
na podstawie wzorów
dla prętów o
niepodatnych
podporach
Metoda
sił:
i
k
1
X
ki
1
M
X
Dane:
-obrót
podpory
-obrót pręta
k
ik
L
v
v
i
k
ik
L
1
L
1
1
M
1
X
1
1
i
i
2
i
L
0
2
1
11
K
3
1
EJ
3
L
L
1
EJ
1
1
3
2
L
1
2
1
1
L
1
L
1
dx
EJ
M
EJ
L
K
3
i
i
ik
k
k
i
k
p
1
v
L
1
v
L
1
ik
k
11
p
1
1
3
K
K
L
EJ
3
X
3
K
K
L
EJ
3
T
T
;
3
K
K
L
EJ
3
M
ik
k
2
ki
ik
ik
k
ki

- brak
podpory
i
0
K
,
0
i
0
M
,
0
3
K
K
lim
ki
0
K
K
,
i
1
K
3
1
1
lim
3
K
K
lim
K
K
1
L
EJ
3
M
k
k
ki
- podpora
niepodatna
i
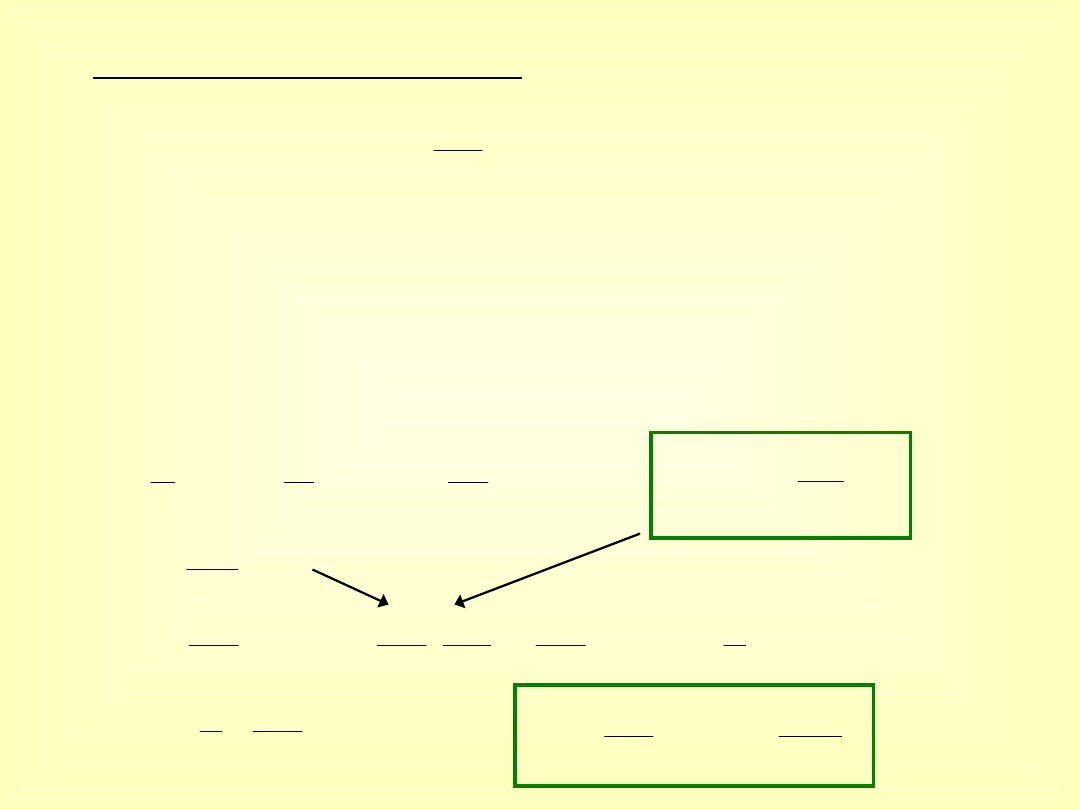
Wykorzystanie znanych wzorów
podpora niepodatna:
podpora podatna:
ik
i
o
ki
L
EJ
3
M
ki
M
ki
o
ki
ki
M
M
M
ki
M
- dodatkowy moment,
który powstanie przez
obrót pręta
wynikający z podatności
podpory
L
M
R
,
R
,
L
ki
i
i
i
i
i
i
2
ki
L
M
L
EJ
3
M
ki
ki
ik
k
i
2
ki
ik
k
ki
M
K
3
L
EJ
3
L
M
L
EJ
3
L
EJ
3
M
ik
k
ki
ki
L
EJ
3
K
3
M
M
K
3
K
L
EJ
3
M
ik
k
ki
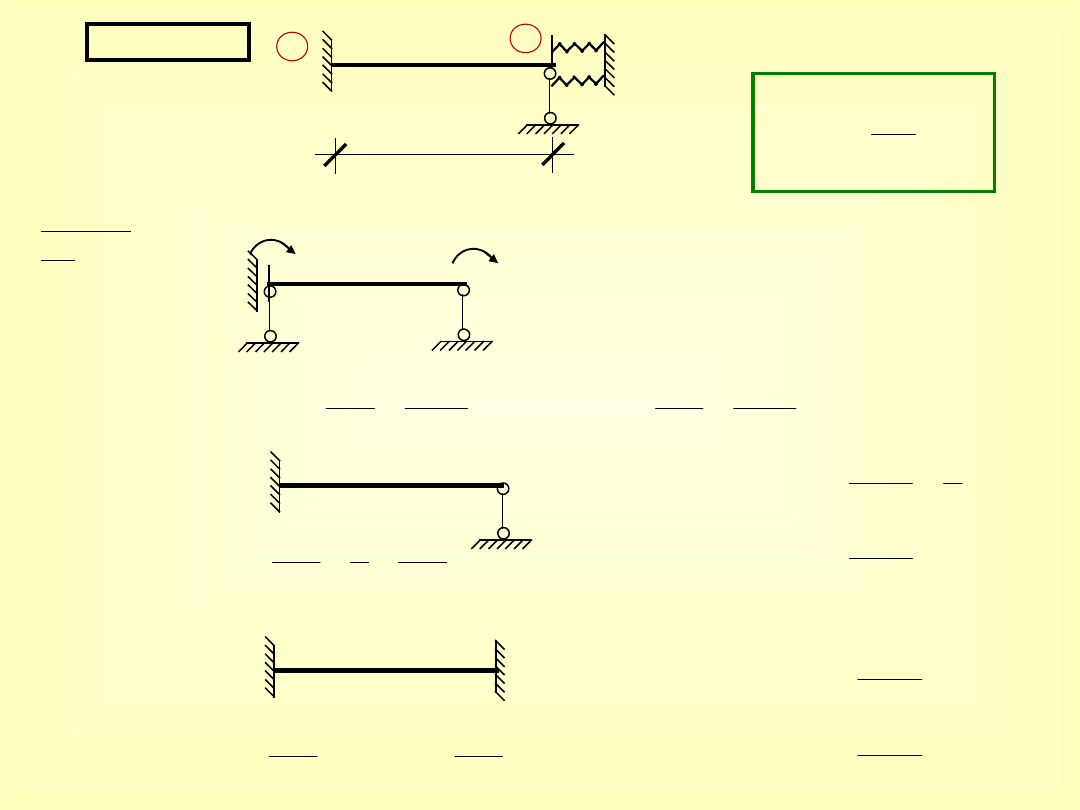
2)
kątowa
EJ
L
K
i
k
L
Metoda
sił:
1
X
2
X
wymuszeni
e:
i
4
K
K
L
EJ
2
M
X
;
4
K
3
K
L
EJ
4
M
X
i
ki
2
i
ik
1
przypadek
1)
0
K
,
0
0
4
K
K
lim
4
3
4
K
3
K
lim
0
K
0
K
0
M
L
3EJ
4
3
L
EJ
4
M
ki
i
i
ik
2)
K
,
1
4
K
K
lim
1
4
K
3
K
lim
K
K
i
ki
i
ik
L
EJ
2
M
,
L
EJ
4
M
Sztywność podpory k
EJ
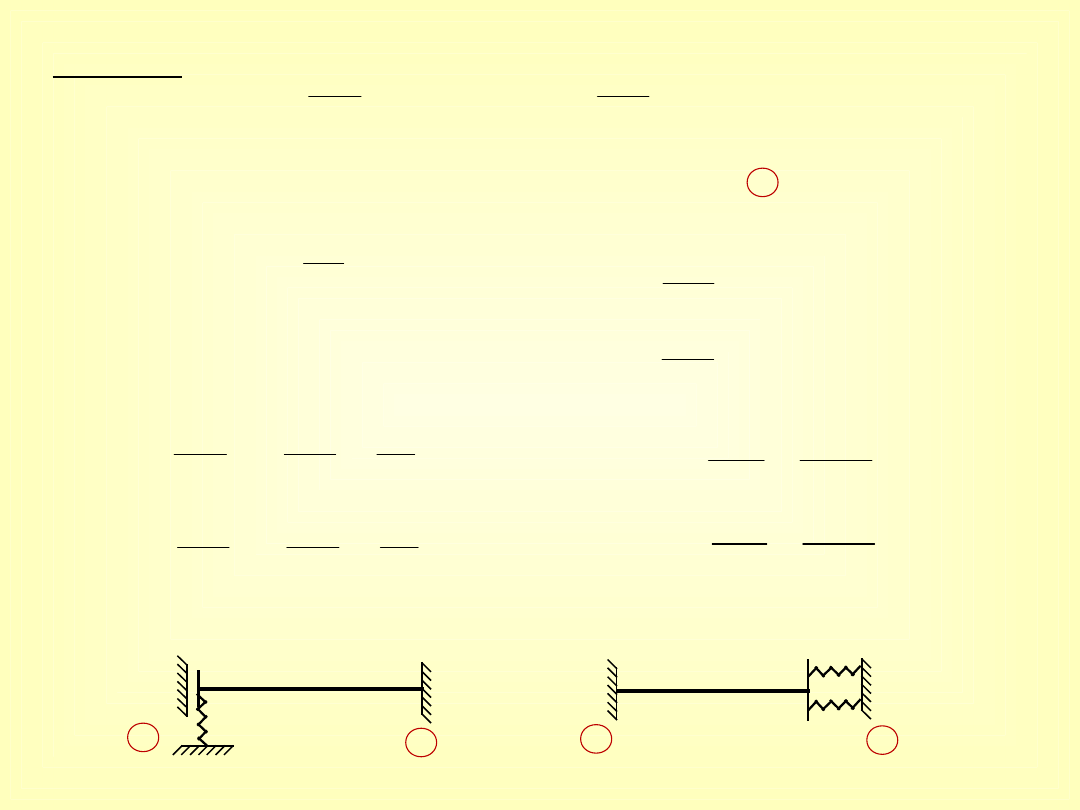
II sposób:
ki
i
ki
ik
i
ik
M
L
EJ
2
M
,
M
L
EJ
4
M
M
- momenty wywołane dodatkowym obrotem podpory
k
;
M
ki
k
L
4EJ
M
L
2EJ
M
k
ki
k
ik
2
ki
1
ik
X
M
;
X
M
2
i
2
2
i
1
X
L
EJ
4
L
EJ
2
X
X
L
EJ
2
L
EJ
4
X
4
K
K
L
EJ
2
X
4
K
3
K
L
EJ
4
X
i
2
i
1
inne przypadki:
i
k
i
i
k
i
k
itd….
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
Wyszukiwarka
Podobne podstrony:
Schemat oceniania do arkusza 1
LINUX, SZKOLNE PLIKI-mega zbiory (od podstawówki do magisterki), Systemy operacyjne
Schemat blokowy Do While 2
fe3c wykres1, Wykres fazowy Fe - Fe 3 C (żelazo węgiel) stanowi podstawę do dyskusji nad mikrostrukt
Brak podstaw do postawienia przed Trybunałem Ziobry i Kaczyńskiego
RODZAJE I FUNKCJE KANAŁÓW DYSTRYBUCYJNYCH, SZKOLNE PLIKI-mega zbiory (od podstawówki do magisterki),
schemat prostownika do ?owania akumulator w samochodowych
metodyka pracy opiekuńczo wychowawczej, Konspekt do zajęć wychowawczych - schemat, Konspekt do zajęć
PROGRAM PROFILAKTYCZNY DOTYCZĄCY ZWALCZANIA AGRESJI WŚRÓD UCZNIÓW SZKOŁY PODSTAWOWEJ ( do poprawek )
PROGRAM PROFILAKTYCZNY DOTYCZĄCY ZWALCZANIA AGRESJI WŚRÓD UCZNIÓW SZKOŁY PODSTAWOWEJ ( do poprawek )
język C dla mikrokontrolerów AVR od podstaw do zaawansowanych aplikacji
19 Konstrukcje powojenne podstawy do 7,62 mm ckm systemu Goriunowa wz 1943
Instrukcja obsługi Przenośna podstawka do ładowania bezprzewodowego Nokia DC 50
Jezyk C dla mikrokontrolerow AVR Od podstaw do zaawansowanych aplikacji jcmikr
JAK WYKOŻYSTAĆ EFEKTY PRZYNIESIONE PRZEZ TRANSFORMACJĘ GOSPODARCZĄ, SZKOLNE PLIKI-mega zbiory (od po
2003-2004 wojewódzki klucz, SCHEMAT ODPOWIEDZI DO ZADAŃ OTWARTYCH
w sprawie, stawki opłaty stanowiącej podstawę do obliczania kary wymierzonej w wyniku obowiązkowe
więcej podobnych podstron