Wybrane wiadomości z

teorii błędów

Spostrzeżeniami - nazywamy wyniki pomiarów
np. geodezyjnych. Każdy pomiar obarczony jest
różnego rodzaju błędami wynikającymi z
przyjętej metody pomiarów, zastosowanych
instrumentów pomiarowych oraz staranności w
wykonywaniu pomiarów.

Błędy spostrzeżeń i ich klasyfikacja

Błędy spostrzeżeń dzielimy na:

-grube (omyłki)
-systematyczne
-przypadkowe

Błąd gruby lub omyłka, różni się znacznie od

wyników innych pomiarów tej samej
wielkości.

O tym czy dany błąd zakwalifikujemy jako

omyłkę, decyduje jego wielkość.

Np. w ciągu wyników pomiaru długości

jednego boku: 150.10; 150.12; 170.12;
150.11 widać wyraźnie wartość obarczoną
błędem grubym.

Błędy systematyczne wynikają z oddziaływania
czynników związanych z warunkami pomiaru i zwykle
dają się wyrazić za pomocą formuły matematycznej.

Np. jeżeli pomiar długości wykonujemy taśmą która jest
krótsza od swej nominalnej wartości (np. ma 19.90 m
zamiast 20.00 m), możemy łatwo obliczyć poprawną
długość. Powiedzmy że mierząc długość przyłożyliśmy
taśmę 5 razy. Wtedy zmierzona długość nie wynosi
20.00 x 5 =100.00m, ale 100.00 - 5x 0.10 = 99.50 m.

W najgorszym przypadku możemy nie znać dokładnej
wartości błędu systematycznego, ale zwykle orientujemy
się co do znaku, z jakim wpływa na wyniki pomiarów.
Błędy systematyczne związane są zwykle z zastosowana
metodą pomiaru lub narzędziem pomiarowym.

Błędy przypadkowe - zmieniają się w czasie
wykonywania pomiaru zarówno co do znaku
jak i co do wielkości.

Przyczyny ich występowania na ogół nie są
znane.

A gdyby nawet były znane, to nie można
ustalić

ani

wielkości,

ani

znaku

powodowanego przez nie błędu.

Inny podział błędów, oparty na wzorach

matematycznych, dzieli błędy na prawdziwe i
pozorne.

Błąd prawdziwy jest różnicą między

wartością prawdziwą mierzonej wielkości -
X, a wynikiem jej pomiaru L:

= X - L

Bląd prawdziwy = wartość prawdziwa -

wartość zaobserwowana

W

większości

wypadków

nie

znamy

wartości prawdziwych i musimy poprzestać
na ich oszacowaniach zwanych wartościami
wyrównanymi x.





Błąd pozorny v jest różnicą między wartością wyrównaną
mierzonej wielkości - x, a wynikiem jej pomiaru L:

 
 

Poprawka spostrzeżenia v jest to wielkość, którą należy
dodać do wyniku pomiaru, aby otrzymać jego wartość
wyrównaną.

 

Błąd pozorny = wartość wyrównana - wartość zaobserwowana

L

x

v





x

v

L





Prawo błędów przypadkowych
Błędy przypadkowe, są trudne do uchwycenia.

Nie można przewidzieć ich wielkości, znaku
i przyczyny powstawania. Jednak na
podstawie

doświadczeń

ustalono

następujące własności prawdziwych błędów
przypadkowych:

1) błędy o tej samej wartości i różnych

znakach są jednakowo prawdopodobne;

2) błędy mniejsze są bardziej prawdopodobne

niż większe;

3)

bezwzględna

wartość

błędów

przypadkowych nie może przekraczać
pewnej określonej dla danych warunków
pomiarowych wartości a, czyli | \ <. a





Przytoczone własności błędów przypadkowych można
ująć w jedno równanie zwane prawem błędów
przypadkowych:

gdzie: 



- błąd przypadkowy (prawdziwy)

spostrzeżenia,

e - zasada logarytmów naturalnych,
h - parametr zależny od dokładności

pomiaru.

2

2

)

(





h

e

h

x

f

y









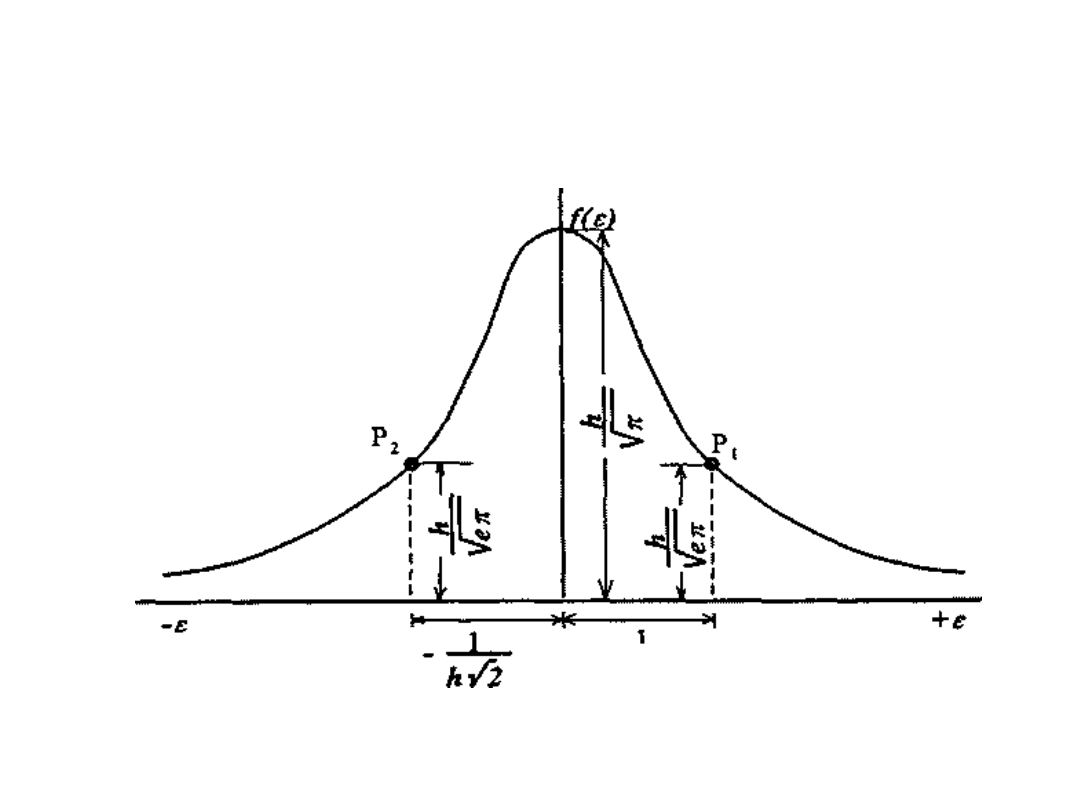
Wykres prawa błędów
przypadkowych

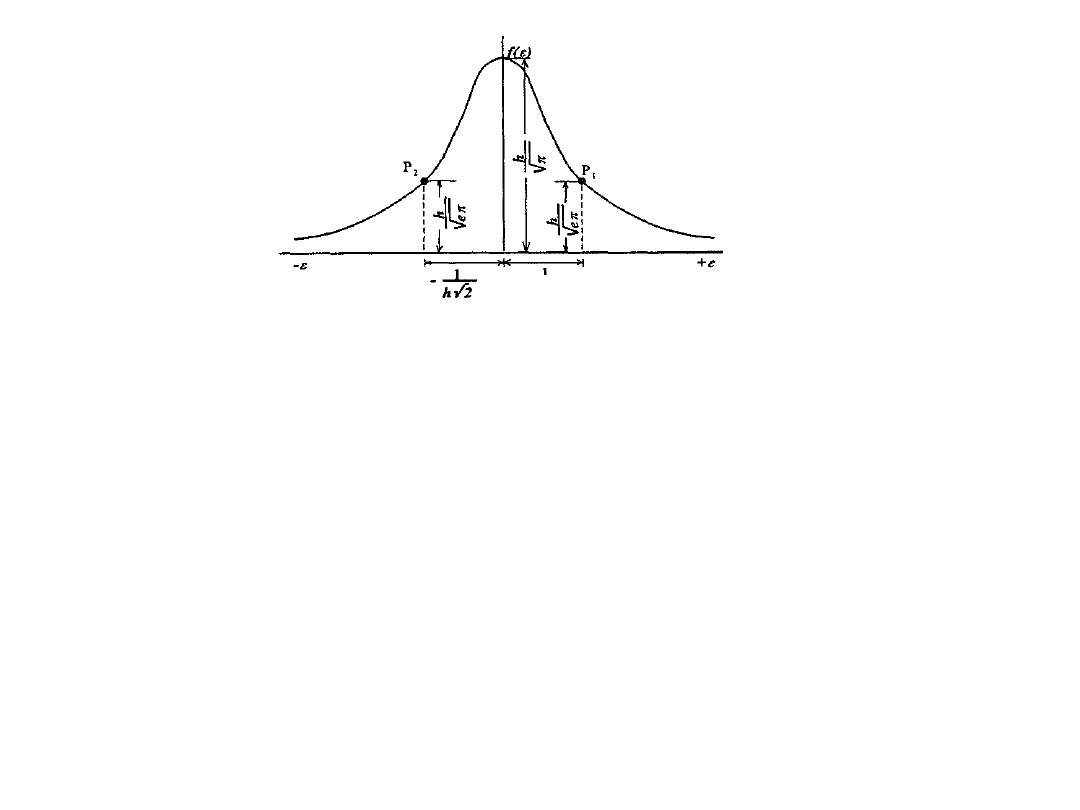
Krzywa jest symetryczna względem osi rzędnych.
Dla  = O osiąga f (e) maksymalną wartość — ,

natomiast dla  = - i  = + wartość zera.

Krzywą charakteryzują dwa punkty przegięcia: P

1

i P

2

położone symetrycznie względem osi rzędnych.

Prawdopodobieństwo pojawienia się błędu w przedziale

[= a,  = b ] przedstawia pole zawarte między krzywą

f(), osią odciętych a rzędnymi f(a) i f (b), co odpowiada

całce:







b

a

d

f





)

(