Metody analizy i

odkrywania wiedzy w

niekompletynych zbiorach

danych

Łukasz Ryniewicz 25.04.2007

Plan prezentacji

• Typy niekompletności informacji
• Metody uzupełniania danych

• Statystyczne
• k-najbliższych sąsiadów, drzewa

decyzyjne

• Metody analizy niekompletnych

danych

• Rozmyte reguły asocjacyjne
• Zbiory przybliżone i modyfikacje
• Modyfikacje algorytmów

Etapy eksploracji danych

Analiza problemu

dane

Selekcja i czyszczenie danych

dane wyselekcjonowane

Transformacja danych

•Wybór strategii co do
badania danych

•Konwersja

•Dyskretyzacja

•Zmiana reprezentacji z
relacyjnej na transakcyjną

dane przetworzone

Etapy eksploracji danych

Eksploracja danych

wzorce

Przygotowanie wyników do oceny

dane wygodne
do
analizowania

Analiza wyników

•Wybór
narzędzi

•Wybór
algorytmów

•Zastosowania
ich

Obróbka żeby było miłe dla oka

Zastosowanie uzyskanej wiedzy w praktyce

Typy niepełności danych

• Niepewność – gdy nie wiemy czy dane

są poprawne

• Niedokładność – np. gdy mamy dane

w postaci przedziałów: 100-200, dane
opisowe : dość ciepło

• Niekompletność – nie znamy wartości

atrybutu

• Niespójność – np. jednemu obiektowi

są przypisane różne wartości

• Ignorancja – gdy mamy brak wiedzy

Niekompletność

• Brakujące dane – są możliwe do

uzupełnienia

• chwilowa – nie jest dostępna dana w

momencie jej wstawiania

• niedokładność urządzeń, metod –

możliwe do oszacowania

• Niedostępne dane

• nie są możliwe do uzupełnienia,
• gdy są instancje do których nie mają

zastosowania wartości atrybutów (np.
baza z polami: bramki, strzelcy w
przypadku meczu bezbramkowego)

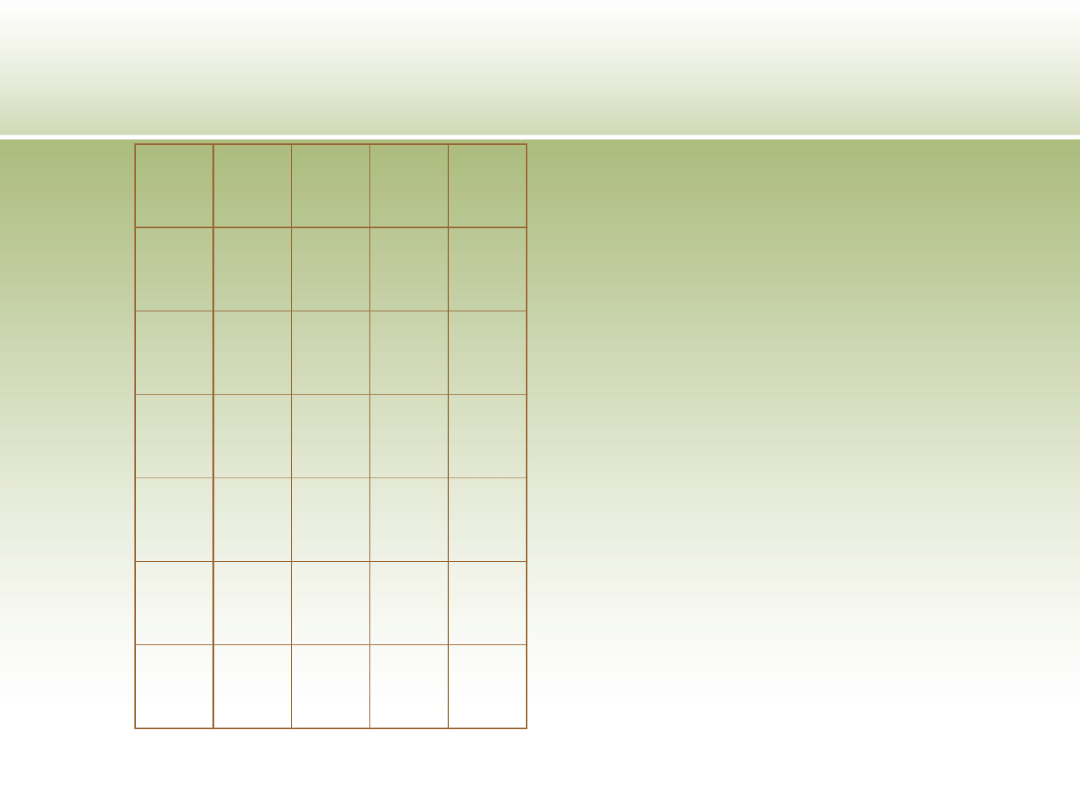
Model transakcyjny danych

A

B

C

d

1

0

1

1

1

2

*

0

*

1

3

1

*

2

1

4

0

1

2

1

5

1

*

1

0

6

0

1

*

0

A

a



A

a

a

V

V





U – zbiór obiektów

A – zbiór atrybutów

d - atrybut decyzyjny

dziedzina

})

{

,

(

d

A

U

DT







a

V

a

V

a

x

f

a

x

V

A

U

f







)

,

(

)

,

(

:

:



}

,...

2

,

1

:

{

n

j

K

K

j





- zbiór klas decyzyjnych

Metody stosowane podczas
transformacji danych

•

Usuwanie niekompletności danych

• Pomijanie obiektów zawierających braki

danych

• W bazach traznsakcyjnych pomijanie

brakującego atrybutu

• Zastępowanie brakujących wartości

• Użycie stałej – np. nowej nie występującej w

zbiorze wartości danego atrybutu

• Użycie mody, mediany, wartości średniej dla

wartości danego atrybutu

• Użycie metod data mining – np. k-najbliższych

sąsiadów gdzie porównujemy obiekt z
brakującą wartością z obiektami sąsiednimi i na
ich podstawie odtwarzamy brakujący atrybut

Metody statystyczne

• Procedury oparte na kompletnych rekordach – gdy

mało braków

• Procedury ważące – ustawiane są wagi rekordów by

zminimalizować odchylenia związane z brakami

• Procedury oparte o uzupełnianie danych

• Jawne w postaci formalnego modelu

(średnia, mediana, regresja, badanie

korelacji)

• Niejawne ukierunkowane na algorytmy

implikujące modele (uzupełnianie na

podstawie podobieństw, zastępowanie

innymi rekordami, zastępowanie stałymi)

• Procedury oparte o modele – definiuje się model

kompletnych danych i zależności są wyliczane na

podstawie rozkładu prawdopodobieństw

Metody statystyczne -
przykład

1. Podziel zbiór U na klasy decyzyjne

2. Dla każdej klasy wyznacz za

pomocą statystyki S

3. Dla każdego braku uzupełnij według

przynależności do odpowiedniej klasy
decyzyjnej

}

)

(

:

{

di

x

d

U

x

U

di







a

di

V

s 

*})

)

,

(

:

({











a

di

a

di

v

x

a

f

U

x

v

S

s

k-najbliższych sąsiadów

1. Bazę – U dzielimy na 2 podzbiory

• - przynajmniej 1 wartość

atrybutu nie jest znana

• - pozostałe

2. Dla każdego rekordu r należącego do

znajdujemy k najbliższych sąsiadów z
Odległość liczona tylko przy
wykorzystaniu znanych w r atrybutów.
Uzupełnienie braku (np. poprzez
wyznaczenie mody z wartości
atrybutów k sąsiadów i wstawienie jej
do r)

N

DR

N

DR

Z

DR

Z

DR

Drzewa decyzyjne

1. Bazę – U dzielimy na 2 podzbiory

• - przynajmniej 1 wartość atrybutu nie

jest znana

• - pozostałe

2. Wyznaczamy zbiór atrybutów gdzie pojawiła sie wartość

nieznana –

3. Dla każdego atrybutu a należącego do tworzymy

drzewo decyzyjne na podstawie gdzie każda

wartość a tworzy klasę decyzyjną

4. Klasyfikujemy rekord r z z brakującym atrybutem a

do odpowiedniej klasy

5. W przypadku gdy rekord r ma więcej niż jeden brak to:

1. Dla braku a klasyfikacja
2. W r uzupełnienie braku tylko wtedy gdy

osiągnięto liść

3. Powrót do 5.1
4. Gdy nie osiągamy już liści klasyfikujemy na

podstawie najbardziej licznego zbioru

N

DR

Z

DR

N

A

N

A

a

DT

Z

DR

N

DR

Metody stosowane na etapie
odkrywania wiedzy

• Użycie standardowych metod gdy

przeprowadziliśmy już proces
uzupełniania danych

• Użycie zmodyfikowanych metod analizy

pod kątem braków danych

• Użycie metod używających podejście

do danych i klasyfikacji zbiorów
rozmytych i przybliżonych

• Podejście probabilistycznie

•Dla każdego atrybutu jest definiowany zbiór
lingwistycznych termów które określają jakieś
pojęcie z dziedziny, np wysoki

• jest reprezentowany przez zbiór rozmyty na
dziedzinie A, ozn: d(A), o funkcji przynależności

Reguły asocjacyjne oparte na
zbiorach rozmytych

i

tA

L

]

1

,

0

[

)

(

:



A

d

i

tA

L



i

tA

L

•Stopień w jakim term charakteryzuje pewien
rekord r to wartość funkcji przynależności:

•Stopień w jakim zbiór termów
charakteryzuje rekord r to:

•Reprezentacja termów za pomocą zbiorów
rozmytych pozwala obliczyć stopień gdy
potrzebna wartość nie jest znana. Wtedy funkcja
zwraca wartość ½

Reguły asocjacyjne oparte na
zbiorach rozmytych

i

tA

L

)

.

(

)

,

(

i

L

tA

A

r

r

L

St

i

tA

i





m

t

tA

tA

tA

L

L

L

L

Z

,...,

,

:

2

1

)}

.

(

),...,

.

(

),

.

(

min{

)

,

(

2

1

2

1

m

L

L

L

L

A

r

A

r

A

r

r

Z

St

m

tA

tA

tA

t









)

,

(

r

L

St

i

tA

)

.

(

i

L

A

r

i

tA



•Generacja reguł dla różnych atrybutów
i w postaci:

Zamiast wsparcia jest liczona różnica
między prawdopodobieństwami:

Reguły asocjacyjne oparte na
zbiorach rozmytych











U

r

tA

U

r

tA

tA

tA

tA

r

L

St

r

L

L

St

L

L

ki

mj

ki

ki

mj

)

,

(

)

},

,

({

)

,

Pr(

mj

ki

tA

tA

L

L

R



:

k

A

m

A















U

r

tA

tA

Am

s

Ak

p

U

r

tA

tA

r

L

L

St

r

L

St

L

ms

kp

mj

mj

)

},

,

({

)

,

(

)

Pr(

Ai

-liczba termów zdefiniowana dla atrybutów Ai

•Jeżeli różnica ta jest statystycznie istotna,
wtedy jest akceptowana taka reguła i jest
obliczane zaufanie reguły

Reguły asocjacyjne oparte na
zbiorach rozmytych

)

|

Pr(

)

|

Pr(

log

)

,

(



j

p

tA

tA

tA

tA

tA

tA

o

mj

ki

mj

ki

mj

ki

L

L

L

L

L

L

W





•Dane wykluczone Dis(X)
•Obowiązująca baza vdb(X)

Rekord r jest wykluczony dla danego
zbioru X jeśli zawiera przynajmniej jedną
wartość nieznaną dla jednego atrybutu
który znajduje się w zbiorze X. Zbiór tych
rekordów – Dis(X), vdb(X) = U\Dis(X)

Definicje reguł asocjacyjnych
uwzględniające braki danych

)

(

)

(

X

vdb

U

X

wsparcie

X



X

X

XY

U

Y

Dis

U

U

Y

X

zaufanie









)

(

)

(

•Nieznane wartości atrybutu są zastępowane
przez wszystkie znane wartości. Każda wartość
w zastępuje nieznaną daną dla której
prawdopodobieństwo prob(w,a) jest równe
względnej częstości jej występowaniu w
wektorach dla których jest określona wartość
tego atrybutu.

•Wsparcie elementu elem(w,a) o wartości w z
dziedziny atrybutu a dla pojedynczego rekordu
r:

•Wsparcie zbioru
dla pojedynczego rekordu r:

Podejście probabilistyczne I



))

,

(

(

w

a

elem

probWsp

r







k

i

i

i

r

r

a

w

elem

probWsp

X

probWsp

1

))

,

(

(

)

(

{

1 gdy r.a = w

prob(w,a) gdy r.a = ?

0 w p. p.

)}

,

(

),...,

,

(

),

,

(

{

2

2

1

1

k

k

a

w

elem

a

w

elem

a

w

elem

X 

•Normalnie transakcja t wspiera zbiór X
albo nie

•Każdy element występujący w transakcji t
wspieranej przez k-elementowy zbiór Zk
wnosi 1/k do wartości całkowitego
wsparcia zbioru Zk

•Całkowita wartość wsparcia Zk jest sumą
wsparć wnoszone przez poszczególne
elementy

•Znalezienie rozkładu
prawdopodobieństwa na brakującym
atrybucie, i wtedy przemnażamy wartość
wnoszoną przez to prawdopodobieństwo

•Zk={a,b,c} t={a,b,*} p(c)=3/5
=> wsp(Zk)=1/3+1/3+(1/3)*(3/5)

Podejście probabilistyczne
II

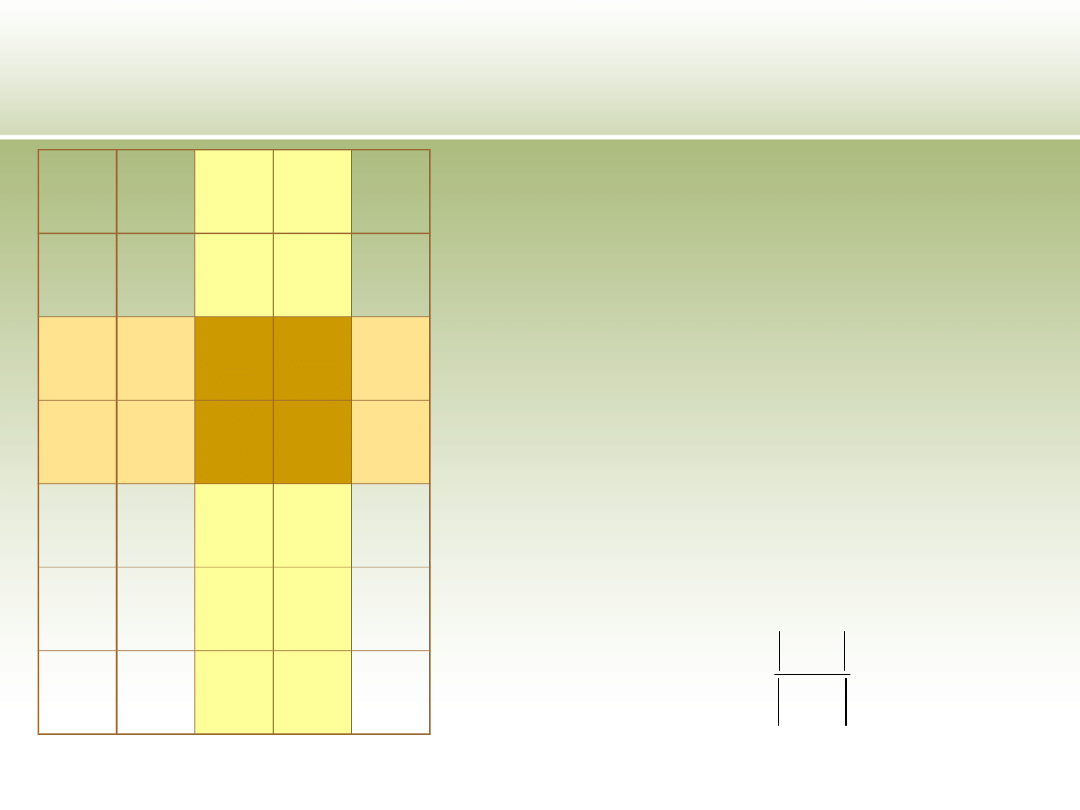
Podejścia wykorzystujące
zbiory przybliżone – relacja
nierozróżnialności

A

B

)}

(

)

,

(

:

{

)

(

B

IND

x

y

U

y

x

I

B







)}

,

(

)

,

(

:

)

,

{(

)

(

a

y

f

a

x

f

U

U

y

x

B

IND

B

a













A

B

C

d

1

0

1

1

1

2

1

0

1

1

3

1

1

2

1

4

0

1

2

1

5

1

1

1

0

6

0

1

0

0

}

)

(

:

{

X

x

I

U

x

X

B

B









}

)

(

:

{













X

x

I

U

x

X

B

B

U

X 

X

B

X

B

X

B







)

(



Używana w algorytmach generacji reguł indukcyjnych

Współczynnik aproksymacji:

Przybliżenia zbiorów klas decyzyjnych
służy do utworzenia zbioru reguł
decyzyjnych w postaci:

Gdzie

Relacja nierozróżnialności może być
stosowana jedynie w kompletnych
zbiorach, dlatego istnieją jej modyfikacje

Podejścia wykorzystujące
zbiory przybliżone – relacja
nierozróżnialności

)

)

,

(

(

d

v

x

d

f

P





)

,

:

)

,

(

(

ai

ai

i

ai

i

V

v

A

a

v

x

a

f

P









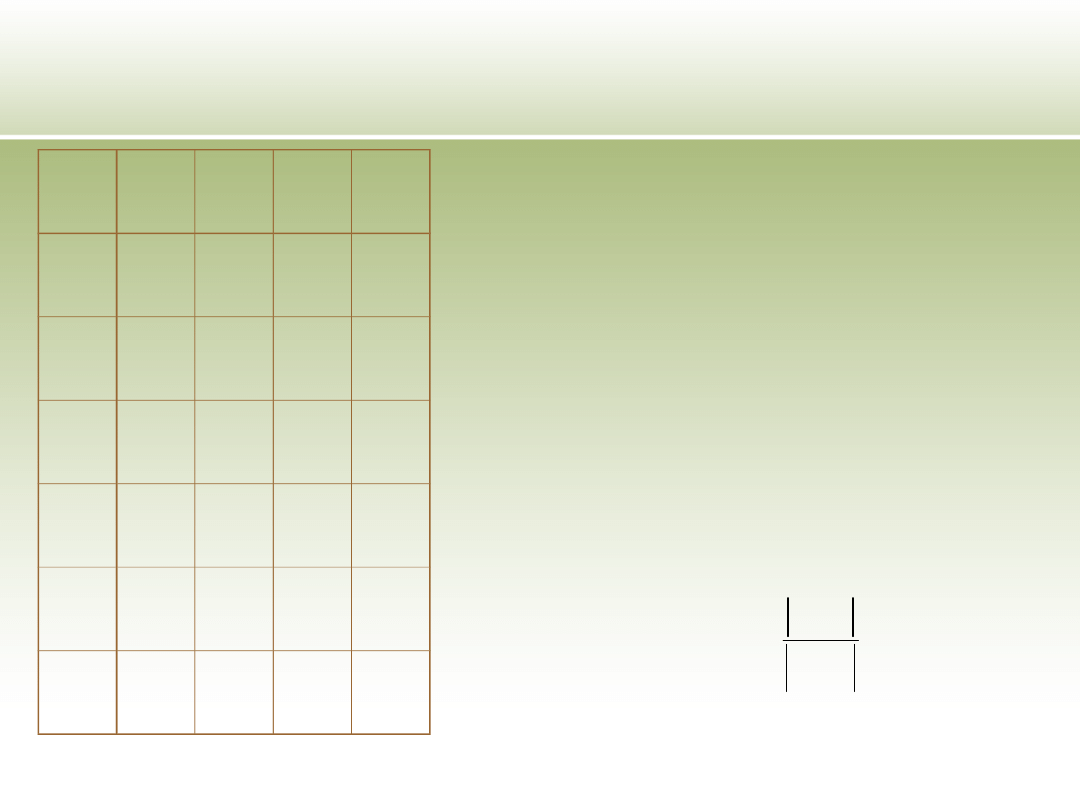
Podejścia wykorzystujące
zbiory przybliżone - relacja
tolerancji

A

B

*}

)

,

(

*

)

,

(







a

y

f

a

x

f















)

,

(

)

,

(

:

)

,

{(

)

(

a

y

f

a

x

f

U

U

y

x

B

T

B

a

A

B

C

d

1

0

1

1

1

2

1

*

1

1

3

1

1

*

1

4

0

1

2

1

5

*

*

1

0

6

0

1

0

0

}

)

(

:

{

X

x

T

U

x

X

B

B









}

)

(

:

{













X

x

T

U

x

X

B

B

U

X 

X

B

X

B

X

B







)

(



Używana w algorytmach generacji reguł indukcyjnych

Używana przy uzupełnianiu braków

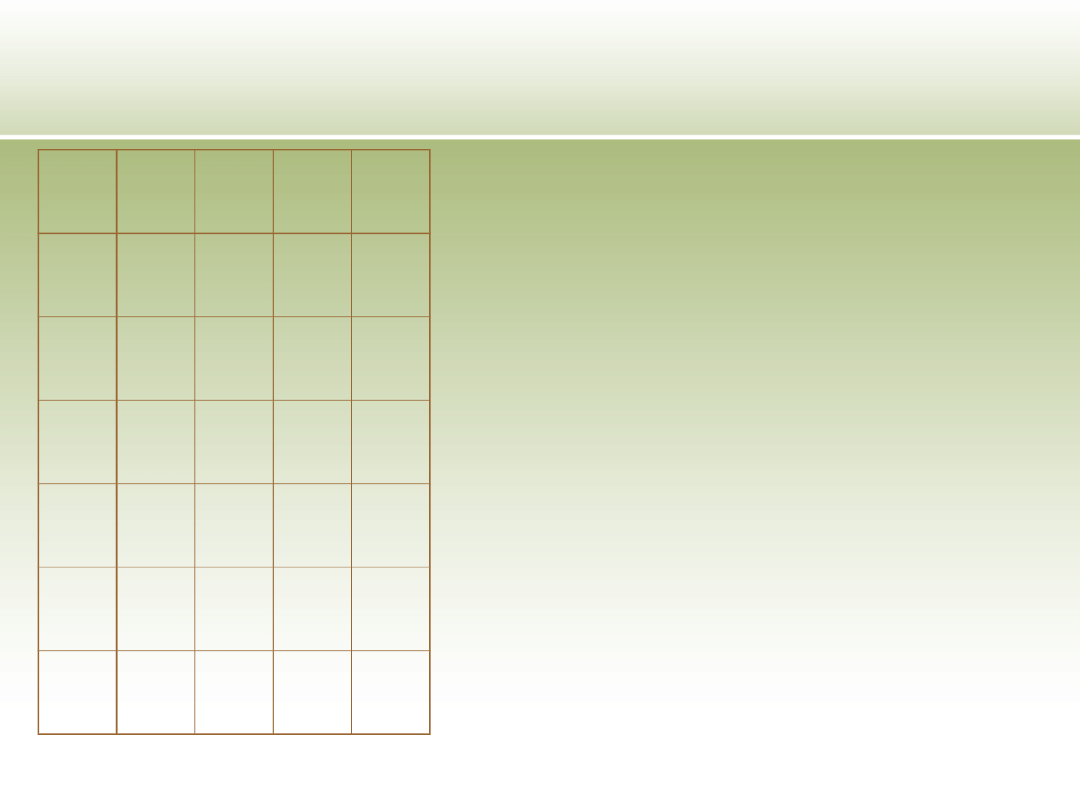
•Elementów podobnych do x

•Elementów do których x jest podobny

Podejścia wykorzystujące
zbiory przybliżone - relacja
podobieństwa

A

B

)

,

(

)

,

(

*

)

,

(

:

y

a

f

x

a

f

y

a

f

x

yS

B

a

B













A

B

C

d

1

0

1

1

1

2

1

*

1

1

3

1

1

*

1

4

0

1

2

1

5

*

*

1

0

6

0

1

0

0

}

:

{

)

(

x

yS

U

y

x

S

B

B





}

)

(

:

{

)

(

1

X

x

S

U

x

X

B

B











Używana w algorytmach generacji reguł indukcyjnych

y podobny do x

Dla każdego x są definiowane 2 klasy:

}

:

{

)

(

1

y

xS

U

y

x

S

B

B









}

:

)

(

{

)

(

X

x

x

S

X

B

B







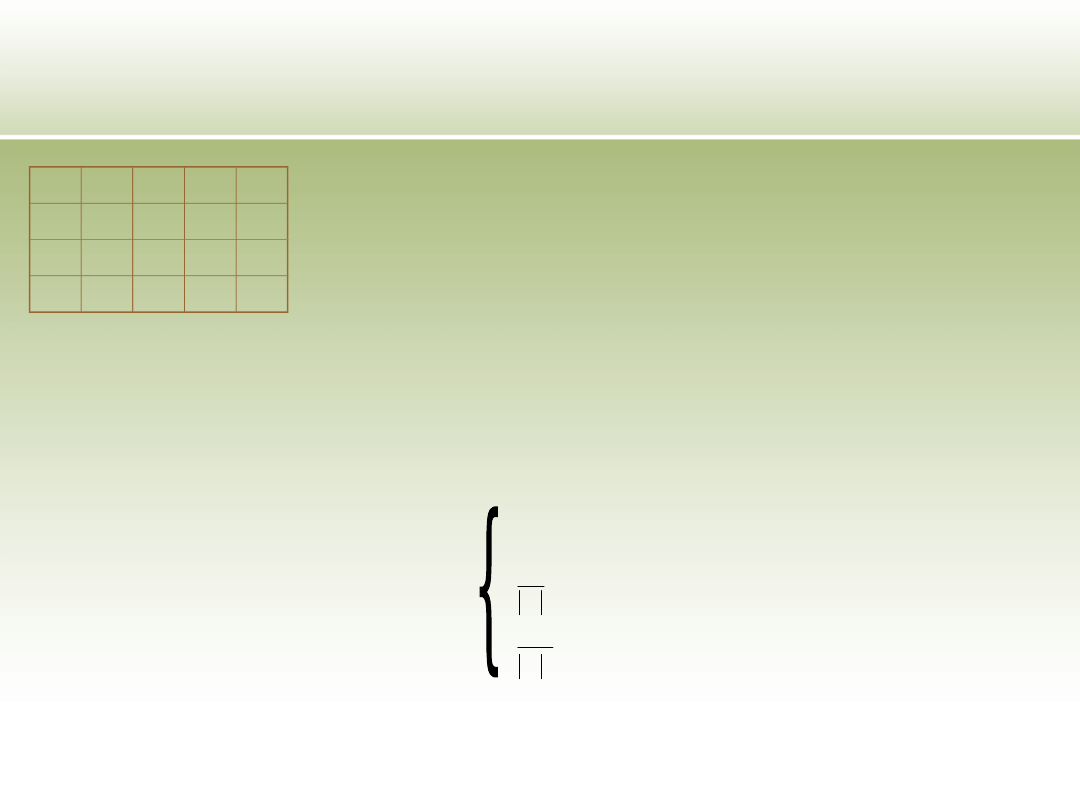
Podejścia wykorzystujące zbiory
przybliżone – rozmyta relacja
podobieństwa



)

,

( y

x

R

a

a

b

c

D

X1

1

2

3

1

X2

*

2

3

1

X3

*

*

3

2

•Intuicja- x2 jest bardziej podobny do
x1 niż x3 do x1

•Zwykła relacja tolerancji nie
rozróżnia

•Zakładamy że pod brakującymi
wartościami dla ustalonego atrybutu
może występować znana wartość z
jednakowym prawdopodobieństwem

•Podobieństwo obiektów x,y
względem a można zapisać:

*

)

,

(

*

)

,

(

1

*)

)

,

(

*

)

,

(

(

*)

)

,

(

*

)

,

(

(

1

*

)

,

(

*

)

,

(

)

,

(

)

,

(

0

*

)

,

(

)

,

(

1

2



































y

a

f

x

a

f

V

y

a

f

x

a

f

y

a

f

x

a

f

V

y

a

f

x

a

f

y

a

f

x

a

f

y

a

f

x

a

f

a

a







B

a

a

A

y

x

R

y

x

B

R

)

,

(

)

,

)(

(

I możemy zapisać
rozmytą relacje
podobieństwa:

•Metoda polega na klasyfikacji n>2 klas decyzyjnych
•Tworzone są klasyfikatory niezależne Cij których
celem jest stwierdzenie czy nowy obiekt należy do
klasy i-tej czy j-tej (odpowiednio Cij = 1, Cij = 0)

•Do budowy klasyfikatorów są wykorzystywane
powyższe relacje które pozwalają stwierdzić do
której klasy bardziej obiekt klasyfikowany należy

•Do każdego klasyfikatora określa sie współczynnik
wiarygodności w fazie uczenia

•Decyzja klasyfikacyjna:

Metoda kwadratowa

i

ij

i

ij

ncor

nerror

ncor

P













i

j

ij

ij

i

i

x

C

P

S

i

x

d

)}

(

{

max

)

(

Oczekiwana ilość informacji potrzebna do
klasyfikacji:

Maksymalizujemy przyrost informacji
G(U,T) w wyniku podziału testem T:

Żeby uniknąć zbyt wielkiej ilości podziałów
wprowadzamy współczynnik:

Gdzie P(U,T) – wartość informacyjna testu:

Drzewa decyzyjne – C4.5

U

Ki

U

K

U

I

n

i

i

log

)

(

1









)

(

)

(

)

,

(

1

i

k

i

i

U

I

U

U

U

I

T

U

G









)

,

(

)

,

(

)

,

(

T

U

P

T

U

G

T

U

WI



U

U

U

U

T

U

P

i

k

i

i

log

)

,

(

1









Uo – zbiór tych obiektów w których
występuje brak na atrybucie potrzebnym do
testu T
Przyrost informacji

Wartość informacyjna testu

Drzewa decyzyjne – C4.5
modyfikacja

)

,

(

)

,

(

'

0

0

T

U

U

G

U

U

U

T

U

G







U

U

U

U

U

U

U

U

T

U

P

i

k

i

i

o

log

log

)

,

(

1

0











Drzewa decyzyjne – podejście
probabilistyczne

T

L

I 

)

)

(

,...,

)

(

|

)

(

(

...

)

)

(

|

)

(

(

)

)

(

(

)

|

(

1

1

1

1

1

1

2

2

1

1

























m

m

m

m

r

x

t

r

x

t

r

x

t

P

r

x

t

r

x

t

P

r

x

t

P

x

I

P

t1

t2

t3

tm

I

n1

n2

n3

nm

T:

r1

r2

rm

m

n

n ,...,

1

m

t

t ,...,

1

m

m

R

r

R

r



 ,...,

1

1

-liść

-węzły

-testy

-wyniki testów

Dla przykładu x (bez braków
danych) prawdopodobieństwo
osiągnięcia liścia I wynosi:

Gdy wyniki testów są znane (x nie zawiera braków
potrzebnych przy testach) to prawdopodobieństwo
osiągnięcia liścia wynosi 0 lub 1

Drzewa decyzyjne – podejście
probabilistyczne

Jeżeli test tk w węźle nk nie może być ustalony
dokładnie (występuje brak danych) to możemy
przyjąć prawdopodobieństwo z rozkładu Ω
określone następująco:

]

[

,

]

[

,

,

1

1

1

1

)

)

(

,...,

)

(

|

)

(

(

k

k

k

k

k

k

t

n

T

t

r

t

n

T

k

k

k

k

x

U

U

r

x

t

r

x

t

r

x

t

P

















Gdzie podzbiór przykładów dla których wartość testu jest znana

]

[t

U

Metoda podziału

Polega na podzieleniu danych na
mniejsze porcje tak by nie zawierały one
braków i niosły maksymalną ilość
informacji o klasyfikacji. Następnie dla
każdej porcji jest stosowany odrębny
model klasyfikacji, i następuje synteza
wyników

a

b

c

d

1

0

*

1

0

1

*

1

0

1

1

0

1

1

0

1

*

0

1

0

*

1

0

0

a

b

d

1

0

1

0

1

1

0

1

0

1

1

1

b c

d

1 1

0

1 0

1

0 1

0

1 0

0

a

b

c

d

0

1

1

0

1

1

0

1

M1

M2

M3

d

1

1

0

1

0

0

a

b

d

1

0

1

0

1

1

0

1

0

1

1

1

b c

d

1 1

0

1 0

1

0 1

0

1 0

0

a

b

c

d

0

1

1

0

1

1

0

1

Literatura

•Imieliński T., Lipiński W., Incomplete Information in Relational
Databases, Journal of the AEM, tom 31, 1984

•Chan K. C. C., Wai-Ho A., Mining Fuzzy Association Rules,
Proceedings of the Sixth International Conference on Information and
Knowledge Managment, Las Vegas, 1997

•Regel A., Cremilleux B., Treatment of Missing Values for Association
Rules, Proceedings of Research and Development in Knowledge
Discovery and Data Mining, Second Pacific-Asia Conference, PAKDD-
98, Melbourne, 1998

•Protaziuk G., Odkrywanie wiedzy w niekopletnych zbiorach danych,
rozprawa doktorska, Warszawa 2005

•Kryszewicz M., Rybiński H., Incomplete database issues for
representative association rules, Proceedings of Foundations of
Inteligent Systems, 11th International Symposium, Warszawa 1999

•Nayak J. R., Cook D. J., Approximate Association Rule Mining,
Proceedings of the Fourteenth International Articital Inteligence
Research Society Conference, Key West, Floryda, 2001

•Feelders A., Handling missing data in trees: surrogate splits of
statistical ipmutation?, Proceedings of Principles of Data Mining and
Knowledge Discovery Third European Confereance, PKDD ’99, Praga,
1999

Dziękuję za
uwagę