PN-EN 1999-1-4

PROJEKTOWANIE KONSTRUKCJI  

ALUMINIOWYCH. K0NSTRUKCJE 

PROFILOWANE NA ZIMNO

Wykład 6

 

 

 

 

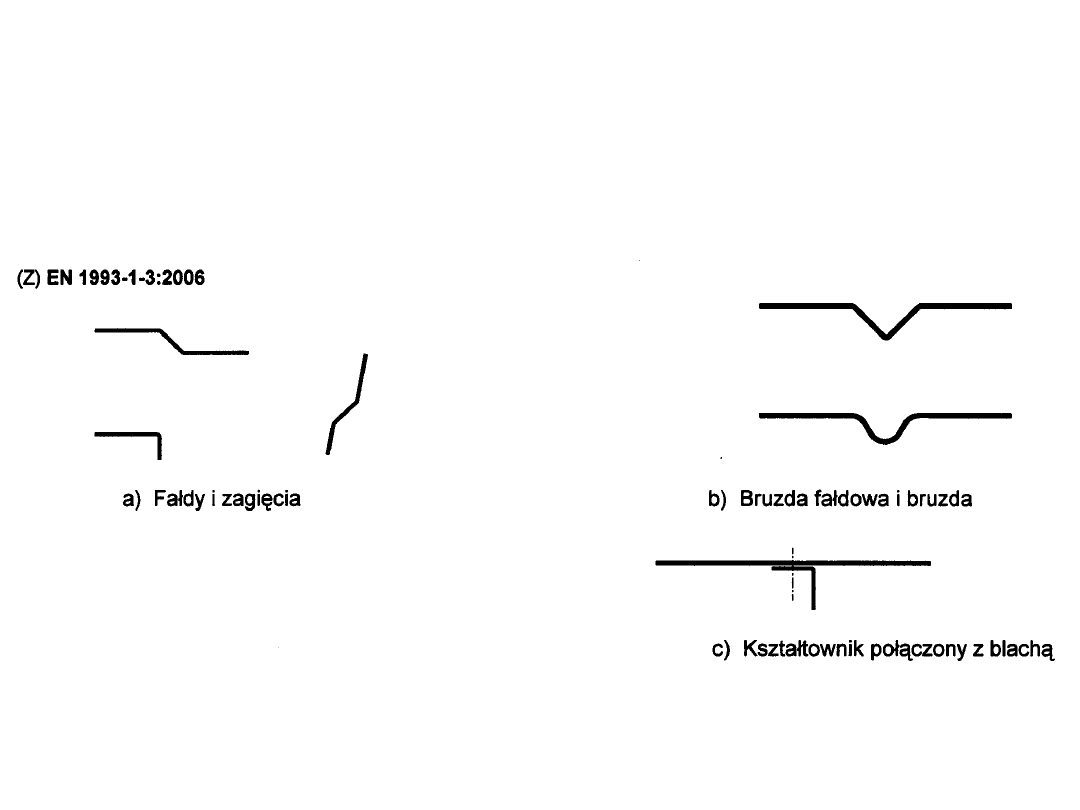
Formy usztywnień kształtowników i 

blach

 

 

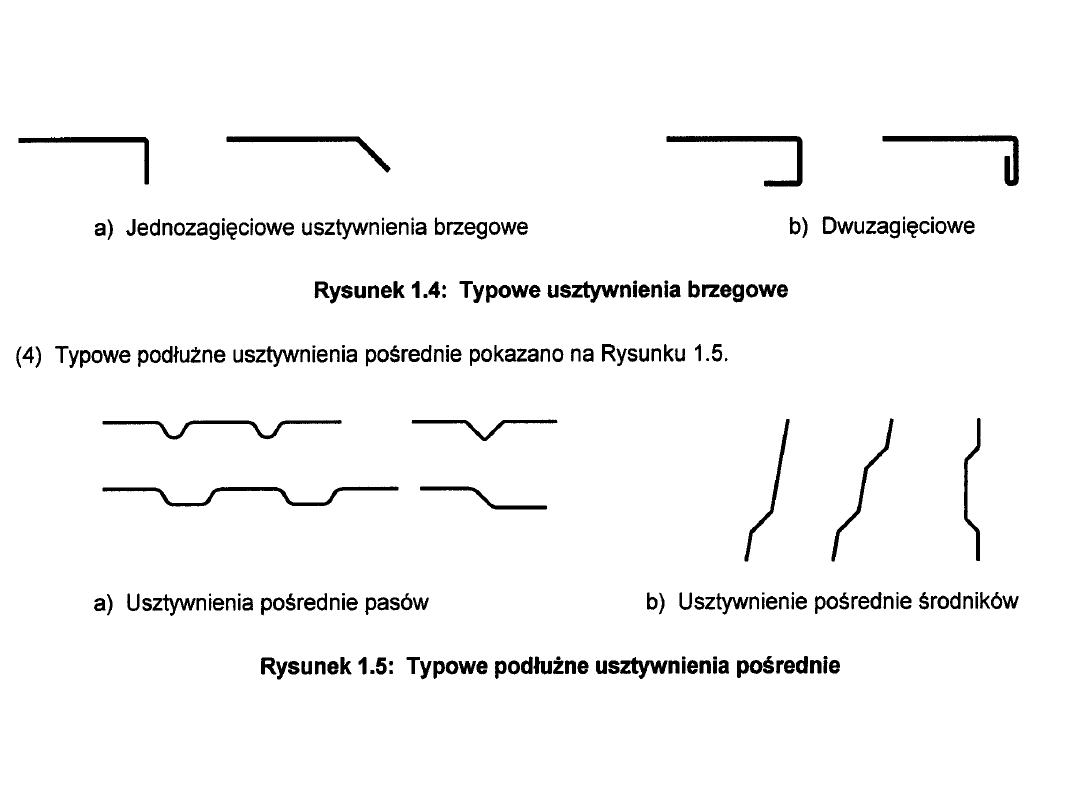
Usztywnienia brzegowe i podłużne 

pośrednie

 

 

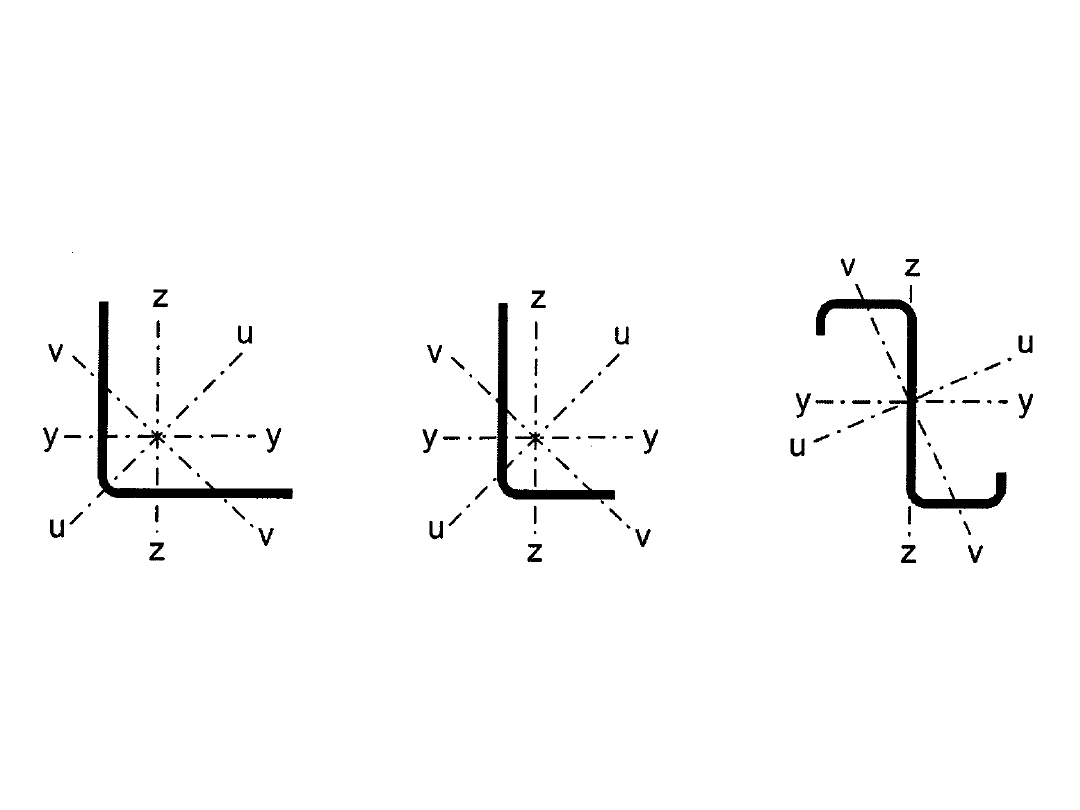
KONWENCJA OSI PRZEKROJU

 

 

 

 

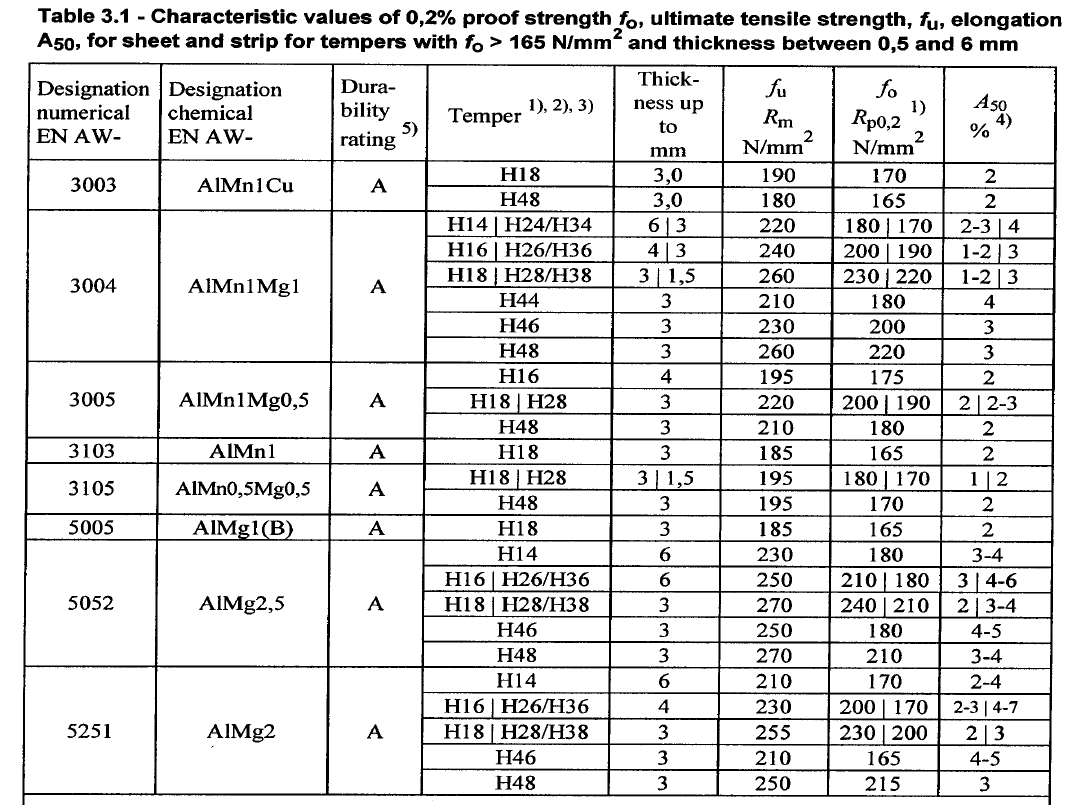
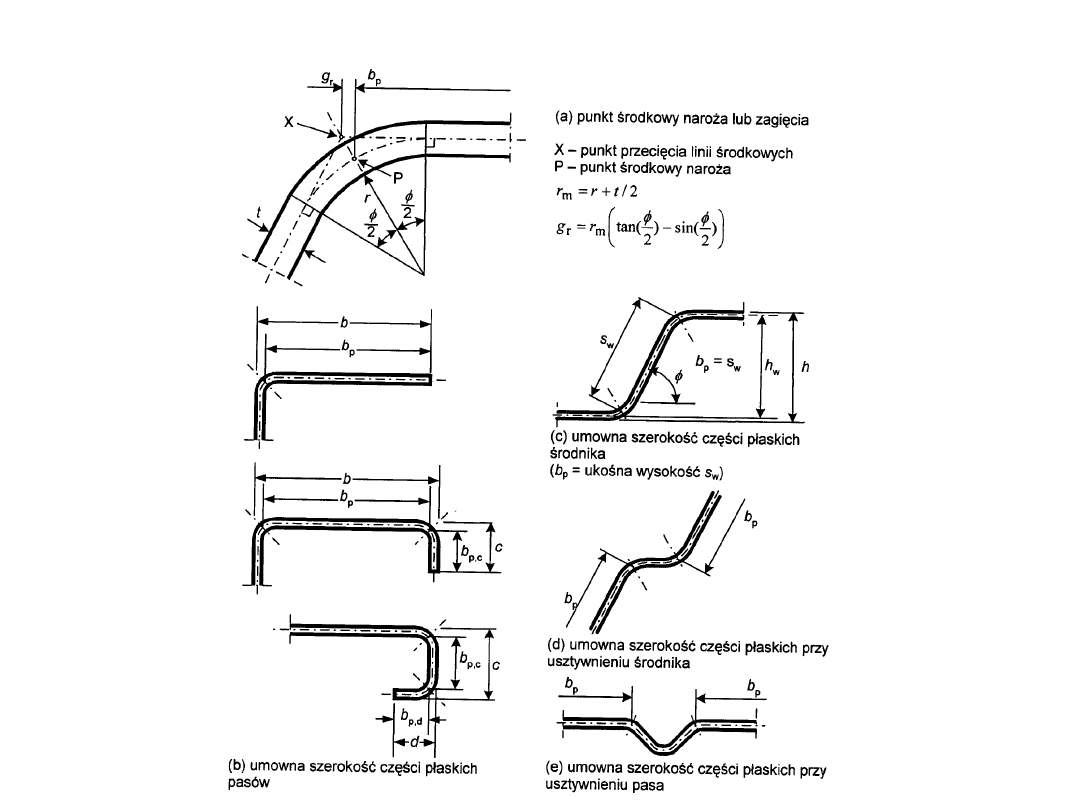
Umowne szerokości części płaskich 

przekroju

 

 

Wpływ wyokrąglenia naroży na cechy 

przekroju 

Charakterystyki geometryczne

A

g

  A

gsh

(1 - )

I

g

  I

gsh

(1 - 2)

I

w

  I

wsh

(1 - 4)

A

g 

I

g

 I

w

 -  pole przekroju, moment bezwładności, 

wycinkowy moment bezwładności przekroju z 

wyokrąglonymi narożami

A

gsh 

I

gsh

 I

wsh

 -  pole przekroju, moment bezwładności, 

wycinkowy moment bezwładności przekroju z 

ostrymi narożami







m

1

pi

n

1

o

j

j

b

90

φ

r

0,43

δ

 

 

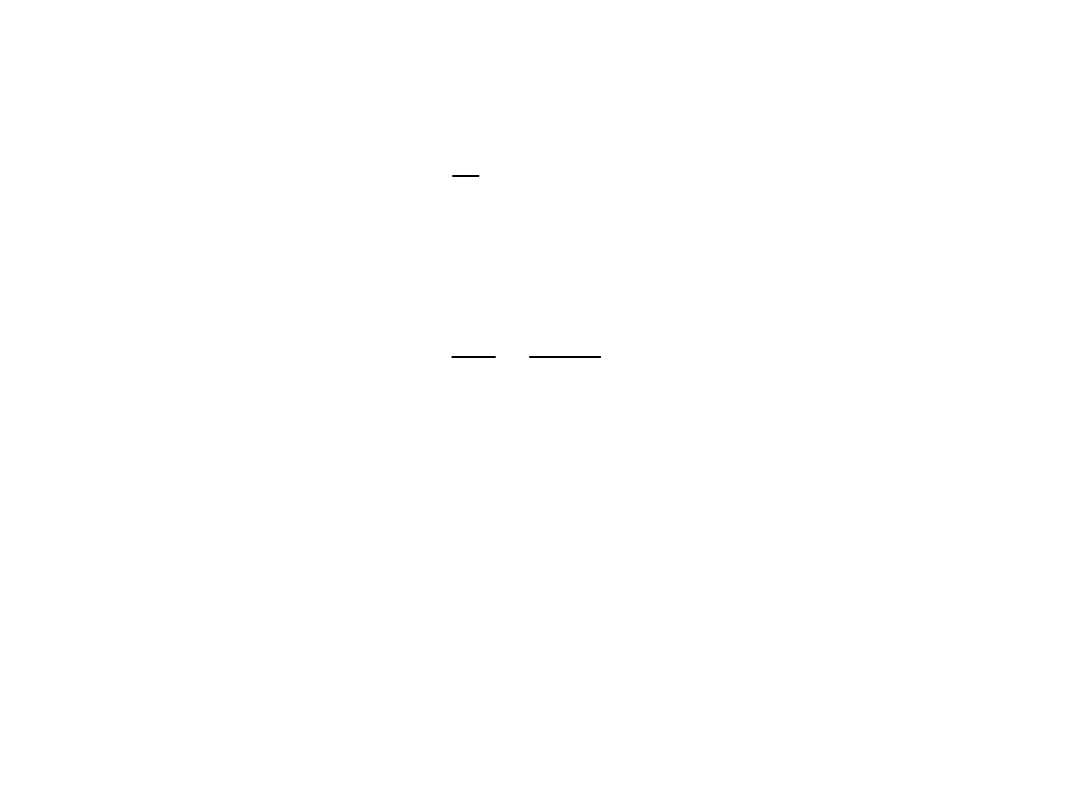
Maksymalne smukłości ścianek

• Maksymalne smukłości pasów ściskanych

• Maksymalne smukłości środników

• Grubość ścianek

t  0,5 mm

300

t

b



o

w

f

0,5E

t

s



 

 

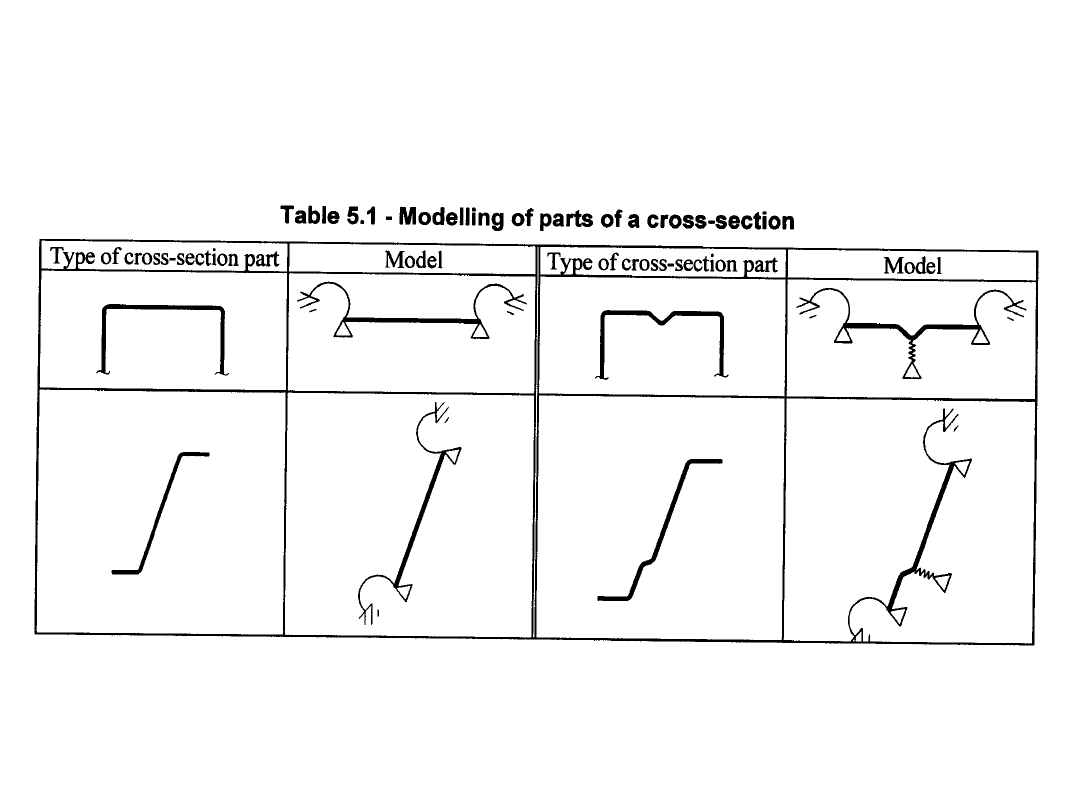
Modelowanie ścianek kształtowników

 

 

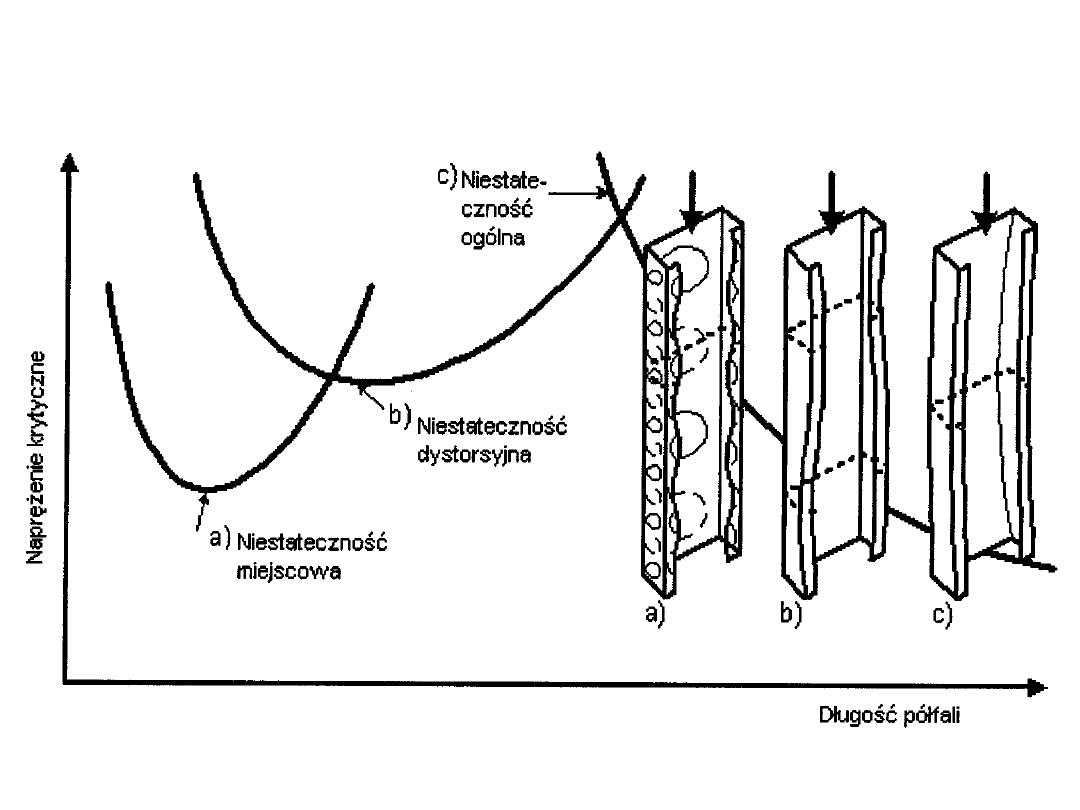
Formy niestateczności

 

 

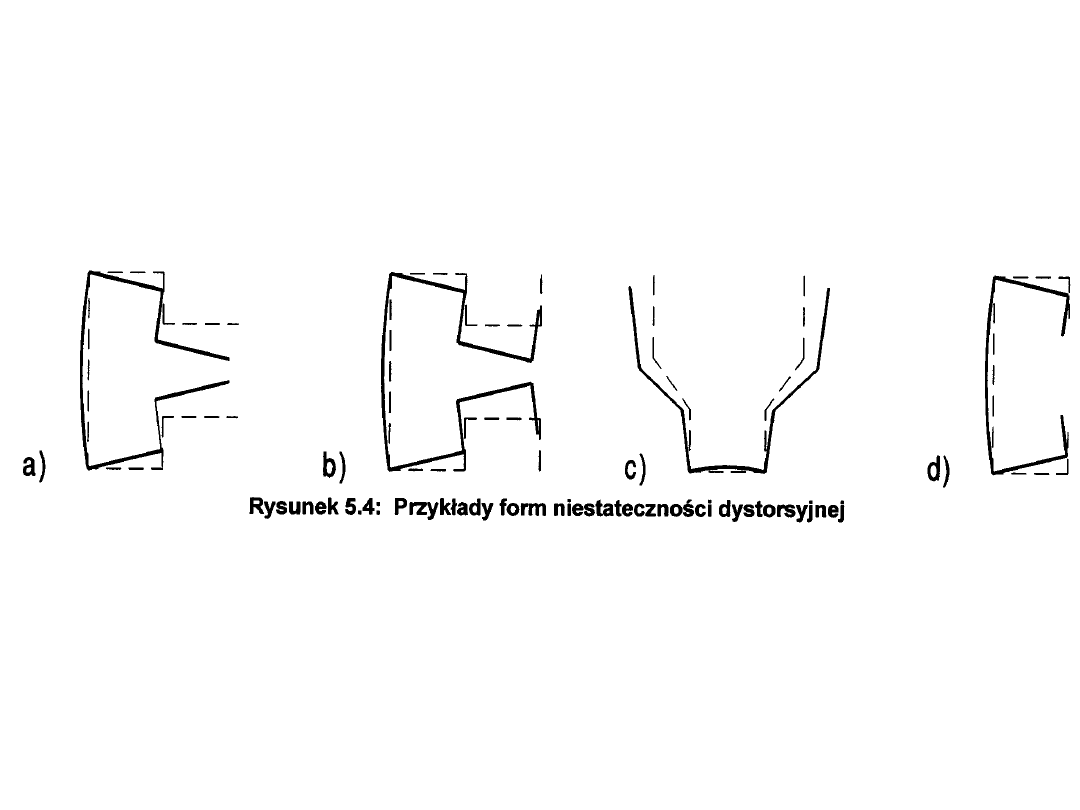
Niestateczność dystorsyjna

 

 

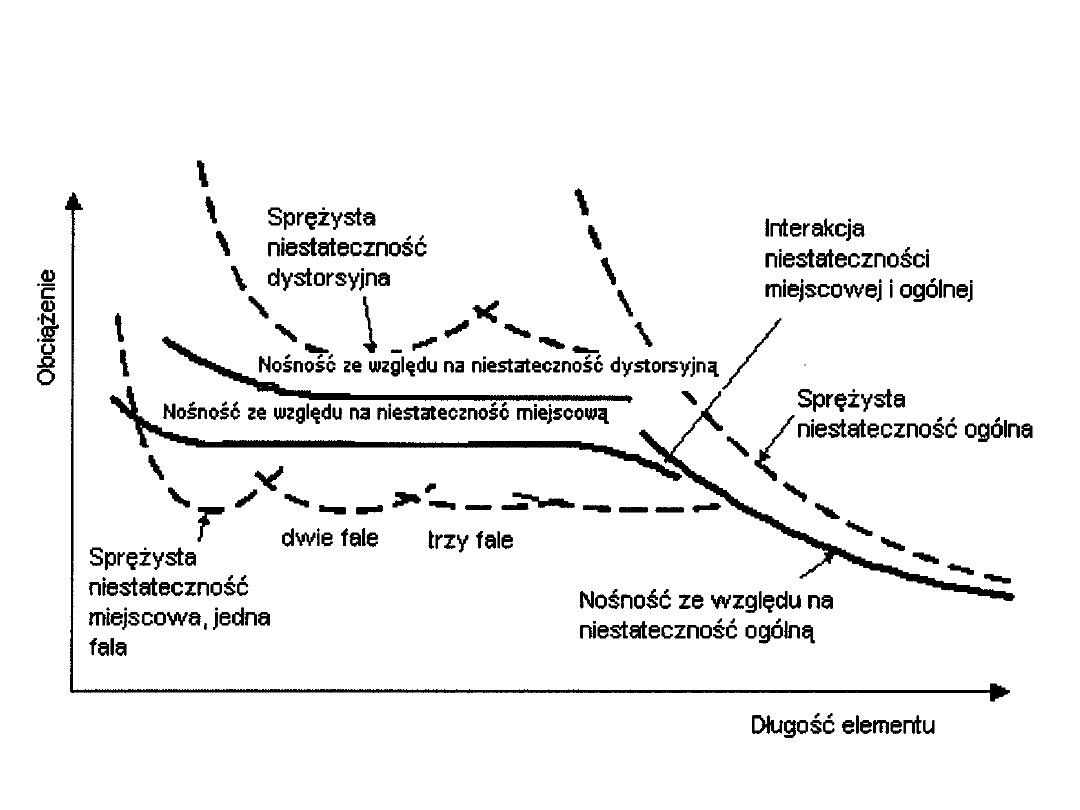
Formuły niestateczności sprężystej 

P

cr

(L)

 

 

Ścianki bez usztywnień 

współczynnik stateczności miejscowej 

• Grubość efektywna ścianki płaskiej t

ef

 

t

ef

 = t

σ

o

p

σ

2

o

2

p

cr

o

p

p

p

p

lim

p

Ek

f

t

b

1,052

Ek

π

)f

12(1

t

b

σ

f

λ

0,90

 

 

α

 

oraz

 

0,517;

λ

  

dla

     

,

λ

0,22

1-

α

ρ

0,517

λ

λ

  

dla

       

          

          

1,00

ρ







































 

 

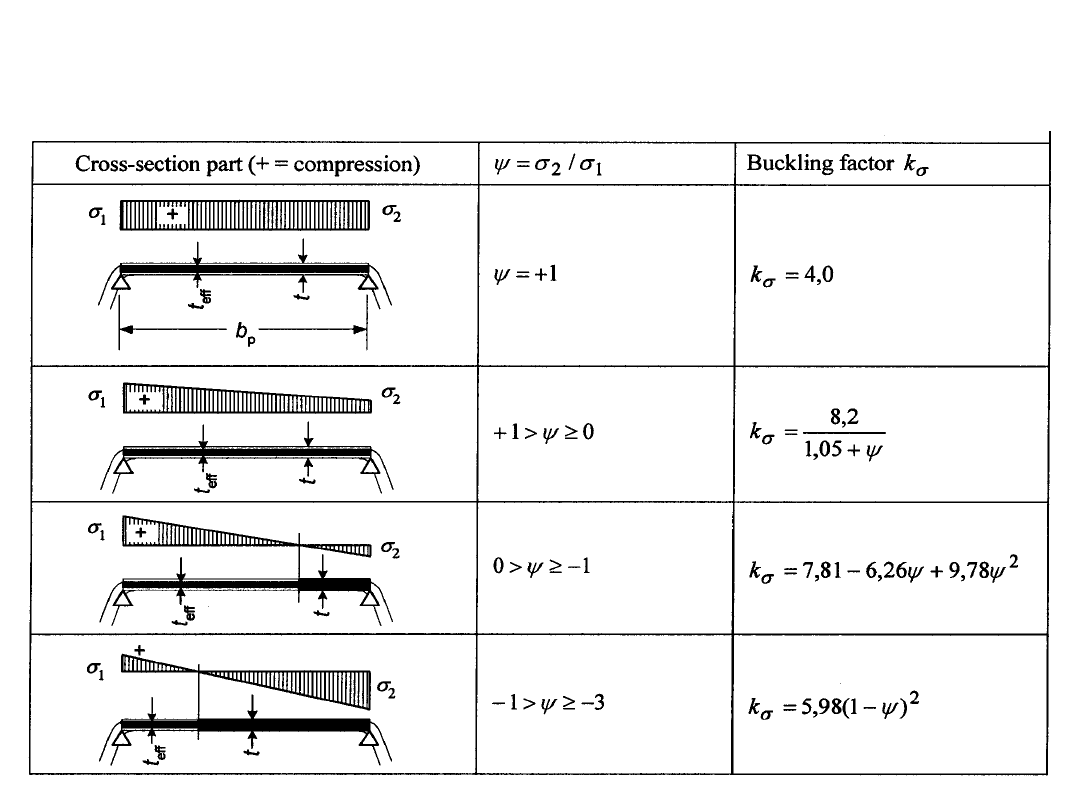
Ścianki bez usztywnień – PN EN 1999-

1-4

 

współczynnik stateczności miejscowej k



 

 

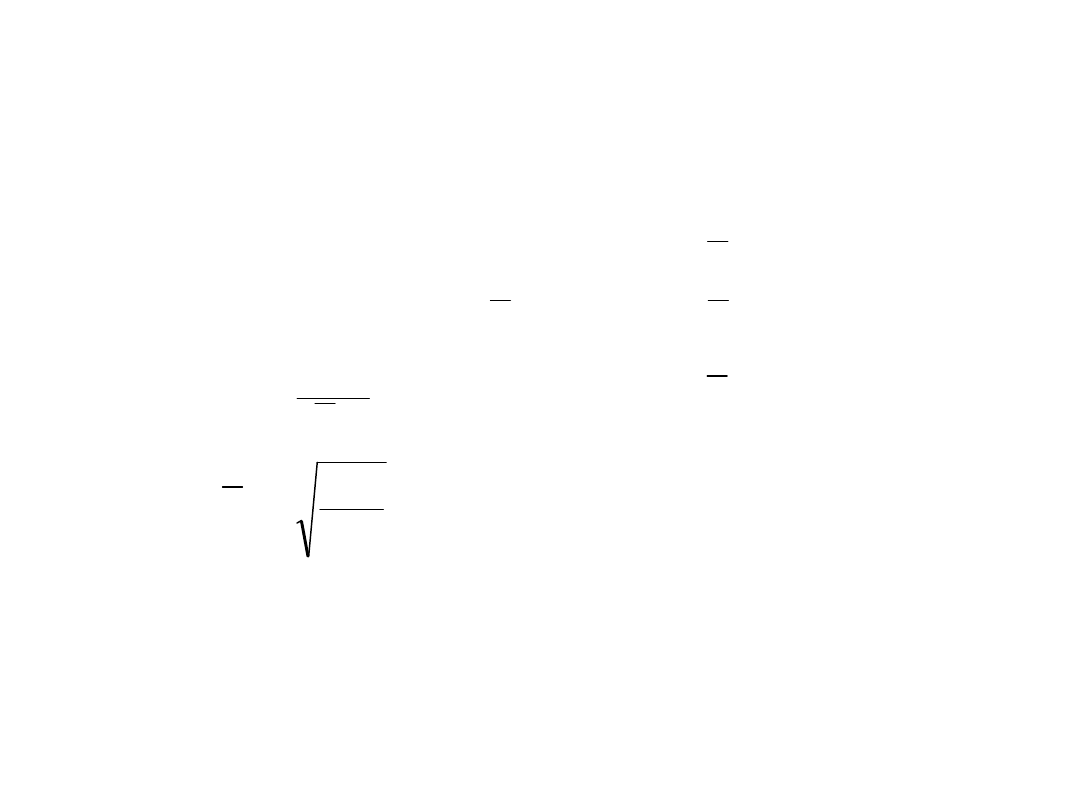
Ścianki płaskie 

 

współczynnik stateczności dystorsyjnej 

d

crs

o

s

s

s

s

s

d

s

σ

f

λ

1,04

λ

  

dla

      

          

          

,

λ

0,53

1,04

λ

0,25

 

dla

  

λ

 

0,62

1,155

0,25

λ

  

dla

        

          

          

1,00



















d

d







 

 

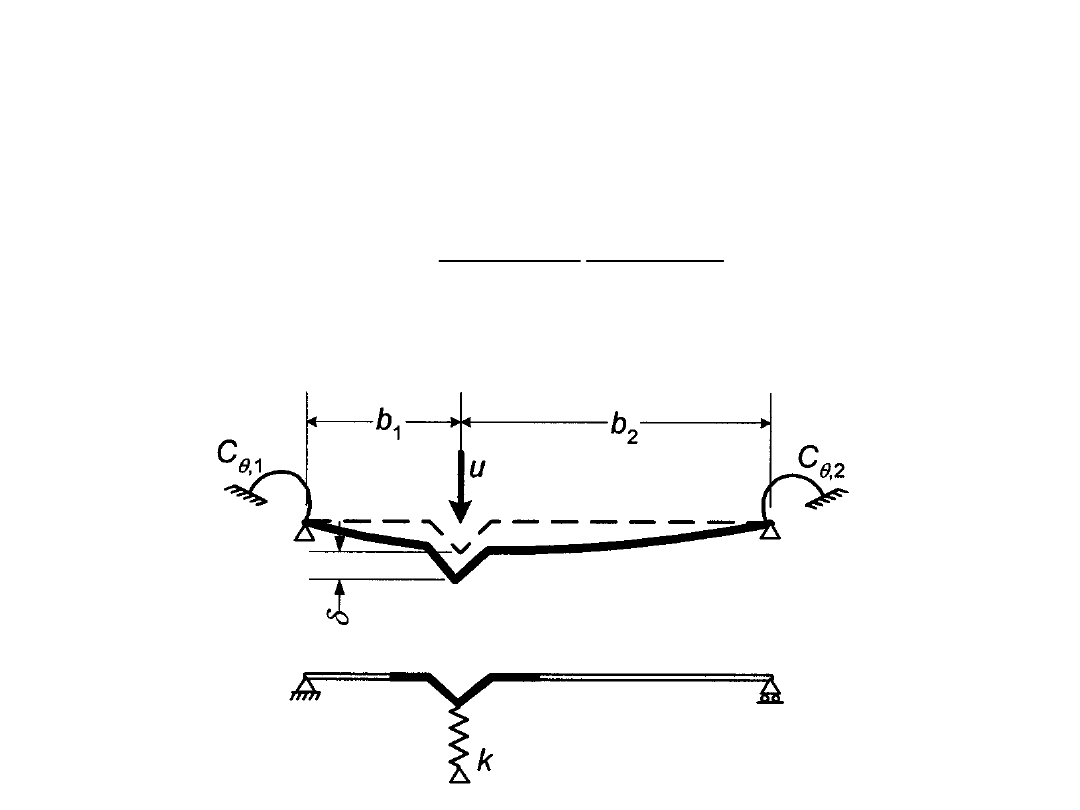
Ścianki płaskie z usztywnieniami 

pośrednimi

Jednostkowa sztywność usztywnienia k

k = u/;

    

Model do wyznaczania sztywności ścianki:









3

2

2

1

2
2

2

1

Et

1

12

b

b

3

b

ub

δ









 

 

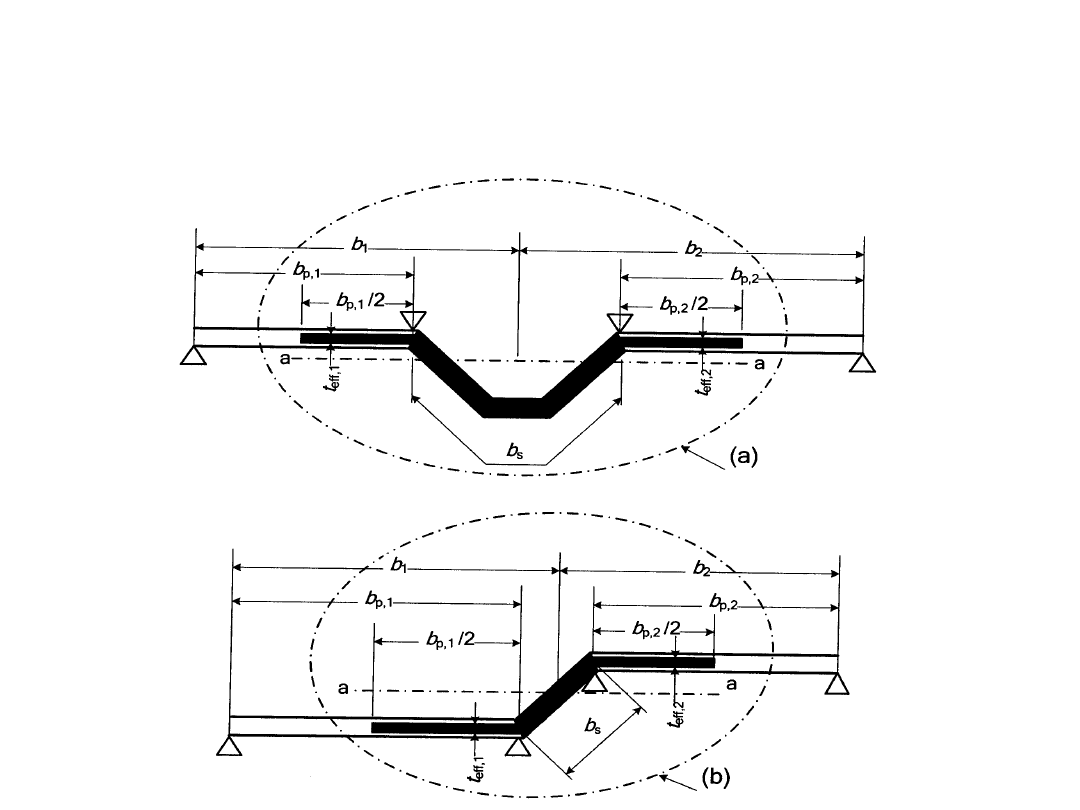
Ścianki płaskie z usztywnieniami 

pośrednimi

Efektywne pole przekroju usztywnienia pośredniego

 

 

Ścianki płaskie z usztywnieniami 

pośrednimi

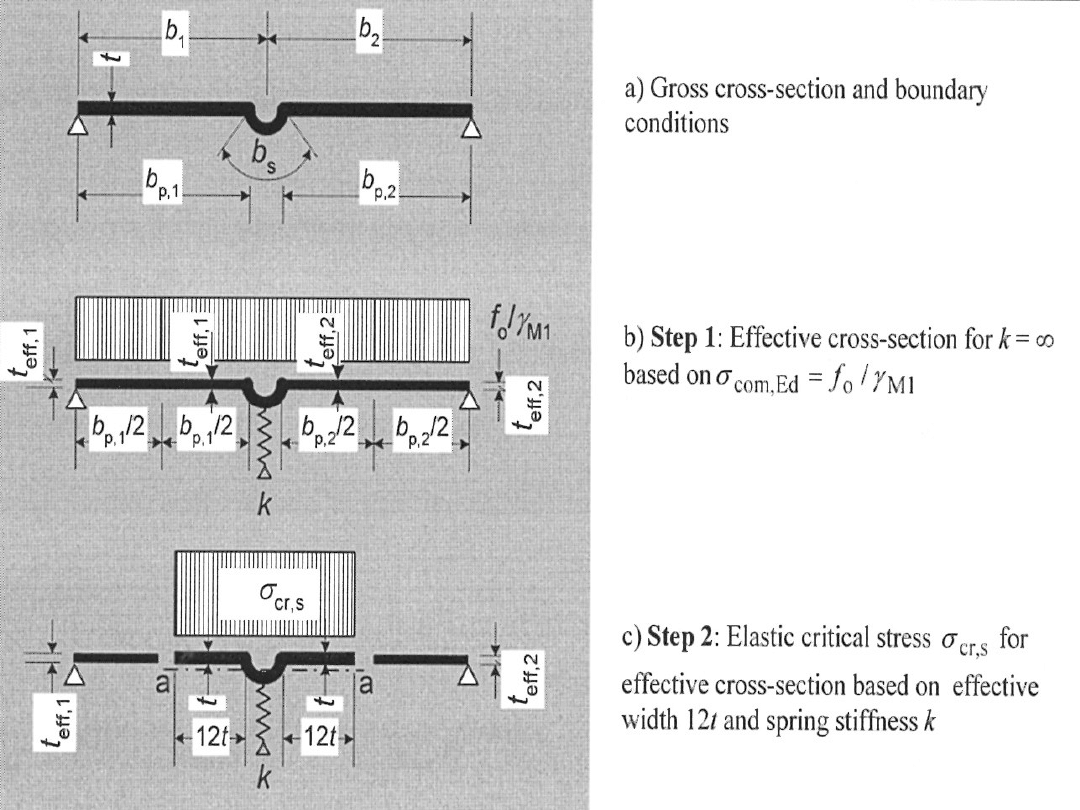
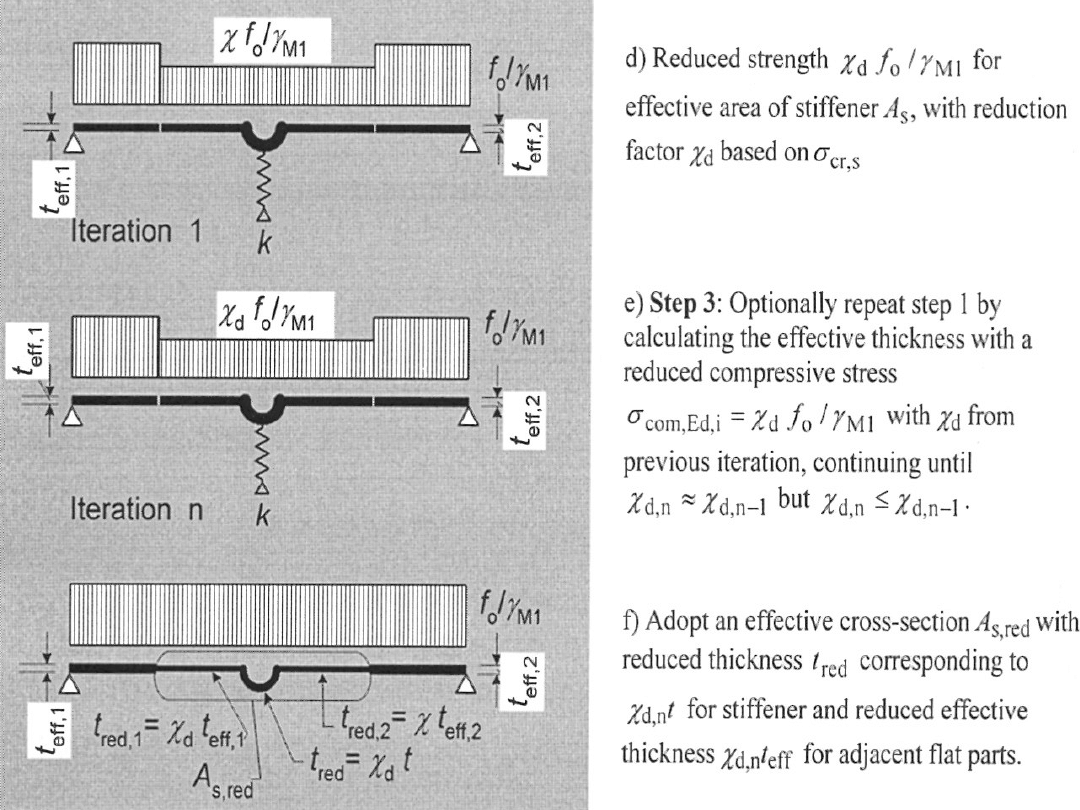
Procedura obliczeniowa przekroju efektywnego

Krok 1: wyznacz przekrój efektywny usztywnienia 

zakładając niepodatność podpór k =  dla naprężeń 

ściskających 



com,Ed

 = f

o

 /

M1

Krok 2:  wyznacz współczynnik k dla usztywnienia o 

zasięgu efektywnym 12 t i obciążenia naprężeniem 

cr,s

 

 zastosuj tak obliczony przekrój do wyznaczenia 

współczynnika stateczności dystorsyjnej 



d

Krok 3: opcjonalnie zastosuj iterację w celu uściślenia 



d

 

 

 

 

 

 

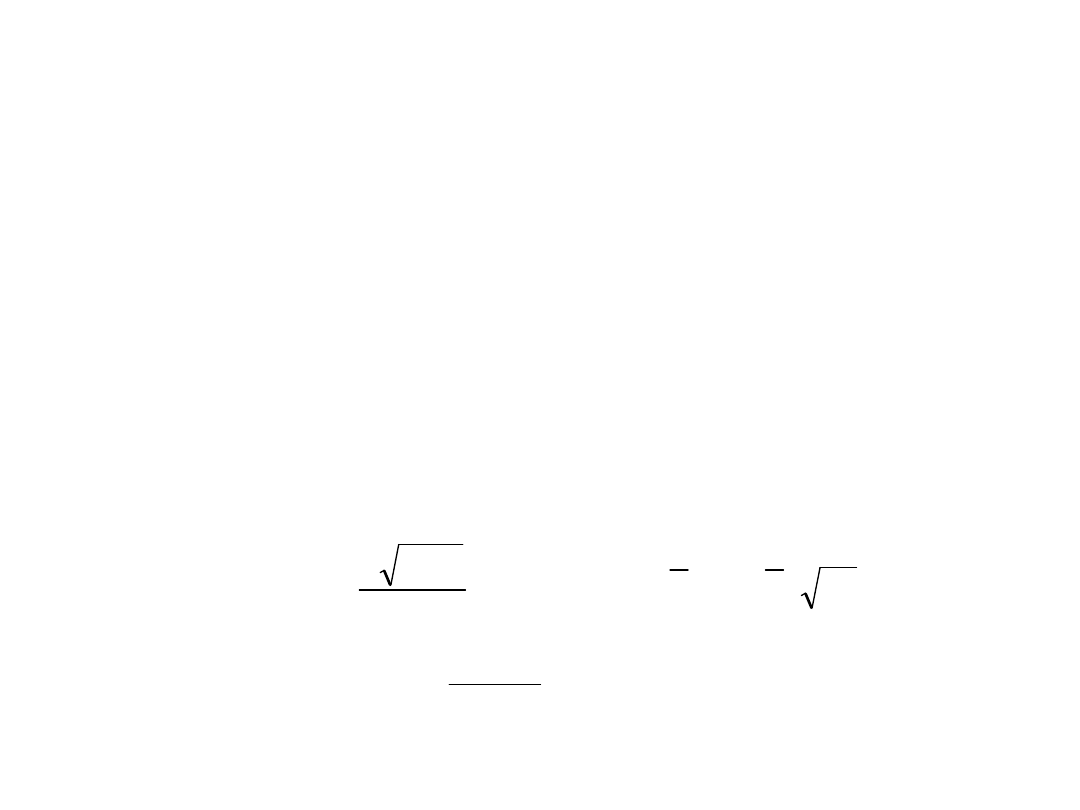
Ścianki płaskie z usztywnieniami 

pośrednimi

Pole usztywnienia brzegowego A

s

 na planszy 22

A

s

 = t (b

e2

 + c

ef

)

A

s

 = 0,5 t

ef1

b

e2

 + t b

s

 + 0,5 t

ef1

b

e2

 

Naprężenia krytyczne i przekrój zredukowany

ef

d

red

comEd

M1

o

s

d

sred

d

p

pred

d

s

s

crs

t

t

σ

/

f

A

A

λ

λ

 

dla

 

ρ

A

kEI

2

σ

























 

 

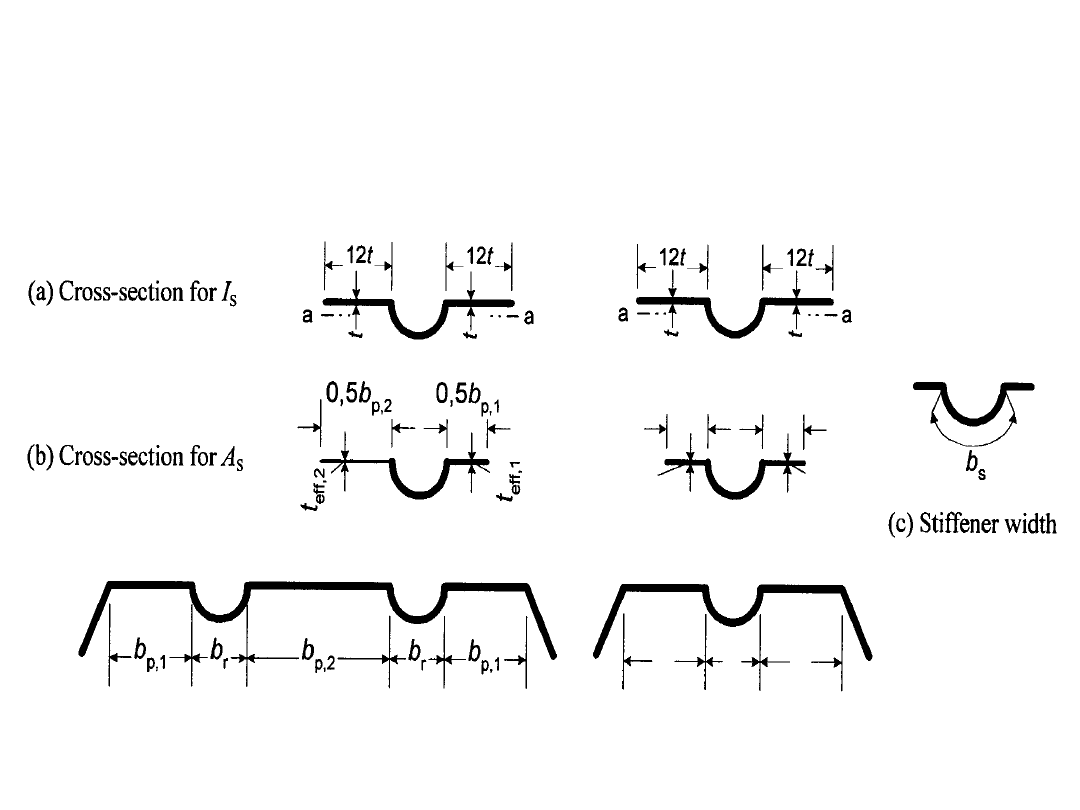
BLACHA TRAPEZOWA Z USZTYWNIENIAMI 

POŚREDNIMI

Pasy z usztywnieniami pośrednimi

 

 

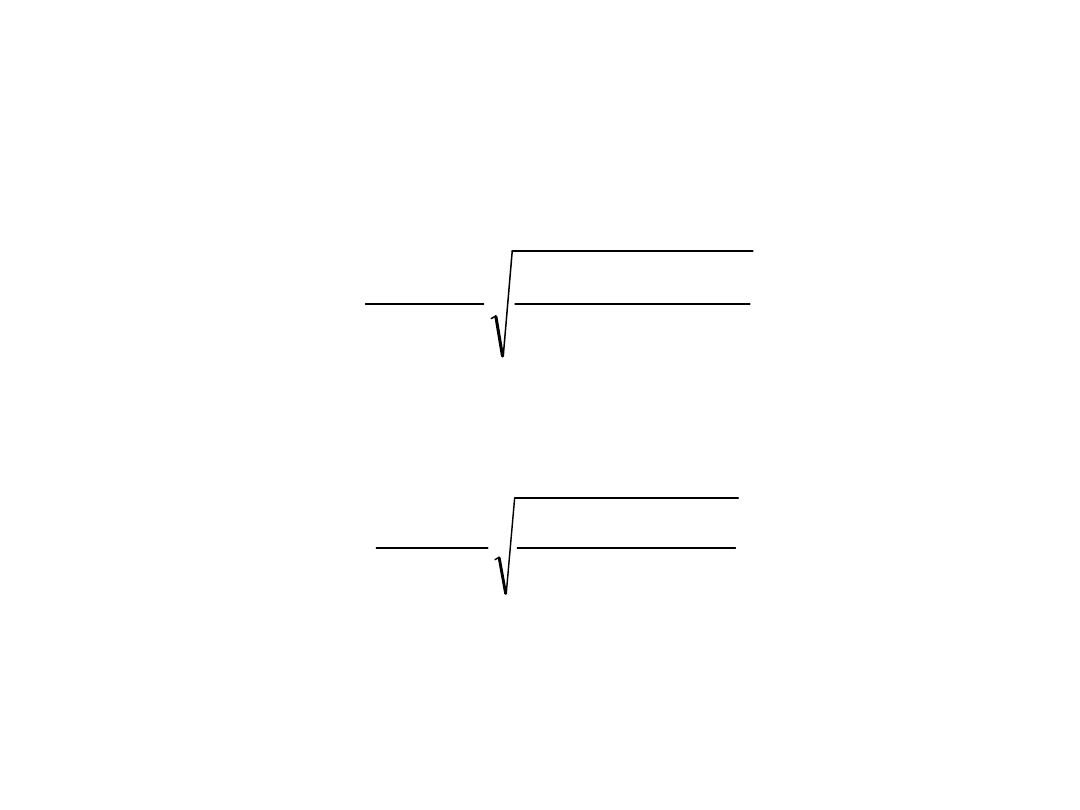
BLACHA TRAPEZOWA Z 

USZTYWNIENIAMI POŚREDNIMI

-Naprężenia krytyczne trapezu z jednym usztywnieniem 

pośrednim

Naprężenia krytyczne pasa trapezu z dwoma usztywnieniami 

pośrednimi





s

p

2

p

3

s

s

w

3b

2b

4b

t

I

A

E

4,2









s

cr,





1

e

2

1

3

s

s

w

3b

2b

8b

t

I

A

E

4,2









s

cr,

 

 

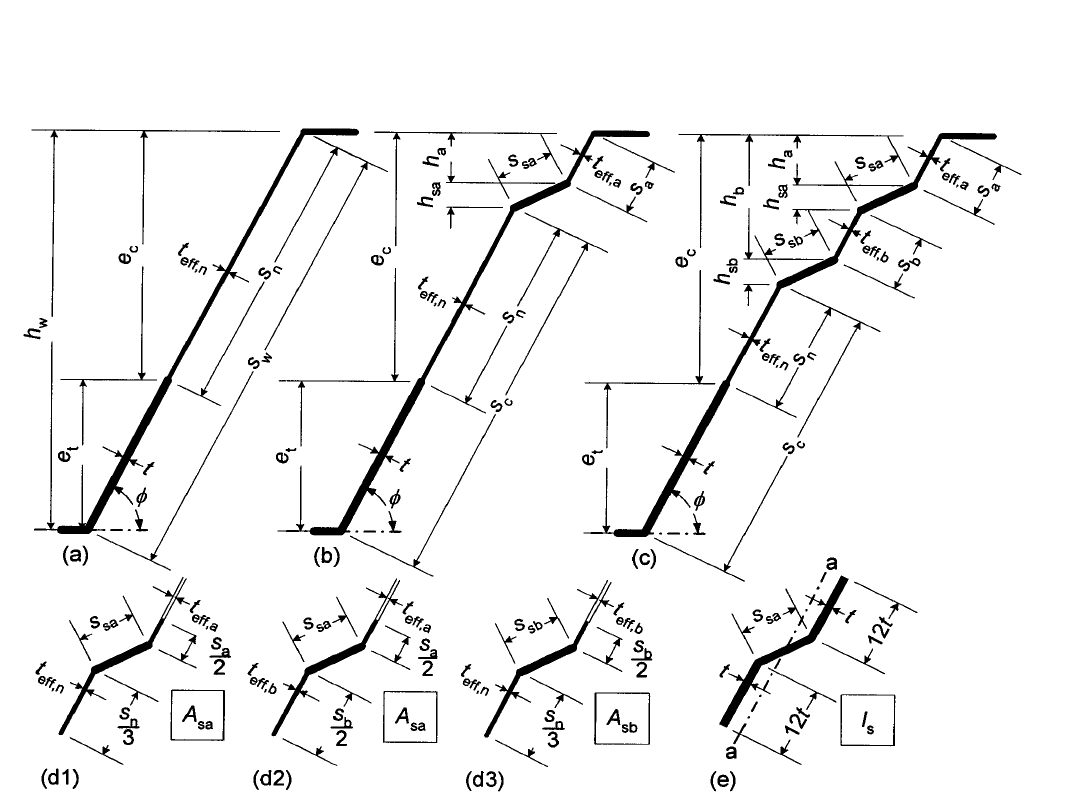
BLACHA TRAPEZOWA Z 

USZTYWNIENIAMI POŚREDNIMI

 

 

BLACHA TRAPEZOWA Z 

USZTYWNIENIAMI W PASACH I 

ŚRODNIKACH

 

 

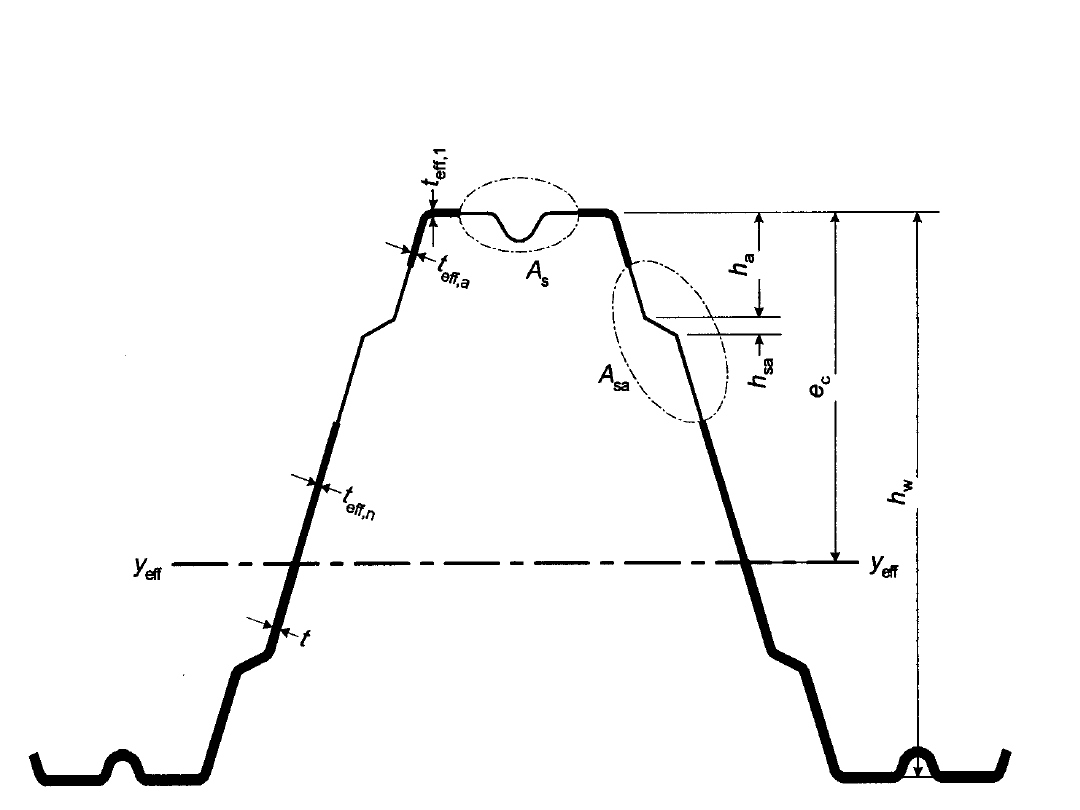
BLACHA TRAPEZOWA Z 

USZTYWNIENIAMI W PASACH I 

ŚRODNIKACH

• Zmodyfikowane naprężenie krytyczne przy 

wyboczeniu dystorsyjnym:





zginanie

e

0,5h

h

1

ściskanie

β

1

β

s

s

s

A

s

t

I

E

1,05

σ

gdzie

σ

σ

β

1

σ

σ

c

ha

s

s

s

2

1

a

sa

1

3

s

f

crsa

4

4

crsa

crs

s

crs

mod

cr,







































d

 

 

BLACHA TRAPEZOWA Z 

USZTYWNIENIAMI W PASACH I 

ŚRODNIKACH

• Końcowy rezultat obliczeń przekrojów 

cienkościennych:

• A

ef

• J

ef

• W

ef

 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Ściskanie osiowe

N

Ed

  N

cRd

 = f

o

 A

ef

 /

M1

gdzie 
A

ef

 < A

g

 gdy zachodzi redukcja wskutek niestateczności 

miejscowej lub dystorsyjnej

 A

ef

 = A

g

 gdy nie zachodzi redukcja jak wyżej

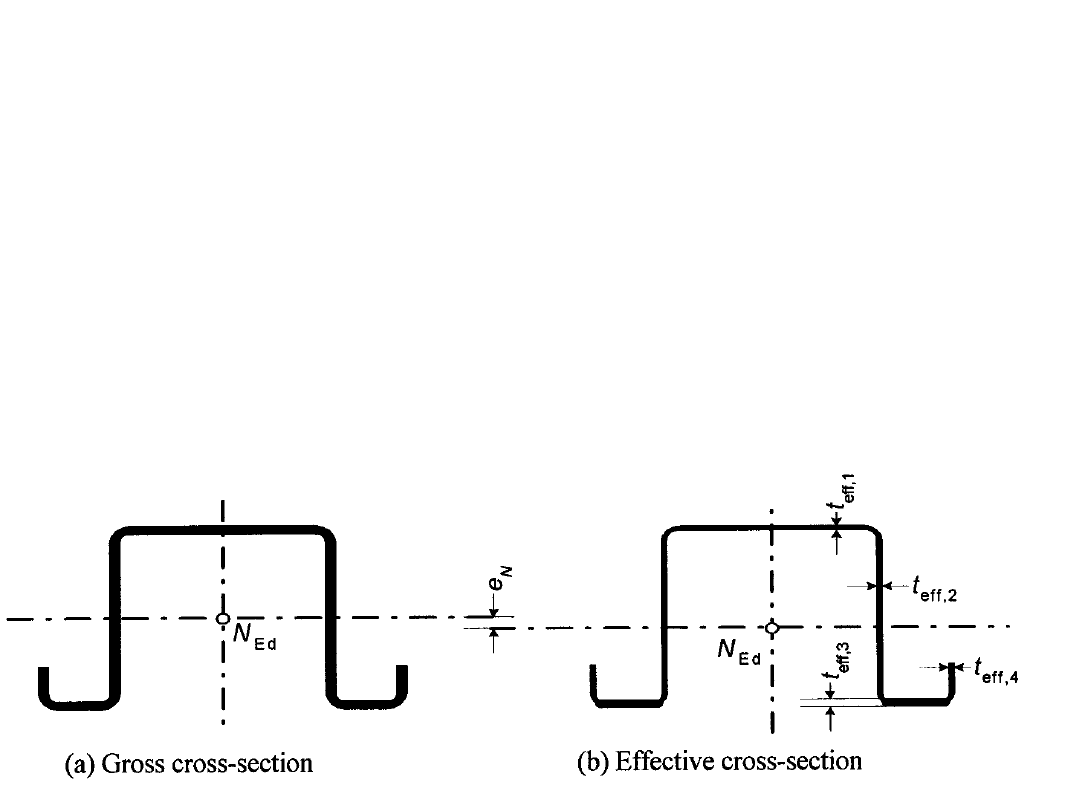
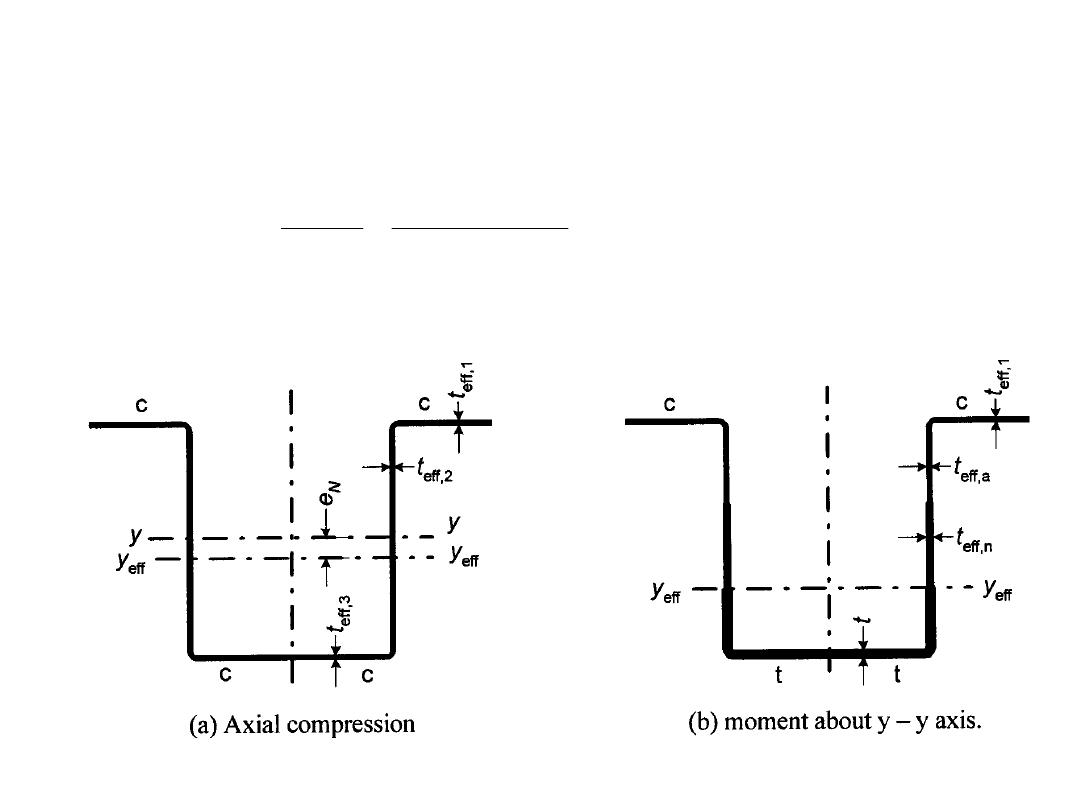
Należy uwzględnić wpływ mimośrodu e

N

 :

 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Zginanie

M

Ed

  M

cRd

 = f

o

 W

ef

 /

M1

gdzie
W

ef

 < W

el

 gdy zachodzi redukcja wskutek 

niestateczności miejscowej lub 
dystorsyjnej

 W

ef

 = W

el

 gdy nie zachodzi redukcja jak 

wyżej

 

M

Ed

  M

cRd

 = 4f

o

W

pl

(1 - /

el

) /

M1

 

 

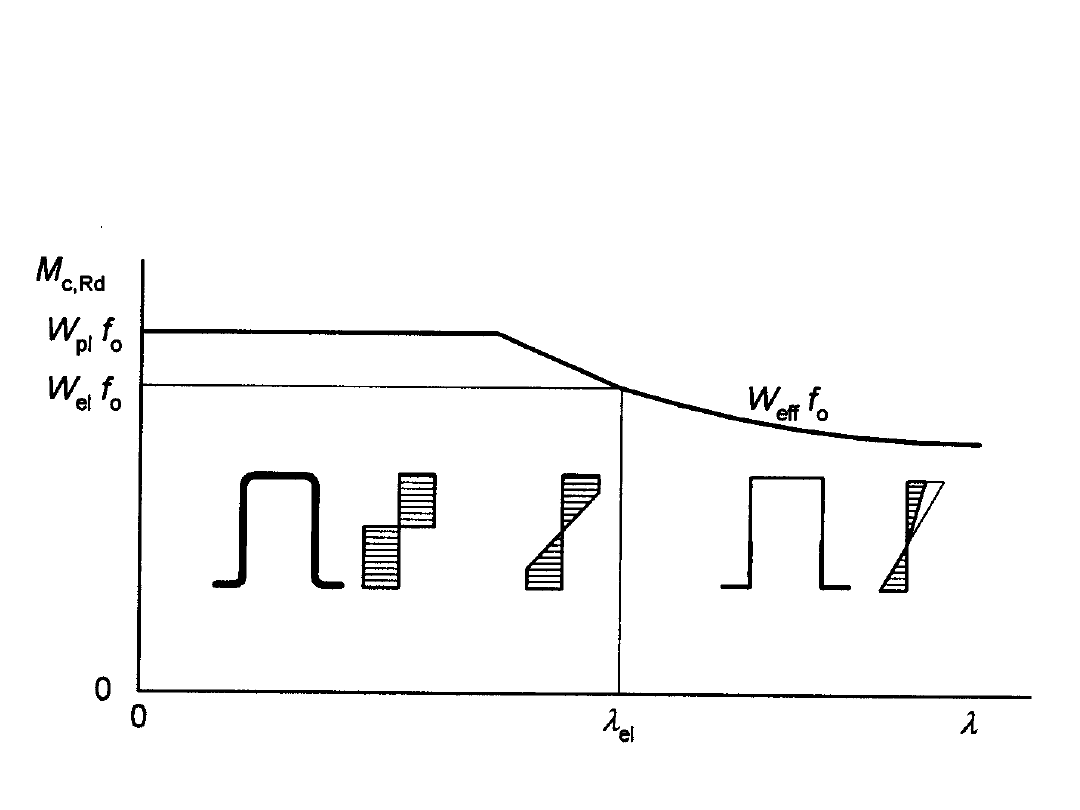
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Zginanie – nośność przekroju jako funkcja smukłości 

ścianek

 

 

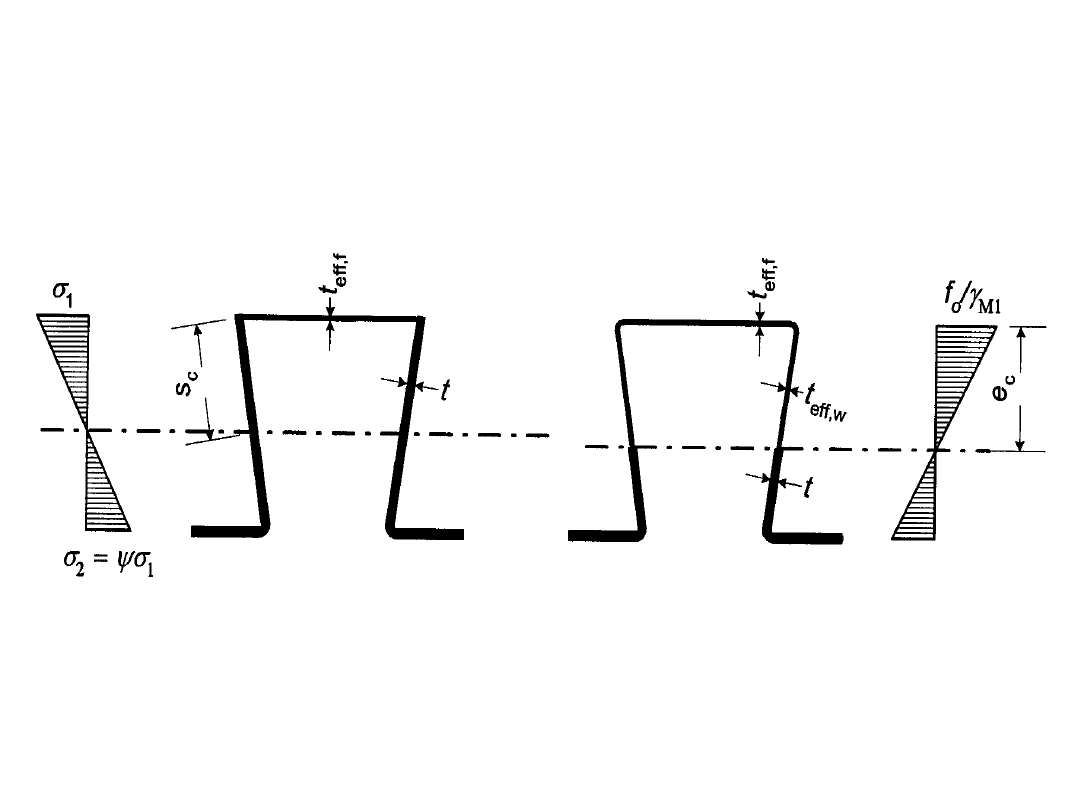
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Przekrój współpracujący przy zginaniu

 

 

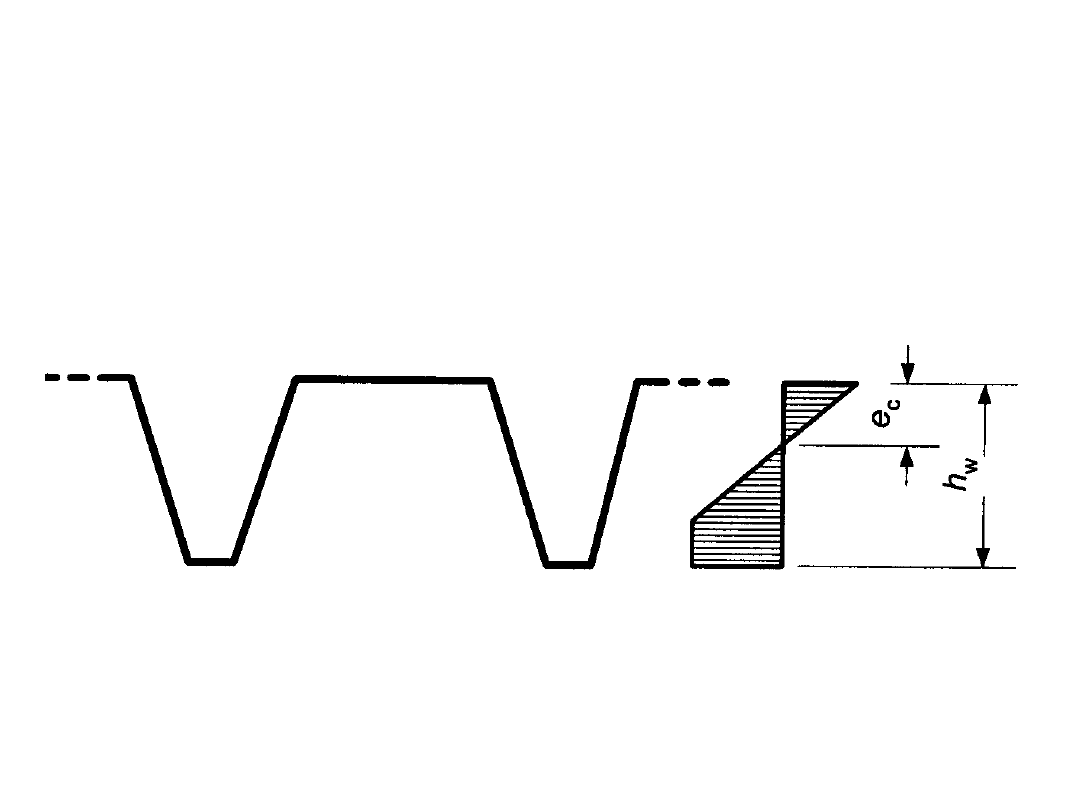
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Jednostronne uplastycznienie strefy rozciąganej przy 

zginaniu

 

 

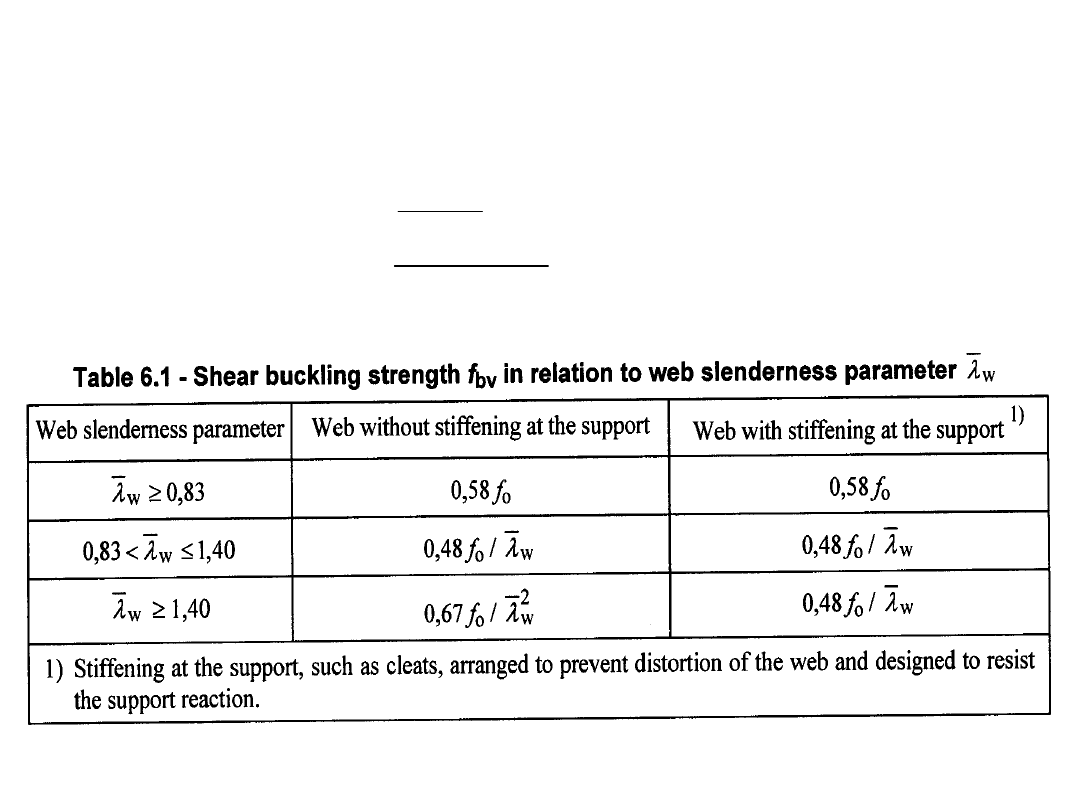
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Ścinanie

:

tablicy

 

wg

f

tf

sin

h

V

V

bv

M1

bv

w

bRd

Ed











 

 

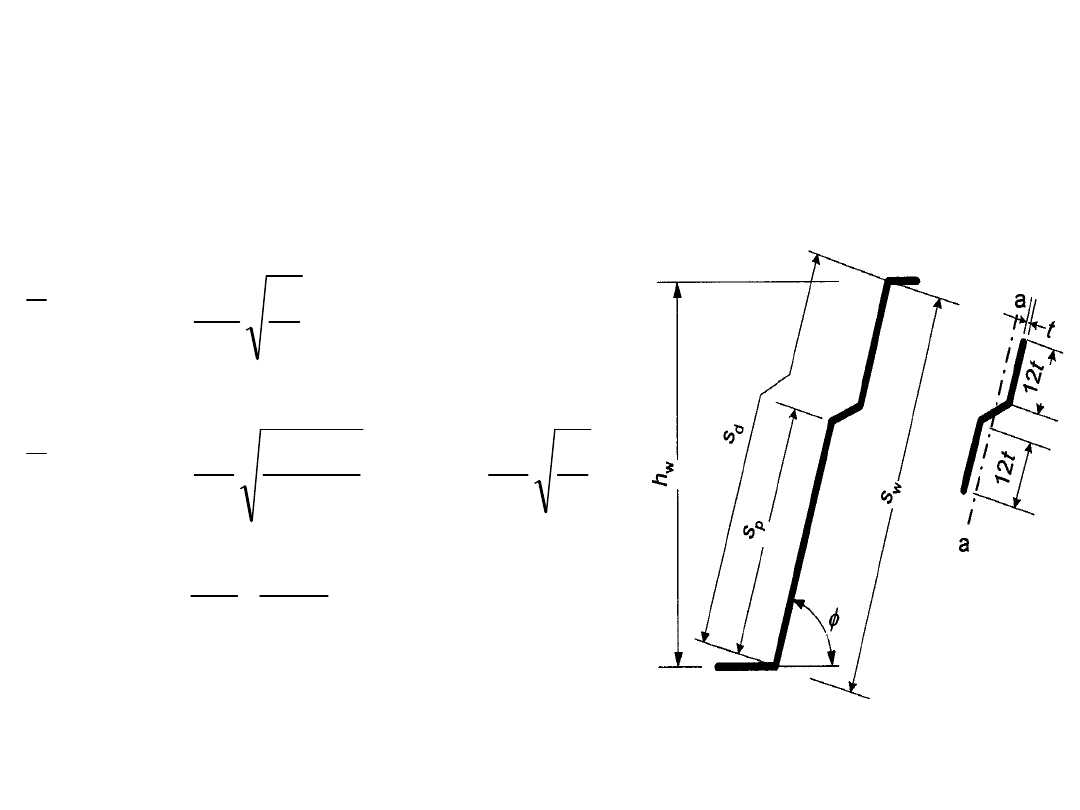
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Ścinanie

1/3

d

s

τ

o

d

o

d

w

o

w

w

s

I

t

2,1

5,34

k

E

f

t

s

0,346

E

k

5,34f

t

s

0,346

λ

podłodłużn

 

iami

usztywnien

 

z

 

środniki

E

f

t

s

0,346

λ

podłodłużn

 

usztywnie

ń

 

bez

 

środniki

































 

 

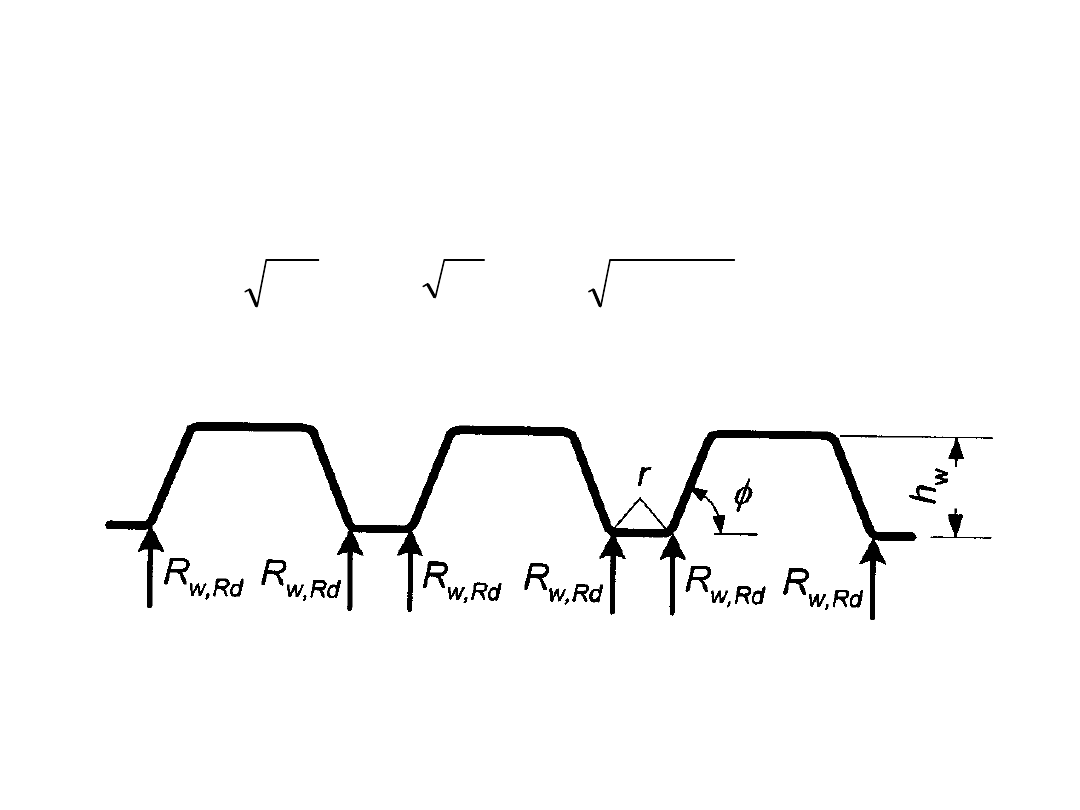
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

Obciążenie skupione – belki bez usztywnienia 

F

Ed

Ed

  R

wRd

 











M1

2

a

o

2

wRd

/

/90)

(

2,4

/t

0,02l

0,5

r/t

0,1

1

E

f

αt

R













 

 

 

 

 

 

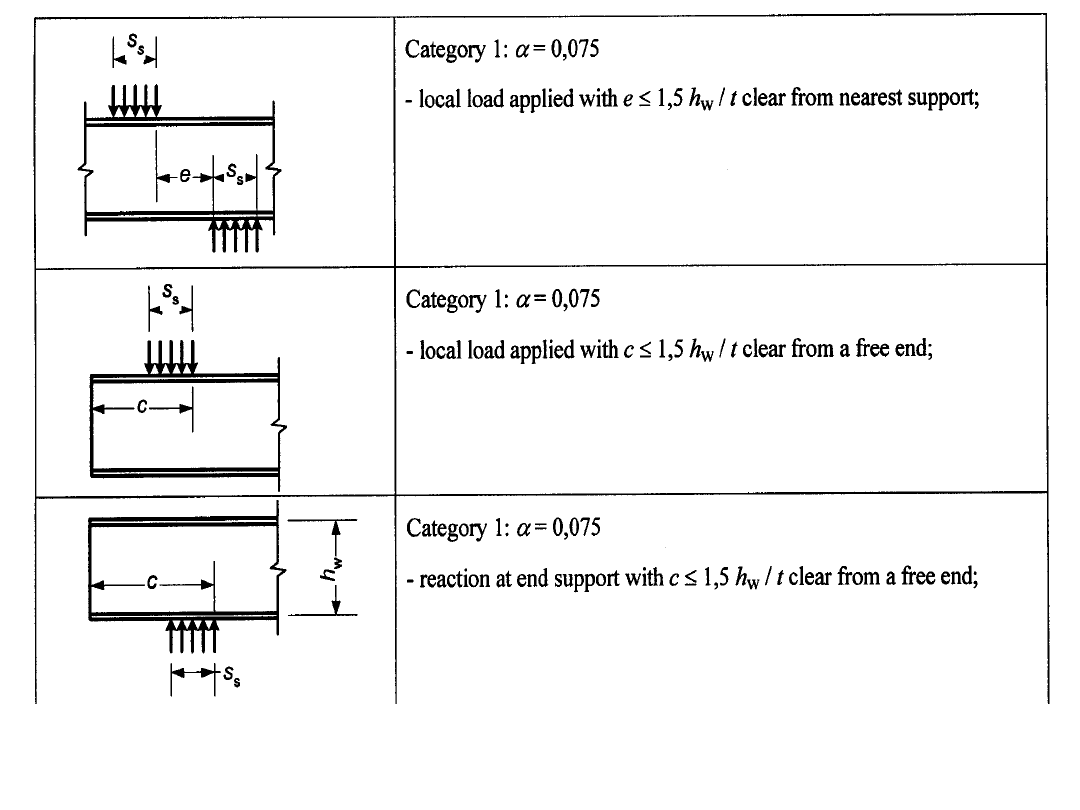
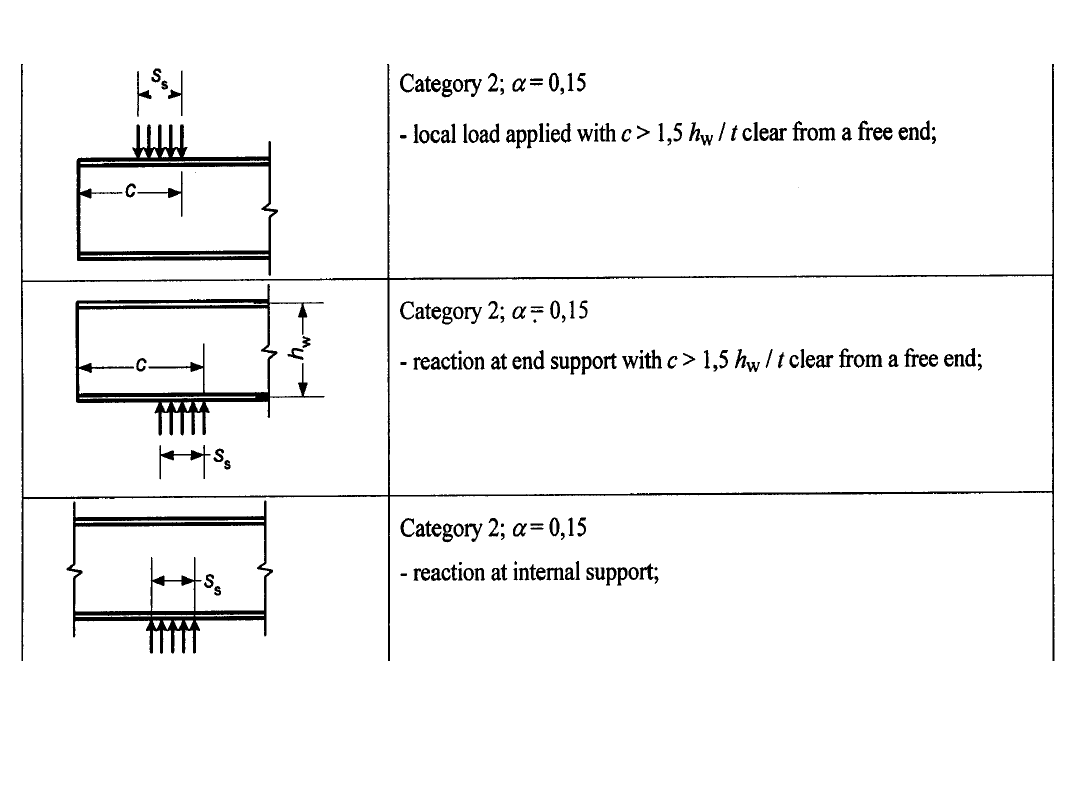
STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Rozciąganie ze zginaniem

N

tRd

 – obliczeniowa nośność na rozciąganie

M

cyRd,ten

 – obliczeniowa nośność na zginanie względem 

silnej osi ustalona dla wskaźnika wytrzymałości 

odpowiadającego krawędzi rozciąganej

1

M

M

N

N

ten

cyRd,

yEd

tRd

Ed





 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Rozciąganie ze zginaniem

Gdy M

cyRd,com

  M

cyRd,ten

 należy sprawdzić dodatkowo 

warunek:

  

1

M

M

N

N

com

cyRd,

yEd

tRd

Ed







 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Ściskanie ze zginaniem

Gdy M

cyRd,ten

  M

cyRd,com

  należy sprawdzić dodatkowo 

warunek:

Ny

Ed

yEd

com

cyRd,

yEd

yEd

cRd

Ed

e

N

M

1

M

M

M

N

N













1

M

M

M

N

N

ten

cyRd,

yEd

yEd

cRd

Ed











 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Zginanie ze ścinaniem i siłą podłużną

przekroju

 

plastyczna

 

nośośno

M

pasów

 

przekrojów

 

h

efektywnyc

 

nośośno

M

środnika

 

nośośno

 

wa

obliczenio

V

1

1)

V

2V

)(

M

M

(1

M

M

N

N

plRd

fRd

wRd

2

wRd

Ed

Rd

pl,

fRd

yRd

yEd

Rd

Ed

















 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność przekrojów

• Zginanie i obciążenie skupione

1

R

F

1

M

M

1,0

R

F

M

M

0,94

wRd

Ed

cRd

Ed

2

wRd

Ed

2

cRd

Ed









)

(

)

(

 

 

WYMIAROWANIE STALOWYCH 

PRĘTÓW ŚCISKANYCH

Współczynnik wyboczenia wg EN 1999-1-1:

gdzie

dla prętów dowolnej klasy:

2

2

λ

Φ

Φ

1

















2

O

λ

λ

λ

α

1

0,5

Φ









0,2

λ

  

oraz

  

0,13

α

E

f

iπ

l

λ

o

o









 

 

STANY GRANICZNE NOŚNOŚCI

 Nośność prętów

Zginanie ze ściskaniem wg EN 1999-1-4:

M1`

com

y,

ef,

o

yRd

M1

ef

x

o

y

Rd

yRd

yEd

yEd

Rd

y

Ed

/

W

f

M

   

,

/

A

ω

f

N

1

M

ΔM

M

N

N



















 

 

STANY GRANICZNE 

UŻYTKOWALNOŚCI

• Moment bezwładności przekroju klasy 4 :

I

gr

 – moment bezwładności przekroju brutto



gr

 – maksymalne naprężenie ściskające w SGU

I

ef

 – moment bezwładności przekroju efektywnego





ef

gr

o

gr

gr

ser

ef,

I

I

f

σ

I

I





