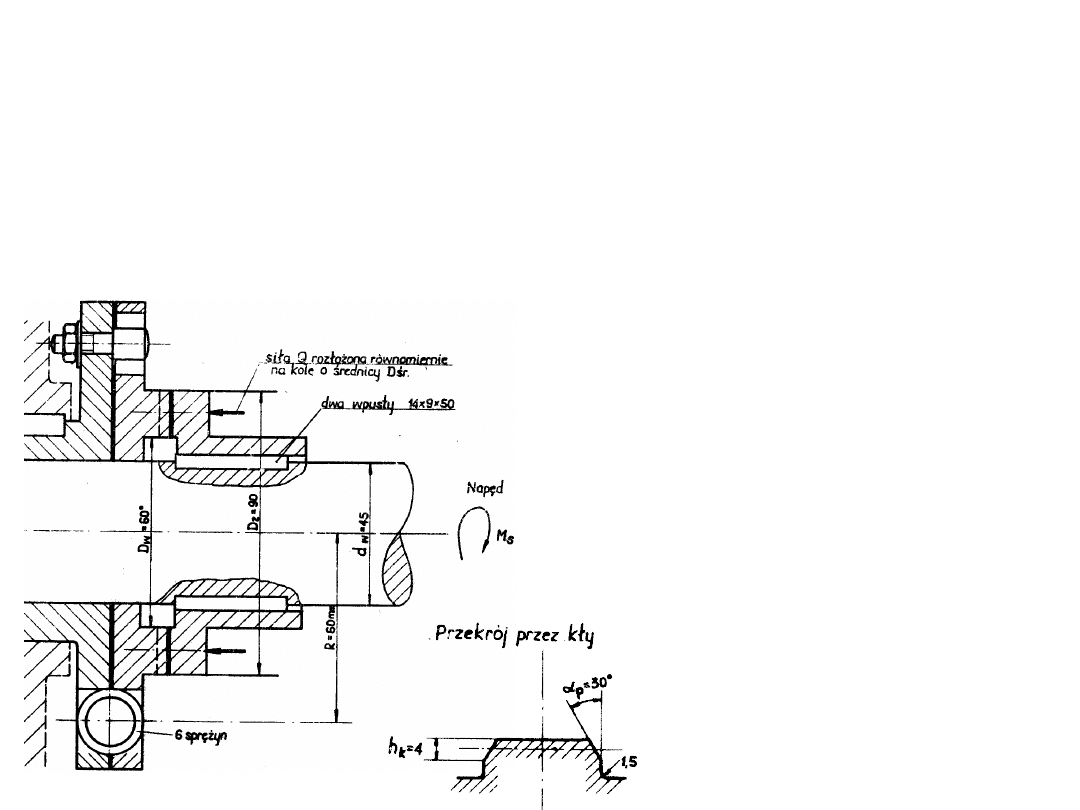
ZADANIE 2:

Sprzęgło bezpieczeństwa kłowe oraz sprzęgło podatne o budowie i wymiarach
pokazanych na rysunku są obciążone momentem nominalnym wynikającym z
przenoszenia mocy N=15 kW przy obrotach n=750 obr/min. W trakcie pracy mogą
występować przeciążenia. Dla momentu maksymalnego M

smax

=k·M

snom

, gdzie k=1,25

ma

następować

blokowanie

sprzęgła

podatnego

i wyłączenie sprzęgła kłowego.

1. Sprawdzić wytrzymałość wpustów mocujących piastę do wału jeśli p

dopw

=40 MPa.

2. Sprawdzić wytrzymałość kłów (sześciu) jeśli p

dopk

=40 MPa.

3. Wyznaczyć siłę Q wywieraną na

prawą część sprzęgła kłowego
aby sprzęgło wyłączało się pod
działaniem

momentu

maksymalnego

M

smax

jeżeli

współczynnik tarcia na wpustach i
powierzchniach roboczych kłów
wynosi μ=0,1.

4. Wyznaczyć sztywność każdej z

sześciu

sprężyn

sprzęgła

podatnego tak, aby skręcanie
sprzęgła rozpoczynało się przy
M

s0

=0.25·M

snom

oraz by dla M

smax

następowało blokowanie sprzęgła.
Podatność

sprzęgła

wynosi

dφ/dM

s

=0,02 deg/Nm.

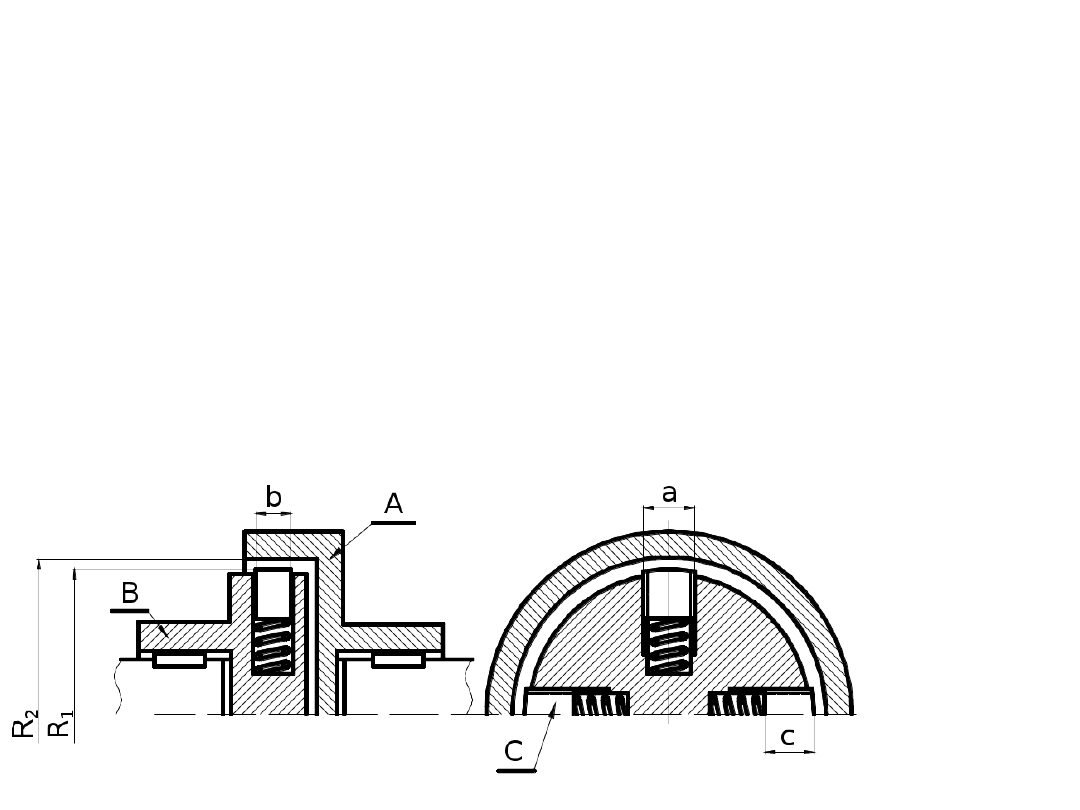
ZADANIE 3:

Sprzęgło rozruchowe o budowie podanej na rysunku składa się z członu napędzanego
A, napędzającego B oraz n = 4 jednakowych elementów ruchomych C. Elementy te
połączone

są

z członem B za pomocą sprężyn o podatności k = 1·10

-6

m/N. Zakładając, że elementy

C wykonane są ze stali o gęstości ρ = 7,8·10

3

kg/m

3

i mają kształt jednorodnych

prostopadłościanów
o wymiarach a x b x c = 20 x 40 x 50 mm oblicz:

1. prędkość obrotową wału napędzanego ω

0

, przy którym sprzęgło się włączy (ω

2

 > 0);

2. moment M

s

przenoszony przez sprzęgło, gdy nie występują na nim poślizgi, zaś

prędkość obrotowa członu B wynosi ω

1

= 2·ω

0

;

3. maksymalną ilość ciepła jaka może się wydzielić w sprzęgle, jeśli masa

nagrzewających się elementów wynosi m = 10 kg, ciepło właściwe tych elementów
c = 0,6 kJ/kg/K, zaś przyrost temperatury nie może przekroczyć ΔT = 250 K;

4. maksymalny czas pracy sprzęgła jeśli człon napędzający B kręci się ze stałą

prędkością

ω

1

a człon napędzany A zostanie nagle zatrzymany, zaś przyrost temperatury nie może
przekroczyć wartości ΔT.

R

1

 = 119 mm;

R

2

 = 120 mm;

 = 0,4

(wsp.

tarcia
pomiędzy
członem A oraz
elementami C).
Tarcie
pomiędzy
członem B oraz
elementami C
zaniedbać.

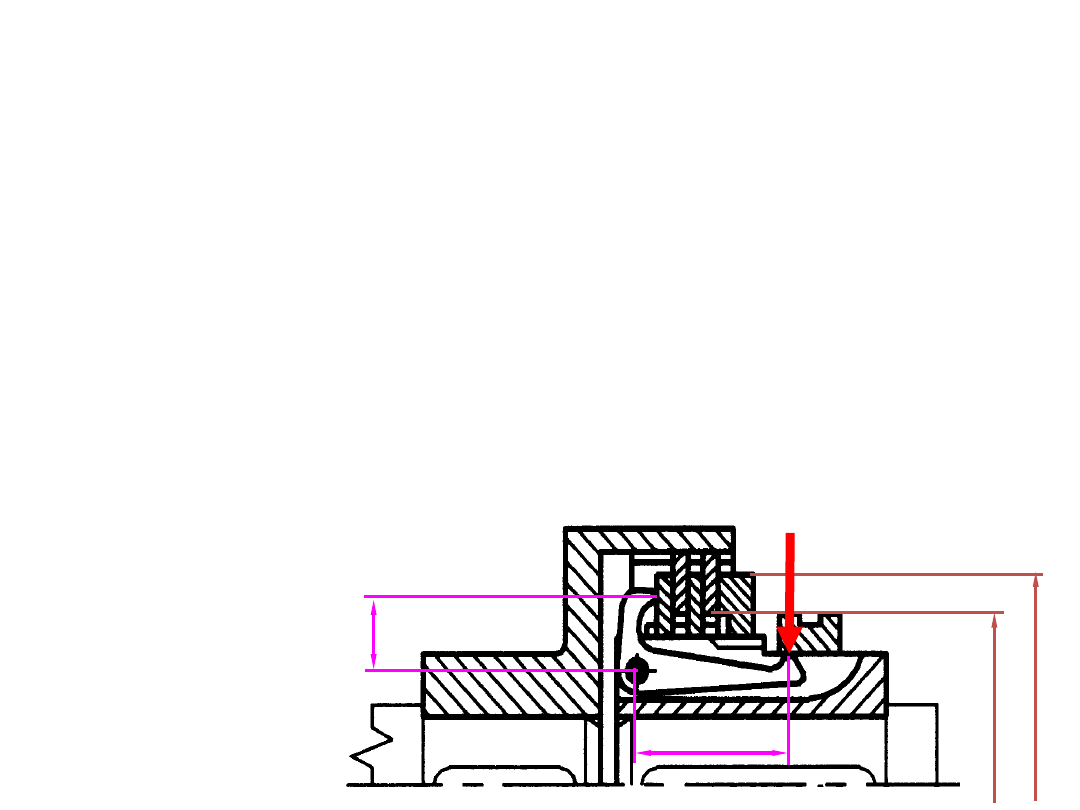
ZADANIE 4:

Pokazane na rysunku sprzęgło wielopłytkowe przeznaczone jest do
przenoszenia mocy N=10 kW przy prędkości obrotowej wału n=600 obr/min.
Zredukowany moment bezwładności członu napędzającego I

1

=0.02 kg·m

2

;

zaś

członu

napędzanego

I

2

=0.5 kg·m

2

. Średnice płytek przyjąć odpowiednio D

w

=80 mm; D

z

=110 mm.

Obliczyć:

1. Maksymalny moment M

s

przenoszony przez sprzęgło przy zerowym

momencie odbieranym.

2. Maksymalną siłę Q wywieraną na każdą dźwignię jeżeli liczba dźwigni

wynosi z=4, liczba płytek zewnętrznych wynosi n=3, zaś współczynnik

tarcia pomiędzy płytkami wynosi μ=0.07. Wymiary dźwigni: a = 20 mm; b

= 70 mm.

3. Maksymalne naciski na płytki p

n

.

4. Przyrost temperatury sprzęgła ΔT w czasie jednego włączenia jeżeli masa

nagrzewających się części wynosi m=1 kg, zaś ciepło właściwe c=0,55

kJ/kg/°C. Pominąć oddawanie ciepła do otoczenia.

D

w

D

z

Q

a

b

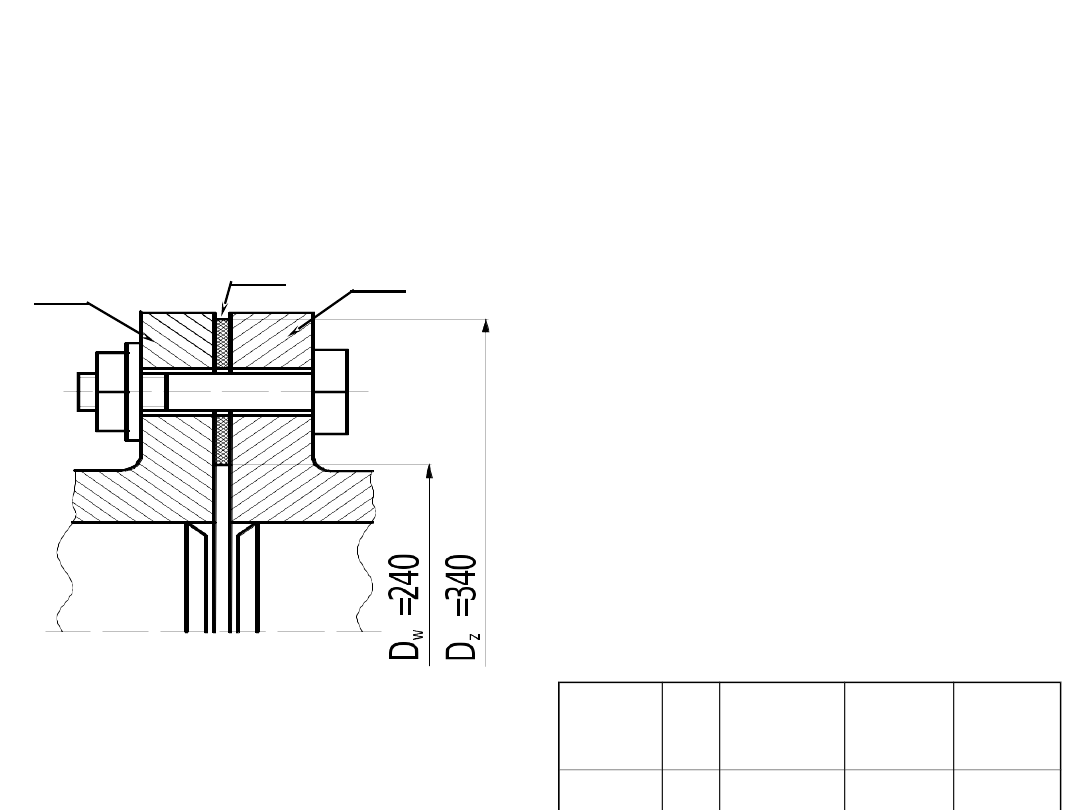
1

2

3

Sprzęgło cierne sztywne składające się z dwóch tarcz (1) i (3) oraz okładziny
ciernej (2) przeznaczone jest do przenoszenia momentu obrotowego
M

0

 = 2000 Nm. Docisk tarcz realizowany jest za pomocą z = 10 śrub M16.

Współczynnik

tarcia

pomiędzy

śrubą

a nakrętką przyjąć

 = 0,15; pomiędzy nakrętką a podkładką 

n

 = 0,1

(przyjąć średnicę tarcia pomiędzy nakrętką a podkładką D

n

 = 24 mm); zaś

pomiędzy tarczą a okładziną



0

 = 0,3. Obliczyć:

1. Naciski p na okładzinie ciernej.
2. Siłę naciągu Q każdej ze śrub.
3. Moment

M

s

,

jakim

należy

dokręcić każdą ze śrub.

4. Naprężenia zredukowane σ

z

w

każdej ze śrub.

5. Narysować wykres siły

rozciągającej oraz momentu
skręcającego w śrubie

ZADANIE 5:

W obliczeniach pominąć
istnienie otworów na śruby.

d = D

P

d

2

 = D

2

d

1

 = 

D

1

d

3

16

2

14,701

13,83

5

13,54

6