Zakład Systemów Elektronicznych i
Telekomunikacyjnych

POLITECHNIKA
RZESZOWSKA

ul. W. Pola 2, 35–959 Rzeszów,

tel.: [phone], w.

1239

Włodzimierz Kalita, Wiesław Sabat – Rok Akad.
2010/2011

Materiały do wykładu

–

tylko do użytku wewnętrznego

(na prawach

rękopisu)

Technika bardzo wielkich częstotliwości

Technika bardzo wielkich częstotliwości

PROPAGACJA

FAL W LINIACH

TRANSMISYJNYCH

Propagacja fal w liniach transmisyjnych

Propagacja fal w liniach transmisyjnych



1

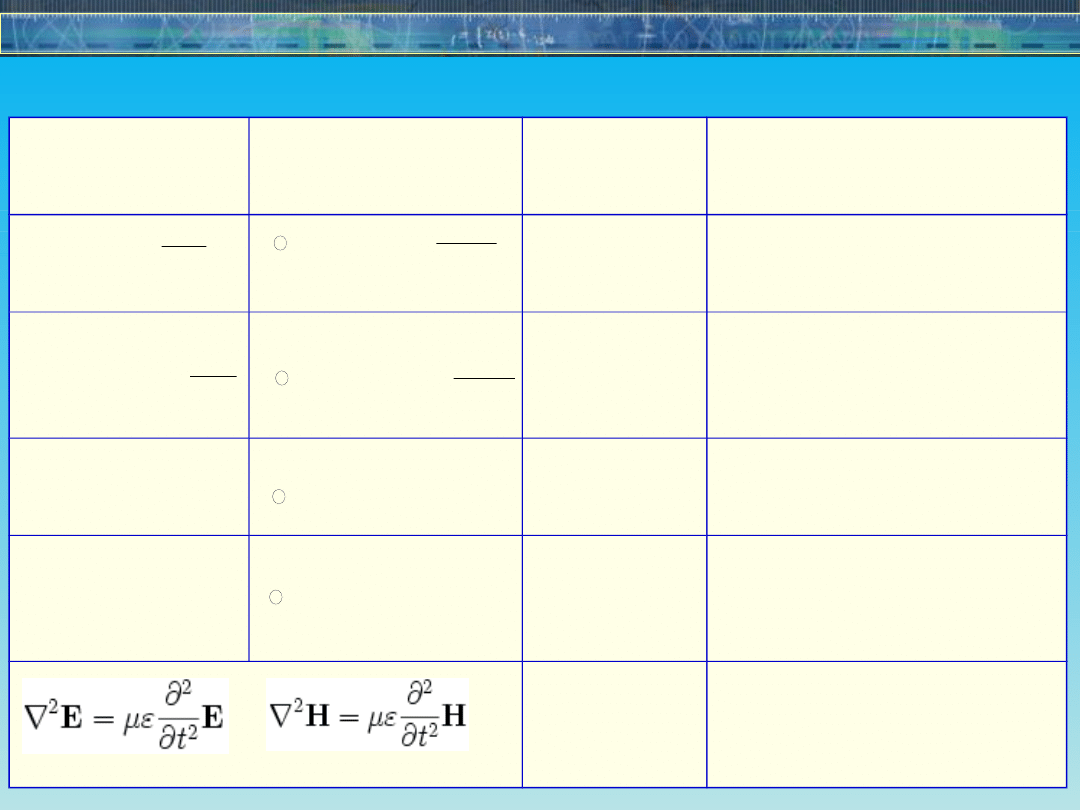
Postać

różniczkowa

Postać całkowa

Prawo

Zjawisko fizyczne

opisywane przez

równanie

Faradaya

Zmienne w czasie pole

magnetyczne wytwarza

wirowe pole elektryczne

Ampère'a

rozszerzone

przez

Maxwella

Przepływający prąd oraz

zmienne pole elektryczne

wytwarzają wirowe pole

magnetyczne

Gaussa dla

elektrycznoś

ci

Źródłem pola elektrycznego

są ładunki

Gaussa dla

magnetyzmu

Pole magnetyczne jest

bezźródłowe, linie pola

magnetycznego są

zamknięte

Równania

Maxwella w

postaci

falowej

Równania liniowe fali

rozcho-dzącej się z

prędkością

1()

-1/2

t

B

E

















t

D

j

H

























 D



0

B 







dt

d

l

d

E

B

L















dt

d

I

l

d

H

D

L



























V

L

dV

s

d

D 



0

s

d

B

S











Równania Maxwella - przypomnienie

Równania Maxwella -

przypomnienie

Propagacja fal w liniach transmisyjnych

Propagacja fal w liniach transmisyjnych

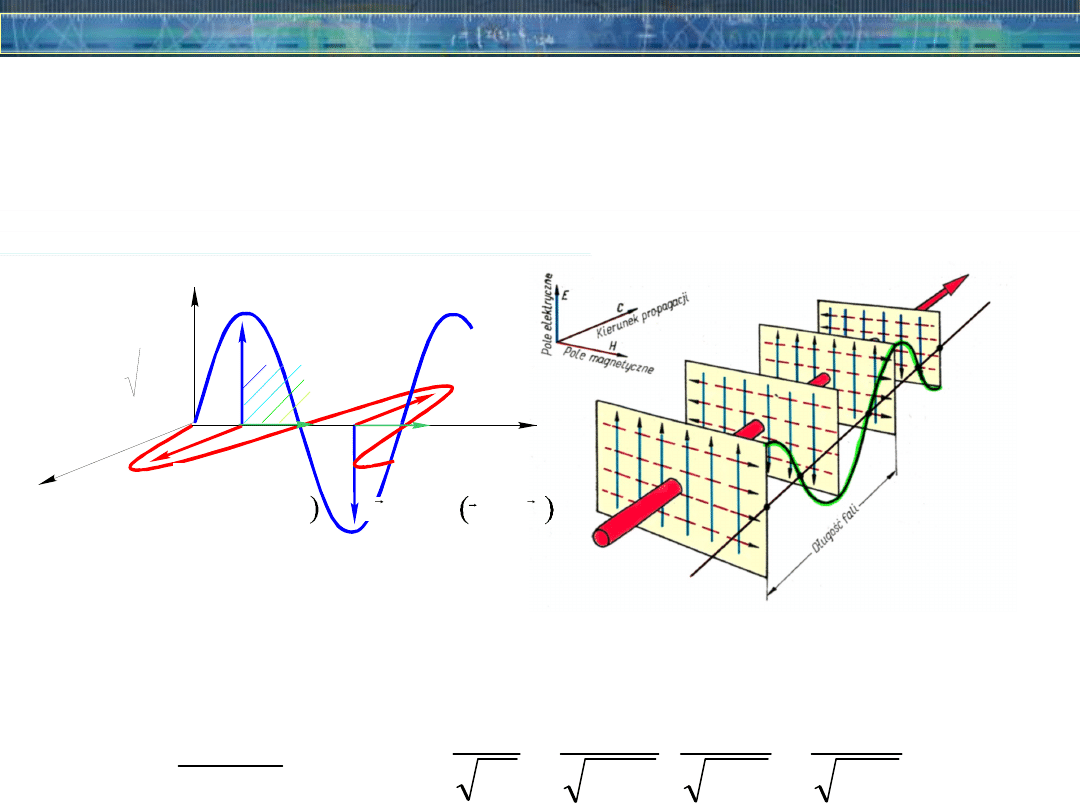
Fala płaska typu TEM – warunki brzegowe

Fala płaska typu TEM – warunki brzegowe





H

a

E

z



















E

a

1

H

z



















f

Z

c

c

z

y

a

a

z

a

d l’

a ’

a

n

n

H

E

d l

+ + +

+ +

z

- a

d l’

z

a

d l

_ _

_

_

_

 

 

y

z

X

E

H

a

z

a

z

H

a

E

z











E

a

1

H

z



















f

Z

Fala - to zaburzenie, które się rozprzestrzenia w ośrodku lub przestrzeni.
Fale przenoszą energię z jednego miejsca do drugiego bez transportu
jakiejkolwiek materii. Rzeczywiste źródła wytwarzają fale kuliste,
cylindryczne lub stanowiące efekt superpozycji. Fala płaska – każda fala w
dużej odległości od źródła, lokalnie (na małym obszarze) posiada czoło w
postaci płaszczyzny (

TEM – Transverse ElectroMagnetic)

.

Fala - to zaburzenie, które się rozprzestrzenia w ośrodku lub przestrzeni.
Fale przenoszą energię z jednego miejsca do drugiego bez transportu
jakiejkolwiek materii.

Rzeczywiste źródła wytwarzają fale kuliste,

cylindryczne lub stanowiące efekt superpozycji.

Fala płaska

– każda fala w

dużej odległości od źródła, lokalnie (na małym obszarze) posiada czoło w
postaci płaszczyzny (

TEM – Transverse ElectroMagnetic)

.

Parametry fali: f - częstotliwość – liczba pełnych drgań na sekundę, T –
okres (czas
trwania jednego drgania), L – długość fali (λ), Vp – prędkość propagacji fali
(zależy od własności ośrodka)  związek Vp i λ (w powietrzu):

Parametry fali:

f

- częstotliwość – liczba pełnych drgań na sekundę,

T

–

okres (czas
trwania jednego drgania),

L

– długość fali (λ),

Vp

– prędkość propagacji fali

(zależy od własności ośrodka)  związek Vp i λ (w powietrzu):

GHz

,

f

30

cm

,





r

r

r

r

o

o

p

c

1

1

1

v























Propagacja fal w liniach transmisyjnych

– linie TEM

– linie TEM

Linia transmisyjna – struktura przenosząca sygnały elektryczne, złożona z

dwóch równoległych przewodników, o długości od kilku milimetrów do
kilku metrów, łącząca elementy i podzespoły systemów wielkiej
częstotliwości.

Linia transmisyjna

– struktura przenosząca sygnały elektryczne, złożona z

dwóch równoległych przewodników, o długości od kilku milimetrów do
kilku metrów, łącząca elementy i podzespoły systemów wielkiej
częstotliwości.

Linie transmisyjne TEM – posiadają tylko składowe pola elektrycznego i

magnetycznego poprzeczne do kierunku propagacji sygnałów w linii.

Linie transmisyjne TEM

– posiadają tylko składowe pola elektrycznego i

magnetycznego poprzeczne do kierunku propagacji sygnałów w linii.

Poprzeczne pole elektryczne E

t

i magnetyczne H

t

w linii transmisyjnej TEM

określają zależności:

Poprzeczne pole elektryczne E

t

i magnetyczne H

t

w linii transmisyjnej TEM

określają zależności:

U

E

t







t

t

E

z

1

H







gdzie

gdzie

r

1

377













Podstawowe parametry charakteryzujące linie transmisyjne:
• Impedancja charakterystyczna (falowa)
• Współczynnik fazy
• Stała tłumienia

Podstawowe parametry charakteryzujące linie transmisyjne:

•

Impedancja charakterystyczna (falowa)

•

Współczynnik fazy

•

Stała tłumienia

 

 

  



0

t

,

z

z

u

t

t

,

z

i

z

L

t

,

z

i

z

R

t

,

z

u



























 







 



0

t

,

z

z

i

t

t

,

z

z

u

z

C

t

,

z

z

u

z

G

t

,

z

i



































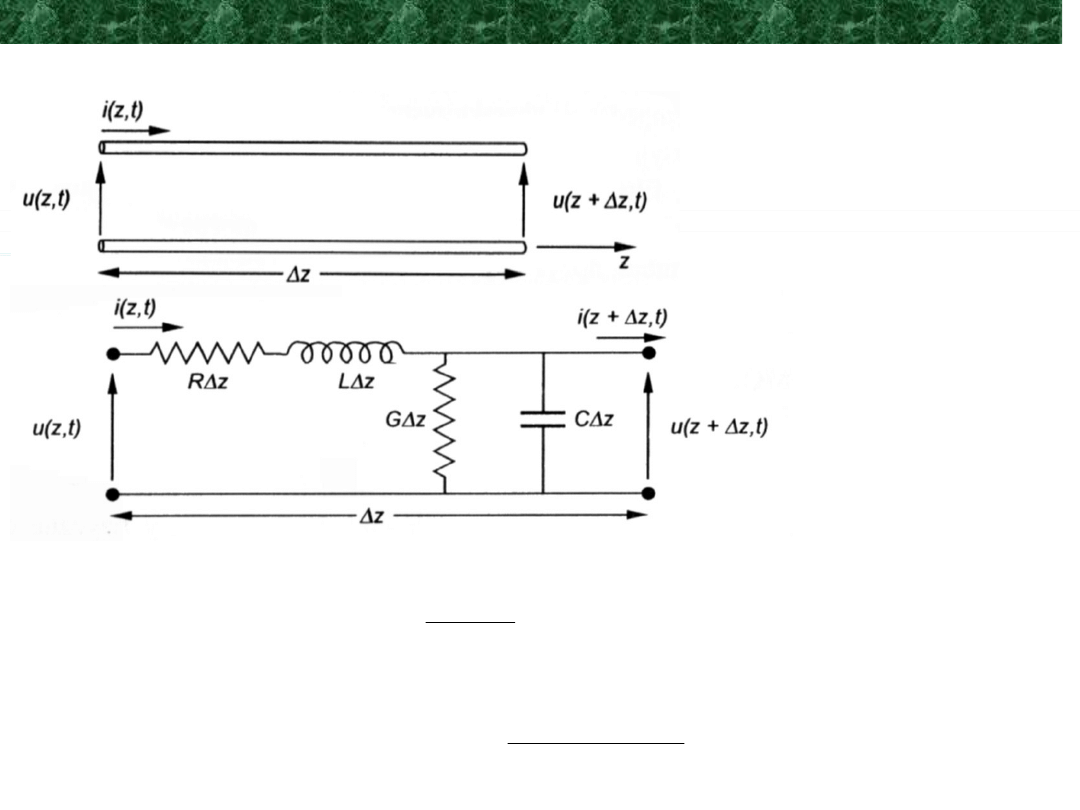
Prawo Kirchoffa dla napięć:

Prawo Kirchoffa dla napięć:

Prawo Kirchoffa dla prądów:

Prawo Kirchoffa dla prądów:

Propagacja fal w liniach transmisyjnych – równania linii

Propagacja fal w liniach transmisyjnych – równania linii

Równania linii transmisyjnej – model o parametrach skupionych

Obwód elektryczny

– rozmiary

mniejsze od

�

,

linia

transmisyjna

(długa) –

rozmiary porównywalne lub
większe od

�

- obwód o

parametrach rozłożonych,

u

oraz

i

zmieniają się wzdłuż

długości –

układ

jednowymiarowy 

kaskadowe połączenie sekcji

z

 

 

 

 

 

 













































t

,

z

u

t

C

t

,

z

u

G

t

,

z

i

z

t

,

z

i

t

L

t

,

z

i

R

t

,

z

u

z

Po podzieleniu obu równań przez z i założeniu, że z0 otrzymujemy:

Po podzieleniu obu równań przez z i założeniu, że z0 otrzymujemy:

Są to równania linii transmisyjnej w dziedzinie czasu – Równania
telegrafistów
Dla napięć i prądów harmonicznych opisanych za pomocą liczb
zespolonych:

Są to równania linii transmisyjnej w dziedzinie czasu –

Równania

telegrafistów

Dla napięć i prądów harmonicznych opisanych za pomocą liczb
zespolonych:

 

   

 

   

























s

,

z

s

s

,

z

dz

d

s

,

z

s

s

,

z

dz

d

U

Y

Z

U

I

I

Propagacja fal w liniach transmisyjnych – równania linii

Propagacja fal w liniach transmisyjnych – równania linii

[u(z+z,t) – u(z,t)]/z 

u(z,t) z

�

/�

[i(z+z,t) – i(z,t)]/z 

i(z,t) z

�

/�

otrzymuje się równania falowe linii długiej:

Z(s)  Z(j) = R +

jL

Y(s)  Y(j) = G + jC

Równania linii długiej (inna forma równań telegrafistów) w postaci:

Równania linii długiej

(inna forma równań telegrafistów)

w postaci:

 

 

 

 

























0

z

I

z

I

dz

d

0

z

U

z

U

dz

d

2

2

2

2

2

2

Stała propagacji fali (współczynnik przenoszenia, tamowność
charakterystyczna) linii (wartość zespolona, uwarunkowana parametrami
fizycznymi linii: R, G, L, C):

Stała propagacji fali

(współczynnik przenoszenia, tamowność

charakterystyczna)

linii

(wartość zespolona, uwarunkowana parametrami

fizycznymi linii: R, G, L, C)

:







C

j

G

L

j

R

j

























LG

RC

j

RG

LC

2

















Rozwiązania równań linii długiej mają postać fal: napięcia i prądu,
prowadzonych w tej linii:

Rozwiązania równań linii długiej mają postać

fal: napięcia i prądu

,

prowadzonych w tej linii:

 

z

0

z

0

e

U

e

U

z

U















 

z

0

z

0

e

I

e

I

z

I















Propagacja fal w liniach transmisyjnych – równania linii

Propagacja fal w liniach transmisyjnych – równania linii

„

+

” – fala poruszająca się w

kierunku +z
„

–

” – fala poruszająca się w

kierunku -z

Propagacja fal w

liniach transmisyjnych - równania linii

liniach transmisyjnych - równania linii

Po przekształceniach:

Po przekształceniach:

 





z

0

z

0

e

U

e

U

L

j

R

z

I





















C

j

G

L

j

R

L

j

R

Z

0



















Zapis uproszczony

Zapis uproszczony

 





z

0

z

0

0

e

U

e

U

Z

1

z

I















gdzie:

gdzie:

Z

0

– impedancja charakterystyczna (falowa) linii transmisyjnej:

Z

0

– impedancja charakterystyczna (

falowa

) linii transmisyjnej:















0

0

0

0

0

I

U

I

U

Z

Długość fali w linii
transmisyjnej

Długość fali w linii
transmisyjnej









2

Prędkość
propagacji

Prędkość
propagacji

f

v

p











Napięcie wzdłuż linii, w dziedzinie czasu:

u(z,t) = U

+

0

e

-z

cos(t-z+

+

) + U

-

0



e

z

cos(t+z+

-

)

Prędkość fazowa

– prędkość

poruszania się punktu styku
czoła fali
ze ścianką, większa niż
prędkość światła (pojęcie
abstrakcyjne);

analogia z

brzegiem morza.

 -

przesunięcie fazy fali

Propagacja fal w liniach transmisyjnych - ró

wnania linii

wnania linii

Linia bezstratna

Linia bezstratna

0

G

,

0

R





LC

,

0

LC

j

j



























Stała propagacji

Stała propagacji

Impedancja falowa

Impedancja falowa

C

L

Z

0



Rozwiązania dla napięcia i prądu bezstratnej linii transmisyjnej:

Rozwiązania dla napięcia i prądu bezstratnej linii transmisyjnej:

 

z

j

0

z

j

0

e

U

e

U

z

U















 

z

j

0

0

z

j

0

0

e

Z

U

e

Z

U

z

I















Długość fali w linii transmisyjnej

Długość fali w linii transmisyjnej









2

Prędkość propagacji

Prędkość propagacji

LC

1

v

p









Propagacja fal w

Równania linii transmisyjnej

Równania linii transmisyjnej

Linia o małych stratach

Linia o małych stratach

C

G

,

L

R









LC

j

C

G

L

R

LC

2

1

j















 













Stała propagacji

Stała propagacji

Impedancja falowa

Impedancja falowa

Długość fali w linii transmisyjnej

Długość fali w linii transmisyjnej









2

Prędkość propagacji

Prędkość propagacji

LC

1

v

p









C

L

Z

0





























 





0

0

GZ

Z

R

2

1

C

G

L

R

LC

2

1

LC







Propagacja fal w liniach transmisyjnych - p

arametry obwodowe linii

arametry obwodowe linii

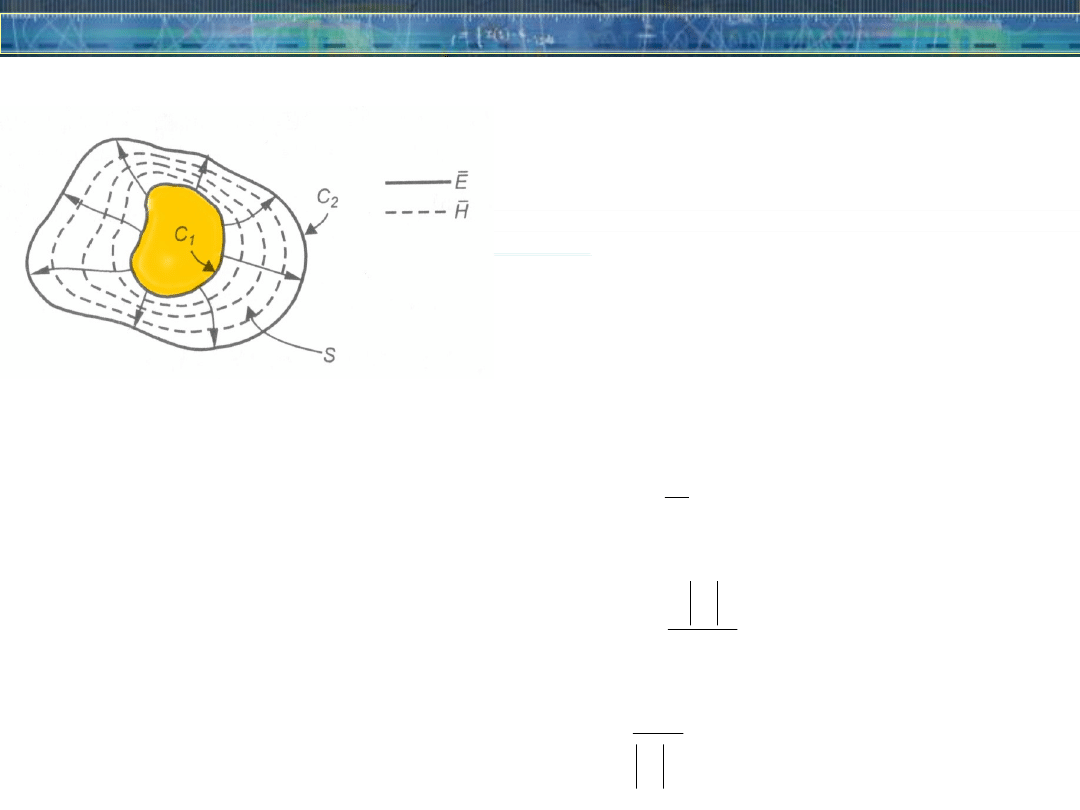
Linie sił pola elektromagnetycznego
w linii TEM

Linie sił pola elektromagnetycznego
w linii TEM

Wg teorii pola
elektromagnetycznego
Średnia w czasie energia
magnetyczna W

m

magazynowana w odcinku linii o
jednostkowej długości ( - operacja

sprzężenia zespolonego)

Wg teorii pola
elektromagnetycznego

Średnia w czasie energia
magnetyczna W

m

magazynowana w odcinku linii o
jednostkowej długości ( - operacja

sprzężenia zespolonego)

Wg teorii obwodów
Energia zmagazynowana w
indukcyjności L

Wg teorii obwodów

Energia zmagazynowana w
indukcyjności L

4

I

L

W

2

0

m











S

m

ds

HH

4

W

Stąd indukcyjność jednostkowa
(własna, na jednostkę długości
linii):

Stąd

indukcyjność jednostkowa

(własna, na jednostkę długości
linii):

m

/

H

,

ds

HH

I

L

S

2

0









Indukcyjność linii
transmisyjnej

Indukcyjność linii
transmisyjnej

Parametry obwodowe linii transmisyjnej

Przekrój poprzeczny linii
transmisyjnej

C1, C2 – droga całkowania po
powierzchni
przewodników linii
S – powierzchnia przekroju
poprzecznego
linii transmisyjnej

Propagacja fal w liniach transmisyjnych - p

arametry obwodowe linii

arametry obwodowe linii

Wg teorii pola
elektromagnetycznego
Średnia w czasie energia elektryczna
magazynowana w odcinku linii
o jednostkowej długości

Wg teorii pola
elektromagnetycznego

Średnia w czasie energia elektryczna
magazynowana w odcinku linii
o jednostkowej długości

Wg teorii obwodów
Energia zmagazynowana w
indukcyjności L

Wg

teorii obwodów

Energia zmagazynowana w
indukcyjności L

4

U

C

W

2

0

e











S

e

ds

EE

4

W

Stąd pojemność jednostkowa:

Stąd

pojemność jednostkowa:

m

/

F

,

ds

EE

U

C

S

2

0









Pojemność linii transmisyjnej

Pojemność linii transmisyjnej

Rezystancja linii
transmisyjnej

Rezystancja linii
transmisyjnej

Wg teorii pola elektromagnetycznego

Moc strat przypadająca na jednostkę
długości linii

(R

s

– powierzchniowa

rezystancja przewodników linii, 

s

– głębokość

wnikania prądu,  - konduktywność)

Wg teorii pola elektromagnetycznego

Moc strat przypadająca na jednostkę
długości linii

(R

s

– powierzchniowa

rezystancja przewodników linii, 

s

– głębokość

wnikania prądu,  - konduktywność)

Wg teorii obwodów
Moc strat w jednostkowej rezystancji szeregowej

Wg teorii obwodów

Moc strat w jednostkowej rezystancji szeregowej









2

1

C

C

s

c

ds

HH

4

R

P

2

I

R

P

2

0

c



Stąd rezystancja jednostkowa:

Stąd

rezystancja jednostkowa:

m

/

,

ds

HH

I

R

R

2

1

C

C

2

0

s











s

s

1

R





Konduktancja strat linii transmisyjnej

Konduktancja strat linii transmisyjnej

Wg teorii pola elektromagnetycznego

Średnia w czasie moc strat w
dielektryku
wypełniającym linię transmisyjną,
przypadająca na jednostkę długości;
” – urojona część zespolonej

przenikalności elektrycznej  = ’ - j”

= ’(1 – j tg)

Wg teorii pola elektromagnetycznego

Średnia w czasie moc strat w
dielektryku
wypełniającym linię transmisyjną,
przypadająca na jednostkę długości;
” – urojona część zespolonej

przenikalności elektrycznej  = ’ - j”

= ’(1 – j tg)

Wg teorii obwodów
Średnia w czasie moc strat w
dielektryku

Wg teorii obwodów

Średnia w czasie moc strat w
dielektryku









S

"

d

ds

EE

2

P

2

U

G

P

2

0

d



Stąd równoległa konduktancja
jednostkowa strat:

Stąd

równoległa konduktancja

jednostkowa strat:

m

/

S

,

ds

EE

U

G

S

2

0

"









Propagacja fal w liniach transmisyjnych - p

arametry obwodowe linii

arametry obwodowe linii

Propagacja fal w liniach transmisyjnych -

Struktury transmisyjne

Struktury transmisyjne

Struktury transmisyjne - najczęściej stosowane w technice
mikrofalowej

Struktury transmisyjne -

najczęściej stosowane w technice

mikrofalowej

Linie TEM

Struktury

planarne

Falowody metalowe i

dielektryczne

•

Linia współosiowa

•

Symetryczna linia

paskowa

•

Linia symetryczna

•

Linia symetryczna

ekranowana

•

Drut nad płaszczyzną

przewodzącą

•

Linia

mikropaskowa

•

Linia szczelinowa

•

Falowód

koplanarny

•

Koplanarne paski

•

Falowód metalowy

prostokatny

•

Falowód metalowy

kołowy

•

Falowód dielektryczny