PROPAGACJA FAL

ELEKTROMAGNETYCZNYC

H

W ATMOSFERZE

Całokształt zjawisk związanych z rozchodzeniem się fali

elektromagnetycznej w jakimś ośrodku, nazywamy propagacją. W
interesującym

nas

przypadku

- w powietrzu. Ośrodek ten oddziałuje w różny sposób na falę
elektromagnetyczną, w zależności od długości fali oraz od jego składu
i

stanu

fizycznego.

Do

najważniejszych wpływów tego ośrodka na rozchodzącą się w nim falę
elektro-
magnetyczną należą:

1) zmiany prędkości fali,
2) zakrzywienie toru fali,
3) zmiany wiązki promieniowania wywołane turbulencją powietrza

(tylko w zakresie

optycznym),
4) rozpraszanie i absorpcja promieniowania.
Pomiar

odległości

wykonujemy

za

pośrednictwem

fal

elektromagnetycznych, więc wszystkie te zjawiska w większym lub
mniejszym stopniu wpływają na wynik pomiaru odległości, oraz zasięg
pomiaru.

Propagacji fal elektromagnetycznych w zakresie mikrofalowym

mogą towarzyszyć również zjawiska wywołane stycznością wiązki
mikrofal

z

powierzchniami

obiektów leżących na trasie jej przelotu; są to głównie:

a) ugięcie fali nośnej na przeszkodach,
b) odbicie fali od powierzchni terenu.

Prędkość rozchodzenia się fal elektromagnetycznych w próżni jest
dla całego widma promieniowania elektromagnetycznego jednakowa
i stanowi uniwersalną stałą fizyczną c. Aktualnie obowiązująca w
geodezji wartość liczbowa stałej c została zalecona przez
Międzynarodową Asocjacje Geodezyjną i wynosi:

c= 299 792 4581,2 m/s

Prędkość rozchodzenia się fali w danym ośrodku określa się wzorem

n

c

v

t

t

o

o

















1

1

gdzie:


o

, 

o –

przenikalność elektryczna i magnetyczna próżni



t

, 

t

– względne przenikalności ośrodka

c – prędkość fali elektromagnetycznej w próżni
n – współczynnik refrakcji atmosfery

Prędkość rozchodzenia się fal elektromagnetycznych w powietrzu
zależy głównie od trzech parametrów meteorologicznych: t, p, e
ośrodka oraz od długości  fali nośnej. Zależność ta wyraża się

ogólnie poprzez współczynnik załamania (refrakcji)

)

,

,

,

(



e

p

t

f

n

v

v

g

d

dv

v

v













v

d

dv





0



v

d

dv





Prędkość danej fali monochromatycznej jest identyfikowana z
prędkością rozchodzenia się fazy i dlatego nazywana jest prędkością
fazowa 



. Sygnał pomiarowy wytworzony poprzez modulacją fali

nośnej stanowi grupę fal monochromatycznych rozchodzącymi się w
powietrzu z różnymi prędkościami fazowymi, natomiast ten sam
sygnał rozchodzi się w tymże ośrodku z prędkością grupowa v

g

.

Wielkości tej nie można utożsamiać ze średnią prędkością fazową dla
całej grupy fal. Zjawisko to zwane jest dyspersją, a ośrodek w którym
ono zachodzi – ośrodkiem dyspersyjnym. Związek między prędkością
grupowa a prędkością fazową określony jest wzorem Rayleigha.

charakterystyka dyspersyjna
ośrodka

charakterystyka dyspersyjna
próżni

Dlatego w próżni

c

v

v

g







Z pojęciem prędkości fazowej i grupowej wiążą się pojęcia
fazowego

współczynnika

załamania

n



oraz

grupowego

współczynnika załamania n

g

. Ta ostatnią wielkość wyraża się

wzorem













d

dn

n

n

g





Dla próżni n

g

= n



=1

Zależność fazowego współczynnika załamania od długości fali
wyraża się wzorem Cauchy’ego

4

2

1

v

v

C

B

A

n















Po zróżniczkowaniu według zmiennej  oraz podstawieniu, wzór na n

g

otrzymuje postać

4

2

5

3

1

v

v

g

C

B

A

n













Gdzie A, B, C – współczynniki dyspersji fali
elektromagnetycznej dla powietrza

Jak widzimy, dwa ostatnie człony prawej strony w

z

oru mogą mieć

istotne znaczenie tylko dla małych wartości v. W praktyce, jako

wielkość graniczną przyjmuje się 

v

=1 cm, powyżej której zjawisko

dyspersji nie wywiera istotnego wpływu na wartość v.

.

W związku z

tym grupowy współczynnik załamania wyznacza się tylko w przypadku
stosowania fali lub grupy fal o długościach v  l cm, a więc dla

milimetrowych fal radiowych i dla fal z zakresu optycznego.
Natomiast dla mikrofal o długościach v> l cm wpływ dyspersji jest

praktycznie niewyczuwalny i z tego względu dla tego zakresu
przyjmuje się v

g

=v



.

W związku z powyższym do wyznaczania fazowego i grupowego
współczynnika załamania stosuje się odrębne wzory matematyczne.

Współczynnik refrakcji mikrofal

W zakresie mikrofalowym, z wyjątkiem częstotliwości bliskich 60 i 22
GHz, współczynnik refrakcji atmosferycznej nie zależy od długości fali,
a jedynie od temperatury, ciśnienia i wilgotności atmosfery. Zależność
tę opisują empiryczne wzory Essena,. Smitha-Weintrauba oraz Essena-
Frooma. Międzynarodowa Unia Geodezji i Geofizyki IUGG zaleciła w
1960 r. zastosowanie wzoru Essena-Frooma. Ma on postać:

e

T

T

e

p

T

n

N

)

5748

1

(

70

.

64

)

(

624

.

77

10

)

1

(

6













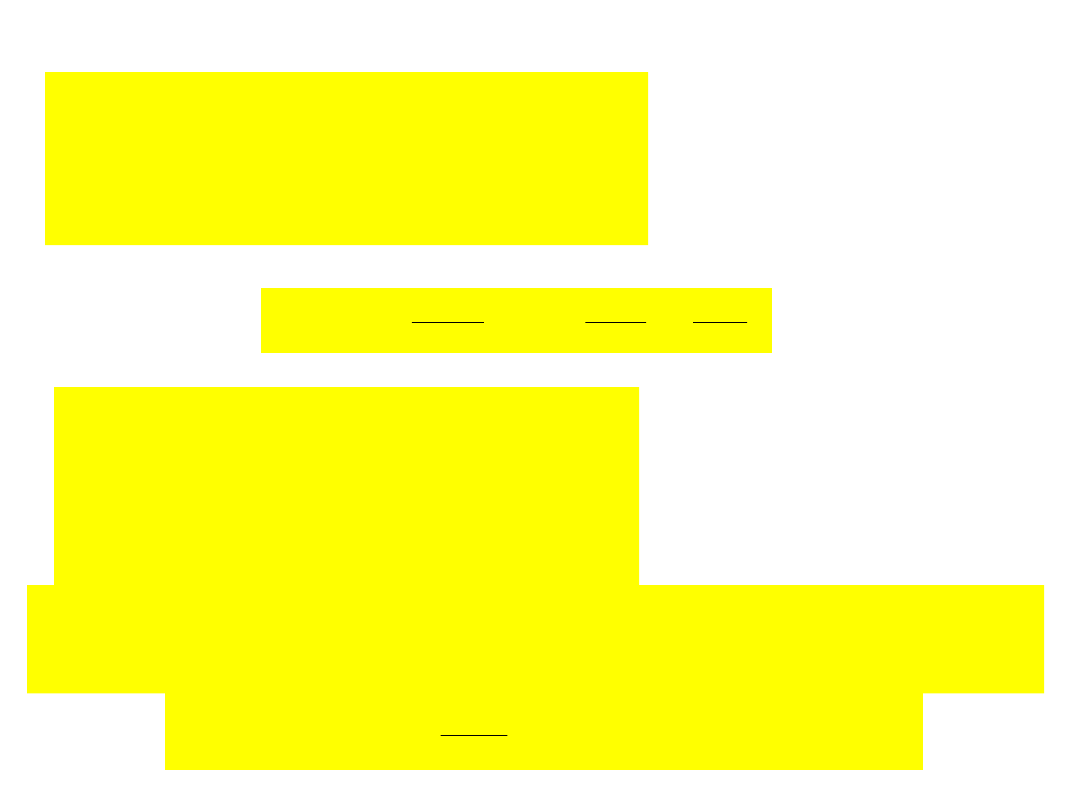
n = 1+N x 10

-6

– współczynnik refrakcji

T – temperatura powietrza wK

P – ciśnienie atmosferyczne w hPa
e – cząstkowa prężność pary wodnej hPa
Można też spotkać ten wzór w postaci:

e

T

T

e

p

T

n

)

5748

1

(

26

,

86

)

(

49

,

103

10

)

1

(

6













gdzie
n = 1+N x 10

-6

– współczynnik refrakcji

T – temperatura powietrza wK

P – ciśnienie atmosferyczne w mm Hg
e – cząstkowa prężność pary wodnej w
mmHg

Prężność pary wodnej e jest określana w praktyce pomiarowej poprzez
pomiar temperatury suchego t i zwilżonego t

’

, termometru w

psychrometrze aspiracyjnym

)

(

10

67

.

0

)

(

)

8

.

827

1

(

10

67

.

0

'

3

'

'

'

3

'

t

t

p

e

t

t

p

t

e

e























gdzie:
t i t

’

– temperatura suchego i zwilżonego termometru w C

e

’

– prężność pary nasyconej w temperaturze t

’

(z tablic)

p, e

– w jednakowych jednostkach

Współczynnik refrakcji fal optycznych

Podobnie jak dla mikrofal MUGG zaleciła stosowanie współczynników
Barella i Searsa. Dla suchego powietrza o:
temperaturze 0C (273.15°K),

ciśnieniu 760 mm Hg (1013.25 hPa)
zawartości CO

2

0.03%

 - wyrażono w m.

4

2

6

068

.

0

8864

.

4

604

.

287

10

)

1

(















go

go

n

N

Dla dowolnych warunków meteorologicznych współczynnik

refrakcji według wzoru Barrela i Searsa ma postać:
gdzie T wyrażono w K, e i p w hPa

T

e

T

p

N

n

N

g

g

g

27

.

11

2696

.

0

10

)

1

(

0

6











Jest stosowany wzór równoważny

T

e

T

p

N

n

N

g

g

g

02

.

15

3594

.

0

10

)

1

(

0

6











gdzie: T wyrażono w K, e i p w mm Hg:

W literaturze można spotkać inną postać

tego wzoru:









e

t

p

t

n

n

g

g

























1

10

55

760

1

1

1

9

0

Dokładność wyznaczania współczynnika

załamania z pomiarów meteorologicznych

Z powyższego wzoru wynika że błąd średni m

D

wyznaczenia

współczynnika
załamania wywiera poważny wpływ na dokładność pomiaru
odległości D dalmierzami elektronicznymi.
Wartość m

n

można ocenić jako błąd średni funkcji niezależnych

parametrów
meteorologicznych: t, p, e, która to funkcja dana jest jednym z
wzorów, np:

2

2

































m

n

m

D

m

n

D

e

T

T

e

p

T

n

)

5748

1

(

26

,

86

)

(

49

,

103

10

)

1

(

6













Skorzystamy tu z ogólnego wzoru na błąd średni funkcji

2

2

2

2

2

2

2

e

p

t

n

m

e

n

m

p

n

m

T

n

m























































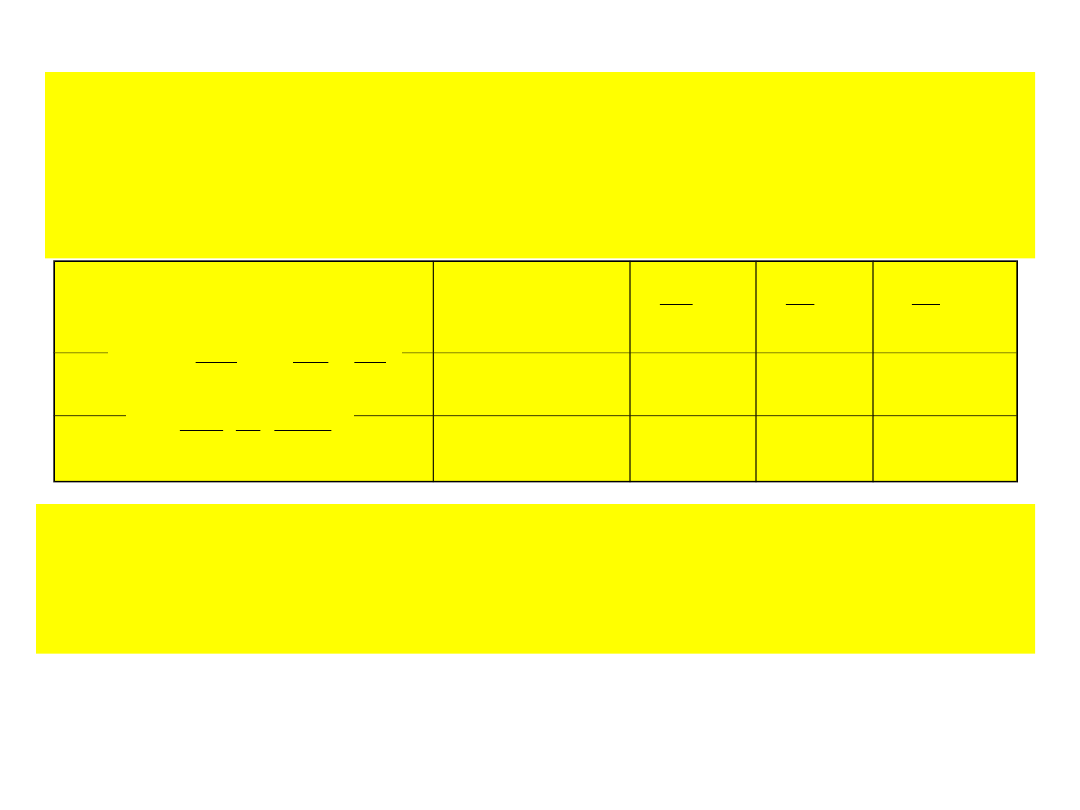
gdzie
m

t

— błąd średni temperatury w °C,

m

p

— błąd średni ciśnienia powietrza w mm sł. rtęci,

m

e

— błąd średni cząstkowego ciśnienia pary wodnej w powietrzu w

mm sł. rtęci.

Wzór

Rodzaj fali

elektromagnety

cznej

mikrofale



w

>1 cm

1.0 x 10

-4

0.4 x 10

-

4

6.6 x 10

-6

światło



w

0.54m

0.9x10

-6

0.4x10

-6

0.06 x10

-6

t

m

T

n





p

m

p

n





e

m

e

n





e

T

T

e

p

T

n

)

5748

1

(

26

,

86

)

(

49

,

103

10

)

1

(

6





















e

t

p

t

n

n

g

g

























1

10

55

760

1

1

1

9

0

Wartości w tabeli obliczono przy następujących założeniach:
t=20°C,

m

t

=m

T

=±l°C

p=760 mm sł. rt.,

m

p

= l mm sł. rt.

e=10 mm sł. rt.,

Z porównania odpowiednich danych zawartych w tabeli wynika, że

taka sama niedokładność określenia temperatury i ciśnienia wywiera w
przybliżeniu

taki

sam

wpływ na odległość mierzoną dalmierzem mikrofalowym, jak
dalmierzem elektrooptycznym. Natomiast ten sam błąd w określeniu
wilgotności e ma przy pomiarze dalmierzem mikrofalowym 100-krotnie
większy wpływ niż w pomiarze dalmierzem elektrooptycznym.

Powyższe rozważania i wnioski dotyczą tylko zależności funkcyjnych

współ-
czynnika

n

od

błędów

średnich

wyznaczania

parametrów

meteorologicznych.

W

praktyce wartości tych błędów są niewielkie i wynoszą średnio:
mt=±0.1°C
(pomiar termometrem rtęciowym), mp=+0,1 mm sł. rtęci (pomiar
aneroidem),
me=±0,l mm sł. rtęci (z pomiarów wykonanych psychrometrem
aspiracyjnym
Assmanna).

O wiele większy wpływ na wartość n ma niejednorodność atmosfery na

trasie

x

przelotu sygnałów pomiarowych, z powodu której wartości parametrów
meteorologicznych na tejże trasie, t

x

, p

x

, e

x

, zmieniają się od punktu do

punktu.

W

związku

z tym dane meteorologiczne pomierzone w dyskretnych punktach trasy
x

nie

będą

reprezentatywne dla całej odległości D.

W ogólnym przypadku, atmosferę niejednorodną na trasie przelotu
sygnałów
można przedstawić jako szereg ściśle przylegających do siebie
nieskończenie cienkich warstewek powietrza o grubości dx i
współczynniku załamania n(x) , gdzie

n(x)

=

f(t

x

, p

x

, e

x

)

jest funkcją ciągłą reprezentującą rozkład wartości n na linii
mierzonej odległości D.
Droga D przebyta przez sygnał pomiarowy będzie jednak równa
drodze wyrażonej wzorem

jeżeli przyjmiemy, że występująca w nim wartość n jest równa
średniej wartości określonej wzorem









n

c

D

2

1









D

x

x

dx

x

n

D

n

0

)

(

1



Ponieważ funkcja n(x) jest na ogół nieznana, więc średnią wartość
n

wyznacza

się z pomiarów wielkości t

x

, p

x

, e

x

, wykonanych w k punktach

odcinka

D.

Wtedy

wzór ścisły zastępujemy wzorem przybliżonym

)

,.....,

2

,

1

(

1

1

k

i

n

k

n

k

i

i

i

























Gdy wartości n, wyznaczone są w trzech punktach odcinka D, tj. na
jego końcach l i 2 oraz w środku 3, zaleca się stosowanie ogólnej
średniej





3

2

1

4

6

1

n

n

n

n









W praktyce pomiary meteorologiczne wykonywane są najczęściej
tylko na końcach mierzonego odcinka D, a wartość n wyznaczana
jest według wzoru:

)

(

2

1

2

1

n

n

n







Zależność współczynnika załamania od
wysokości

Przy mniejszych wymaganiach dokładnościowych można wyznaczać
współczynnik załamania jako funkcję średniej wysokości mierzonego
odcinka nad poziomem morza. Metoda ta opiera się na założeniu, że
zmiany warunków meteorologicznych następują wraz z wysokością, na
ogół bowiem ze wzrostem wysokości maleje temperatura powietrza,
ciśnienie

i

wilgotność.

Przeciętne

warunki

meteorologiczne

reprezentowane są przy tym przez atmosferę standardową, określoną
przez konwencję międzynarodową. W atmosferze tej parametry
meteorologiczne określone są jako następujące funkcje wysokości h nad
poziomem morza

h

T

T







0



















h

g

g

dT

dh

R

M

p

p

0

0

exp





6

0

064

,

0

1

h

e

e





h w km ( h  10 km )

T

0

= 288,15 K

– temperatura powietrza na poziomie

morza

P

0

= 1013,25 hPa

– ciśnienie powietrza na poziomie

morza

e

0

– prężność pary wodnej na poziomie

morza

 = dT/dh

– pionowy gradient temperatury

M

g

= 28,9 kg/kmol

– masa molowa powietrza (przy

g=9,80665 m/s

2

)

R

g

=8,31436 x 10

3

J/kmol

– uniwersalna stała gazowa

W atmosferze standardowej gradient temperatury
wynosi:

km

K

km

K

km

K

1

0

5

,

6















dla h od 0 do 10 km

dla h od 11 do 20 km

dla h od 20 do 30 km

Gradient ciśnienia dla niewielkich wysokości wynosi w

przybliżeniu

m

hPa

dh

dp

/

12

,

0



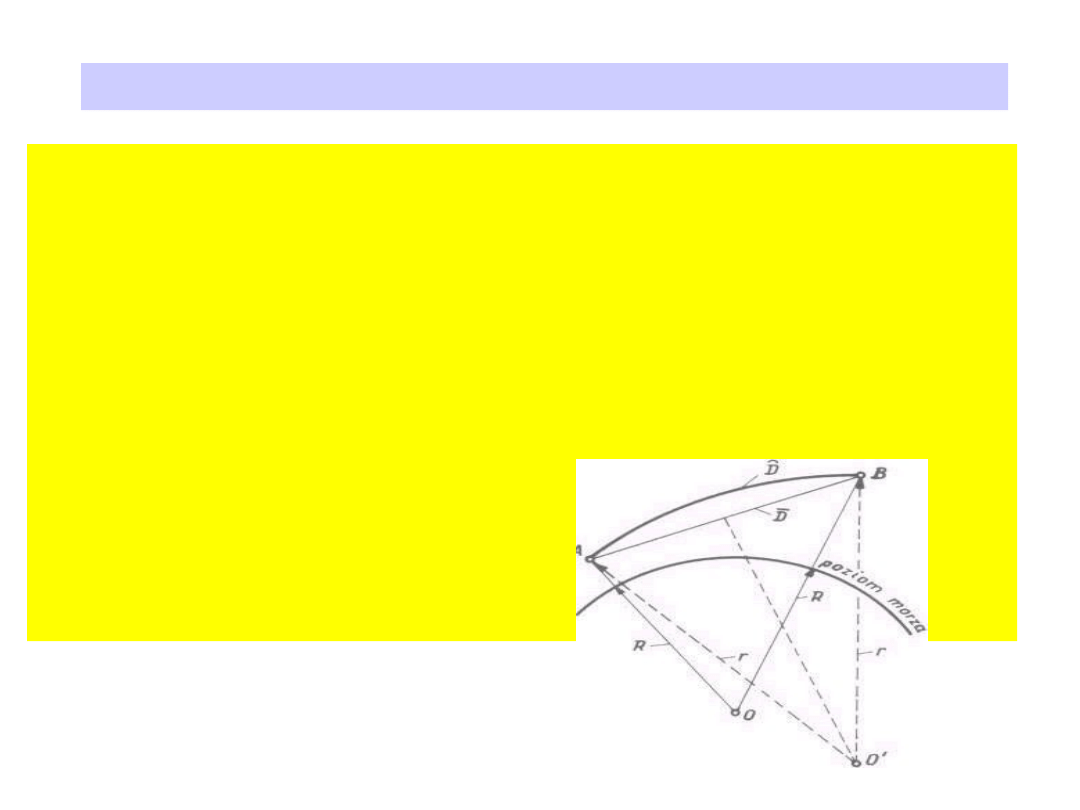
Tor fali elektromagnetycznej w atmosferze

Posłużymy się tu uproszczonym modelem atmosfery ziemskiej
zakładając,

że

atmosfera ta składa się z wielu koncentrycznie ułożonych cienkich
warstw powietrza, w przybliżeniu sferoidalnych. W modelu tym każdej
takiej warstwie przypisuje się pewien stały współczynnik załamania
oraz zakłada się, że wartość tego współczynnika zmienia się od
warstwy do warstwy wraz z wysokością. Fala biegnąca w takiej
atmosferze od punktu A do punktu B przebywa swą drogę po pewnej
krzywej, która w płaszczyźnie pionowej zbliżona jest do koła o
średnim promieniu r. Tak więc wielkością mierzoną jest długość łuku
AB, którego cięciwa stanowi odległość poszukiwaną AB = D (rys)
Przy normalnych warunkach atmosferycznych przyjmuje się:
dla fal optycznych r = 8R
dla mikrofal r = 4R,
gdzie R oznacza promień Ziemi.

Przeliczenie długości łuku AB

=

D, który jest faktycznie mierzony,

na

długość

cięciwy AB

=

D, która jest poszukiwaną odległością D, odbywa się

według wzoru

2

3

24r

D

D

D









D [km]

20

0 mm

30

2 mm

50

8 mm

100

70 mm

2

3

24r

D

Dla fal świetlnych poprawki takie są oczywiście o wiele
mniejsze

Tłumienie energii fali elektromagnetycznej w

atmosferze

Energia sygnału pomiarowego ulega w atmosferze tłumieniu,
które powodowane jest przez dwa zjawiska fizyczne:
— absorpcję energii fali przez poszczególne składniki atmosfery,
— rozpraszanie przez cząstki materialne (np. kropelki wody,
igiełki

lodu,

pyły,

dymy i molekuły związków chemicznych).
Straty mocy sygnału elektromagnetycznego zależą od składu
fizycznego atmosfery, od długości drogi D przebytej przez sygnał
oraz

od

długości

fali nośnej.
Wartość transmisji dla zakresu fal optycznych jest bardzo
zróżnicowana.
Można tu wyodrębnić szereg pasm falowych, dla których
przepuszczanie

promieni

świetlnych jest znacznie lepsze niż dla pozostałych części widma.
Tego

rodzaju

„okna" atmosferyczne leżą m.in. w pasmach: 0,5—0,9 m, 1,0—

1,1

m,

1,2—1,3 m. Wraz ze wzrostem wysokości tłumienie światła

maleje i przy wysokościach ok. 60—70 km można go już nie brać
pod uwagę.
W przyziemnej warstwie atmosfery (do wysokości 10—12 km) fale
optyczne
pochłaniane są głównie przez cząsteczki pary wodnej i dwutlenku
węgla. Na wysokościach ok. 30 km składnikiem silnie
absorbującym jest ozon.

Druga przyczyna tłumienia — rozpraszanie — zależy silnie od
długości

fali

nośnej . W zależności od wymiaru d (średnicy) cząstek,

rozróżniane są trzy typy rozpraszania.
Pierwszy typ to rozpraszanie typu Rayleigha, które następuje na
cząstkach

o

średnicy d  0,2v. Jest to tzw. dyspersja molekularna

wywoływana przez oddziaływanie fali świetlnej (fotonów) z
cząstkami

gazów

zawartych

w

atmosferze.

Tłumienie

pochodzące od tego zjawiska zachodzi nawet w zupełnie
czystym powietrzu i może być dla widzialnej części widma
znacznie silniejsze niż absorpcja. Natomiast dla podczerwieni
rozpraszanie molekularne jest bardzo słabe.
Drugi typ — rozpraszanie Mie’go — zachodzi na tzw. aerozolach
(mgła,

pyły),

których średnice zawarte są w przedziale: 0,2  d  5.

Tłumienie zależy silnie od wielkości cząstek i stopnia
koncentracji zawiesin.
Trzeci typ – rozpraszanie geometryczne – występuje przy
cząstkach o wymiarach d > 5 (deszcz, śnieg, grad, owady) i nie

zależy od .

W zakresie mikrofal tłumienie absorpcyjne jest bardzo małe.
Mikrofale rozpraszają się na cząstkach opadowych (deszcz,
śnieg, grad)

Wpływ turbulencji atmosferycznej

Składowa turbulentna ruchu powietrza charakteryzuje się fluktuacją jego

parametrów, a zmienność prędkości ma charakter pulsacji o okresie od 2
godzin do 1 sek. Fluktuacje te występują na skutek nieregularności
wymiany energii i pędu miedzy warstwami powietrza na różnych
poziomach, zachodzącej za pośrednictwem tzw. elementów turbulencyjnych
(turbulentów). Elementami tymi są wiry powietrza, które na skutek jego
lepkości rozbijają się — po przekroczeniu prędkości krytycznej — na
mniejsze wiry o zmniejszonej prędkości. Proces rozkładu na coraz to
mniejsze wiry o coraz to mniejszych prędkościach toczy się do chwili, gdy
wiry pochodne osiągną prędkość mniejsza od prędkości krytycznej.
Maksymalne wymiary wirów wynoszą od 1 do 100 m, minimalne zaś od 1do
10 mm. Turbulencja atmosfery powoduje oczywiście fluktuacje wartości
współczynnika załamania. Gdy przekrój wiązki fali jest mniejszy od
wymiaru wiru, to cala wiązka doznaje jednakowego załamania (zmiany
prędkości v), a czoło fali nie ulega deformacjom. W przeciwnym przypadku
następuje zniekształcenie czoła fali. Przejściu fali elektromagnetycznej
przez

atmosferę

turbulentna

mogą

towarzyszyć

następujące

zniekształcenia:
- fluktuacja amplitudy i fazy,
- zakłócenie przestrzennej spójności czoła fali,
- kątowe rozszerzenie przekroju wiązki fali (efekt scyntylacji),
- fluktuacja kąta odbioru fali (efekt migotania)
Wszystkie te zniekształcenia wpływają na jakość odbieranych sygnałów
pomiarowych i w konsekwencji — na dokładność pomiarów odległości i
ograniczają zasięg dalmierzy.