Ćwiczenie 2
Temat:
I. Obliczanie przepływów
charakterystycznych.
II. Projektowanie nowej trasy i przekroju
poprzecznego cieku.
I.Obliczanie przepływów charakterystycznych
Przepływ
(natężenie przepływu) – ilość (objętość)
wody przepływającej w danym miejscu w jednostce
czasu. Symbol „
Q”
(m
3.
s
-1
)
Metody określania przepływów charakterystycznych:
- metody bezpośrednie,
- metody pośrednie (metody analogii
hydrologicznej),
- metody empiryczne.
Metody empiryczne
Wzory
Iszkowskiego
:
Q
S
=
SQ = 0,03171 C
S
●
P
●
A
(m
-3
·s
-1
)
Q
S
- przepływ średni, przepływ teoretyczny służący do wyznaczenia
trzech charakterystycznych niskich przepływów:
Q
O
,
Q
1
,
Q
2
;
C
S
- współczynnik odpływu dla całej zlewni
P
- opad roczny w zlewni [m],
A
- powierzchnia zlewni [km
2
]
Q
O
=
NNQ
= 0,2
●
ν
●
Q
S
(m
-3
·s
-1
)
Q
O
- przepływ absolutnie najniższy z okresu obserwacyjnego minimum
20-letniego
ν
- („ni”) – współczynnik uzależniony od zdolności retencyjnej zlewni;
Q
1
=
SNQ
= 0,4
●
ν
●
SQ
(m
-3
·s
-1
)
Q
1
- przepływ średni niski, średni z najmniejszych corocznych z okresu
min. 20-letniego
Q
2
=
ZQ = 0,7
●
ν
●
Q
S
(m
-3
·s
-1
)
Q
2
- przepływ średni normalny, odpowiada przepływowi z około 270
dni w ciągu roku
Q
4
= WWQ = C
w
●
m
●
P
●
A
(m
-3
·s
-1
)
Q
4
- przepływ katastrofalny (najwyższy wielki przepływ z okresu min.
20-letniego)
C
w
- współczynnik uwzględniający urzeźbienie terenu i
przepuszczalność gleby w zlewni,
m
- współczynnik zależny od wielkości zlewni,
P
- opad roczny w zlewni [m],
A
- powierzchnia zlewni [km
2
]
Q
3L
=
WQ
L
= 0,2
●
Q
4
(m
-3
·s
-1
)
Q
3L
- wielki przepływ wody letniej
Q
3Z
= WQ
Z
= 0,4
●
Q
4
(m
-3
·s
-1
)
Q
3L
- wielki przepływ wody zimowej
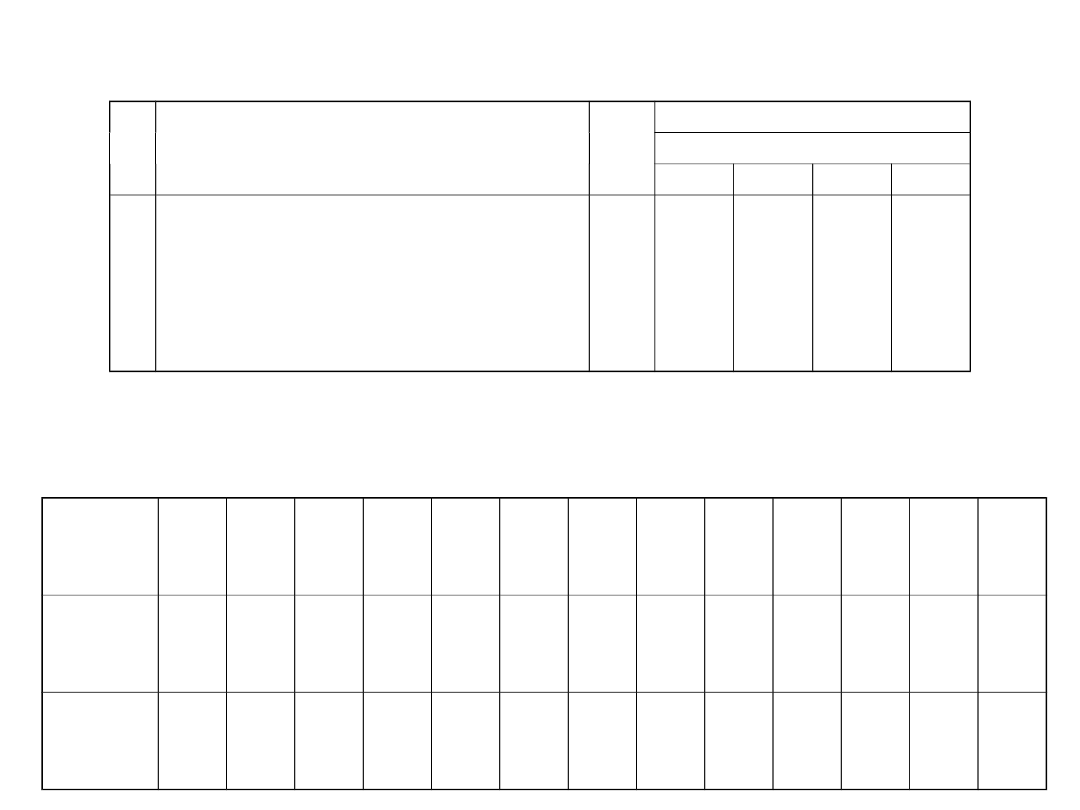
C
W
Lp
Rzeźba terenu
C
S
Kategoria zlewni
I
II
III
IV
1.
2.
3.
4.
5.
6.
Bagna i niziny
Płaszczyzny i płaskowzgórza
Płaszczyzny połączone z pagórkami
Pagórki o łagodnych stokach
Pagórki bardziej strome i podgórza
Wzgórza i wyskoki większych pasm
górskich
0,20
0,25
0,30
0,35
0,40
0,45
0,019
0,025
0,029
0,034
0,039
0,045
0,030
0,043
0,055
0,067
0,079
0,100
--
--
--
0,124
0,160
0,200
--
--
--
--
0,390
0,440
Tabela 1.Wartości współczynników
C
S
i
C
W
wg
Iszkowskiego
w modyfikacji A. Wierzchowskiego
Tabela 1a. Wartości współczynników
m
F - km
2
1
10 20 30 40 50 100 150 200 250 300 500 100
0
Podgó
rze
25,
0
22,
3
19,
8
17,
8
16,
3
14,
8
10,
7
8,8
0
7,1
6
7,0
3
6,5
5
5,9 4,7
Niziny 20,
0
17,
0
14,
0
12,
0
10,
8
9,8 7,4 7,1
0
6,8
7
6,7
0
6,5
5
5,9 4,7
Wyznaczenie współczynnika m
m
metodą interpolacji prostej
np. A = 68 km
2
m dla 50 km
2
- 9,8
100 km
2
- 7,4
50 km
2
- 2,4
18 km
18 km
2
2
- x
68 km
2
- 50 km
2
=
18 km
18 km
2
2
x = (18 · 2,4) : 50 = 0,864
stąd:
m
(dla A = 68 km
2
) = 9,8 – 0,864 = 8,936
50 km
2
- 2,4 lub 100 km
2
- 68 km
2
=
32 km
32 km
2
2
32 km
32 km
2
2
- x
x = (32 · 2,4) : 50 = 1,536
stąd:
m
(dla A = 68 km
2
) = 7,4 + 1,536 = 8,936
Lp. Powierzchn
ia
zlewni w
km
2
Warunki
w zlewni
Kategori
a zlewni
1.
2.
3.
4.
> 1000
0 - 1000
0 - 1000
0 – 300
Zlewnie nizinne - teren uprawny,
przepuszczalny, zarosły
Zlewnie nizinne i podgórskie - warunki
średnie
Zlewnie podgórskie i górskie, gleby mało
przepuszczalne, słaba roślinność
Zlewnie górskie - bez roślin, grunt
nieprzepuszczalny
I
II
III
IV
Tabela 2. Klucz do oznaczania
kategorii zlewni
Tabela 2a. Wartości współczynników
1. Zlewnie z przewagą gruntów nieprzepuszczalnych:
---------------------------------------------------------------------------------------------------------
---
a) na równinie, przy odpływie wyrównanym przez jeziora i
stawy............................. 1,5
b)
na
równinie
bez
jezior
i
stawów.............................................................................. 1,0
c)
w
terenie
słabo
pofałdowanym............................................................................... 0,8
d)
w
okolicy
pagórkowatej
i
w
mniejszych
górach.................................................... .. 0,6-0,5
2. Zlewnie z przewagą gruntów przepuszczalnych:
---------------------------------------------------------------------------------------------------------
---
a)
w
gruncie
średnio
przepuszczalnym,
roślinność
normalna..................................... 1,0
b)
w
gruncie
niezbyt
przepuszczalnym,
roślinność
bogata.......................................... 0,8
c)
w
gruncie
wybitnie
przepuszczalnym,
roślinność
skąpa.......................................... 0,4
UWAGA
: Dla zlewni o F< 200 km
2
współczynniki przyjęte w pkt. 1 lub 2
należy zmniejszyć o 25%
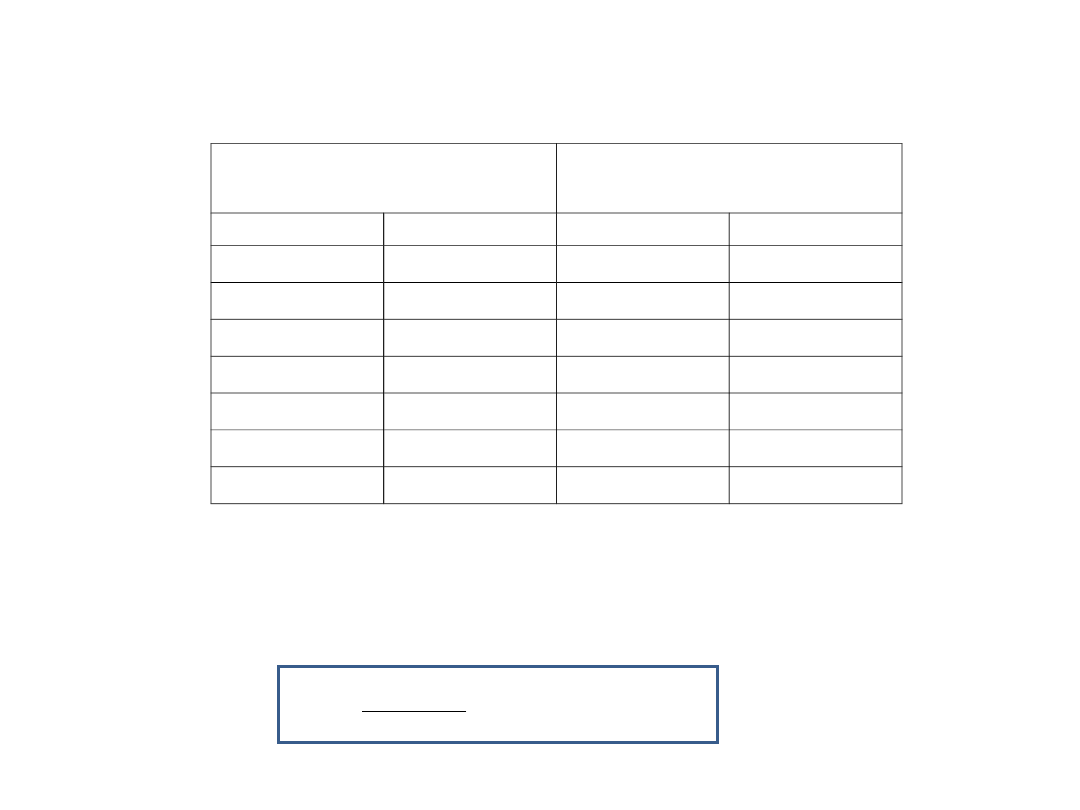
Przepływ
charakterystyczny
Spływ (odpływ)
jednostkowy
Q
[m
3 .
s
-1
]
q
[l
.
s
-1.
km
-2
]
Q
O
q
O
Q
1
q
1
Q
2
q
2
Q
S
q
S
Q
3L
q
3L
Q
3Z
q
3Z
Q
4
q
4
[l·s
-
1
·km
-2
]
Zestawienie przepływów
oraz odpływów
jednostkowych
A
1000
Q
q
Odpływ jednostkowy
q
:
- objętość (ilość) wody spływająca z powierzchni 1
km
2
zlewni w czasie 1 sekundy.
II. Projektowanie nowej trasy i przekroju
poprzecznego cieku
Podstawy hydrologiczne:
●
przepływy na podstawie których projektuje się przekroje
poprzeczne rzeki, nazywa się
miarodajnymi
lub
regulacyjnymi
,
●
przepływy
na podstawie których sprawdza się warunki przepływu -
kontrolnymi
.
Najczęściej spotykaną koncepcją jest regulowanie rzeki na
podstawie z góry założonego przepływu charakterystycznego, np.
na:
●
przepływ średni roczny,
●
najdłużej trwający w okresie wegetacji,
●
najdłużej trwający w ciągu roku.
Przepływy charakterystyczne przyjmowane jajko miarodajne lub
kontrolne podczas projektowania regulacji rzek i w ochronie
przeciwpowodziowej, można zaliczyć do jednej z trzech stref
przepływów: strefy przepływów niskich, średnich i wysokich
(maksymalnych). Niektóre przepływy charakterystyczne - zwane
umownymi, trudno jest od razu zakwalifikować do którejś z tych
stref. Dotyczy to :
●
przepływów nienaruszalnych
Q
n
,
●
kształtujących koryto
Q
kk
- przepływy przy których koryta ulegają
największym przeobrażeniom.
Przepływ nienaruszalny
Jest to przepływ najniższy, który musi pozostać w korycie ze
względu na zachowanie życia biologicznego i wymogi gospodarcze.
W Polsce stosuje się następujące kryteria ich doboru:
●
hydrobilologiczne - warunkujące zachowanie podstawowych
siedlisk floty i fauny cieku,
●
wędkarsko-rybackie - wynikające z potrzeb ichtiofauny, ochrony
gatunków i rekreacji,
●
ochrony przyrody - parki i rezerwaty przyrody,
●
zachowania piękna krajobrazu terenów przybrzeżnych rzek,
●
turystyczno-sportowe, zachowanie wymagań dla szlaków
kajakowych i żeglarskich.
Strefa przepływów niskich
Najczęściej określa się przepływy:
●
minimalne
NQ
,
●
średnie niskie
SNQ
- stosowane najczęściej,
●
najdłużej trwające: w roku
NTQ
, w okresie wegetacyjnym
NTQ
weg
i
żeglugowym
NTQ
żeg.
Strefa przepływów średnich
Zaliczamy do nich:
●
średnie
SQ
- oblicza się bezpośrednio, dzieląc sumy przepływów
dobowych przez liczbę dób,
lub pośrednio z krzywych hydrologicznych (hydrogramy, krzywe sum
czasów trwania, krzywe sumowe odpływu,
●
zwyczajne
ZQ
- odpowiadające wartościom środkowym
Q
50%
w
ciągu przepływów dobowych, lub można je też określić z sum czasów
trwania.
Strefa przepływów wysokich
W regulacji rzek przepływy maksymalne roczne
WQ
lub sezonowe
przyjmowane są jako miarodajne oraz kontrolne o określonym
prawdopodobieństwie wystąpienia.
Ogólne zasady projektowania trasy regulacyjnej
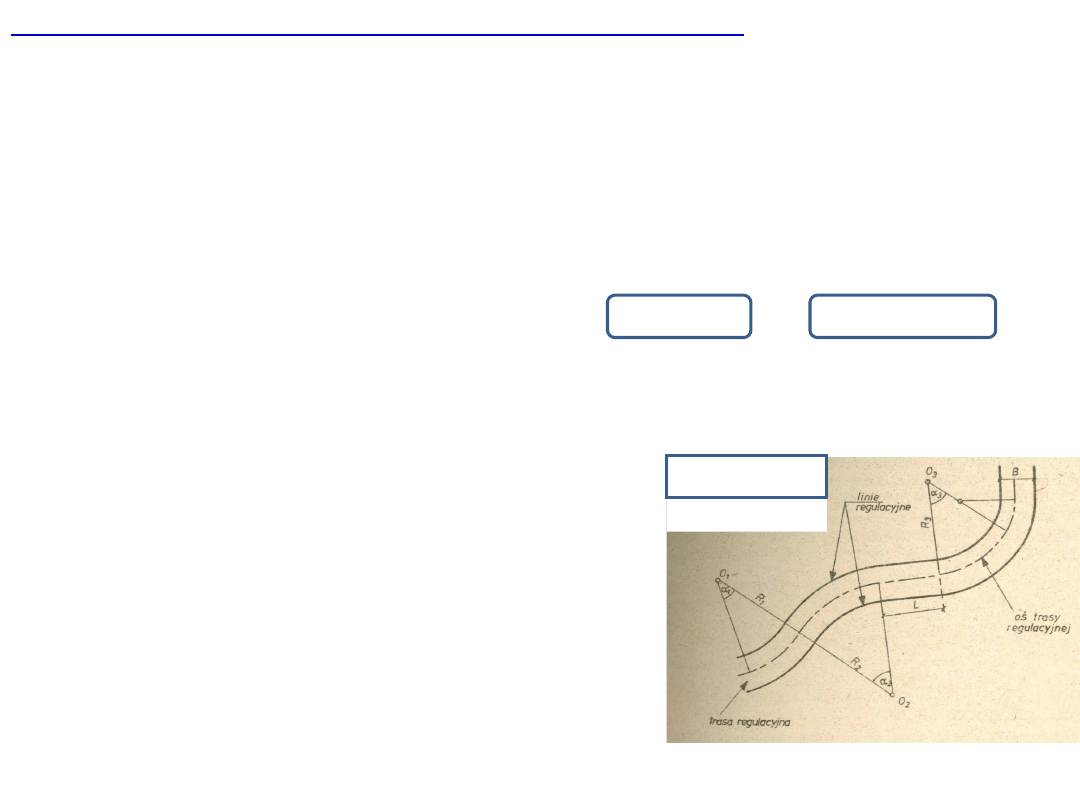
Trasa regulacyjna
rzeki to pas wody zawarty między sztucznymi
brzegami uregulowanej rzeki. Linia biegnąca środkiem trasy nazywa
się
osią trasy regulacyjnej. Oś trasy
składa się na przemian z łuków
(kołowych lub koszowych) oraz odcinków prostych. Oś winna mieć
linię płynną, czyli łuk w łuk odwrotny lub w odcinek prostej winien
przechodzić stycznie.
1. Trasa. Na małych ciekach nizinnych winna składać się z odcinków
prostych oraz łuków na zmianach ich kierunków. Dla zmniejszenia
niebezpieczeństwa niszczenia brzegów wklęsłych, należy stosować
następujące zasady projektowania łuków:
●
kąt środkowy łuku
α
nie powinien przekroczyć
≤ 60
o
wyjątkowo do
90
o
●
minimalny promień łuku winien spełniać warunki:
R
min
≥ 10 b
lub
R
min
≥ (6-8) B
gdzie:
b
-
szerokość lustra wody średniej normalnej
Q
2
,
B
- szerokość lustra wody dużej dorocznej
Q
3Z
2. Prędkość minimalna wody, aby uniknąć zamulania i zarastania:
Q
2
- V
min
nie mniej niż 0,15-0,20 m
.
s
-1
,
Q
3Z
- V
min
nie mniej niż 0,4 m
.
s
-1
.
3. Prędkości maksymalna wody, aby uniknąć rozmywania
skarp: V
max
dla skarp nieubezpieczonych
nie większa niż 0,6-0,9 m
.
s
-1
,
4. Napełnienie koryta
h
- zależy od wielkości zlewni:
przy zlewni > 100 km
2
h = 0,4-0,5 m,
przy zlewni 20-100 km
2
h = 0,3-0,4 m,
5. Spadki
I
: najmniejsze dopuszczalne – 0,2-0,3 ‰
najwłaściwsze - rowy większe zbliżone do 0,5 ‰, rowy
mniejsze zbliżone do 1,0 ‰.
Trasa
cieku
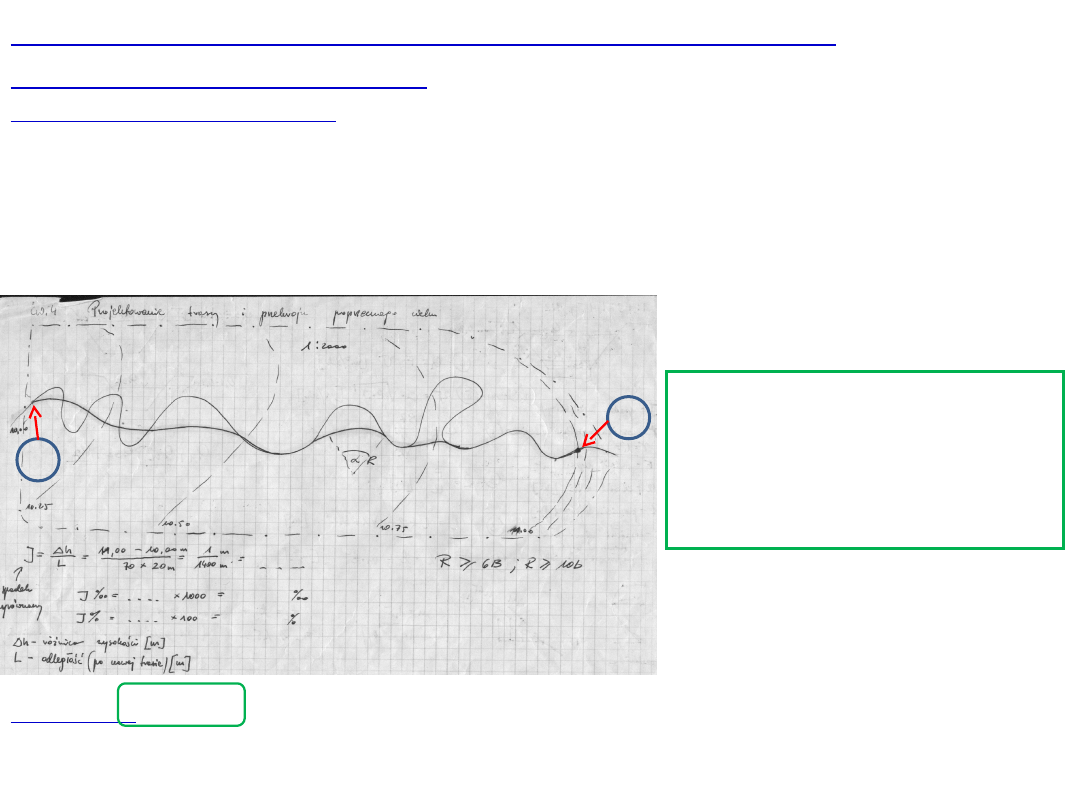
II. Projektowanie nowej trasy i przekroju
poprzecznego cieku:
Przepływ regulacyjny,
czyli przepływ, w oparciu o który projektujemy
przekrój poprzeczny cieku. Dla regulacji rzek w celach melioracyjnych i
rolniczych przyjmuje się następujące przepływy regulacyjne:
- dla ochrony przeciwpowodziowej
→
Q
4
- dla cieków przechodzących przez pola uprawne
→
Q
3Z
- napełnienie
przepływem + zapas 0,5 m
- dla cieków przechodzących tereny zadarnione
→
Q
3L
- napełnienie
przepływem + zapas 0,3 m
- dla projektowania dna cieku
→
Q
2
– służy do ustalenia szerokości dna cieku
Spadek
:
I = Δ h : L Spadek
wyrażamy w postaci: wartości
bezwzględnych; w %; lub w ‰,
gdzie:
Δ h
– różnica wysokości w m; między dwoma punktami (h
1
i h
2
)
L
– długość w m, po linii biegu cieku
My przyjmujemy:
- przepływy regulacyjne:
Q
3L
i
Q
2
- głębokość
cieku
t
c
= min 1,5 m
- szerokość dna b = min
0,4 m
- pochylenie skarp 1:1,5
h
1
h
2
Wyznaczanie parametrów regulacyjnych koryta
rzeki
●
Podstawą do projektowania są trzy parametry: przepływy regulacyjne
Q
3L
,
Q
2
i spadek cieku
I
w
‰
●
Z nomogramów odczytujemy parametry przekroju koryta rzeki: głębokości
t
3
,
t
2
i szerokość dna
b
1. Kształt przekroju poprzecznego:
trapez równoramienny,
nachylenie skarp
1:1,5
.
2. Głębokość koryta rzeki (
t
c
). Głębokość przyjmujemy tak, aby można było
odprowadzić wody z drenów i rowów odwadniających teren. Orientacyjnie
przyjmujemy
t
c
większe o 0,2-0,4 m od głębokości zbieracza (
t
z
) lub rowu
(
t
r
)odprowadzającego wodę, zatem
t
c
=
t
3
+ 0,3 m.
Minimalna głębokość
wynosi 1,5 m.
3. Maksymalna dopuszczalna prędkość wody w rzece dla gliny piaszczystej
V
max
= 0,9 m
.
s
-1
4. Projektowanie przekroju poprzecznego tak, aby pomieściły się wody
przepływu regulacyjnego
Q
3L
z zapasem minimum 0,3 m do wierzchu terenu, z
zachowaniem dopuszczalnej maksymalnej prędkości
V
max
.
Podstawą projektowania jest wzór
Q = F · V
,
który posłuży nam do
sprawdzenia poprawności przyjętych parametrów koryta rzeki. Stąd też
kolejno sprawdzamy czy przyjęte wymiary przekroju poprzecznego (
t
3
,
t
2
i
b
)
będą właściwe do pomieszczenia przepływu
Q
3L
.
Orientacyjnie możemy też
wyliczyć
: F = Q
3L
: V
max
5. Obliczenie przekroju poprzecznego rzeki
F
F = b·t + n·t
2
[m
2
]
(wyliczenia prowadzimy osobno dla
F
2
i
F
3
, wstawiając
odpowiednio wartości
t
3
i
t
2
)
6. Obliczenie obwodu zwilżonego i promienia hydraulicznego:
U = b + 2t·√1
+ n
2
[m] (wyliczamy osobno
U
2
i
U
3
, wstawiając
odpowiednio wartości
t
2
i
t
3
)
R
h
= F : U
[m
2
] (wyliczamy osobno
R
h2
i
R
h3
, wstawiając
odpowiednio wartości
U
2
i
U
3
oraz
F
2
i
F
3
)
7. Obliczenie współczynnika prędkości wg
wzoru Bazina
C
C
= 87 : 1 + [
= 87 : 1 + [
γ
γ
: √
: √
R
R
h
h
]
]
, jak poprzednio wyliczamy osobno
C
2
i
C
3
8. Obliczenie prędkości dopuszczalnej
V
ze
wzoru Chezy
(liczymy dla obu
głębokości
t
3
i
t
2
, czyli
V
3
i
V
2
)
V = C√R
h
· I
[m/s], jak poprzednio osobno
wyliczamy
V
2
i
V
3
9. Sprawdzenie wzorem:
Q = F · V,
wyliczając
Q
3
oraz
Q
2
i porównując
następnie z
Q
3L
i
Q
2
obliczonymi wzorami Iszkowskiego. Za rozbieżność
dopuszczalną uznajemy różnicę do 10%. Gdy rozbieżność jest większa,
wprowadzamy korektę pomniejszając lub powiększając
t
3
lub
t
2
.
10. Gdy spadek cieku
I
jest większy od dopuszczalnego (najlepiej do 0,5 ‰, a
max. do 1 ‰), projektujemy progi (od jednego do kilku), każdy o wysokości
od 0,2 do 0,3 m. Ilość progów zależy od przyjętego spadku.
h
R
c
k
1
87
Wzór Bazina
Wzór Bazina
C
- współczynnik oporu i tarcia - tarcie między innymi
ma miejsce:
- o brzegi koryta,
- strugi wody między sobą,
- o powietrze.
R
h
h
– promień hydrauliczny,
γ
– (gamma) – współczynnik szorstkości koryta
zależny od stanu utrzymania i konserwacji koryta
cieku.
Przykładowe wartości współczynnika
γ
:
0,85 - koryto ziemne dobrze utrzymane,
1,30
- koryto ziemne w zwykłym (średnim) stanie
utrzymania,
1,75 - koryto ziemne źle utrzymane.
h
R
c
k
1
87
γ
C
Przykład obliczenia przepływu
Przykład obliczenia przepływu
regulacyjnego WQ
regulacyjnego WQ
Dane:
t
t
max
max
= 1,7 m; b
b
= 14,0; n
n
= 1,5; γ
γ
= 1,3;
I
I
= 0,0003
Obliczenia:
1)
1)
U = 14 + 2
U = 14 + 2
●
●
1,7
1,7
●
●
√
√
1 + 1,5
1 + 1,5
2
2
2)
2) F
= 14
= 14
●
●
1,7 + 1,5
1,7 + 1,5
●
●
1,7
1,7
2
2
(m
(m
2
2
)
)
U = 14 + 3,4
U = 14 + 3,4
●
●
1,8 F =
1,8 F =
23,8 + 4,3
23,8 + 4,3
U = 14 + 6,12
U = 14 + 6,12
U = b + 2t·√1 + n
2
F = 28,1
F = 28,1
m
m
2
2
F = b·t + n·t
2
U = 20,12 m
U = 20,12 m
3) R
3) R
h
h
= 28,1 : 20,12 4) C = 87 : 1
= 28,1 : 20,12 4) C = 87 : 1
+ [1,3 :
+ [1,3 :
√
√
1,4] -
1,4] - wz. Bazina
wz. Bazina
R
R
h
h
= 1,40 m C = 87 :
= 1,40 m C = 87 :
1 + [ 1,3 : 1,18]
1 + [ 1,3 : 1,18]
C = 87 :
C = 87 :
1 + [ 1,10]
1 + [ 1,10]
R
h
= F : U
C = 87 :
C = 87 :
2,1
2,1
C =
C =
41,42
41,42
C = 87 : 1 + [γ : √R
h
]
5) V = 41,42
5) V = 41,42
●
●
√
√
1,4
1,4
●
●
0,0003 -
0,0003 - wz. Chezy
wz. Chezy
6)
6) Q
3
= 28,1
= 28,1
●
●
0,83
0,83
V = 41,42
V = 41,42
●
●
0,02
0,02 Q
3
= 23,3
= 23,3
m
m
3
3
·
·
s
s
-
-
1
1
Q = F
· V
V = 0,83
V = 0,83
m
m
·
·
s
s
-1
-1
V = C√R
h
· I
Analogicznie obliczamy przepływ regulacyjny
Analogicznie obliczamy przepływ regulacyjny
Q
3
, podstawiając
, podstawiając
Dane:
Dane:
t
t
3
3
= 1,15 m;
b
b = 14;
n
n = 1,5;
γ
γ = 1,3;
I
I = 0,0003
Nomogram do projektowania przekroju poprzecznego cieku – dla
małych cieków
Nomogram do projektowania przekroju poprzecznego cieku – dla
dużych cieków
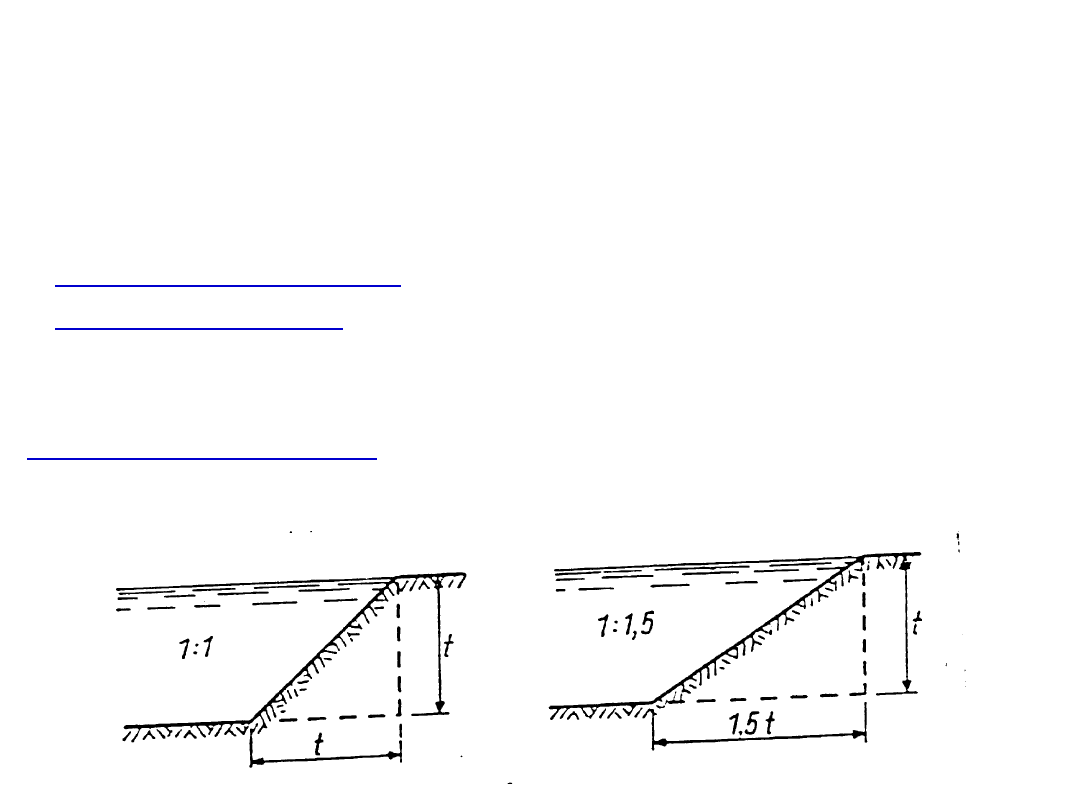
Wskazówki do projektowania przekroju
poprzecznego cieku:
Aby ciek (np. rów) dobrze funkcjonował, należy
zaprojektować
odpowiednie:
-
nachylenie skarp
(ścianek bocznych rowu),
-
szerokość dna
- dostosowaną do objętości
odprowadzanej wody
Q
.
Nachylenie skarp
– stosunek głębokości rowu do
rzutu skarpy na płaszczyznę poziomą. Nachylenie
skarpy zależy od odporności gleby na
rozmywanie. Rowy o łagodniejszym nachyleniu są
trwalsze i łatwiejsze do konserwacji (głównie
wykaszania skarp), ale zajmują większą
powierzchnię.
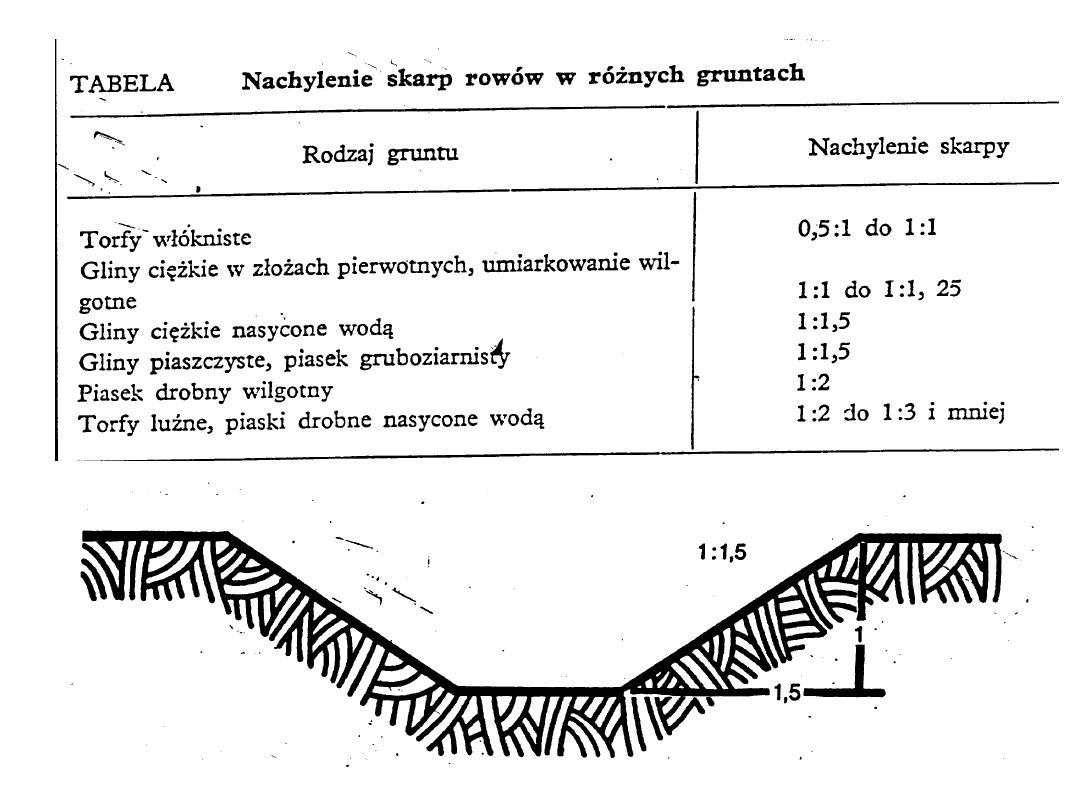
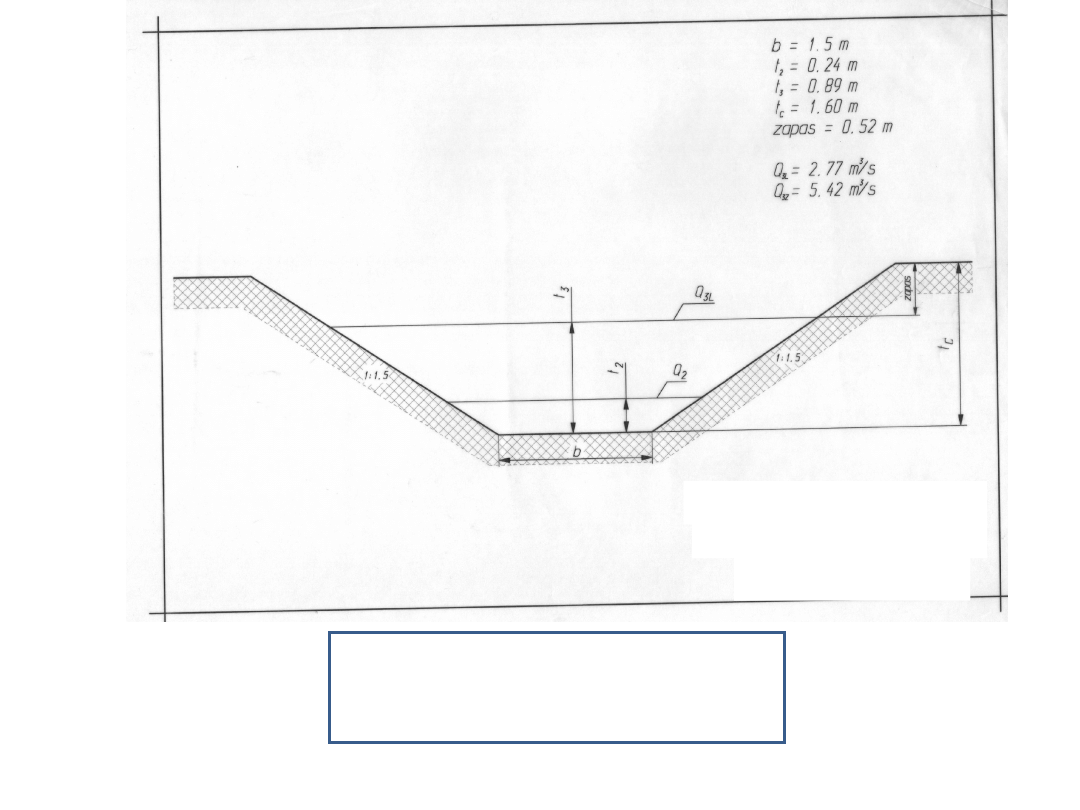
Przekrój poprzeczny
cieku
Skala 1 : 20 do 1 : 50