Wykład 1

Wykład 1

Kinematyka punktu

MECHANIKA (OGÓLNA)

- jest nauką badającą ogólne

prawa ruchu obiektów materialnych (ciał) i ich wzajemne

oddziaływania.

Mechanikę ogólną dzielimy na:

STATYKĘ, KINEMATYKĘ i DYNAMIKĘ

Semestr III:

KINEMATYKA i DYNAMIKA.

1.1 Pojęcia

podstawowe

Pojęcia podst.

1

• Obiekty materialne:

wyidealizowane schematy ciał rzeczywistych.

• Wyróżniamy:

punkt materialny ( w skrócie PM),
układ punktów materialnych (UPM),
ciało sztywne (CS).

• Ruch - j

est to zjawisko zmiany położenia

ciała względem innego ciała uznanego
umownie za nieruchome.
Nieruchome ciało nazywamy ciałem
odniesienia.

•

W

W

niosek

niosek

:

:

ruch jest wzgl

ruch jest wzgl

ę

ę

dny tzn. zale

dny tzn. zale

ż

ż

y od

y od

wyboru

wyboru

cia

cia

ł

ł

a odniesienia.

a odniesienia.

•Czas -

jest w mechanice klasycznej (Newtona)

pojęciem pierwotnym i absolutnym.

•Czas nie zależy od wyboru układu odniesienia i
jest taki sam w każdym punkcie przestrzeni.

•Przyjmuje się, że czas jest stale nieujemny

t



0

i występuje tylko wtedy gdy występuje ruch.

•Układ odniesienia -

jest to układ

współrzędnych sztywno związany z ciałem

odniesienia, który służy do opisu ruchu obiektu

(-ów).

Pojęcia podst. 2

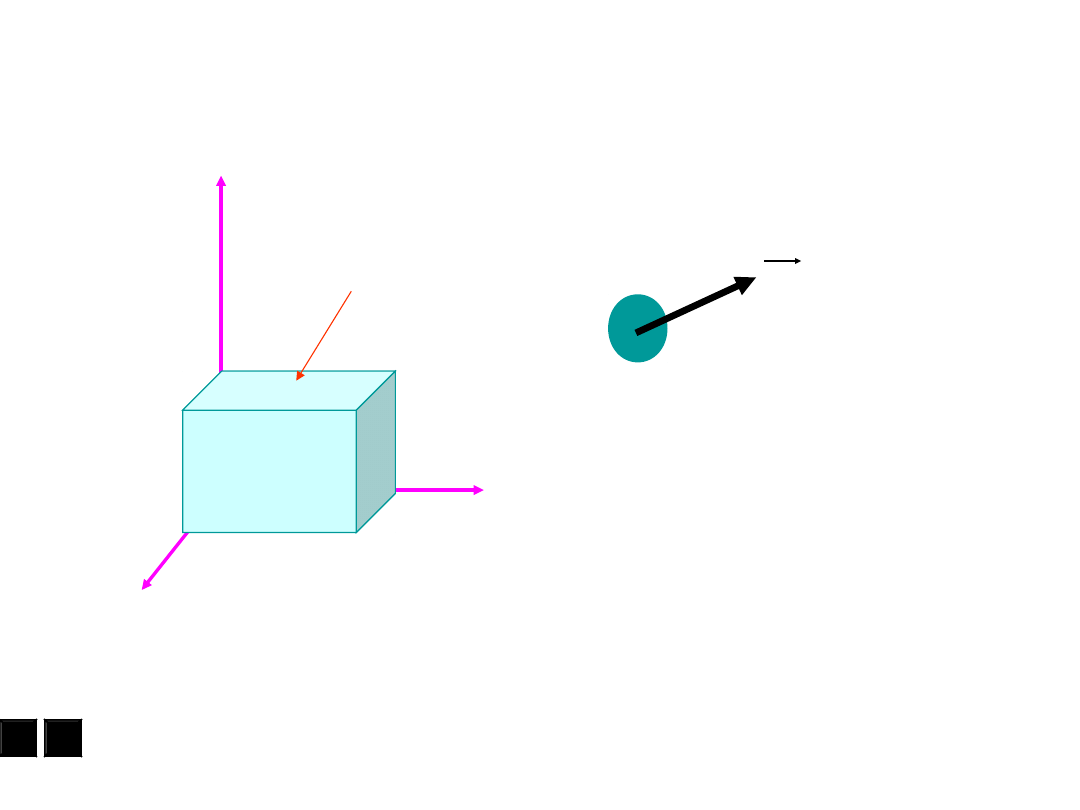
Układ odniesienia

Oxyz – układ odniesienia, prostokątny prawoskrętny układ
współrzędnych

Obiekt ruchomy
względem Oxyz

V

UKŁAD ODNIESIENIA

O

x

y

z

 Ciało
odniesienia
(nieruchome)

Kinematyka p-
tu 1

• Kinematyka

- jest to dział mechaniki,

w którym bada się ruch obiektów bez

wnikania w przyczyny wywołujące ten

ruch.

• Można ją nazwać geometrią ruchu,

bowiem do opisu tego ruchu stosujemy

pojęcia przestrzeni i czasu.

1.2 Kinematyka punktu w
układzie Oxyz

Wielkości

kinematyczne

Wielkości fizyczne w
kinematyce

1.

Droga, przesuni

Droga, przesuni

ę

ę

cie, przemieszczenie

cie, przemieszczenie -

[translacja -

m

, obrót -

rad

]

2. 

Pr

Pr

ę

ę

dko

dko

ść

ść - [

m/s

,

rad/s

]

3. 

Przyspieszenie

Przyspieszenie - [

m/s

2

,

rad/s

2

]

4.

Tor ruchu punktu

Tor ruchu punktu - równanie krzywej, po

której następuje ruch tego punktu, np.:

y = y(x)  y = 3x

2

– 6x + 5

Opis ruchu p-

tu

Matematycznie ruch punktu opisujemy w
postaci wektorowej lub skalarnej. Opisy te
są równoważne.

Opis ruchu punktu

Równanie wektorowe

ruchu:

)

t

(

r

r







Równania skalarne w układzie
Oxyz:

x=x(t), y=y(t), z=z(t)

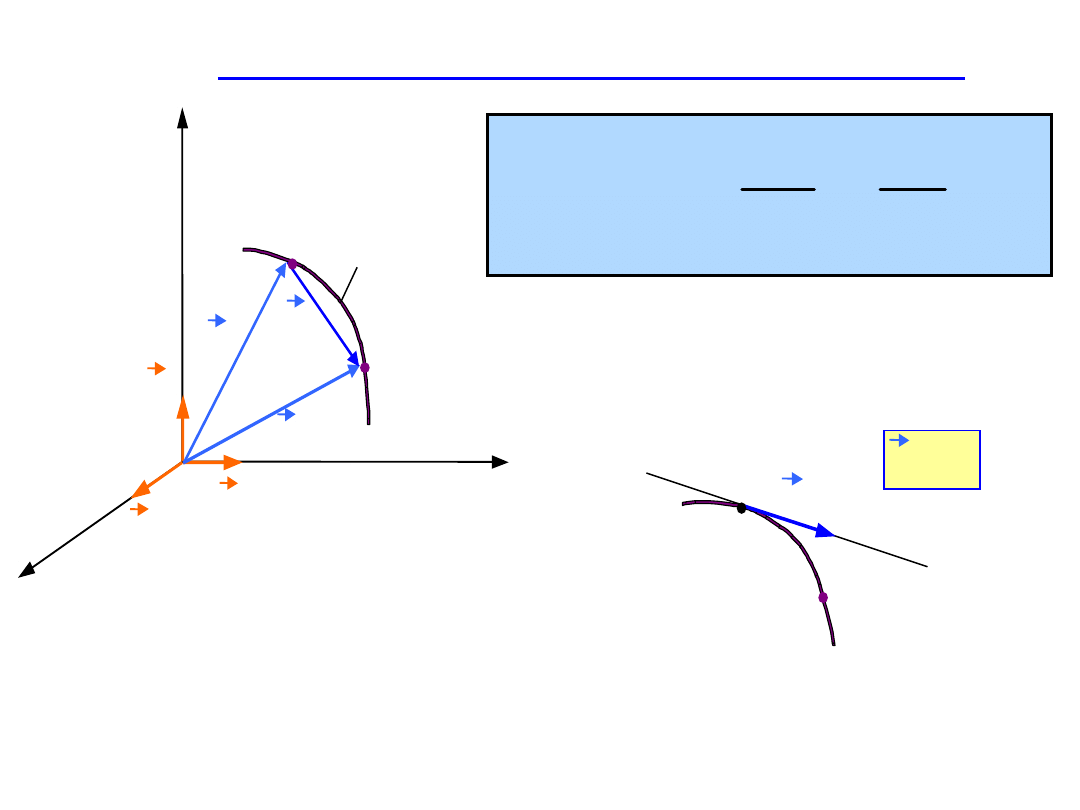
y

x

O

y

z

x

e

e

z

e

r



r(t+

t)

r

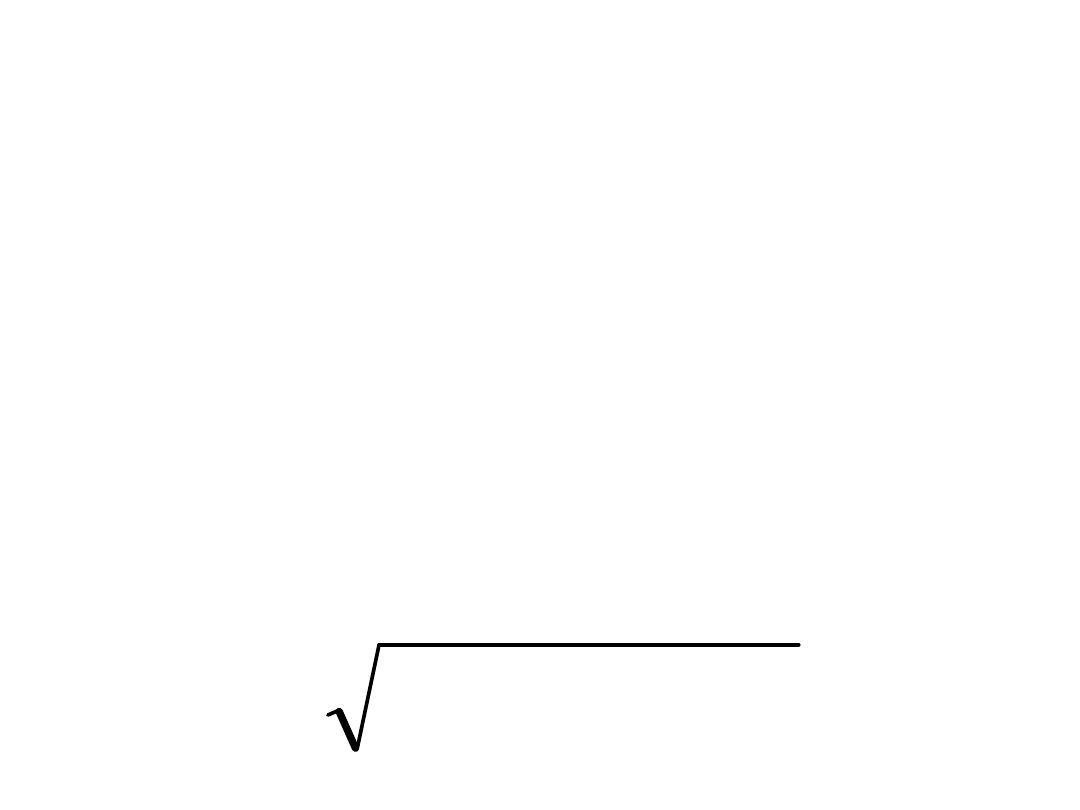
Prędkość p-tu w

Oxyz

A(t +

t)

tor

A(t)

 s



r

dt

r

d

t

r

v

lim

0

t

























- styczna do toru w punkcie A(t)

A(t)

A(t+

t)



v(t)

TOR



v 



Prędkość punktu w Oxyz

Prędkość

c.d.

Moduł wektora prędkości jest wartością prędkości.
NIE MYLIĆ pojęć wektora prędkości i jej wartości !

Wektor prędkości:

]

v

,

v

,

v

[

v

e

v

e

v

e

v

z

y

x

z

z

y

y

x

x























2

2

2

z

y

x

v

v

v

|

v

|

v











Wartość prędkości (długość
wektora):

przy czym

z

v

,

y

v

,

x

v

z

y

x













Prędkość c.d.

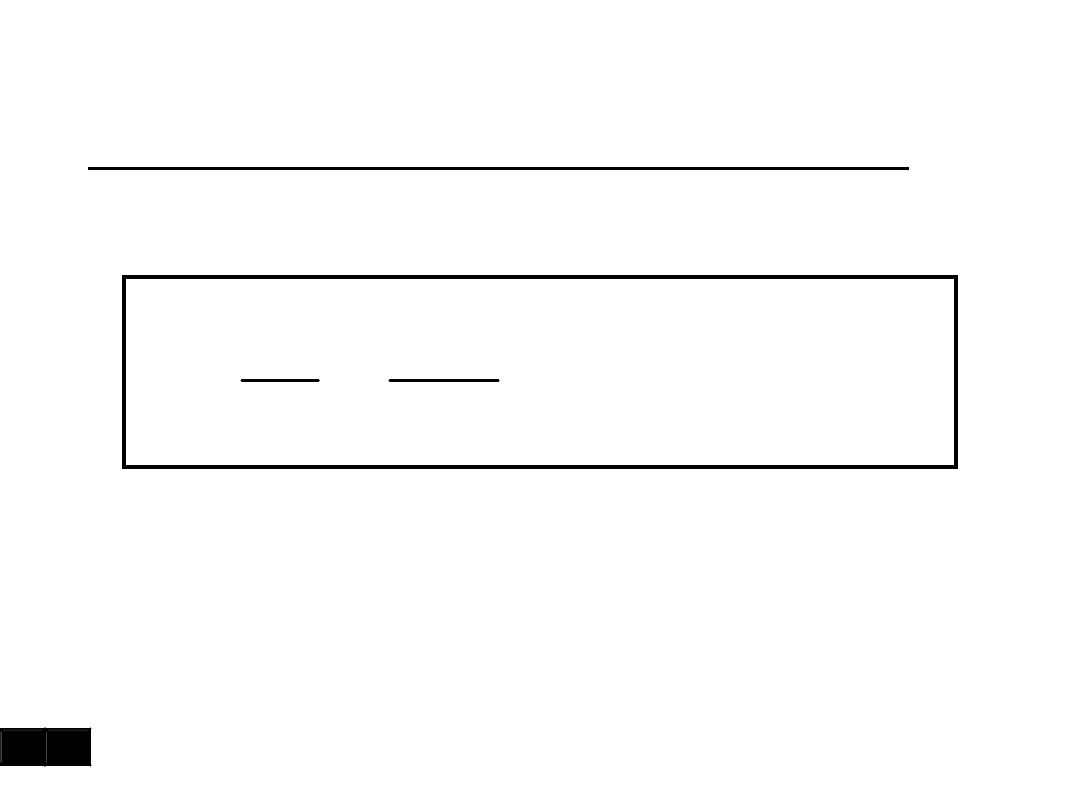
Elementarna droga po torze:

dt

v

v

v

ds

z

y

x

2

2

2







Jeśli znamy s=s(t) to prędkość możemy obliczyć z
zależności:

s

dt

ds

v







Przysp. p-tu w

Oxyz

r

v

a

lub

;

dt

r

d

dt

v

d

a



















2

2

Przyspieszenie punktu w Oxyz

UWAGA: wektor przyspieszenia punktu ma na ogół

inny kierunek niż wektor prędkości !

Moduł przyspieszenia (długość wektora
przyspieszenia):

2

2

2

z

y

x

a

a

a

|

a

|

a











Przysp. p-tu c.d

;

z

v

a

;

y

v

a

;

x

v

a

)

e

v

e

v

e

v

(

dt

d

a

z

z

y

y

x

x

z

z

y

y

x

x







































Wektor przyspieszenia i jego współrzędne:

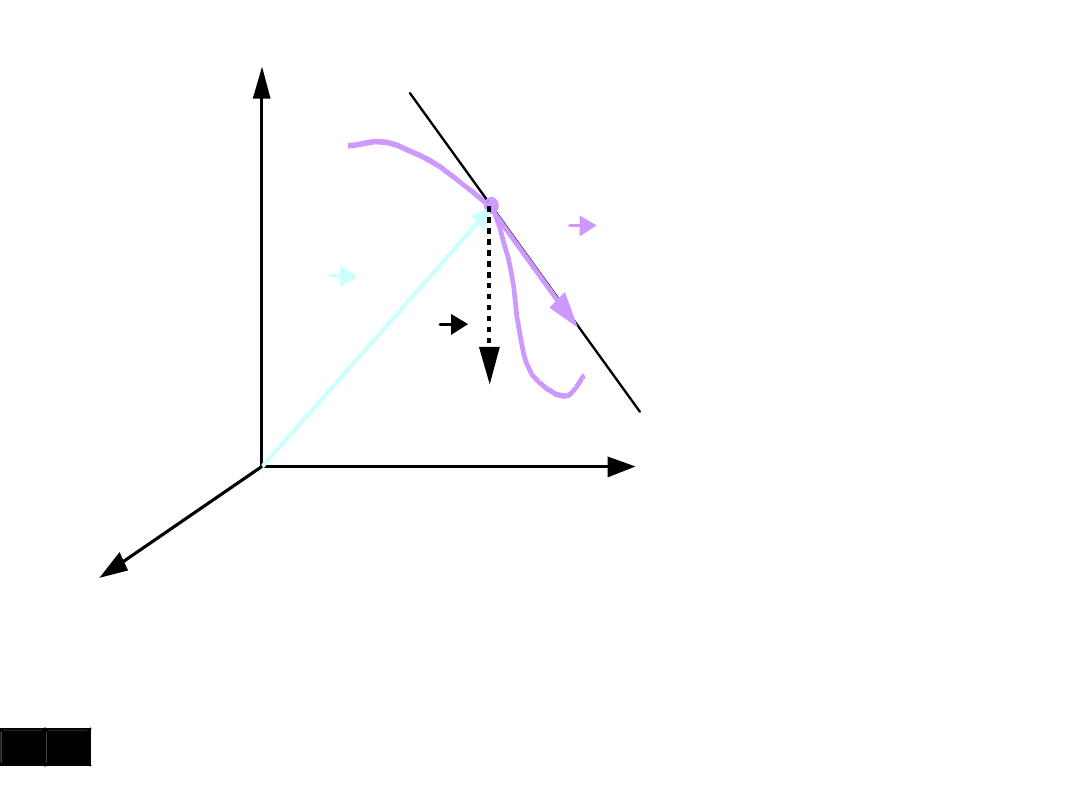
O

y

z

x

r(t)

A

V

a

!

()









a

v





Uwaga: wektor przyspieszenia ma na
ogół inny kierunek niż wektor
prędkości.

Przysp. p-tu c.d.

14

1.3 Kinematyka p-tu w układzie

naturalnym

Założenia:

s(t)

s

gdzie

);

s

(

r

r









- Ruch punktu jest dany w postaci:

- Początek układu współrzędnych jest
związany
z ruchomym punktem A na torze.
Układ taki nazywamy naturalnym
lub
trójścianem Freneta.

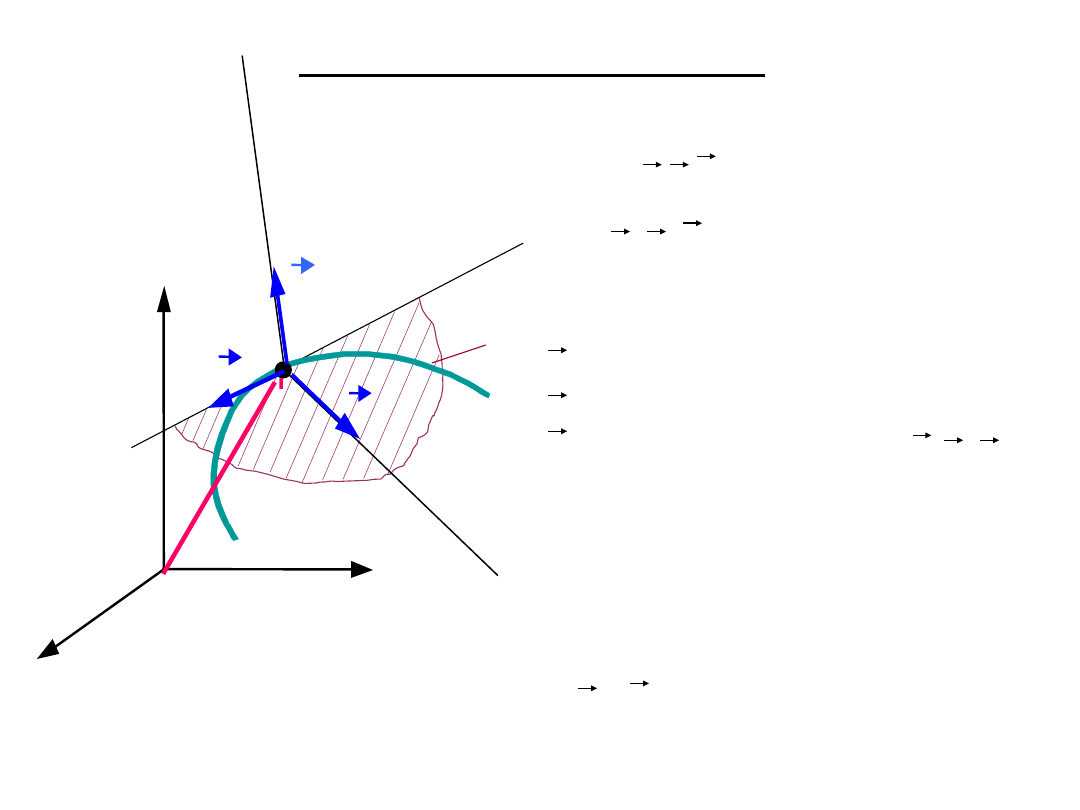
– wersor ściśle styczny,
n – wersor normalny
główny,
b – wersor binormalny
b=n

Tróścian
Freneta

Trójścian Freneta

A  n b – układ naturalny

, n, b - zależą od czasu.

Wektory  i n wyznaczają

płaszczyznę
ściśle styczną do toru -



(b)

()

(n)

O

y

z

x

)

s

(

r

A

tor



b

n

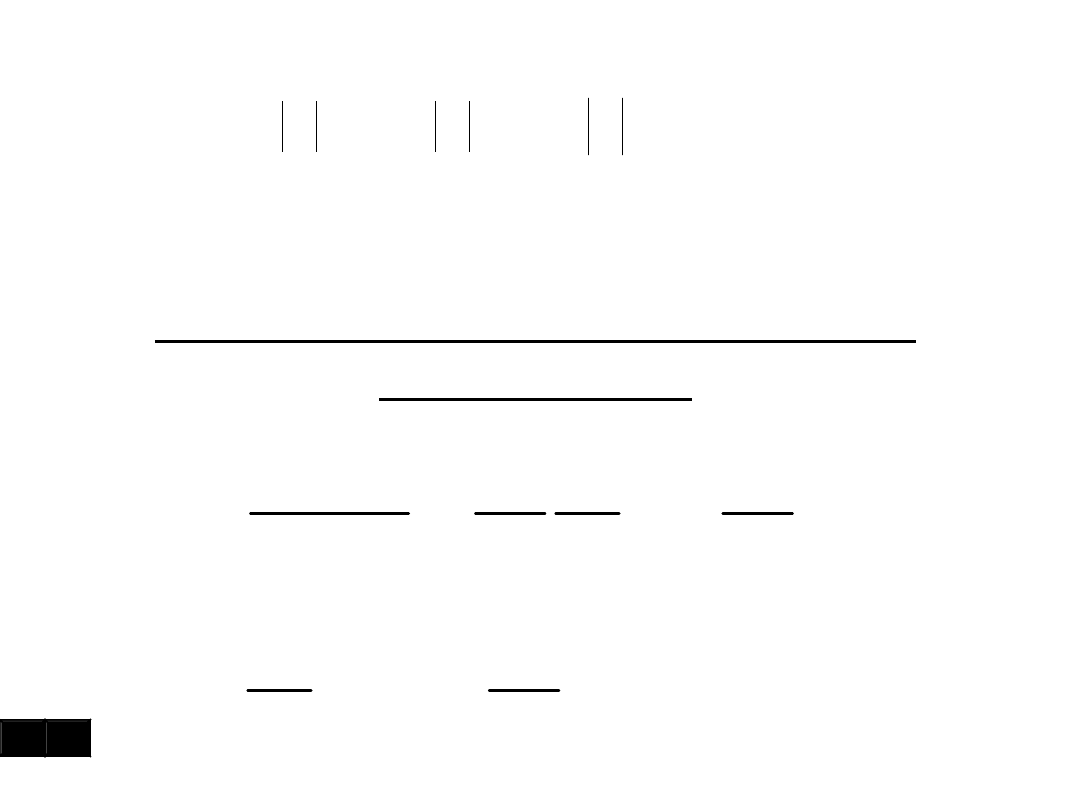
v

;

ds

r

d

;

dt

ds

v

v

ds

r

d

v

dt

ds

ds

r

d

dt

)

s

(

r

d

v





































Predkość w ukł.
Freneta 1

Prędkość punktu w układzie

naturalnym



























,

1

1

1











n

i

b

,

n

b

,

n

,

















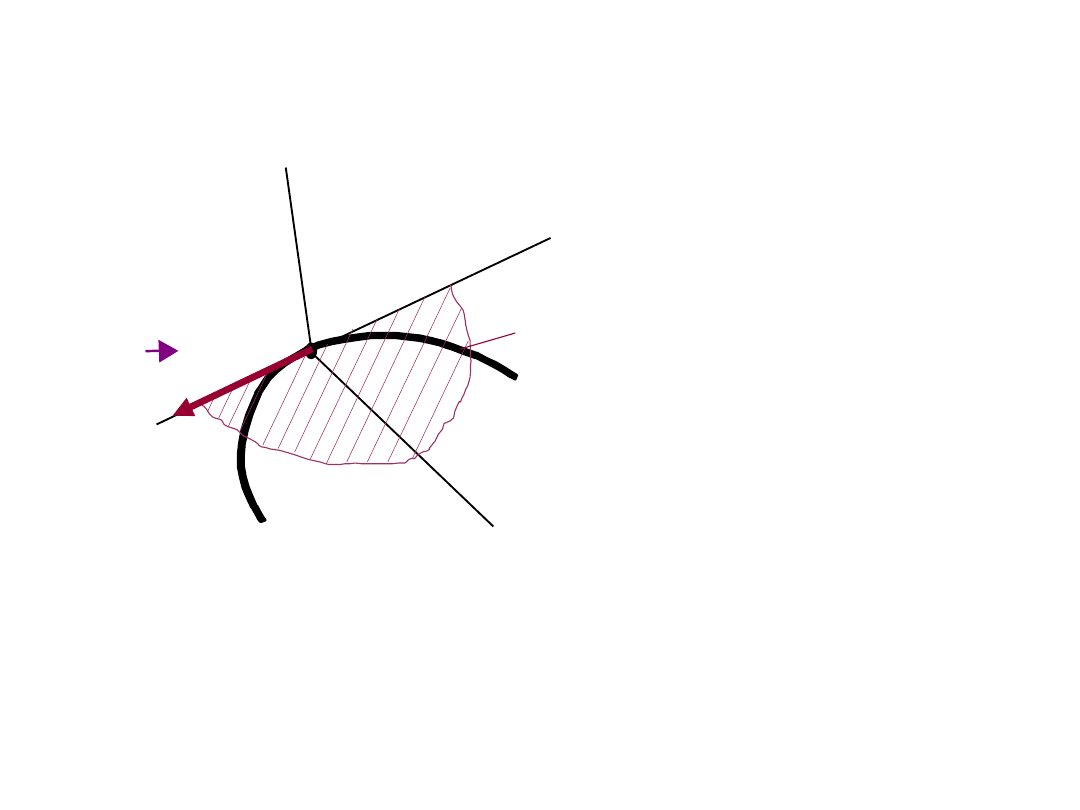
Prędkość w ukł. Freneta 2

(n)

A

(b)

()



V

normalne;

enie

przyspiesz

styczne;

enie

przyspiesz

n

v

a

dt

dv

a

dt

ds

ds

d

v

dt

dv

)

v

(

dt

d

dt

v

d

a

2

n











































Przyspieszenie punktu w układzie naturalnym



-

promień krzywizny toru w punkcie A

Przysp. w ukł.
Freneta 1









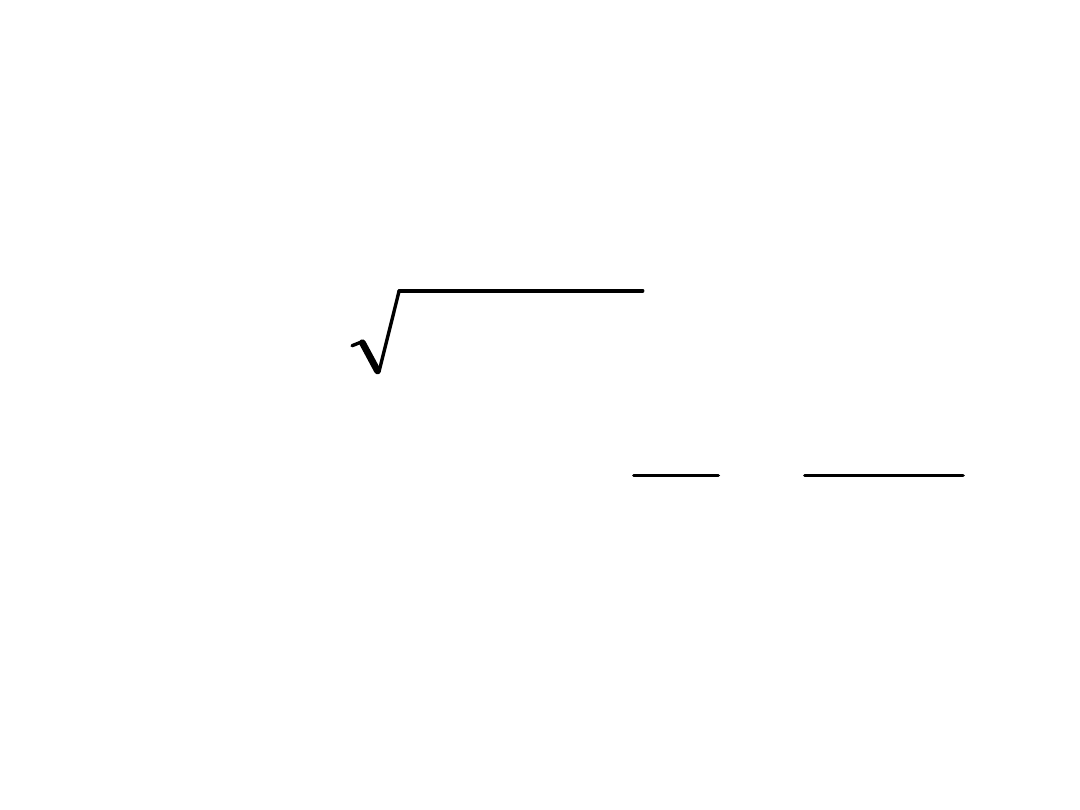
2

2

2

2

)

s

(

v

a

;

s

v

a

;

a

a

|

a

|

a

n

n

























Moduł i współrzędne wektora przyspieszenia:

Przysp. w ukł. Freneta
2

(n)

A

(b)

()



Przysp. w ukł.
Freneta 3



a



n

a



2
n

2

b

n

n

a

a

a

(zawsze),

0

a

,

n

a

a

,

a

a

,

a







































a



Przykład
y

1.4 Przykłady

1.

Punkt materialny A porusza się zgodnie z

równaniami ruchu: x(t)=bsin(t), y(t)=c



cos(t).

Wyznacz równanie toru punktu, jego prędkość i

przyspieszenie w dowolnej chwili czasu t. Wyznacz

przyspieszenie styczne i normalne tego punktu.

Układ naturalny jest na ogół stosowany do badania
krzywoliniowego ruchu punktu.

Przykład
1/1

Rozwiązanie:

Dokonajmy przekształcenia:

)

t

cos(

c

y

),

t

sin(

b

x













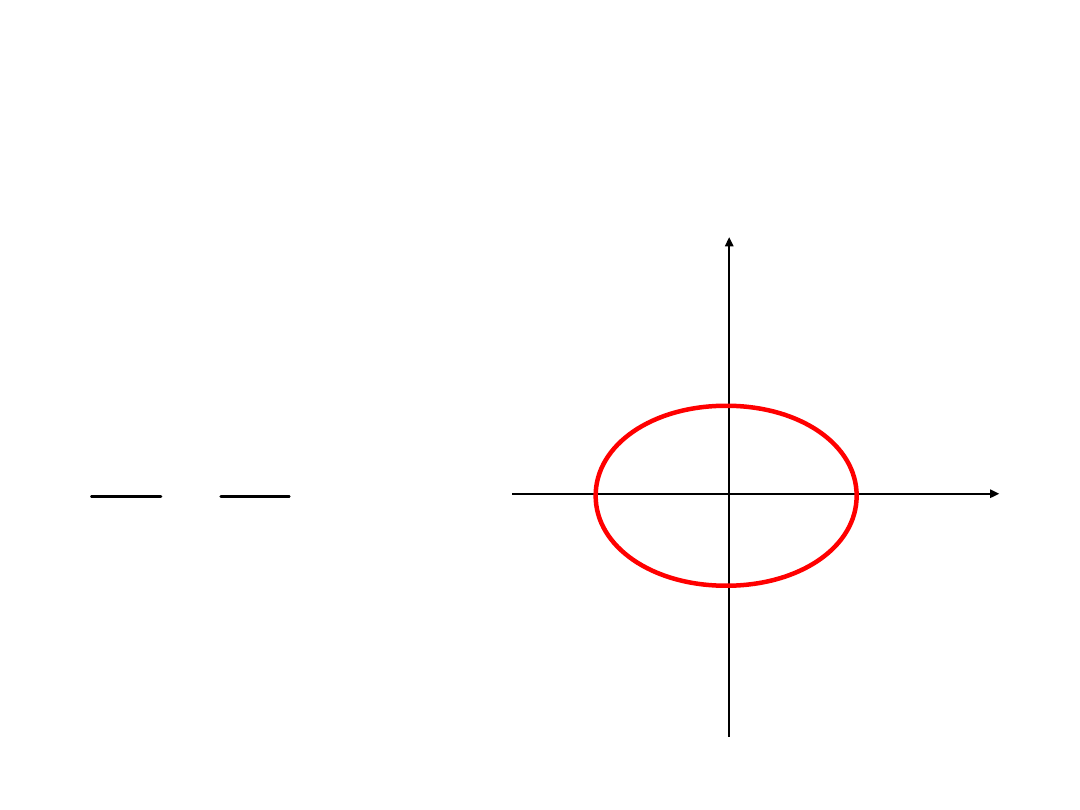
i podnieśmy obustronnie równania do kwadratu:

)

t

(

cos

c

y

),

t

(

sin

b

x

2

2

2

2

2

2













Przykład
1/2

Po dodaniu stronami mamy równanie
toru w postaci elipsy:

1

c

y

b

x

2

2

2

2





O

x

y

c

-c

-b

b

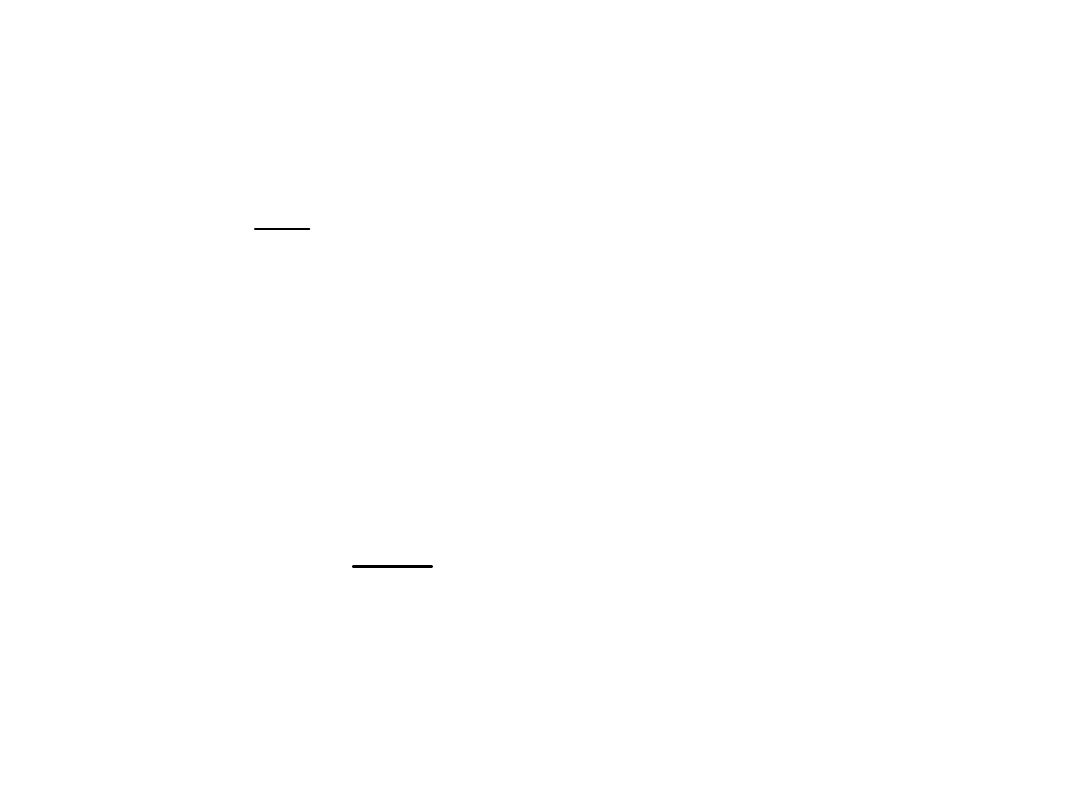
Przykład
1/3

Prędkość i przyspieszenie
punktu:

)]

t

(

y

),

t

(

x

[

dt

r

d

)

t

(

r

v

















)

t

sin(

c

)

t

(

y

)

t

cos(

b

)

t

(

x































)]

t

(

y

),

t

(

x

[

dt

r

d

)

t

(

r

v

a

2

2





















)

t

cos(

c

)

t

(

y

)

t

sin(

b

)

t

(

x

2

2

































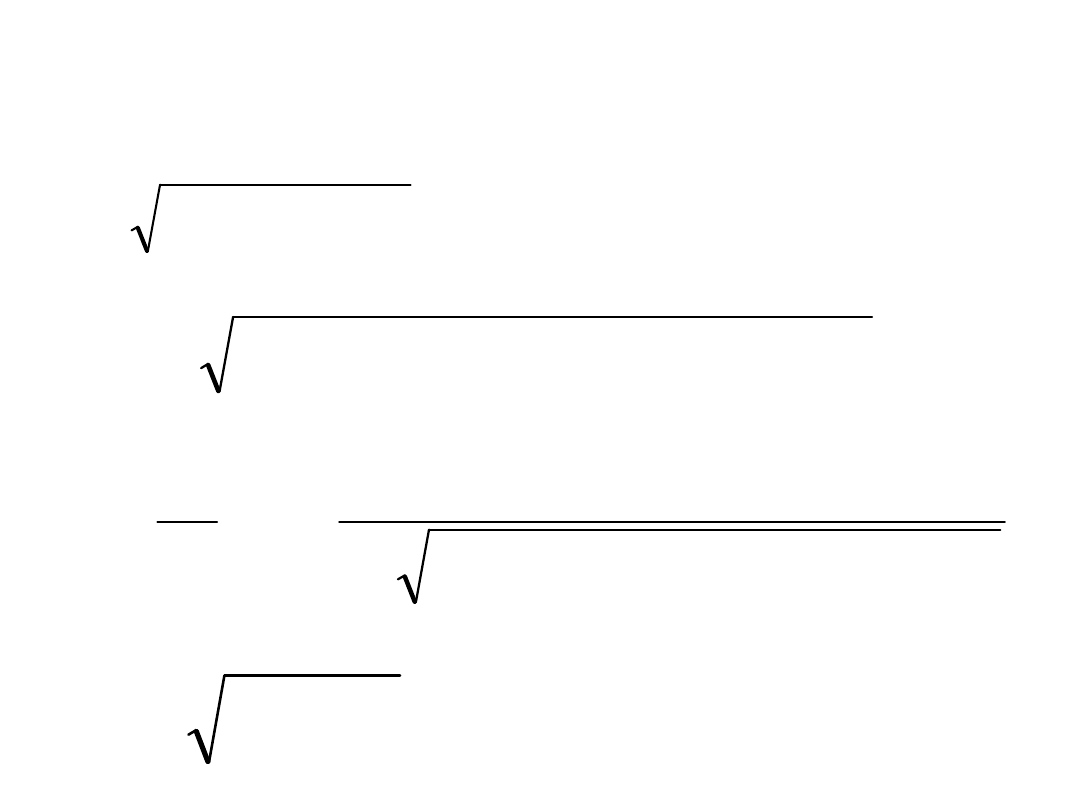
Przykład
1/4

Przyspieszenie styczne i
normalne:

)

t

(

y

)

t

(

x

v

2

2









)

t

(

sin

c

)

t

(

cos

b

v

2

2

2

2





















)

t

(

sin

c

)

t

(

cos

b

2

)

t

2

sin(

)

b

c

(

dt

dv

a

2

2

2

2

2

2

2



























2

2

n

a

a

a







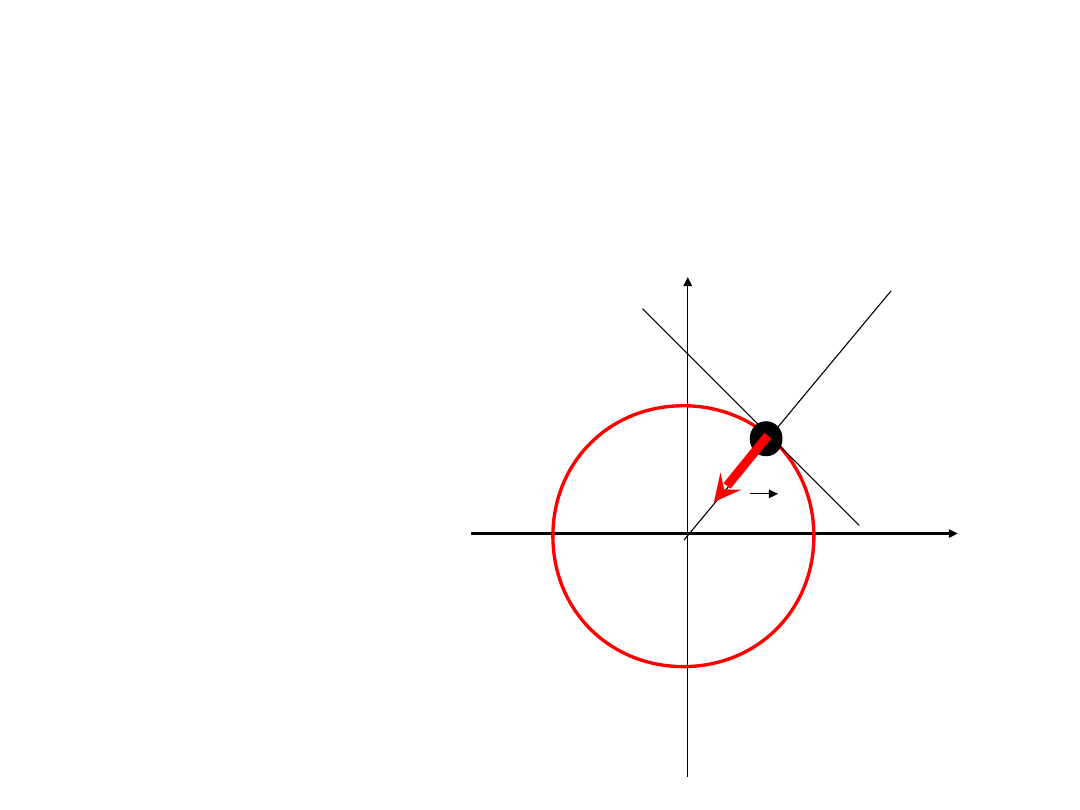
Przykład
1/5

Ruch po okręgu o promieniu r z prędkością

v=const.

Dla okręgu mamy:

b=c=r,

r

a



=0

a

n

=



2

r =

v

2

/r

n

O

x

y



a

n

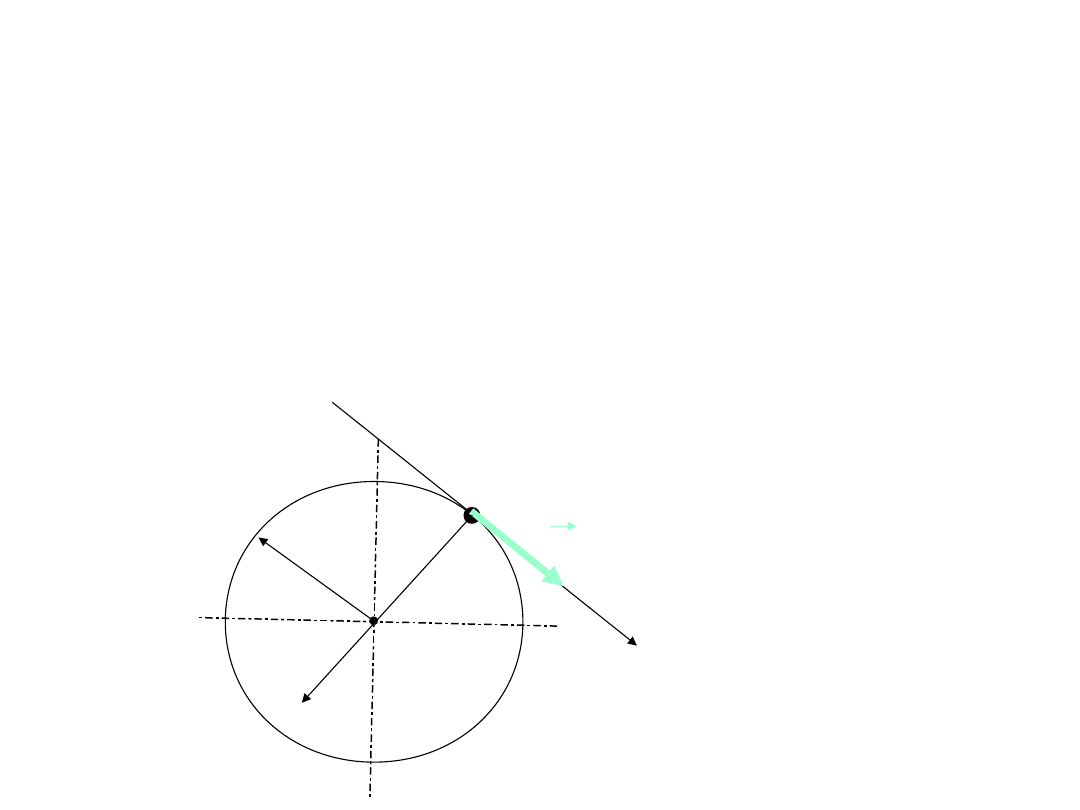
Przykład
2/1

Przykład 2.

Punkt materialny A zaczął poruszać się

po okręgu o promieniu

r =0.1

[m] w ten sposób, że jego

przyspieszenie styczne

a



jest stale równe

2

[m/s

2

] . Po

jakim czasie jego przyspieszenie normalne będzie
równe stycznemu?

A

r



a



n

Przykład
2/2

Rozwiązanie:

t

a

)

t

(

v

dt

a

v

0

C

0

v

;

C

t

a

)

t

(

v

dt

a

v

dt

a

dv

dt

dv

a

1

0

t

1















































]

s

[

20

1

t

;

s

m

2

t

40

a

a

t

40

1

.

0

t

4

a

r

v

a

2

2

n

2

2

n

2

n

































Przykład
3/1

Przykład 3.
Obliczyć promień krzywizny toru środka kulki
w początku ruchu, jeżeli równania ruchu mają
postać: x=2t, y=t

2

; przy czym t [s], x i y [m].