Metoda naukowa
2

Metoda naukowa 2

2

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

Metoda naukowa 2

3

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

„(ja) poszukuję…” = S(a, x)



x S(a, x) …

Metoda naukowa 2

4

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

„(ja) poszukuję…” = S(a, x)

„…jest pokojem” = P(x)



x

[

S(a, x)  P(x) …

Metoda naukowa 2

5

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

„(ja) poszukuję…” = S(a, x)

„…jest pokojem” = P(x)

„…jest z…” = Z(x, y)



x

[

S(a, x)  P(x)  Z(x, y) …

Metoda naukowa 2

6

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

„(ja) poszukuję…” = S(a, x)

„…jest pokojem” = P(x)

„…jest z…” = Z(x, y)

„…jest oddzielnym wejściem” = Q(y)



x

{

S(a, x)  P(x)  y [Q(y)  Z(x, y)] …

Metoda naukowa 2

7

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.

„(ja) poszukuję…” = S(a, x)

„…jest pokojem” = P(x)

„…jest z…” = Z(x, y)

„…jest oddzielnym wejściem” = O(y)

„…jest starszą panią” = R(z)



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)]  z R(z) …

Metoda naukowa 2

8

Błędy logiczne:

amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla starszej

pani.

„(ja) poszukuję…” = S(a, x)

„…jest pokojem” = P(x)

„…jest z…” = Z(x, y)

„…jest oddzielnym wejściem” = O(y)

„…jest starszą panią” = R(z)

„…jest dla…” = D(?, z)



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)]  z [R(z)  D(

?

,

z)

]

}

Metoda naukowa 2

9

Amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)  z R(z) 

D(

x

, z)

]

}

Metoda naukowa 2

10

Amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)  z R(z) 

D(

x

, z)

]

}



Poszukuję pokoju

dla starszej pani

z

oddzielnym wejściem

.

Metoda naukowa 2

11

Amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla

starszej pani.



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)  z R(z) 

D(

x

, z)

]

}



Poszukuję pokoju

dla starszej pani

z oddzielnym

wejściem



Metoda naukowa 2

12

Amfibologie



Poszukuję pokoju z oddzielnym wejściem

dla starszej

pani.



x

{

S(a, x)  P(x) 

[

y Q(y)  Z(x, y)  z R(z)  D(

x

,

z)

]

}



Poszukuję pokoju

dla starszej pani

z oddzielnym

wejściem

.



Dla starszej pani

poszukuję pokoju z oddzielnym

wejściem.

Metoda naukowa 2

13

Amfibologie



Przedsiębiorstwo zamieni obiekt kolonijny

na

100 dzieci

.



x y

[

Z(a, x, y)  Q(x) 

R

(

?

)

]

Metoda naukowa 2

14

Amfibologie



Przedsiębiorstwo zamieni obiekt kolonijny

na 100

dzieci

.



x y

[

Z(a, x, y)  Q(x) 

R

(

?

)

]



Przedsiębiorstwo zamieni (z innym
przedsiębiorstwem) obiekt kolonijny

na

równorzędny, mieszczący

100 dzieci

.

Metoda naukowa 2

15

Amfibologie



Buzek jest przyjacielem Krzaklewskiego, który
zawsze słucha jego rad.



P(b, k)  S(

?

,

?

)

Metoda naukowa 2

16

Amfibologie



Buzek jest przyjacielem Krzaklewskiego, który
zawsze słucha jego rad.



P(b, k)  S(

?

,

?

)



Buzek przyjaźni się z Krzaklewskim i zawsze
słucha jego rad.

Metoda naukowa 2

17

Niejawne kwantyfikatory



Marks postulował, aby
człowiek panował nad społeczeństwem.

Metoda naukowa 2

18

Niejawne kwantyfikatory



Marks postulował, aby
człowiek panował nad społeczeństwem.



Powstaje jednak pytanie,

który

człowiek (L.

Kołakowski).

Metoda naukowa 2

19

Niejawne kwantyfikatory



Marks postulował, aby
człowiek panował nad społeczeństwem.



Powstaje jednak pytanie,

który

człowiek (L.

Kołakowski).



x

[

H(x)  P(x)

];



x

[

H(x)  P(x)

]

Metoda naukowa 2

20

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.

Metoda naukowa 2

21

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



xP(x) ...

Metoda naukowa 2

22

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)
…”;



x(P(x) ? 

y

[

Q(?

,

?

) …

Metoda naukowa 2

23

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)
…”;



x

{

P(x)  

y

[

Q(?

,

?

) …

Metoda naukowa 2

24

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)
…”;



x

{

P(x)  

y

[

Q(y

,

x

) …

Metoda naukowa 2

25

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x) 

R(

?

,

?

)

]

}

Metoda naukowa 2

26

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x,

y)

]}

y[Q(y, x) :=
istnieje

przynajmniej
jeden

ogonek

pliszki

Metoda naukowa 2

27

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x,

y)

]}

y[Q(y, x) :=
istnieje
przynajmniej
jeden ogonek
(pliszki)
… R(x, y)] :=
(który) ona chwali

Metoda naukowa 2

28

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x,

y)

]}



Każda pliszka ma co
najmniej jeden
ogonek, który
chwali (może mieć

inne

i ich nie

chwalić).

Metoda naukowa 2

29

Niejawne kwantyfikatory



Każda pliszka

swój

ogonek

chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x, y)

]}



Każda pliszka ma co
najmniej jeden
ogonek, który
chwali (może mieć

inne

i ich nie

chwalić).



Może nie być ani
jednej pliszki.

Metoda naukowa 2

30

Niejawne kwantyfikatory



Każda pliszka swój ogonek
chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x, y)

]}



x

{

P(x)  

y

[

Q(y

, x)  R(x,

y)

]}



Każda pliszka ma co
najmniej jeden ogonek,
który chwali (może
mieć inne i ich nie
chwalić).



Każda pliszka chwali
każdy swój ogonek (ale
może nie mieć

żadnego

).

Metoda naukowa 2

31

Niejawne kwantyfikatory



Każda pliszka swój ogonek chwali.



P = „…jest pliszką”;



Q = „…jest ogonkiem (czyim?)…”;



R = „…chwali (co?) …”



x

{

P(x)  

y

[

Q(y

, x)  R(x, y)

]}



Niech pliszka ma
dokładnie jeden ogonek,
który chwali

• x{P(x)  y[Q(y, x)  R(x, y)] 

z[Q(z, x)

 z = y]

}

Metoda naukowa 2

32

Niejawne kwantyfikatory



Każda pliszka

tylko

swój ogonek chwali.

Niech nie chwali
żadnego
cudzego ogonka

Metoda naukowa 2

33

Niejawne kwantyfikatory



Każda pliszka

tylko

swój ogonek chwali.



x

{

P(x)  y

{

Q(y, x)  R(x, y) 

z[(Q(y, z)  R(x,

y)  z = x)]

}

}



Każda pliszka chwali swój ogonek, a żadnego cudzego (ale
nadal może mieć więcej niż jeden ogonek, wystarczy, że
tylko jeden z nich chwali i nadal może w ogóle nie być
żadnych pliszek).

Metoda naukowa 2

34

Niejawne kwantyfikatory



Każda pliszka tylko swój ogonek chwali.



x

{

P(x)  y

{

Q(y, x)  R(x, y)  z[(Q(y, z)  R(x, y) 

z = x)]

}

}



Niech każda pliszka chwali swój ogonek, a poza tym nic innego
nie chwali



x

{

P(x)  y

[

Q(y, x)  R(x, y) 

z(R(x, z)  z = y)

]

}



Teraz na dodatek każda pliszka chwali tylko jeden ze swoich
ogonków, o ile w ogóle są jakieś pliszki.



Metoda naukowa 2

35

Niejawne kwantyfikatory



x

{

P(x)  y

[

Q(y, x)  R(x, y)  z(R(x, z)  z =

y)

]

}



Teraz na dodatek każda pliszka chwali tylko jeden ze swoich
ogonków, o ile w ogóle są jakieś pliszki.

Dopuśćmy, że

(niektóre) pliszki mają więcej ogonków i też je chwalą, a
poza tym nic innego.

Metoda naukowa 2

36

Niejawne kwantyfikatory



x

{

P(x)  y

[

Q(y, x)  R(x, y)  z(R(x, z)  z = y)

]

}



Teraz na dodatek każda pliszka chwali tylko jeden ze swoich
ogonków, o ile w ogóle są jakieś pliszki. Dopuśćmy, że
(niektóre) pliszki mają więcej ogonków i też je chwalą, a poza
tym nic innego.



x

{

P(x)  y

[

R(x, y)  Q(y, x)

]

}



Każda pliszka, jeżeli cokolwiek chwali, to to, co chwali, jest jej
ogonkiem.

Metoda naukowa 2

37

Niejawne kwantyfikatory



x

{

P(x)  y

[

Q(y, x)  R(x, y)  z(R(x, z)



z = y)

]

}



Teraz na dodatek każda pliszka chwali tylko jeden ze swoich
ogonków, o ile w ogóle są jakieś pliszki. Dopuśćmy, że
(niektóre) pliszki mają więcej ogonków i też je chwalą, a poza
tym nic innego.



x

{

P(x)  y

[

R(x, y)  Q(y, x)

]

}



Każda pliszka, jeżeli cokolwiek chwali, to to, co chwali, jest jej
ogonkiem.



Niestety, to dopuszcza także, że (niektóre) pliszki, o ile jakieś
istnieją, w ogóle nic nie chwalą. Jak to poprawić?

Metoda naukowa 2

38

Niejawne kwantyfikatory



x

{

P(x)  y

[

Q(y, x)  R(x, y)  z(R(x, z)



z = y)

]

}



Teraz na dodatek każda pliszka chwali tylko jeden ze swoich
ogonków, o ile w ogóle są jakieś pliszki. Dopuśćmy, że
(niektóre) pliszki mają więcej ogonków i też je chwalą, a poza
tym nic innego.



x

{

P(x) 

x

R(x, y)



y

[

R(x, y)  Q(y, x)

]

}



Każda pliszka, jeżeli cokolwiek chwali, to to, co chwali, jest jej
ogonkiem.



Każda pliszka coś chwali, w tym przynajmniej jeden ze swoich
ogonków. Niekoniecznie wszystkie swoje ogonki.

Metoda naukowa 2

39

Empiryzm logiczny

Koło Wiedeńskie, 1922-1936

(1929-1931)



Kryterium demarkacji:
sensowne (naukowe) są zdania

weryfikowalne

empirycznie i

tylko one



związek z behawioryzmem

Moritz Schlick

(1882-1936)

Rudolf

Carnap

(1891-

1970)

Metoda naukowa 2

40

Empiryzm logiczny



Logika i matematyka są
narzędziami nauki



Zadanie filozofii: analiza
języka nauki

Moritz Schlick

(1882-1936)

Rudolf

Carnap

(1891-

1970)

Metoda naukowa 2

41

Trudności empiryzmu
logicznego



Czy jakakolwiek weryfikacja jest
możliwa?



Wymóg weryfikowalności można
zastąpić słabszym wymogiem

potwierdzalności

(stopniowalnej).

Metoda naukowa 2

42

Nauka i pseudonauka



Dążenie do potwierdzeń jest
właściwe pseudonauce.



Przykłady:



astrologia



marksizm



psychoanaliza Freuda

Karl Popper (1902-1994)

Logik der Forschung 1934

The Logic of Scientific Discovery

1959

Metoda naukowa 2

43

Nauka i pseudonauka



Zdania, które mogą się tylko
potwierdzić, nie mówią nic o
świecie.



Kryterium demarkacji: zdanie jest
naukowe wtedy i tylko wtedy, gdy
jest

falsyfikowalne

.

Metoda naukowa 2

44

Zasada krytycyzmu



Należy wysuwać śmiałe hipotezy, a następnie
usiłować je obalić.



Logiczny schemat falsyfikacji:



x(W(x)  Z(x)), W(a)

------------------------------

Z(a)

W(a), Z(a)

--------------------------





x(W(x)  Z(x))



Nauka składa się ze zdań przyjętych na próbę.

Metoda naukowa 2

45

Uteoretyzowanie obserwacji



Uteoretyzowanie obserwacji (theory-
impregnation, theory-ladeness):



Nie istnieje zdanie, które można byłoby
rozstrzygnąć na podstawie samej
obserwacji



bez wcześniejszych założeń
teoretycznych



bez wcześniejszych oczekiwań

Metoda naukowa 2

46

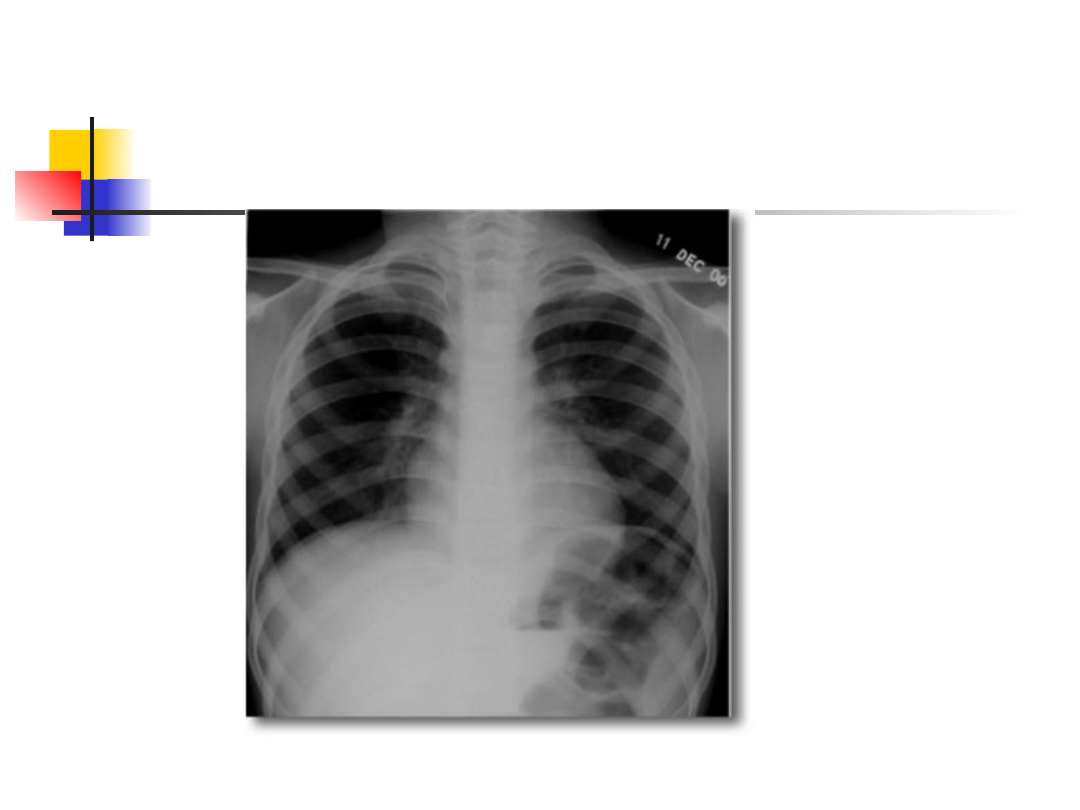
Uteoretyzowanie obserwacji

Metoda naukowa 2

47

Uteoretyzowanie obserwacji

Małe dzieci widzą na
zdjęciu obok dziewięć
delfinów.

Metoda naukowa 2

48

Hipoteza a eksperyment



Hipoteza poprzedza eksperyment.



Hipoteza jest niezależnym od doświadczenia
domysłem, który następnie jest sprawdzany w
doświadczeniu.

Metoda naukowa 2

49

Hipoteza a eksperyment



Hipotezy są genetycznie a priori, metodologicznie
empiryczne



hipotezy organizują eksperyment podobnie jak według
Kanta formy zmysłowości organizują doświadczenie



ale inaczej niż formy zmysłowości, hipotezy są
falsyfikowalne (podważalne przez doświadczenie

)



Falsyfikacjonizm jest formą

fallibilizmu

(antyfundamentyzmu)

Metoda naukowa 2

50

Realizm naukowy

Instrumentalizm

Przedmioty

teoretyczne

(hipotetycznie) istnieją

są dogodnymi fikcjami

Teorie naukowe

są

domys

ł

ami na temat

prawdy

narzędziami przewidywania

zjawisk

Celem nauki

jest

poszukiwanie prawdy

przewidywanie zjawisk

panowanie nad przyrodą

postęp techniczny

Argumenty

(motywy)

Potrzeby: wyjaśniania

heurystyki

  idei regulatywnej

nieufno

ść

do metafizyki

(empiryzm)

niejasno

ść

pojęcia prawdy