Mechanika

Mechanika

Ogólna

Ogólna

Statyka

Statyka

Wykład II

Wykład II

Adam F.

Adam F.

Bolt

Bolt

2

Plan wykładu

Plan wykładu

Część I Statyka



Pojęcia i zasady mechaniki technicznej



Zbieżne układy sił



Podstawy redukcji układów sił



Redukcja i równowaga płaskich układów
sił



Tarcie



Przestrzenny układ sił



Środki ciężkości

Wykład II
Zbieżne układy
sił

Plan wykładu

Zbieżne układy
sił



Płaski układ sił zbieżnych



Przestrzenny układ sił zbieżnych



Równowaga płaskiego układu sił
zbieżnych



Równowaga trzech sił
nierównoległych



Równowaga przestrzennegogo
układu sił zbieżnych

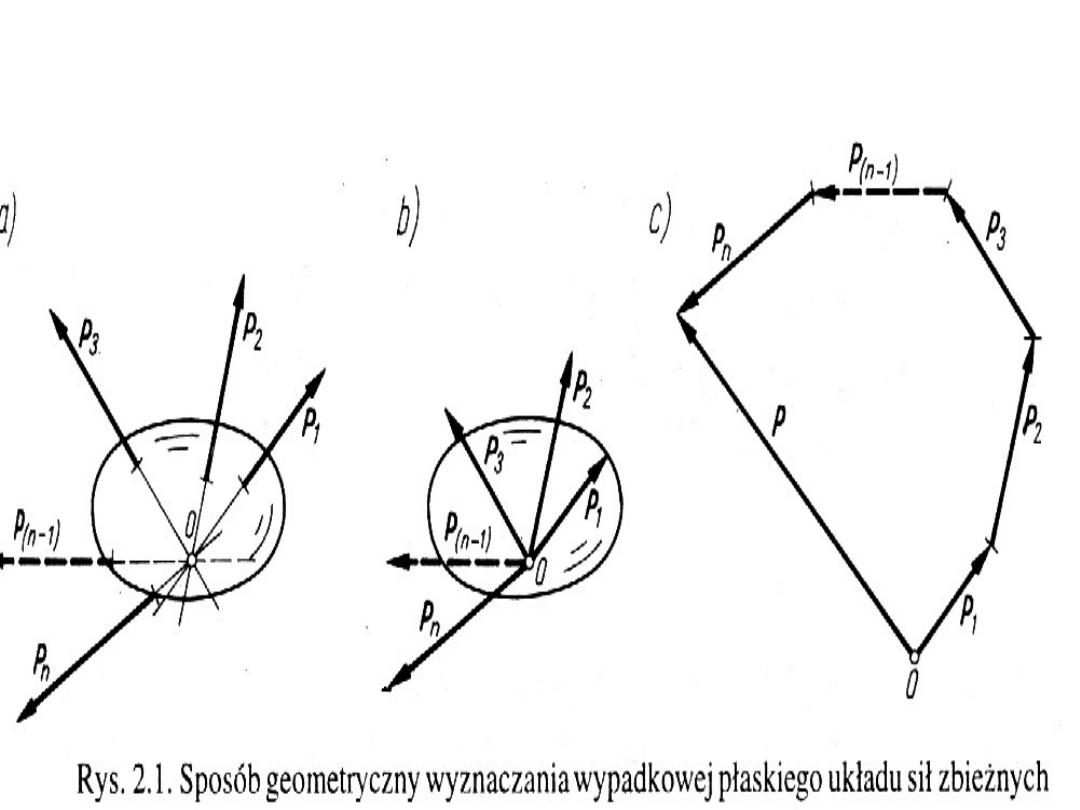
Sposób geometryczny
wyznaczania wypadkowej



Polega na zbudowaniu woieloboku
sił, w którym wektory sił odkłada
się rónolegle do ich linii działania
(jako wektory swobodne)

Płaski układ sił zbieżnych:



Płaski układ sił zbieżnych P

1

,

P

2

,P

3

, ... P

n

przyłożonych do punktu

O można zastąpić siłą wypadkową P
równą sumie geometrycznej tych sił
i przyłożoną również w punkcie O.

Płaski i przestrzenny układ sił

zbieżnych:

Sposób

Sposób

analityczny

analityczny

Sposób

Sposób

analityczny

analityczny

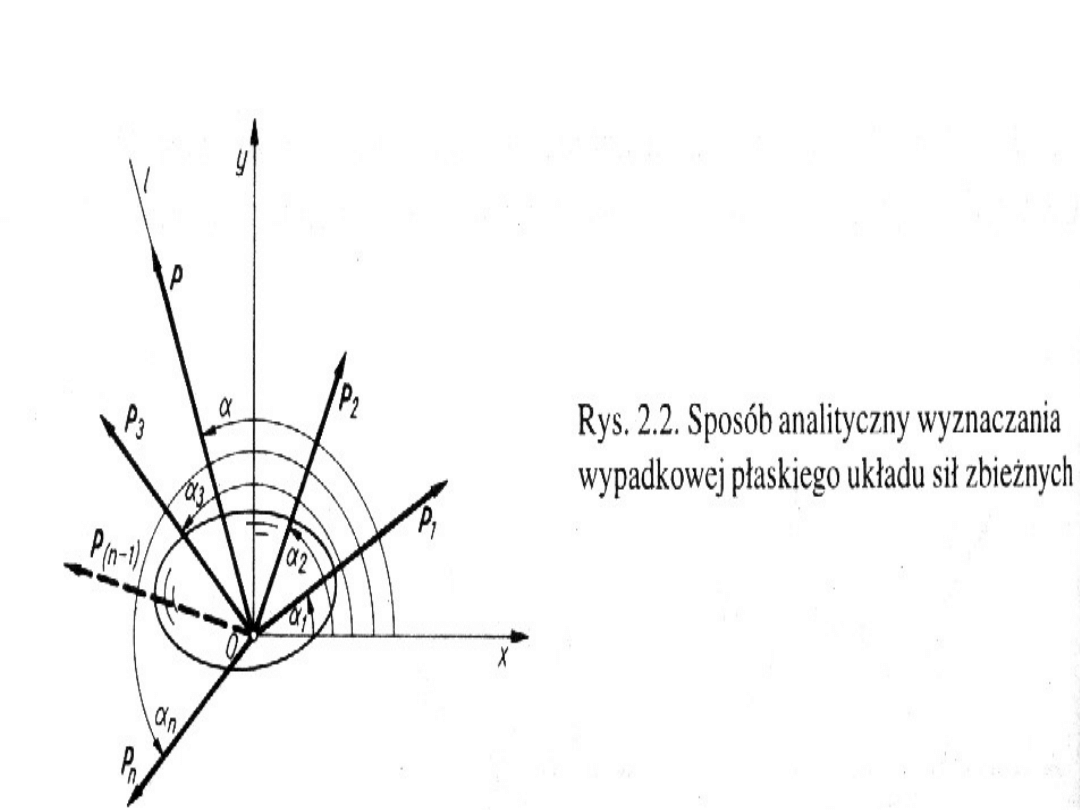
Sposób analityczny

Sposób analityczny

Twierdzenie o rzucie sumy wektorów

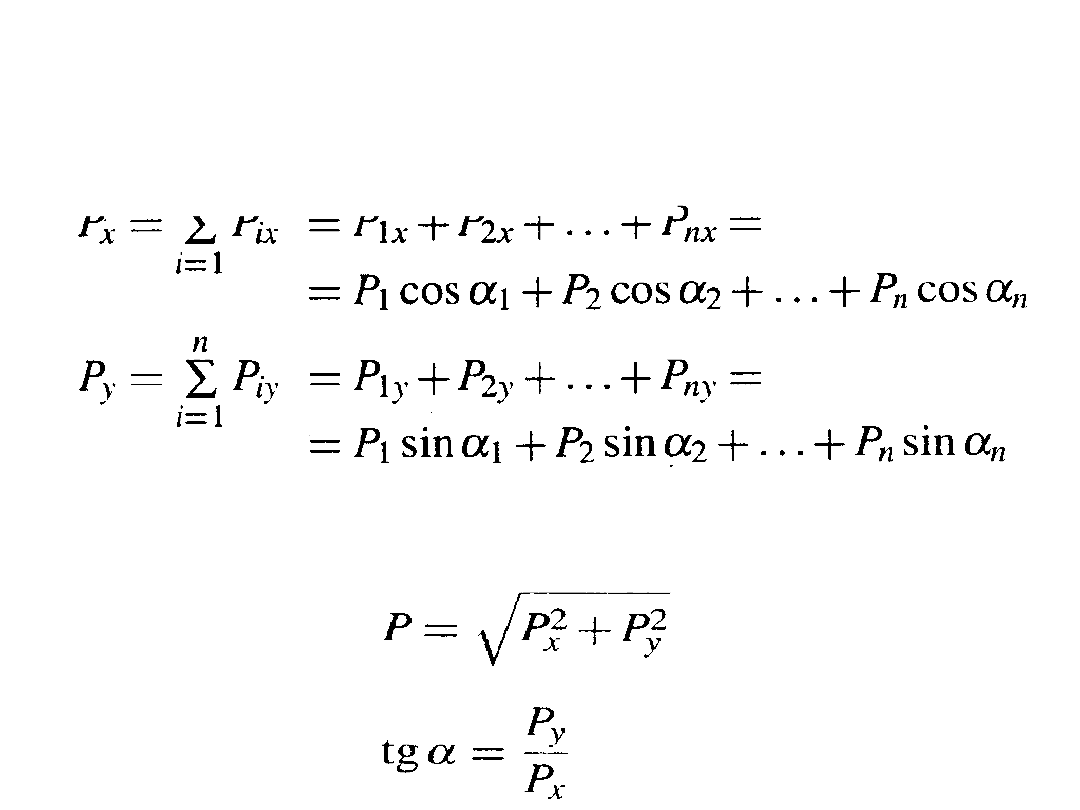
Wyznaczenie wypadkowej P i kąta

Wyznaczenie wypadkowej P i kąta





• wyznaczenie składowych P

x

i P

y

Określenie wartości liczbowych wypadkowej P
i kąta



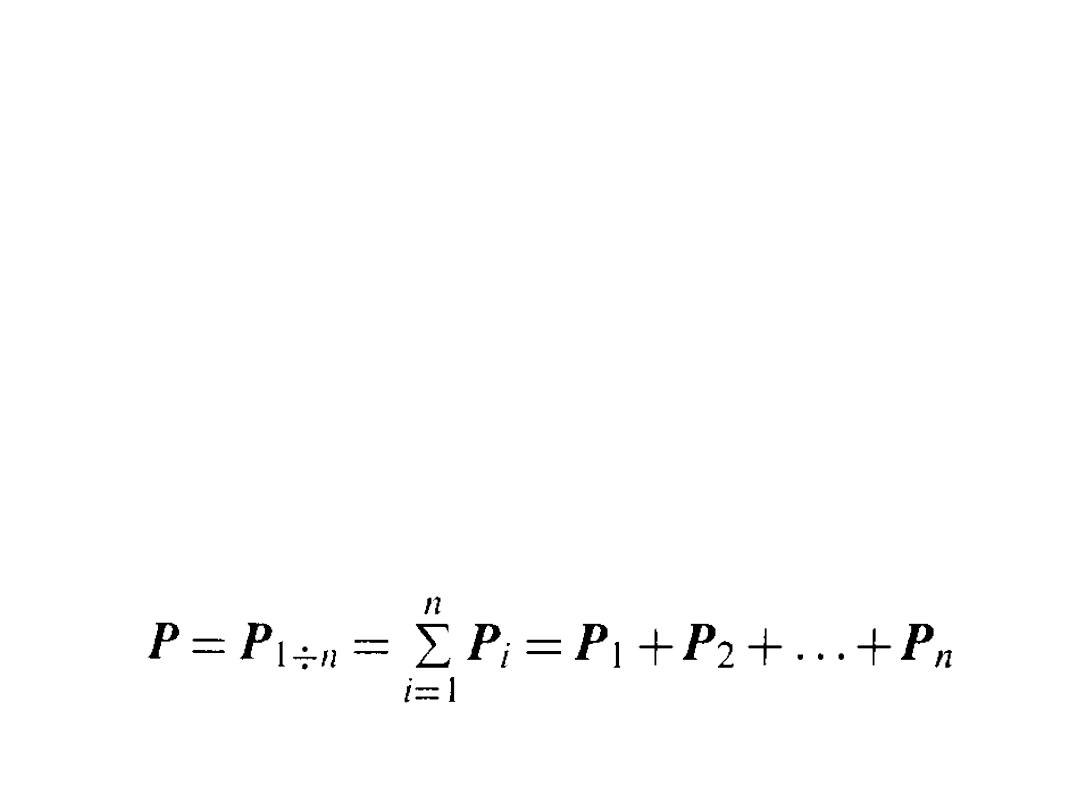
Przestrzenny układ sił zbieżnych

Przestrzenny układ sił zbieżnych P P . .
„ P, przyłożonych do jednego punktu O
można zastąpić jedną siłą wypadkową P
przyłożoną w tymże punkcie i równą
sumie geometrycznej tych sił.

Wypadkowa dowolnej liczby n sił przyłożonych do jednego

Wypadkowa dowolnej liczby n sił przyłożonych do jednego

punktu

punktu

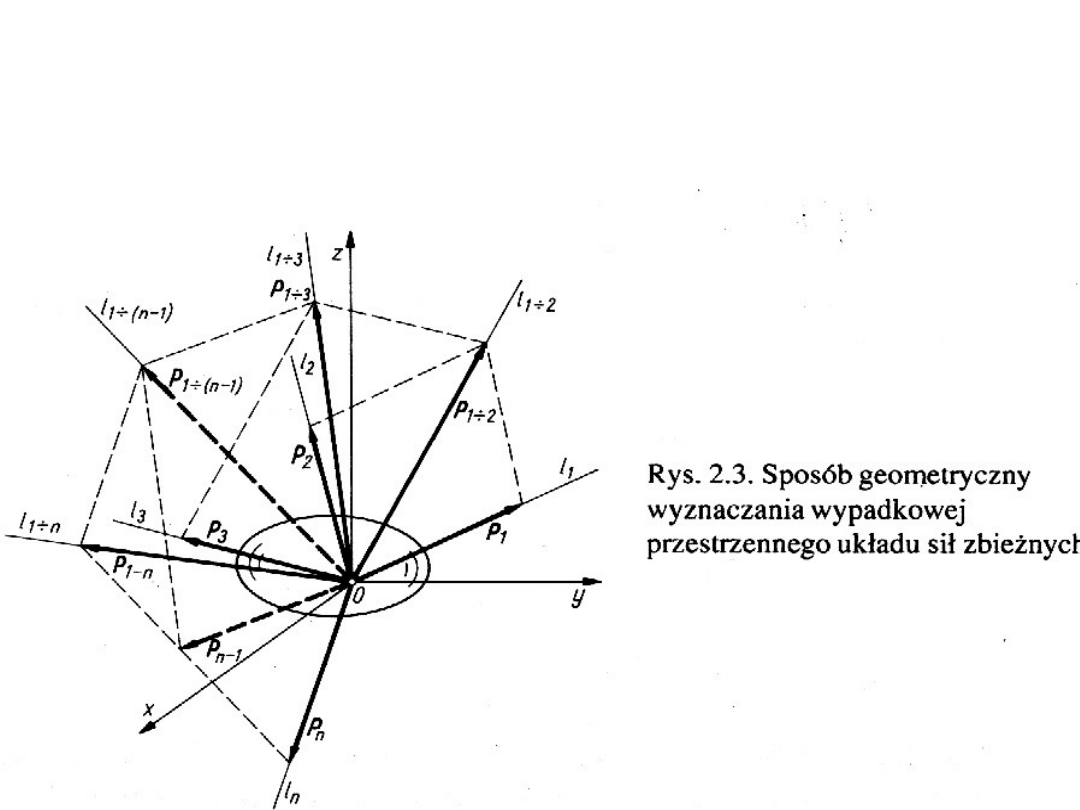
Sposób geometryczny
wyznaczania wypadkowej

Zastosowanie zasday równoległoboku

Zastosowanie zasday równoległoboku

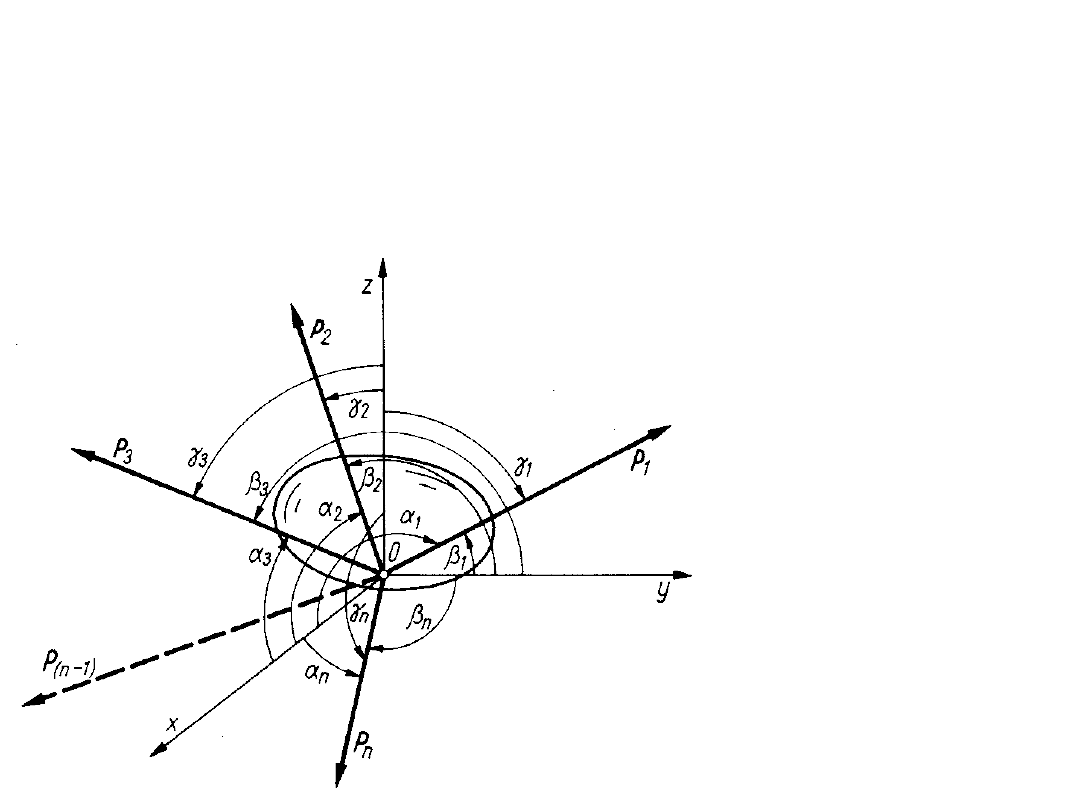
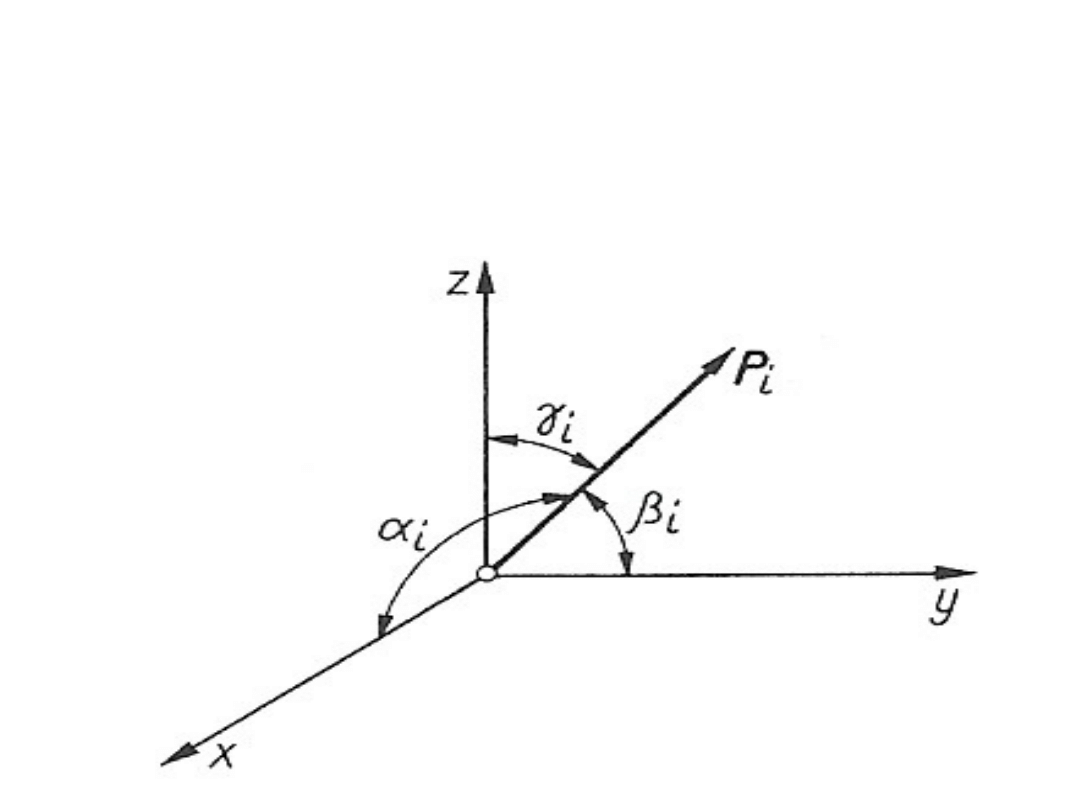
Oznaczając kąty
nachylenia sił do
osi x, y, z przez:












, (i

=1,2,..,n),
Oblicza się
wartości
algebraiczne
rzutów
wypadkowej P
sił P

i

, na

odpowiednie osie
układu

Sposób analityczny wyznaczenia
wypadkowej

Aby wyznaczyć wypadkową układu sił P

1,

P

2

,....,P

n

, których

linie działania przechodzą przez punkt 0, przyjmuje się
prostokątny układ osi Oxyz.

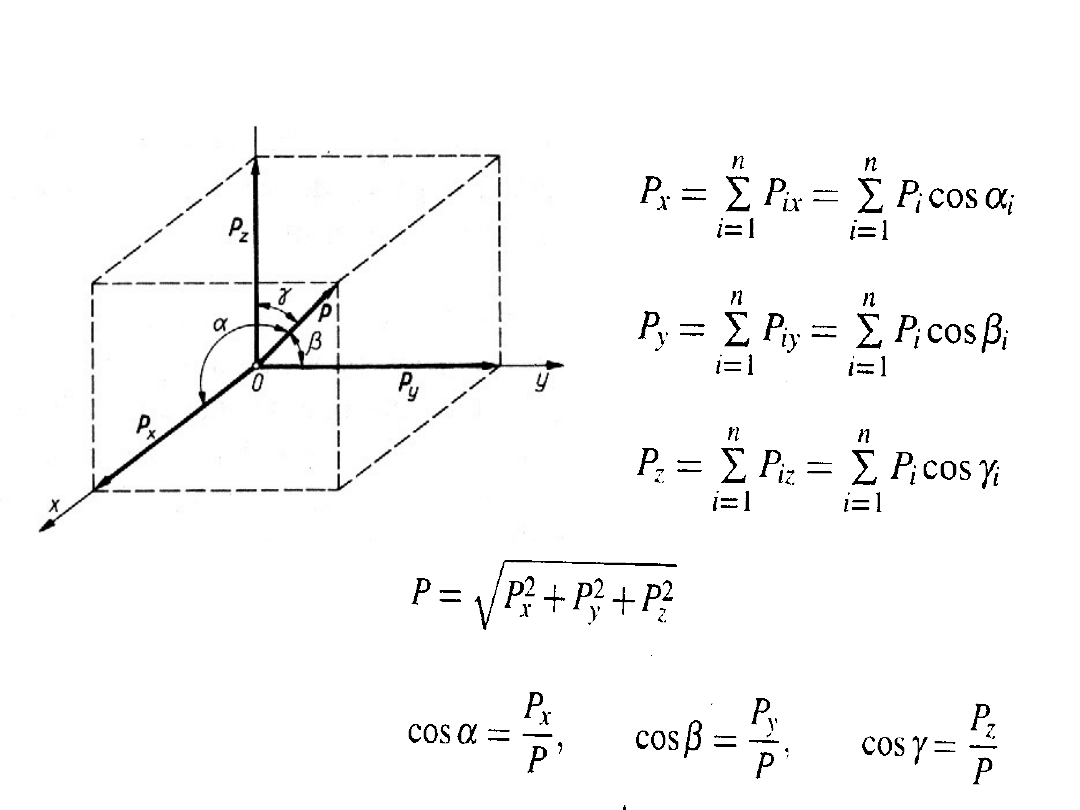
Obliczenie wartości

Obliczenie wartości

składowych

składowych

Sposób analityczny wyznaczenia
wypadkowej

Określenie

Określenie

wartości

wartości

liczbowej

liczbowej

( modułu )

( modułu )

wypadkowej

wypadkowej

P

P

oraz jej

oraz jej

cosinusów

cosinusów

kirunkowych

kirunkowych

Sposób analityczny wyznaczenia
wypadkowej cd.

Równowaga
płaskiego i przestrzennego
układu sił zbieżnych

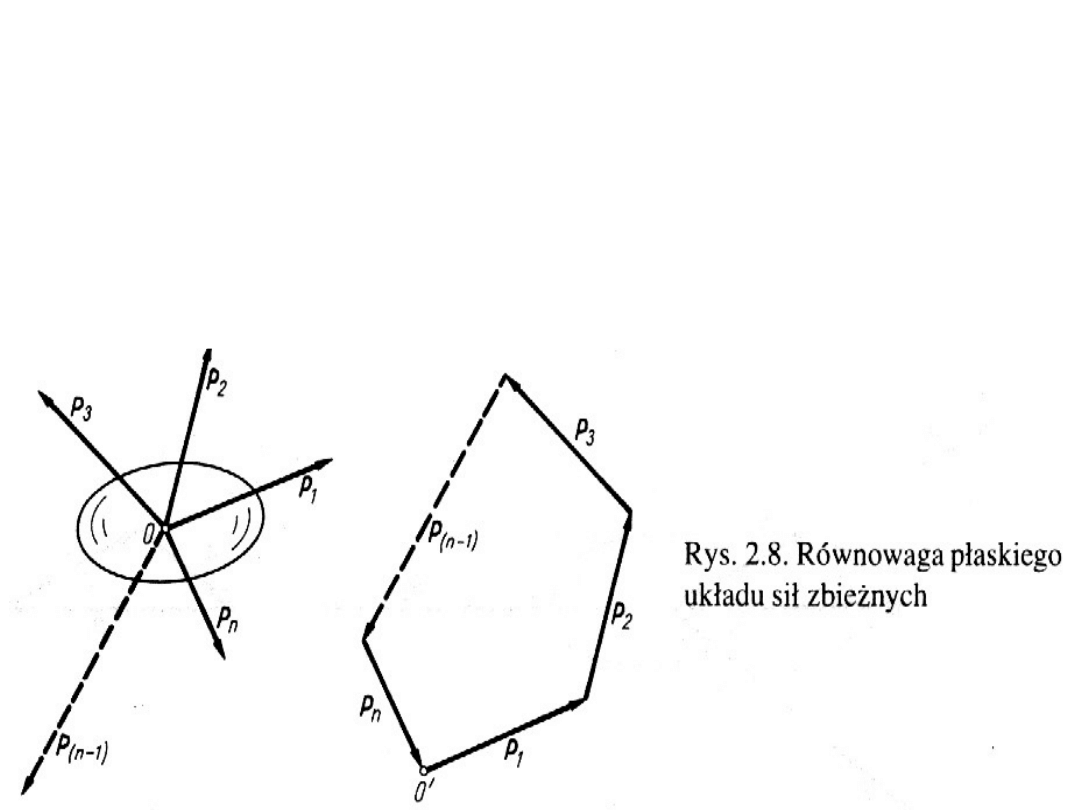
Równowaga płaskiego układu sił

zbieżnych

•W szczególnym przypadku suma geometryczna
płaskiego układu sił zbieżnych może być równa
zeru.

•Wielobok zbudowany z tych sił jest wielobokiem
zamkniętym a układ jego jest w równowadze.

Warunki równowagi płaskiego układu sił

zbieżnych

Rozwiązywanie zagadnień równowagi
płaskiego układu sił zbieżnych

•

Dla układu sił zbieżnych o

określonych liniach działania, należy
dysponować danymi liczbowymi (n —
2) sił.
• Wartości liczbowe dwóch
niewiadomych sił można wyznaczyć z
warunku równowagi

• Zakłada się, że na bryłę działają trzy
nierównoległe siły P P i P (rys. a), będące w
równowadze.

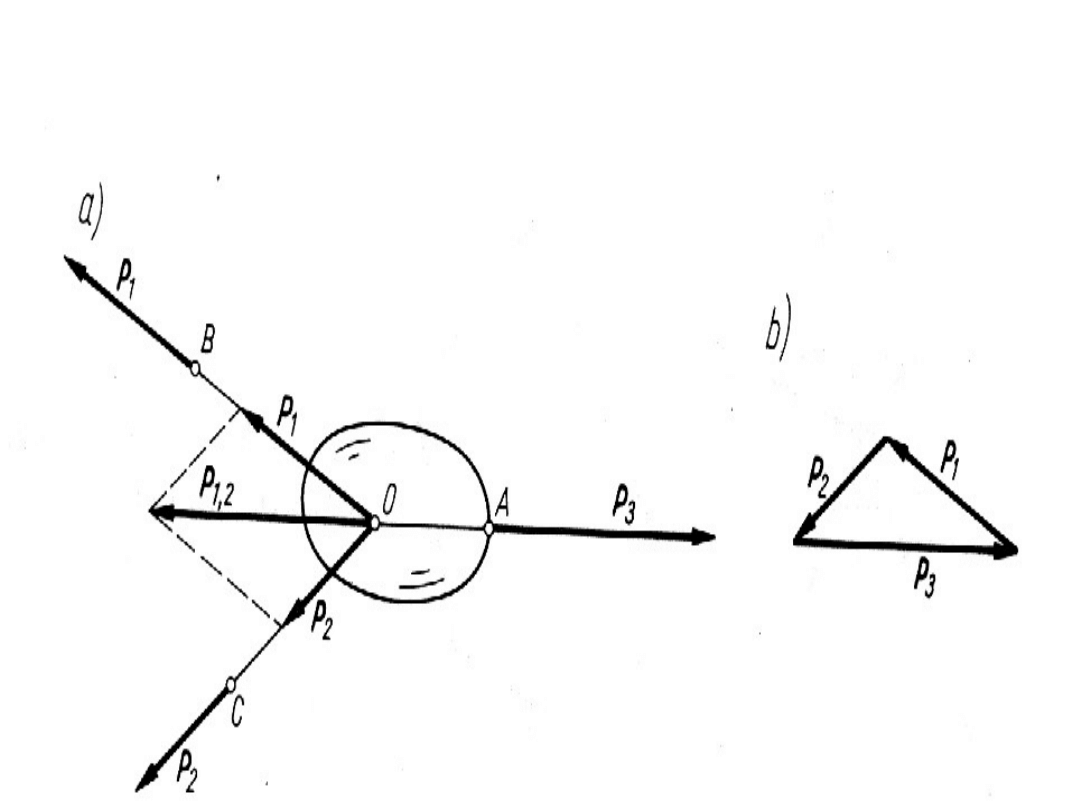
Równowaga trzech sił nierównoległych

m

m

m

m



wypadkowa dwóch z tych sił (np. P

1

i P

2

czyli

P

1,2

musi się równoważyć z siłą trzecią P

3

a

więc siły P

1,2

i P

3

muszą być równe co do

wartości liczbowych, przeciwne co do
kierunku i muszą działać wzdłuż jednej
prostej.



Stąd wynika, że linia działania siły P

3

musi

przechodzić także przez punkt 0, w którym
przecinają się linie działania sił P

1

i P

2

.



Oprócz tego, wielobok (trójkąt) sił P

1

,P

2

i P

3

musi być zamknięty (rys. b).

Równowaga trzech sił nierównoległych

Równowaga przestrzennego układu sił
zbieżnych

Równowaga przestrzennego układu sił
zbieżnych

Warunek równowagi w postaci

Warunek równowagi w postaci

wektorowej

wektorowej

Równowaga przestrzennego układu sił
zbieżnych

Przy rozwiązywaniu zagadnień równowagi
dotyczących n sił zbieznych o określonych
liniach działania musimy dysponować
danymi liczbowymi (n-1) sił.

Wartości pozostałych trzech niewiadomych
możemy wyznaczyć z równań równowagi.

Przy układaniu równań równowagi możemy
rzutować siły na trzy dowolne nierównoległe
do jednej płaszczyzny osi i nie musimy
ograniczać się do osi wzajemnie
prostopadłych ( rzut wypadkowej na każdą
oś jest równy zeru).

Dziekuje:D