Mechanika

Mechanika

Ogólna

Ogólna

Statyka

Statyka

Wykład VII

Wykład VII

Adam F.

Adam F.

Bolt

Bolt

Wykład VII

Wykład VII



Redukcja przestrzennego uładu sił
równoległych



Środki ciężkości



Środki ciężkości brył



Środki ciężkości powierzchni
(powłoki)



Środki ciężkości figur płaskich



Środki ciężkości linii



Twierdzenie Guldina (Pappusa)

Środki ciężkości

Środki ciężkości

Redukcja przestrzennego

Redukcja przestrzennego

układu sił równoległych

układu sił równoległych

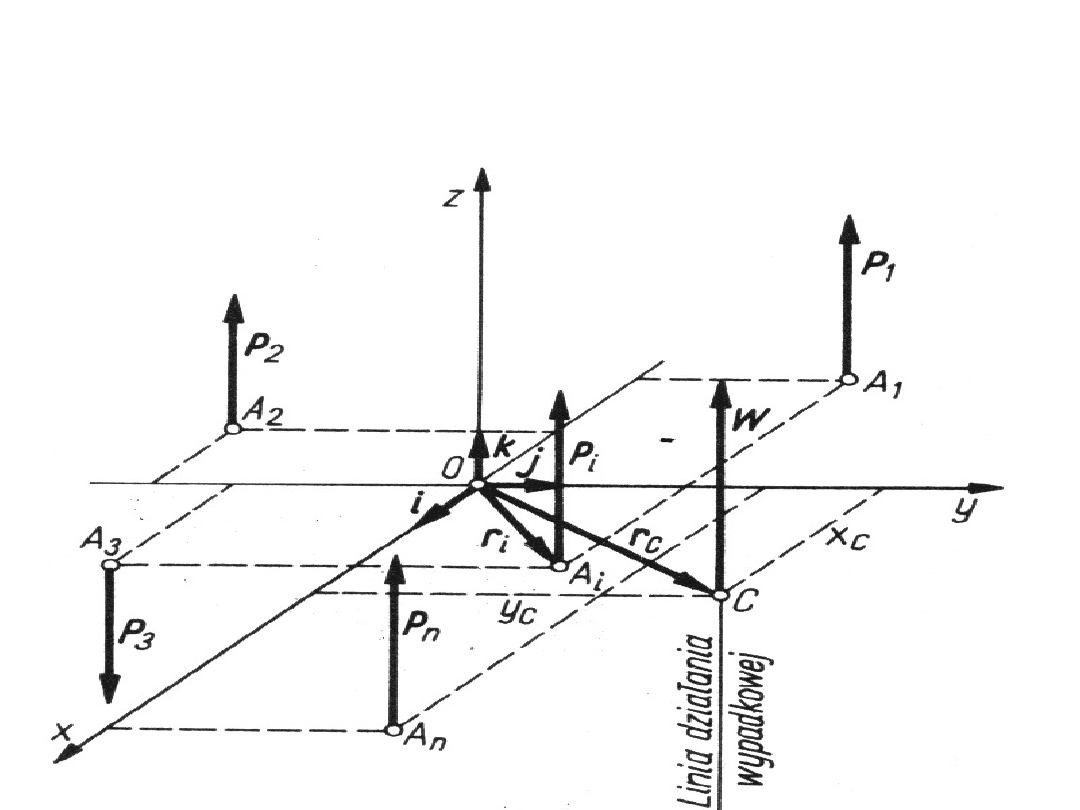
Redukcja przestrzennego układu
sił równoległych

Redukcja przestrzennego układu sił
równoległych

Twierdzenie Varignona

Ze wzoru (7.3) wynika, że moment główny jest
wektorem prostopadłym do osi z, czyli jest
również prostopadły do wektora głównego układu
sił (M

o

 R).

W takim przypadku układ sił równoległych
redukuje się do wypadkowej W = R =  P

i

.

Kierunek działania wypadkowej (linia działania
wypadkowej) jest równoległy do linii działania sił
równoległych.

Linię działania wypadkowej wyznaczamy na podstawie

Twierdzenia Varignona:
Moment siły wypadkowej W względem
dowolnego punktu równa się sumie
momentów układu sił względem tego
samego punktu (rys.)

Redukcja przestrzennego
układu sił

Równania (7.7) określają linię działania
wypadkowej, ponieważ wyznaczają jej
punkt przebicia z płaszczyzną Oxy, do
której jest ona prostopadła.
Wypadkową układu sił równoległych
określają jednoznacznie wektor główny R =
W i punkt C o współrzędnych x

C

i Y

C

Obróćmy teraz wszystkie siły P, o pewien kąt 

wokół ich punktów przyłożenia tak, aby były nadal
równoległe do siebie (rys. b).
Niech kierunki sił będą określone wersorem e.
Wypadkowa W jest wtedy równoległa do linii
działania wersora i równa:

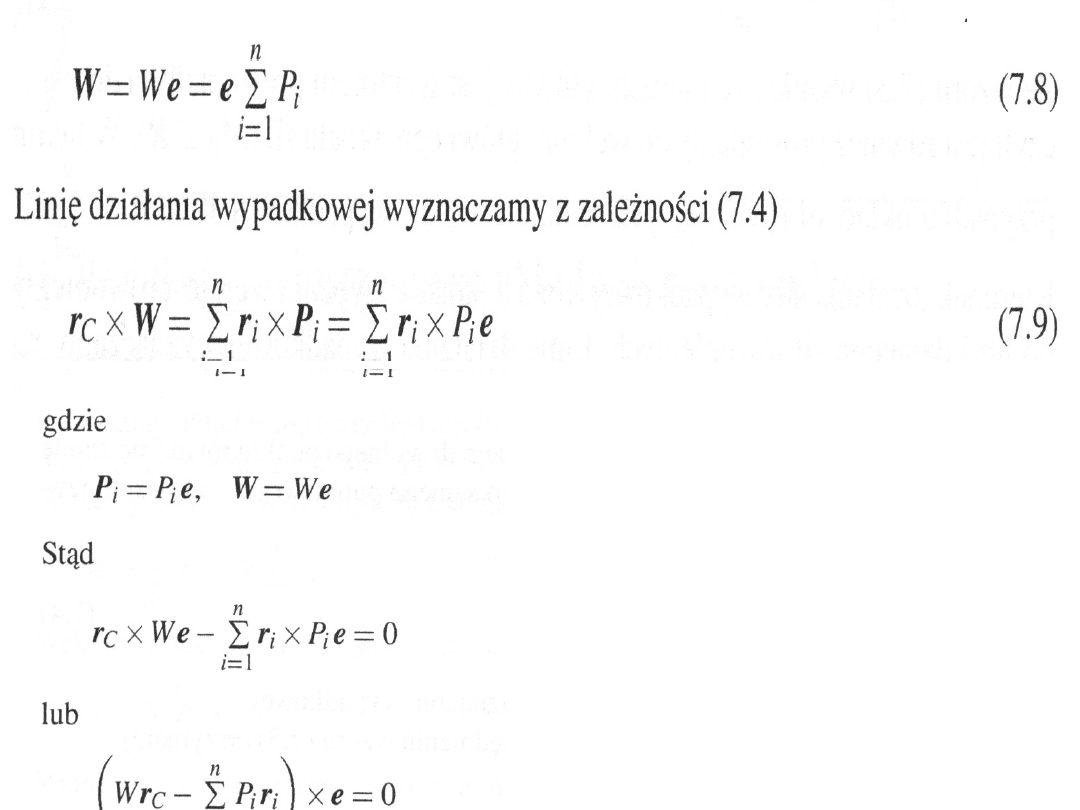
Punkt C mający tę własność, że przechodzi
przez niego wypadkowa układu sił
równoległych, niezależnie od kierunku tych
sił (przy niezmienionych punktach
przyłożenia i wartościach sił), nazywa się
środkiem sił równolegŁych.

Środek sił równoległych

Równania (7.1 1) określają współrzędne punktu C
— środka sił równoległych, którego położenie nie
zależy od wyboru kierunku wersora e. Przez punkt
ten przechodzi wypadkowa danego układu sił
równoległych.

Środki ciężkości

Siły ciężkości jako układ sił równoległych

 Najczęściej spotykanym przykładem sił
równoległych są siły ciężkości (tj. siły
przyciągania cząstek ciała materialnego
przez kulę ziemską), skierowane pionowo do
środka Ziemi.

Siły te możemy traktować jako równoległe,
gdyż wymiary ciał rozważanych w
zastosowaniach technicznych są bardzo
małe w porównaniu z promieniem kuli
ziemskiej.

Siły ciężkości są szczególnym przypadkiem
sił objętościowych, a więc działąją na każdy
element objętości danego ciała.

Środek sił równoległych w odniesieniu do
sił ciężkości nazywamy środkiem ciężkości.

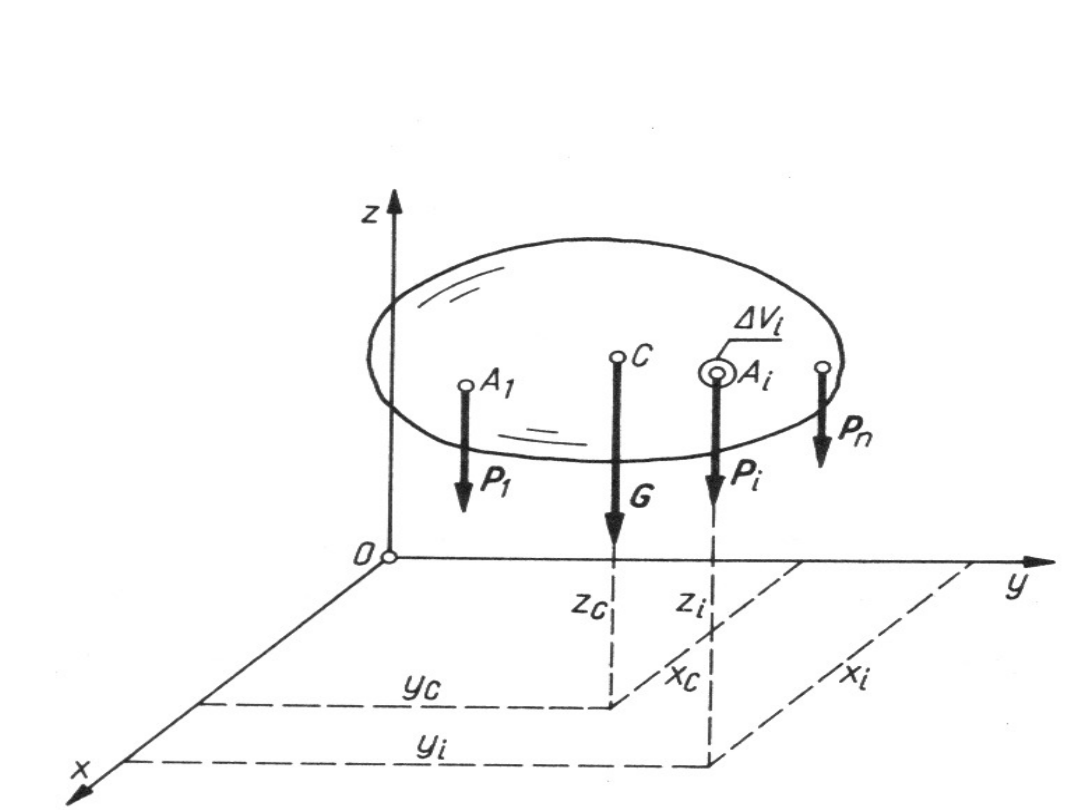
Siły ciężkości jako układ sił równoległych

Siły ciężkości jako układ sił równoległych

Ciężar ciała, czyli wypadkową sił ciężkości,
możemy uważać za przyłożony stale w
środku ciężkości C, niezależnie od położenia
ciała.

Przyjmując układ współrzędnych sztywno
związany z danym ciałem, powodu jemy, że
w przypadku obrócenia ciała, siły ciężkości
zmienią swój kierunek w stosunku do
układu współrzędnych. Natomiast punkty
ich przyłożenia w stosunku do tego układu
współrzędnych pozostają nie zmienione.

Zgodnie z własnością środka sił
równoległych wypadkowa sił ciężkości
będzie przechodziła zawsze przez ten sam
punkt C — środek ciężkości.

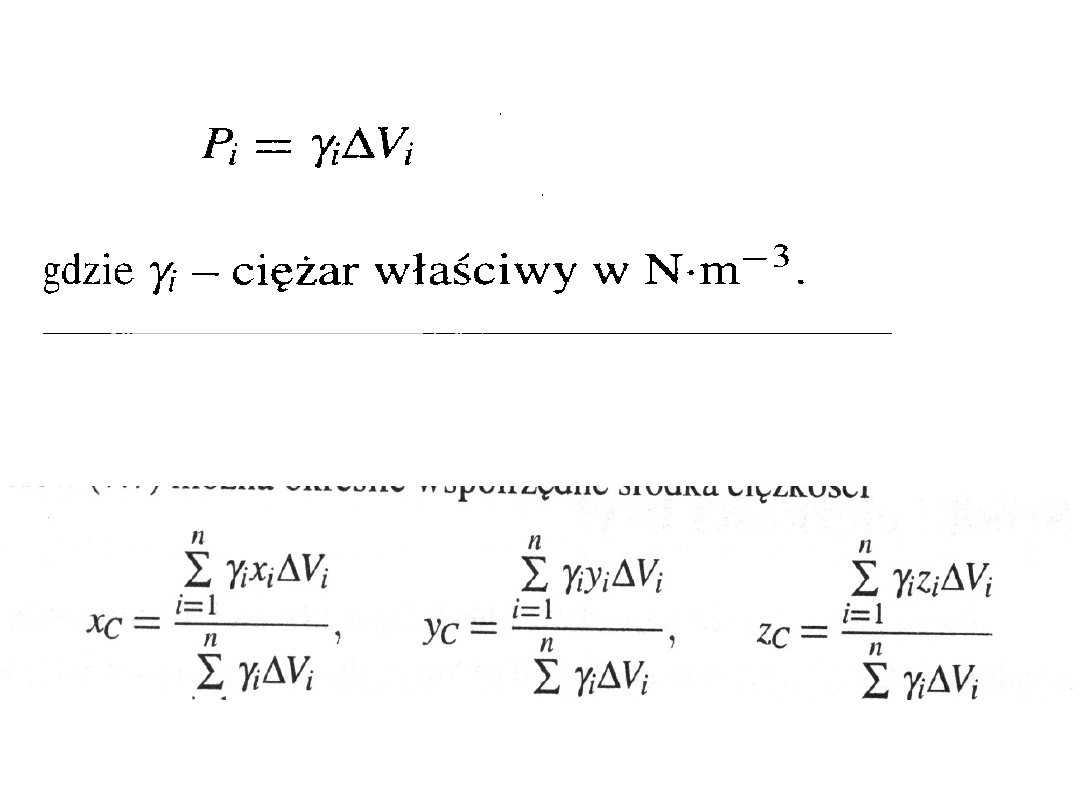
Wartość siły ciężkości

Współrzędne środka ciężkości

(Wzory przybliżone)

7.1
2

7.13

Wzory dokładne

7.1
4

7.1
5

Aby otrzymać wzory dokładne należy
rozpatrzyć graniczny przypadek, gdy liczba
elementów n dąży do nieskończoności a ich
wymiary dążą do zera.

Przypadek ogólny

7.1
6

7.17

7.18

7.14

Współrzędne środka ciężkości C zależą od kształtu ciała oraz
rozkładu masy

Środki ciężkości brył

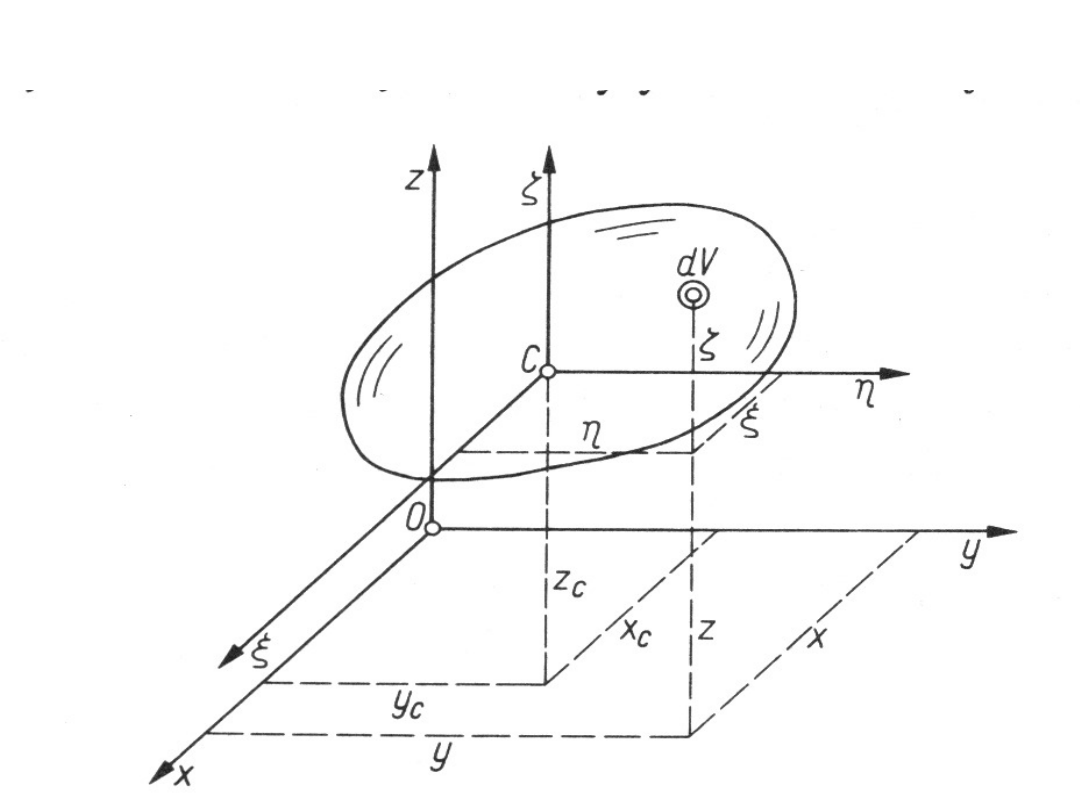
Położenie środka ciężkości dowolnej
bryły

W przypadku ciał jednorodnych  =const)

7.19

Położenie środka ciężkości dla ciała
jednorodnego zależy tylko od kształtu
geometrycznego ciała. Dlatego środek
ciężkości ciała jednorodnego nazywamy

środkiem ciężkości bryły geometrycznej

.

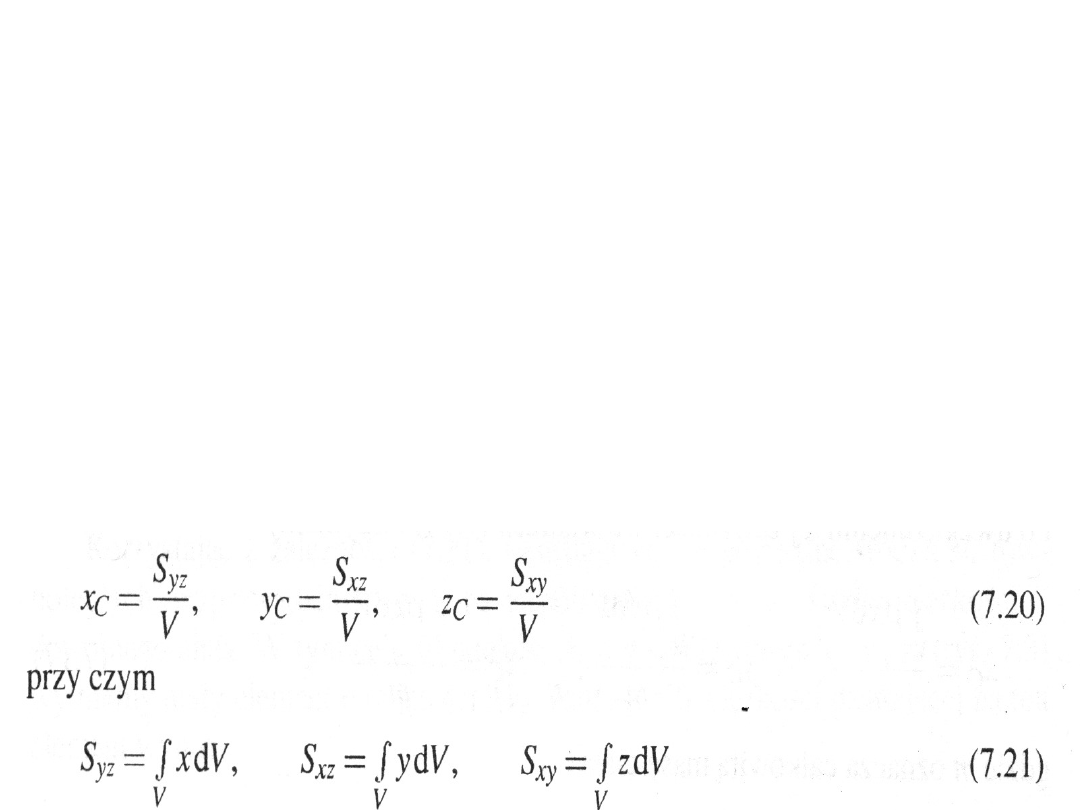
Wyrażenia w licznikach wzorów (7.19) noszą
nazwę

momentów statycznych objętości

bryły

względem odpowiednich płaszczyzn

układu, a ich wymiar jest równy jednostce
długości do potęgi czwartej.
Momenty statyczne oznaczamy literą S z
odpowiednim indeksem, określającym
płaszczyznę, względem której oblicza się
moment statyczny.

Po wprowadzeniu tych oznaczeń wzory
(7.19) przyjmują postać:

Współrzędne elementarnej objętośći
dV są równe:

Moment statyczny bryły względem
płaszczyzny równa się objętości bryły
pomnożonej przez współrzędną środka
ciężkości bryły, prostopadłą do tej
płaszczyzny.

Położenie środka ciężkości brył
geometrycznych można wyznaczyć:

 metodą analityczną polegającą na
zastosowaniu wzorów (7.19).

 metodą momentów statycznych, w której
korzystamy z twierdzenia, że moment
statyczny bryły względem płaszczyzny
przechodzącej przez środek ciężkości jest
równy zeru (wzory (7.22),

metodą dzielenia ( stosowaną najczęściej
w praktyce inżynierskiej przy obliczaniu
środka ciężkości bryły),

metodą uzupełniania ( metoda mas
ujemnych)

Metoda dzielenia składa się z
następujących etapów:



dokonujemy podziału bryły na proste

elementy, których położenie środków
ciężkości jest znane,

 obliczamy momenty statyczne bryły
względem płaszczyzn przyjętego układu
współrzędnych x, y, z (sumując iloczyny
objętości brył prostych i współrzędnych
środków ciężkości),

obliczamy ze wzorów (7.20)
współrzędne środka ciężkości bryły
(dzieląc momenty statyczne bryły przez
całkowitą objętość bryły).

W szczególnych przypadkach przy
zastosowaniu metody symetrii;
(twierdzenia ułatwiające określenie
położenia środka ciężkości)

Jeżeli bryła ma płaszczyznę symetrii, to
środek ciężkości leży w tej płaszczyźnie.

Gdy bryła ma dwie płaszczyzny symetrii,
środek ciężkości leży na linii ich przecinania
się.

Gdy bryła ma trzy płaszczyzny symetrii,
środek ciężkości leży w punkcie przecięcia
się tych płaszczyzn.

Metoda uzupełniania ( metoda mas
ujemnych)

 polega na tym, że bryłę uzupełnia się
inną bryłą tak dobraną, aby uzyskać
bryłę o możliwie prostej postaci.

 Wyznaczenie środka ciężkości
sprowadza się wówczas do metody
momentów statycznych, odejmując od
momentu statycznego otrzymanej bryły
moment statyczny bryły uzupełniającej.

Środki ciężkości
powierzchni (powłoki)

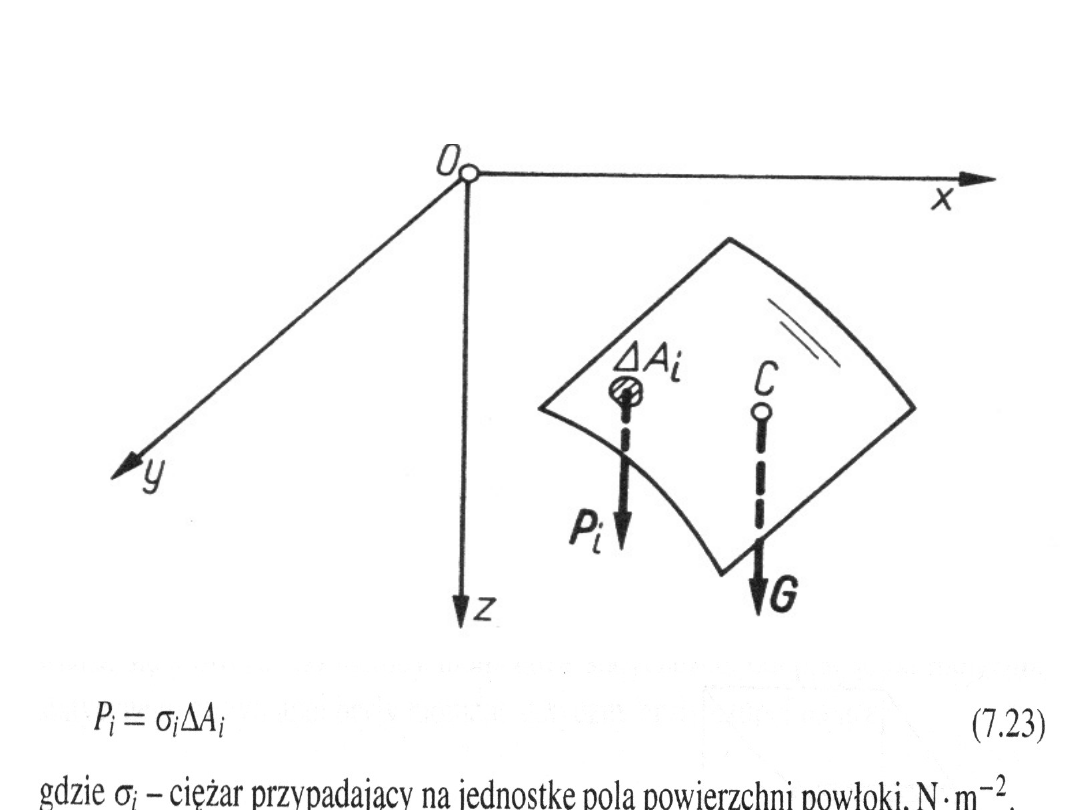
Wyznaczenie położenia środka
ciężkości dowolnej powłoki

Wyznaczenie położenia środka ciężkości dowolnej
powłoki

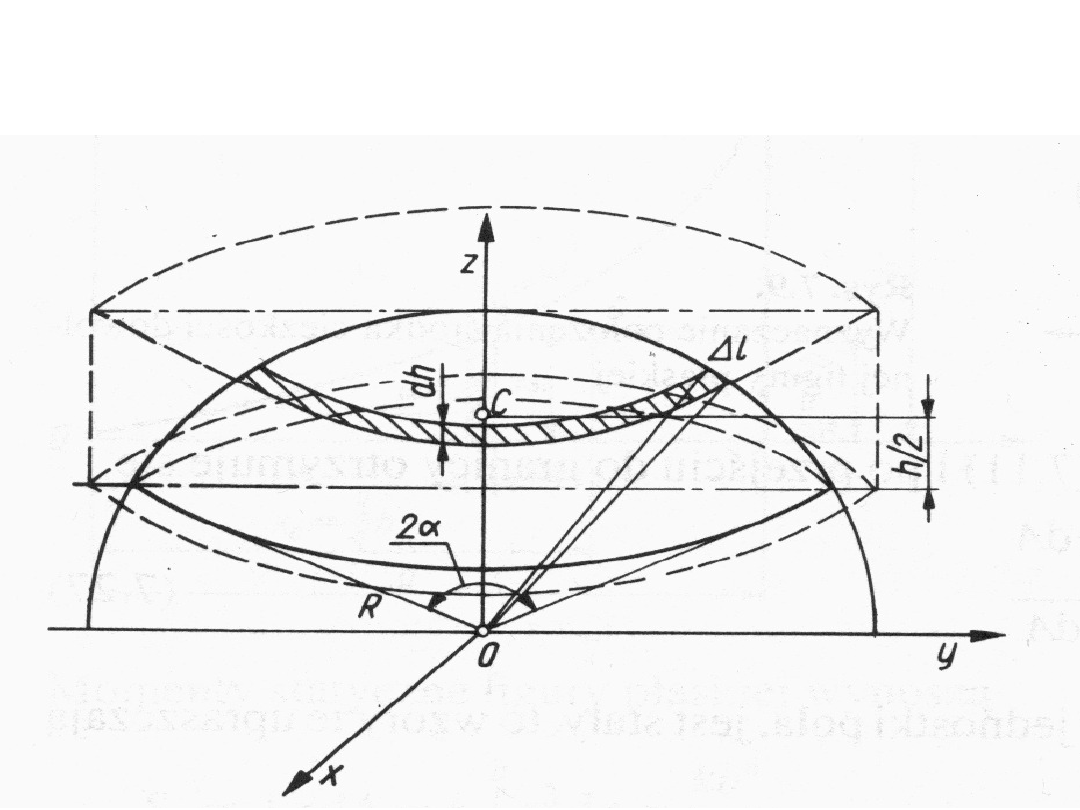
Wyznaczenie położenia środka
ciężkości powłoki czaszy kulistej

Wyznaczenie położenia środka
ciężkości powłoki czaszy kulistej

Środki ciężkości figur płaskich

Wyznaczenie położenia środka ciężkości
dowolnej figury płaskiej

Wyznaczenie położenia środka ciężkości figur
płaskich

Wyznaczenie położenia środka ciężkości figur
płaskich

Środki ciężkości linii

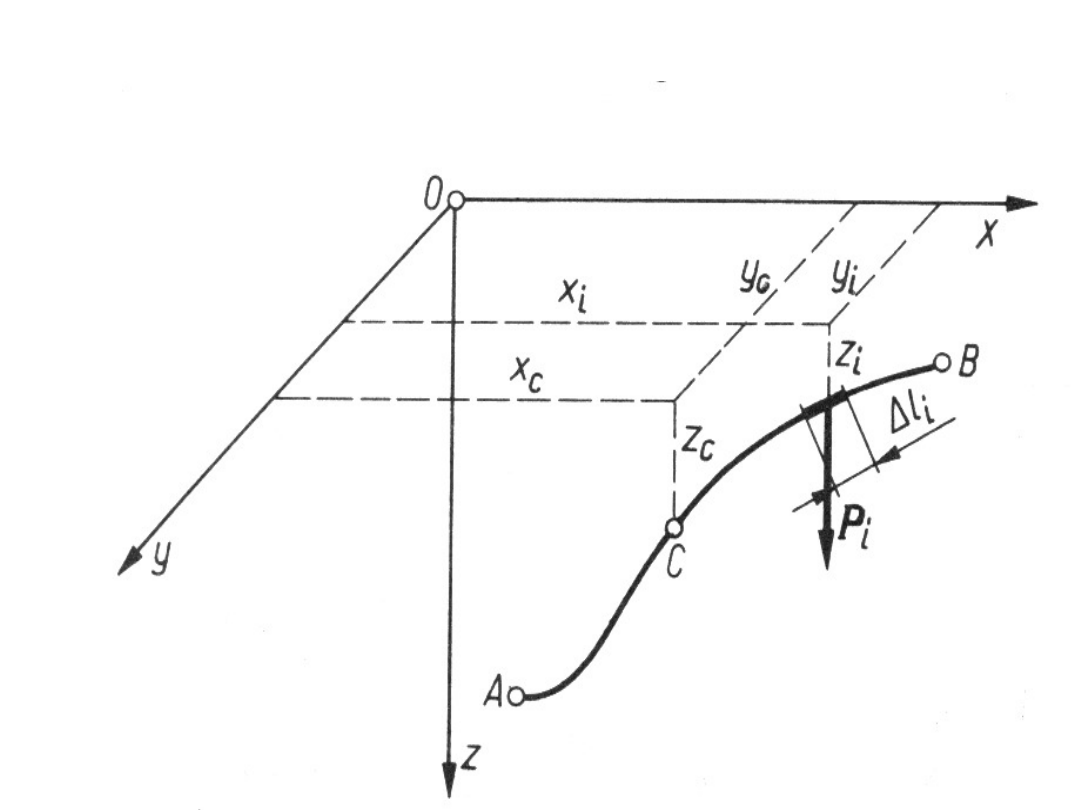
Wyznaczenie położenia środka ciężkości dowolnej
linii

Ciężar elementu o długości l

i

jest określony wzorem:

Twierdzenia Guldina -
Pappusa

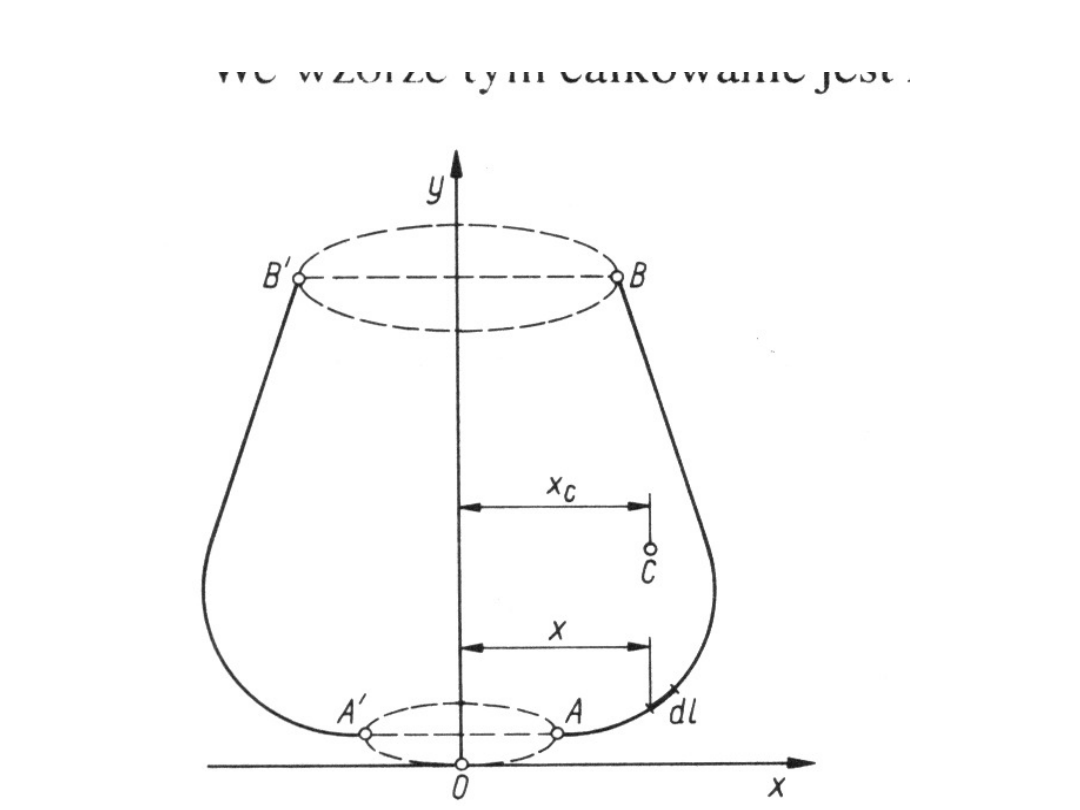
Twierdzenie I Guldina - Pappusa

I Twierdzenie Guldina -
Pappusa

Pole powierzchni A powstałej
przez obrót płaskiej linii o
długości l dookoła osi leżącej
w płaszczyźnie tej linii i nie
przecinającej jej jest równe
iloczynowi długości linii I
przez długość obwodu okręgu
2x

c

, który opisuje jej środek

ciężkości.

Twierdzenie I Guldina - Pappusa

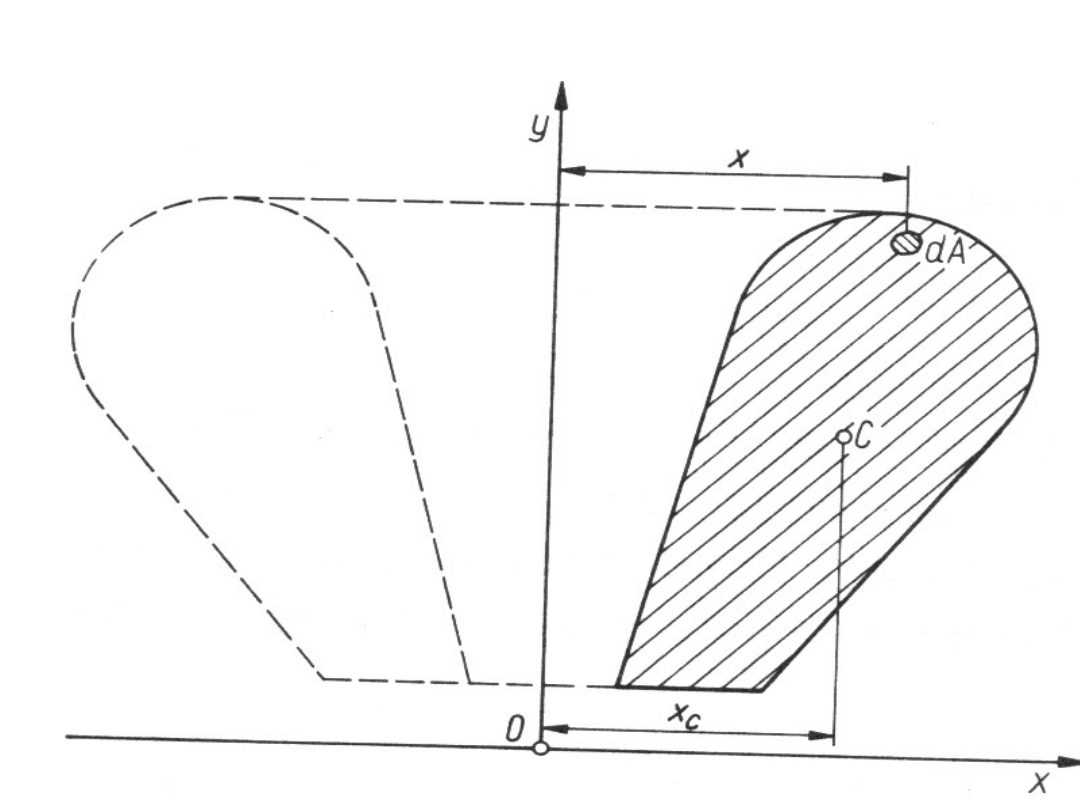
Twierdzenie II Guldina - Pappusa

Twierdzenie II Guldina -
Pappusa

Objętość bryły powstałej wskutek
obrotu figury płaskiej, o polu A,
dookoła osi leżącej w jej
płaszczyźnie i nie przecinającej
tej figury równa się iloczynowi
pola powierzchni A przez długość
obwodu okręgu 2 x

c

, który

opisuje środek ciężkości.

Twierdzenie II Guldina - Pappusa