Mechanika
Mechanika
Ogólna
Ogólna
Statyka
Statyka
Wykład VI
Wykład VI
Adam F.
Adam F.
Bolt
Bolt
Mechanika
Mechanika
Ogólna
Ogólna
Statyka
Statyka
Wykład VI
Wykład VI
Adam F.
Adam F.
Bolt
Bolt
Wykład VI
Wykład VI
Redukcja dowolnego przestrzennego
układu sił
Redukcja dowolnego przestrzennego
układu sił do skrętnika
Redukcja dowolnego przestrzennego
układu sił do dwóch sił skośnych
Redukcja dowolnego przestrzennego
układu sił do siły wypadkowej
Redukcja dowolnego przestrzennego
układu sił do pary sił
Równowaga dowolnego przestrzennego
układu sił
Dowolny przestrzenny układ
Dowolny przestrzenny układ
sił
sił
3
Redukcja dowolnego
przestrzennego
uładu sił
4
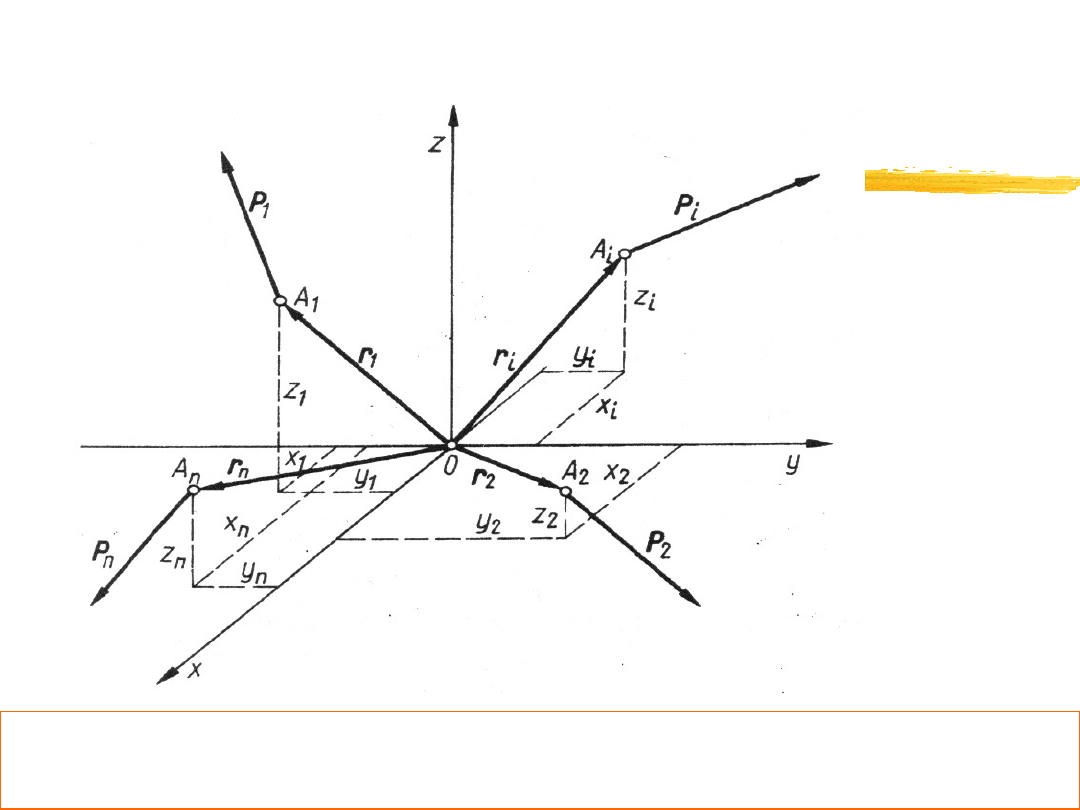
Przestrzenny układ sił
Układ sił o dowolnie rozmieszczonych w przestrzeni
liniach działania
5
Przestrzenny układ sił
6
Redukcja pzestrzennego układu
sił
Przestrzenny układ sił działających na ciało
sztywne można zastąpić siłą R przyłożoną
do dowolnie wybranego środka redukcji 0,
równą sumie geometrycznej wszystkich sił
układu, oraz parą sił o momencie M
o
równym sumie geometrycznej momentów
tych sił względem środka redukcji.
R - wektor główny
Mo - moment główny względem środka
redukcji O
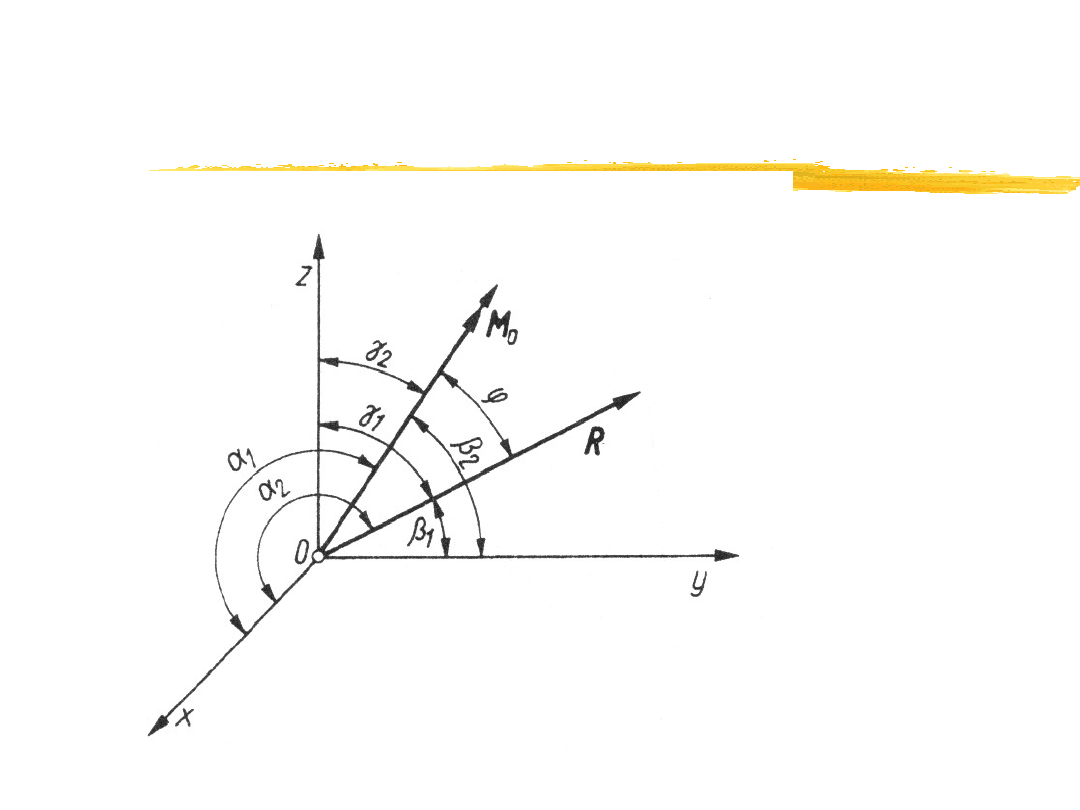
7
Wektor główny R i moment główny M
o
przestrzennego układu sił
8
Wektor główny R
9
Moment główny M
o
przestrzennego układu
sił
10
Moment główny M
o
przestrzennego układu
sił
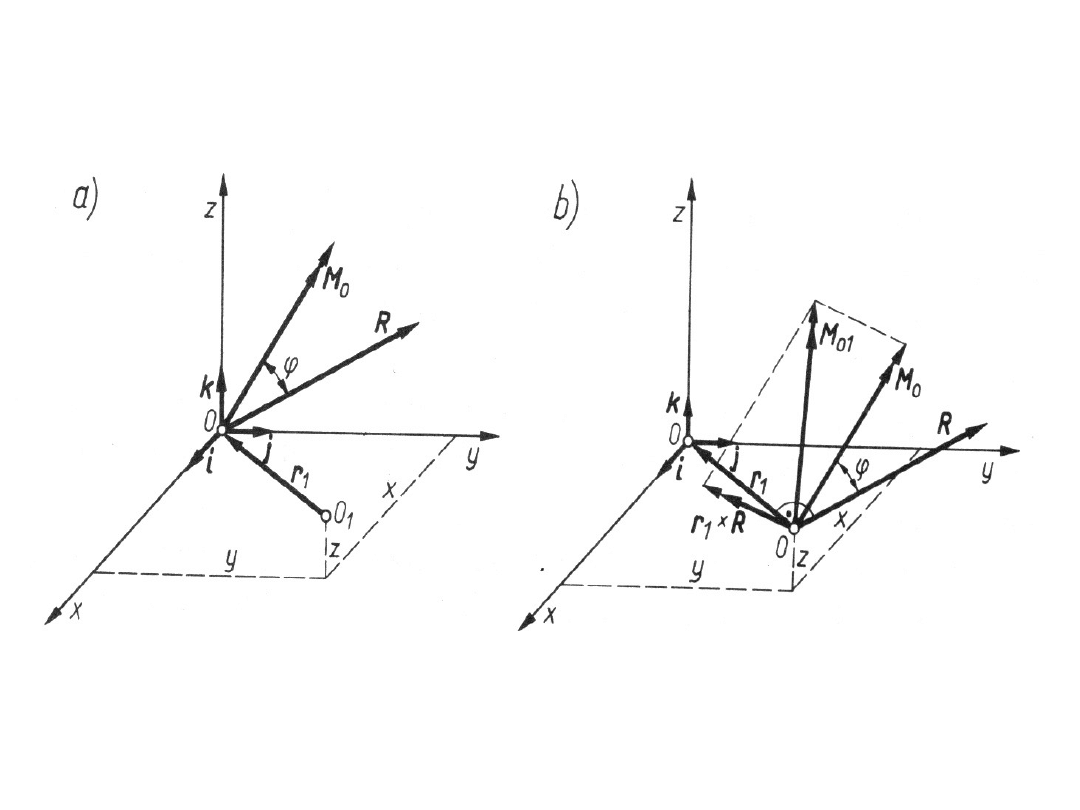
11
Redukcja układu sił do nowego środka
Redukcja układu sił do nowego środka
redukcji
redukcji
O
O
1
1
Zakłada się,że układ n sił, zredukowany
względem środka redukcji O można zredukować
względem innego środka redukcji np. punktu
O
1
12
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
nowego środka redukcji
nowego środka redukcji
Zredukowanie układu n sił względem
innego środka redukcji powoduje
jedynie zmianę momentu głównego
układu, nie wywołując zmiany wektora
głównego.
Moment główny względem środka redukcji O
1
wynosi:
M
o1
= M
o
= r
1
x R (6.8)
13
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
nowego środka redukcji
nowego środka redukcji
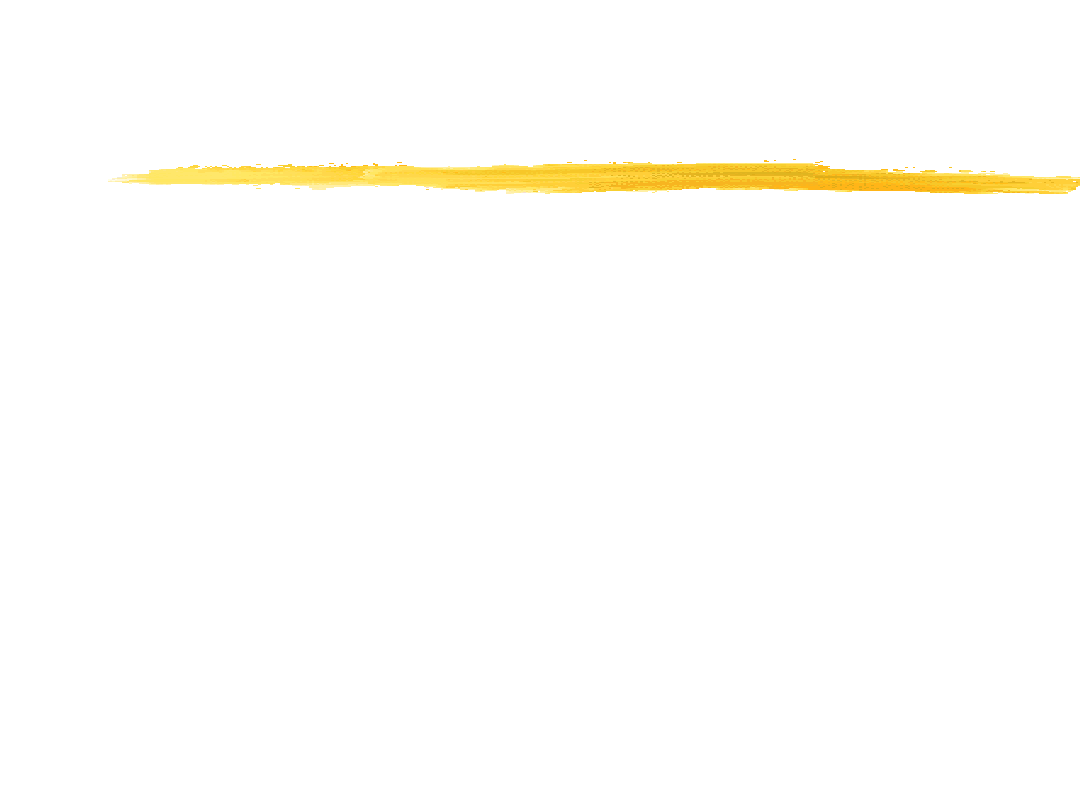
14
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
nowego środka redukcji
nowego środka redukcji
Iloczyn skalarny momentu głównego układu
względem dowolnego środka redukcji i
wektora głównego jest stały, ponieważ
wektor główny R nie zależy od wyboru
środka redukcji.
15
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
nowego środka redukcji
nowego środka redukcji
Z zależności (6.10) dodatkowo wynika, że
iloczyn M
o
cos
jako wartość rzutu
momentu głównego M
o
na kierunek
wektora głównego jest także wielkością
stałą.
Zatem każdy układ sił ma dwa
niezmienniki (tj. wielkości niezależne od
położenia środka redukcji), którymi są:
wektor główny R oraz rzut momentu
głównego M obliczonego względem
dowolnego środka redukcji O na kierunek
wektora głównego R.
16
Redukcja
dowolnego
przestrzennego
układu sił do
skrętnika
17
Redukcja przestrzennego układu
Redukcja przestrzennego układu
n
n
sił do
sił do
skrętnika
skrętnika
Układ wektora głównego R i momentu głównego Mo,
obliczonego względem środka redukcji O mozna
zredukować
do prostszej postaci.
18
Redukcja przestrzennego układu
Redukcja przestrzennego układu
n
n
sił do
sił do
skrętnika
skrętnika
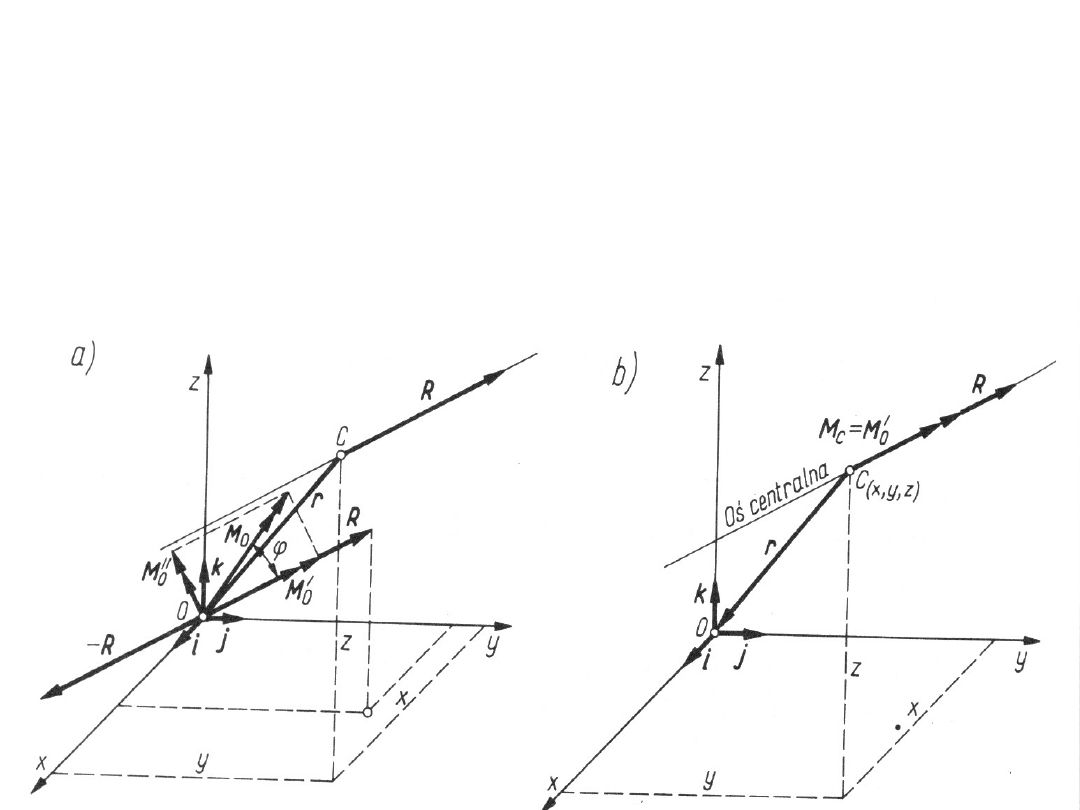
Moment główny Mo rozkłada się na dwie
składowe:
M’o— zgodną z kierunkiem wektora głównego R
M”o— prostopadłą do tego wektora.
Następnie składową M”o zastę puje się parą sił
(—R, R), leżącą w płaszczyźnie prostopadłej do
M”o przy czym siła (—R) jest przyłożona w
punkcie O.
Linia działania drugiej siły R będzie przechodzić
przez pewien szczególny punkt C, którego
położenie jest opisane promieniem wektorem r,
wynikającym z następującej zależności:
która określa równoważność zastępowania wektora
M”o
parą sił (—R, R).
19
Redukcja przestrzennego układu
Redukcja przestrzennego układu
n
n
sił do
sił do
skrętnika
skrętnika
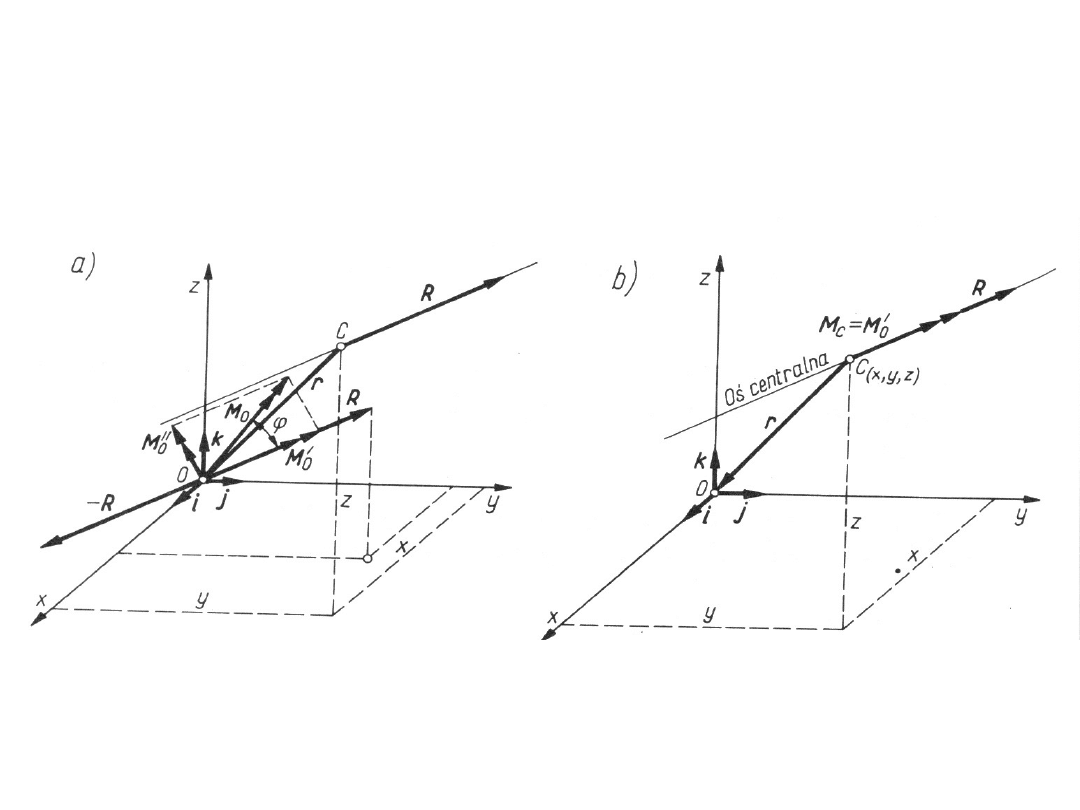
W wyniku tych przekształceń otrzymuie sie dwie siły (—R,
R) przyłożone w punkcie O, które można usunąć jako
układ równoważący się. Cały układ redukuje się wóczas do
siły R przyłożonej do punktu C oraz składowej momentu
głównego M’o równoległej do R
20
Dowolny przestrzenny układ n sił można
zredukować do dwóch wektorów kolinearnych:
- wektora głównego R
- wektora głównego M’
o
Układ złożony z wektora głównego R i składowej
momentu głównego M’
o
leżącego na linii
działania wektora R nazywamy skrętnikiem
21
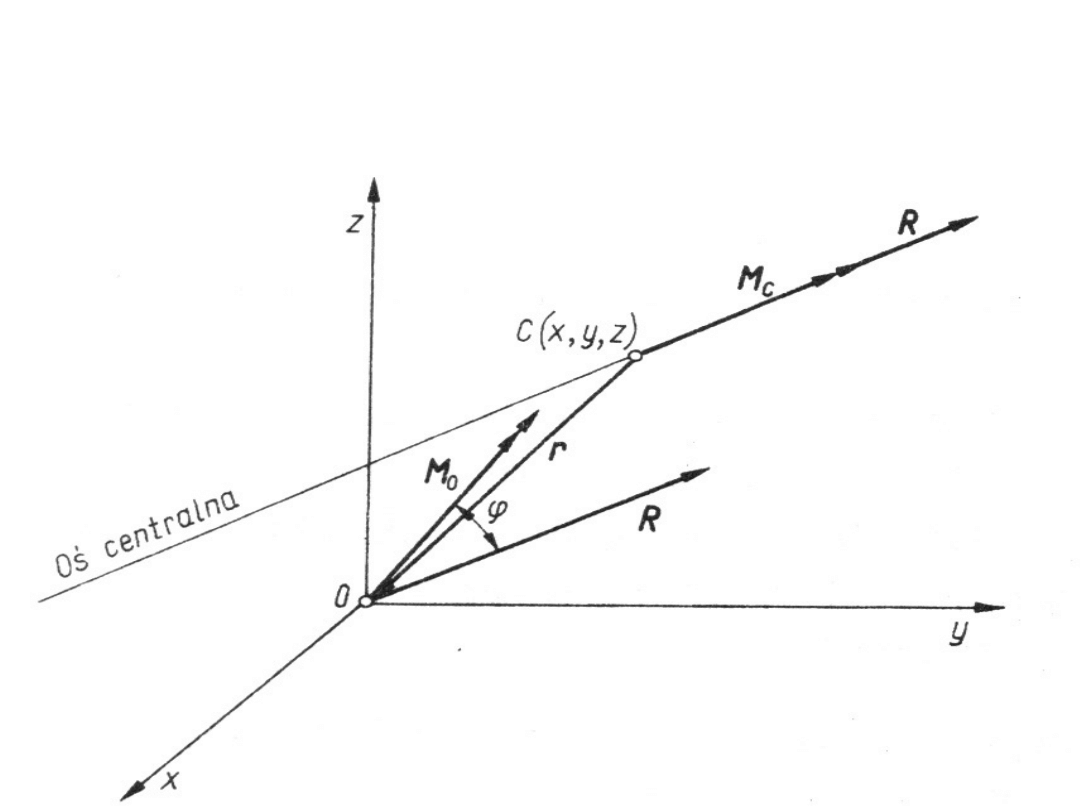
Ilustracja osi centralnej układu sił
Ilustracja osi centralnej układu sił
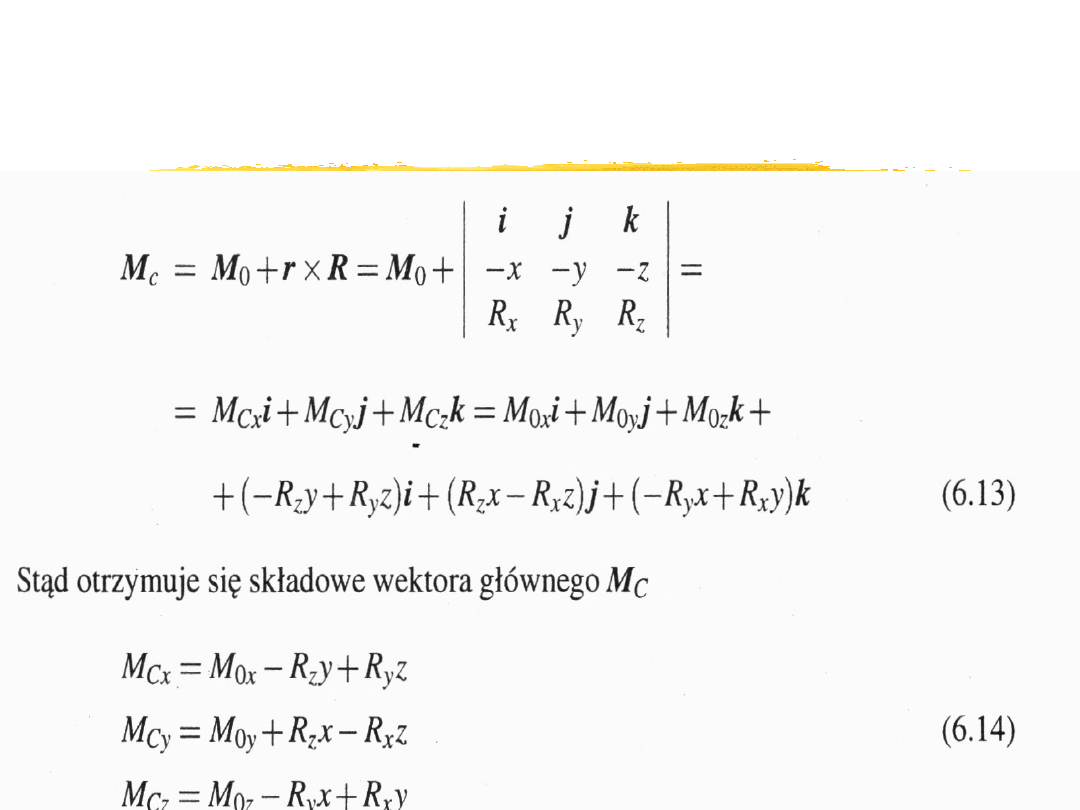
22
Moment główny M
C
względem punktu C
opisanego wektorem r o składowych (-x,-y,-z)
wynosi:
23
Równanie osi centralnej
Równanie osi centralnej
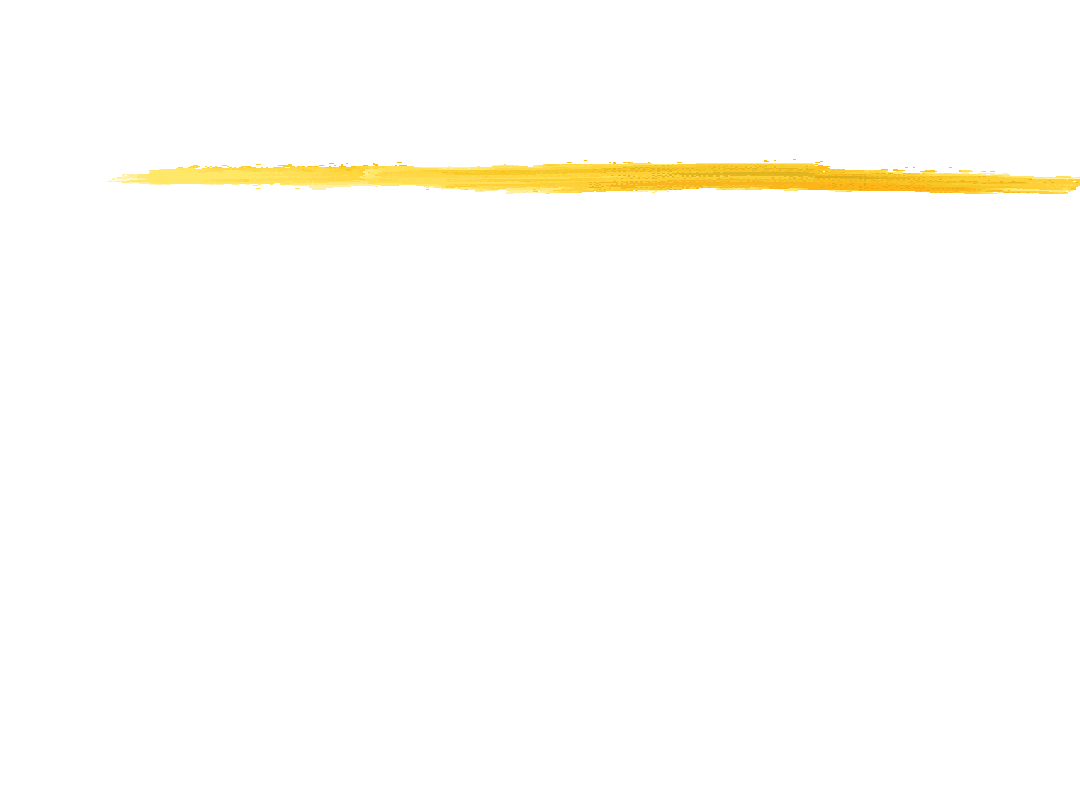
24
Redukcja dowolnego
przestrzennego układu
sił do dwóch sił
skośnych
25
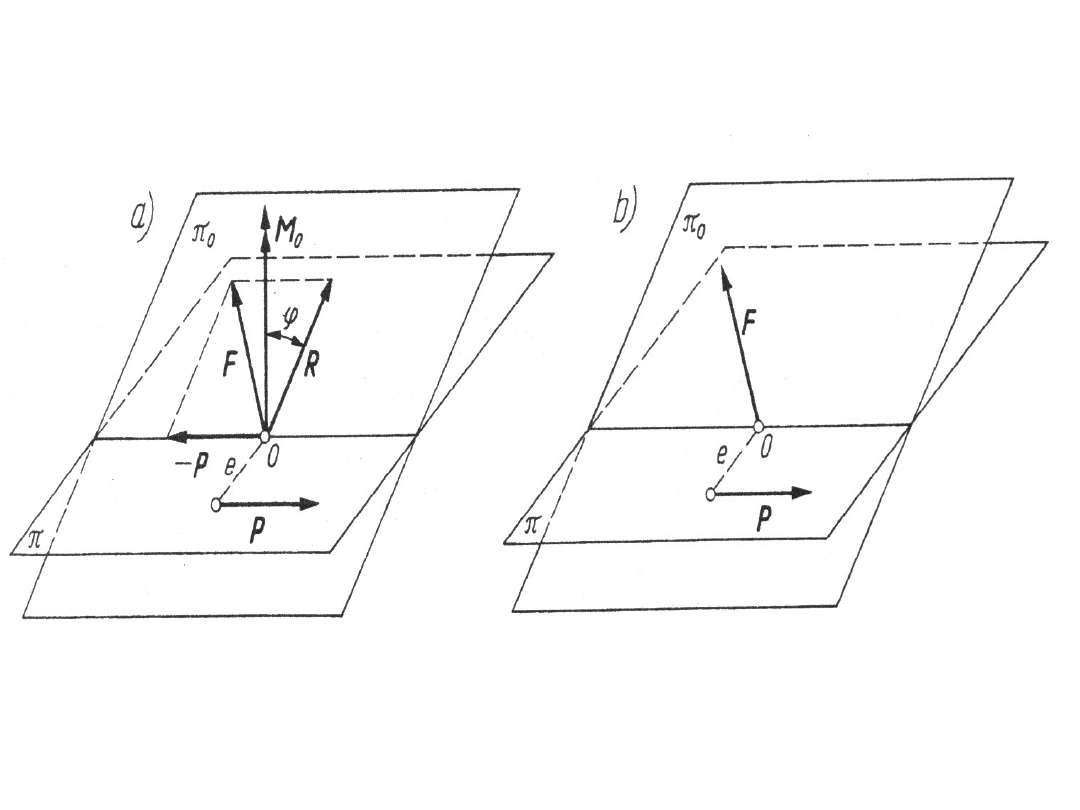
Redukcja dowolnego przestrzennego
Redukcja dowolnego przestrzennego
układu n sił do dwóch skośnych
układu n sił do dwóch skośnych
Przestrzenny układ sił daje się sprowadzić do
dwóch sił wichrowatych ( skośnych), z których
jedna przechodzi przez środek redukcji O.
26
Redukcja dowolnego
przestrzennego układu
sił do pary sił
27
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
pary sił
pary sił
28
Redukcja przestrzennego układu sił do
Redukcja przestrzennego układu sił do
pary sił
pary sił
Gdy wektor główny równa sie zeru
Układ redukuje się do pary sił, których moment jest równy
momentowi głównemu układu (M
o
= r x P).
Moment główny nie zależy od wyboru punktu O, gdyż
suma geometryczna momentów sił tworzacych jest stała
dla wszystkich punktów przestrzeni i równa się
momentowi pary.
29
Redukcja dowolnego
przestrzennego układu
sił do siły wypadkowej
30
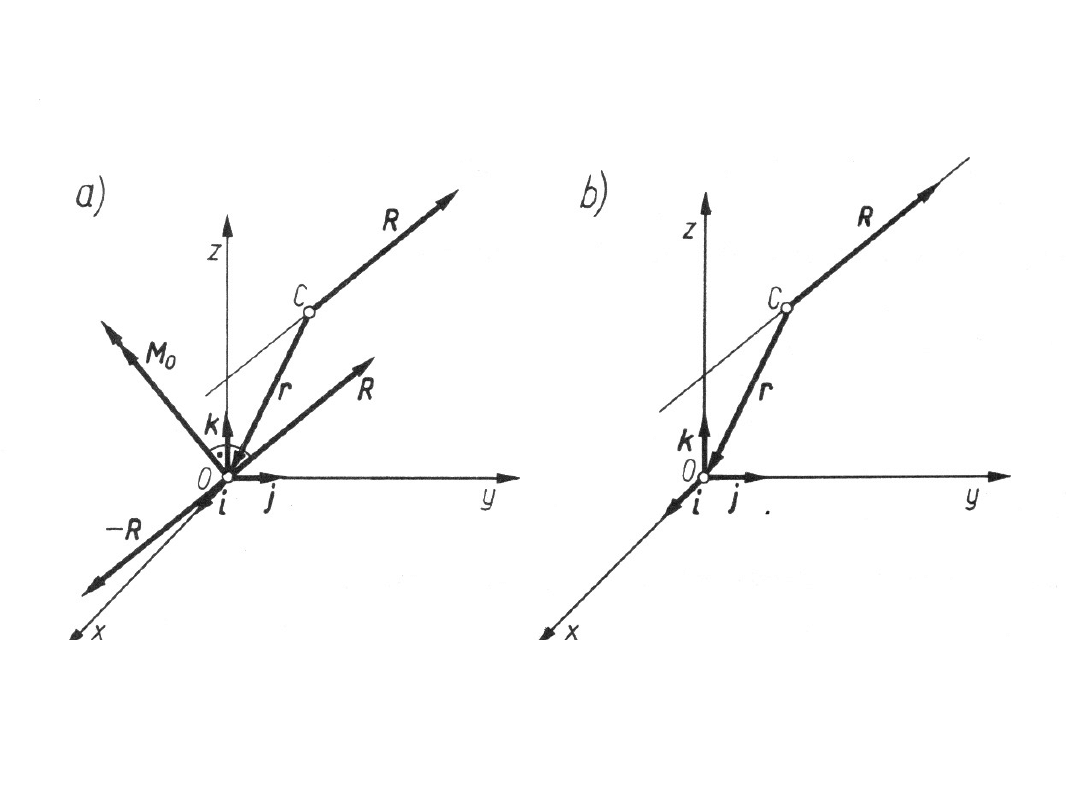
Redukcja przestrzennego układu sił do siły
wypadkowej
gdy wektor momentu głównego M
o
obliczony względem
dowolnego punktu 0, będzie prostopadły do wektora
głównego R
31
Redukcja przestrzennego układu sił do siły
wypadkowej
•składowa momentu głównego M
o
będzie
równa zeru i układ redukuje się wyłącznie
do wektora głównego R, prze chodzącego
przez punkt C.
•taki układ sił P
i
daje się zredukować
wyłącznie do jednej siły R, która jest
wypadkową układu sił, leżącą na osi
centralnej układu. W tym przypadku oś
centralna staje się linią działania
wypadkowej (rys. b).
32
Redukcja przestrzennego układu sił do siły
wypadkowej
Warunkiem koniecznym i dostatecznym,
aby przestrzenny układ sił P
i
, redukował
się do wypadkowej, jest istnienie różnego
od zera wektora głównego R i
prostopadłość głównego wektora momentu
M
o
względem dowolnie wybranego punktu
O do linii działania wektora głównego R.
Jeżeli moment główny M obliczony
względem punktu 0, jest równy zeru, to
układ sił redukuje się do siły wypadkowej
przechodzącej przez środek redukcji O.
33
Przypadki, które zachodzą przy redukcji
Przypadki, które zachodzą przy redukcji
dowolnego przestrzennego układu sił
dowolnego przestrzennego układu sił
działajacego na ciało sztywne
działajacego na ciało sztywne
34
Równowaga
dowolnego
przestrzennego układu
sił
35
Równowaga dowolnego przestrzennego
układ sił
Przestrzenny układ n sił jest w
równowadze, jeżeli jego suma
geometryczna R jest równa zeru oraz
moment główny M
o
układu względem
dowolnego punktu O jest równy zeru.
Moment główny układu będącego w równowadze
jest równy zeru względem każdego punktu w
przestrzeni.
Układy sił będących w równowadze są ukłądami
równoważnymi.
36
Równania równowagi dowolnego
przestrzennego układu sił
Wektory te będą równe zeru, jeżeli wszystkie ich składowe
będą równe zeru
37
Warunek równowagi:
Przestrzenny układ sił P
i
jest w
równowadze, jeżeli suma rzutów wszystkich
sił na trzy osie jest równa zeru i suma
momentów wszystkich sił względem trzech
osi układu jest równa zeru
38
Jeżeli rozpatruje się równowagę ciała
sztywnego pod działaniem dowolnego
przestrzennego układu sił, to liczba
niewiadomych może być równa sześciu,
gdyż tyle mamy równań do ich
wyznaczenia.
Jeżeli niewiadomych jest więcej niż sześć,
to zadanie jest statycznie niewyznaczalne i
nie można go rozwiązywać przy
zastosowaniu metod statyki ciała
sztywnego.
Z sześciu równań równowagi (6.19)
wynikają szczególne przypadki równań
równowagi prostszych układów sił, które
rozpatrzono poprzednio.
39
Wskazówki metodyczne:
a
) wydzielić ciało sztywne bądź ciała
sztywne, których równowagę
rozpatrujemy,
b) narysować siły czynne i reakcje
więzów, obciążające te ciała,
c) sprawdzić czy układ sił jest
statycznie wyznaczamy i obrać układ
współ rzędnych Oxyz,
d) napisać równania równowagi
według wzorów
e) rozwiązać układ równań zestawiony
w punkcie d) i wyznaczyć wielkości
niewiadome,
f) dokonać sprawdzenia.