Mechanika

Mechanika

Ogólna

Ogólna

Statyka

Statyka

Wykład V

Wykład V

Adam F.

Adam F.

Bolt

Bolt

Plan

Plan

wykładu

wykładu



Tarcie ślizgowe



Tarcie cięgna o krążek



Tarcie toczenia

Tarcie i prawa tarcia

Tarcie



Tarciem nazywamy zjawisko
powstawania sił stycznych do
powierzchni styku dwóch ciał (sił
tarcia).



Siły tarcia to siły oporu zapobiegające
ruchowi, który by powstał, gdyby tarcia
nie było.



Są siłami biernymi i składowymi
reakcji, które wystąpią dla zachowania
równowagi stykających się ciał.

Chropowatość



Chropowatość powierzchni ciał, które
pod wpływem obciążeń zewnętrznych
wykazują tendencję do przesunięcia się
względem siebie jest przyczyną
powstawania sił tarcia.



Jeżeli wartość liczbowa chropowatości
maleje (wpływ obróbki mechanicznej i
smarowania), to również maleją siły
tarcia, stając się równe zeru w
przypadku styku powierzchni idealnie
gładkich (reakcje zawsze mają kierunek
prostopadły do powierzchni).

Tarcie ślizgowe

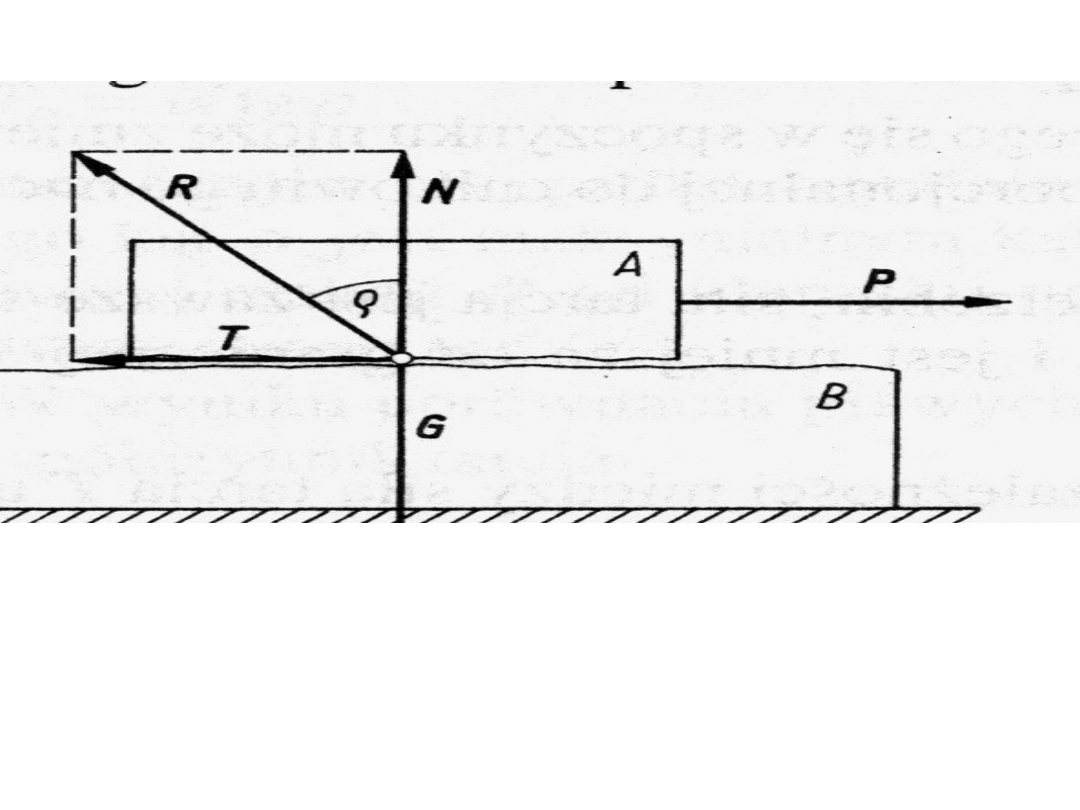
Doświadczenie
Coulomba

Ciało A o ciężarze G spoczywające na podłożu B do
którego jest przyłożona siła P, powodująca przesunięcie
tego ciała. Występująca na powierzchni styku siła tarcia T
zależy od chropowatości obu powierzchni i reakcji
normalnej N, wywołanej ciężarem G. Występuje wtedy
zjawisko klinowania się bruzd i grzbietów obu
powierzchni.

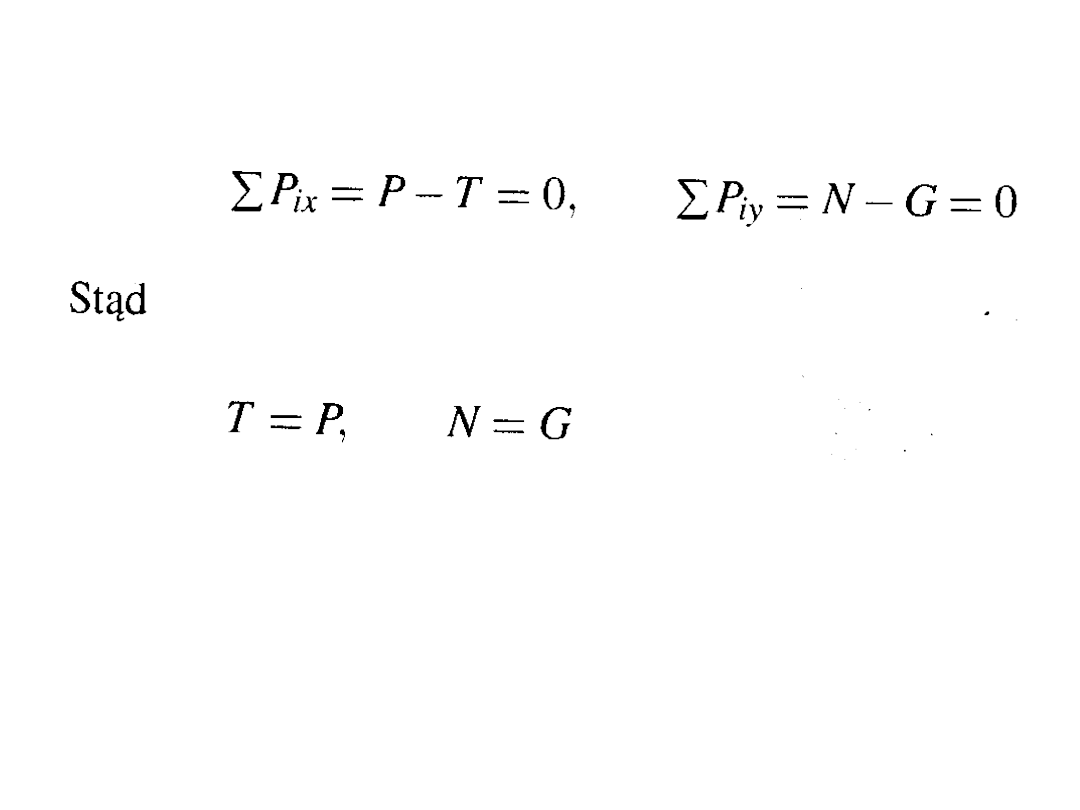
Równania rzutów sił w równowadze

Wzrastaniu siły P towarzyszy wzrost siły tarcia Tdo
pewnej wartości granicznej Tg, poza którą nie jest ona
w stanie (przy stałym nacisku N) opierać się nadal
przesunięciu.

Tarcie ślizgowe statyczne( spoczynkowe)
Tarcie kinematyczne ( ślizgowe)

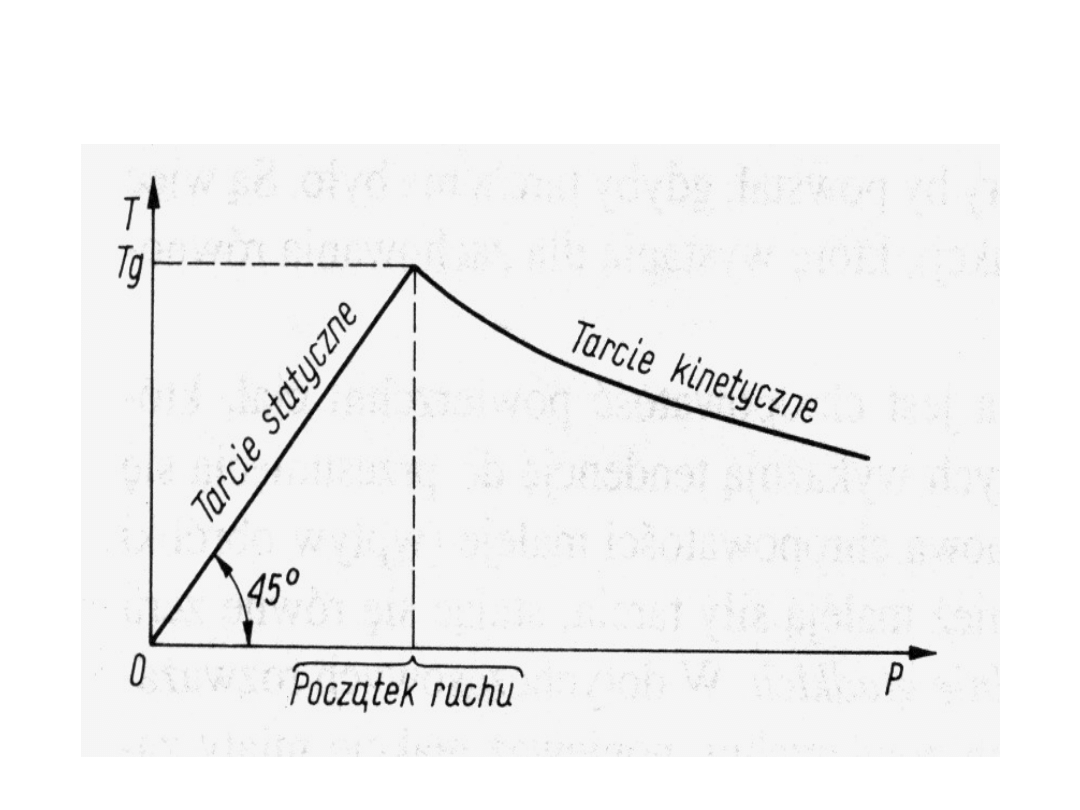
Zależność między siłą tarcia T a działającą

Zależność między siłą tarcia T a działającą

siłą P

siłą P

Prawa tarcia

Prawa tarcia

1. Siła tarcia jest niezależna od wielkości
powierzchni stykających się ze sobą ciał i
zależy jedynie od ich rodzaju.

2. Wartość siły tarcia dla ciała znajdującego
się w spoczynku może zmie niać się od zera
do granicznej wartości, proporcjonalnej do
całkowitego nacisku normalnego.

3. W przypadku gdy ciało ślizga się po
pewnej powierzchni, siła tarcia jest zawsze
skierowana przeciwnie do kierunku ruchu i
jest mniejsza od granicznej wartości.

Zależność między siłą tarcia T a naciskiem

Zależność między siłą tarcia T a naciskiem

normalnym N

normalnym N

N

T

N

T

N

T

'

'

G















współczynnik tarcia

ślizgowego (statycznego)
zależny od rodzaju
materiału trących się
ciał,wartości
chropowatości i stanu ich
powierzchni
(suche,wilgotne,
zimne ,gorące)



’



wspłczynnik tarcia

ślizgowego
(kinetycznego) zależny
od względnej prędkości
ciała

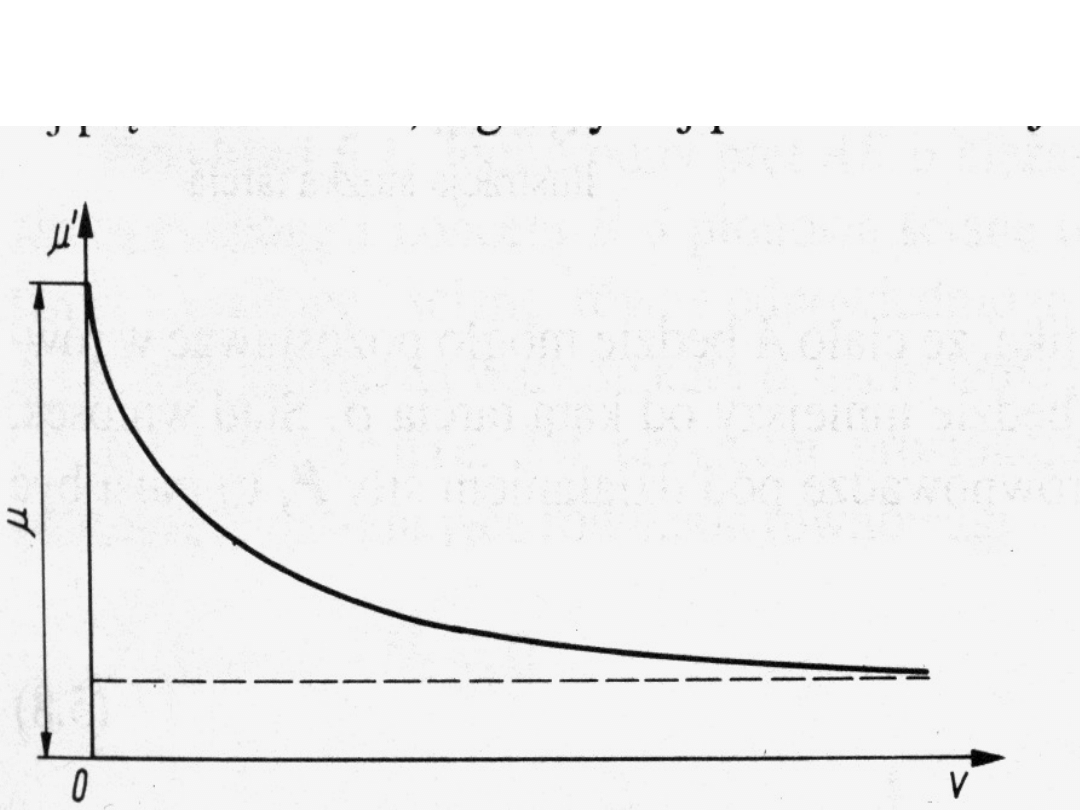
Zależność kinetycznego współczynnika

Zależność kinetycznego współczynnika

tarcia od prędkości względnej ciała

tarcia od prędkości względnej ciała

Kąt tarcia i wspólczynnik

Kąt tarcia i wspólczynnik

tarcia

tarcia

•

gdy siła tarcia działająca na ciało

osiągnęła wartość graniczną, reakcja
podłoża R. będąca wypadkową sił N i T jest
nachylona pod kątem



do składowej

normalnej.

•gdy N = G = const, kąt



jest

maksymalnym kątem, o jaki może odchylić
się linia działania całkowitej reakcji R
Tg = N tg



Tg =



N

•po porównaniu prawych stron otrzymamy
wzór na współczynnik tarcia



= tg



Zależność między siłą tarcia

Zależność między siłą tarcia

T

T

a działającą

a działającą

siłą

siłą

P

P



- jest maksymalnym współczynnikiem

tarcia, odpowiadającym tarciu
rozwiniętemu (na granicy tarcia ślizgowego
statycznego i kinetycznego).

•kąt



jest maksymalnym kątem

nachylenia reakcji R, zapewniającym
jeszcze równowagę ciała A.

• jeżeli na ciało A spoczywające na
chropowatej powierzchni działa siła P (jako
wypadkowa wszystkich sił czynnych)
nachylona do prostej n (normalnej do
płaszczyzny styku) pod kątem  to siłę tę

równoważy reakcja R będąca wypadkową
siły normalnej N i siły tarcia T.

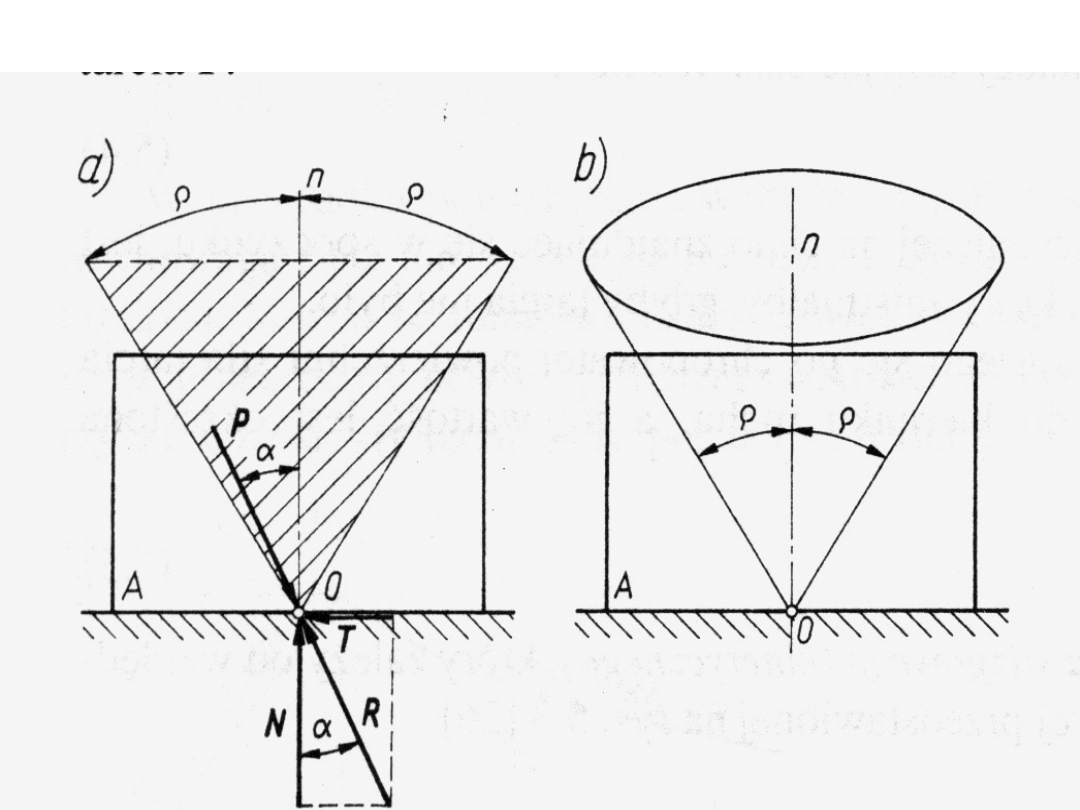
Ilustracja stożka tarcia

Ilustracja stożka tarcia

Zależność między siłą tarcia T a działającą

Zależność między siłą tarcia T a działającą

siłą P

siłą P

•jeżeli ciało A ma pozostać w równowadze
pod działaniem siły P, to musi być
spełniona następująca zależność

czyli siła P musi leżeć w obszarze
zakreskowanym (rys.a), ograniczonym
dwiema prostymi tworzącymi z normalną n
kąty równe , gdyż jedynie w tym obszarze

może leżeć linia działania całkowitej reakcji
R.







Zależność między siłą tarcia

Zależność między siłą tarcia

T

T

a działającą

a działającą

siłą

siłą

P

P

W przypadku ciał izotropowych, jak stal i inne
metale, tarcie nie zależy od kierunku działania
siły T, wobec czego reakcja R może leżeć w
każdej z płasz czyzn przechodzących przez
normalną n i odchylać się od tej normalnej o
ten sam kąt tarcia p, tworząc powierzchnię
boczną kołowego stożka.
Stożek ten nazywa się stożkiem tarcia (rys. b).

Ciała anizotropowe np drewno wykazuja
większe tarcie w poprzek niż wzdłuż włokien,
dlatego stożek tarcia dla takich ciał ma
podstawę eliptyczną

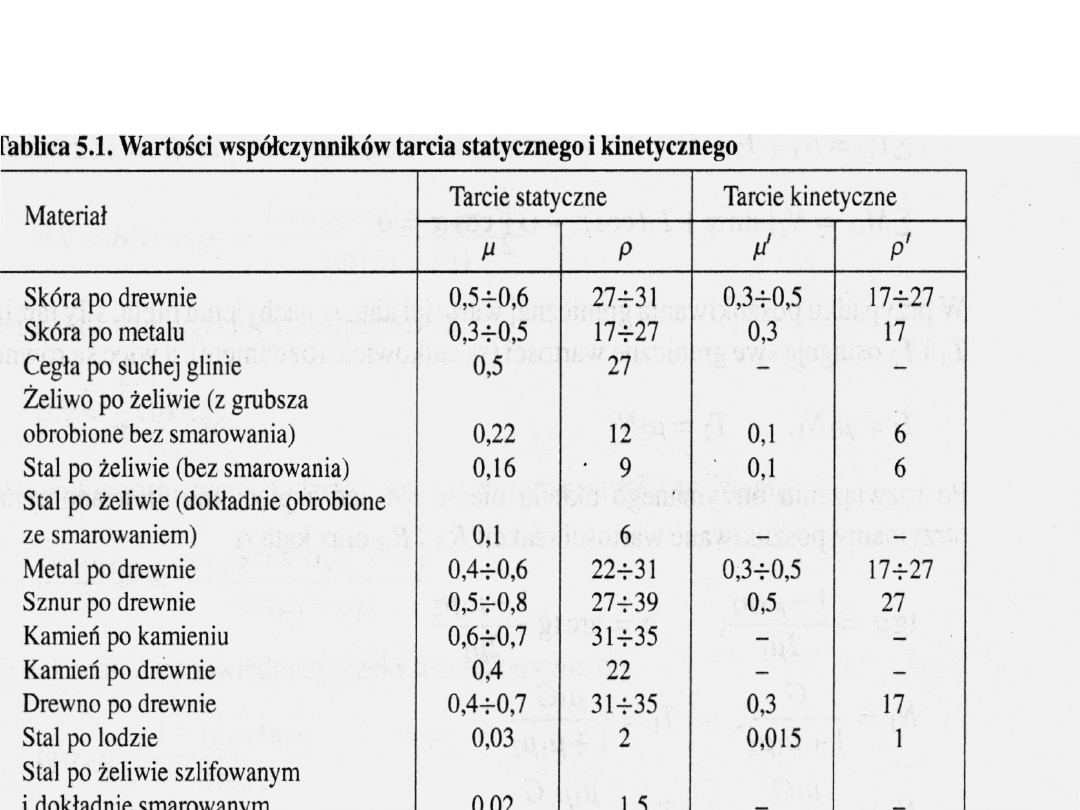
Wartości współczynników tarcia ślizgowego

Wartości współczynników tarcia ślizgowego

statycznego i kinematycznego

statycznego i kinematycznego

Tarcie cięgna o krążek

Tarcie cięgna o krążek

Tarciem cięgna o krążek nazywa się siły
tarcia występujące między
powierzchniami cylindrycznymi a
cięgnami, taśmami, sznurami, pasami
lub linami na nie nawiniętymi.
Siły te w hamulcach taśmowych hamują
wzajemny poślizg koła i taśmy,
natomiast w przypadku kół pasowych nie
dopuszczają do wzajemnego poślizgu
koła i pasa.

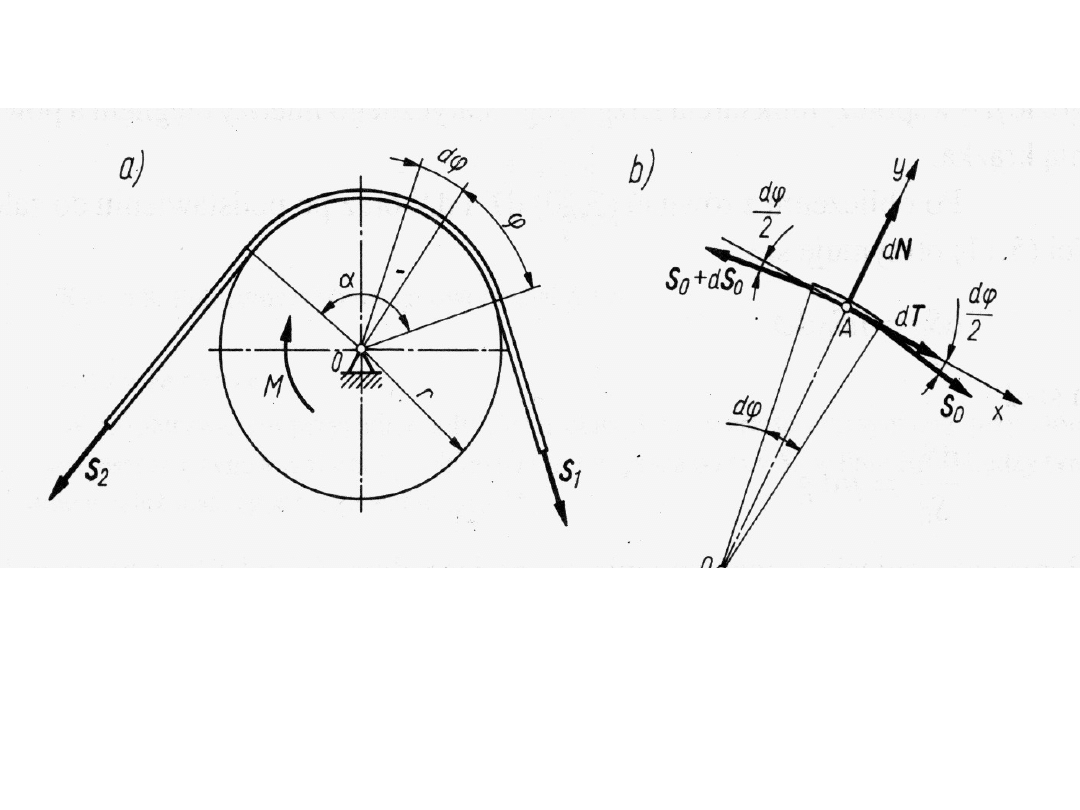
Tarcie cięgna o krążek

Zakłada się, że cięgno obciążone siłami S

1

i S

2

znajduje się w płaszczyźnie prostopadłej do osi
krążka.
Siły tarcia występują na całej długości cięgna
stykającego się z krążkiem.

Tarcie cięgna o krążek

Siły te mają różne wartości, gdyż zmienia się w
sposób ciągły kierunek nacisku cięgna na krążek
i wartość napięcia w cięgnie.
Uniemożliwia to zbadanie równowagi cięgna jako
całości.

Należy rozważyć zatem elementarny odcinek
cięgna odpowiadający kątowi środkowemu d



.

Aby powstały siły tarcia T, trzeba spowodować
docisk cięgna do krążka przez wstępne napięcie
przyłożone do jego końców.
Jeżeli krążek obróci się względem cięgna w
prawo po przyłożeniu mo mentu M, to powstaną
siły tarcia, które spowodują, że siła S

2

będzie

większa od S

1

Tarcie cięgna o krążek

Na rozpatrywany odcinek cięgna (rys.b)
działają następujące siły:

• nacisk krążka dN,

• siła tarcia dT — przeciwdziałająca
ślizganiu się cięgna pod wpły wem siły
maksymalnej S

2

> S

1

oraz napięcia odciętych

części cięgna S

o

i S

o

+ dS

o

,

gdzie d S

o

oznacza przyrost napięcia

odpowiadający przyrostowi kąta



o d



.

Tarcie cięgna o krążek

Na rozpatrywany odcinek cięgna (rys.b)
działają następujące siły:

• nacisk krążka dN,

• siła tarcia dT — przeciwdziałająca
ślizganiu się cięgna pod wpły wem siły
maksymalnejS

2

> S

1

oraz napięcia odciętych

części cięgna S

o

i S

o

+ dS

o

,

gdzie d S

o

oznacza przyrost napięcia

odpowiadający przyrostowi kąta  o d .

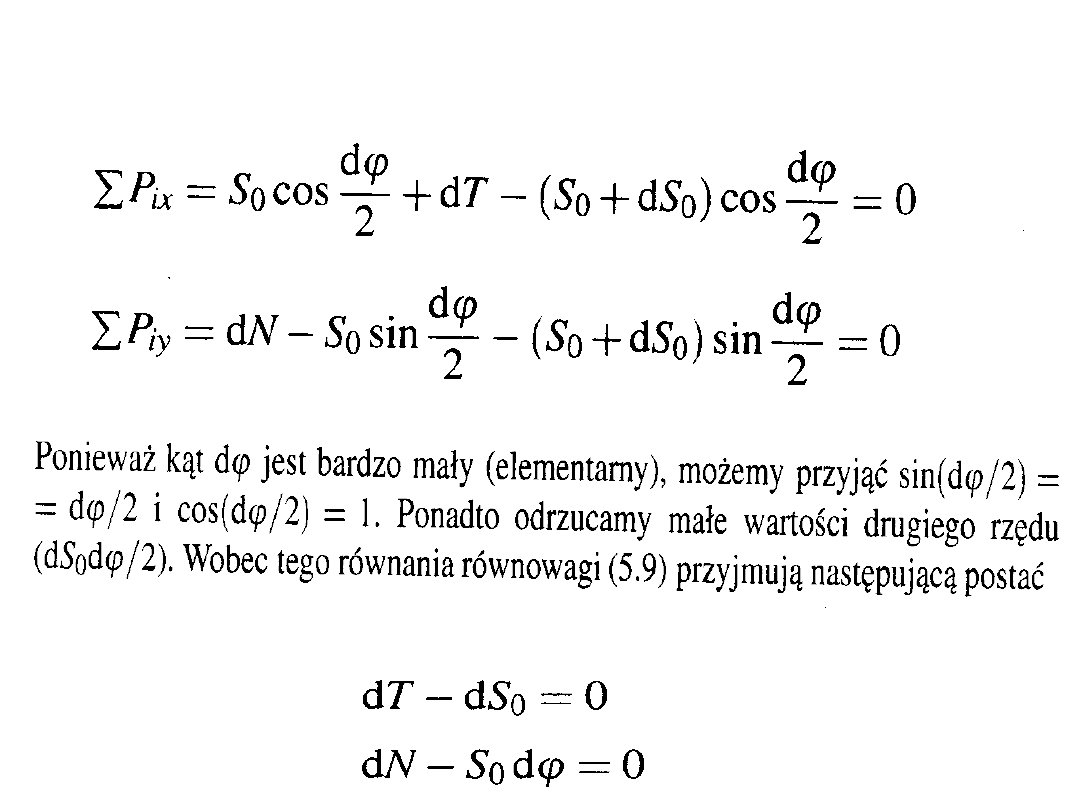
Równania równowagi odciętego elementu

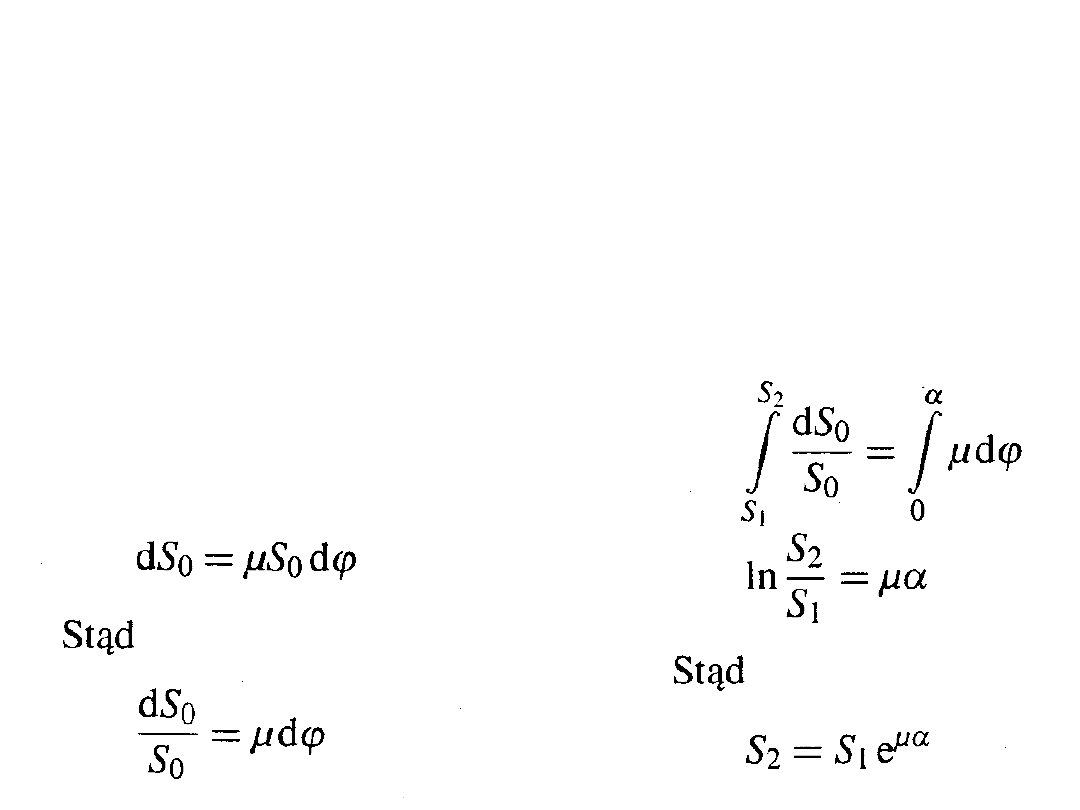
Równania równowagi

dT =

dT =





dN

dN

Napodstawie zwiazku między
dT a dN w rozpatrywanym
granicznym stanie równowagi
otrzymuje się:

Po obliczeniu dt i dN oraz
po podstawieniu
otrzymuje się:

Ponieważ napięcie
cięgna zmienia się na
jego długości od S

1

do

S

2

a kąt



przyjmuje



= 0 do



=



Tarcie cięgna o krążek

Wzór ten został wyprowadzony przez Eulera.
Wartość e



jest zawsze większa od jedności,

gdy



> 0, a więc siła S

2

jest większa od siły S

1

Stosunek tych sił S jest tym większy, im większy
jest współczynnik tarcia



między cięgnem a

krążkiem oraz im większy jest kąt (kąt

opasania), na którym cięgno przyiega do krążka.
Ponieważ wartość e



bardzo szybko rośnie ze

wzrostem kąta opasania , dlatego np.

kilkakrotne owinięcie liny okrętowej na koło
linowe powoduje, że niewielka siła przyłożona
przez człowieka, wywołująca wstępne napięcie
liny S

1

, jest w stanie zahamować ruch statku.

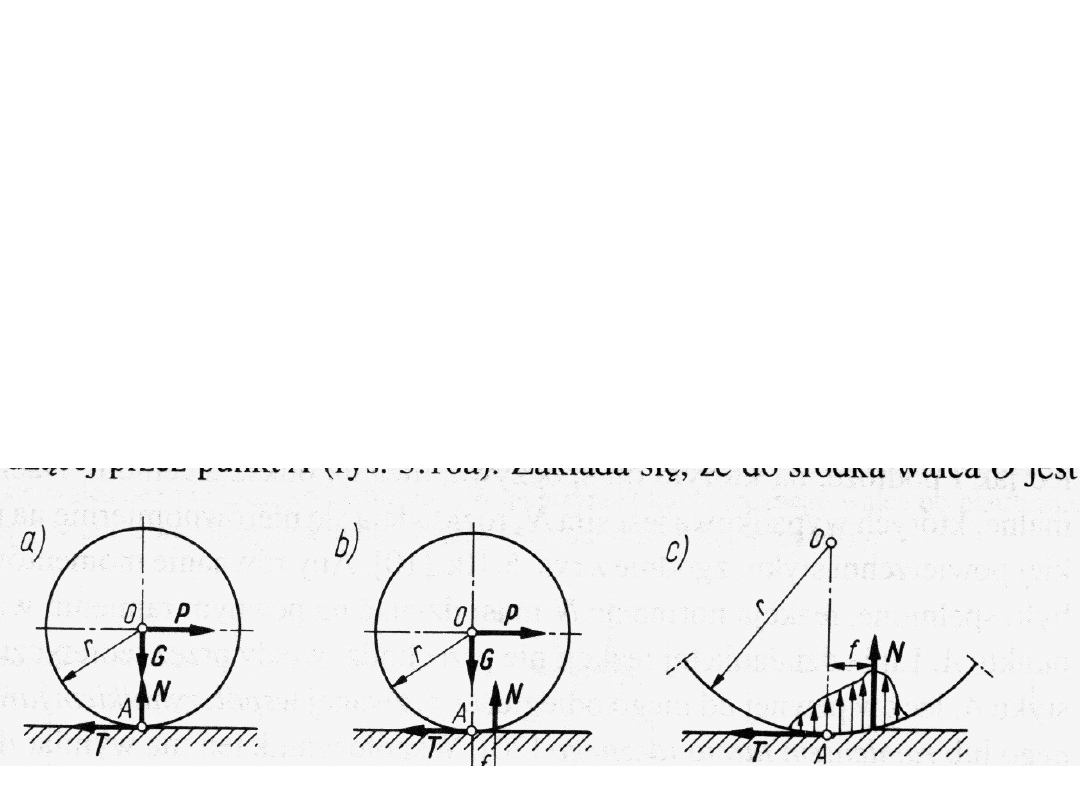
Tarcie toczenia

Tarcie toczenia

Tarcie toczenia

Tarcie toczenia lub opór toczenia powstaje przy
usiłowaniu przetoczenia walca o ciężarze G po
poziomej płaszczyźnie. Gdyby walec toczący się
po podłożu i podłoże były idealnie sztywne, to
styk występowałby tylko wzdłuż tworzącej walca,
przechodzącej przez punkt A (rys. a).

Równania równowagi walca

Współczynniki tarcia tocznego

Dziekuje:D