„Signal Theory” Zdzisław Papir

Signal Filtering

Signal Filtering

• Signal filtering – Fourier series

• Signal filtering - examples

• Signal filtering – Fourier transform

• Frequency characteristics of a signal after filtration

• Signal filtering – example

„Signal Theory” Zdzisław Papir

)

(s

H

)

(t

x

 

st

e

s

H











n

t

jn

n

e

X

t

x

o

)

(



























n

t

jn

n

n

t

jn

Y

n

e

Y

e

jn

H

X

t

y

n

o

o

o

)

(







 

 



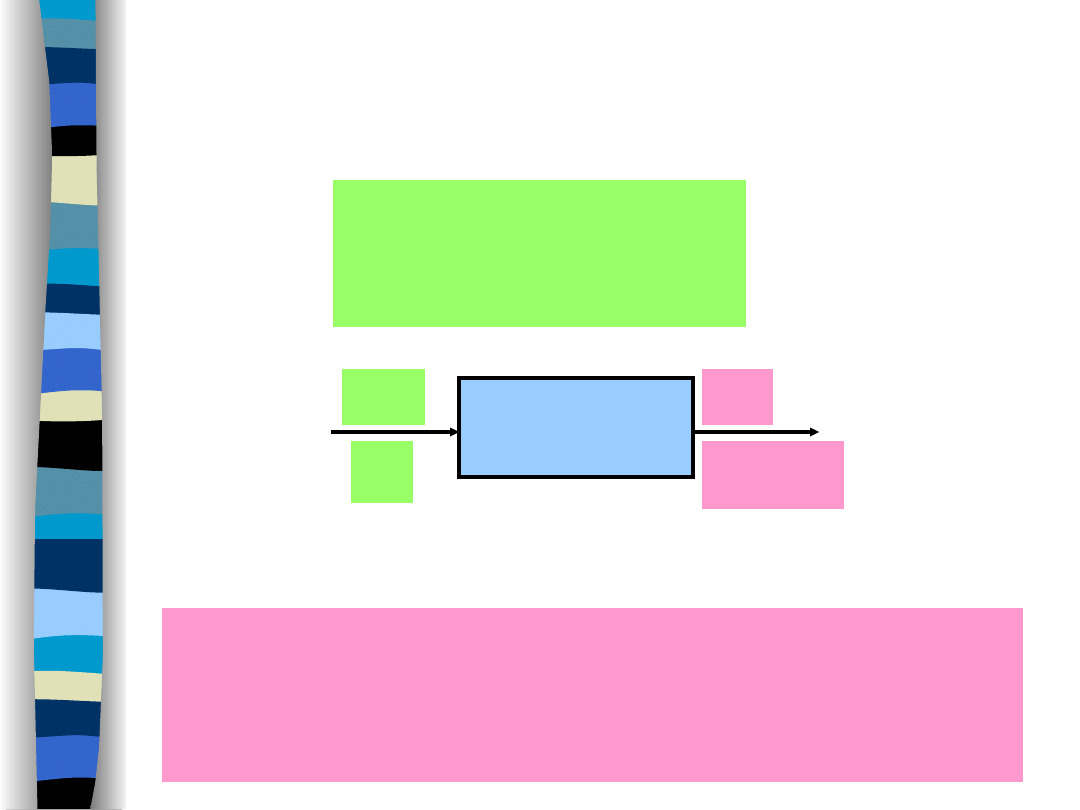
The Fourier series of the output signal y(t)

Signal filtering – Fourier series

st

e

 

t

y

„Signal Theory” Zdzisław Papir

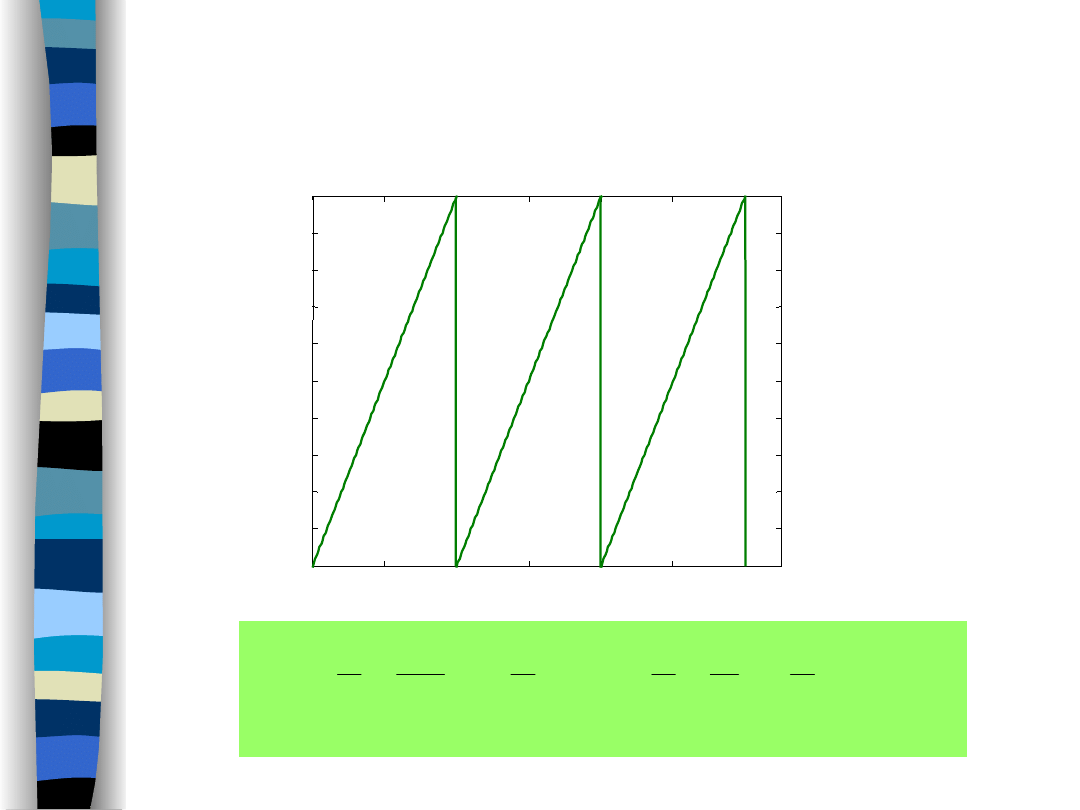
Sawtooth input signal x(t)

0

0.5

1

1.5

2

2.5

3

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Sawtooth signal (period T)

time t/T

x(t)

 





t

n

n

e

n

j

t

x

n

t

jn

n

n

o

1

2

0

sin

1

1

2

1

1

2

2

1

































Signal filtering - examples

„Signal Theory” Zdzisław Papir

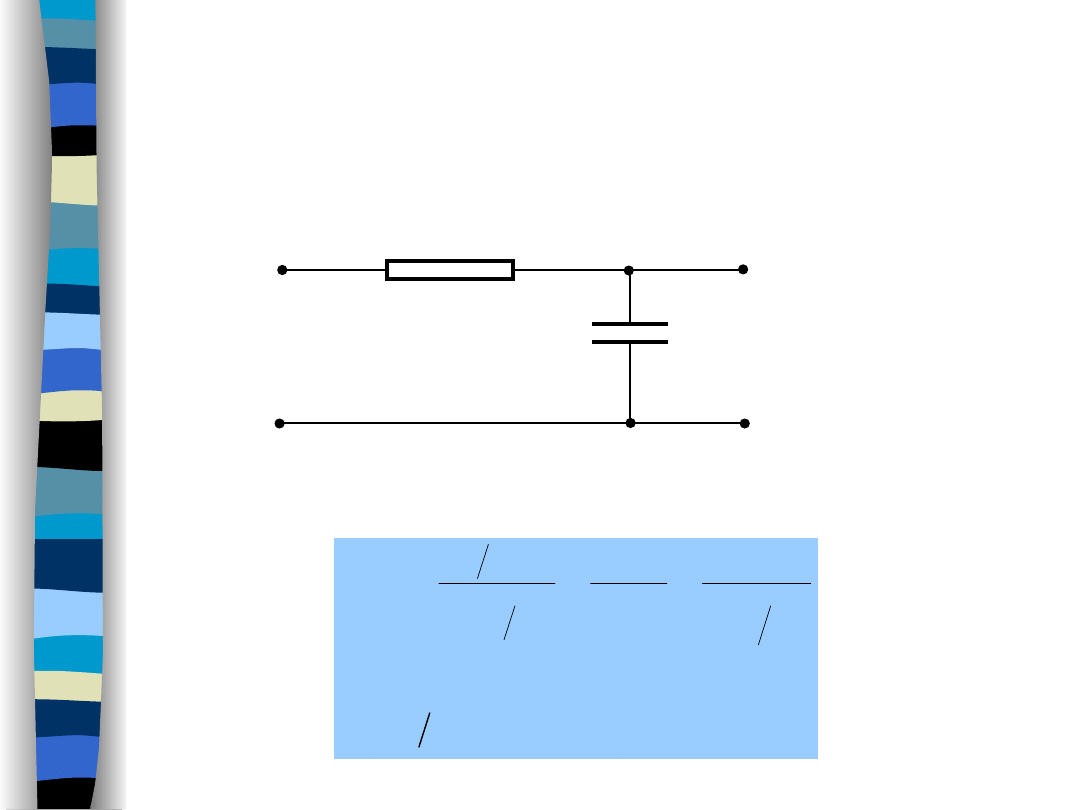
Lowpass filter

 

RC

T

T

s

Ts

Cs

R

Cs

s

H

















,

1

1

1

1

1

1

1

g

g





R

C

„Signal Theory” Zdzisław Papir

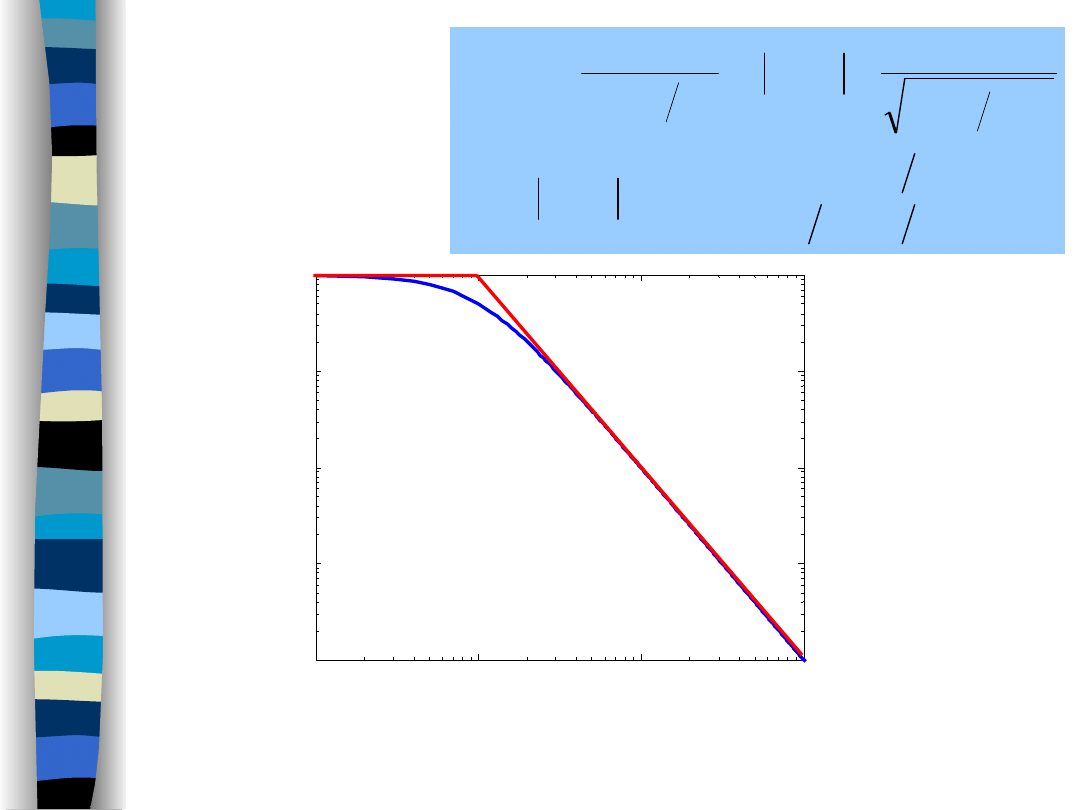
Lowpass
filter

 

 





 



























1

,

log

20

1

,

0

log

20

1

1

,

1

1

g

g

g

2

g

g



























H

H

j

j

H

„Signal Theory” Zdzisław Papir

10

-1

10

0

10

1

10

2

10

-4

10

-3

10

-2

10

-1

10

0

g



 

dec



 

 

dB



H

log-log amplitude characteristics of the LPF (1st order)

Input/output signals – Fourier
series

 

t

jn

n

n

e

jn

n

j

t

y

o

g

o

o

1

1

1

2

2

1



























 





t

n

n

e

n

j

t

x

n

t

jn

n

n

o

1

o

sin

1

1

2

1

1

2

2

1

o

































 

g

1

1







j

j

H





„Signal Theory” Zdzisław Papir

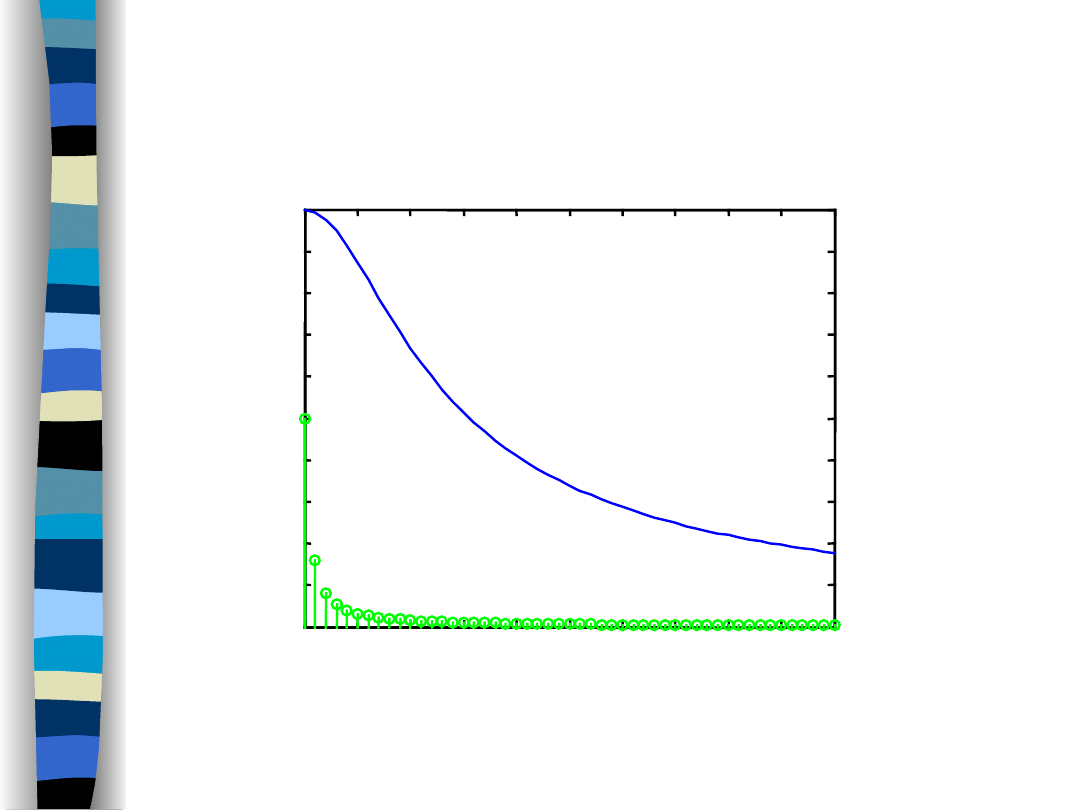
Amplitude spectra (f

g

/f

o

= 9)

0

5

10

15

20

25

30

35

40

45

50

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Lowpass filter and sawtooth signal – amplitude spectra

n

f

o

Lowpass filter

Sawtooth signal

f

g

/f

o

= 9

„Signal Theory” Zdzisław Papir

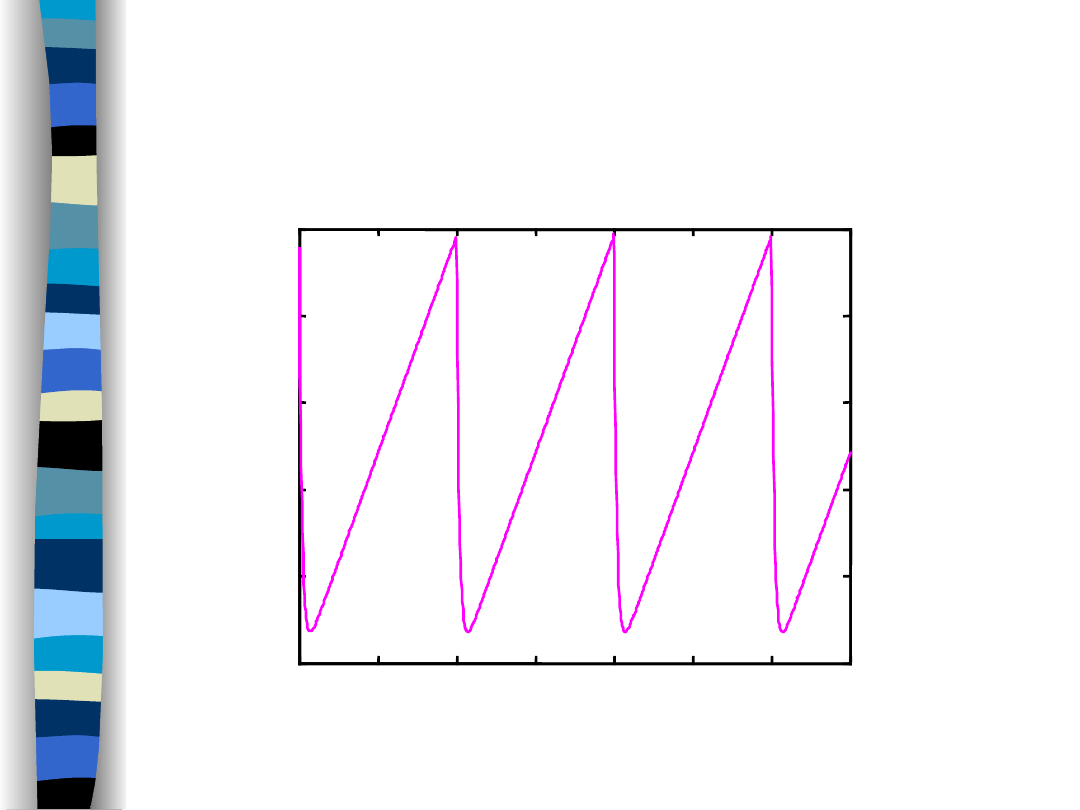
Output signal y(t) (f

g

/f

o

= 9)

0

0.5

1

1.5

2

2.5

3

3.5

0

0.2

0.4

0.6

0.8

1

Lowpass filter response

time t/T

f

g

/f

o

= 9

„Signal Theory” Zdzisław Papir

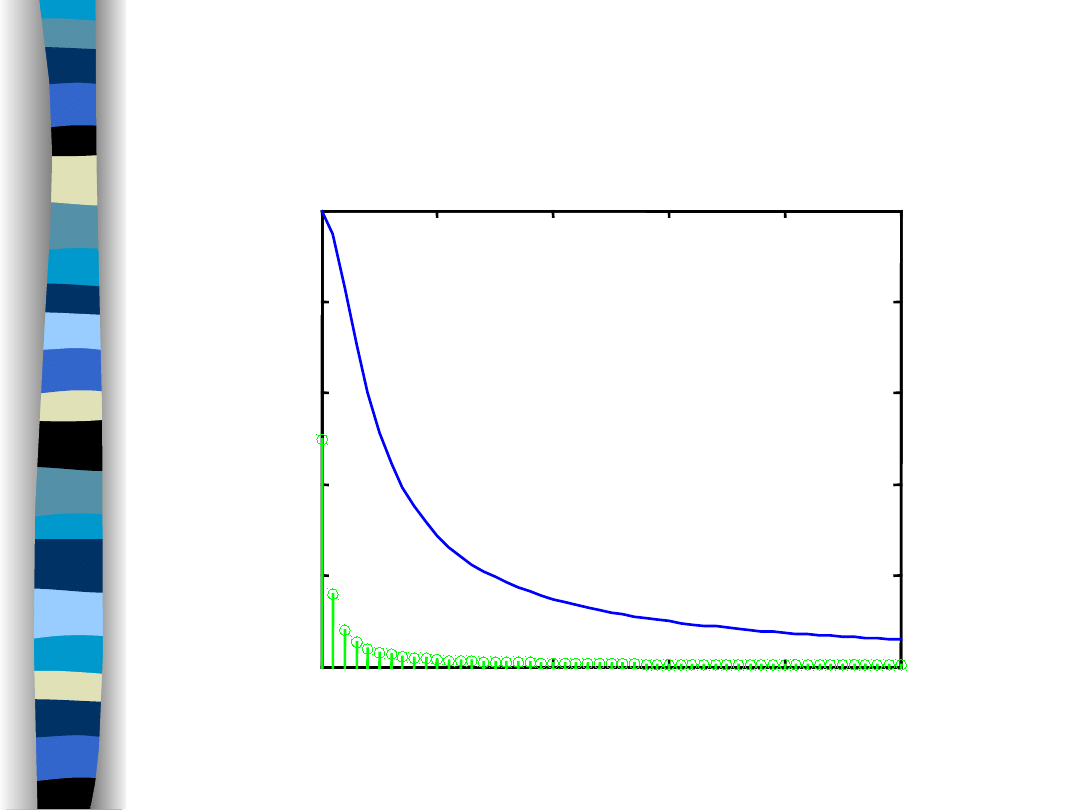
Amplitude spectra (f

g

/f

o

= 3)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Lowpass filter and sawtooth signal – amplitude spectra

Lowpass filter

Sawtooth signal

f

g

/f

o

= 3

n

f

o

„Signal Theory” Zdzisław Papir

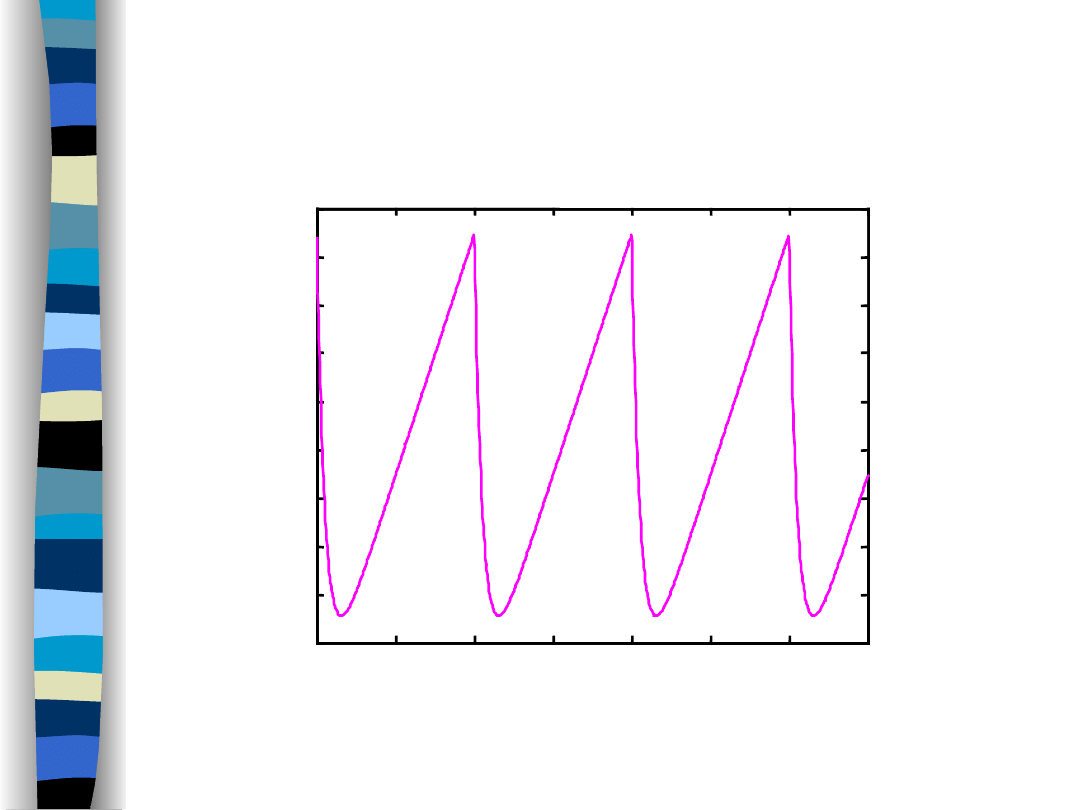
Output signal y(t) (f

g

/f

o

= 3)

0

0.5

1

1.5

2

2.5

3

3.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Lowpass filter response

time t/T

f

g

/f

o

= 3

„Signal Theory” Zdzisław Papir

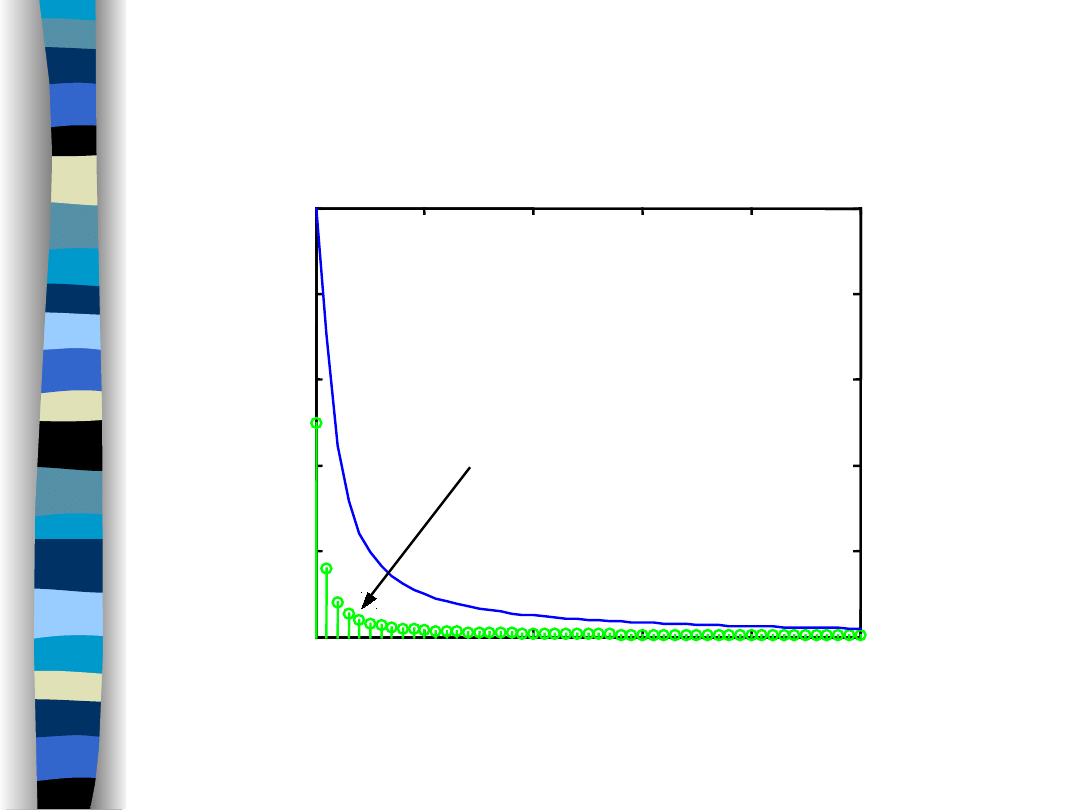
Amplitude spectra (f

g

/f

o

= 1)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Lowpass filter and sawtooth signal – amplitude spectra

Lowpass filter

Sawtooth signal

f

g

/f

o

= 1

n

f

o

„Signal Theory” Zdzisław Papir

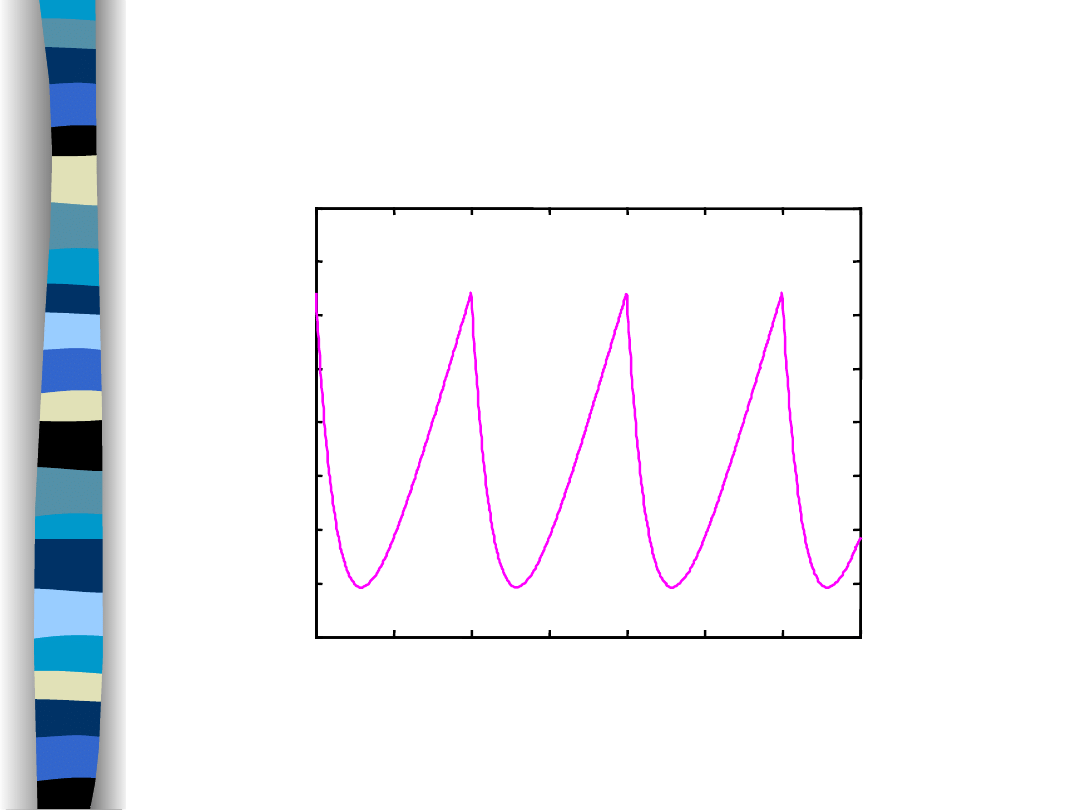
Output signal y(t) (f

g

/f

o

= 1)

0

0.5

1

1.5

2

2.5

3

3.5

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Lowpass filter response

time t/T

f

g

/f

o

= 1

„Signal Theory” Zdzisław Papir

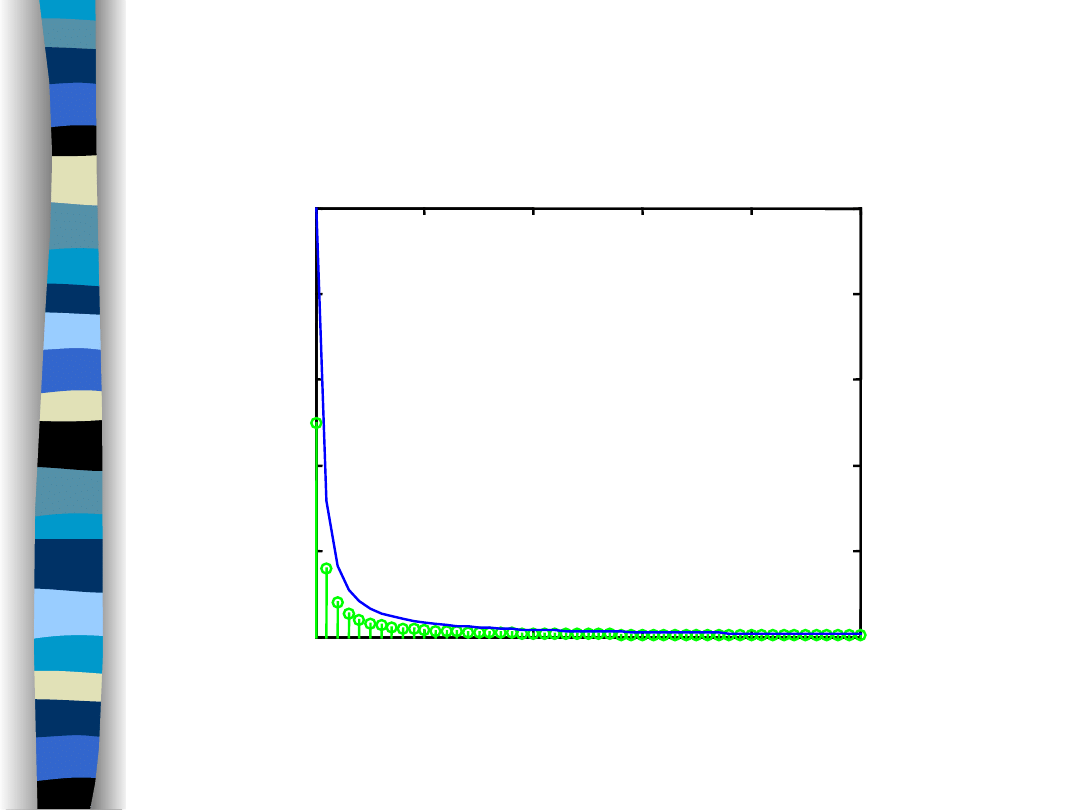
Amplitude spectra (f

g

/f

o

= 1/3)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Lowpass filter and sawtooth signal – amplitude spectra

f

g

/f

o

= 1/3

n

f

o

„Signal Theory” Zdzisław Papir

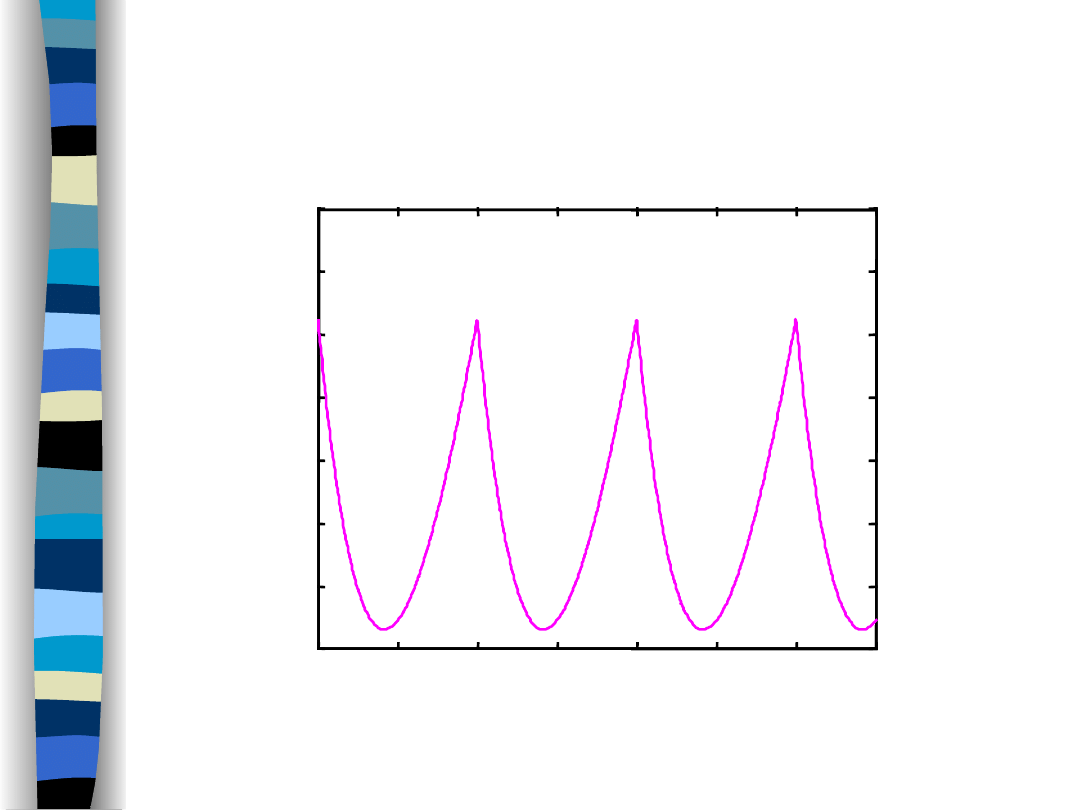
Output signal y(t) (f

g

/f

o

= 1/3)

0

0.5

1

1.5

2

2.5

3

3.5

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

Lowpass filter response

time t/T

f

g

/f

o

= 1/3

„Signal Theory” Zdzisław Papir

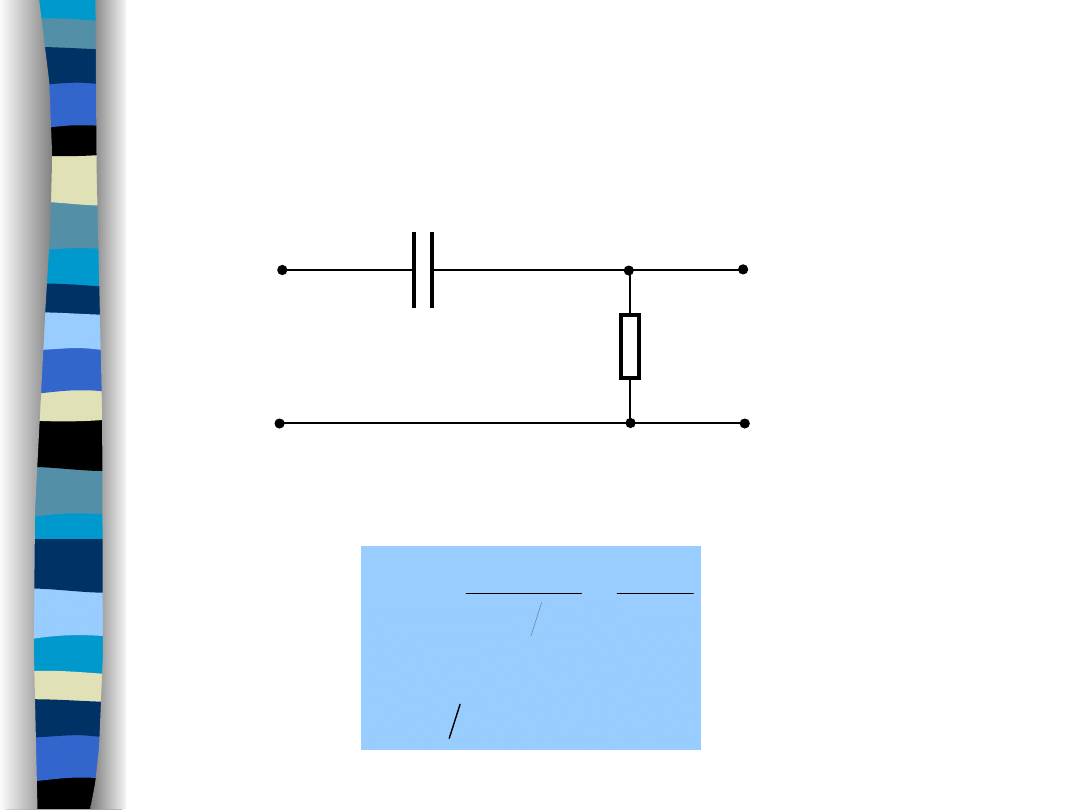
Highpass filter

 

RC

T

T

Ts

Ts

Cs

R

R

s

H

g













,

1

1

1



R

C

„Signal Theory” Zdzisław Papir

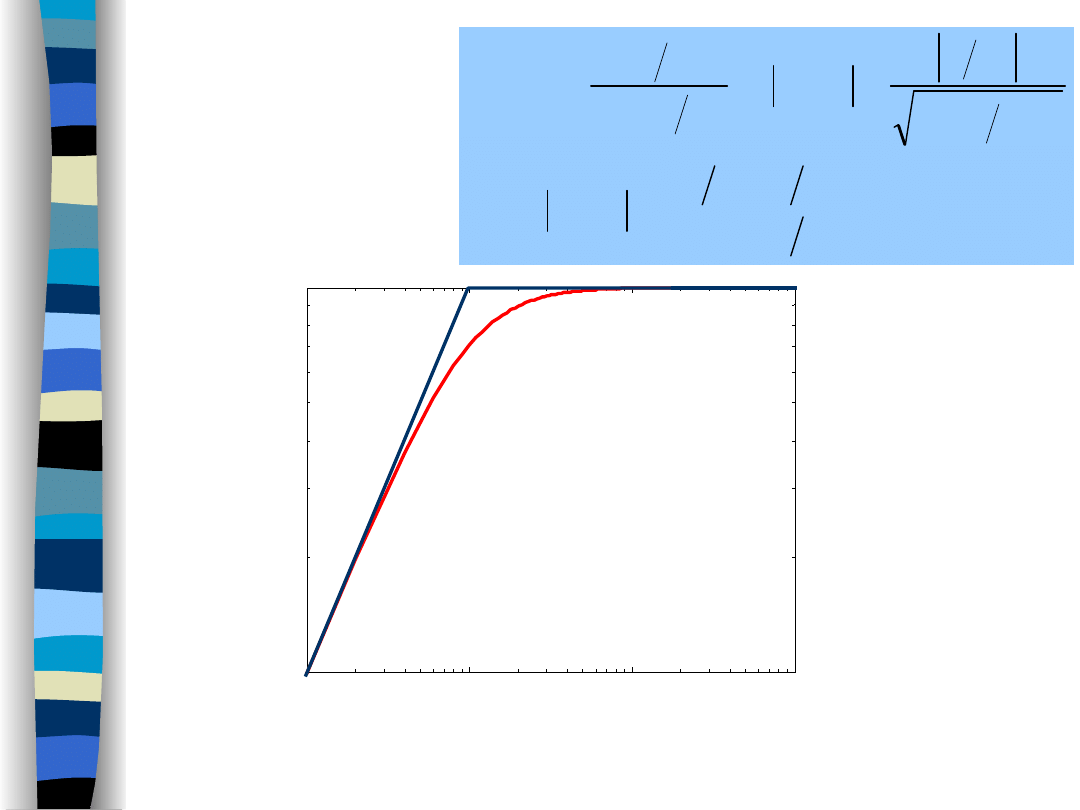
Highpass
filter

„Signal Theory” Zdzisław Papir

10

-1

10

0

10

1

10

2

10

-1

10

0

g



 

dec



 

 

dB



H

log-log amplitude characteristics of the HPF (1st order)

 

 





 





















1

,

0

1

,

log

20

1

,

1

g

g

g

2

g

g

g

g



































H

H

j

j

j

H

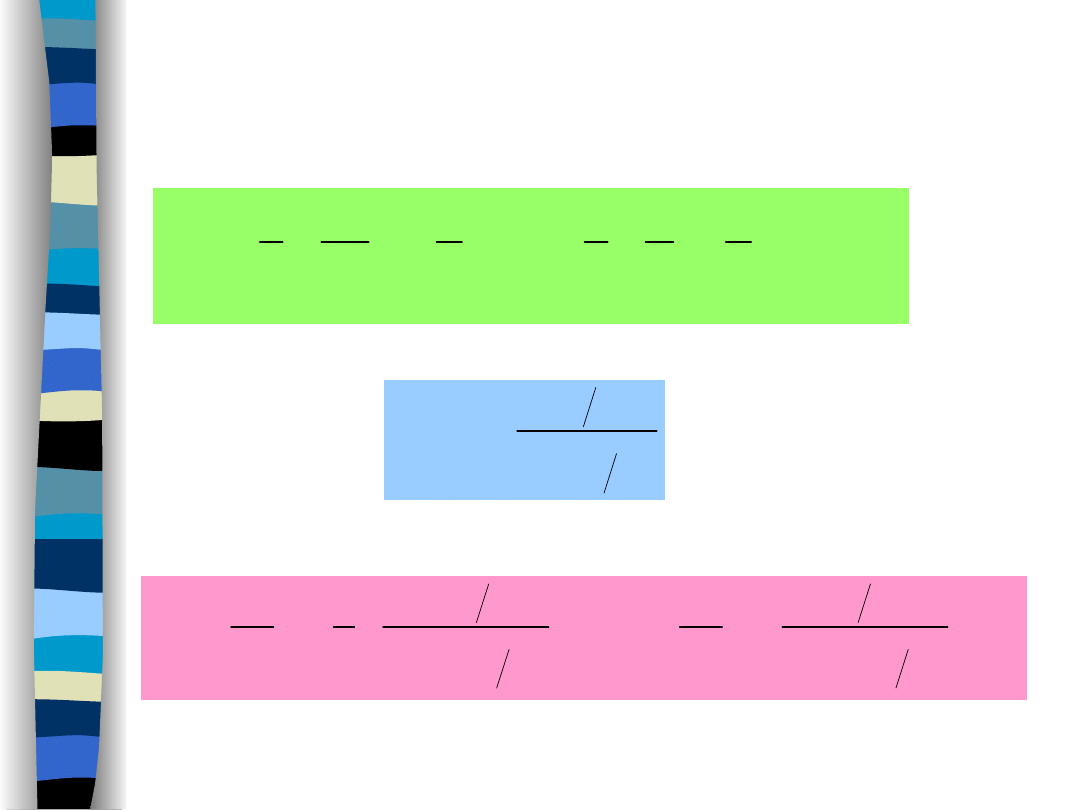
„Signal Theory” 

Zdzisław Papir

 

































o

g

o

g

o

g

o

g

o

o

o

o

1

2

1

1

1

2

n

n

t

jn

t

jn

n

n

e

jn

e

jn

jn

n

j

t

y

























 





t

n

n

e

n

j

t

x

n

t

jn

n

n

o

1

o

sin

1

1

2

1

1

2

2

1

o

































 

g

g

1











j

j

j

H





Input/output signals – Fourier
series

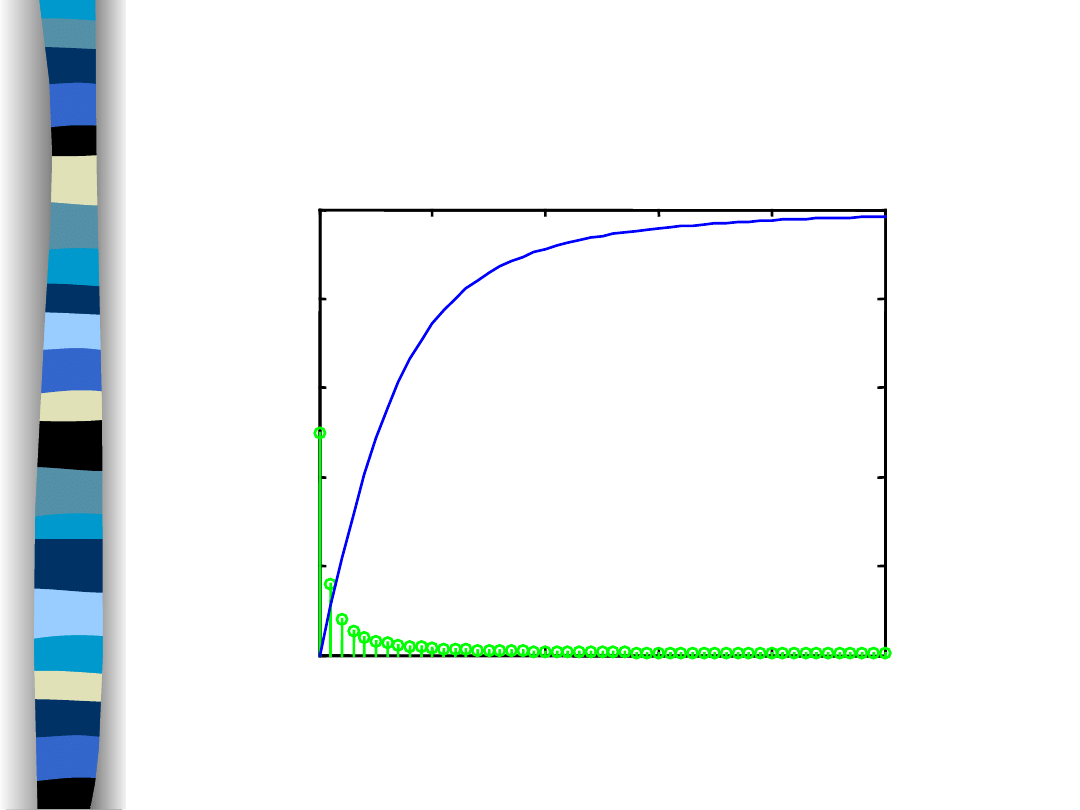
Amplitude spectra (f

g

/f

o

= 9)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Highpass filter and sawtooth signal – amplitude spectra

Highpass filter

Sawtooth signal

f

g

/f

o

= 9

n

f

o

„Signal Theory” 

Zdzisław Papir

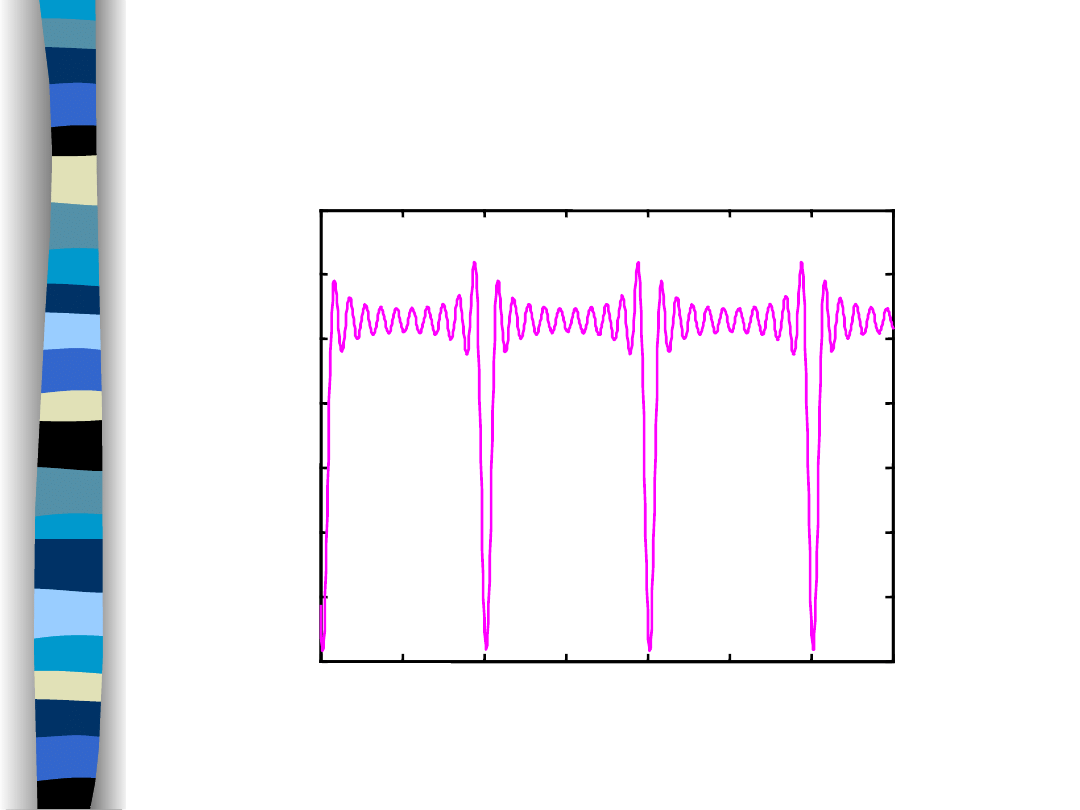
Output signal y(t) (f

g

/f

o

= 9)

0

0.5

1

1.5

2

2.5

3

3.5

-25

-20

-15

-10

-5

0

5

10

Highpass filter response

time t/T

f

g

/f

o

= 9

„Signal Theory”  Zdzisław Papir

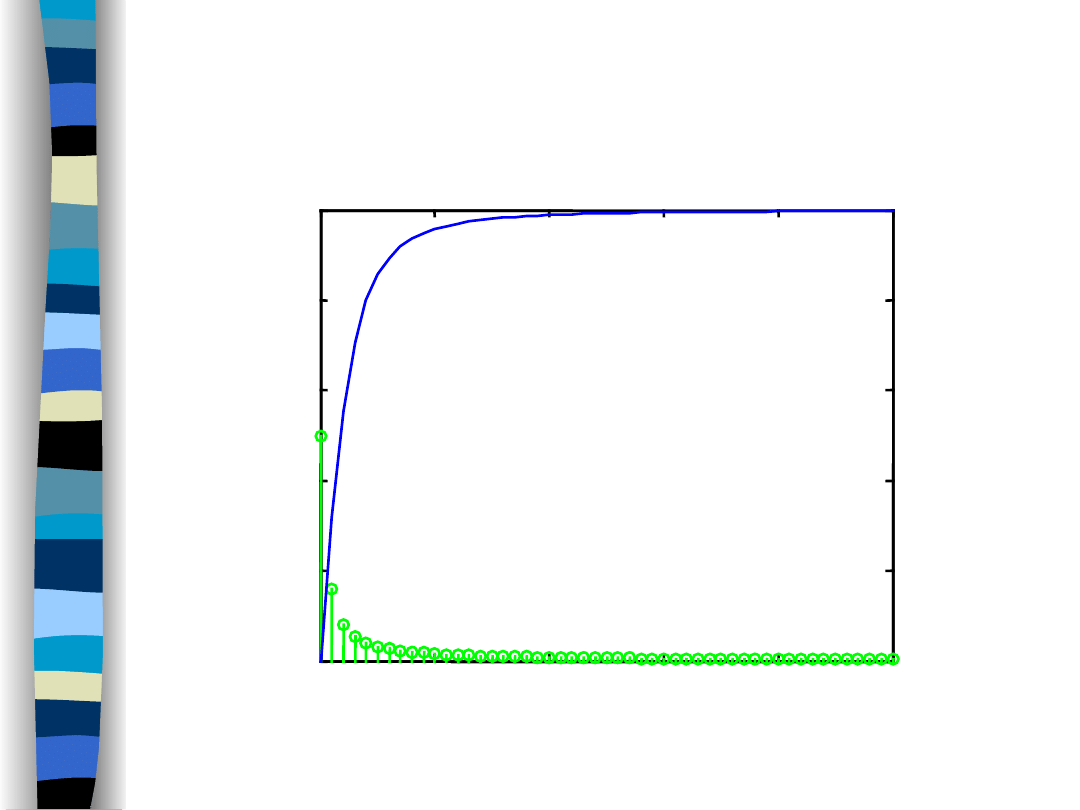
Amplitude spectra (f

g

/f

o

= 3)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Highpass filter and sawtooth signal – amplitude spectra

Highpass filter

Sawtooth signal

n

f

o

f

g

/f

o

= 3

„Signal Theory”  Zdzisław Papir

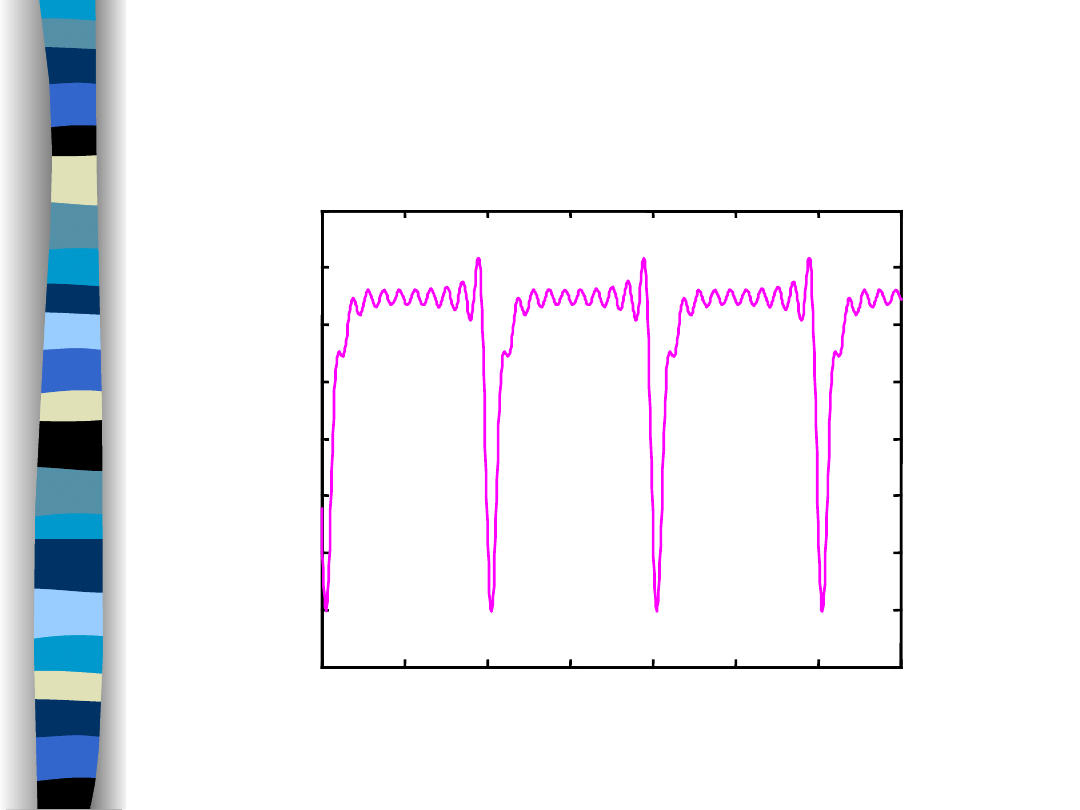
Output signal y(t) (f

g

/f

o

= 3)

0

0.5

1

1.5

2

2.5

3

3.5

-6

-5

-4

-3

-2

-1

0

1

2

Highpass filter response

time t/T

f

g

/f

o

= 3

„Signal Theory”  Zdzisław Papir

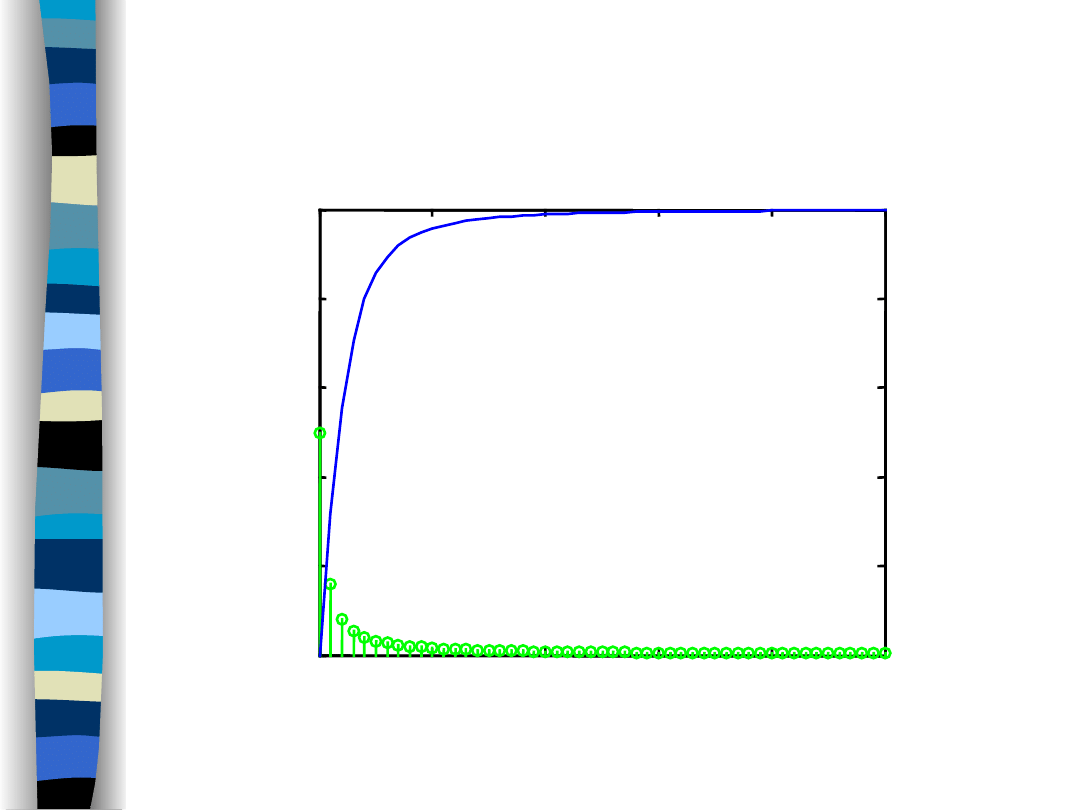
Amplitude spectra (f

g

/f

o

= 1)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Highpass filter and sawtooth signal – amplitude spectra

Highpass filter

Sawtooth signal

n

f

o

f

g

/f

o

= 1

„Signal Theory”  Zdzisław Papir

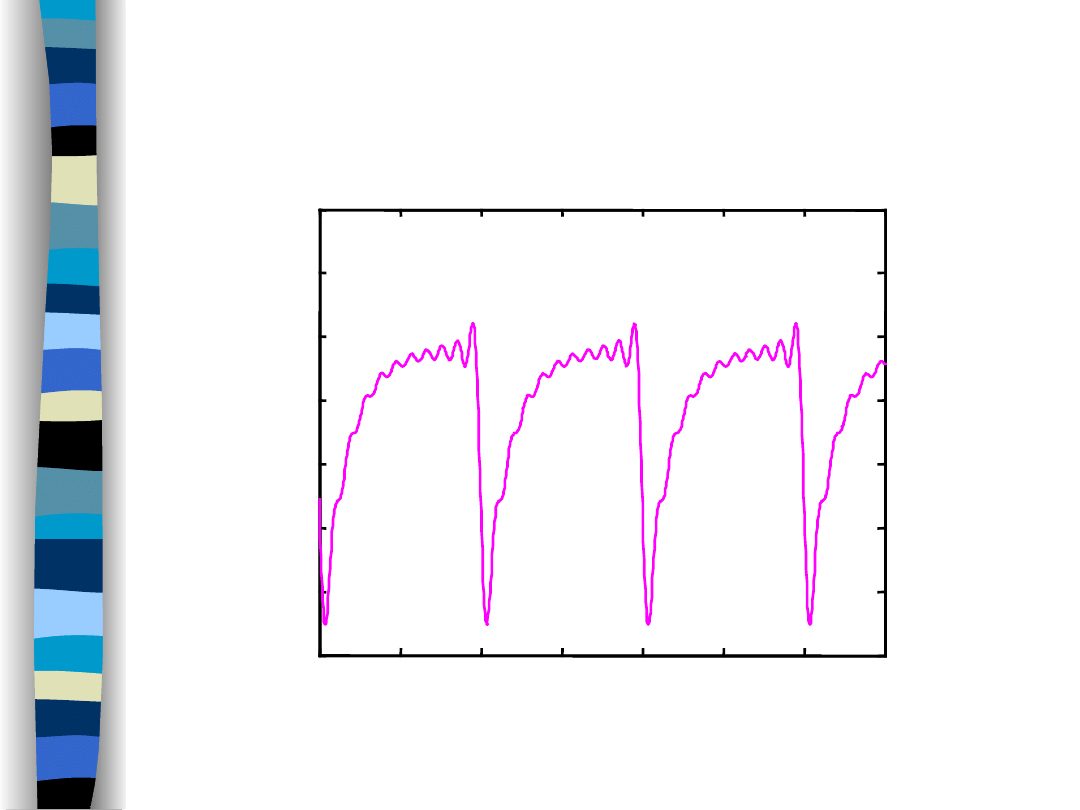
Output signal y(t) (f

g

/f

o

= 1)

0

0.5

1

1.5

2

2.5

3

3.5

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

High pass filter

time t/T

f

g

/f

o

= 1

„Signal Theory”  Zdzisław Papir

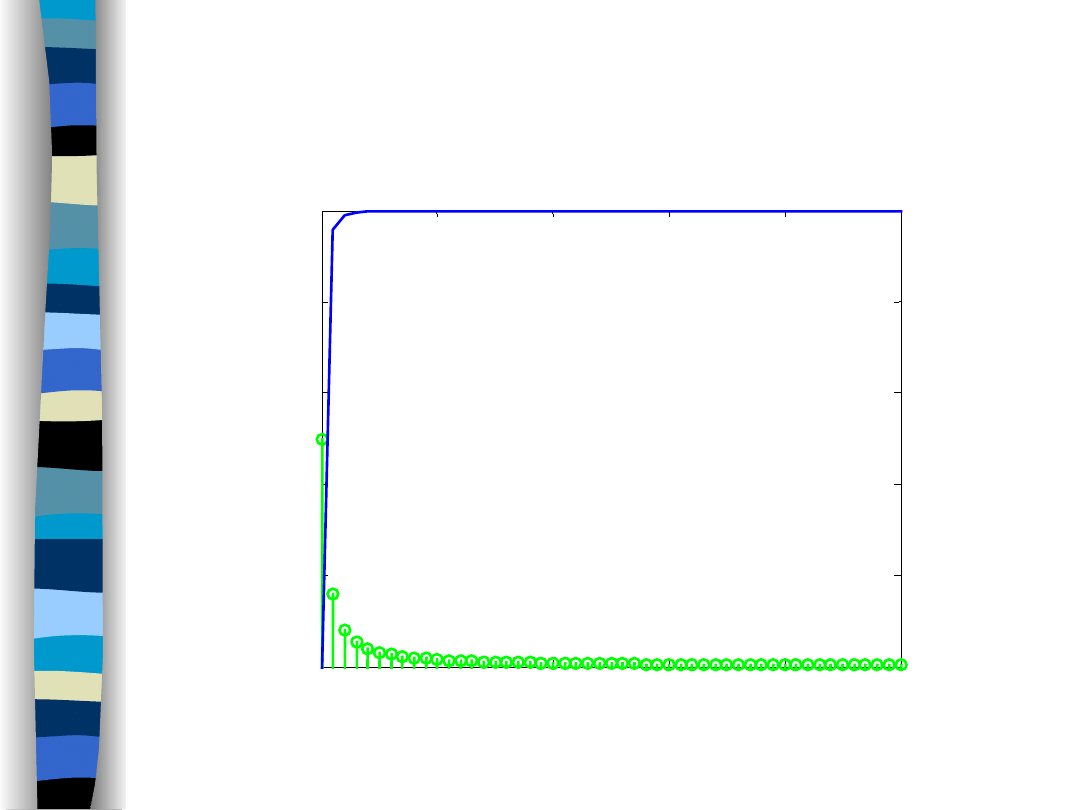
Amplitude spectra (f

g

/f

o

= 1/3)

0

10

20

30

40

50

0

0.2

0.4

0.6

0.8

1

Highpass filter and sawtooth signal – amplitude spectra

Highpass filter

Sawtooth signal

n

f

o

f

g

/f

o

= 0,3

„Signal Theory”  Zdzisław Papir

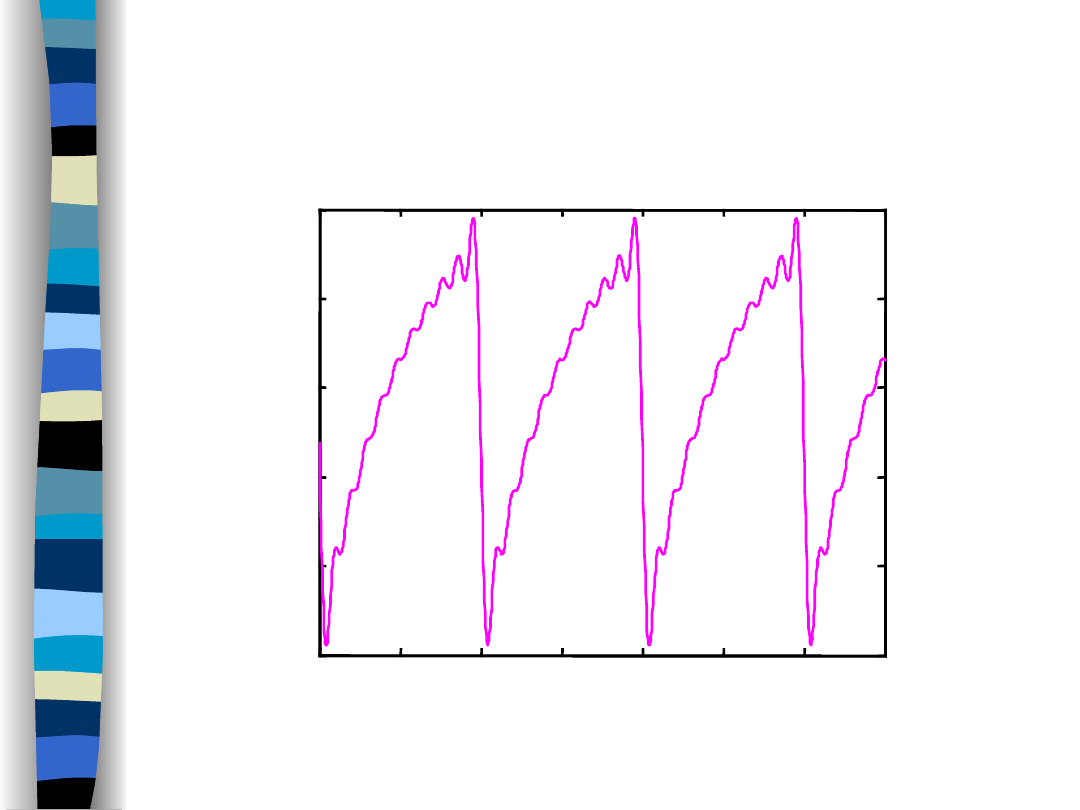
Output signal y(t) (f

g

/f

o

= 1/3)

Highpass filter response

0

0.5

1

1.5

2

2.5

3

3.5

-0.06

-0.04

-0.02

0

0.02

0.04

time t/T

f

g

/f

o

= 0,3

„Signal Theory”  Zdzisław Papir

„Teoria sygnałów”  Zdzisław Papir

 



















d

e

j

X

t

x

t

j

2

1

)

(

   

 

   

















j

X

j

H

j

Y

d

e

j

X

j

H

t

y

t

j













2

1

)

(

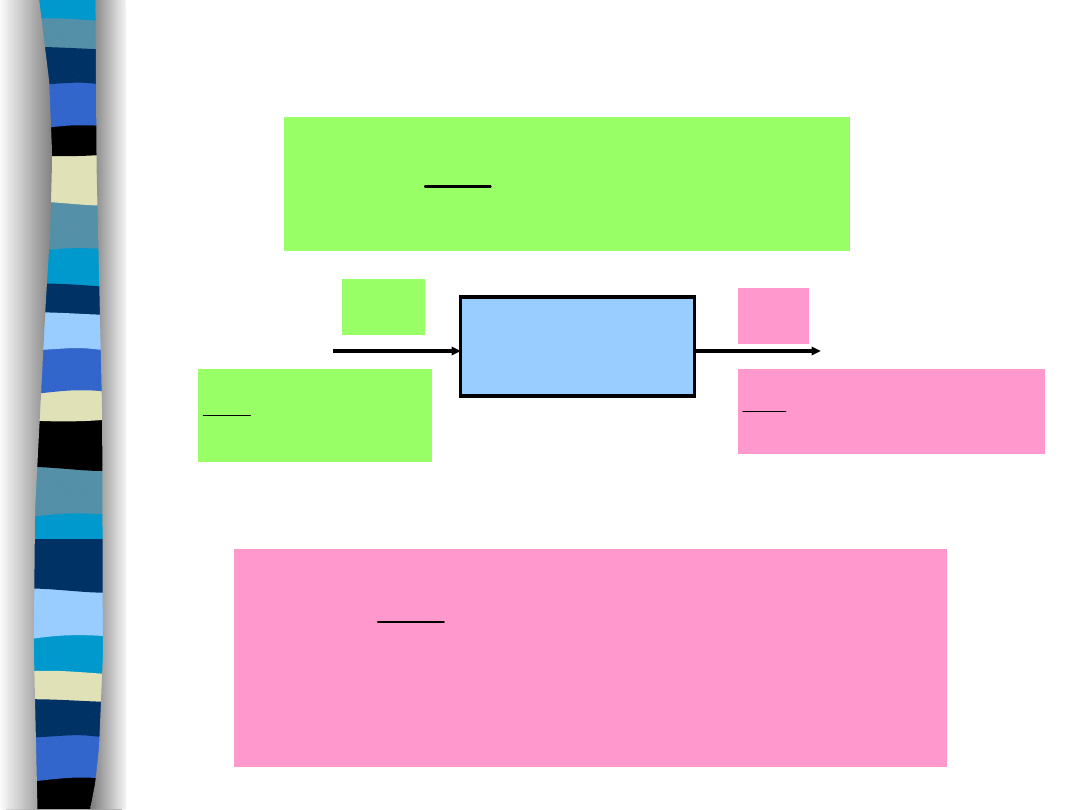
Transformata Fouriera sygnału wyjściowego y(t)

)

(s

H

)

(t

x

   

t

j

e

j

X

j

H









2

1

 

t

j

e

j

X







2

1

 

t

y

Signal filtering - Fourier transform

 

 

 

   









j

X

j

H

j

Y

j

Y

t

y





 

   

   

   

 

 

t

t

x

t

h

t

y

t

x

t

h

j

X

j

H

j

Y





















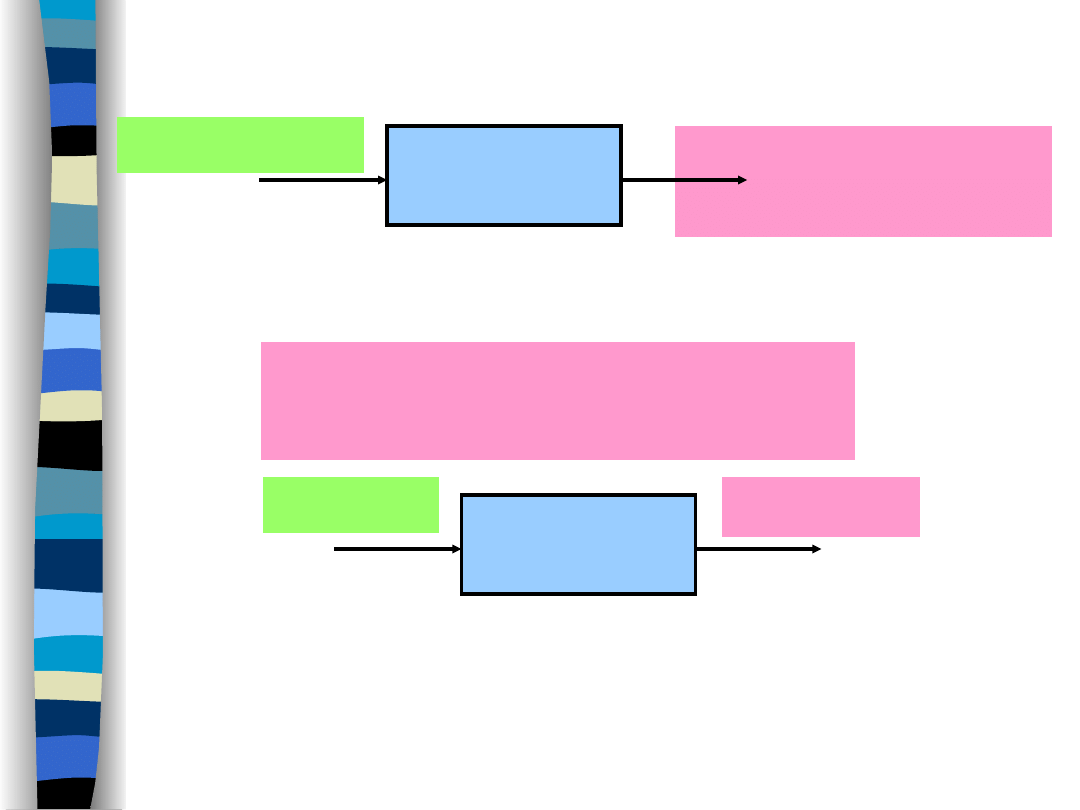
Impulse response of the filter

Signal filtering - Fourier transform

)

(s

H

 



j

X

t

x 

)

(

)

(t

h

 

)

(t

h

t

y 

 

t

t

x





)

(

Impulse response of a filter is its output signal when
input of a filter is excited by the Dirac delta impulse



(t).

„Signal Theory” 

Zdzisław Papir

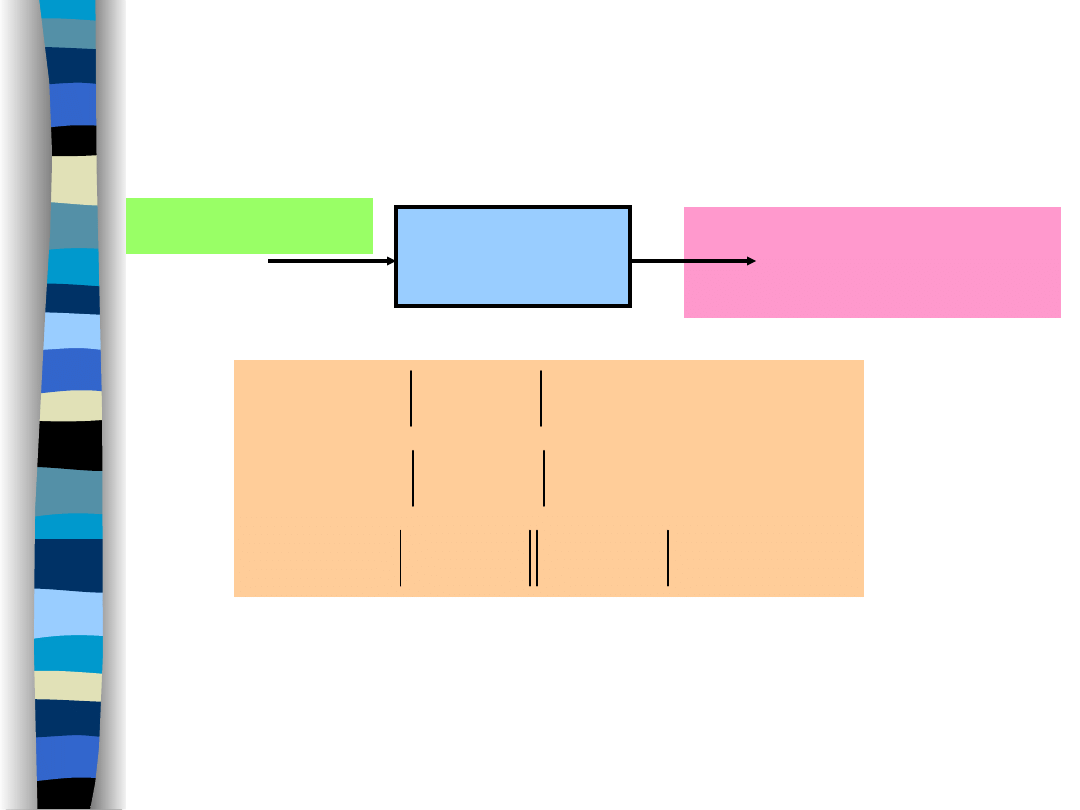
Frequency characteristics
of a signal after filtration

 

 

 

   









j

X

j

H

j

Y

j

Y

t

y





)

(s

H

 



j

X

t

x 

)

(

 

 

 

 

 

 

 

   

   











































j

j

j

e

j

H

j

X

j

Y

e

j

H

j

H

e

j

X

j

X

Filtration changes both:

• amplitude spectrum

• phase spectrum
of an input signal.

„Signal Theory”  Zdzisław Papir

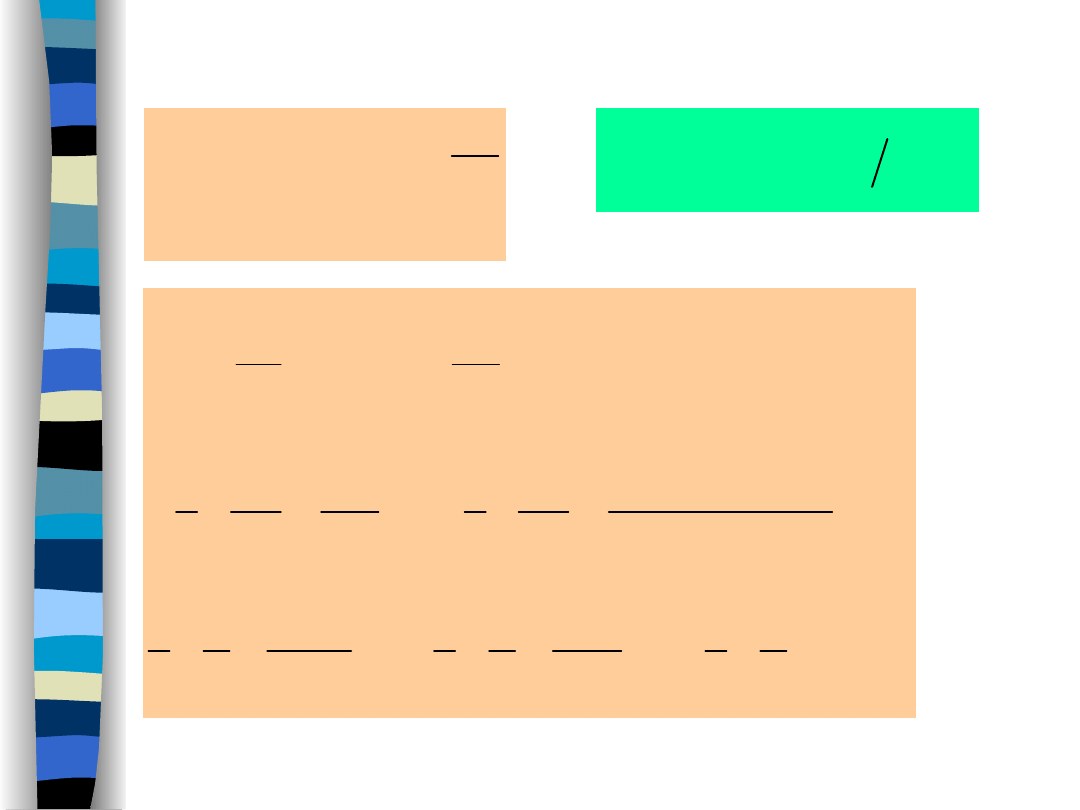
Signal filtering - example

   

 

 

 











W

j

H

j

t

t

x

2

1









1

 

 

 

Wt

d

d

t

d

t

j

t

j

d

e

j

d

e

j

t

y

Wt

W

W

W

W

W

t

j

t

j

W

W

Si

1

2

1

sin

1

2

1

sin

1

2

1

sin

cos

2

1

2

1

2

1

2

1

1

2

1

0

0





















































































































 





x

d

x

0

sin

Si







„Signal Theory” 

Zdzisław Papir

Sinus integral
properties

 





x

d

x

0

sin

Si







„Signal Theory”  Zdzisław Papir

1. Sinus integral is an odd function

 

 

x

du

u

u

du

d

u

d

x

x

x

Si

sin

sin

Si

0

0







































2. Sinus integral in zero vicinity (x  0)

 

0

sin

0

Si

0

0













d





0

sin

,

0

Si

0

















x

d

x

x

Sinus integral
properties

 





x

d

x

0

sin

Si







„Signal Theory” 

Zdzisław Papir

3. Horizontal asymptote (x )

 

2

sin

Si

lim

0

x





















d

x





0

0

sin

2

1

sin

2

1

sin







































F

d

d

4. Local extrema

 

0

,

0

sin

Si











k

k

x

x

x

dx

x

d



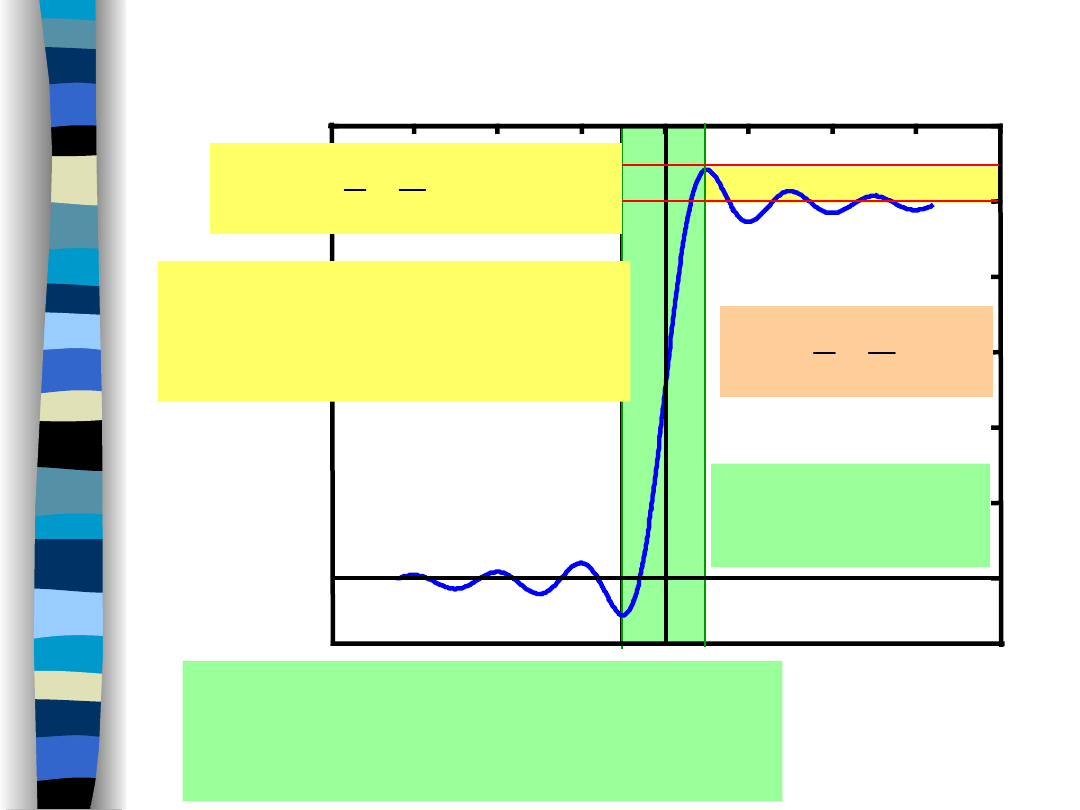
Rising time of a filter output
is inversely proportional
to its bandwidth.

Signal filtering - example

„Signal Theory”  Zdzisław Papir

1

0

 

 

Wt

t

y

Si

1

2

1







+



/W

-



/W

t

r

= 2



/W =

1/B

 

 

 

W

f

W

y













Si

1

2

1

The peak output value
does not depend on
the filter bandwidth.

Summary

• The output signal of the filter excited by a periodic signal
is a periodic signal as well; in most cases its Fourier series
is not summable to a closed form expression.

•

The Fourier transform of the output signal is a product of the

filter transfer function and input signal Fourier transform.

• The impulse response of the filter is its output signal when
the filter is driven by the Dirac delta



(t).

•

The filter output signal is a convolution of the filter

impulse response and the input signal.

„Signal Theory” 

Zdzisław Papir