More on statistical

distributions

Więcej o rozkładach

statystycznych

Agnieszka Piernik

1. Rozkład zero-jedynkowy
2. Rozkład Pascala
3. Rozkład geometryczny
4. Rozkład Poissona
5. Rozkład hypergeometryczny

Funkcje rozkładu

prawdopodobieństwa cech

nieciągłych

dr Agnieszka Piernik

Rozkład zero-jedynkowy – jest rezultatem takiego doświadczenia
(zwanego próbą Bernoulliego), w wyniku którego określone
zdarzenie A wystąpi lub nie wystąpi
Wówczas jeżeli

P(A) = p to P(Ā) = 1-p = q

gdzie Ā oznacza zdarzenie przeciwne, oraz

P(X = 1) = p
P(X = 0) = q

__

x



p

pq



SD



2

= pq = p(1-p)

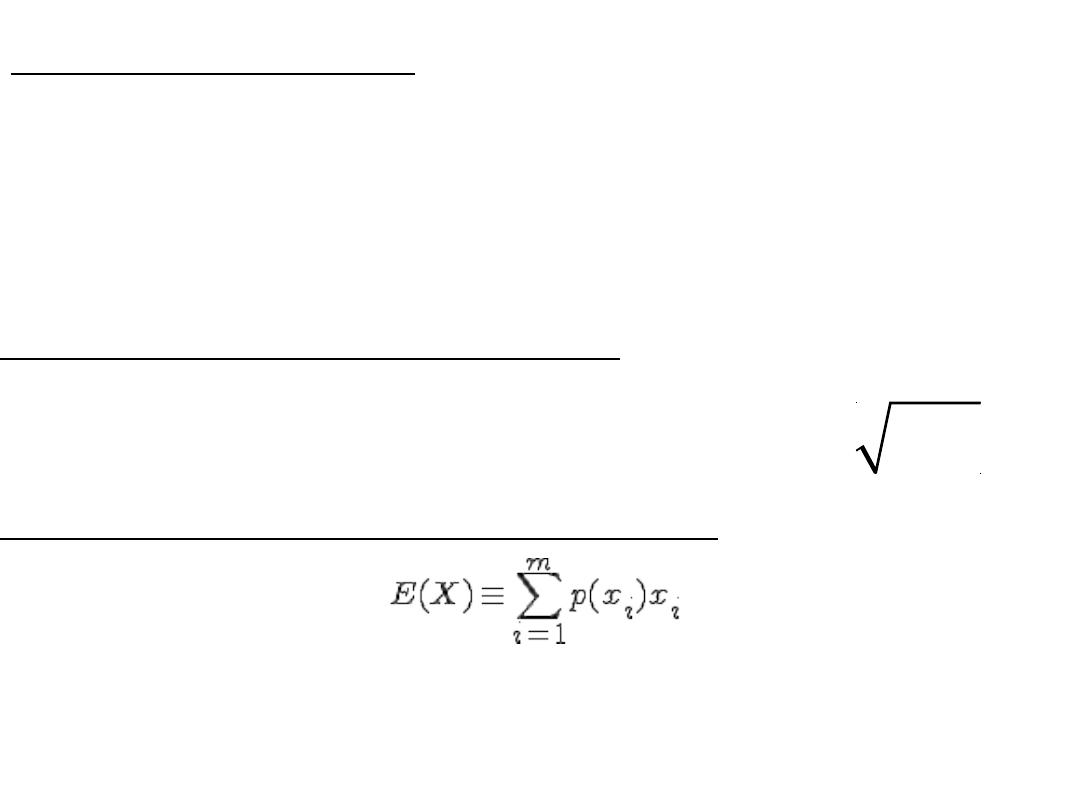
Średnia (wartość oczekiwana)

Wariancja

Odchylenie standardowe

Dla doświadczeń, gdzie sukces jest tylko jeden:

Dla doświadczeń, gdzie sukcesów jest więcej niż jeden:

Wariancja

Średnia (wartość oczekiwana)

x

i

- kolejna wartość zmiennej losowej



2

=



(x

i

– E(X))

2

p

i

n

i=1

Zadanie 1
Wysiewamy kolejno 10 ziaren żyta i notujemy, czy ziarno wykiełkuje, czy
nie. W wyniku uzyskujemy, że wykiełkowało 9 ziarniaków. Jak wygląda
zero-jedynkowy rozkład prawdopodobieństwa dla pojedynczego
doświadczenia?

Zadanie 2
Przyjmijmy, że prawdopodobieństwo uzyskania przez studenta oceny
bardzo dobrej, dobrej, dostatecznej i niedostatecznej jest takie samo. Z
jakim prawdopodobieństwem zmienna losowa przybiera wartość x=1

Zadanie 3
Rzucamy raz kostką do gry. Jak wygląda rozkład zmiennej losowej w tym
doświadczeniu?
Ile wynosi średnia rozkładu zmiennej losowej oraz wariancja?

p(k)=k/n

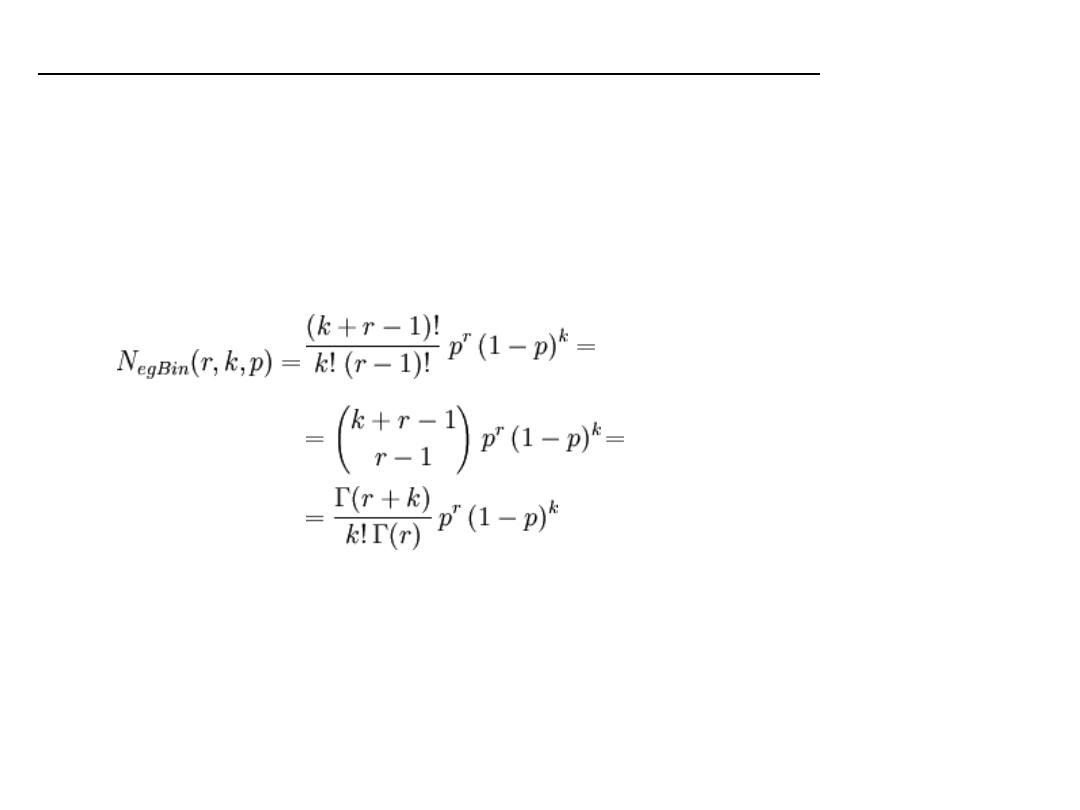
Rozkład Pascala (ujemny rozkład dwumianowy) –
rozkład prawdopodobieństwa opisujący m.in. liczbę sukcesów i
porażek w niezależnych i posiadających równe
prawdopodobieństwo sukcesu próbach Bernoulliego.

Jeśli r-liczba sukcesów, k-liczba porażek, p-
prawdopodobieństwo sukcesu w badanych próbach
Bernoulliego, to:

opisuje, jakie jest prawdopodobieństwo, że w k + r próbach
wystąpi r sukcesów.

__

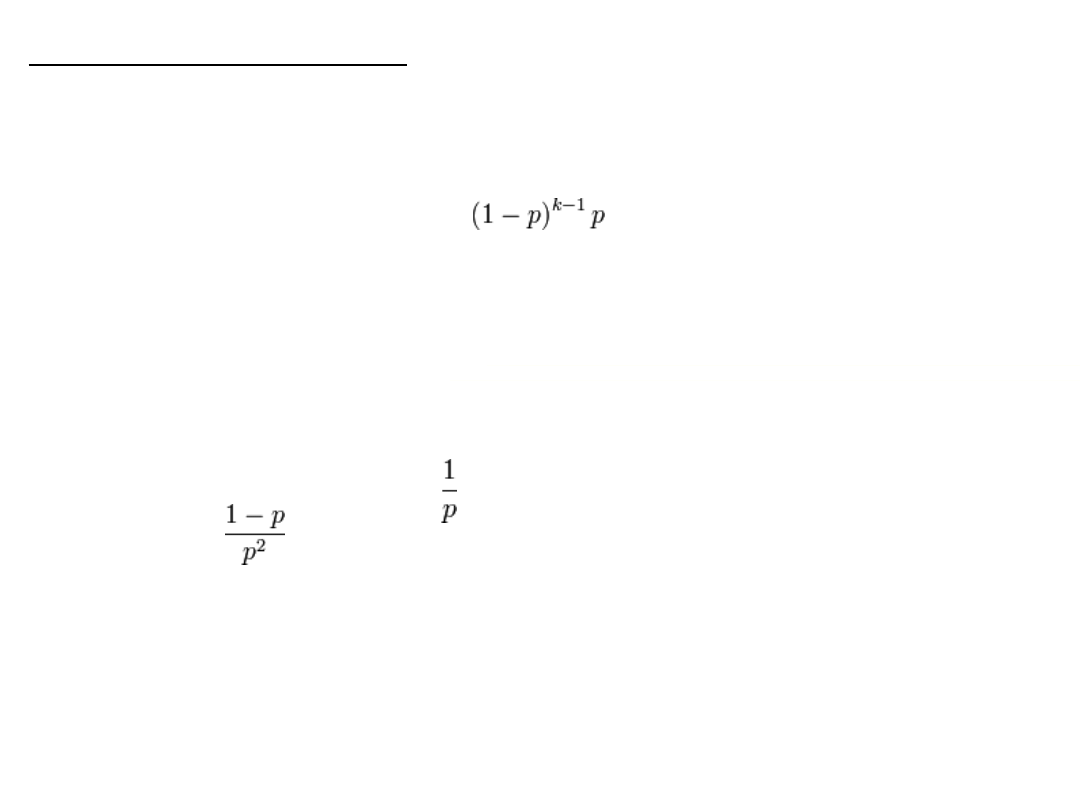
x





2

=

Średnia (wartość oczekiwana)

Wariancja

Rozkład geometryczny
jest dyskretnym rozkładem prawdopodobieństwa opisującym
prawdopodobieństwo zdarzenia, że proces Bernoulliego odniesie
pierwszy sukces dokładnie w k-tej próbie. k musi być liczbą
naturalną dodatnią.

Niekiedy zamiast badać w której próbie odniesiemy pierwszy sukces,
badamy ile prób z rzędu kończy się porażką. Wówczas tak zdefiniowane k
jest o jeden mniejsze, więc we wszystkich wzorach należy dodać do niego
1.
Rozkład geometryczny to szczególny przypadek

ujemnego rozkładu

dwumianowego

dla r = 1.

P(X=1)=

Rozkład Poissona

 Rozkład ten wprowadził S. D. Poisson i reprezentuje
matematyczny model dla wielu bardzo różnych zjawisk
biologiczno-medycznych i nie tylko. Gwiazdy w przestrzeni,
rozmieszczenie zwierząt na badanym terenie, rodzynki w cieście
czy oddziaływanie promieniowania na komórkę jest zgodne z
rozkładem Poissona.

 Prawdopodobieństwo P(x) zajścia zdarzenia korzystnego x,
wyrażone jest wzorem:

( )

( )

!

x

np

np

P x

e

x





_

X=



2

=np

Średnia (wartość oczekiwana)

Wariancja

x- oczekiwna wartość zmiennej losowej
(średnia liczba zajścia zdarzenia r w populacji)
n-liczba prób
p-prawdopodobieństwo sukcesu
e-podstawa logarytmu naturalnego 2,718

Zadanie 4
Próbkę kwasu acetylosalicylowego, wyznakowaną izotopowo przy weglu

14

CH

3

-COO-C

2

H

5

O

2

, zliczano przez 5 minut w liczniku scyntylacyjnym.

Liczba zliczeń wynosiła 2905. Jaki jest błąd standardowy oznaczenia?

Zadanie 5
Tą sama próbkę zliczano trzykrotnie i uzyskano następujące wyniki:

Liczba
zliczeń

Czas
(min)

1

1799

3

2

2453

4

3

4387

8

Suma

8639

15

Jaka jest średnia liczba zliczeń na minutę i jaki jest błąd oznaczenia?

Zadanie 6
Dopuszczalna wadliwość produkowanych szczepionek wynosi 1,5‰. Do
sprawdzenia jakości produkcji pobrano losowo próbkę 700 fiolek. Niech x
oznacza liczbę złych fiolek spośród 700 wylosowanych. Obliczyć: a)
wartość oczekiwaną zmiennej x b) wariancję i odchylenie standardowe.

_

X=



2

=np

Zadanie 7
W każdej serii torebek z nasionami jarzyn znajduje się średnio 1,5 nasion
chwastów. Jakie jest prawdopodobieństwo, że losowo wybrana torebka z
nasionami będzie zawierała więcej niż 3 nasiona chwastów?

Zadanie 8
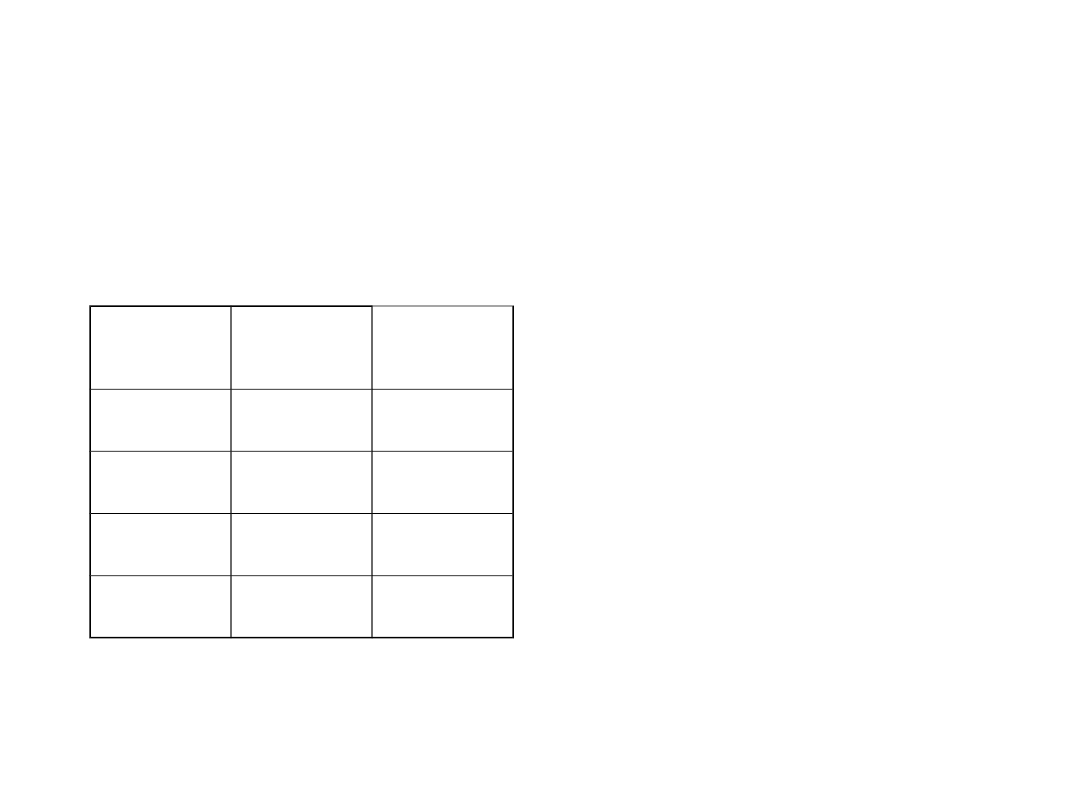
Metodą kolejnego zliczania próbowano ocenić gestość zawiesiny bakterii.

Po starannym wytrząśnięciu pobrano próbki zawiesiny o objętości
0,5ml i rozporowadzono (w aseptycznych warunkach) na płytkach z
pożywką agarową. Po inkubacji policzono kolonie bakteryjne na każdej
ze 100 płytek. Wyniki podane są w postaci tabeli częstości:

Liczba kolonii na płytkę 0 1 2 3 4 5 6 7 8 9 10 11
Częstość 3 9 17 22 20 14 8 4 2 1 0 0
a) Obliczyć całkowitą liczbę kolonii oraz ich średnią liczbę przypadającą

na płytkę

b) Obliczyć błąd standardowy dla średniej przypadającej na płytkę

zakładając, że w oryginalnym inokulum bakterie były rozmieszczone w
sposób losowy.

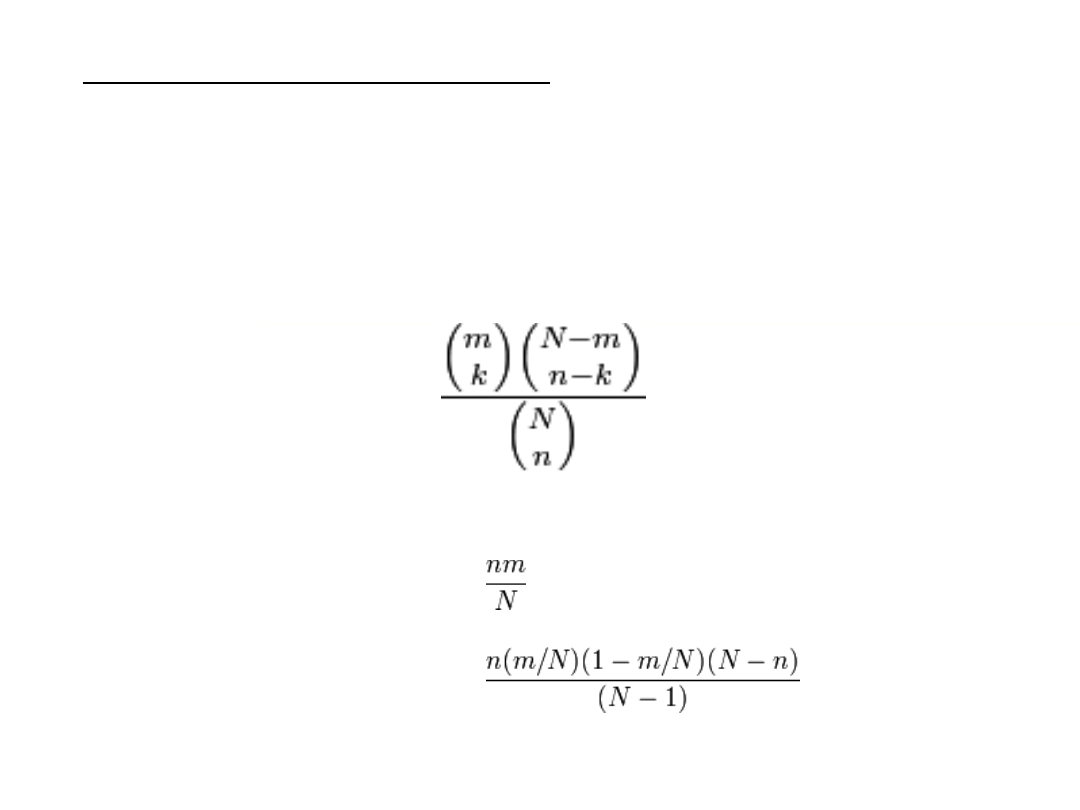
Rozkład hipergeometryczny to rozkład prawdopodobieństwa
związany z tzw. schematem urnowym
Zmienna losowa o tym rozkładzie określa liczbę elementów
jednego typu występujących w n-elementowej próbie
wylosowanej z urny zawierającej m elementów tego typu wśród
N wszystkich elementów.

X
=

Średnia (wartość oczekiwana)

Wariancja

_



2

=

P(x) =

k – liczba sukcesów
m – liczba elementów danego typu
n – liczba prób
N – liczba wszystkich elementów

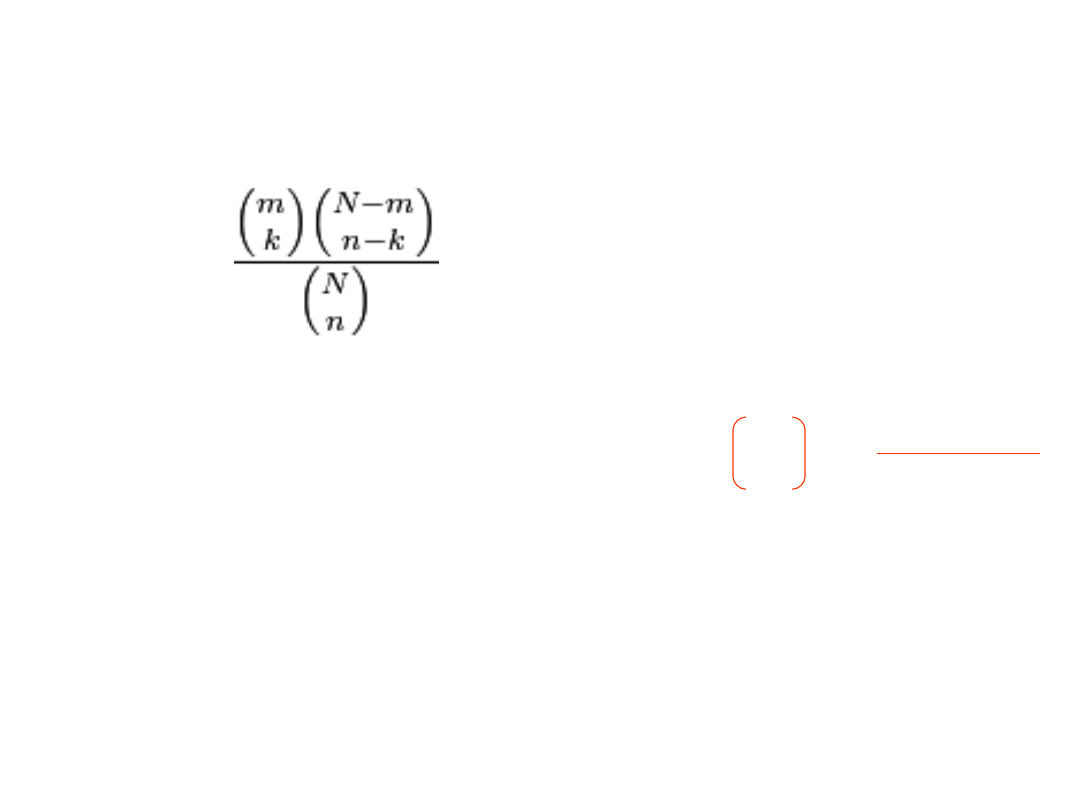
Zadanie 9
W hodowli znajdują się dwa rodzaje ryb – białe i czarne. Ryb białych jest
5 a czarnych 45. Odłowienie ryby białej oznacza sukces. Odławiano ryby
kolejno 10 razy bez zwracania. Jakie jest prawdopodobieństwo, że
dokładnie 4 ryby spośród odłowionych 10 są białe?

P(x) =

k – liczba sukcesów
m – liczba elementów danego typu
n – liczba prób
N – liczba wszystkich elementów

n
k

=

n !

k !(n - k)!