Przykładowe wahadła - modelowanie

Elementy

Elementy

Mechatroniki

Mechatroniki

Wykład nr 3

Wykład nr 3

dr inż. Tomasz Trawiński

Politechnika Śląska

Politechnika Śląska

Wydział Elektryczny

Wydział Elektryczny

Katedra Mechatroniki

Katedra Mechatroniki

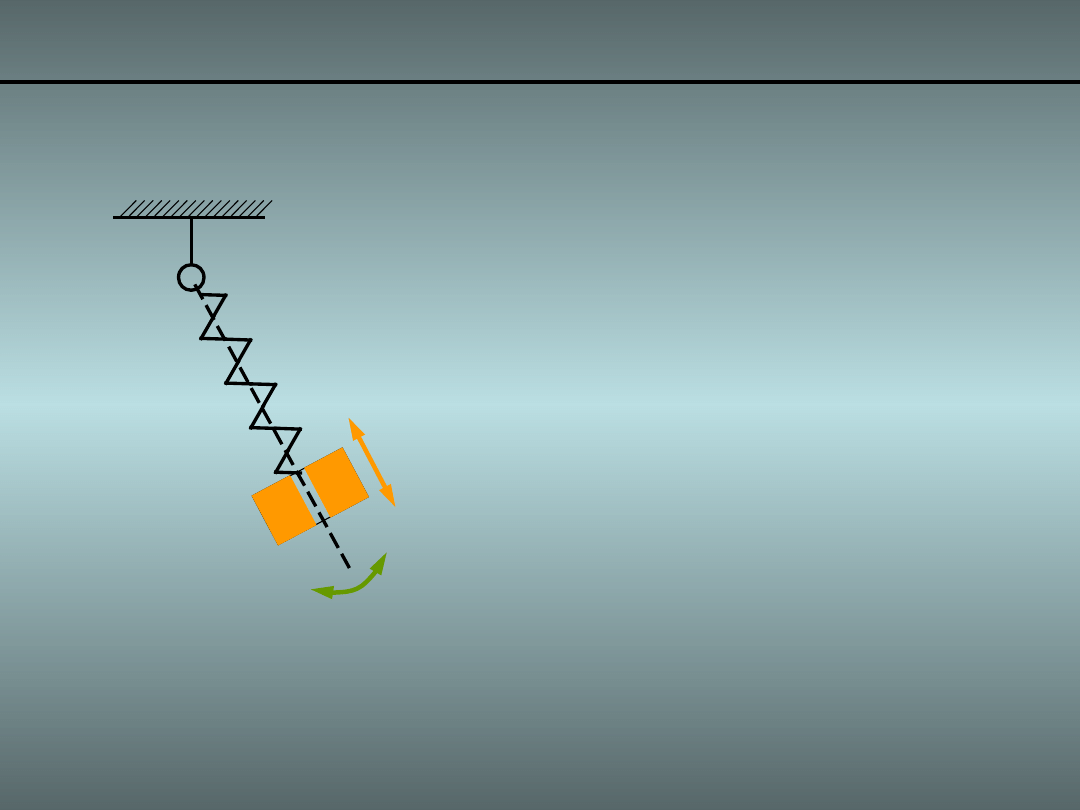
Przykład1. Wahadło z masą ślizgającą się 1/

Przykład1. Wahadło z masą ślizgającą się 1/

•

Niech będzie dane wahadło o strukturze kinematycznej:

Niech będzie dane wahadło o strukturze kinematycznej:

k

k

m

m

• Masę „m” możemy traktować jako punktową

• Masa „m” może wykonywać ruch postępowy

wzdłuż prowadnicy

• Prowadnica ma znikomo małą masę

w porównaniu do masy „m”

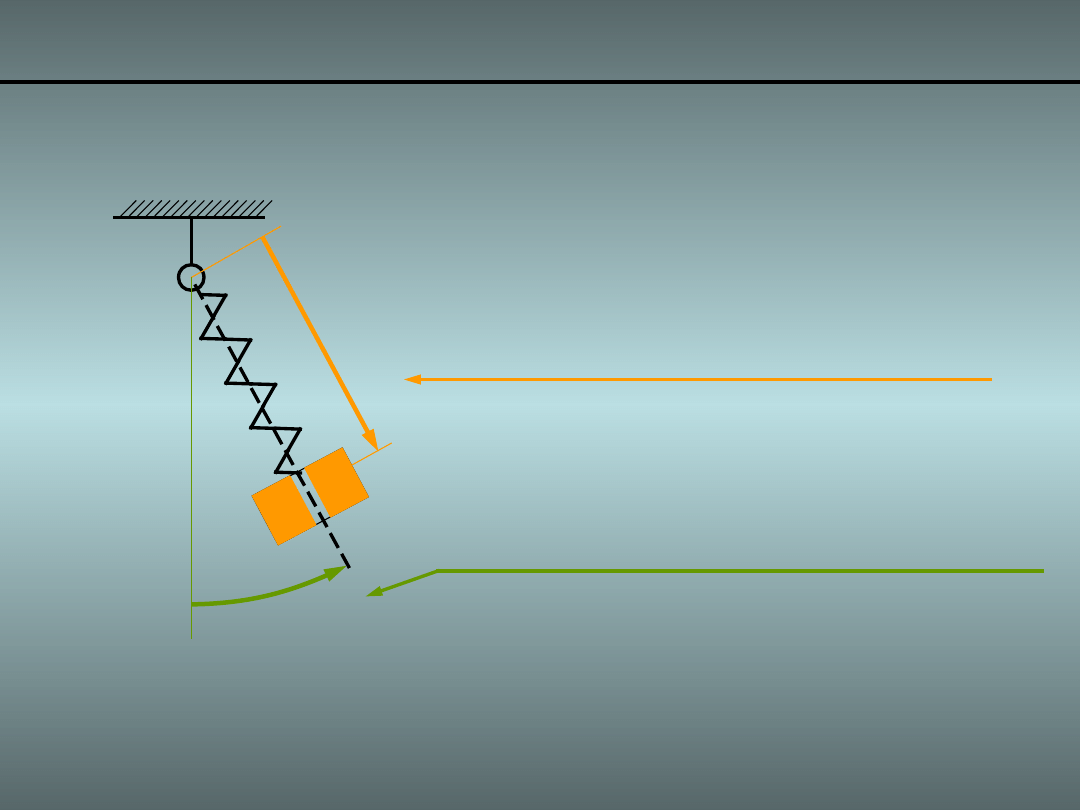
• Zmienną reprezentującą wydłużenie sprężyny

• Zmienną związaną z wychyleniem całego wahadła

Przykład 1. Wahadło z masą ślizgającą się 2/

Przykład 1. Wahadło z masą ślizgającą się 2/

•

Przyjmujemy następujące zmienne uogólnione:

Przyjmujemy następujące zmienne uogólnione:

k

k

m

m

q

q

1

1

q

q

2

2

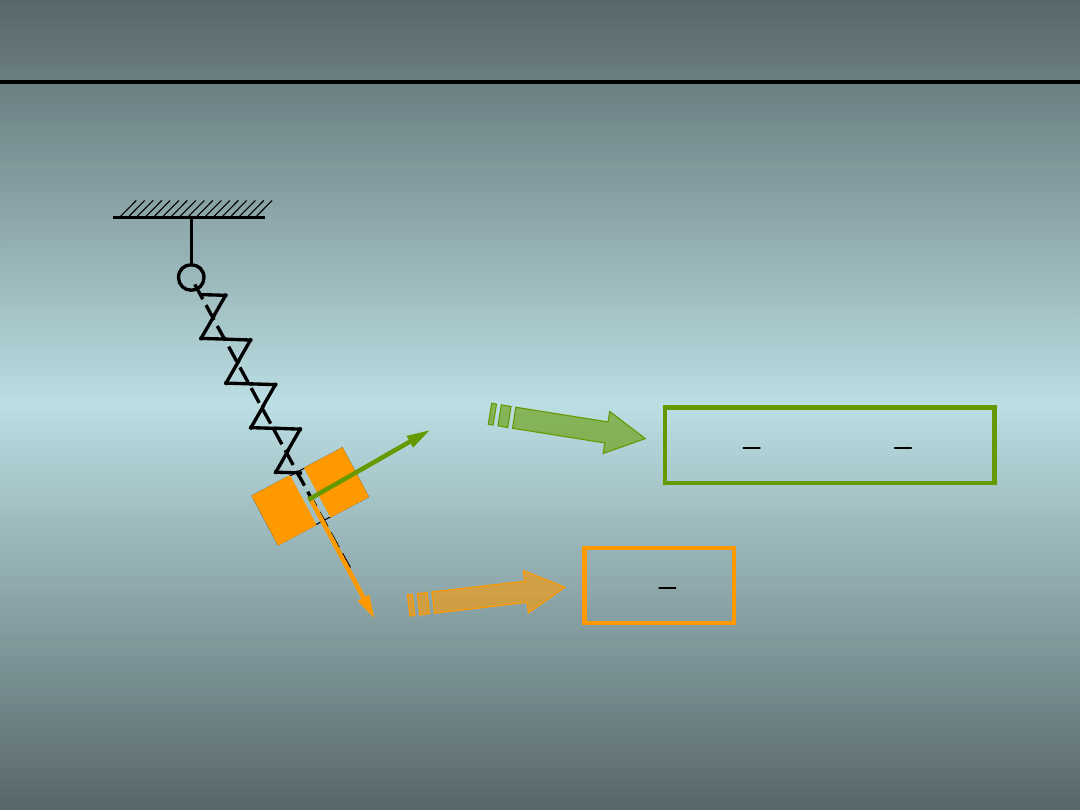
• Wprowadzając prędkość styczną

do trajektorii ruchu masy „m”

Przykład 1. Wahadło z masą ślizgającą się 3/

Przykład 1. Wahadło z masą ślizgającą się 3/

•

Możemy przejść do współrzędnych prostokątnych:

Możemy przejść do współrzędnych prostokątnych:

k

k

m

m

q

q

1

1

q

q

2

2

•

•

q

q

1

1

2

1

1

2

1

q

m

E

k









2

2

2

1

2

2

1

2

2

1

2

1

q

mq

q

q

m

E

k









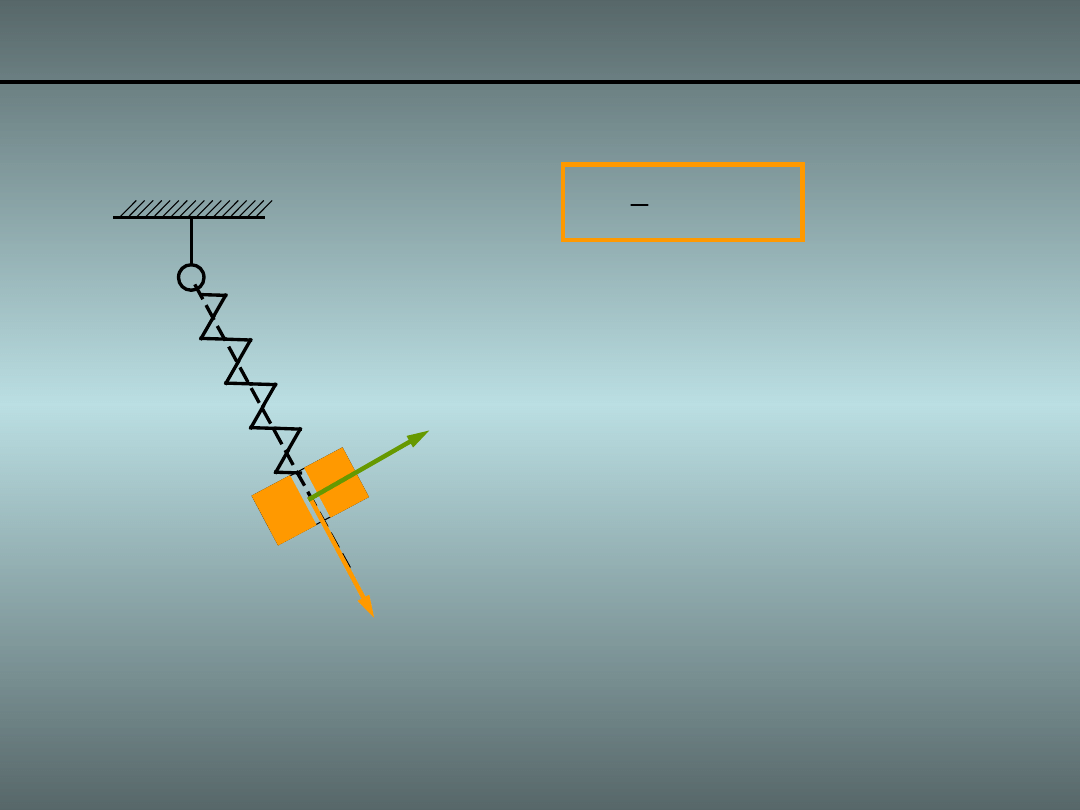
Przykład 1. Wahadło z masą ślizgającą się 4/

Przykład 1. Wahadło z masą ślizgającą się 4/

•

Całkowita energia kinetyczna wynosi:

Całkowita energia kinetyczna wynosi:

k

k

m

m

q

q

1

1

q

q

2

2

•

•

q

q

1

1





2

2

2

1

2

1

2

1

q

q

q

m

E

k



 



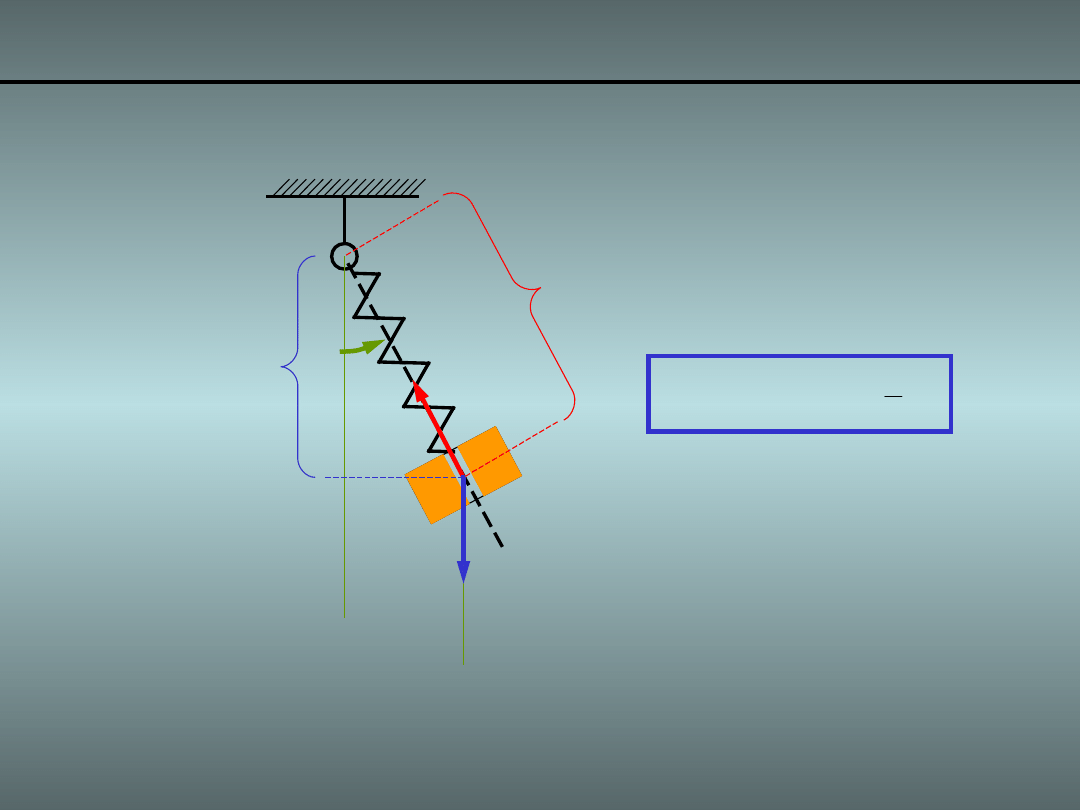
Przykład 1. Wahadło z masą ślizgającą się 5/

Przykład 1. Wahadło z masą ślizgającą się 5/

•

Energia potencjalna wynosi:

Energia potencjalna wynosi:

k

k

m

m

2

1

2

1

2

1

cos

kq

q

mgq

E

p







q

q

2

2

mg

mg

l=q

l=q

1

1

cos(q

cos(q

2

2

)

)

kq

kq

1

1

Siła sprężystości sprężyny przeciwdziała
sile wywołanej grawitacją.

q

q

1

1

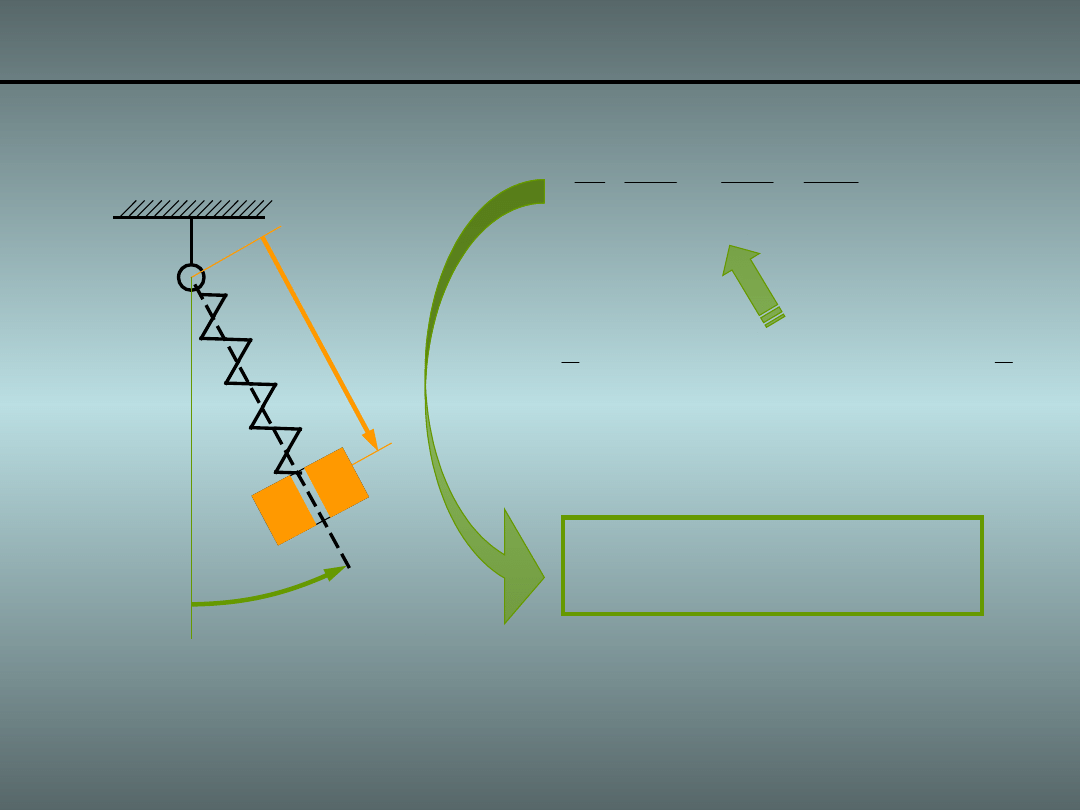
Przykład 1. Wahadło z masą ślizgającą się 6/

Przykład 1. Wahadło z masą ślizgającą się 6/

•

Równania Lagrange’a II rodzaju:

Równania Lagrange’a II rodzaju:

2

1

2

1

2

1

cos

kq

q

mgq

E

p







k

k

m

m

q

q

1

1

q

q

2

2

i

i

p

i

k

i

k

Q

q

E

q

E

q

E

dt

d





































;

2

1

2

2

2

1

2

1

q

q

q

m

E

k



 



0

sin

2

0

cos

2

1

1

1

2

2

1

2

1

2

2

2

1

1















q

mgq

q

q

q

m

q

q

m

kq

q

mg

q

mq

q

m











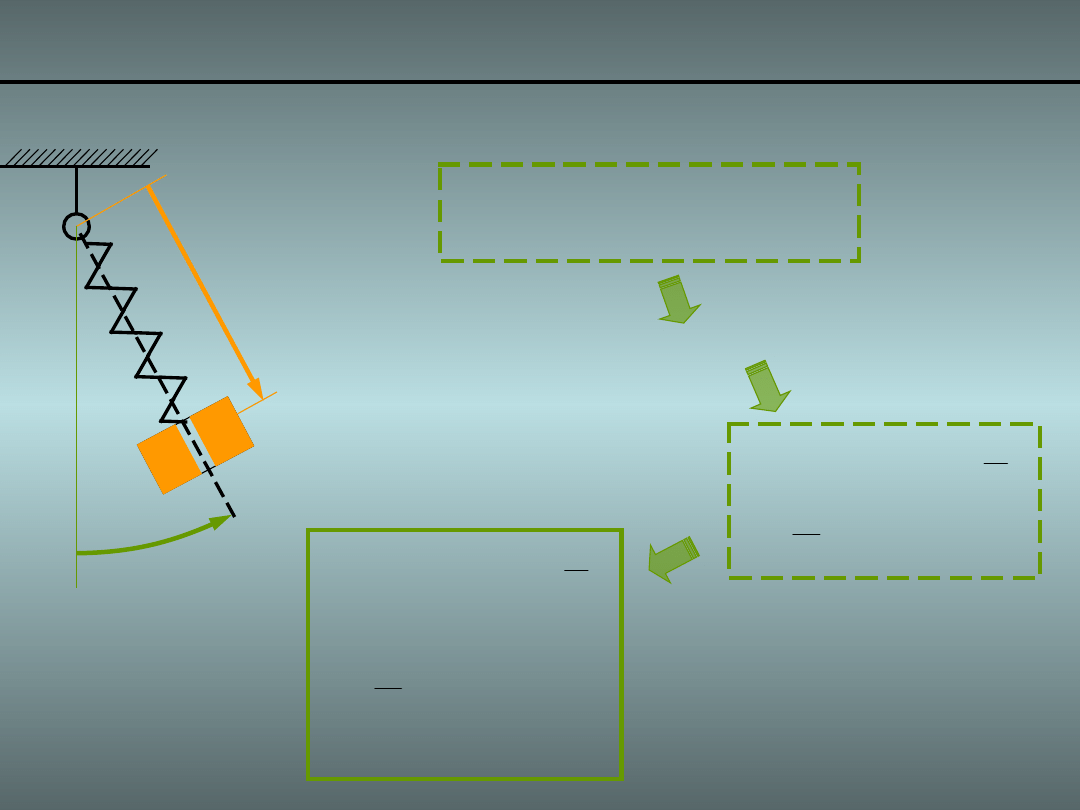
Przykład 1. Wahadło z masą ślizgającą się 7/

Przykład 1. Wahadło z masą ślizgającą się 7/

•

Implementacja równań Lagrange’a II rodzaju:

Implementacja równań Lagrange’a II rodzaju:

k

k

m

m

x

x

1

1

, v

, v

1

1

q

q

2,

2,

,

,





2

2

0

sin

2

0

cos

2

1

1

1

2

2

1

2

1

2

2

2

1

1















q

mgq

q

q

q

m

q

q

m

kq

q

mg

q

mq

q

m











Sprowadzić do postaci kanonicznej

)

sin

2

(

1

cos

2

2

1

1

2

1

2

2

2

1

1

q

g

q

q

q

q

q

m

k

q

g

q

q

q























2

2

2

2

1

1

2

1

1

1

2

2

2

1

1

)

sin

2

(

1

cos

























q

q

g

v

x

v

x

x

m

k

q

g

x

v









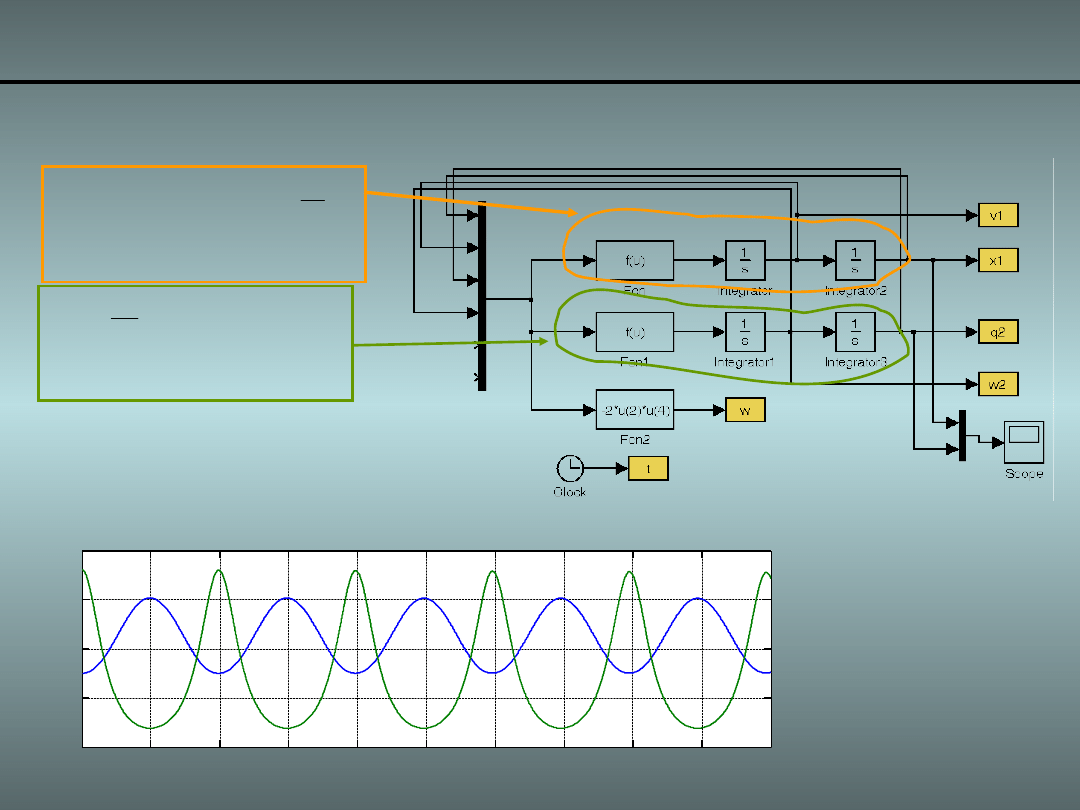
Przykład 1. Wahadło z masą ślizgającą się 8/

Przykład 1. Wahadło z masą ślizgającą się 8/

•

Implementacja równań Lagrange’a II rodzaju:

Implementacja równań Lagrange’a II rodzaju:

2

2

2

2

1

1

2

1

1

1

2

2

2

1

1

)

sin

2

(

1

cos

























q

q

g

v

x

v

x

x

m

k

q

g

x

v









0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

5

-0.2

0

0.2

0.4

0.6

x

x

1

1

q

q

2

2

wahadlo_slizgajace_v1.mdl

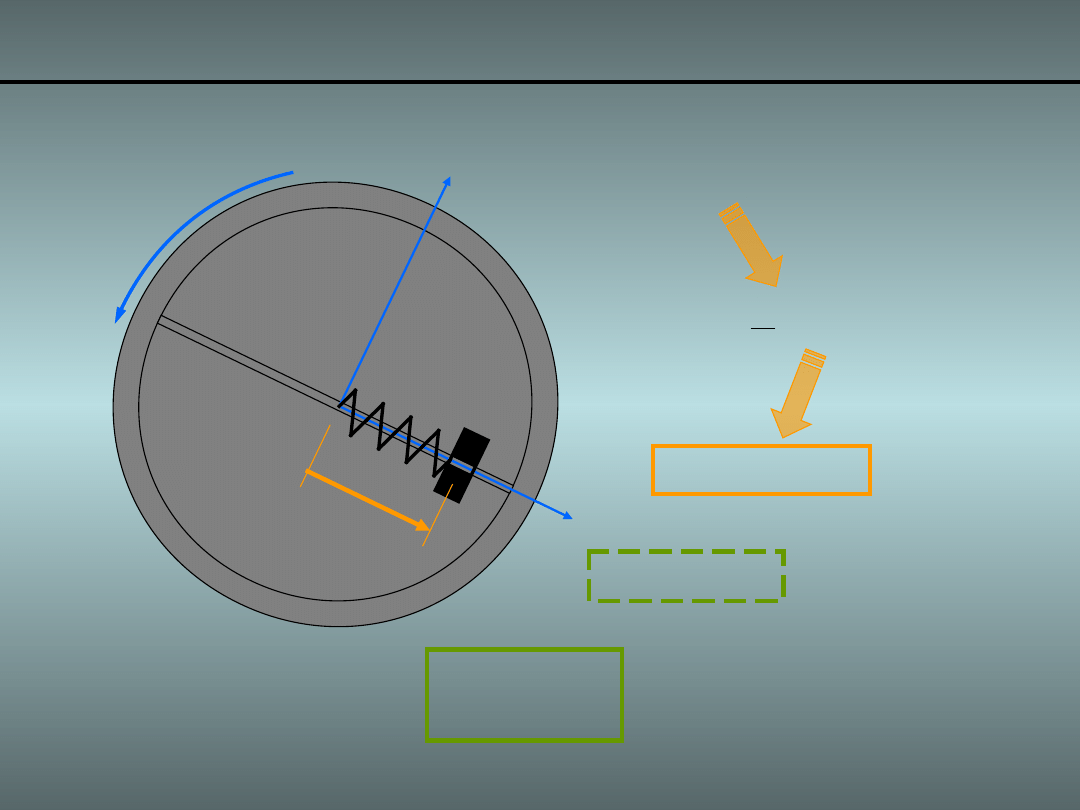
Przykład 2. Obracający się układ masa i sprężyna

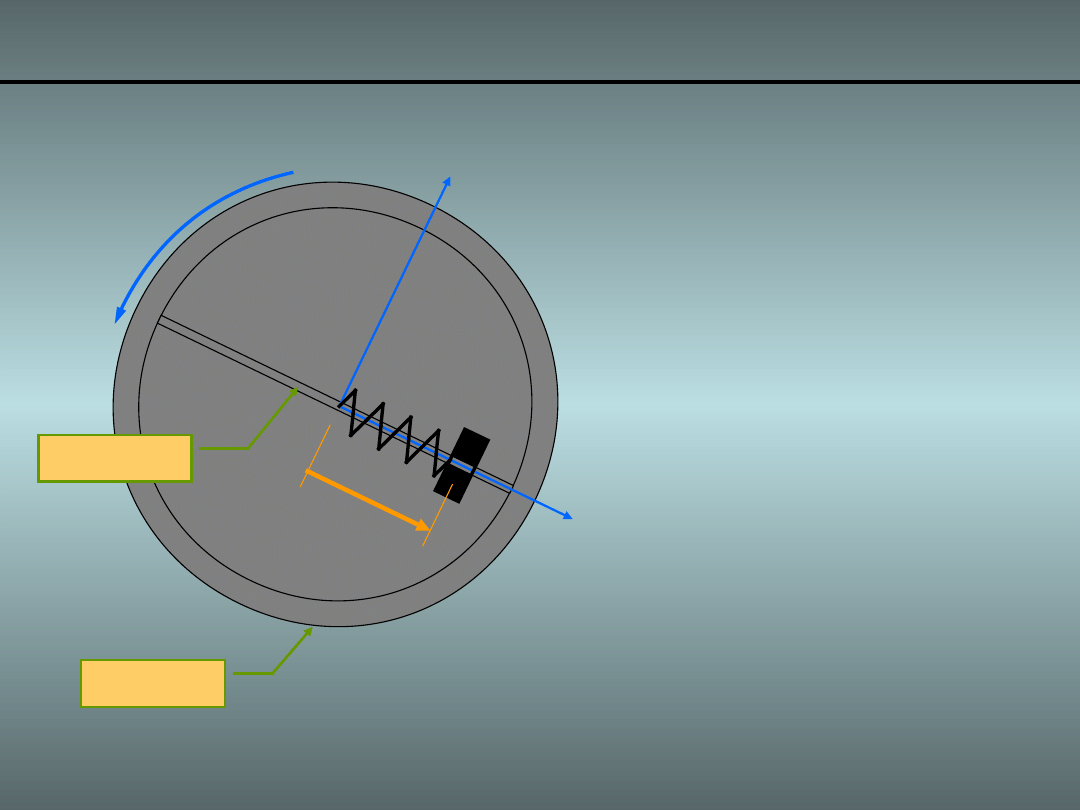
Przykład 2. Obracający się układ masa i sprężyna

1/

1/

•

Niech będzie dane układ o strukturze kinematycznej:

Niech będzie dane układ o strukturze kinematycznej:

• Masę „m”

możemy
traktować jako
punktową

• Masa „m”

może
wykonywać
ruch
postępowy
wzdłuż
prowadnicy

• Wprowadzamy

układ
współrzędnych
„xy”

• Układ wiruje

ze stałą
prędkością
kątową

y

y





x

x

q

q

1

1

k

k

m

m

Pierścień

Prowadnica

Przykład 2. Obracający się układ masa i sprężyna

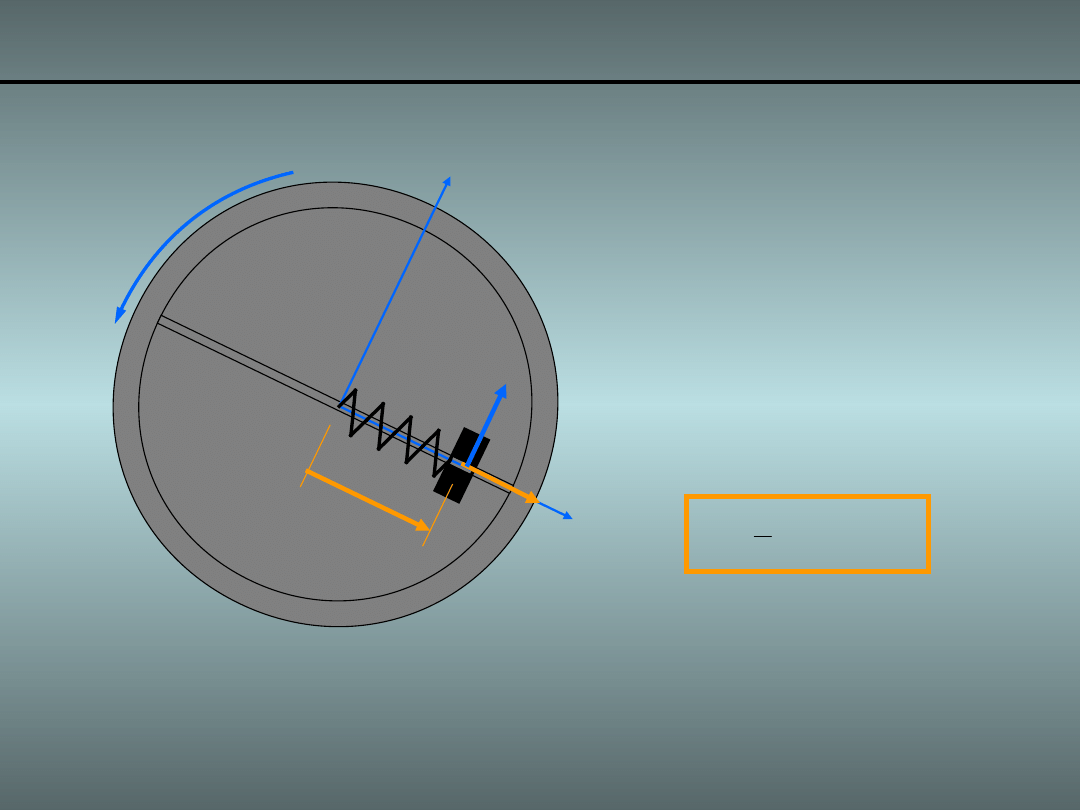
Przykład 2. Obracający się układ masa i sprężyna

2/

2/

•

Energia kinetyczna:

Energia kinetyczna:

y

y





x

x

q

q

k

k

m

m





2

2

2

2

1



q

q

m

E

k







Mamy 1 stopień swobody:

- ruch postępowy masy

q

q

.

.

q

q





Przykład 2. Obracający się układ masa i sprężyna

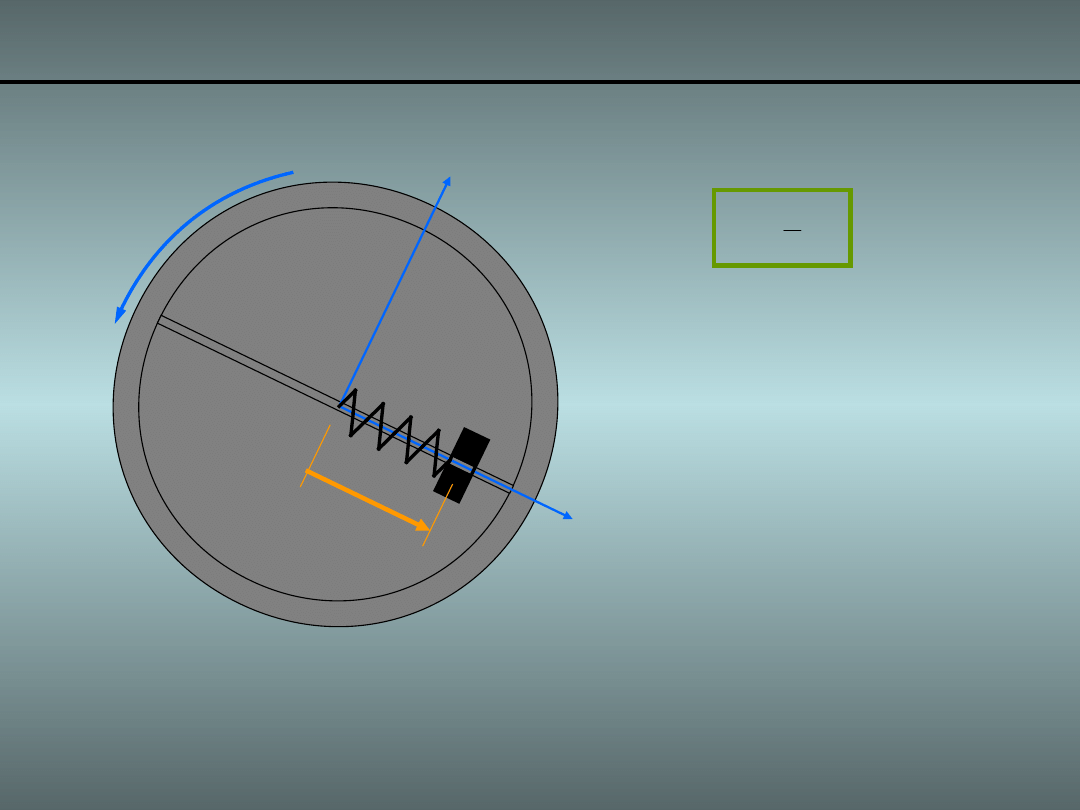
Przykład 2. Obracający się układ masa i sprężyna

3/

3/

•

Energia potencjalna:

Energia potencjalna:

y

y





x

x

q

q

k

k

m

m

2

2

1

kq

E

p



Przykład 2. Obracający się układ masa i sprężyna

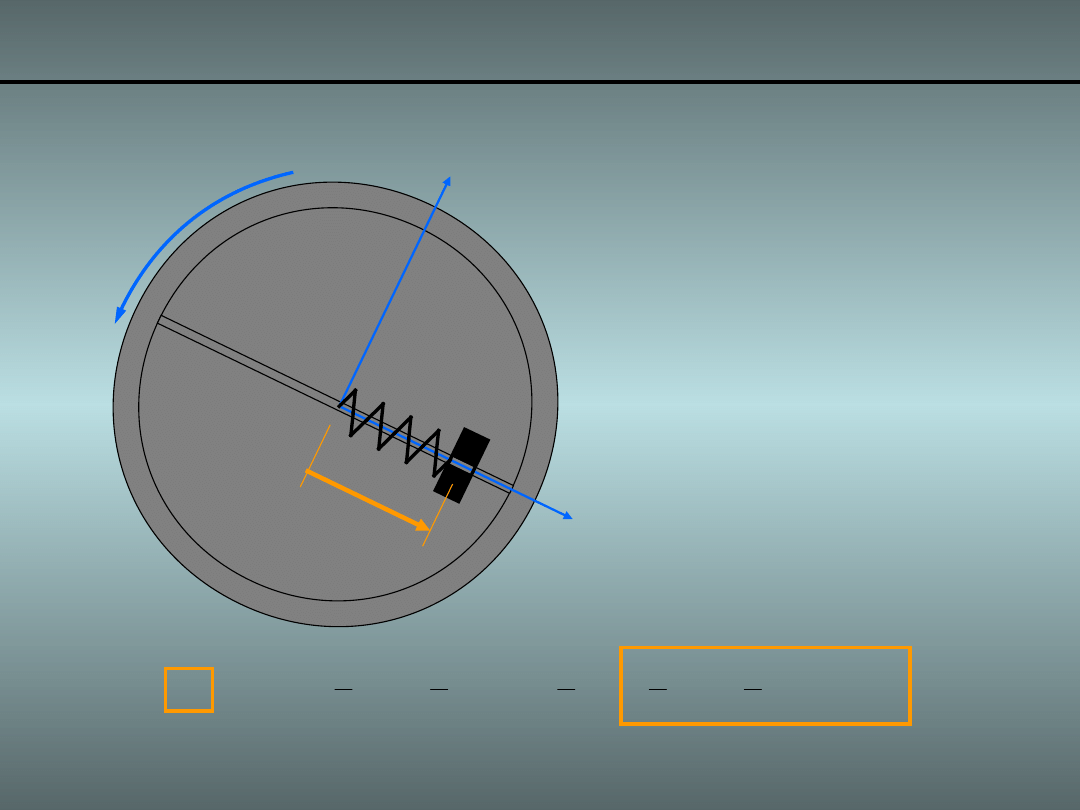
Przykład 2. Obracający się układ masa i sprężyna

4/

4/

•

Lagrangian:

Lagrangian:

y

y





x

x

q

q

k

k

m

m

2

2

2

2

2

2

2

)

(

2

1

2

1

2

1

2

1

2

1

q

m

k

q

m

kq

q

m

q

m

E

E

L

p

k

























Przykład 2. Obracający się układ masa i sprężyna

Przykład 2. Obracający się układ masa i sprężyna

5/

5/

•

Równanie Lagrange’a:

Równanie Lagrange’a:

y

y





x

x

q

q

k

k

m

m

0

)

(

2







q

m

k

q

m





0

)

(

2







q

m

k

q





0

)

(

2

2







q

q

n







q

q

n

)

(

2

2













v

q

q

v

n













)

(

2

2





Tu zmienna uogólniona „q” jest
przemieszczeniem liniowym masy

krecona_masa_1dof_v2.mdl

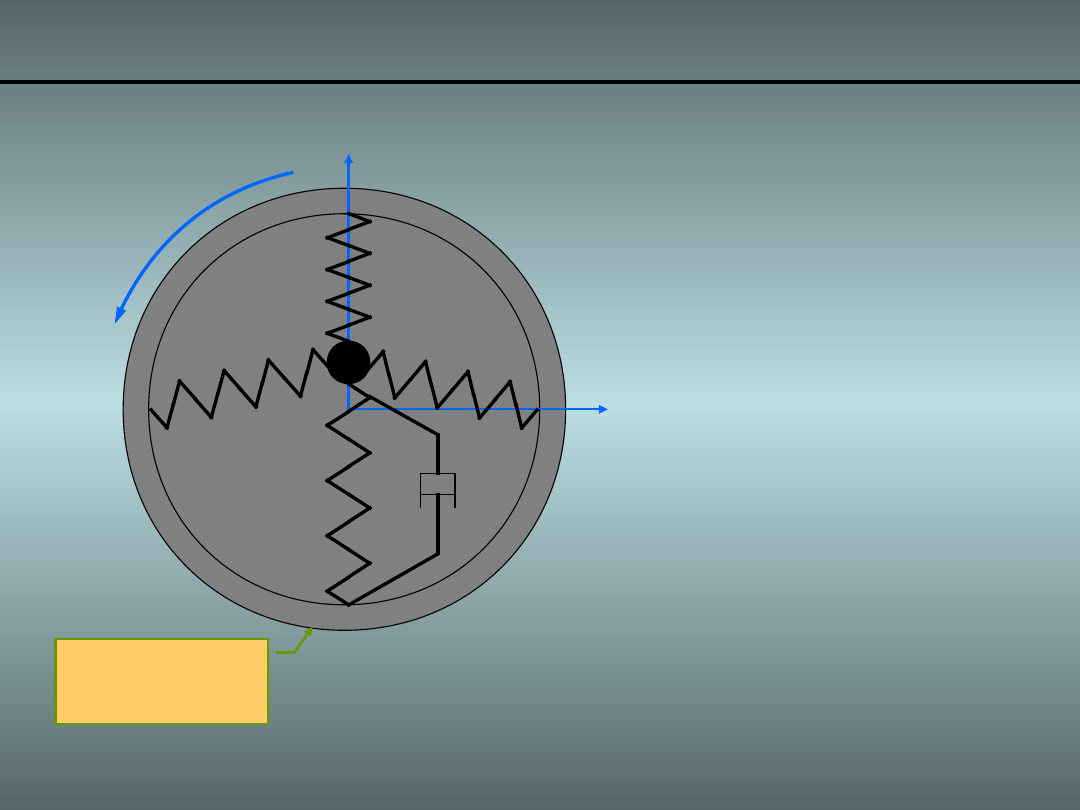
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

1/

1/

•

Niech będzie dane układ o strukturze kinematycznej:

Niech będzie dane układ o strukturze kinematycznej:

• Masę „m”

możemy
traktować jako
punktową

• Masa „m”

może
wykonywać
ruch
postępowy
wzdłuż dwóch
osi „x” i „y”

• Wprowadzamy

układ
współrzędnych
„xy”

• Układ wiruje

ze stałą
prędkością
kątową

x

x





z

z

y

y

m

m

Pierścień wirujący

ze stałą

prędkością kątową

k

k

2

2

k

k

1

1

c

c

1

1

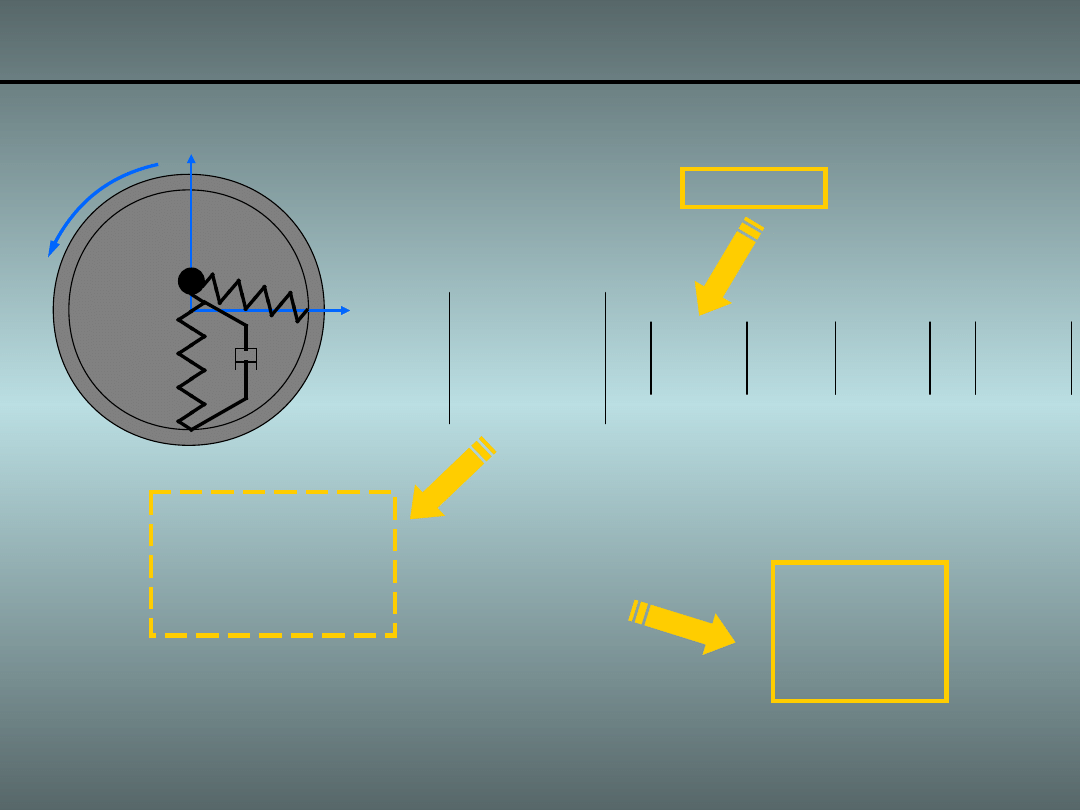
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

1/

1/

•

Związek pomiędzy prędkością kątową a liniową:

Związek pomiędzy prędkością kątową a liniową:

• Ale gdy ruch

obrotowy
dokonuje się
tylko wokół osi
„z”, to:

r

ω

v





y

x

k

z

x

j

z

y

i

z

y

x

k

j

i

v

v

v

y

x

z

x

z

y

z

y

x

z

y

x





























































)

1

(























































x

y

x

z

y

z

v

v

v

y

x

z

x

z

y

z

y

x























































0

x

y

v

v

v

z

z

z

y

x





x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1





z

z

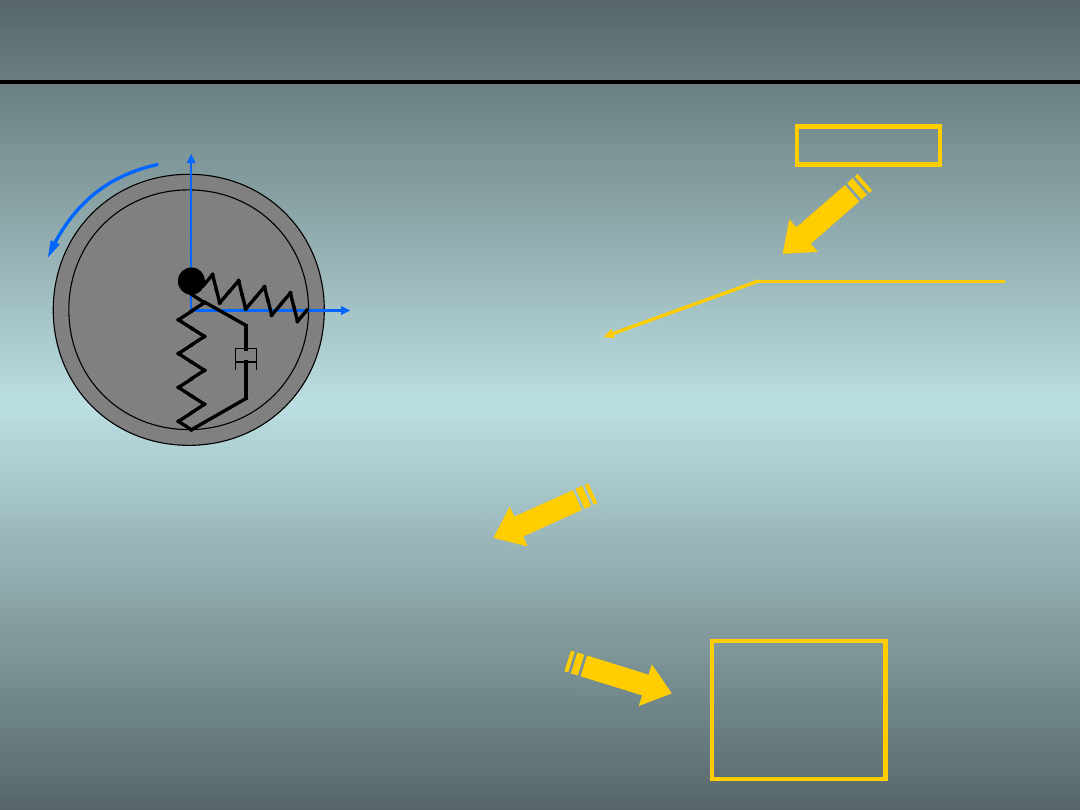
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

2/

2/

•

Związek pomiędzy prędkością kątową a liniową:

Związek pomiędzy prędkością kątową a liniową:

• Wykorzystując macierze skośnie

symetryczne

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1

r

ω

v



















































































































































x

y

x

z

y

z

y

x

z

x

z

y

z

y

x

v

v

v

y

x

z

x

z

y

x

y

x

z

y

z

x

y

x

z

y

z

z

y

x





































0

0

0











































0

x

y

v

v

v

z

z

z

y

x





• Ale gdy ruch

obrotowy
dokonuje się
tylko wokół osi
„z”, to:





z

z

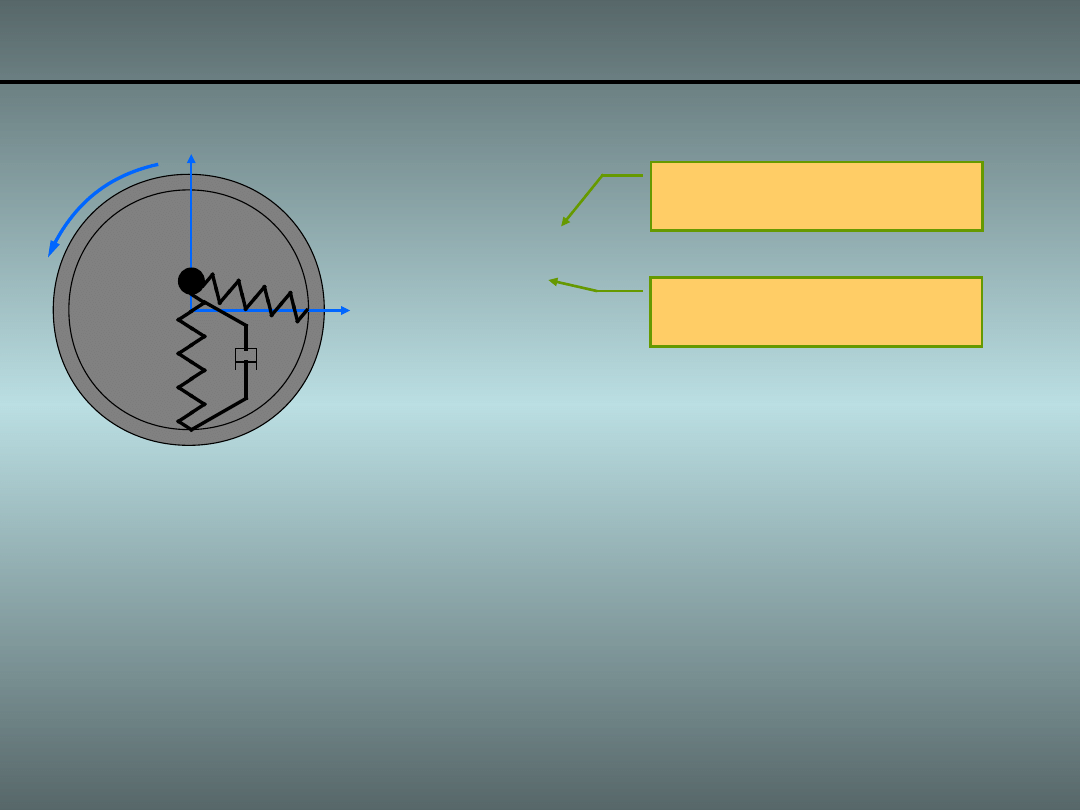
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

4/

4/

•

Składowe prędkości liniowej:

Składowe prędkości liniowej:

• Stąd całkowity wektor prędkość liniowej masy

skupionej „m” w rotującym układzie współrzędnych
ma postać:

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1











































0

x

y

v

v

v

z

z

z

y

x









z

z

Składowa prędkości

liniowej działająca w

kierunku osi „x”

Składowa prędkości

liniowej działająca w

kierunku osi „y”



























0

x

y

y

x

z

z









v

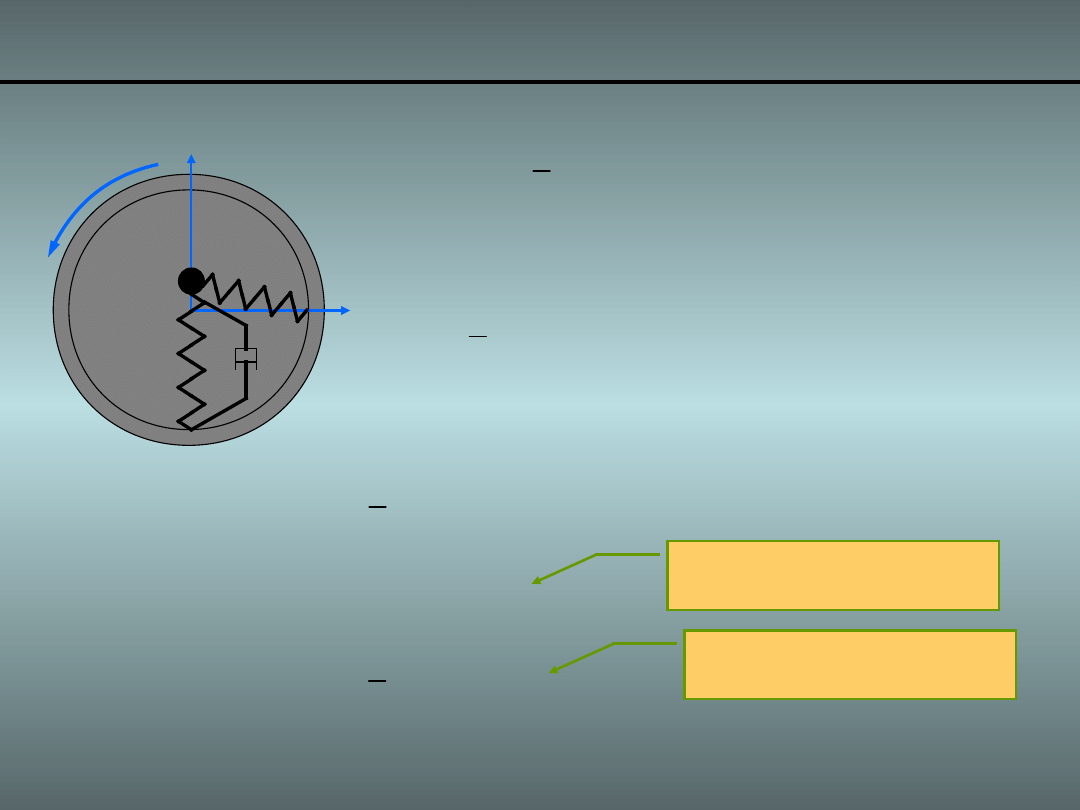
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

5/

5/

•

Energia kinetyczna układu:

Energia kinetyczna układu:

• Po rozpisaniu wyrażenia na energię

kinetyczną otrzymujemy:

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1





z

z

Składnik odpowiedzialny

za siły żyroskopowe

)

)

(

)

((

2

1

2

2

x

y

y

x

m

E

z

z

k

















)

2

2

(

2

1

2

2

2

2

2

2

x

x

y

y

y

y

x

x

m

E

z

z

z

z

k





























• Grupując wyrażenia wewnątrz nawiasu

otrzymujemy:

)

(

2

1

2

2

2

y

x

m

E

k



 



)

(

1

x

y

y

x

m

E

z

k



 







)

(

2

1

2

2

2

0

x

y

m

E

z

k







Składnik potencjalny

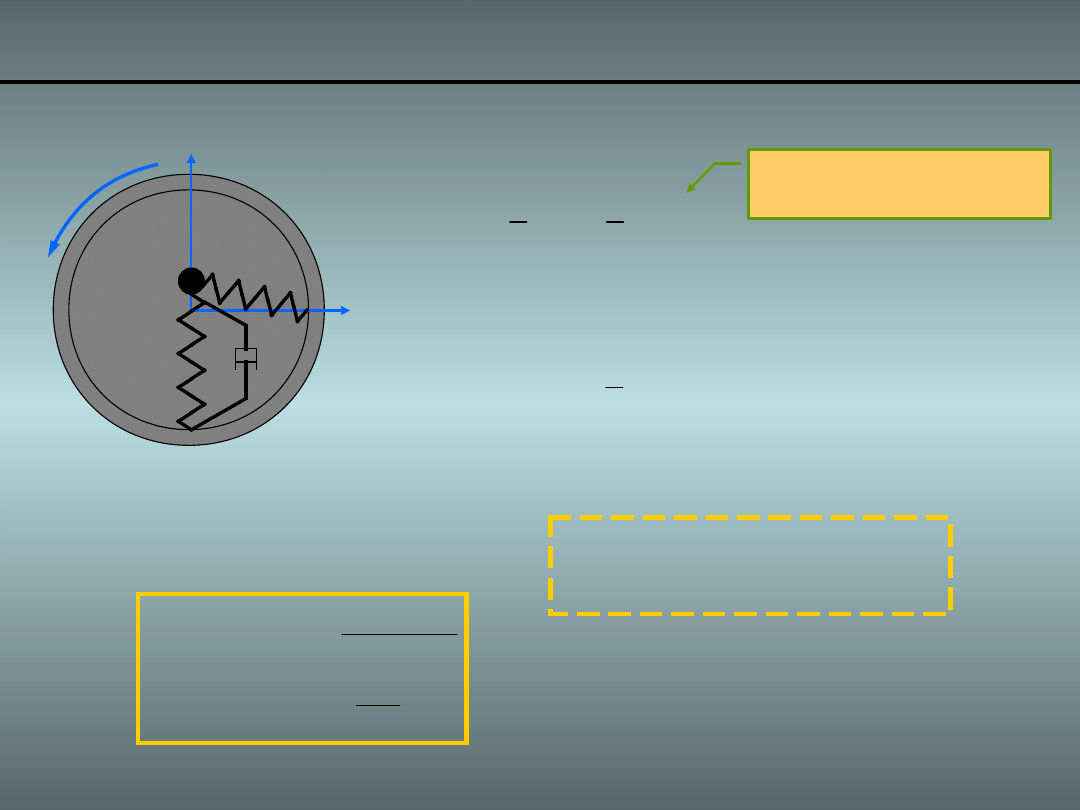
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

6/

6/

•

Energia potencjalna układu i funkcja dyssypacji:

Energia potencjalna układu i funkcja dyssypacji:

• Funkcja dyssypacji:

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1





z

z

Zakładamy niewielkie

deformacje sprężyn

2

2

2

1

2

1

2

1

y

k

x

k

E

p





2

1

2

1

x

c

D





• Równania Lagrange’a mają postać:

0

2

0

2

2

2

1

2

1



















y

m

y

k

x

m

y

m

x

c

x

m

x

k

y

m

x

m

z

z

z

z



















m

y

k

y

x

y

m

x

c

x

k

x

y

x

z

z

z

z

2

2

1

1

2

2

)

(

2



































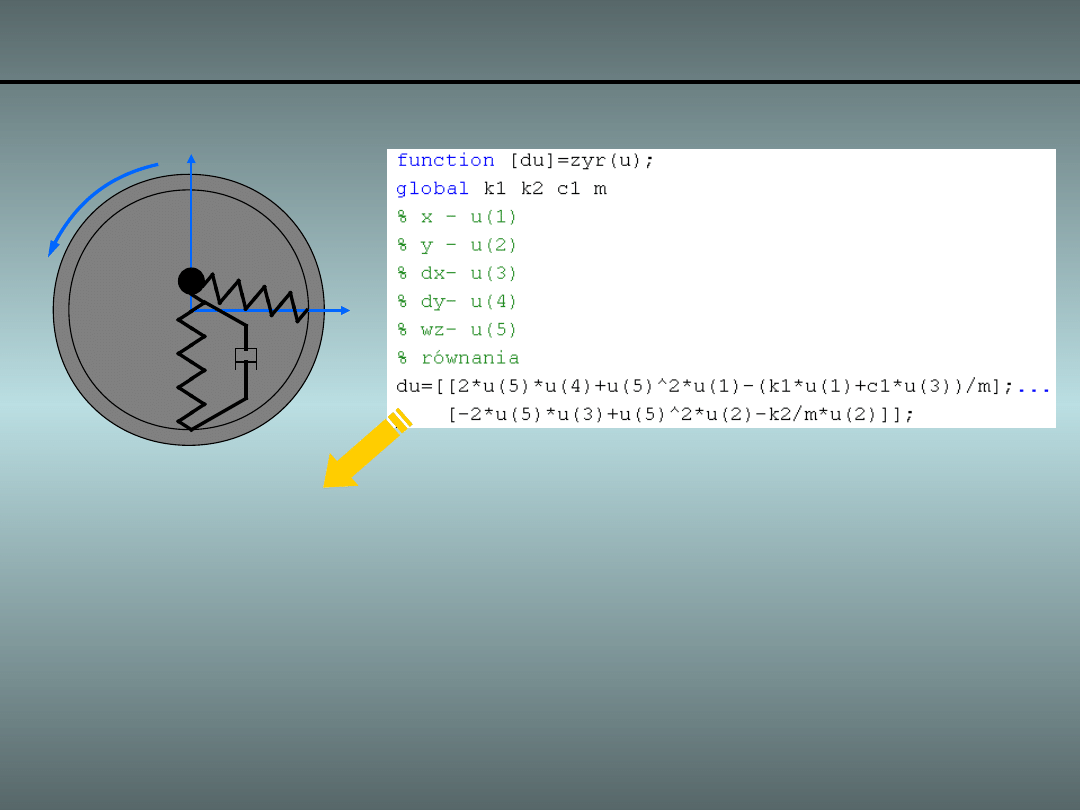
Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

7/

7/

•

Implementacja w programie Matlab – „m-funkcja”:

Implementacja w programie Matlab – „m-funkcja”:

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1





z

z

• Zapisano w pliku o nazwie:

„efekt_zyroskopowy_1.m”

Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

8/

8/

•

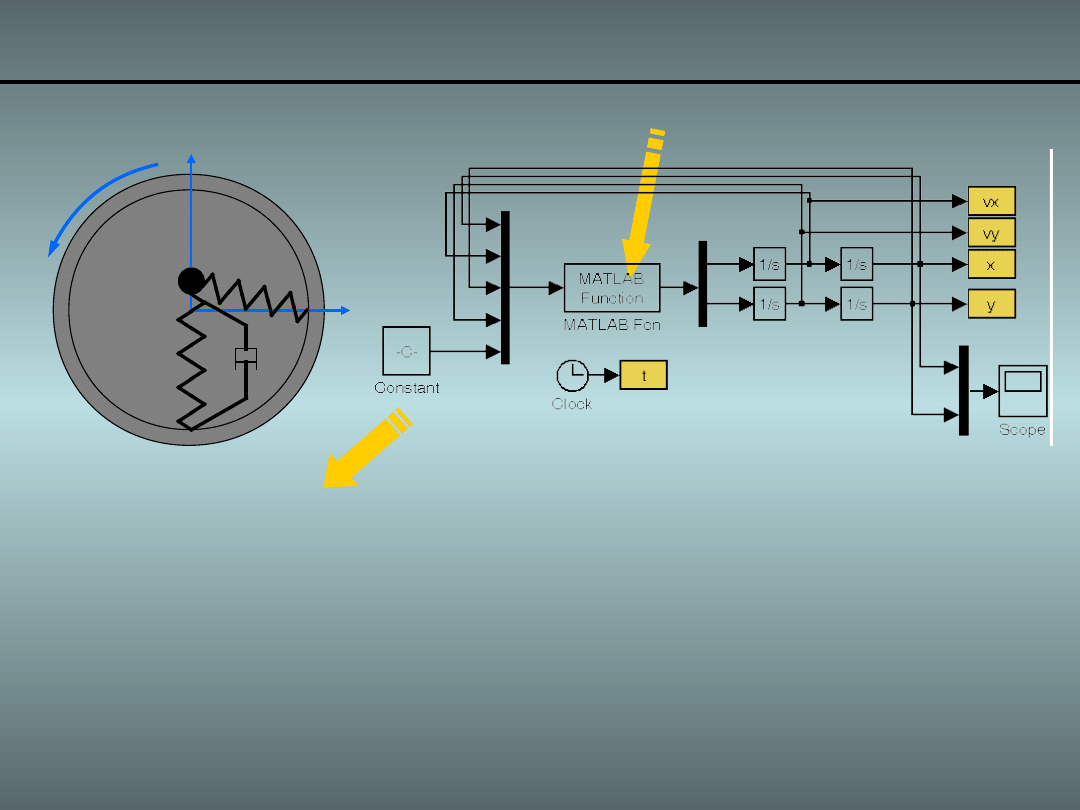
Implementacja w programie Matlab – „m-funkcja”:

Implementacja w programie Matlab – „m-funkcja”:

x

x

y

y

m

m

k

k

2

2

k

k

1

1

c

c

1

1





z

z

• dane:
>> global k1 k2 c1 m
>> k1=1000;k2=1000;c1=4;m=100;

efekt_zyroskop_nr_1_v1.mdl

Przykład 3. Obracająca się masa i sprężyny o 2DoF

Przykład 3. Obracająca się masa i sprężyny o 2DoF

9/

9/

•

Przykładowe wyniki symulacji:

Przykładowe wyniki symulacji:

• dane:

>> global k1 k2 c1 m
>>

k1=1000;k2=1000;c1=4;m=
100;

0

1

2

3

4

5

6

7

8

9

10

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

x

x

y

y