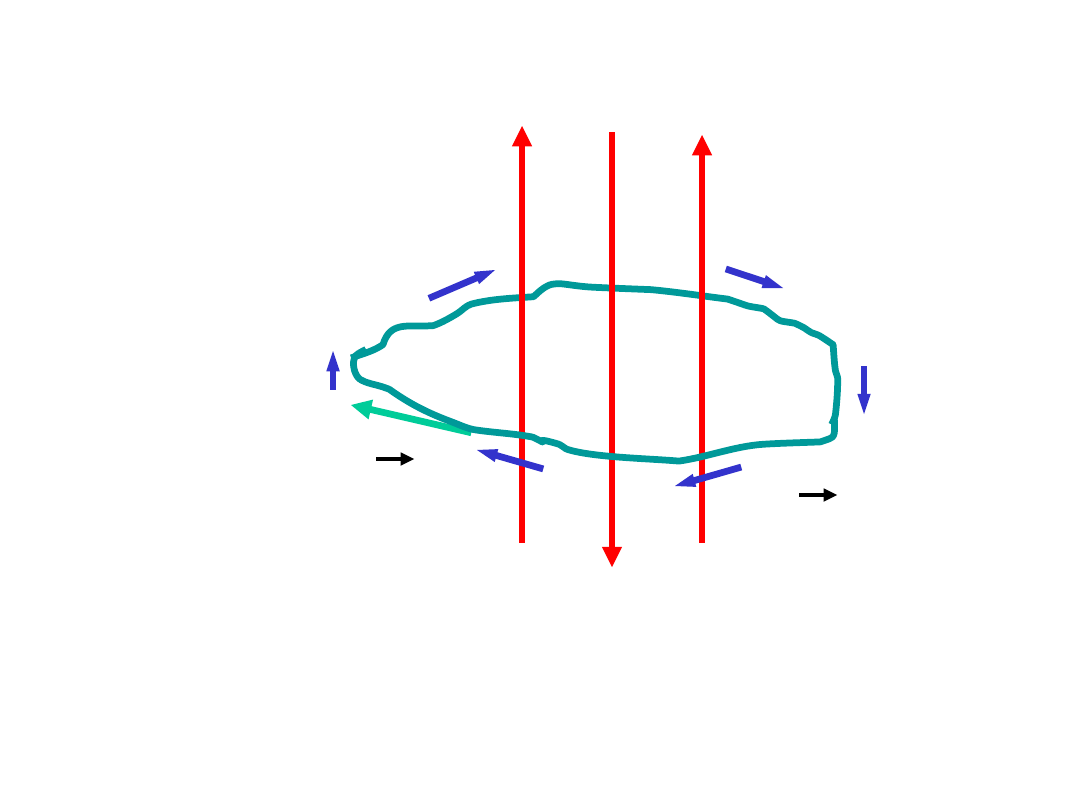
Prawo Ampere’a

C

Przenikalność magnetyczna próżni



0

= 410

-7

Tm/A

B - wektor indukcji magnetycznej

i - natężenie prądu

dl - wektor przesunięcia wzdłuż linii C

(1)

Bdl =

0

i

i

1

i

2

i

3

dl

B

C

i = i

1

- i

2

+ i

3

i - suma prądów wewnątrz linii

C

r

d

l

B

B dl = 

0

i = B

dl = B2r

i

B

i

r







0

2

B ||
dl

(2

)

(1a

)

Indukcja magnetyczna wokół

przewodnika z prądem i

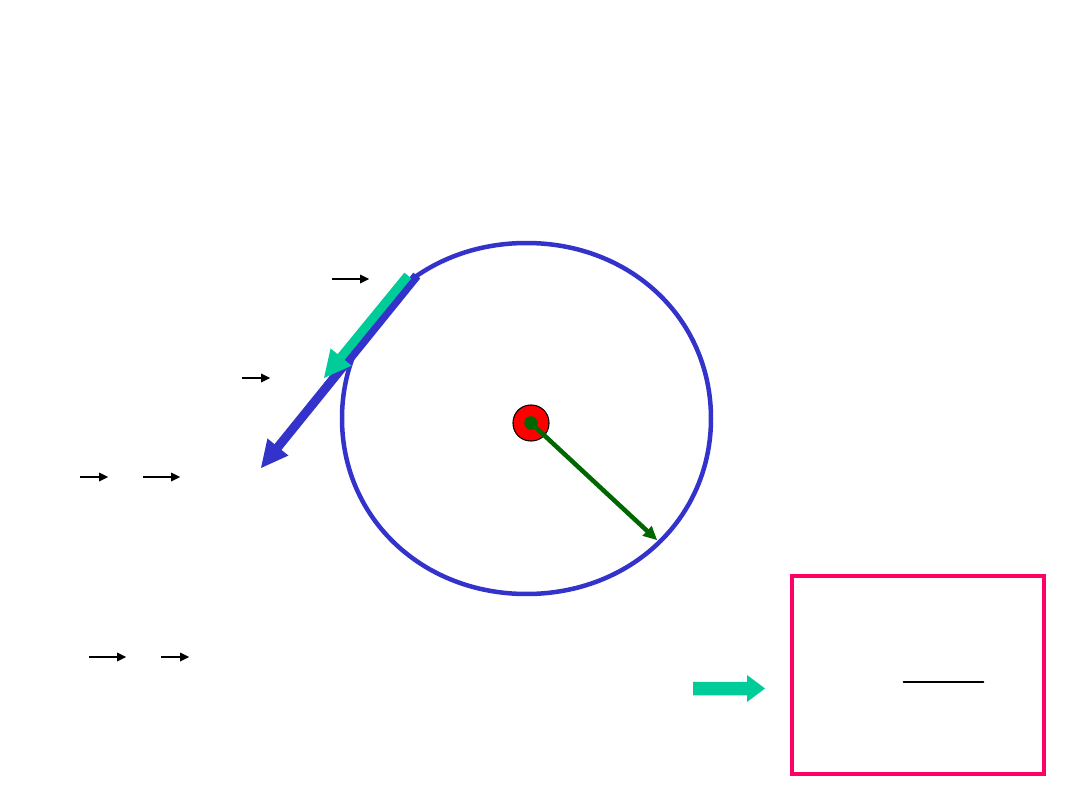
Siła Lorentza

W przestrzeni istnieje pole

magnetyczne o indukcji B. Na
ładunek próbny q

0

poruszający się w

tej przestrzeni z prędkością v działa
siła F wyrażona wzorem

)

(

0

B

v

q

F











(3)

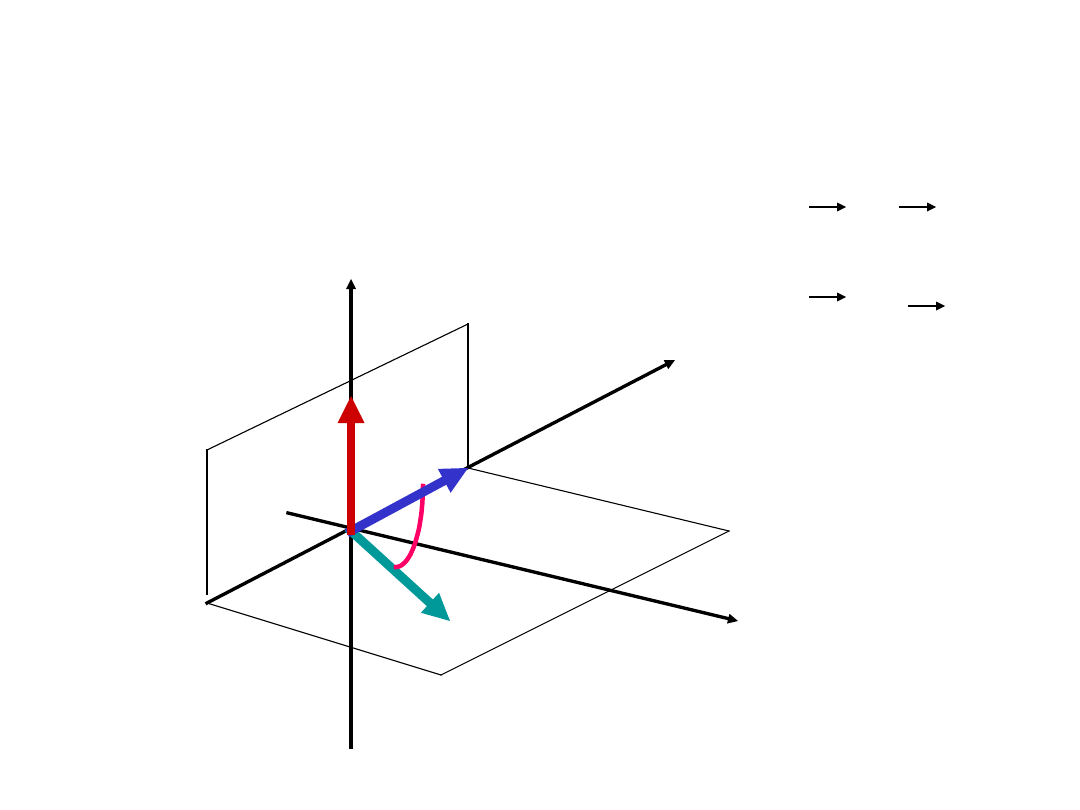
Wartość bezwzględna tej siły wyraża się wzorem:

F q vB



0

sin



x

y

z



F

B

v

F  B

F  v

(3a

)

Działanie pola

magnetycznego na

przewodnik z prądem

Prąd jest uporządkowanym ruchem ładunków

elektrycznych, należy się spodziewać, że pole
magnetyczne będzie wywierać siłę na przewodnik,
przez który płynie prąd. Jeżeli w jednostce objętości
przewodnika znajduje się n elektronów, to w
przewodniku o przekroju S i długości l zawartych
jest

N = nSl elektronów.

Na każdy elektron działa siła opisana wzorem

(3 )

.

Wartość wypadkowej siły działającej na przewodnik
wyniesie

F = evBsin nSl

(4)

(5)

Natężenie prądu i można określić jako ładunek
przepływający w jednostce czasu przez przekrój
poprzeczny tego przewodnika S, możemy zapisać to
wzorem

i = enSv

Z porównania wzorów

(4, 5, 6)

otrzymujemy

F = ilBsin

Wzór ten w zapisie wektorowym ma postać

F = i(l  B)

Na podstawie tego wzoru można wyznaczyć siłę
wzajemnego oddziaływania dwóch przewodników z
prądem.

(6)

(7)

(7a
)

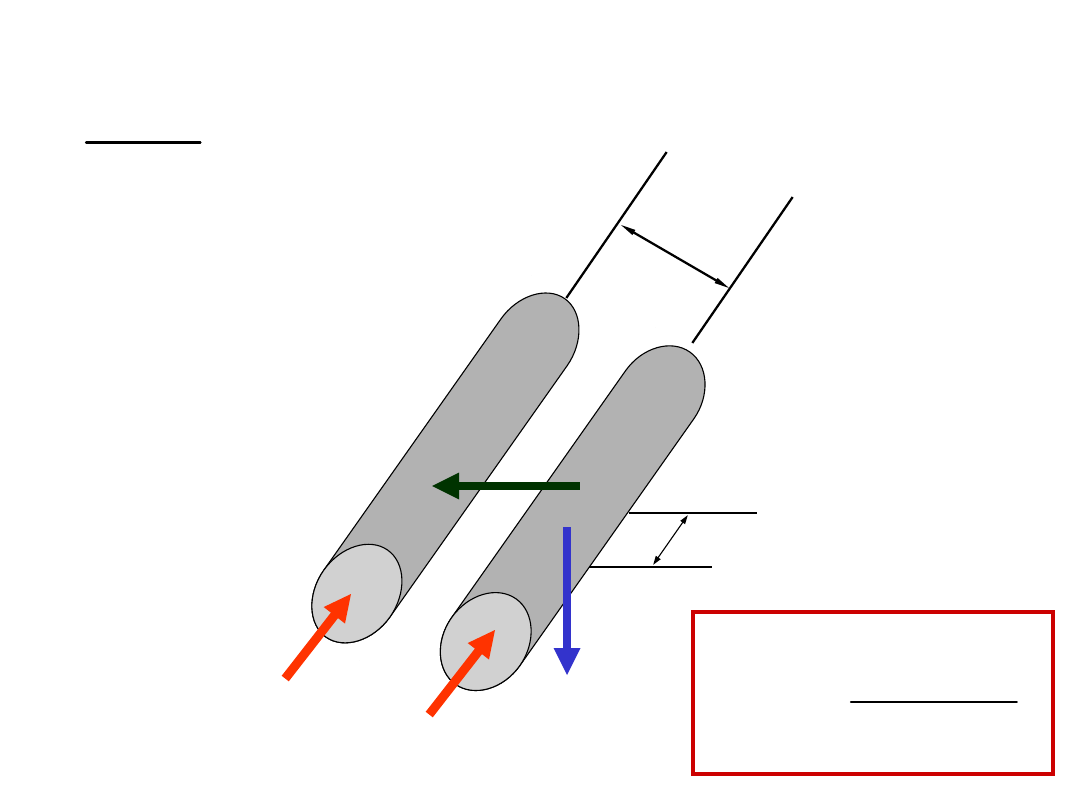
F

B

d

l

i

b

i

a

a

b

B

i

d

a

a







0

2

F

li i

d

b

o a b







2

a

b

b

B

l

i

F











F

i lB

b

b

a



(8)

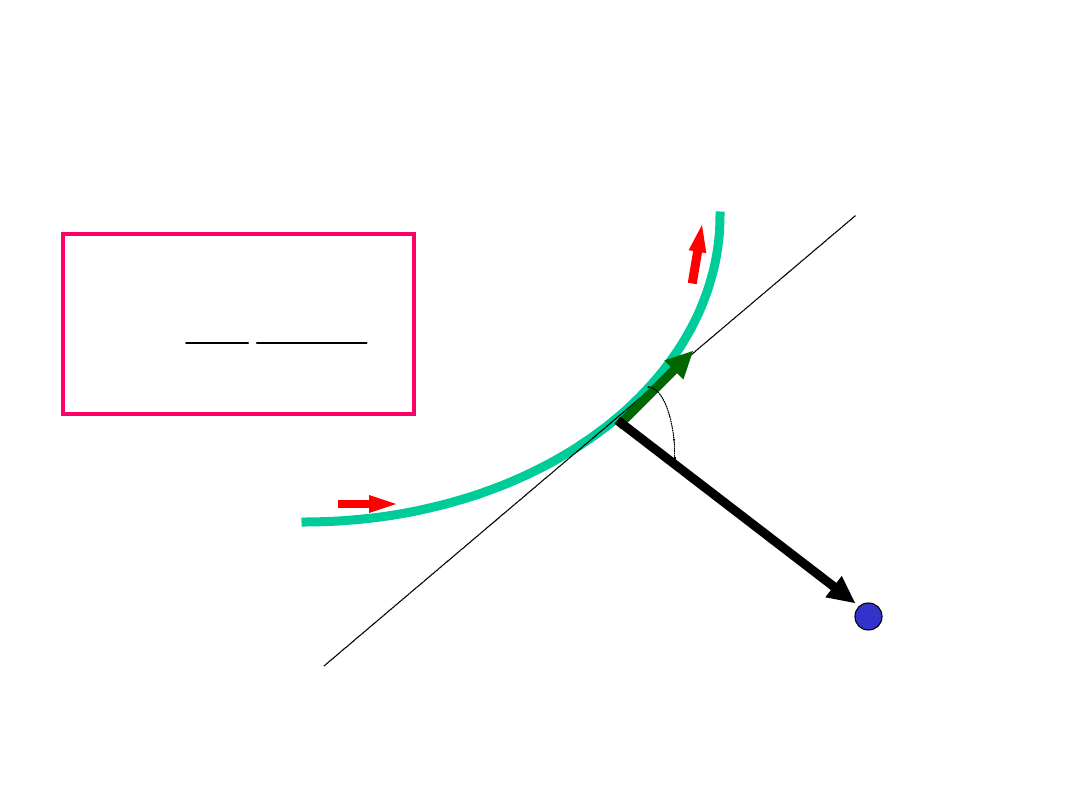
Prawo Biota -
Savarta

P

r

dl

i

i

dB

3

0

4

r

r

l

d

i

B

d

















(9

)

d

B

i

d

l

r









0

2

4

s

i

n

B

dB





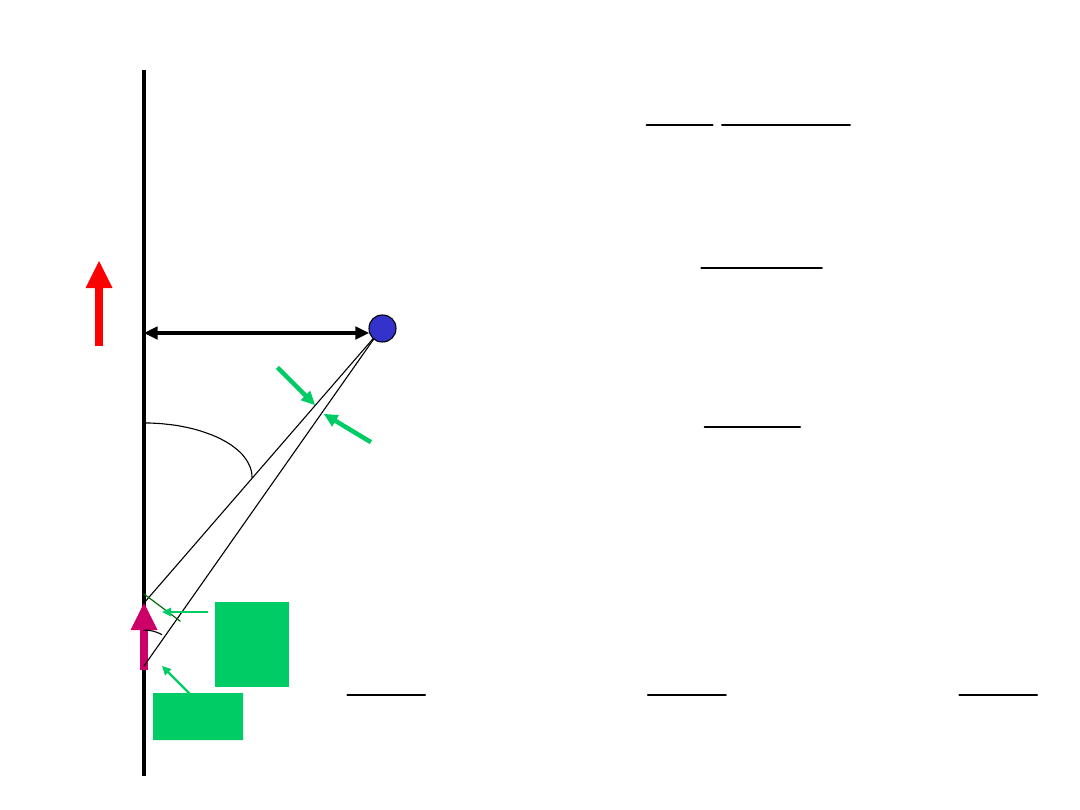
Przykład 1.

Korzystając z prawa Biota - Savarta obliczyć wektor
indukcji magnetycznej B dla dowolnego punktu
leżącego na zewnątrz prostoliniowego, cienkiego,
nieskończenie długiego przewodnika, przez który
płynie prąd o natężeniu i.

(9a)

(10)

dB i B
zapisane
skalarnie

i

dl



d

P

rd


r

sinθ

a

r 

a

dl

rd







sin





B

i

a

d

i

a

i

a















 















0

0

0

0

0

4

4

2

sin

cos

d

B

i

d

l

r









0

2

4

s

i

n

(1
1)

(1
2)

(13)

 

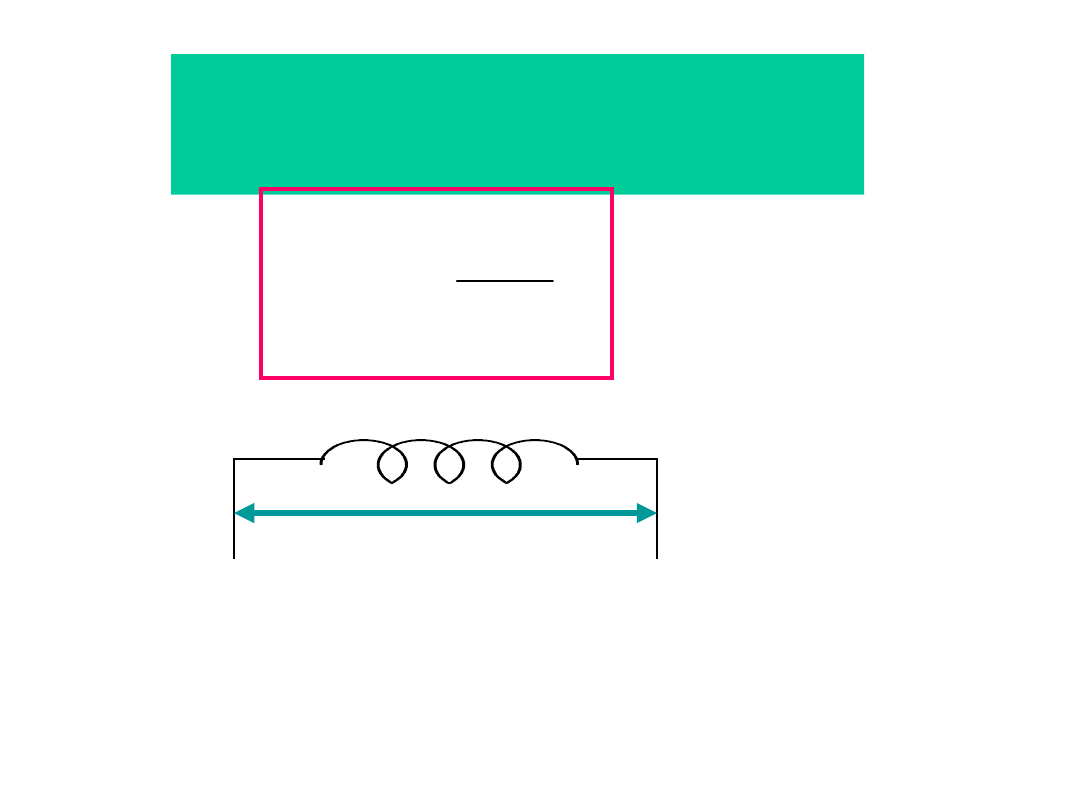
Prawo indukcji
Faradaya

E

d

dt

B





E

L

Indukowana w obwodzie SEM jest równa

szybkości, z jaką zmienia się strumień pola B,
przechodzący przez ten obwód. Znak „-”
dotyczy kierunku indukowanej SEM.

•

•

(14

)

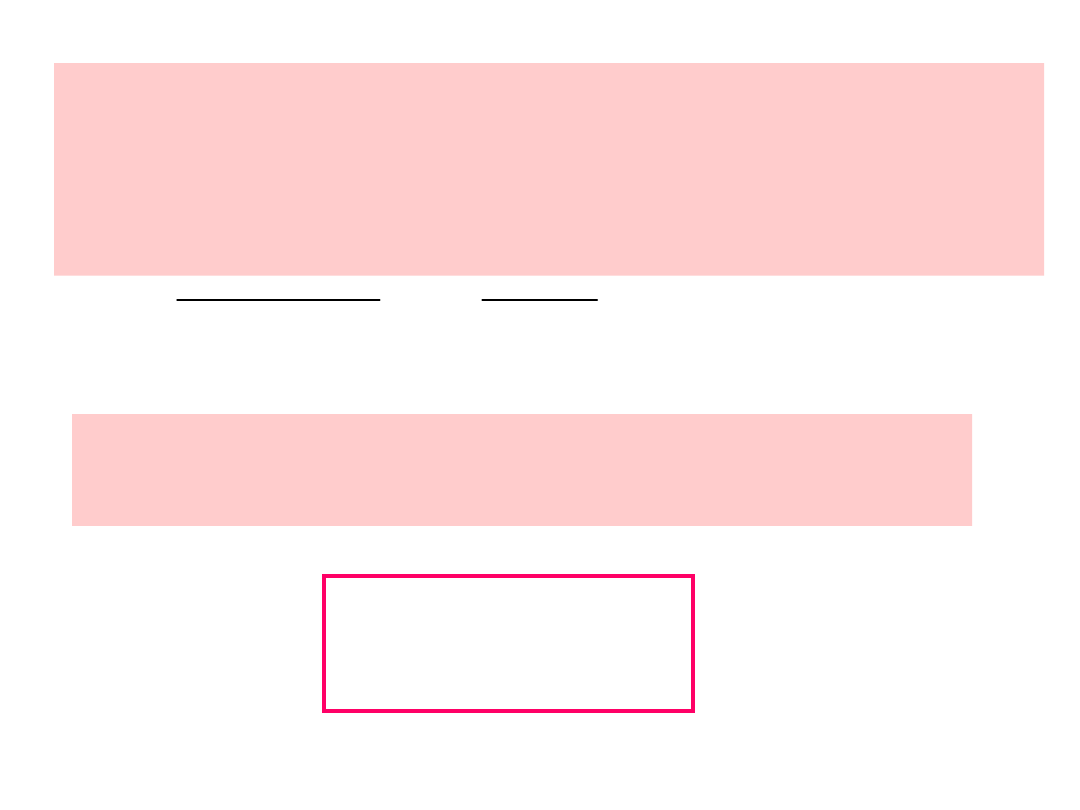
Jeżeli podane równanie zastosować do
zwojnicy o N zwojach, to w każdym z nich
pojawi się SEM i te siły elektromotoryczne
dodadzą się.

E

N

d

d t

dN

d t

B

B









(

)

Strumień pola magnetycznego
definiowany jest w sposób następujący:









S

d

B

B





(14

a)

(1
5)

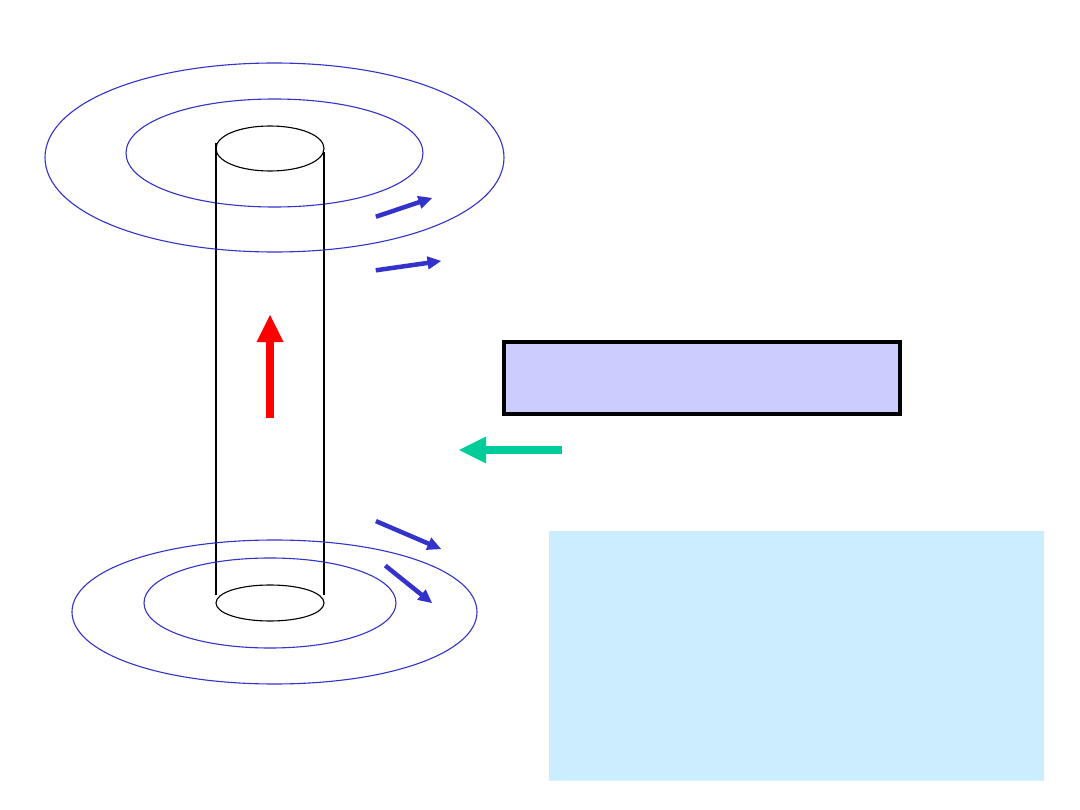
i

S

S

S

S

S

S

N

N

N

N

N

N

N

S

v

W przewodzie zaczyna
płynąć prąd o natężeniu i.

Powstające pole
przeciwdziała ruchowi
magnesu.

Reguła
Lenza

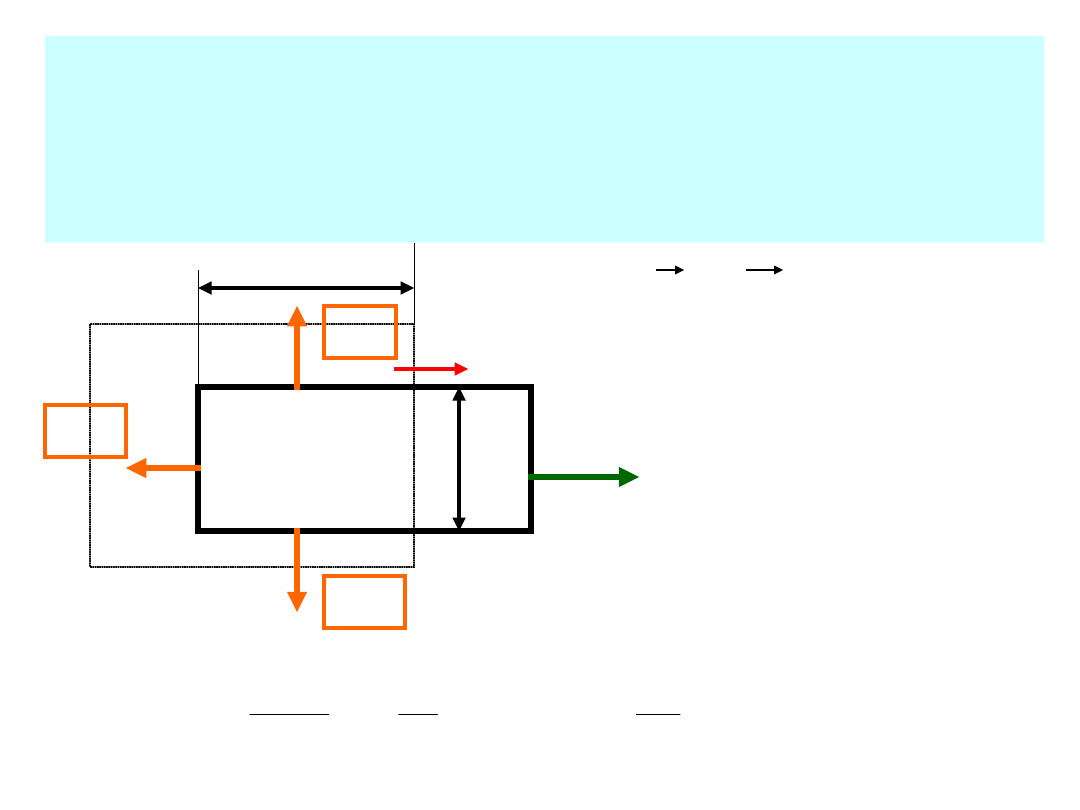
Przykład 2.

Jaka siła elektromotoryczna SEM powstanie w w
obwodzie o kształcie prostokąta przesuwanym z
prędkością v w jednorodnym polu magnetycznym B?

       

       

       

       

       

       

       

       

       

i

v

l

x

F

1

F

2

F

3

F

2

= F

3

B



B

=Blx

Blv

dt

dx

Bl

Blx

dt

d

dt

d

SEM

B

















)

(

B  F  SEM  i

F

1



0

(16

)

(1
7)

Jeżeli opór obwodu wynosi R, to w obwodzie zacznie
płynąć prąd o natężeniu i.

R

Blv

R

SEM

i





Siła F

1

przeciwdziałająca przesuwaniu się

obwodu:

F

ilB

B l v

R

1

0

2 2

90





sin

Moc tracona:

P

F v

Blv

R





1

2

(

)

F

1

=il  B

(18)

(1
9)

(2
0)

     

     

     

     

     

     

     

     

    



Siła elektromotoryczna indukowana

w zmiennym polu magnetycznym






 

 
 





   

 

r

E

B

Szybkość zmian
pola B:

d

dt

B





E r

2











l

d

E















dt

d

l

d

E

B





(21

)

(21a

)

(22)

 

ponieważ

zwój

Zmienne pole



magnetyczne

wytwarza pole
elektryczne

Indukcyjność

E

N

d

d t

dN

d t

B

B









(

)

Siła elektromotoryczna indukowana w cewce o
N zwojach:

Strumień pola magnetycznego cewki oddalonej
od wszelkich materiałów magnetycznych jest
proporcjonalny do natężenia prądu i płynącego
przez cewkę.

N

Li

B

 

L - indukcyjność, współczynnik
proporcjonalności między natężeniem
prądu a strumieniem pola magnetycznego
cewki

(14b

)

(23)

E

d N

dt

L

di
dt

L

B





(

)



Korzystając z prawa Faradaya indukowaną SEM
można przedstawić następująco:

A stąd indukcyjność
L

L

E

di
dt

L



Jednostką
indukcyjności jest

(2
4)

(25

)

A

s

V

[H]

henr

1





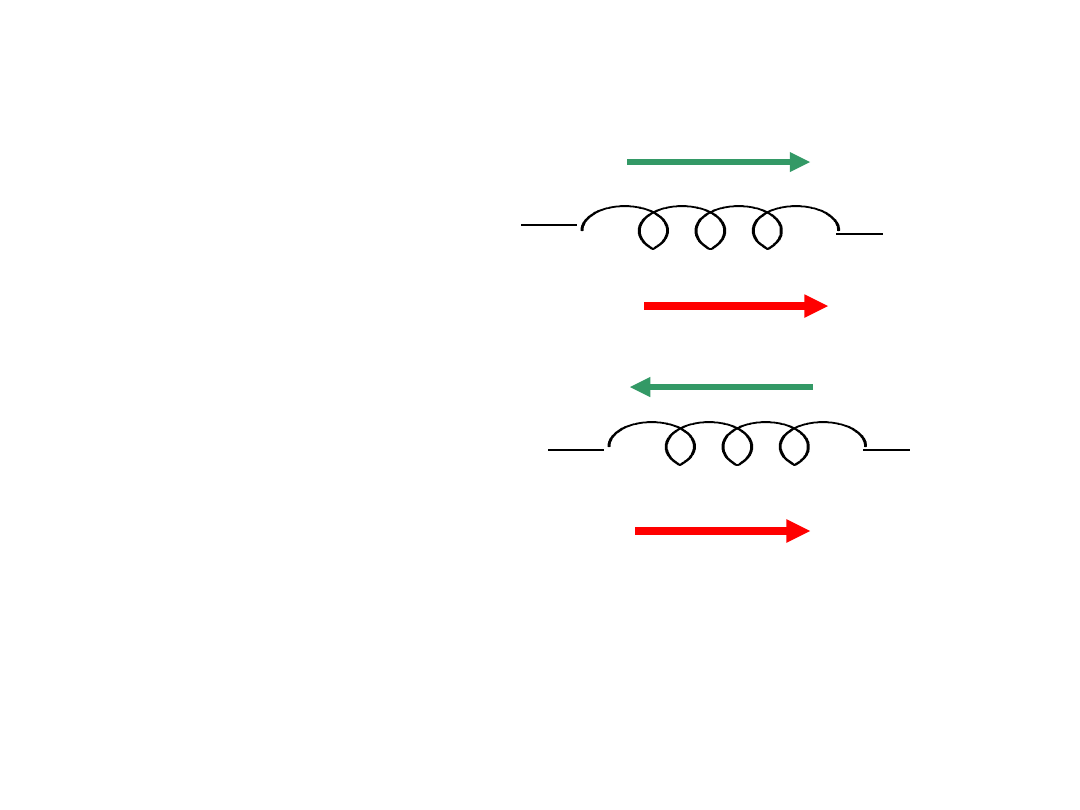
Kierunek SEM można otrzymać z reguły Lenza.

a)

b)

W przewodzie a) prąd maleje, a w przewodzie b)
rośnie. E

L

- siła elektromotoryczna w obu przypadkach

przeciwdziała zmianie prądu.

i

i

E

L

E

L

Wyobraźmy sobie,
że nawinęliśmy
cewkę.
Zauważamy różne
kierunki siły
elektromotorycznej
E

L

.

a) Aby zapobiec zmniejszeniu się prądu, indukowana
SEM musi mieć ten sam kierunek co prąd. b) Jeżeli
prąd wzrasta, indukowana SEM musi mieć kierunek
przeciwny.

Obliczanie indukcyjności

cewki.

L

N

i

B





Indukcyjność ściśle
nawiniętej cewki:

Dla długiego solenoidu
o długości l, przekroju
S i ilości zwojów na
jednostkę długości n:

N

nlBS

B

 

Na podstawie
prawa Ampere’a
można wykazać, że
indukcja B
solenoidu wynosi:

B

ni





0

(26

)

(27)

(28

)

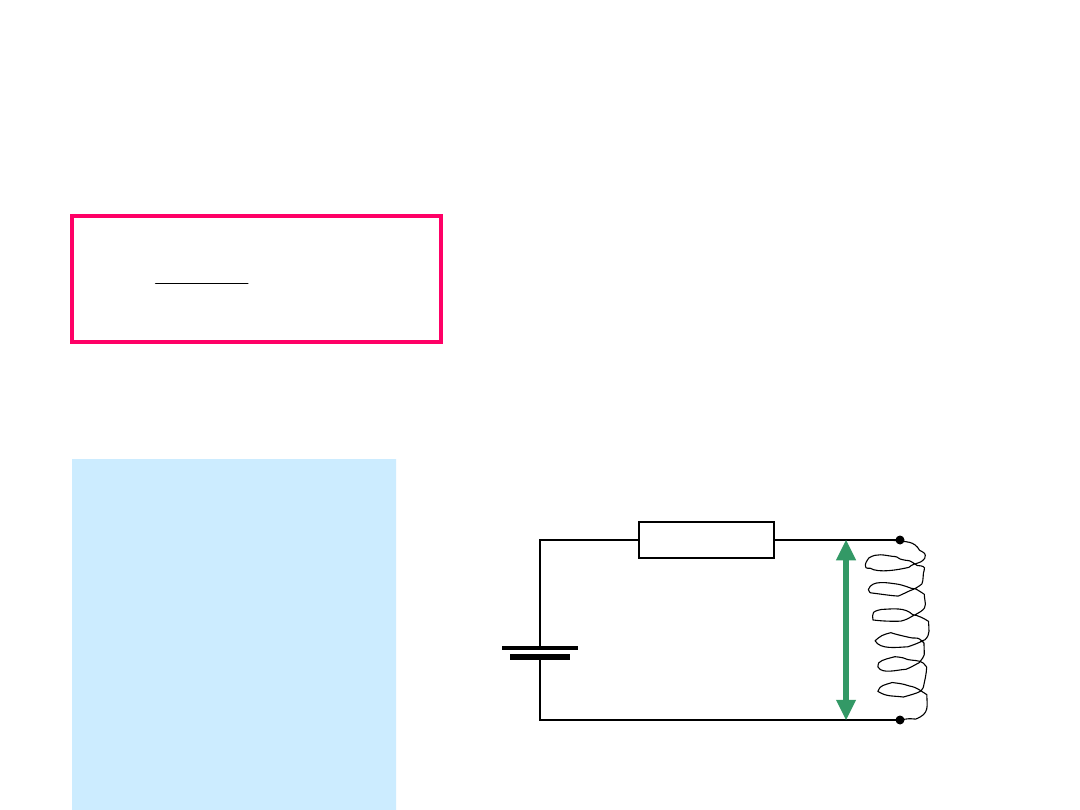
Wstawiając B do
wyrażenia na strumień 

B

i

przekształcając
otrzymujemy L solenoidu:

N

n liS

B

 



0

2

L

N

i

n lS

B









0

2

Obwód RL

R - wartość
oporu

L - indukcyjność

E - SEM baterii

E

L

- SEM cewki

i - natężenie
prądu

(2
9)

(30)

E 

i 

R

L

E

L

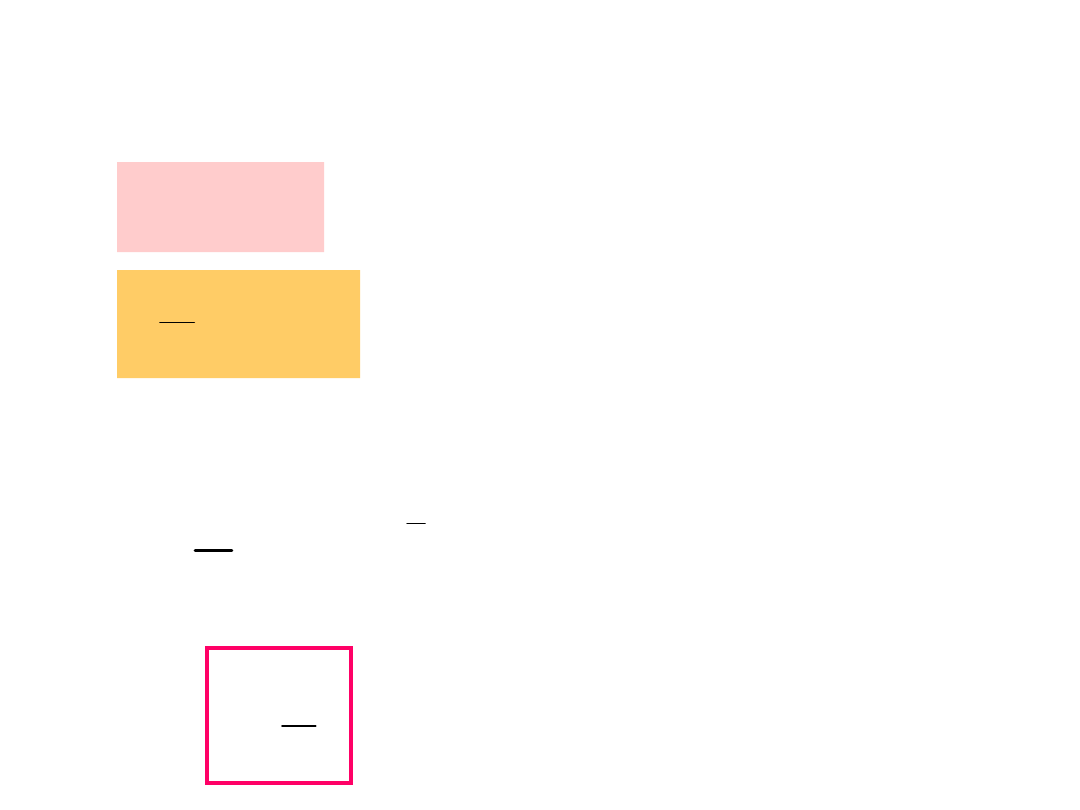
Na podstawie II prawa Kirchoffa zapisujemy
równanie obwodu w postaci

E

L

+

i

R

=

E

L

d

i

d

t

i

R

E



Rozwiązaniem drugiego równania różniczkowego
jest

gdzie





L

R

 nazywamy stałą czasową

(3
1)

(32)

(33)

(34)

i

e

E

R

t







(

)

1



a z tego wynika, że

Szybkość z jaką gromadzi się energia w polu
magnetycznym dW

B

/dt:

dW

dt

Li

di
dt

B



odpowiednio

W

dW

Lidi

Li

B

B

W

i

B











0

0

2

1

2

dW

B

= Lidi

Po scałkowaniu tego
wyrażenia otrzymamy
całkowitą energię pola
magnetycznego zawartą w
cewce o indukcyjności L.

(35)

(36
)

Iloczyn prądu i
napięcia na cewce

Przykład 3

Wyznaczyć gęstość energii pola magnetycznego w

B

cewki o długości l i przekroju S.

B

ni





0

L =



0

n

2

lS

w

W

Sl

B

B



w

Li

Sl

B



1

2

2

Po uwzględnieniu tych związków
otrzymujemy gęstość energii pola
magnetycznego w

B

.

w

B

B



1

2

2

0



(37
)

(37a
)

(38)

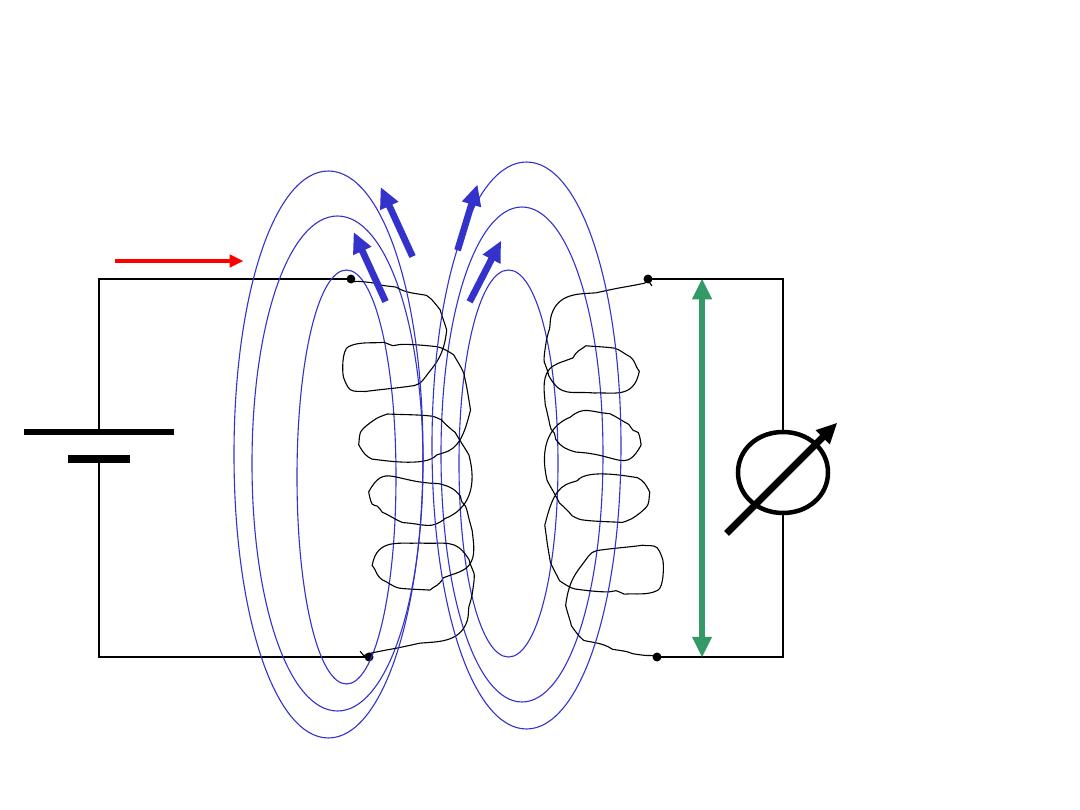
Indukcja wzajemna

E

i

1

i

2

E

2

Nawijamy teraz
dwie cewki,
umieszczamy je
w blisko siebie.

Dwie cewki umieszczone blisko siebie mogą na siebie
oddziaływać wzajemnie. Stały prąd i

1

płynący w jednej

cewce utworzy strumień pola magnetycznego 

obejmującego drugą cewkę.

Jeżeli zmienimy prąd i

1

w czasie, to w drugiej cewce

pojawi się siła elektromotoryczna E. Zjawisko to
nazywamy

indukcją wzajemną

.

Cewka 2 jest oddzielnym zamkniętym obwodem
elektrycznym, która obejmuje strumień 

21

. Definiujemy

indukcję wzajemną cewki 2 względem 1 jako:

M

N

i

21

2

21

1





M

21

i

1

= N

2



21

Po zróżniczkowaniu względem
czasu otrzymamy:

M

d

i

d

t

N

d

d

t

2

1

1

2

2





(38
)

(39
)

Prawa strona tego równania jest zgodnie z prawem
Faradaya siłą elektromotoryczną E

2

pojawiającą się w

cewce 2 dzięki zmianom prądu w cewce 1.

Jeżeli zamienimy cewki rolami - odłączymy źródło
napięcia z obwodu cewki 1, a umieścimy je w
obwodzie cewki 2, która teraz wytworzy strumień 

12

,

to w obwodzie cewki 1 pojawi się SEM.

E

M

di

dt

1

12

2



SEM w jednej z cewek jest proporcjonalna do
szybkości zmian prądu w drugiej cewki.
Zwykle też

M

21

= M

12

= M

E

M

di

dt

2

21

1



E

M

di

dt

1

12

2



(40)

(41

)

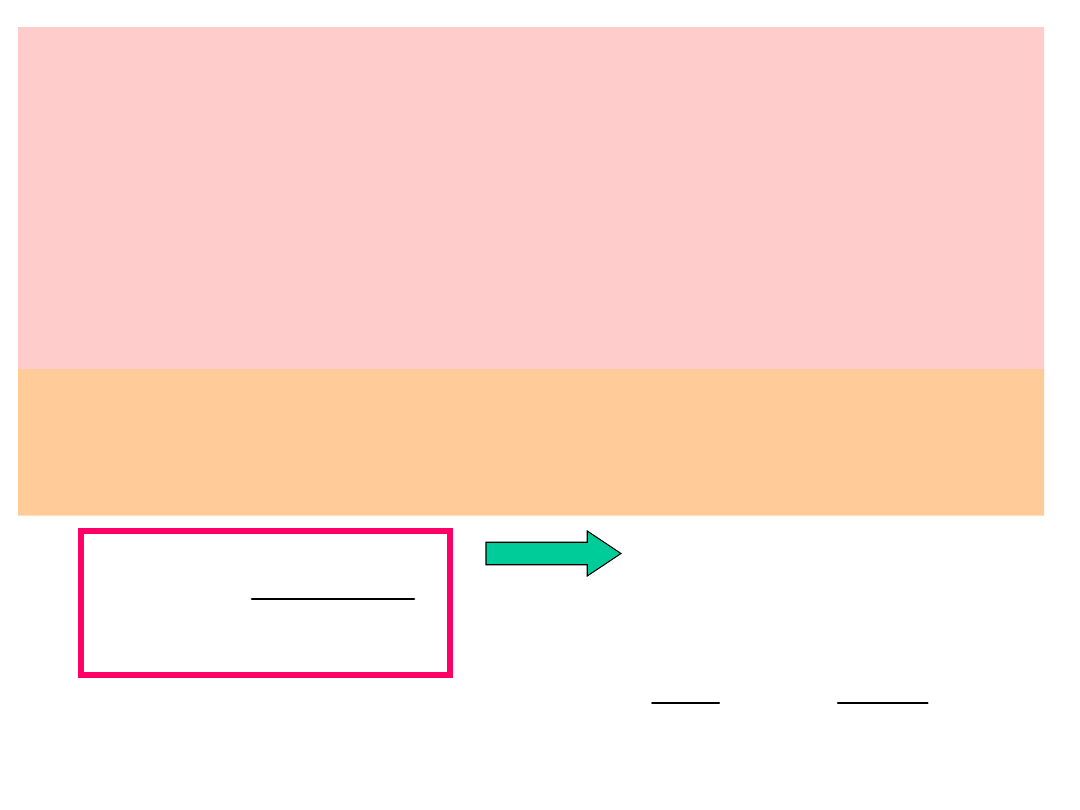
Indukowane pole magnetyczne -

pełne prawo Ampere’a

i

+ -









E

R

B

Pole elektryczne E i indukowane pole magnetyczne B
w trakcie ładowania kondensatora płaskiego.

Prąd i
dopływa
do okładek



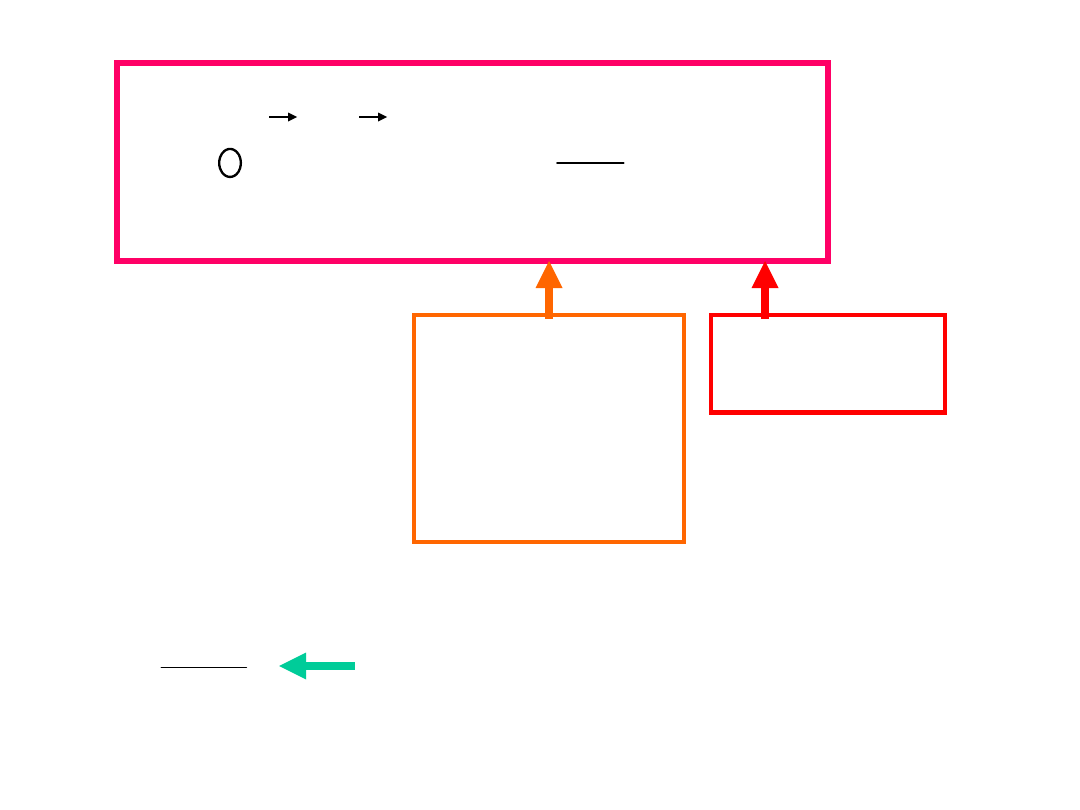
Pole
magnetyczne
jest
wytwarzane
przez

zmienny

strumień

pola

elektryczneg

o

przepływ
prądu

Wcześniej przy obliczaniu indukcji wokół
przewodnika z prądem zakładano, że strumień pola
elektrycznego jest równy zeru.



o

E

d

dt



To wyrażenie ma wymiar
prądu i nosi nazwę prądu
przesunięcia.

(42

)

B dl

i

d

dt

E

 





 





0 0

0

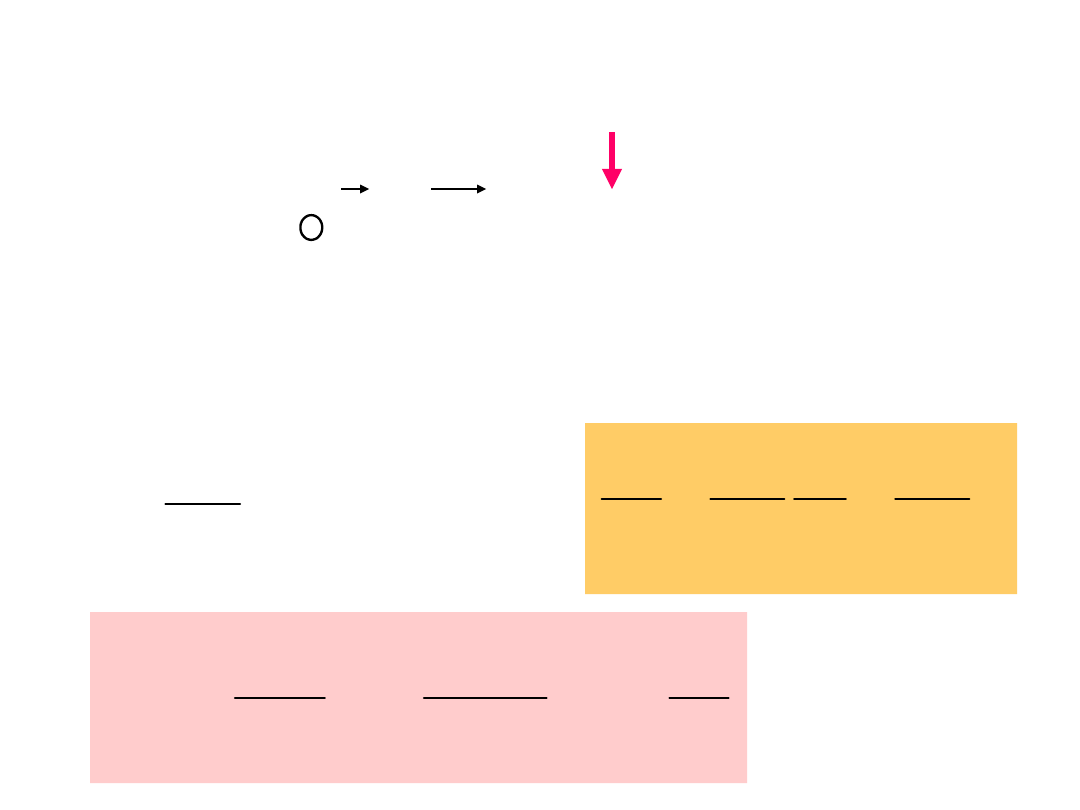
Prąd przesunięcia

B dl

i

i

p











0

(

)

Koncepcja prądu przesunięcia pozwala na
utrzymanie zasady ciągłości prądu.

E

q

S





0

dE

dt

S

dq

dt

S

i





1

1

0

0





Różniczkuje
my po czasie

i

d

dt

d ES

dt

S

dE

dt

p

E

o













0

0



(

)

(42a

)

(43

)

(4
4)

(45)

Prąd przesunięcia jest
równy prądowi
przewodzenia w
obwodzie
zewnętrznym.

Przykład 4.

Obliczyć prąd przesunięcia kondensatora o
okładkach kołowych, promień okładek R = 5 cm,
pole elektryczne zmienia się z szybkością dE/dt
=10

12

V/(m•s).

dt

dE

R

dt

d

i

E

p

2

0

0













i

C

N m

V m s

A

p

















( .

/ (

))( )( .

) (

/ (

))

.

89 10

50 10

10

007

12

2

2

2 2

12



i

S

S

i

i

p





(

)(

)





0

0

1

(46)

(47

)

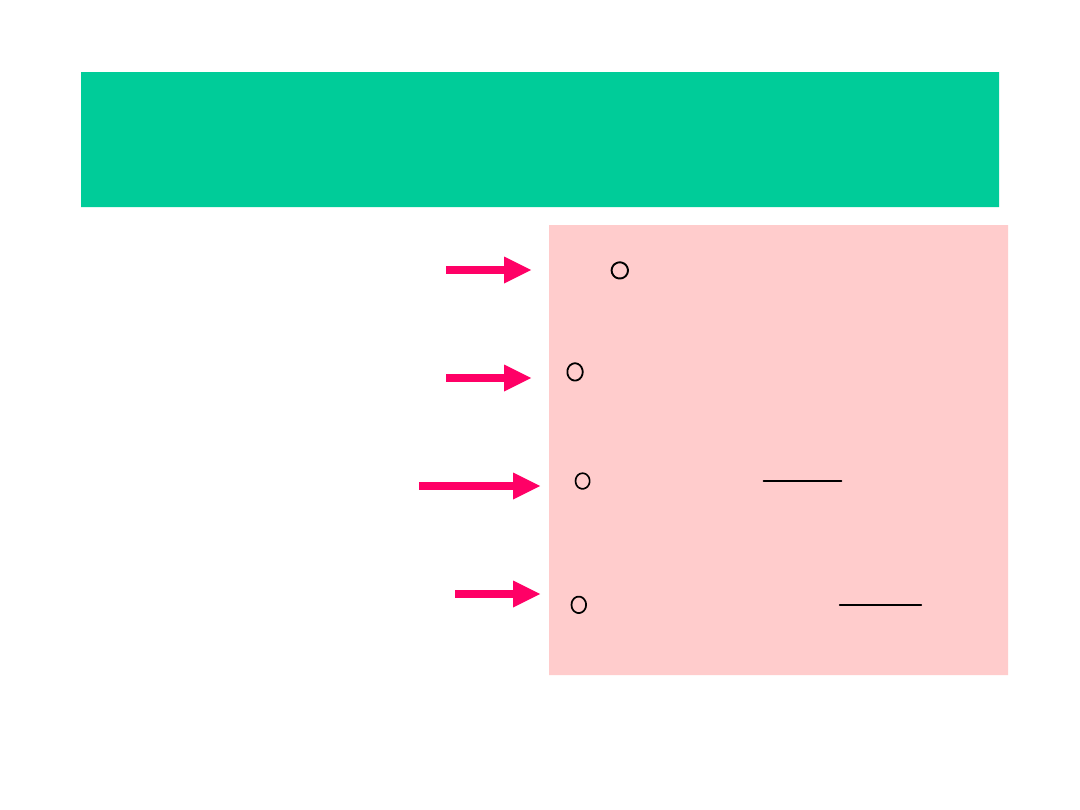
Równania Maxwella

• Prawo Gaussa dla

elektryczności

• Prawo Gaussa dla

magnetyzmu

• Prawo indukcji

Faradaya

• Prawo Ampere’a











dt

d

l

d

E

B





q

s

d

E











0









0

s

d

B





)

(

0

0

i

dt

d

l

d

B

E



















(48

)