OPTYMALIZACJ

A PRZEPŁYWU

W SIECIACH

W porównaniu od klasycznych

zadań

transportowych, problemy

przepływów w sieciach (które są

uogólnieniem zadań

transportowych) dopuszczają

możliwość występowania w sieci

oprócz węzłów:

A

+

(dostawców) i A

-

(odbiorców)

również węzłów oznaczonych jako

A

0

, które traktujemy jako węzły

tranzytowe lub przeładunkowe.

W zadaniach przepływów w sieciach

można zrezygnować z:

• ograniczeń dotyczących

występowania (bądź też braku)

tras (łuków) łączących dane

węzły.

• Można również dodatkowo

uwzględnić ograniczenia

przepustowości (przepływu) na

poszczególnych łukach (trasach) i

to zarówno z dołu, jak i z góry.

W zadaniach przepływów w sieciach

stosuje się najczęściej terminologię

zaczerpniętą z hydrauliki

• węzły reprezentujące dostawców to źródła,
• węzły reprezentujące odbiorców to ujścia,
• wielkości podaży dostawców to potencjały

źródeł (czyli wg przyjętych wcześniej
oznaczeń a

i

to potencjał i-tego źródła),

• wielkości popytu odbiorców to potencjały

ujść (czyli wg przyjętych wcześniej oznaczeń
b

j

to potencjał j-tego ujścia),

• konkretne przewozy to przepływy,
• węzeł tranzytowy (przeładunkowy) to taki

węzeł, w którym potok cieczy wpływającej do
niego jest równy potokowi cieczy
wypływającej z tego węzła.

Przy określaniu poszczególnych warunków

ograniczających dla węzłów można

wszystkie ich typy: dla źródeł, ujść i

punktów tranzytowych potraktować

jednolicie wykorzystując nierówność (a):

potok wypływający – potok wpływający <

potencjał węzła

przy założeniu, że:

potencjał źródła jest dodatni,

potencjał ujścia jest ujemny,

a węzła potencjał tranzytowego równy

zeru.

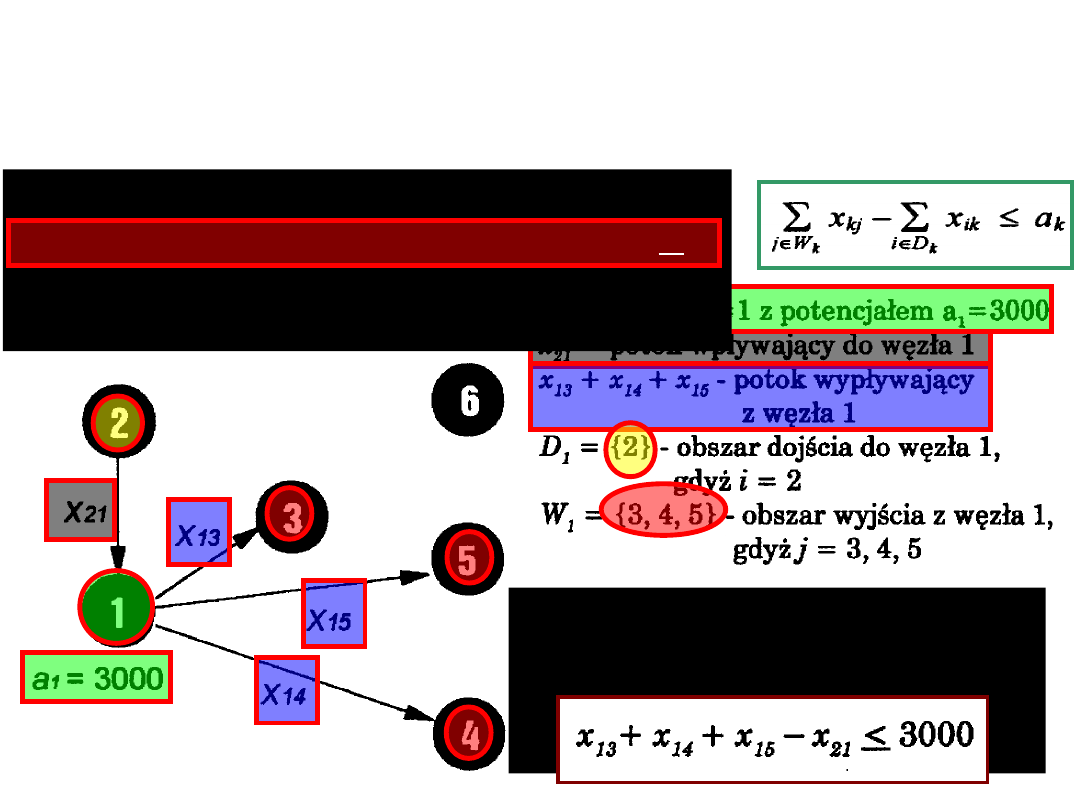
Oto przykład źródła (o numerze k = 1) i

budowa odpowiednich warunków

ograniczających przyjmując jako k

oznaczenie numeru węzła.

Ogólny warunek ograniczający na

podstawie (a)

dla źródła jest następujący

potok wypływający – potok wpływający <

potencjał źródła

co dla naszego węzła źródła

k = 1

jest równoważne

nierówności:

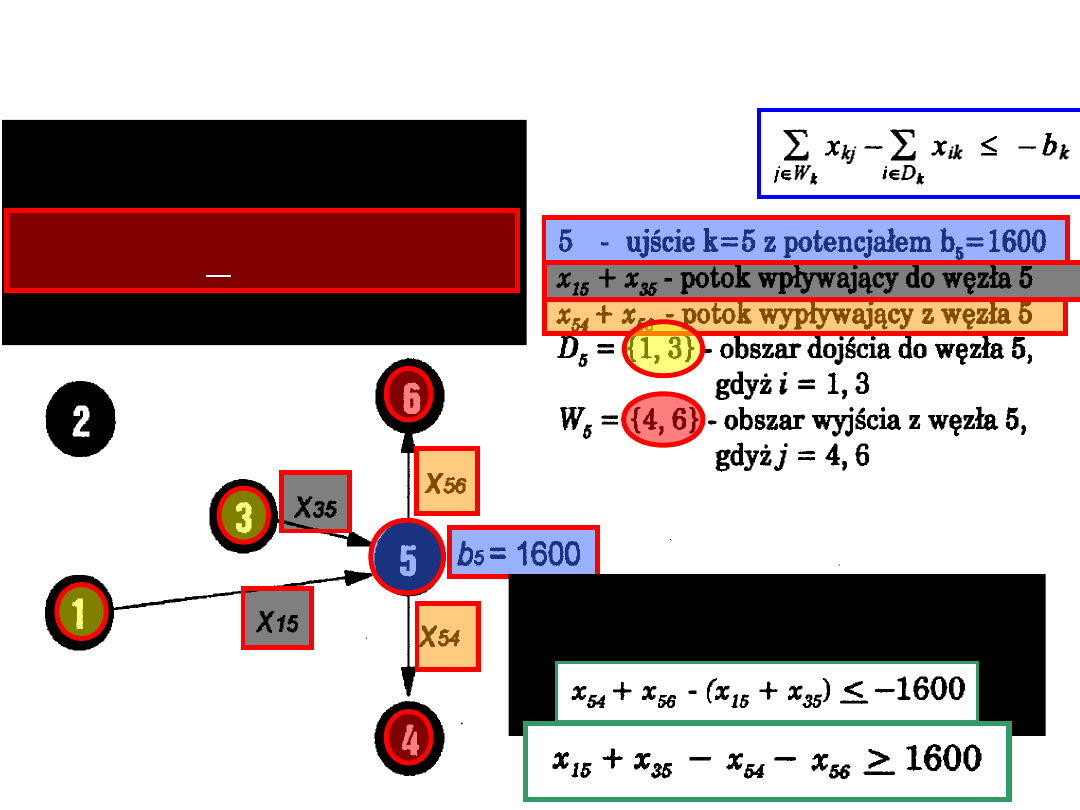
Rozpatrzmy przykład ujścia (o numerze k =

5) i budowę odpowiednich warunków

ograniczających:

Ogólny warunek

ograniczający na

podstawie (a)

dla ujścia jest następujący

potok wypływający – potok

wpływający < - potencjał ujścia

co dla naszego węzła ujścia

k = 5

jest równoważne

nierówności:

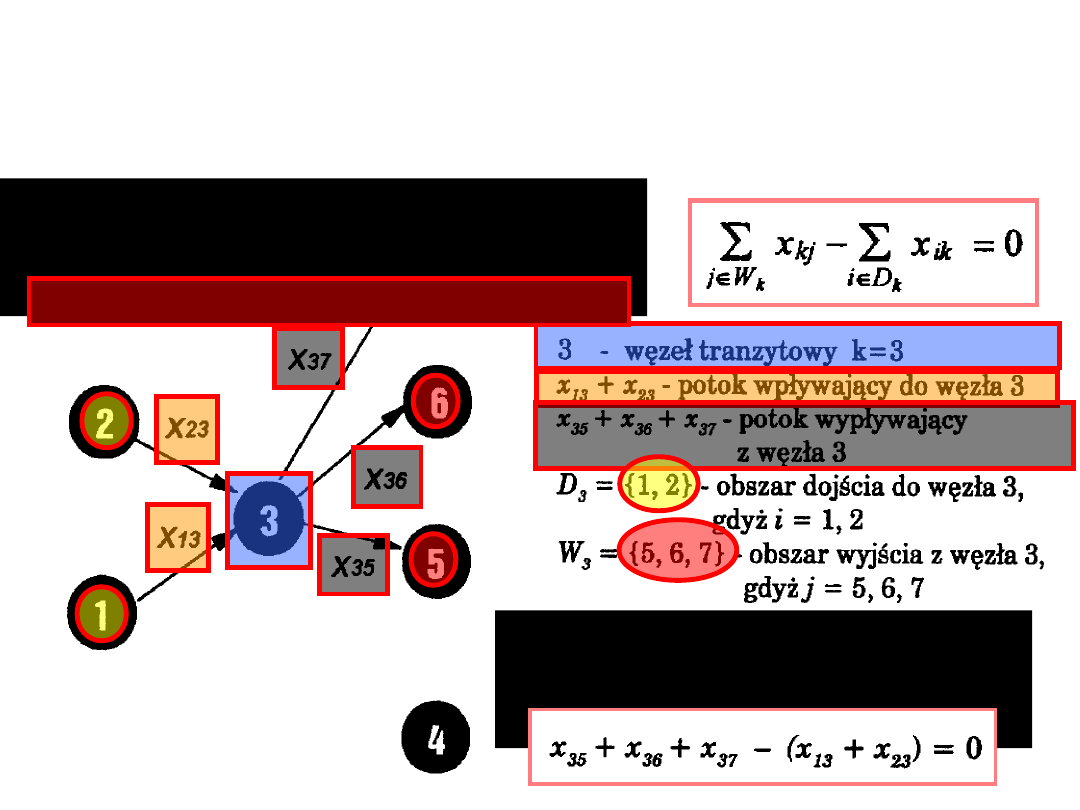
W węźle tranzytowym (przeładunkowym)

potok

cieczy wpływającej do niego jest

równy potokowi

cieczy wypływającej z tego

węzła.

Zrównoważenie potoków

wpływającego i wypływającego w

węźle tranzytowym:

potok wypływający – potok wpływający

= 0

co dla węzła tranzytowego

k = 3 jest równoważne

następującej równości:

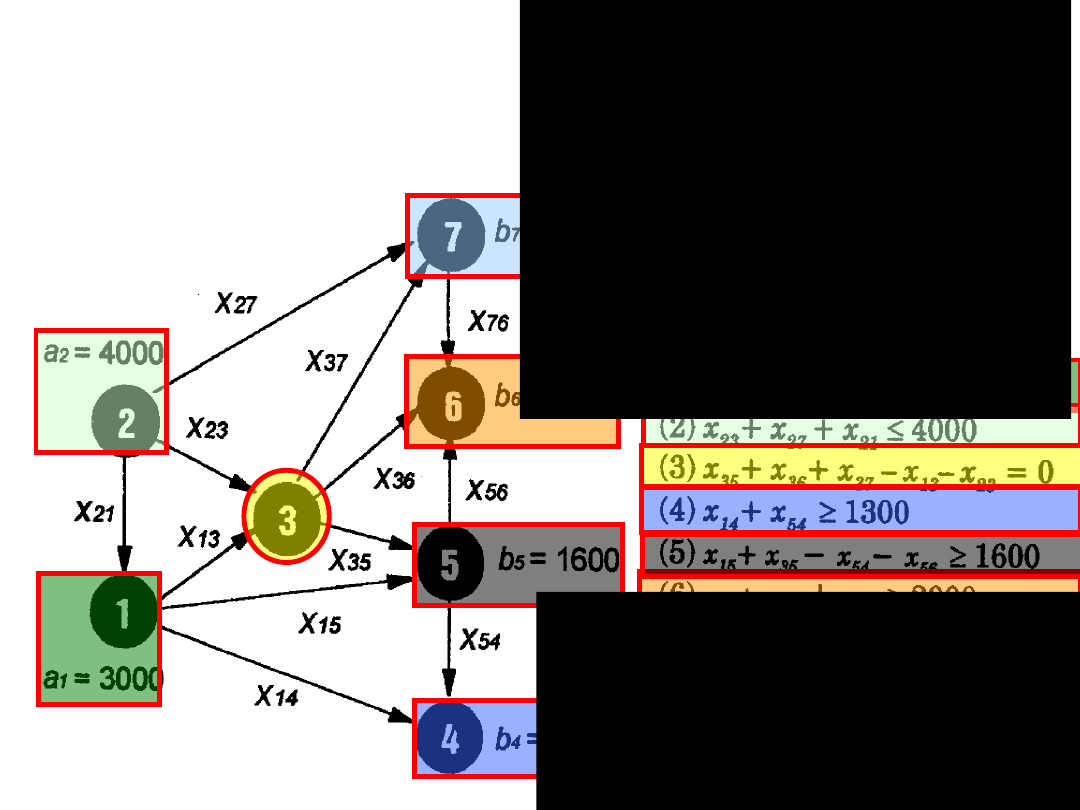
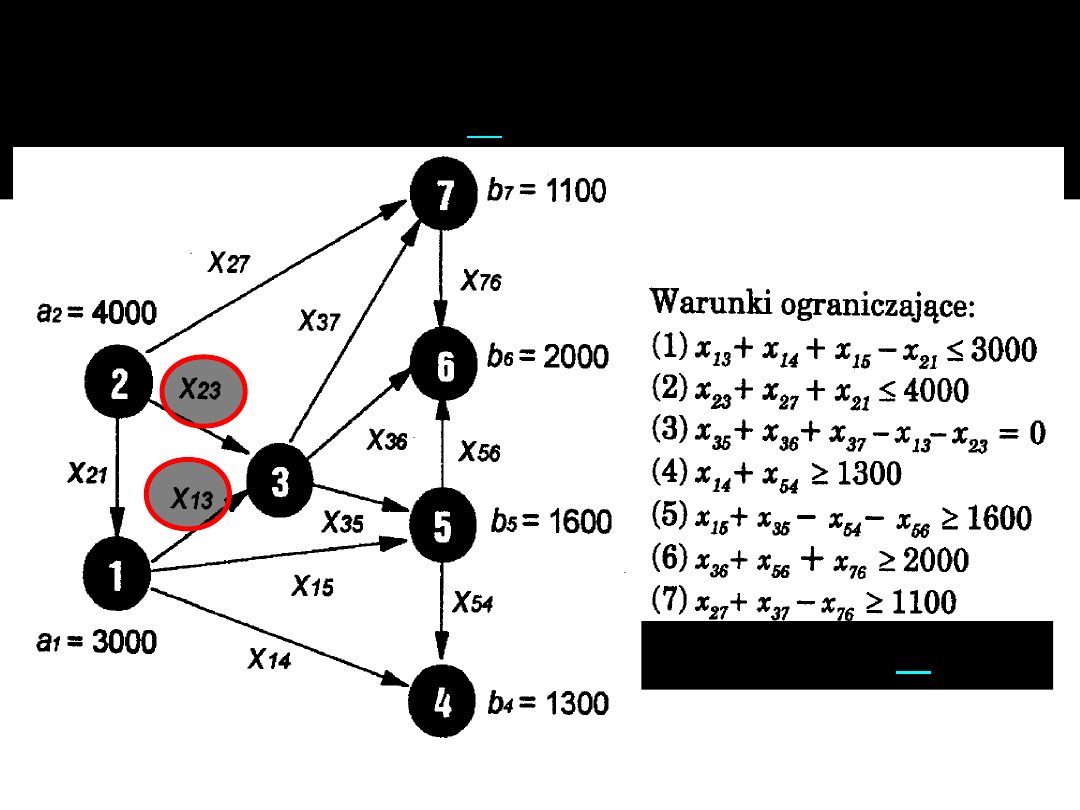
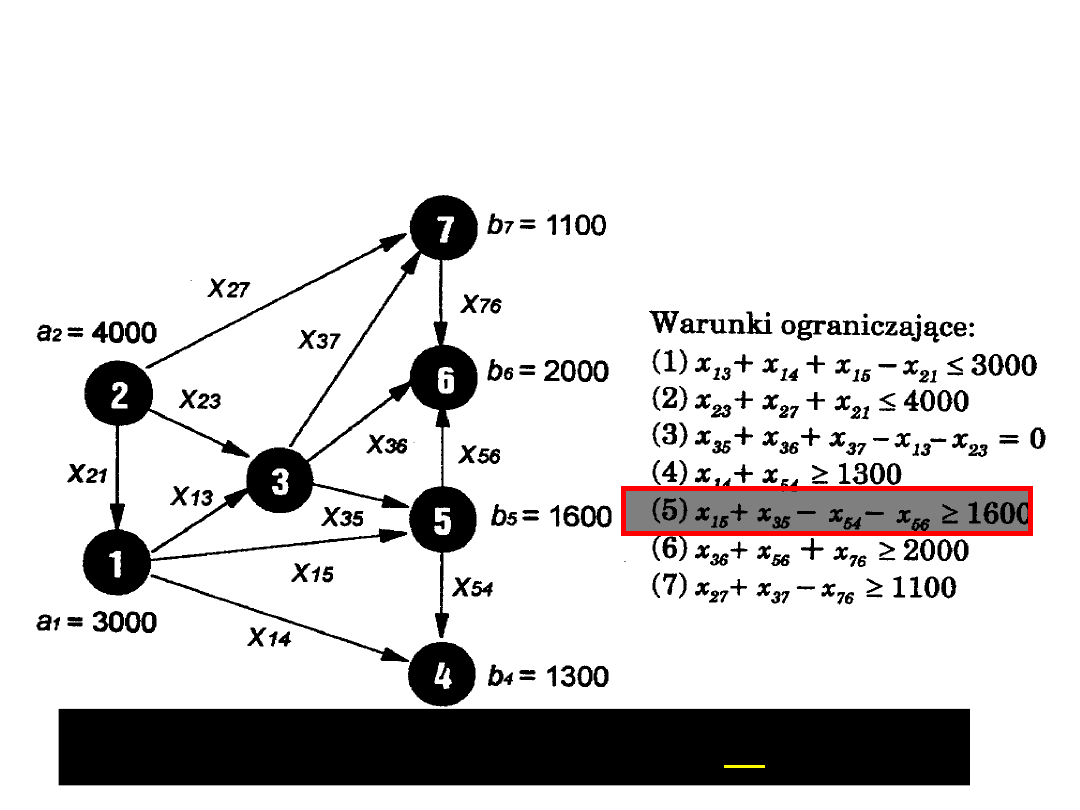
Oto cała sieć wraz ze

wszystkimi warunkami

ograniczającymi, przy

czym numer warunku

odpowiada numerowi

węzła sieci. Wstępnie

założono, że węzłami

źródłowymi są węzły 1

i 2, natomiast ujściami

węzły o numerach 4,

5, 6 i 7.

Dodatkowo dochodzą

jeszcze warunki

ograniczające związane z

łukami sieci, gdyż na

każdym z tych łuków

przepływ musi być liczbą

dodatnią lub równą zeru,

czyli:

x

ij

ł



0

Oprócz tego przepływy te

mogą być ograniczone na

danym łuku (i,j) z

dołu (d

ij

)

i z

góry (g

ij

),

czyli:

d

ij

Ł x

ij

Ł

g

ij

Każde wartości x

ij

będące rozwiązaniem

podanych warunków ograniczających dla

węzłów stanowią tzw.

przepływ

dopuszczalny

, który zaspokaja popyt

odbiorców (ujść) w ramach istniejącej

podaży dostawców (źródeł) i konkretnych

możliwości przewozowych.

W porównaniu do klasycznych

zagadnień transportowych, w których

rozwiązanie (czyli przepływ

dopuszczalny) zawsze istnieje w

zagadnieniach przepływu w sieciach

zdarza się, że przepływ dopuszczalny

nie istnieje (nie potrafimy wskazać

rozwiązania).

W ramach przepływów dopuszczalnych w

zagadnieniach przepływu w sieciach

rozpatrujemy dwa problemy:

1. Wyznaczamy wartości przepływów

dopuszczalnych

aby uzyskać najniższy

koszt przepływu K

p

, mając dane koszty

jednostkowe h

ij

przepływów na

poszczególnych łukach sieci (i,j)

należących do zbioru łuków sieci Q.

Ponieważ całkowity koszt przepływu jest

sumą iloczynów kosztów jednostkowych

h

ij

i odpowiadających im wielkości

przepływów x

ij

(zmiennych decyzyjnych)

na poszczególnych łukach sieci (i,j), więc

rozwiązanie optymalne uzyskamy

opierając się na zadaniu optymalizacji

liniowej

W ramach przepływów dopuszczalnych w

zagadnieniach przepływu w sieciach

rozpatrujemy dwa problemy:

2. Określamy dla jakich wartości

przepływów dopuszczalnych uzyskamy

największą wartość przepływu W

p

,

przez którą rozumiemy sumę masy

towarów transportowanych od

dostawców (źródeł) do odbiorców

(ujść).

Rozwiązanie optymalne uzyskamy

opierając się na zadaniu optymalizacji

liniowej:

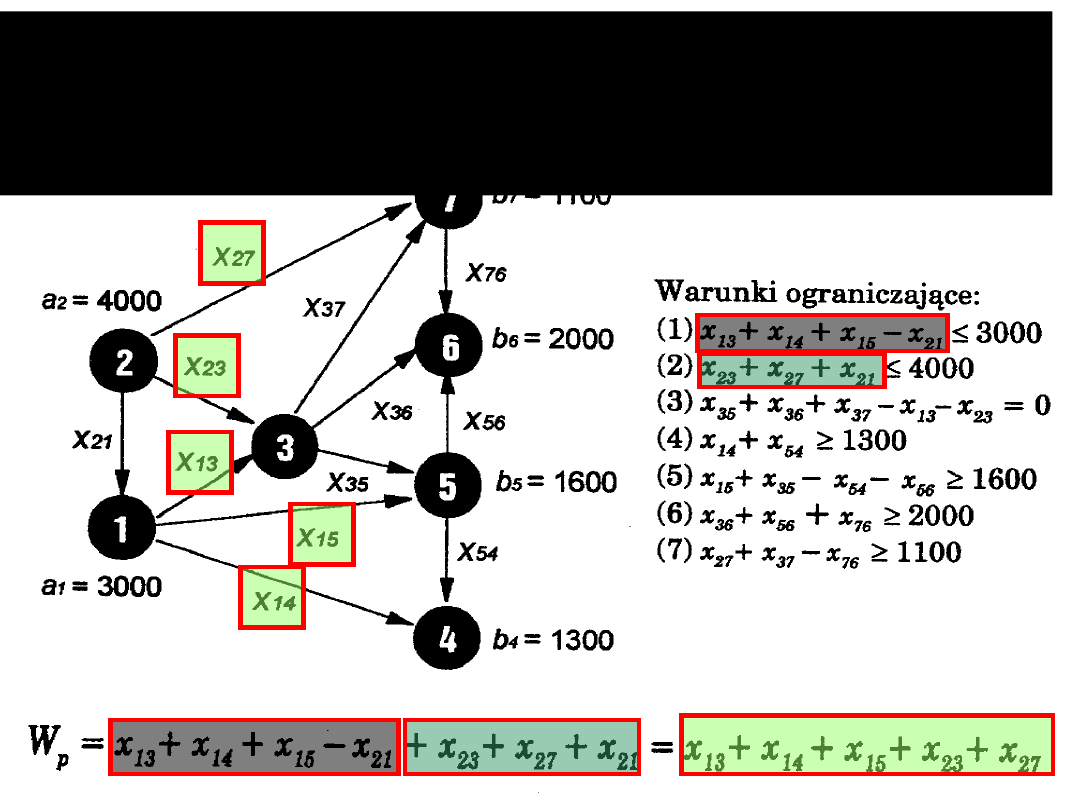
Można zauważyć, że wartość przepływu jest sumą

wszystkich lewych stron warunków

ograniczających dotyczących

źródeł.

Czyli dla

naszej sieci:

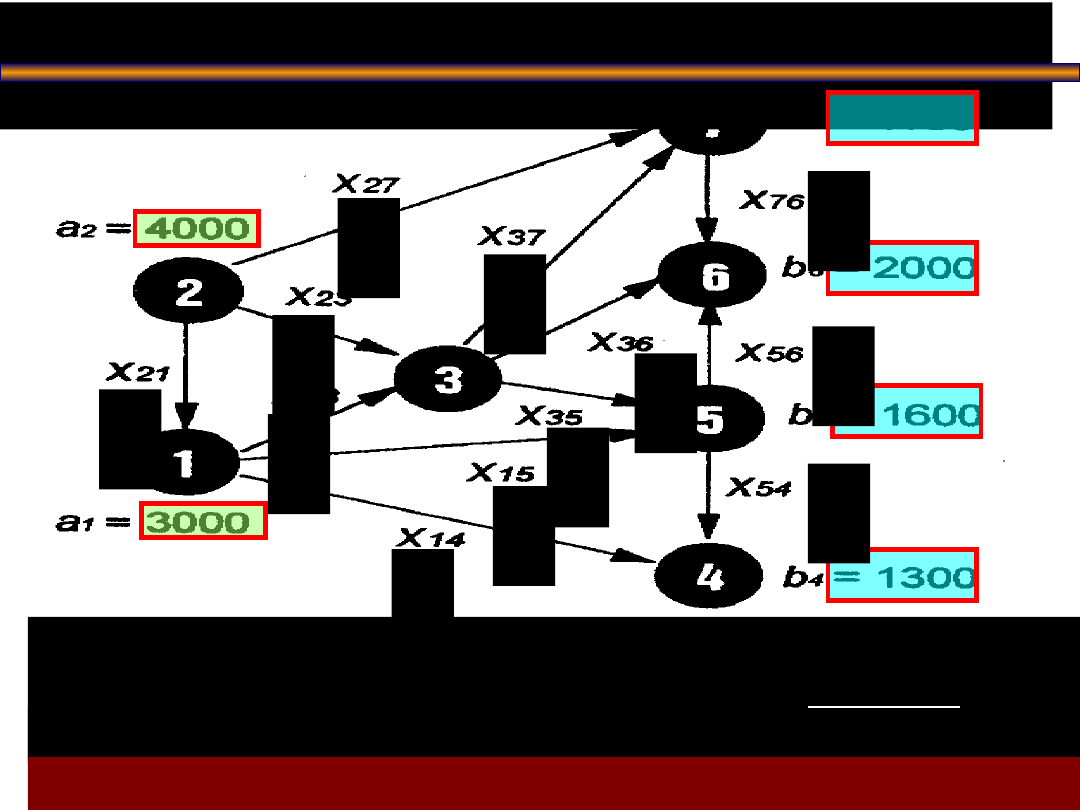
Przykład:

Zadanie przepływu w

sieciach

wielkości popytu w tonach (czyli

potencjały ujść),

Dla sieci o strukturze przedstawionej powyżej,

biorąc pod uwagę podane wielkości podaży w

tonach (czyli

potencjały źródeł

),

oraz jednostkowe koszty przepływu

h

ij

(zł/tonę)

wynoszące:

2

6

2

5

3

4

1

9

3

8

1

1

4

8

5

5

4

2

2

9

4

1

5

1

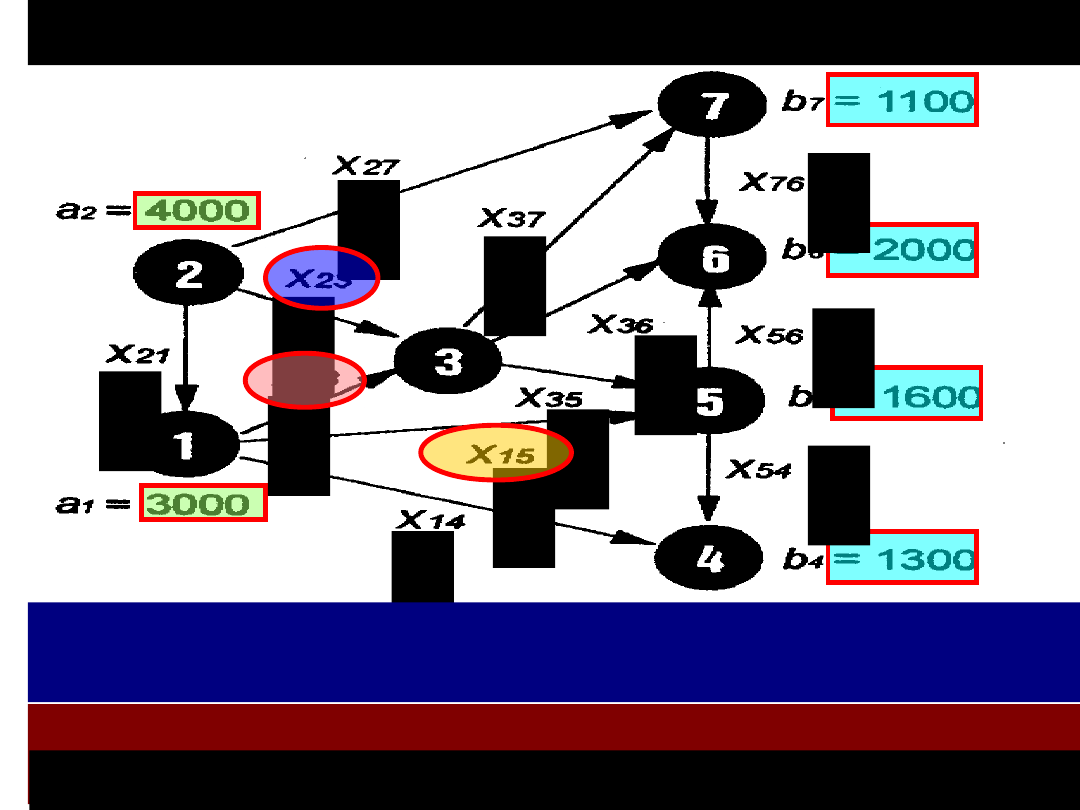
Dodatkowo mamy następujące ograniczenia:

2

6

2

5

3

4

1

9

3

8

1

1

4

8

5

5

4

2

2

9

4

1

5

1

na łuku

13

przepływ powinien być nie mniejszy niż

500 ton, lecz nie większy niż 700 ton,
na łuku

15

przepływ powinien być nie mniejszy niż

300 ton,

na łuku

23

przepływ powinien być nie większy niż

600 ton

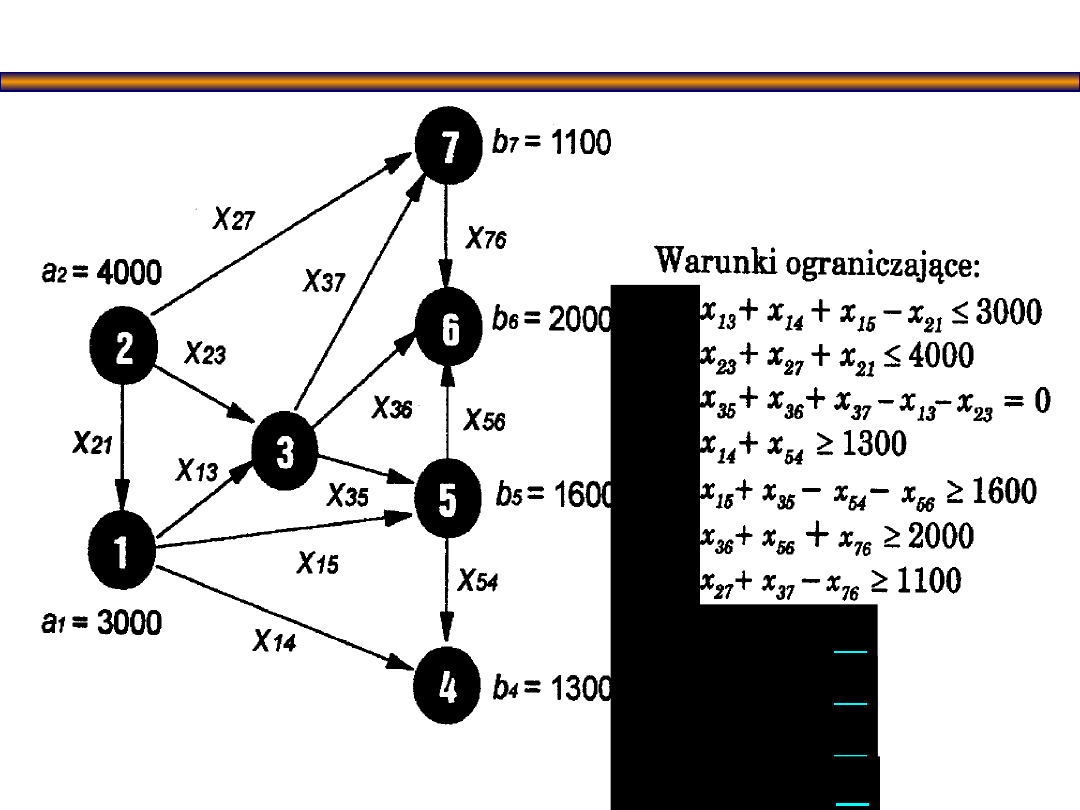
Mamy następujące warunki

ograniczające:

W8: x

13

>

500

W1

:

W2

:

W2

:

W4

:

W5

:

W6

:

W7

:

W9: x

13

<

700

W10: x

15

>

300

W11: x

23

<

600

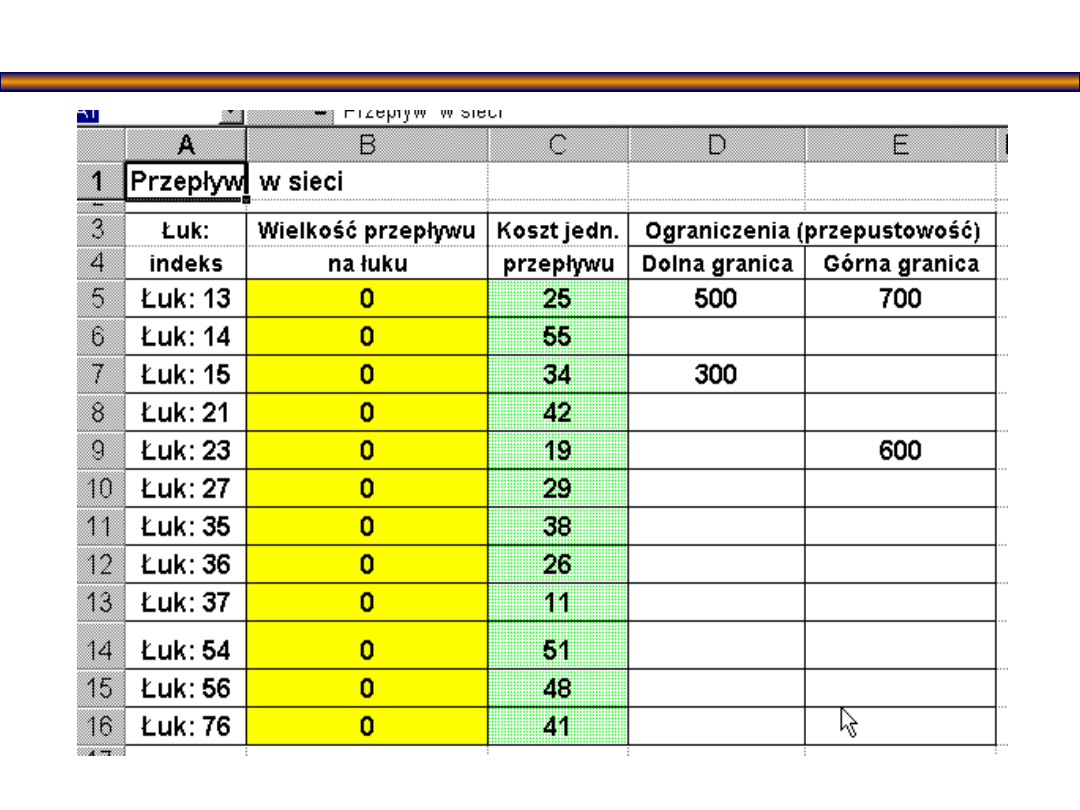
Wprowadzamy dane do EXCELA:

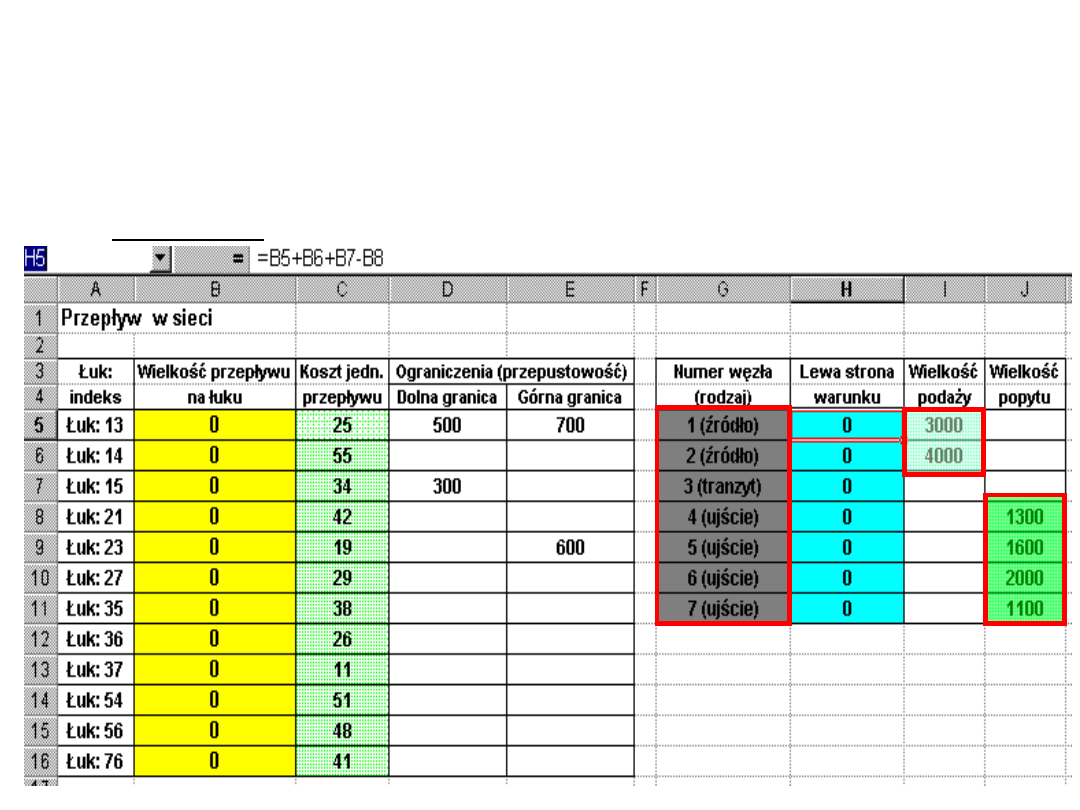
Do bloku komórek G5:G11 wprowadzamy numery

węzłów wraz z opisem ich rodzaju oraz wielkości

podaży węzłów źródłowych (do bloku I5:I6) i

popytu węzłów ujścia (do bloku J8:J11).

Wprowadzamy dane dotyczące wielkości

potencjałów poszczególnych węzłów.

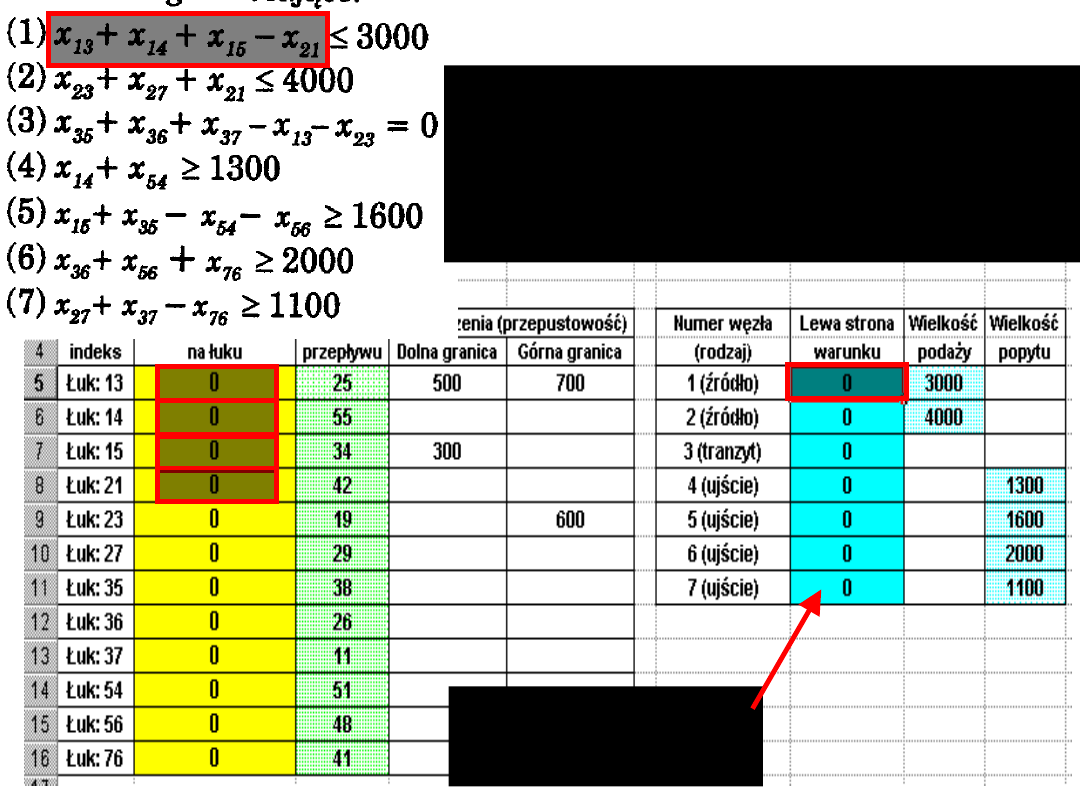
Do bloku komórek

H5:H11

wprowadzamy formuły

ujmujące lewe strony

pierwszych siedmiu (W1:W7)

warunków

ograniczających

, i tak:

=B10+B13-

B16

do komórki H5 wprowadzamy

formułę dotyczącą lewej

strony warunku (W1), czyli:

=B5+B6+B7-B8

itd.

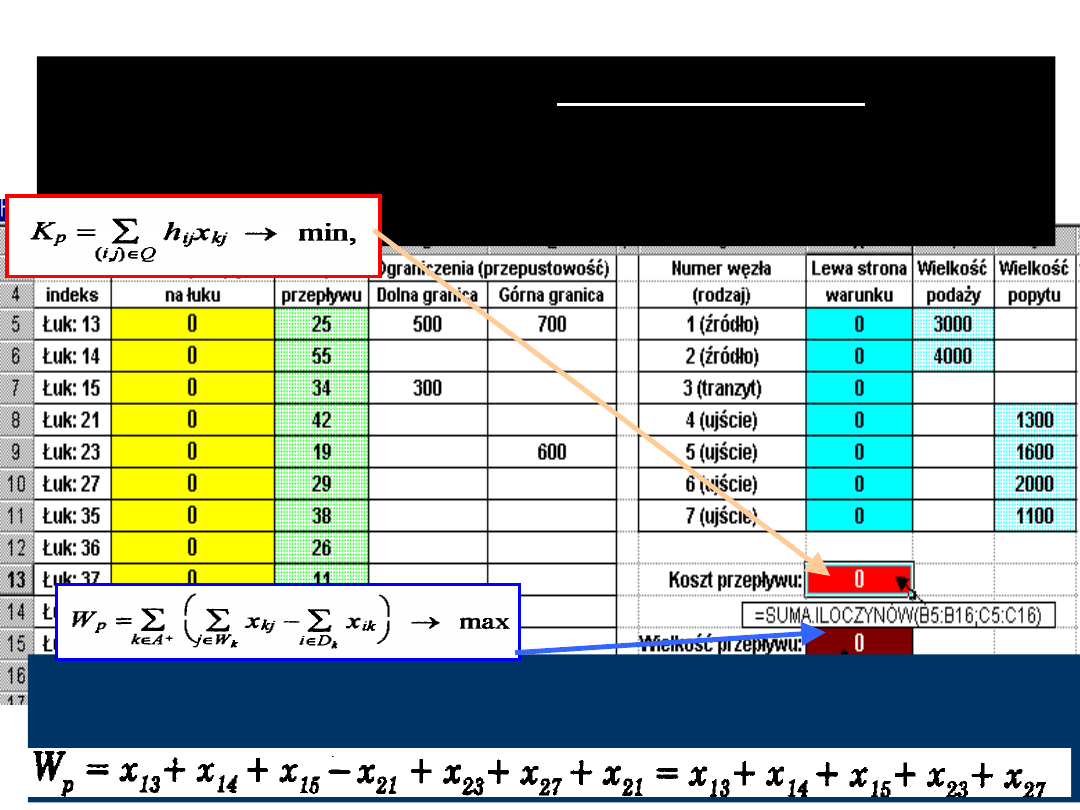
W zadaniu postawimy sobie dwie funkcje

celu.

Pierwsza z nich będzie minimalizować ogólny

koszt przepływu

K

p

i zgodnie ze wzorem

wpiszemy do komórki H13 formułę

=SUMA.ILOCZYNÓW(

B5:B16

;

C5:C16

),

Druga funkcja celu ma za zadanie

zmaksymalizować wielkość przepływu

W

p

do

komórki H15 wpiszemy formułę =H5+H6.

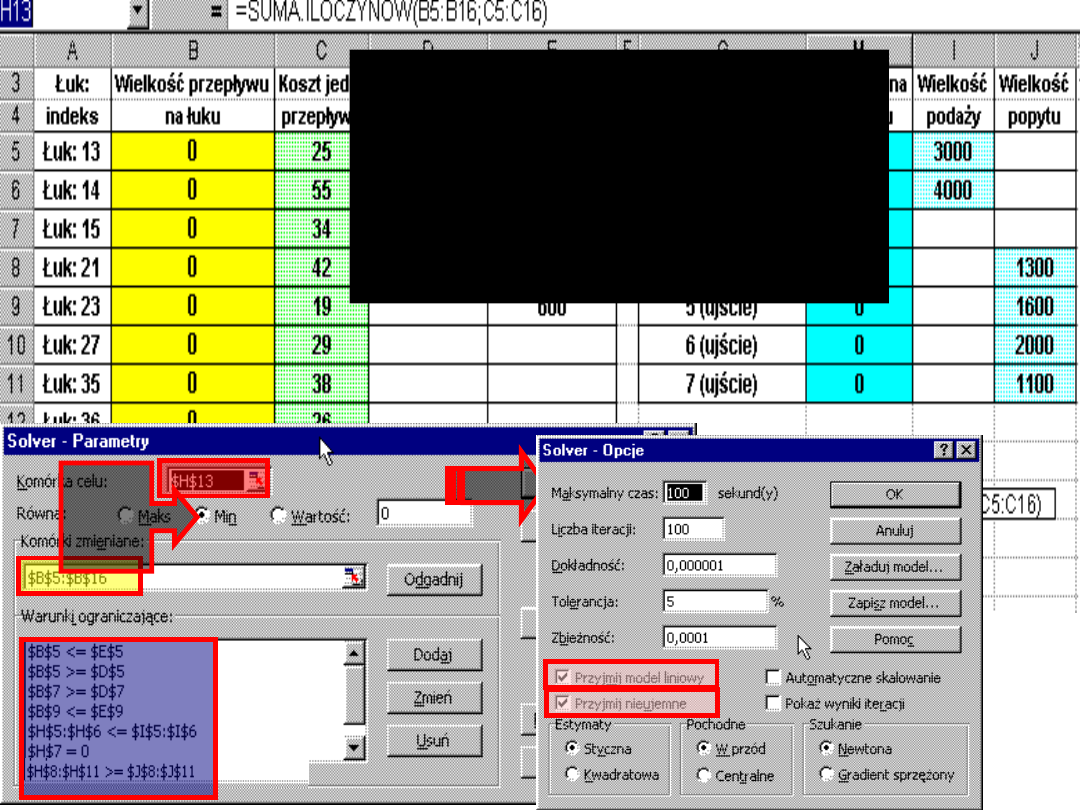
W pierwszej kolejności

dokonamy optymalizacji

wielkości przewozów pod

kątem minimalizacji

ogólnego kosztu przepływu

K

p

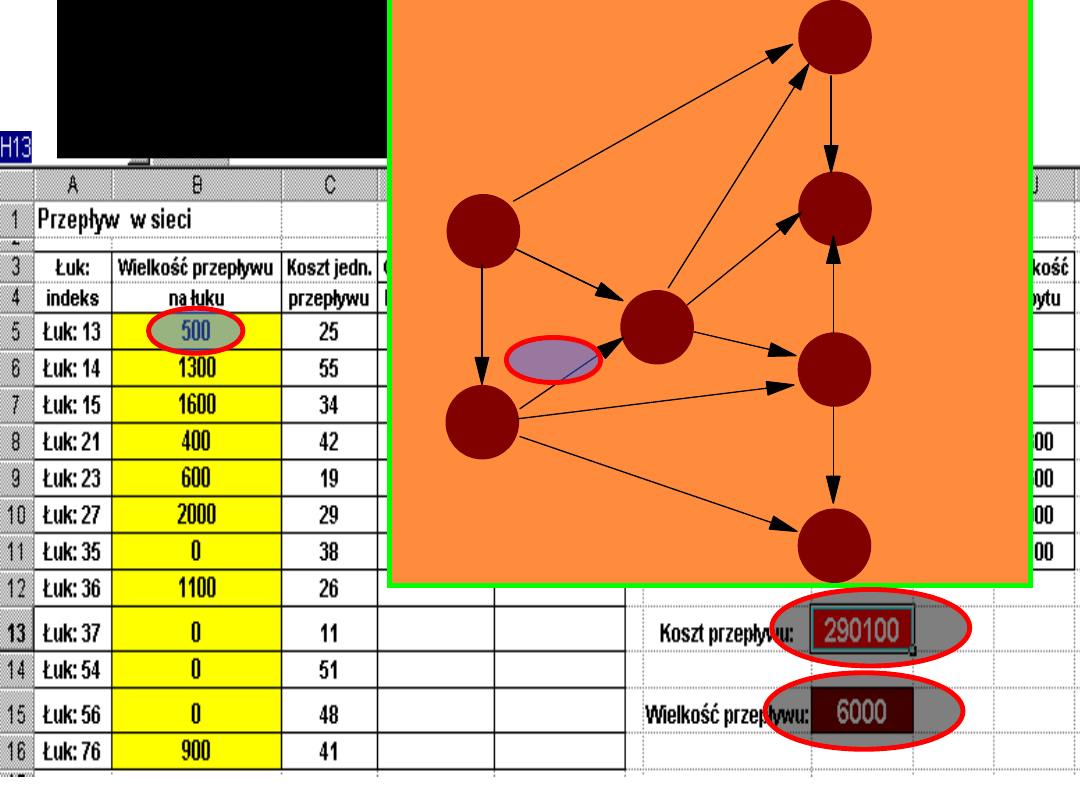
Oto rozwiązanie optymalne wielkości

przewozów pod kątem minimalizacji

ogólnego kosztu przepływu

K

p

1

2

3

4

5

6

7

b

5

= 1600

1600

a

1

= 3000

a

2

= 4000

b

4

= 1300

b

6

= 2000

b

7

= 1100

1100

1300

2000

600

500

400

900

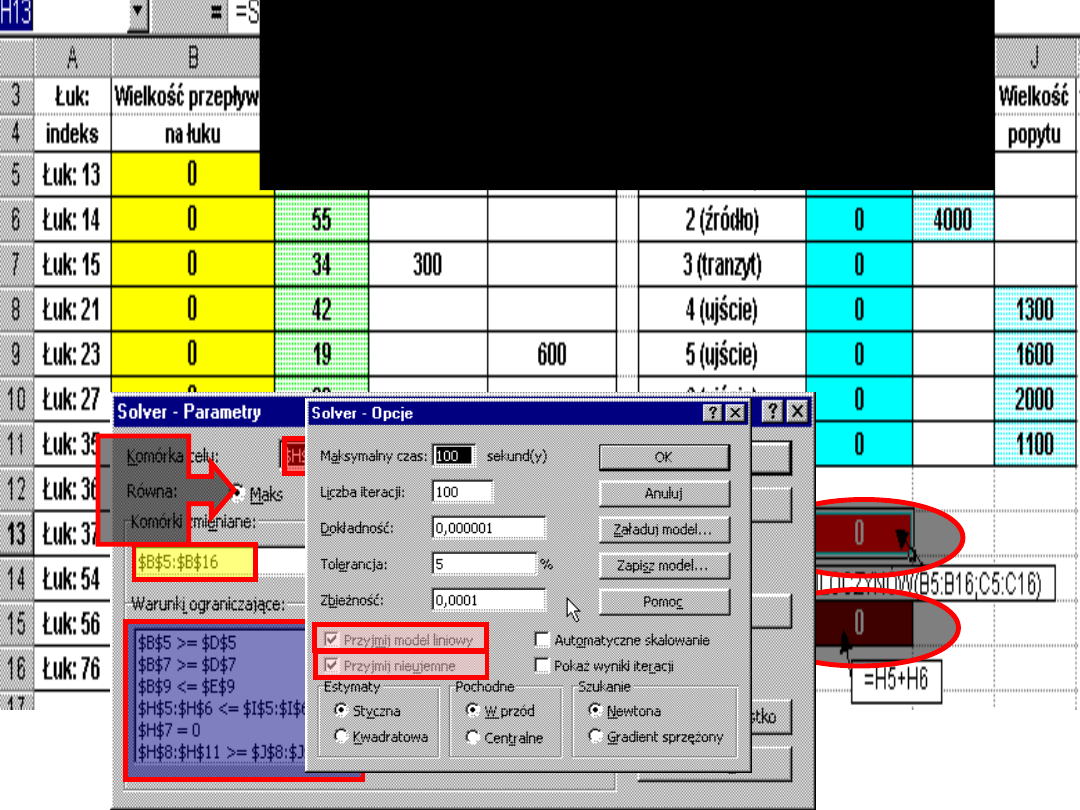
W drugiej kolejności dokonamy

optymalizacji wielkości przewozów

pod kątem

maksymalizacji

wielkości przepływu

W

p

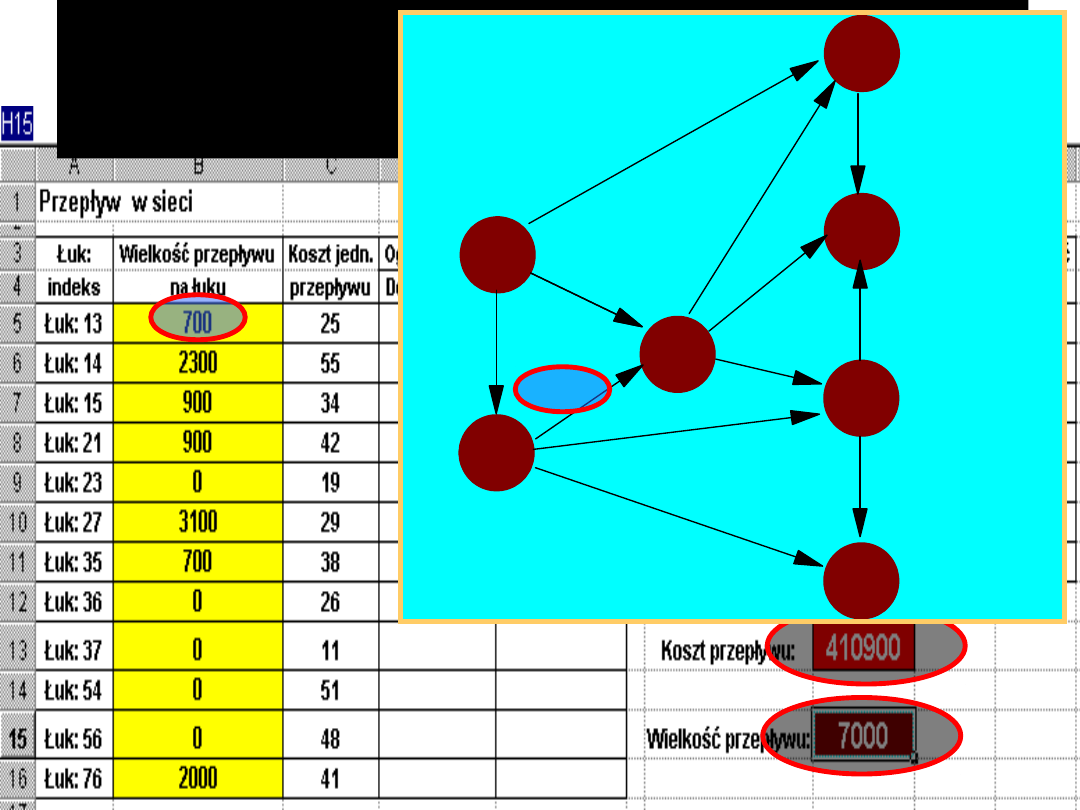
Oto rozwiązanie optymalne wielkości

przewozów pod kątem maksymalizacji

wielkości przepływu

W

p

1

2

3

4

5

6

7

b

5

= 1600

900

a

1

= 3000

a

2

= 4000

b

4

= 1300

b

6

= 2000

b

7

= 1100

3100

2300

2000

900

700

700

1

2

3

4

5

6

7

b

5

= 1600

1600

a

1

= 3000

a

2

= 4000

b

4

= 1300

b

6

= 2000

b

7

= 1100

1100

1300

2000

600

500

400

900

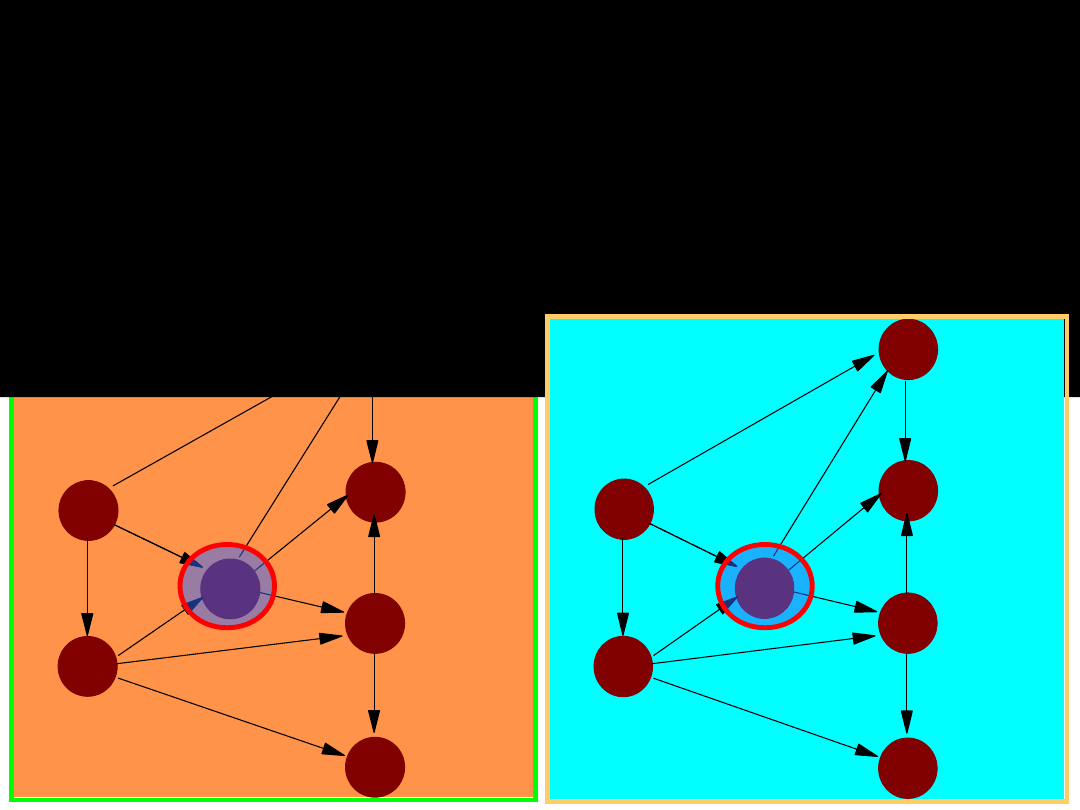
Często ograniczenia przepustowości (najczęściej

z góry) dotyczą również poszczególnych węzłów

sieci.

Gdyby np. w rozwiązywanym przez nas

przypadku węzeł

tranzytowy nr 3

miał

ograniczoną górną granicę przepustowości do

wartości

600

ton, to uzyskane przez nas

rozwiązania przepływów są niedopuszczalne.

1

2

3

4

5

6

7

b

5

= 1600

900

a

1

= 3000

a

2

= 4000

b

4

= 1300

b

6

= 2000

b

7

= 1100

3100

2300

2000

900

700

700

Aby rozwiązać ten problem, do istniejących

warunków ograniczających

dodajemy

warunek:

x

13

+x

23

< 600

i rozwiązujemy to

zadanie ponownie.

(8):

x

13

+x

23

< 600

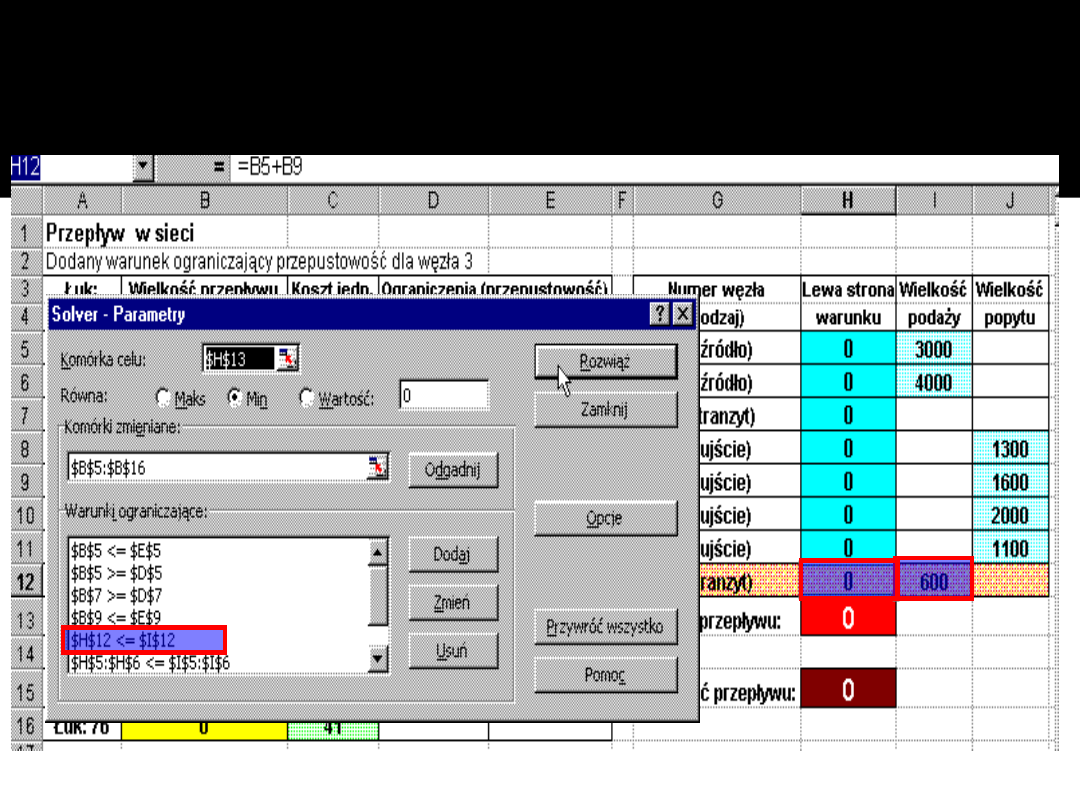
Lewą stronę tego warunku umieszczamy w

komórce

H12

, a cały warunek dodajemy do

warunków ograniczających w oknie dialogowym

Solver-Parametry.

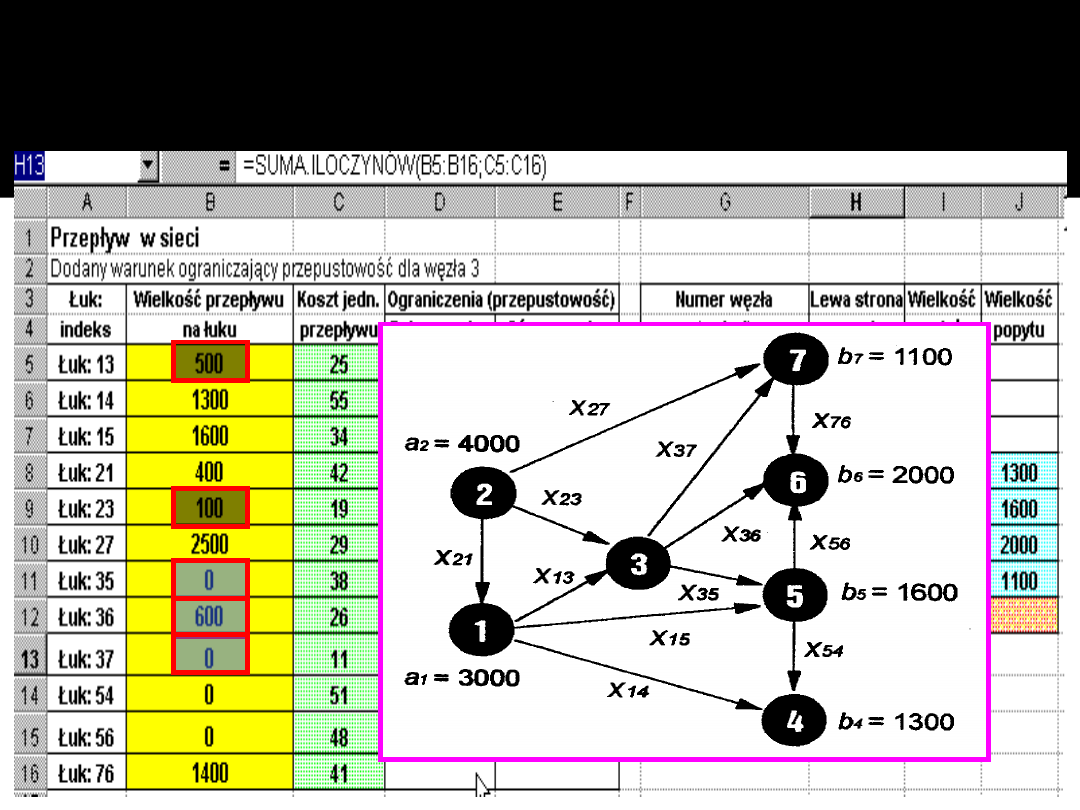
Oto rozwiązanie optymalne poprzedniego

zadania po dodaniu warunku ograniczającego

przepustowość węzła nr 3 do górnej granicy

600

ton pod kątem

minimalnego kosztu przepływu

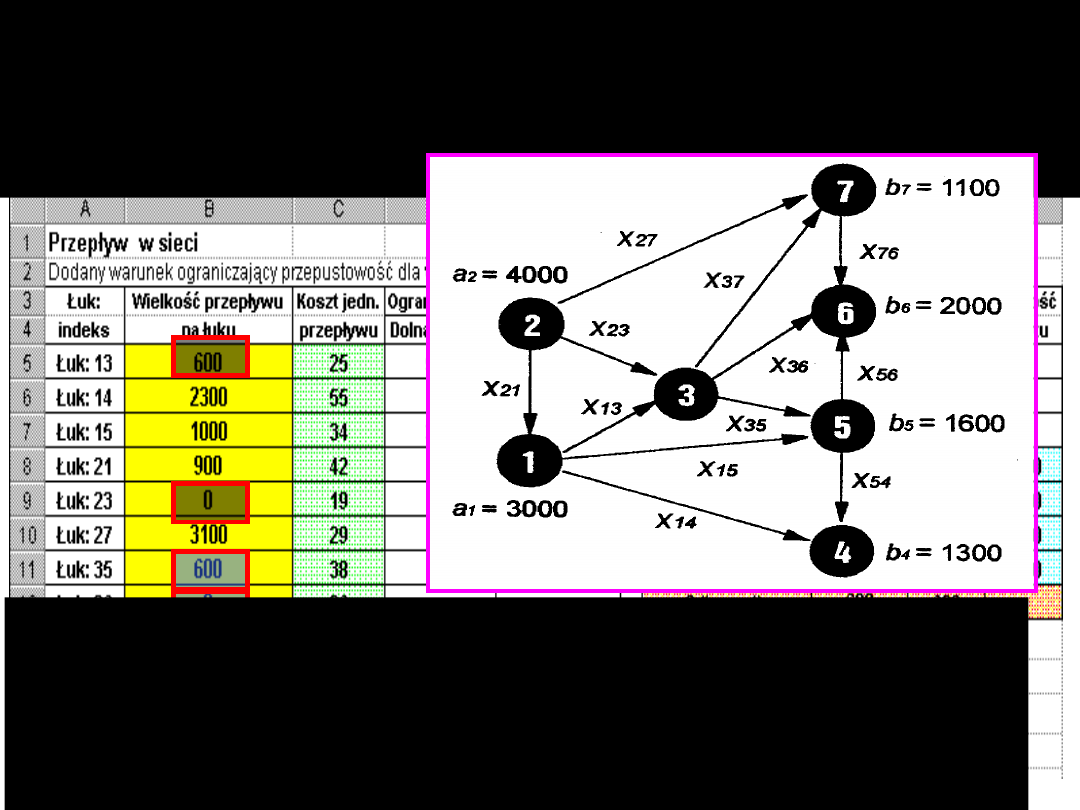
Oto rozwiązanie optymalne poprzedniego

zadania po dodaniu warunku ograniczającego

przepustowość węzła nr 3 do górnej granicy

600

ton pod kątem

maksymalnej wielkości przepływu

Innym sposobem ujęcia warunku

ograniczonej przepustowości dla węzła nr 3

jest wprowadzenie dodatkowego łuku

reprezentującego ten węzeł i przyjęcie na tym

właśnie łuku ograniczonej przepustowości.

Rozwiązując problemy przepływu w

sieciach możemy również uwzględniać

wzmacnianie lub osłabianie przepływu

na łukach sieci.

Dotychczas rozpatrywaliśmy sieci, w

których dany przepływ x

ij

na każdym

łuku (i,j) był taki sam na wejściu i na

wyjściu tego łuku.

Jeśli jednak weźmiemy pod uwagę

przesył energii elektrycznej w sieciach

energetycznych, to musimy uwzględnić

tendencję do zanikania wielkości prądu.

Z kolei w sieciach telekomunikacyjnych,

gdzie sygnały są wzmacniane, musimy

uwzględnić wielkości tego wzmocnienia.

W przypadku np. osłabienia przepływu

na łukach 54 i 56, odpowiednio, o 5% i

10% warunek (W5) dla węzła nr 5

przedstawiałby się następująco:

x

15

+ x

35

– 0,95x

54

– 0,9x

56

> 1600.