PROCESY TRANSPORTU W ROZTWORACH

ELEKTROLITÓW

HENRYK SCHOLL

KATEDRA CHEMII OGÓLNEJ I NIEORGANICZNEJ

WYDZIAŁ FIZYKI I CHEMII

UNIWERSYTETU ŁÓDZKIEGO

E-mail: [e-mail]

2

Omówione do tej pory termodynamiczne metody umożliwiają wyznaczanie

wielkości charakterystycznych dla stanów równowagi.

Określenie rodzaju i szybkości procesów doprowadzających układ do
stanu

równowagi wykracza poza ramy termodynamiki.

Zmiany w układach chemicznych, a więc i w roztworach elektrolitów nie

znajdujących się w stanie równowagi, polegają na reakcjach chemicznych

i na procesach transportu.

Scharakteryzujmy krótko podstawowe rodzaje transportu w

roztworach elektrolitów:

1)

Przewodzenie prądu elektrycznego

- jest transportem

naładowanych cząstek na skutek działania zróżnicowanego pola

elektrycznego.

2) Konwekcja

- jest transportem substancji pod wpływem

zewnętrznych sił mechanicznych lub impulsu związanego z ruchem

części układu, różniących się np. gęstością.

3

3) Przewodzenie ciepła

- jest transportem substancji na skutek istnienia

gradientu temperatury.

4) Dyfuzja

- jest transportem substancji, uwarunkowanym różnymi

wartościami potencjału chemicznego wewnątrz układu oraz między

układem a jego otoczeniem.

Zdefiniujmy na wstępie pojęcie

gęstości przepływu

:

jest to ilość określonej wielkości termodynamicznej (moli, dżuli,

kulombów), która przepływa w jednostce czasu (1s) przez jednostkę

przekroju poprzecznego (1m

2

).

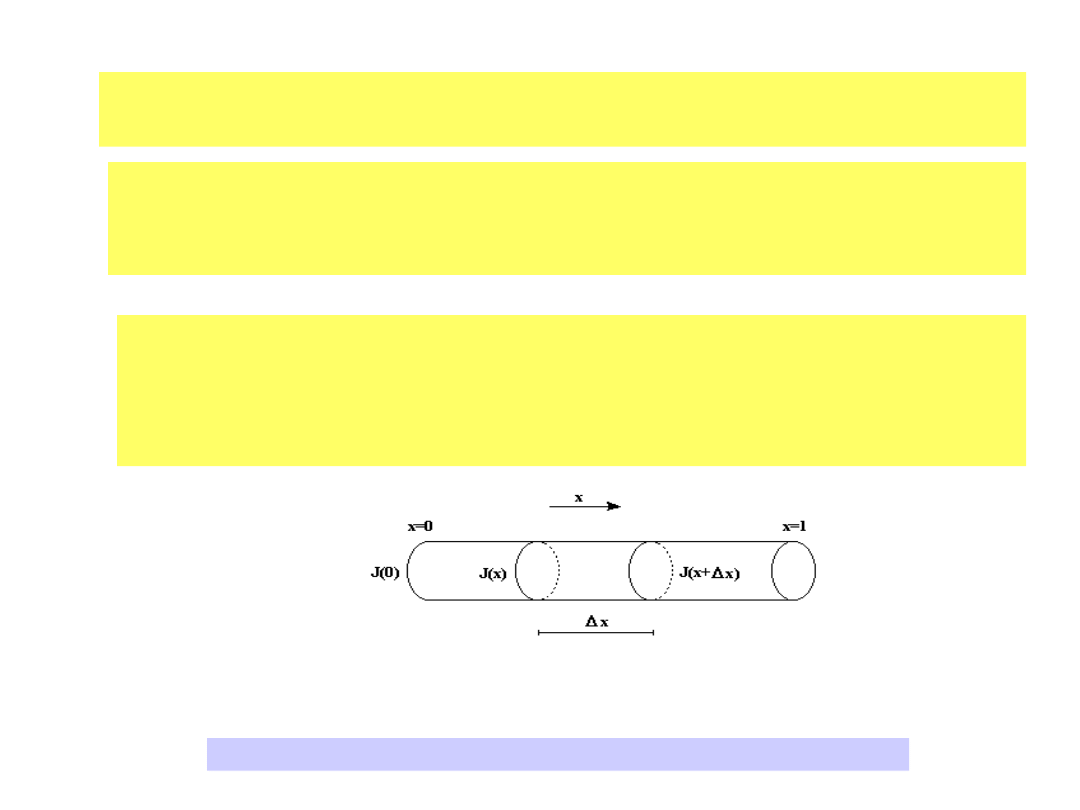
Ilustracja do rozważań o przepływie dyfuzyjnym

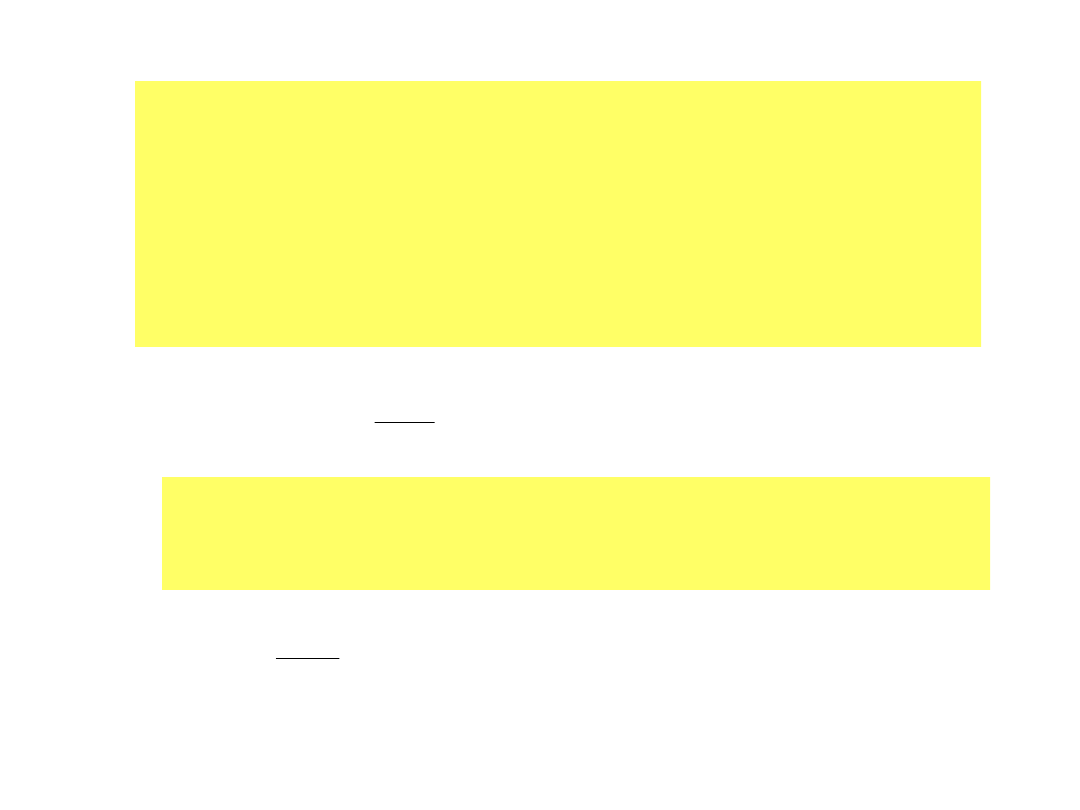
4

Rozważa się rurę o przekroju A i długości l przy założeniu, że

zmiany wielkości termodynamicznych mogą występować

jedynie w kierunku podłużnym.

Gęstość przepływu J jest funkcją osi podłużnej x.

Zmiana ilości wielkości termodynamicznej, np. zmiana ilości

substancji, zachodząca w jednostce czasu jest opisana

zależnością:

   





0

1 J

J

dt

dM







(1)

Dla odcinka x gęstość przepływu J jest ciągłą funkcją x we wnętrzu

rury. Chwilową zmianę ilości wielkości termodynamicznej w tym

odcinku rury można wyrazić wzorem:



  





x

A

x

J

x

x

J

t

M

















(2)

5

Dzieląc obie strony równania przez Ax = V i biorąc pod uwagę

gęstości graniczne otrzymamy:













t

M

V

J

x





(3)

ponieważ wyrażenie na gęstość jest oczywiste:







M

V



(4)









t

J

x



to:

(5)

Dla

ciała

trójwymiarowego,

ograniczonego

przez

powierzchnię S, posługujemy się analizą wektorową. Wektor
dS jest wektorem unormowanym, skierowanym od ciała na
zewnątrz.

6







dS

J

t

M





(6)

Gęstości przepływu wielkości termodynamicznych są wprost

proporcjonalne do wielkości fizycznych charakteryzujących

substancję w rozważanym punkcie układu.

Należy równocześnie pamiętać, że podczas dyfuzji mamy do

czynienia z nieuporządkowanym ruchem cieplnym cząstek.

Ponieważ jednak występuje tu

gradient stężenia

i przepływ

cząstek w kierunku mniejszego stężenia przeważa nad

przepływem w kierunku przeciwnym, to cząstki wędrują

do obszaru o mniejszym stężeniu.

Szybkość dyfuzji

jest określona zależnością empiryczną znaną

również pod nazwą I prawa Ficka:

7

J

D

dc

dx

dyf



(7)

Lub inaczej:

J

D c

dyf

grad



(8)

gdzie

D jest współczynnikiem dyfuzji

o wymiarze [m

2

s

-1

]

lub częściej stosowane [cm

2

s

-1

].

Dla większości nieorganicznych kationów i anionów jest w

roztworach ciekłych rzędu 10

-6

cm

2

s

-1

.

Należy jednocześnie nadmienić, że szczegółowe rozważania

dyfuzji, wysoce przydatne w teorii procesów elektrodowych,

opiera się na tzw. II prawie Ficka o równaniu podstawowym:









c

t

D

c

x



2

2

(9)

8

Rozpatrzmy teraz sposób w jaki rozwiązano zagadnienie obliczenia

wartości prądu dyfuzyjnego w reakcji elektrodowej:

Ox + ne  Red

Przyjęto, dla ułatwienia, że obie formy depolaryzatora nie są

naładowane. Wówczas na powierzchni elektrody będą się

znajdować cząstki "Ox" i "Red" w zależności od odległości od

elektrody i czasu pokonania tej odległości, tj. c

ox

(x,t) i c

Red

(x,t).

Dla opisu zachodzącego procesu przyjęto ponadto kilka założeń:

1)

elektroda ma płaską powierzchnię o wielkości A i jest

dostatecznie duża, by można pominąć zakłócenia dyfuzji na jej

krawędziach;

2) dyfuzja wzdłuż osi x jest do powierzchni A prostopadła

i rozpatrywana wyłącznie na dodatniej części osi x;

3) wyjściowe stężenia cząstek w roztworze , tzn. przed

rozpoczęciem procesu dyfuzji wynoszą:

 c

ox

(x,0) = c

0

Ox

     i      c

Red

(x,0) = 0     dla x  0;

9

4) objętość elektrolitu jest dostatecznie duża, tak, że w czasie przebiegu

reakcji stężenia obu form depolaryzatora w głębi roztworu nie zmieniają

się, tzn.

 c

ox

(x,t)   c

0

ox

      i      c

Red

(x,t)  0     jeśli     x    ;

5) każda cząstka "Ox" po przyjęciu elektronu w reakcji utleniania

i redukcji tworzy formę "Red" depolaryzatora. Oznacza to, że strumienie

przepływu są równe i przeciwne co do znaku: J

ox

(0,t) = -J

Red

(0,t)

6) Reakcja wymiany elektronu w omawianym procesie jest bardzo szybka

i tym samym formy depolaryzatora "Ox" i "Red" są w stanie stałej

równowagi i spełniają równanie Nernsta zapisane w postaci:

 





c

t

c

t

nF E E

RT

Ox

d

( , )

( , )

exp

(

)

Re

0

0

0

(10)

W takich warunkach dyfuzja obydwu rodzajów cząstek spełnia II-gie

prawo Fick'a, co ilustrują równania:









c

t

D

c

x

Ox

Ox

Ox



2

2

(11)









c

t

D

c

x

d

d

d

Re

Re

Re



2

2

(12)

10

Rozwiązaniem tych równań są stężenia form "Ox" i "Red"

w funkcji odległości i czasu dyfuzji. Rozwiązania powyższych

równań przeprowadzono poprzez transformacje Laplace'a.

Jeśli teraz bodziec powodujący migrację jonów (cząstek) jest

proporcjonalny do gradientu potencjału chemicznego,

to współczynnik proporcjonalności nosi nazwę

ruchliwości (u).

Opisuje on przepływ substancji przy jednostkowym stężeniu

i jednostkowym gradiencie potencjału chemicznego. Wówczas

przepływ dyfuzyjny opisuje równanie:

J

uc

dU

dx

u RT

dc

dx

dyf





(13)

PRZEWODNICTWO ROZTWORÓW ELEKTROLITÓW

 

W ramach podstawowego kursu fizyki omówione zostały reguły

rządzące przepływem prądu elektrycznego przez przewodniki

metaliczne i przez półprzewodniki różnych typów.

Omówmy obecnie zjawiska towarzyszące przepływowi prądu

elektrycznego przez roztwory elektrolitów, elektrolity stałe

i stopione sole.

11

Transport ładunku opisuje (na zasadach rządzących dyfuzją) prawo

Ohma podane w postaci:

j

d

dx



 

(14)

Gdzie:  - jest przewodnictwem właściwym,

 - jest potencjałem wewnętrznym fazy  

Z kolei gęstość prądu jest określona prawem Faradaya:

12

j

z FJ

i

i

i





(15)

gdzie J

i

jest gęstością przepływu "i"-tego składnika układu.

 Ta postać prawa Faraday'a wyraża równoważność transportu

naładowanej elektrycznie materii oraz transportu ładunków

elektrycznych. Przypomnijmy, że dla przepływu materii to prawo jest

znane pod postacią:

m = k i t (16)

 Bodziec powodujący elektrolityczne przenoszenie ładunków jest

wielkością analogiczną do gradientu potencjału chemicznego, tj.

gradientu energii elektrycznej odniesionej do jednostki ilości substancji





















x

F

z

c

u

J

i

i



(17)

gdzie u

i

jest ruchliwością "i"-tego składnika.

 Wielkość, która definiuje

ruchliwość elektrostatyczną

ma postać:

U

z Fu

i

i

i



(18)

Co z kolei prowadzi do formuły przewodności właściwej:







z FUc

i

i i

i

(19)

Lub w postaci:







z F uc

i

i i

i

2

2

(20)

Stąd definicja

przewodności molowej

uwzględniająca odpowiednio ruchliwości kationów i

anionów:

13







z F u FU

i

i

i

2

(21)

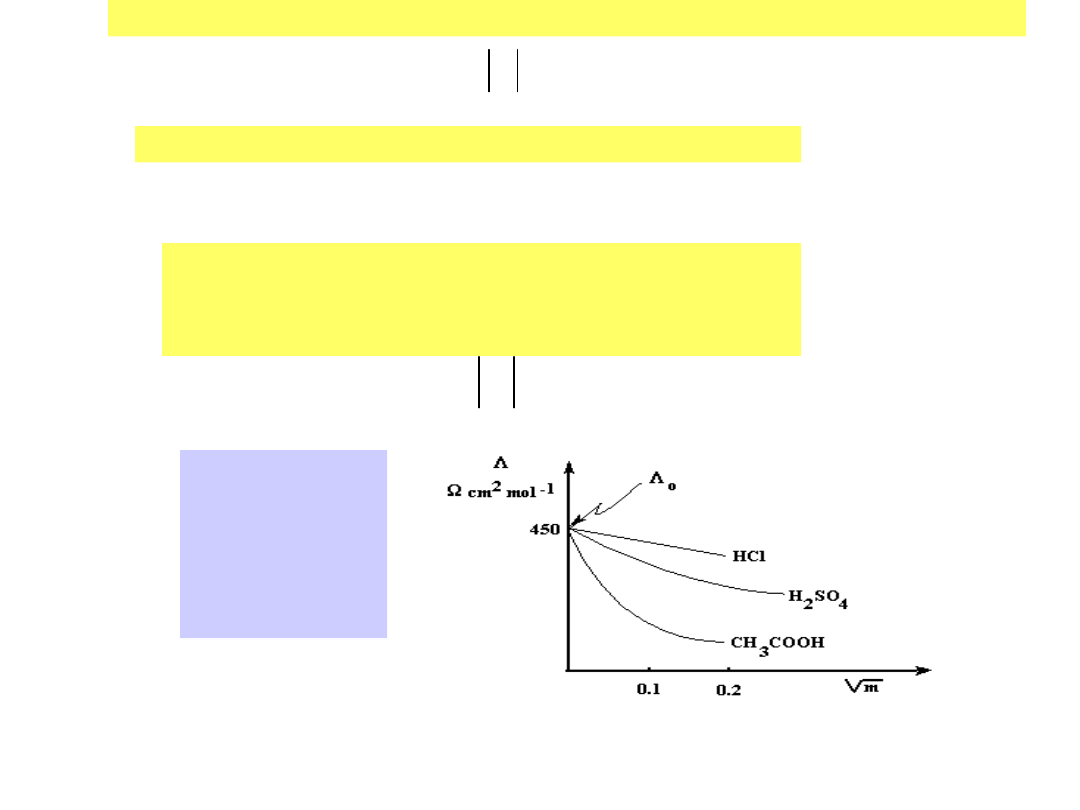
Zależność

przewodnictwa

molowego

=  /

c

od stężenia i

rodzaju

elektrolitu

14

Stąd blisko do sformułowania przez

Ostwalda prawa rozcieńczeń

pozwalającego na obliczenie przybliżonej nietermodynamicznej

stałej dysocjacji:





K

c

c

o

o

'













2

2

1



  

(22)

W miarę zwiększania stężenia roztworu elektrolitu zmienia się

wpływ sił międzyjonowych na prędkość wędrówki jonów.

Zanim sprecyzujemy ten wpływ przypomnijmy ogólne zależności,

jakie występują podczas ruchu kulistej cząstki o promieniu r

(jonu) przez lepkie środowisko (rozpuszczalnik) o współczynniku

lepkości



. Definiuje to

prawo Stokesa

:

u

f

r

i

i



6



(23)

gdzie f

i

jest siłą działającą na cząstki.

Siły międzyjonowe wpływają dwojako na prędkość wędrówki

jonów. Mamy do czynienia z

efektem elektroforetycznym

i z efektem czasu relaksacji

:

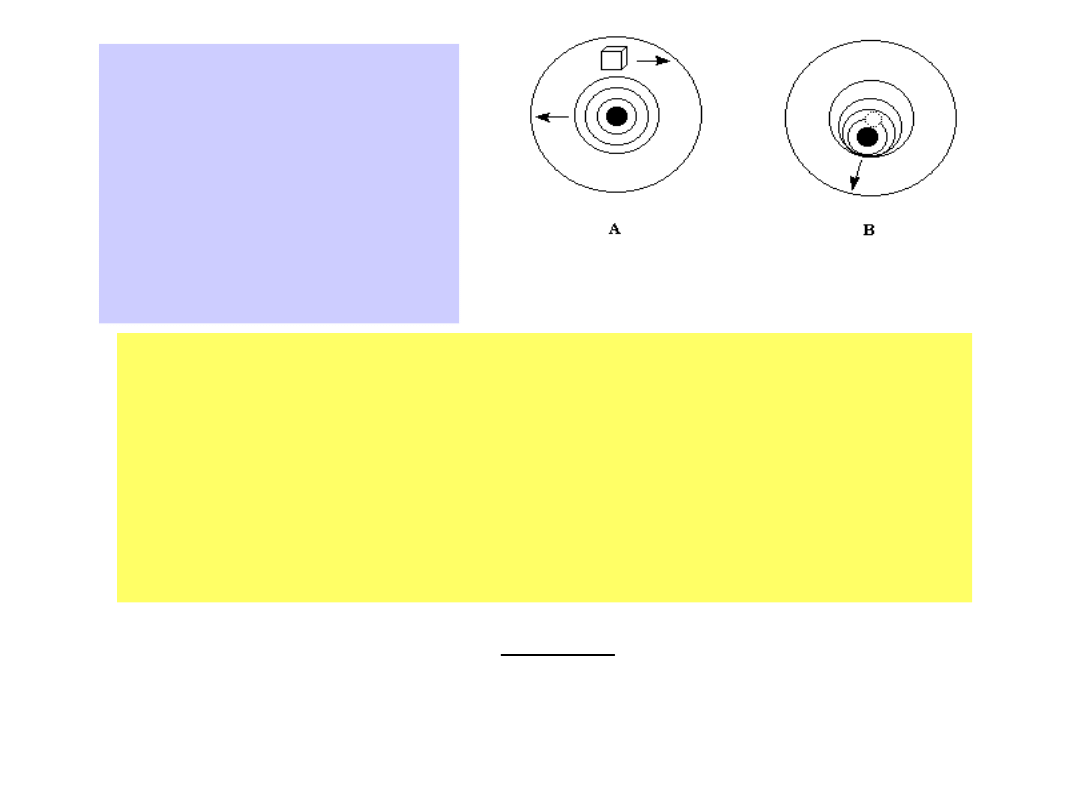
15

A)

Efekt elektroforetyczny. Jon
porusza się w kierunku
przeciwnym niż atmosfera
jonowa.

B)

Efekt

relaksacyjny.

Skończonego

czasu

wymaga

odtworzenie

atmosfery jonowej podczas
ruchu

jonu.

Wtedy

położenie jonu nie

pokrywa

się ze środkiem atmosfery
jonowej

W przypadku

efektu elektroforetycznego

jony pociągają za sobą

cząsteczki rozpuszczalnika, pozostałe poruszają się w kierunku

przeciwnym, więc obydwa ruchy wzajemnie się hamują.

Do prawa Stokesa, jako siłę f

i

powodującą ruch jonu,

wprowadzimy siłę elektryczną (z i e F) stanowiącą iloczyn

ładunku jonu zi i natężenia pola elektrycznego. Mamy wówczas

prędkość ruchu atmosfery jonowej:

V

zeF

x

i







6

(24)

16

Określone opóźnienie (relaksacja) ruchu jonu związane jest

z odtwarzaniem się kulistej symetrii atmosfery jonowej wokół jonu

centralnego, przesuwającego się pod wpływem pola elektrycznego.

Po oddaleniu się jonu centralnego zarówno zanikanie atmosfery

jonowej, jak i jej "reinkarnacja" są wykładniczymi funkcjami czasu.

Zakończenie tych procesów (zanikanie  odtwarzanie) jest podwójnym
upływem czasu (tzw.

czasu relaksacji

) rzędu 10

-7

do 10

-9

s.

Istotą zjawiska jest to, że podczas ruchu jonu centralnego (ruchu

wywołanego wpływem zewnętrznego pola elektrycznego) położenie

centrum jonu nie pokrywa się z położeniem środka atmosfery jonowej –

tym samym wypadkowa oddziaływań jest różna od zera.

Efekt czasu relaksacji jest istotny ze względu na to, że natężenie pola

elektrycznego wytworzonego przez atmosferę jonową powodują małe

zmiany symetrii atmosfery jonowej i osłabiają znaczenie oddziaływania

zewnętrznego pola elektrycznego.

17

Przy jego wysokich wartościach pola elektrycznego jony

przegrupowują się na tyle szybko, że nie zdąży się przegrupować

atmosfera jonowa, zanikają obydwa efekty – relaksacyjny

i elektroforetyczny.

To "prucie" atmosfery jonowej przez jony zostało nazwane "efektem

Wiena", który dla słabych elektrolitów stwierdził ponadto, że silne

pole elektryczne podwyższa wartość stałej dysocjacji słabego

elektrolitu.

Dla sformułowania udziałów ładunków przenoszonych przez kationy

i aniony używa się pojęcia

liczb przenoszenia

t

i

, znanych z kursu

chemii fizycznej.

Podstawiając zależności pomiędzy liczbami przenoszenia

a ruchliwością otrzymuje się

wzór Hendersona

:

E

u u
u u

RT

F

a

a

dyf
























ln

1

2

(25)

18

Potencjał dyfuzyjny jest wielkością wchodzącą w skład potencjałów

składających się na

wartość siły elektromotorycznej

.

Eliminuje się go poprzez stosowanie odpowiednich kluczy

elektrolitycznych, zawierających z reguły nasycony roztwór

obojętnego elektrolitu.

Przedstawiony tu zarys procesów transportu w roztworach

elektrolitów odnosi się do procesów w "nieruchomym" roztworze.

Odrębne zagadnienia wiążą się z procesami transportu,

takimi jak dyfuzja do wirującej elektrody, dyfuzja do narastającej

kropli (w polarografii) itd.

Pozostawmy to do wykładów specjalizacyjnych.

K O N I E C

DZIĘKUJĘ ZA UWAGĘ