Bazy danych, model

Bazy danych, model

relacyjny, normalizacja

relacyjny, normalizacja

relacji

relacji

Paweł Skrzyński,

[e-mail]

http://home.agh.edu.pl/skrzynia/

wste

Zależności funkcyjne

Zależności funkcyjne



Najważniejszy rodzaj więzów z jakim mamy do
czynienia w modelu relacyjnym dotyczy więzów
jednoznaczności nazywanych zależnościami
funkcyjnymi



Wiedza dotycząca tych więzów jest nieodzowna w
przypadku powtórnego definiowania schematu
relacyjnego (np.. W celu wyeliminowania z niego
redundancji)



Definicja. Jeżeli dwie krotki relacji R są zgodne dla
atrybutów A

1

, A

2

, ..., A

n

to muszą być zgodne również

w pewnym innym atrybucie B.



Zapis: A

1

, A

2

, ..., A

n

 B

Uwagi 1

Uwagi 1



Zapis ten czytamy jako A

1

, A

2

, ..., A

n

określają funkcyjnie B”



Jeśli zbiór atrybutów A

1

, A

2

, ..., A

n

określa

funkcyjnie więcej niż jeden atrybut:

A

1

A

2

...A

n

 B

1

...
A

1

A

2

...A

n

 B

m

to zapisujemy to skrótowo jako:

A

1

A

2

...A

n

 B

1

B

2

..B

m

Uwagi 2

Uwagi 2



Zależności funkcyjne dotyczą schematu
bazy a nie określonej instancji. Zatem
patrząc na jakąś instancję nie możemy
stwierdzić, że istnieją jakieś zależności
lub ich nie ma.



Definicja. Zależność trywialna:
zależność funkcyjna A

1

A

2

A

n

B jest

trywialna wtw. gdy B jest równe
któremuś z A.

Wynik zależności

Wynik zależności

funkcyjnej dwóch krotek

funkcyjnej dwóch krotek

A

B

t

u

Jeśli t i u są
zgodne tutaj

To muszą być
też zgodne tutaj

Przykładowa relacja Film

Przykładowa relacja Film

Tytuł Rok Długoś

ć

TypFilm

u

NazwaStu

dia

Nawisk

oGwiaz

dy

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Carrie

Fisher

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Mark

Hamill

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Harrison

Ford

Potężne

Kaczory

1991

104

Kolor

Disney

Emilio

Estevez

Świat

Wayne’a

1992

95

Kolor

Paramount

Dana

Carvey

Świat

Wayne’a

1992

95

Kolor

Paramount

Mike

Meyers

Przykład 1

Przykład 1



Rozważając relację film można

wyodrębnić kilka zależności

funkcyjnych, na przykład:

Tytuł Rok  Długość
Tytuł Rok  TypFilmu
Tytuł Rok  NazwaStudia



Ponieważ lewe strony zależności są

takie same możemy zapisać:

Tytuł Rok  Długość TypFilmu

NazwaStudia

Przykład 1, c.d.

Przykład 1, c.d.



Powyższy zbiór zależności funkcyjnych można

nieformalnie odczytać:

–

jeśli 2 krotki maja takie same wartości składowej

tytuł oraz takie same wartości składowej rok to

muszą mieć również takie same wartości

składowych Długość, TypFilmu oraz NazwaStudia.



Można się spodziewać, że atrybuty tytuł oraz

rok tworzą klucz relacji jednak przy bliższej

obserwacji widać, że te atrybuty nie określają

atrybutu NazwiskoGwiazdy zatem zależność:

Tytuł Rok  NazwiskoGwiazdy jest fałszywa

Klucze relacji

Klucze relacji



Mówimy, że atrybut lub zbiór atrybutów
{A

1

, A

2

, ..., A

n

} tworzy klucz relacji jeżeli:

1.

Wszystkie pozostałe atrybuty relacji są
funkcyjnie zależne od tych atrybutów. Zatem
nie może się zdarzyć, aby 2 różne krotki
relacji R były zgodne dla wszystkich
atrybutów A

1

, A

2

, ..., A

n

.

2.

Nie istnieje taki podzbiór właściwy zbioru
{A

1

, A

2

, ..., A

n

} od którego pozostałe atrybuty

są zależne funkcynie tzn. klucz musi być
minimalny.

Przykład 2

Przykład 2



Atrybuty {Tytuł, Rok, NazwiskoGwiazdy}
tworzą klucz relacji Film



Aby to wykazać należy wykazać, że
wszystkie pozostałe atrybuty są od nich
funkcyjnie zależne oraz że nie istnieje żaden
podzbiór tego zbioru, który również by był
kluczem (zatem określał by funkcyjnie
pozostałe atrybuty)



Zadanie konkursowe: przeprowadzić dowód
(4 minuty czasu)

Przykład 2, dowód

Przykład 2, dowód



Załóżmy, ze 2 krotki są zgodne dla wszystkich 3
wartości atrybutów: Tytuł, Rok,
NazwiskoGwiazdy. Ze względu na to, że są zgodne
dla atrybutów Tytuł i Rok są też zgodne dla
atrybutów Długość, TypFilmu oraz NazwaStudia
(na podstawie zależności funkcyjnych)



Łatwo wykazać, że ani para {Rok,
NazwiskoGwiazdy} (w danym roku gwiazda może
wystąpić w wielu filmach) ani {Tytuł,
NazwiskoGwiazdy} (można nakręcić remake filmu
po paru latach) nie stanowią klucza tej relacji.

Nadklucze

Nadklucze



Definicja. Zbiór atrybutów, który
zawiera klucz nazywa się
nadkluczem.



Jest to skrót od pojęcia nadzbioru
klucza. Zatem każdy klucz jest
nadkluczem ale istnieją nadklucze,
które nie są kluczami gdyż nie
spełniają warunku minimalności.

Reguły dotyczące

Reguły dotyczące

zależności funkcyjnych

zależności funkcyjnych



Załóżmy, że mamy informację na temat zależności

spełnianych przez relację. Często nawet bez

oglądania przykładów krotek można określić pewne

warunki, które muszą być spełnione w relacji.



Jeżeli zależności funkcyjne można określić na różne

sposoby i nie ma to wpływu na instancję relacji to

takie zależności nazywamy równoważnymi.



Ogólniejsza właściwość: zbiór zależności funkcyjnych

S wynika ze zbioru zależności funkcyjnych T. Tzn. dla

dowolnej instancji relacji R spełniającej wszystkie

zależności w T wynika, że spełnia także wszystkie

zależności w S.



Spostrzeżenie: S i T są równoważne wtedy gdy z S

wynika T i z T wynika S.

Reguła przechodniości

Reguła przechodniości



Jeżeli w relacji R z atrybutami A, B, C
zachodzą zależności:

A  B
B  C



To w R zachodzi również zależność
funkcyjna:

A  C



Zadanie konkursowe: wykazać
prawdziwość tej reguły (4 minuty)

Reguła przechodniości,

Reguła przechodniości,

dowód

dowód



Weźmy dowolne dwie krotki z relacji R,

które są zgodne dla atrybutu A.



Zatem mają postać:

–

(a, b

1

, c

1

)

–

(a, b

2

, c

2

)



Ponieważ mamy zależność A  B to b

1

=b

2

(występuje zatem zgodność dla atrybutu B).



Korzystając z drugiej zależności B  C

otrzymujemy: c

1

= c

2

.



Zatem zachodzi A  C.

Zasady podziału i łączenia

Zasady podziału i łączenia



Zasada podziału. Zależność funkcyjną
A

1

A

2

...A

n

 B

1

B

2

..B

m

możemy zastąpić

zbiorem zależności funkcyjnych
A

1

A

2

...A

n

 B

i

gdzie i=1, 2, ..., m.



Zasada łączenia. Zbiór zależności
funkcyjnych A

1

A

2

...A

n

 B

i

gdzie i=1,

2, ..., m możemy zastąpić pojedynczą
zależnością funkcyjną A

1

A

2

...A

n



B

1

B

2

..B

m

.

Zależności trywialne

Zależności trywialne



Zależność trywialna: zależność
funkcyjna A

1

A

2

...A

n

 B jest trywialna wtw.

gdy B jest równe któremuś z A.



Zależność A

1

A

2

...A

n

 B

1

B

2

..B

m

jest:

–

Trywialna, jeśli zbiór B jest podzbiorem zbioru
A

–

Nietrywialna, jeśli co najmniej jeden z
atrybutów B nie znajduje się w A

–

Całkowicie nietrywialna: żaden z atrybutów B
nie znajduje się w A

Reguła zależności

Reguła zależności

trywialnych

trywialnych



Atrybuty, które występują równocześnie
po lewej i po prawej stronie zawsze
można pominąć po prawej stronie. Stąd
wynika reguła zależności trywialnych:



Zależność funkcyjna A

1

A

2

...A

n



B

1

B

2

..B

m

jest równoważna zależności

A

1

A

2

...A

n

 C

1

C

2

..C

k

gdzie C są tymi

elementami z B, które nie są równe A

Reguła zależności

Reguła zależności

trywialnych, c.d.

trywialnych, c.d.

A

B

t

u

Jeśli t i u są
zgodne dla A

To muszą być
też zgodne dla B

C

Zatem na pewno
są zgodne też
dla C

Obliczanie domknięcia zbioru

Obliczanie domknięcia zbioru

atrybutów

atrybutów



Założenia:

–

A={A

1

, A

2

, ..., A

n

}, zbiór atrybutów

–

S, zbiór zależności funkcyjnych



Domknięciem zbioru A nad zbiorem zależności S
nazywamy taki zbiór atrybutów B, że jeżeli pewna
relacja R spełnia wszystkie zależności ze zbioru S, to
spełnia także zależność A

1

A

2

...A

n

B, a zatem

zależność ta wynika z S.



Domknięcie zbioru oznaczamy przez {A

1

, A

2

, ..., A

n

}

+

.



Uwagi: dopuszczamy zależności trywialne zatem {A

1

,

A

2

, ..., A

n

} jest zawsze zawarte w {A

1

, A

2

, ..., A

n

}

+

.

Obliczanie domknięcia zbioru

Obliczanie domknięcia zbioru

atrybutów

atrybutów

Początko

wy zbiór

atrybutów

Wypychanie

Domknięcie

Algorytm

Algorytm

1.

X – nazwa zbiru domknięcia, na początku

X={A

1

, A

2

, ..., A

n

}=A,

2.

Znajdujemy wszystkie zależności funkcyjne

postaci: B

1

B

2

...B

m

C, gdzie B

1

, B

2

,..., B

m

należą do X a C nie należy. Wówczas

dołączamy C do zbioru X.

3.

Powtarzamy krok 2 tak długo jak można

dołożyć jakiś atrybut do X.

4.

Jeśli nie można już dołożyć żadnego

atrybutu do X to koniec. X={A

1

, A

2

, ..., A

n

}

+

Przykład 3

Przykład 3



Relacja R posiada atrybuty: A, B, C, D, E, F.



Zachodzą zależności: ABC, BCAD, DE, CFB.



Szukamy domknięcia zbioru {A, B}:

1.

X={A, B}, bierzemy zależność ABC gdyż

wszystkie lewe atrybuty są w X. Dołączamy C do X.

2.

X={A, B, C}, bierzemy zależność BCAD gdyż

wszystkie lewe atrybuty są w X. Dołączamy D do X
(A już jest w X).

3.

X={A, B, C, D}, bierzemy zależność DE gdyż

wszystkie lewe atrybuty są w X. Dołączamy E do X.

4.

X={A, B, C, D, E}. Nie można dołączy więcej
atrybutów zatem {A, B}

+

={A, B, C, D, E}

Obliczanie domknięcia zbioru,

Obliczanie domknięcia zbioru,

c.d.

c.d.



Jeśli potrafimy obliczyć domknięcie

dowolnego zbioru atrybutów to możemy

sprawdzić czy dana zależność funkcyjna

A

1

A

2

...A

n

B wynika ze zbioru zależności S



Najpierw obliczamy {A

1

, ..., A

n

}

+

dla zbioru

zależności S



Jeśli B należy do {A

1

, ..., A

n

}

+

to A

1

A

2

...A

n

B

wynika z S



Jeśli B nie należy do {A

1

, ..., A

n

}

+

to

A

1

A

2

...A

n

B nie wynika z S

Przykład 4

Przykład 4



Relacja R i zależności funkcyjne
takie jak w przykładzie 3



Zadanie: chcemy ustalić czy z tego
zbioru zależności wynika AB D



Wiemy już że: {A, B}

+

={A, B, C, D,

E}



Ponieważ D należy do {A, B}

+

to AB

D wynika ze zbioru zależności.

Domknięcia i klucze

Domknięcia i klucze



Zauważmy, że zbiór {A

1

, ..., A

n

}

+

zawiera

wszystkie atrybuty relacji R wtedy i tylko

wtedy gdy atrybuty A

1

, ..., A

n

są nadkluczem

w R. Tylko wtedy wszystkie atrybuty są

zależnie funkcyjnie od zbioru A.



Stwierdzenie czy atrybuty A

1

, ..., A

n

stanowią

klucz relacji może polegać na:

–

Stwierdzeniu czy wszystkie atrybuty R należą do

zbioru A

+

–

A następnie czy S

+

otrzymane z dowolnego S,

które tworzymy poprzez usunięcie co najmniej

jednego elementu spośród A

1

, ..., A

n

, nie zawiera

wszystkich atrybutów R

Aksjomaty Armstronga

Aksjomaty Armstronga



Reguły, które umożliwiają z danego zbioru

zależności wyprowadzenie wszystkich tych,

które są od nich zależne funkcyjnie:

1.

Zwrotność. Jeśli {B

1

, ..., B

m

} zawierają się w

{A

1

, ..., An} to A

1

A

2

...A

n

B

1

B

2

..B

m

2.

Rozszerzenie. Jeśli A

1

A

2

...A

n

B

1

B

2

..B

m

to

A

1

A

2

...A

n

C

1

C

2

..C

k

B

1

B

2

..B

m

C

1

C

2

..C

k

dla

dowolnych C

1

, C

2

, ...C

k

3.

Przechodniość. Jeśli A

1

A

2

...A

n

 B

1

B

2

..B

m

oraz

B

1

B

2

...B

m

C

1

C

2

..C

k

to A

1

A

2

...A

n

 C

1

C

2

..C

k

Domknięcie zbioru zależności

Domknięcie zbioru zależności

funkcyjnych

funkcyjnych



Z przedstawionych rozważań wynika, iż

zbiór zależności można rozszerzyć zarówno

o zależności trywialne jak i nietrywialne.



Czasami pożądane jest by odróżniać

zależności zadane w definicji relacji od tych

wyprowadzonych z tego zbioru



Definicja. Każdy zbiór zależności, z którego

można wyprowadzić wszystkie inne

zależności nazywa się bazą tej relacji.



Jeśli żaden z podzbiorów bazy nie umożliwia

wyprowadzenia wszystkich zależności to

baza tak jest bazą minimalną.

Anomalie

Anomalie



Oglądając relację Film łatwo
zauważyć iż występuję redundancja
danych. Źródłem takiej redundancji
często jest próba umieszczenia w
jednej relacji danych
jednowartościowych (np. długość
filmu) wspólnie z danymi
wielowartościowymi (np. zbiór gwiazd
jakie grają w filmie)

Anomalie

Anomalie



Redundancja. Te same dane niepotrzebnie

powtarzają się w kilku krotkach (Długość,

TypFilmu w relacji Film).



Anomalie modyfikacji. Gdy wartość danej zostanie

zmodyfikowana w jednej krotce a w innej nie.



Anomalie usunięć. Gdy dla pewnego atrybutu

zaczyna obowiązywać wartość pusta to jako efekt

uboczny może się zdarzyć utrata części danych.

Jeśli np. ze zbioru gwiazd filmu usuniemy

nazwisko Emilio Estevez to z relacji Film znikną

wszystkie dane dotyczące filmu Potężne Kaczory

Dekompozycja relacji

Dekompozycja relacji



Właściwym sposobem
eliminowania wymienionych
anomalii jest dekompozycja relacji.



Sprowadza się do podziału
atrybutów relacji wejściowej R
pomiędzy nowe relacje (operacja
rzutowania).

Dekompozycja relacji,

Dekompozycja relacji,

algorytm

algorytm



Relację R o schemacie {A

1

, ..., A

n

}

dekomponujemy pomiędzy 2 relacje S i T o

schematach {B

1

, ..., B

m

} oraz {C

1

, ..., C

k

}

według następujących zasad:

1.

{A

1

, ..., A

n

} = {B

1

, ..., B

m

}  {C

1

, ..., C

k

}

2.

Krotki relacji S powstają poprzez rzutowanie

wszystkich krotek relacji R na atrybuty {B

1

,

B

2

, ..., B

m

}

3.

Krotki relacji T powstają poprzez rzutowanie

wszystkich krotek relacji T na atrybuty {C

1

,

C

2

, ..., C

k

}

Dekompozycja, przykład

Dekompozycja, przykład



Dokonamy dekompozycji relacji Film.
Przykładowy wybór atrybutów do
nowych relacji (motywy czemu
właśnie taki podane zostaną później):

–

Do relacji Film1 wchodzą wszystkie
atrybuty oprócz atrybutu
NazwiskoGwiazdy

–

Do relacji Film2 wchodzą atrybuty:
Tytuł, Rok, NazwiskoGwiazdy

Tytuł Rok Długoś

ć

TypFilm

u

NazwaStu

dia

Nawisk

oGwiaz

dy

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Carrie

Fisher

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Mark

Hamill

Gwiezdn

e Wojny

1977

124

Kolor

Fox

Harrison

Ford

Potężne

Kaczory

1991

104

Kolor

Disney

Emilio

Estevez

Świat

Wayne’a

1992

95

Kolor

Paramount

Dana

Carvey

Świat

Wayne’a

1992

95

Kolor

Paramount

Mike

Meyers

Relacja Film

Relacja Film

Relacje Film1 i Film2

Relacje Film1 i Film2

Tytuł

Rok

Długoś

ć

TypFilmu

NazwaStudi

a

Gwiezdne

Wojny

1977

124

Kolor

Fox

Potężne

Kaczory

1991

104

Kolor

Disney

Świat Wayne’a

1992

95

Kolor

Paramount

Tytuł

Rok NazwiskoGwiazdy

Gwiezdne Wojny

1977 Carrie Fischer

Gwiezdne Wojny

1977 Mark Hamill

Gwiezdne Wojny

1977 Harrison Ford

Potężne Kaczory

1991 Emilio Estevez

Świat Wayne’a

1992 Dana Carvey

Świat Wayne’a

1992 Mike Meyers

Postać normalna Boyc’a-

Postać normalna Boyc’a-

Codda

Codda



Zadanie dekompozycji polega na zastąpieniu
relacji równoważnym jej zbiorek relacji,
których struktura wyeliminuje anomalie



Istnieje prosty warunek, którego spełnienie
wyeliminuje omówionej anomalii.



Definicja. Relacja R jest w postaci BCNF
wtw. Dla każdej nietrywialnej zależności
A

1

A

2

A

n

B zbiór {A

1

, A

2

, ..., A

n

} jest

nadkluczem R

Postacie normalne

Postacie normalne



Warunek równoważny do BCNF: lewa
strona każdej nietrywialnej zależności
musi być nadkluczem.



Definicja (alternatywna). Relacja R
jest w postaci BCNF wtw. Dla każdej
nietrywialnej zależności
A

1

A

2

...A

n

B

1

B

2

...B

m

zachodzącej w R

zbiór {A

1

, A

2

, ..., A

n

} jest nadkluczem R

Czy relacja Film jest w

Czy relacja Film jest w

BCNF?

BCNF?



Przypomnijmy iż klucz tej relacji tworzą
atrybuty: Tytuł, Rok, NazwiskoGwiazdy



Każdy zbiór zawierający te trzy atrybuty
jest nadkluczem



W relacji tej mamy zależność:

–

Tytuł Rok  Długość TypFilmu NazwaStudia



Lewa strona tej zależności nie jest
nadkluczem



Zatem relacja Film nie jest w BCNF

Czy relacja Film1 jest w

Czy relacja Film1 jest w

BCNF?

BCNF?



Zachodzi zależność:

–

Tytuł Rok  Długość TypFilmu

NazwaStudia



Jedynym kluczem tej relacji jest para

{Tytuł, Rok}



Zatem jedyna nietrywialna zależność

funkcyjna musi mieć po lewej stronie

te atrybuty



...i ma 

Dekompozycja do postaci

Dekompozycja do postaci

BCNF

BCNF



Spostrzeżenie: każda relacja binarna (dwu

atrybutowa) jest w BCNF. (zadanie

konkursowe: udowodnić to twierdzenie, czas

10 minut)



Jeśli proces dekompozycji będziemy powtarzać

dostatecznie długo to każdą relację zapiszemy

w końcu w postaci kolekcji podzbiorów

atrybutów, które spełnia następujące warunki:

–

Podzbiory te będą relacjami w postaci BCNF

–

Dane z pierwotnej relacji są wiernie

reprezentowane w relacjach powstałych w wyniku

dekompozycji

Strategia dekompozycji

Strategia dekompozycji



Znajdź nietrywialną zależność
A

1

A

2

...A

n

B

1

B

2

...B

m

która narusza BCNF

(czyli A

1

, A

2

, ...A

n

nie są nadkluczem)



Podziel atrybuty na 2 podzbiory:

–

Do jednego należą wszystkie atrybuty, które
pojawiają się w tej zależności

–

A do drugiego atrybuty A (z lewej strony
zależności) oraz wszystkie pozostałe atrybuty,
które nie pojawiają się po prawej stronie tej
zależności

Dekompozycja schematu relacji na

Dekompozycja schematu relacji na

podstawie naruszenia warunku BCNF

podstawie naruszenia warunku BCNF

A B

Inne

Dekompozycja do BCNF -

Dekompozycja do BCNF -

przykład 1

przykład 1



Rozważmy nasza relację Film. Wcześniej

wykazano, że zależność: Tytuł Rok 

Długość TypFilmu NazwaStudia narusza

warunek BCNF



Zatem stosując naszą strategię dokonamy

podziału atrybutów na następujące zbiory:

–

{Tytuł, Rok, Długość, TypFilmu, NazwaStudia}

–

{Tytuł, Rok, NazwiskoGwiazdy}



Zatem są to schematy Film1 i Film2, o

których już wiemy, że są w BCNF

Dekompozycja do BCNF –

Dekompozycja do BCNF –

przykład 2

przykład 2

Tytuł

Rok Długość TypFilmu NazwaStudia AdresStudia

Gwiezdne wojny

1977

124

Kolor

Fox

Hollywood

Potężne kaczory

1991

104

Kolor

Disney

Buena Vista

Świat Wayn’a

1992

95

Kolor

Paramount

Hollywood

Rodzina Adamsów 1991

102

Kolor

Paramount

Hollywood

Spostrzeżenie:
istnieje redundancja -
adres studia
Paramount występuje
dwukrotnie

•W relacji występują dwie zależności:

•Tytuł Rok  NazwaStudia

•NazwaStudia  AdresStudia

•Na podstawie reguły przechodności

•Tytuł Rok  AdresStudia

•Istnieje jeszcze inna oczywista zależność:

•Tytuł Rok  Długość TypFilmu

•Zależność (stosowana w regule przechodności):

•NazwaStudia  AdresStudia

Nie jest zależnością trywialną, jej lewa strona nie
jest nadkluczem

•Wniosek: relacja nie spełnia warunku BCNF

Przykład 2, c.d.

Przykład 2, c.d.



Atrybuty z powyższej zależności wchodzą do

schematu pierwszej relacji powstałej w wyniku

dekompozycji:

–

{NazwaStudia, AdresStudia}



Do drugiego schematu będą należeć wszystkie

atrybuty relacji poza AdresStudia (występuje

po prawej stronie zależności na podstawie,

której dokonujemy dekompozycji), zatem

schemat drugiej relacji wygląda następująco:

–

{Tytuł, Rok, Długość, TypFilmu, NazwaStudia}



Otrzymujemy zatem dwie nowe relacje

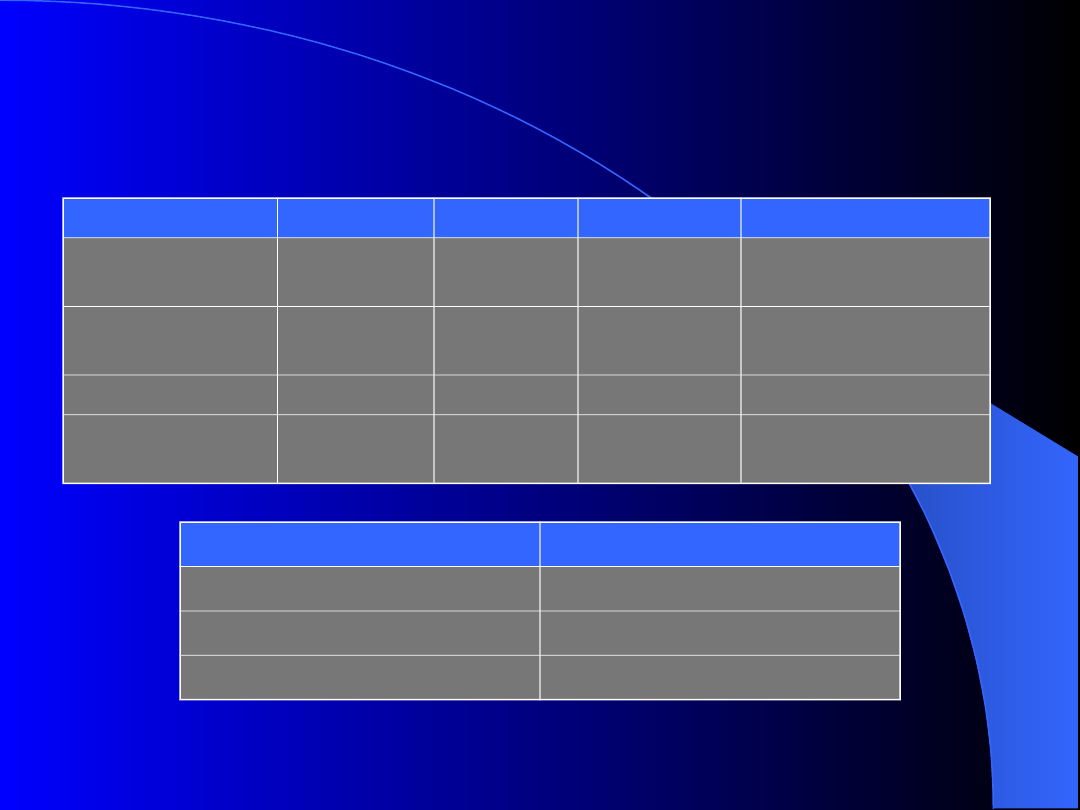
Przykład 2, c.d.

Przykład 2, c.d.

Tytuł

Rok

Długość

TypFilmu

NazwaStudia

Gwiezdne

wojny

1977

124

Kolor

Fox

Potężne

kaczory

1991

104

Kolor

Disney

Świat Wayn’a

1992

95

Kolor

Paramount

Rodzina

Adamsów

1991

102

Kolor

Paramount

NazwaStudia

AdresStudia

Fox

Hollywood

Disney

Buena Vista

Paramount

Hollywood

Projektowanie zależności

Projektowanie zależności

funkcyjnych

funkcyjnych



Po wykonaniu dekompozycji trzeba sprawdzić czy otrzymane nowe
schematy spełniają warunek BCNF.



Problem: jak stwierdzić jakie zależności zachodzą w nowym
schemacie?

Rozwiązanie:



Załóżmy, że w wyniku dekompozycji relacji R powstaje relacja S
oraz jakaś inna relacja T.



Oznaczenie: zbiór zależności prawdziwych w R oznaczamy przez F.



Rozważmy podzbiory X zboru atrybutów S. Dla każdego z nich
obliczamy X

+

(nad zbiorem F). Wówczas jeśli jakiś atrybut B spełnia

warunki:

–

B należy do S

–

B należy do X

+

–

B nie należy do X

To zależność funkcyjna XB jest spełniona w relacji S.

Przykład

Przykład

Sytuacja:



Relacja R: R(A, B, C, D)



Zależności w R: AB, BC



Schemat S: S(A, C) powstał w wyniku

dekompozycji



Obliczamy domknięcia wszystkich podzbiorów:

–

{A}

+

={A, B, C}, atrybut B nie należy do S zatem w

S nie zachodzi AB, zachodzi natomiast AC

–

{C}

+

={C}, nie wprowadza nic nowego

–

{A, C}

+

={A, B, C}={A}

+

, również nie wprowadza

nic nowego



Zatem jedyną zależnością spełnioną w S jest

AC

Przykład 2

Przykład 2

Sytuacja:



Relacja R: R(A, B, C, D, E)



Zależności w R: AD, BE, DEC



Schemat S: S(A, B, C) powstał w wyniku
dekompozycji



Obliczamy domknięcia wszystkich podzbiorów:

–

{A}

+

={A, D}, w schemacie nie występuje atrybut D

–

{B}

+

={B, E}, również nie wprowadza żadnej zależności

–

{C}

+

={C}, jak wyżej

–

{A, B}

+

={A, B, C, D, E}- zatem w S zachodzi ABC

–

Żadna inna para atrybutów nie dostarczy nowych zależności

–

Podobnie zbiór wszystkich trzech atrybutów



Zatem jedyną zależnością spełnioną w S jest ABC

Uproszczenie poszukiwania

Uproszczenie poszukiwania

zależności

zależności



Nie trzeba rozważać domknięcia zbioru
wszystkich atrybutów S



Nie trzeba rozważać zbiorów atrybutów,
do których nie należy żadna lewa strona
jakiejkolwiek zależności



Nie trzeba rozważać zbirów, do których
należy jakikolwiek atrybut, który nie
występuje po lewej stronie jakiejkolwiek
zależności

Odzyskiwanie danych po

Odzyskiwanie danych po

dekompozycji

dekompozycji



Weźmy relację R(A, B, C), w której zachodzi zależność
BC naruszająca BCNF (np.. Jest to jedyna zależność

nietrywialna, wtedy jedynym kluczem jest para A, B)



Dekompozycja dzieli R na schematy S(A, B) i T(B, C)



Niech t będzie pewną krotką z R: t=(a, b, c) (a, b, c,
składowe t dla atrybutów A, B, C)



W wyniku rzutowania t na schemat

–

S otrzymujemy krotkę (a, b),

–

T otrzymujemy krotkę (b, c)



Jeśli wartości składowej B w schematach S i T są równe
to możemy wykonać złączenie odpowiednich krotek ((a,
b) zawsze można połączyć z (b, c) i otrzymać (a, b, c)).

Odzyskiwanie danych po

Odzyskiwanie danych po

dekompozycji 2

dekompozycji 2



Wykonalność odtworzenia krotek sprzed dekompozycji
nie świadczy jeszcze o wiernym reprezentowaniu relacji
R w powstałych schematach S i T



Weźmy krotki t=(a, b, c) i v=(d, b, e), rzutując u na S a
v na T otrzymujemy:

–

u=(a, b)

–

w=(b, e)



Dokonując teraz złączenia otrzymamy krotkę x=(a, b, e)



Pytanie: czy x jest krotką fałszywą? (a, b, e) nie ma w
schemacie R



Przypomnijmy sobie jednak o zależności

BC zachodzącej

w R. Czyli jeśli dwie krotki są zgodne dla atrybutu b to są zgodne
również dla atrybutu C. Krotki t i v są zgodne dla atrybutu b zatem
muszą być zgodne dla atrybutu C czyli c=e. Zatem krotka (a, b, e)
jest w zasadzie krotką (a, b, c).

Złączenie dwóch krotek ze zrzutowanych

Złączenie dwóch krotek ze zrzutowanych

relacji

relacji

t

x

u

w

v

rzutowanie

rzutowanie

złączenie

złączenie

A

C

B

3 postać normalna

3 postać normalna



Czasami okazuje się, że schemat relacji nie

spełnia BCNF ale dekompozycji się nie

przeprowadza



Nieznacznie tylko osłabiając wymagania

BCNF otrzymujemy 3 postać normalną:



Relacja R jest w 3NF wtw. jeśli A

1

A

2

A

n

B jest

zależnością nietrywialną to albo {A

1

, A

2

, ...,

A

n

} jest nadkluczem albo B jest elementem

pewnego klucza.



Jak widać różnica polega na dodaniu: „... albo

B jest elementem pewnego klucza.”

Przykład

Przykład



Mamy relację Zamówienia o następujących

atrybutach: tytuł (tytuł filmu), kino (nazwa kina,

w którym film jest wyświetlany), miasto (siedziba

kina)



Zależności funkcyjne:

–

kinomiasto

–

tytuł miasto  kino



Uwagi: zatem przyjmujemy, że w dwóch różnych

miastach nie mogą istnieć kina o tej samej

nazwie oraz ten sam film nie może być

wyświetlany w dwóch kinach w tym samym

mieście

Przykład, c.d.

Przykład, c.d.



Ustalenie klucza:

–

Żaden pojedynczy atrybut nie jest kluczem (nie

określa funkcyjnie pozostałych atrybutów)

–

{tytuł, miasto} jest kluczem

–

{kino, tytuł} też jest kluczem (stosując zasadę

rozszerzenia dla pierwszej zależności)

–

W relacji nie ma więcej kluczy,



Zależność kinomiasto narusza BCNF gdyż

kino nie jest nadkluczem



Ale miasto jest elementem pewnego klucza

zatem relacja jest w 3NF

Przykład, c.d.

Przykład, c.d.



Stosując dekompozycję musielibyśmy
utworzyć dwa schematy: {kino,
miasto} oraz {kino, tytuł}



W schemacie po dekompozycji
spełniona będzie relacja kino
miasto, ale po złączeniu nie będzie

spełniona zależność tytuł miasto 

kino

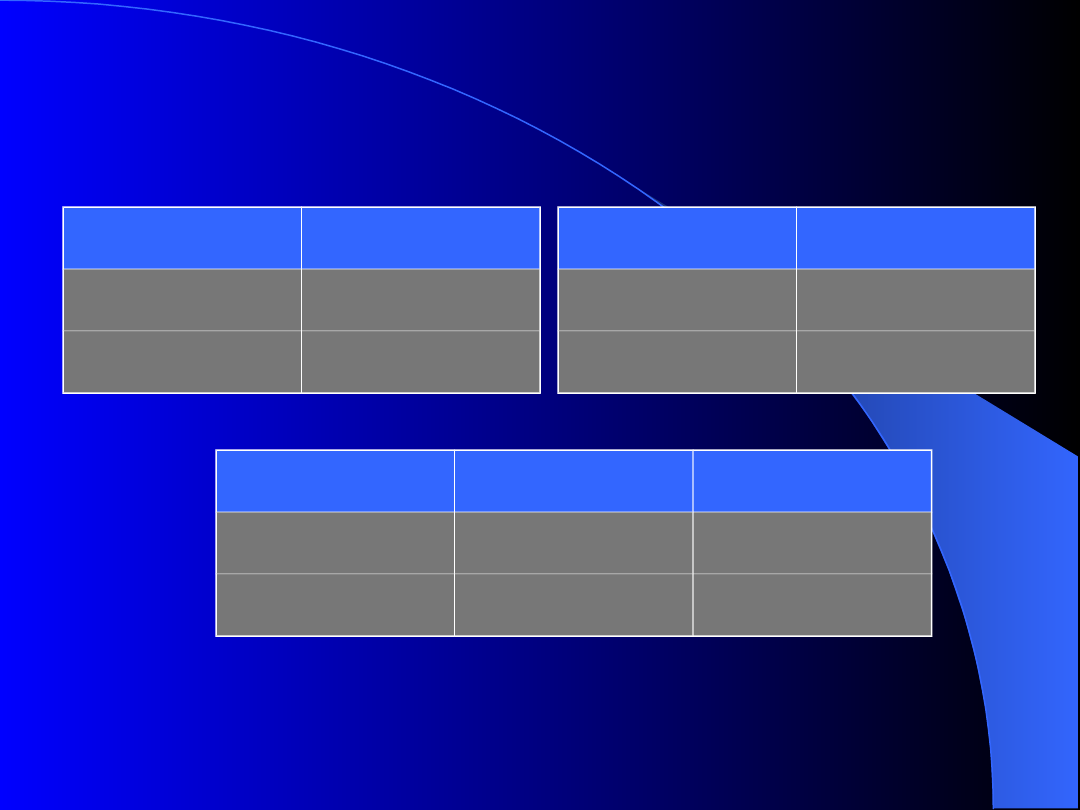
Przykład, c.d.

Przykład, c.d.

Kino

Miasto

Multikino

Kraków

Kijów

Kraków

Kino

tytuł

Multikino

Shrek

Kijów

Shrek

Kino

Miasto

Tytuł

Multikino

Kraków

Shrek

Kijów

Kraków

Shrek

Uwaga: po złączeniu nie jest spełniona zależność

tytuł miasto  kino

2 postać normalna i 1 postać

2 postać normalna i 1 postać

normalna

normalna



1NF  każda składowa w każdej krotce ma

wartość atomową (wszystkie współczesne

SZBD uniemożliwiają tworzenie baz danych

nie będących w 1NF)



2NF  mniej restrykcyjna niż 3NF, zabrania się

wystąpienia takich zależności nietrywialnych,

w których lewa strona jest poprawnym

podzbiorem klucza. Dopuszczalne są w niej

domknięcia przechodnie relacji.



2NF (inaczej)  każdy atrybut nie wchodzący w

skład klucza jest funkcyjnie zależny od

wszystkich kluczy potencjalnych relacji

2 postać normalna,

2 postać normalna,

formalnie

formalnie



Formalnie. Przypomnienie: atrybut główny –
atrybut wchodzący w skład pewnego klucza.



Definicja. Pełna zależność funkcyjna –
zależność funkcyjna A

1

A

2

A

n

B, w której

usunięcie któregokolwiek atrybutu A

i

spowoduje, że zależność nie będzie spełniona



Relacja R jest w drugiej postaci normalnej
wtedy gdy każdy atrybut niekluczowy jest
wpełni funkcyjnie zależny od klucza tej relacji

Przykład

Przykład



Mamy dany schemat relacji R={S,T,D,K} (z

interpretacją odpowiednio Sklep, Towar, Dział,

Kierownik)



Zależności:

–

STD (każdy towar w każdym sklepie sprzedaje się w jednym

dziale)

–

DK (dział ma jednego kierownika)



Jedynym kluczem jest ST



Żaden podzbiór właściwy klucza nie wyznacza

funkcyjnie ani D ani K, STK jest zależnością

przechodnią, zależność STD narusza natomiast 3NF

(D nie jest elementem klucza)



Relacja jest w 2NF

Zależności

Zależności

wielowartościowe

wielowartościowe



Występują gdy 2 lub więcej
atrybutów jest od siebie
niezależnych



Często pomimo, iż schemat spełnia
BCNF występuje w nim
redundancja, której źródlem jest
właśnie niezależność dwóch lub
więcej atrybutów

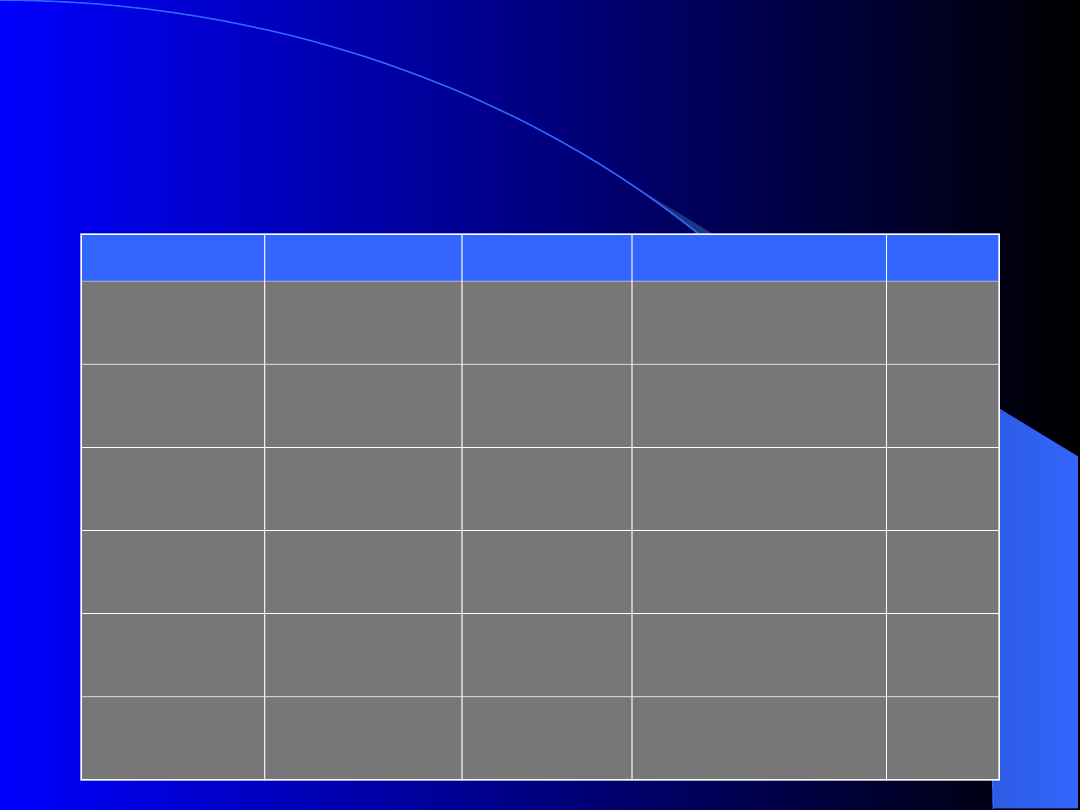
Przykład

Przykład

Nazwisko

Ulica

Miasto

Tytuł

Rok

C. Fisher

123 Maple

St.

Hollywoo

d

Gwiezdne

wojny

1977

C. Fisher

5 Locus

Ln.

Malibu

Gwiezdne

wojny

1977

C. Fisher

123 Maple

St.

Hollywoo

d

Imperium

kontratakuje

1980

C. Fisher

5 Locus

Ln.

Malibu

Imperium

kontratakuje

1980

C. Fisher

123 Maple

St.

Hollywoo

d

Powrót Jedi

1983

C. Fisher

5 Locus

Ln.

Malibu

Powrót Jedi

1983

Przykład, c.d.

Przykład, c.d.



Nie ma powodu by wiązać adres z jednym

filmem a innym nie



Jedyny sposób na to by wyrazić iż adresy filmy są

niezależnymi od siebie właściwościami gwiazdy

polega na tym, że każdy adres w połączeniu z

każdym filmem tworzą osobne krotki



Jak widać jest to źródłem redundancji (każdy

adres powtarza się 3 razy, każdy film 2 razy)



Schemat jednak nie narusza BCNF (żaden z 5

atrybutów nie zależy funkcyjnie od pozostałych

4)

Zależności wielowartościowe -

Zależności wielowartościowe -

definicja

definicja



Zależność wielowartościowa zachodzi dla pewnej relacji R
wówczas, gdy po ustaleniu wartości pewnego podzbioru atrybutów,
wartości pewnych innych atrybutów są niezależne od wszystkich
innych wartości wszystkich pozostałych atrybutów



Zależność wielowartościowa A

1

A

2

...A

n

→→ B

1

B

2

...B

m

zachodzi w

relacji R wówczas, gdy wybierając z R te krotki, które mają
ustalone wartości atrybutów typu A, zbiór wartości typu B nie
zależy od żadnych wartości tych atrybutów R, których nie ma ani w
A ani w B



Dla każdej pary krotek t i u relacji R, które mają takie same
wartości atrybutów typu A, można znaleźć w R taką krotkę v, której
składowe mają wartości równe:

–

Wartościom atrybutów w A w krotkach t oraz u

–

Wartościom atrybutów B krotki t

–

Wartościom tych składowych krotki u, które nie są ani typu A, ani typu
B



W poprzednim przykładzie opisano zależność:

–

nazwisko→→ ulica miasto

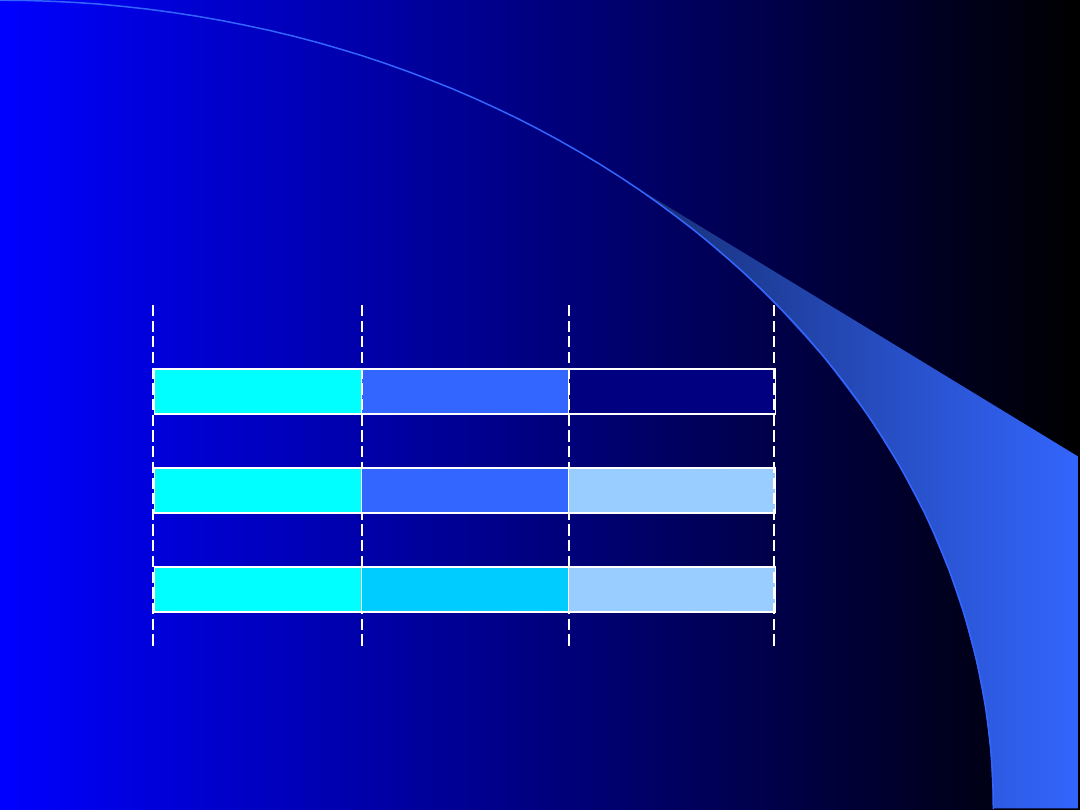
Zależności

Zależności

wielowartościowe -

wielowartościowe -

rysunek

rysunek

t

u

v

A

B

Inne

Przykład, c.d.

Przykład, c.d.



Wróćmy do zależności wielowartościowej:

–

nazwisko→→ ulica miasto



Weźmy pierwszą i czwartą krotkę naszej relacji:

–

t=(C.Fisher, 123 Maple St., Hollywood, Gwiezdne Wojny, 1977)

–

u=(C.Fisher, 5 Locus Ln., Malibu, Imperium kontratakuje,

1980)



Na podstawie definicji w R musi istnieć krotka,

która dla nazwiska ma wartość C. Fisher, dla

ulicy i mieście ma wartości 123 Maple St. i

Hollywood, a pozostałe atrybuty (czyli tytuł i

rok) mają wartości takie jak w drugiej krotce

(Imperium kontratakuje, 1980)



Taka krotka występuje w R (3 z kolei)

Wnioskowanie z zależności

Wnioskowanie z zależności

wielowartościowych

wielowartościowych



Stosuje się reguły, które są podobne do reguł poznanych wcześniej



Reguła zależności trywialnych: jeśli w R zachodzi zależność

A

1

A

2

...A

n

→→B

1

B

2

...B

m

to wówczas, gdy C

1

C

2

...C

k

są wszystkimi

atrybutami B oraz część z nich jest typu A to zachodzi również:

A

1

A

2

...A

n

→→C

1

C

2

...C

k



Ponadto zachodzi również związek odwrotny: A

1

A

2

...A

n

→→D

1

D

2

...D

r

gdzie atrybuty typu D sa tymi atrybutami typu B, które nie są typu

A



Reguła przechodniości: Jeśli w R zachodzą zależności

A

1

A

2

...A

n

→→B

1

B

2

...B

m

oraz B

1

B

2

...B

m

→→C

1

C

2

...C

k

to zachodzi

również A

1

A

2

...A

n

→→ C

1

C

2

...C

k



Reguła dopełnienia: Jeśli w R zachodzi A

1

A

2

...A

n

→→B

1

B

2

...B

m

to

zachodzi również A

1

A

2

...A

n

→→ C

1

C

2

...C

k

gdzie atrybuty typu C są

wszystkimi atrybutami, które nie są ani typu A ani B. (Reguła ta

nie zachodzi dla zależności funkcyjnych)



Nie zachodzą natomiast reguły podziału i łączenia

Czwarta postać normalna

Czwarta postać normalna



Definicja. Zależność wielowartościową
w relacji R:

A

1

A

2

...A

n

→→B

1

B

2

...B

m

nazywamy

nietrywialną jeśli:

–

Żaden atrybut typu B nie jest typu A

–

Każdy atrybut R jest albo typu A, albo typu B



Relacja R jest w czwartej postaci
normalnej (4NF) wtw.
A

1

A

2

...A

n

→→B

1

B

2

...B

m

jest nietrywialną

zależnością wielowartościową; {A

1

,

A

2

,

..., A

n

} jest nadkluczem w R

Dekompozycja do 4NF

Dekompozycja do 4NF



Algorytm stanowi pełną analogię do

algorytmu dekompozycji do BCNF.



Znajdujemy zależność, która nie spełnia

4NF, dla ustalenia uwagi niech to będzie:

A

1

A

2

...A

n

→→B

1

B

2

...B

m

({A

1

, A

2

, ..., A

n

nie jest

nadkluczem)



Dzielimy schemat R na 2 schematy:

–

Pierwszy zawiera wszystkie atrybuty typu A i B

–

Drugi zawiera wszystkie atrybuty A i wszystkie

te, które nie są ani typu A ani typu B

Przykład

Przykład



Wróćmy do przykładu i zależności naruszającej

4NF:

–

nazwisko→→ ulica miasto (nazwisko nie stanowi nadklucza co

wcześniej wykazaliśmy)



Zastępujemy zatem schemat R przez 2 schematy:

–

{nazwisko, ulica, miasto}

–

{nazwisko, tytuł, rok}



W żadnym z tych schematów nie ma nietrywialnych

zależności wielowartościowych (ani funkcyjnych)

zatem spełniają one 4NF



Spostrzeżenie: w pierwszym schemacie zależność

nazwisko→→ ulica miasto jest trywialna ponieważ obejmuje

wszystkie atrybuty, podobnie w drugim schemacie

zależność nazwisko→→ tytuł rok (wyprowadzona w R z

pierwszej zależności na podstawie reguły dopełnienia) jest

trywialna

Rzutowanie zależności

Rzutowanie zależności

funkcyjnych

funkcyjnych



Przed zastosowaniem dekompozycji do

4NF należy określić wszystkie

zależności wielowartościowe spełnione

w relacjach wynikowych



Niestety nie ma prostego algorytmu

takiego jak domknięcie zbioru w

przypadku zależności funkcyjnych



Na szczęście można otrzymać właściwą

zależność dla jednego z wynikowych

schematów dekompozycji poprzez

zastosowanie reguły przechodniości,

dopełnienia lub przecięcia

Zależności pomiędzy

Zależności pomiędzy

postaciami normalnymi

postaciami normalnymi



Z postaci 4NF wynika postać

BCNF a z tej z kolei postać 3NF.



Zatem zbiór instancji schematu

relacyjnego spełniających

poszczególne warunki postaci

normalnych tworzy hierarchię



Przedstawione jest to na

poniższym rysunku

Rysunek – zależności pomiędzy

Rysunek – zależności pomiędzy

postaciami normalnymi

postaciami normalnymi

2NF

3NF

BCNF

4NF

Właściwości postaci

Właściwości postaci

normalnych

normalnych

Właściwość

2NF

3NF

BCN

F

4NF

Eliminowanie
redundancji przez

zależności funkcyjne

Nie

Większo

ść

Tak

Tak

Eliminowanie
redundancji przez

zależności
wielowartościowe

Nie

Nie

Nie

Tak

Zachowanie
zależności
funkcyjnych

Tak

Tak

Możliw

e

Możliw

e

Zachowanie

zależności
wielowartościowych

Możliw

e

Możliwe Możliw

e

Możliw

e

Piąta postać normalna

Piąta postać normalna



Definicja. W schemacie R występuje połączeniowa
zależność funkcyjna (ozn. R*[R

1

, ..., R

n

]) wtw. gdy możliwa

jest dekompozycja relacji R na relacje R

1

, ..., R

n

taka, że

relację R można zrekonstruować przez wykonanie
sekwencji operacji połączenia relacji R

1

, ..., R

n



Dana relacja R jest w piątej postaci normalnej wtw. gdy
jest w czwartej postaci normalnej i w przypadku
występowania w niej połączeniowej zależności
funkcjonalnej *R[R

1

, ..., R

m

] zależność ta wynika z

zależności atrybutów od klucza.



Wynika z tego, że w celu doprowadzenia pewnej relacji do
piątej postaci normalnej konieczne jest podzielenie jej na
takie relacje, które spełniać będą podany wyżej warunek.