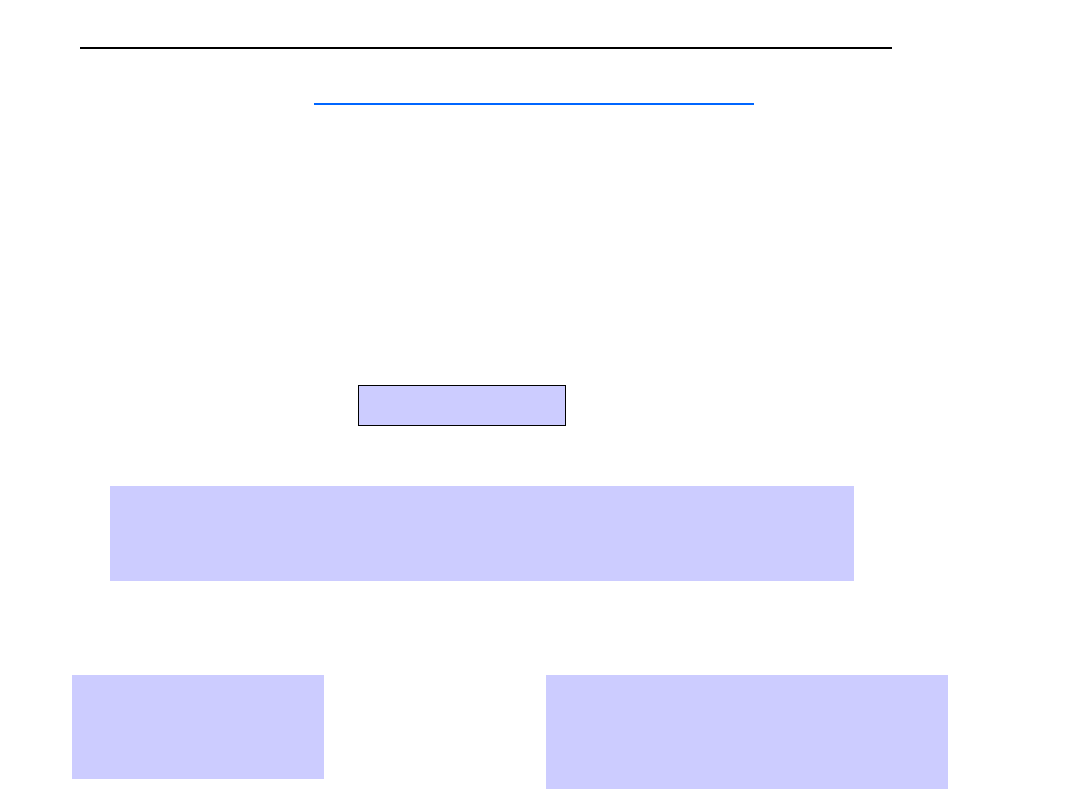
ZMIENNE LOSOWE CIĄGŁE
Są to zmienne, które mogą przyjmować wartości z nieprzeliczalnego
zbioru wartości (przy założeniu, że będą mierzone z wystarczającą
dokładnością).
Zmienna ciągła jest opisywana dwoma funkcjami:
• funkcją gęstości f(X)
• dystrybuantą F(X)
P(X=a) = O
a
dx
x
f
a
F
)
(
)
(
dx
x
xf
X
E
)
(
)
(
dx
x
f
X
E
x
X
D
)
(
)
(
2
2
Twierdzenie:
Definicje:
b
a
a
b
dx
x
f
dx
x
f
dx
x
f
a
F
b
F
b
X
a
P
)
(
)
(
)
(
)
(
)
(
)
(
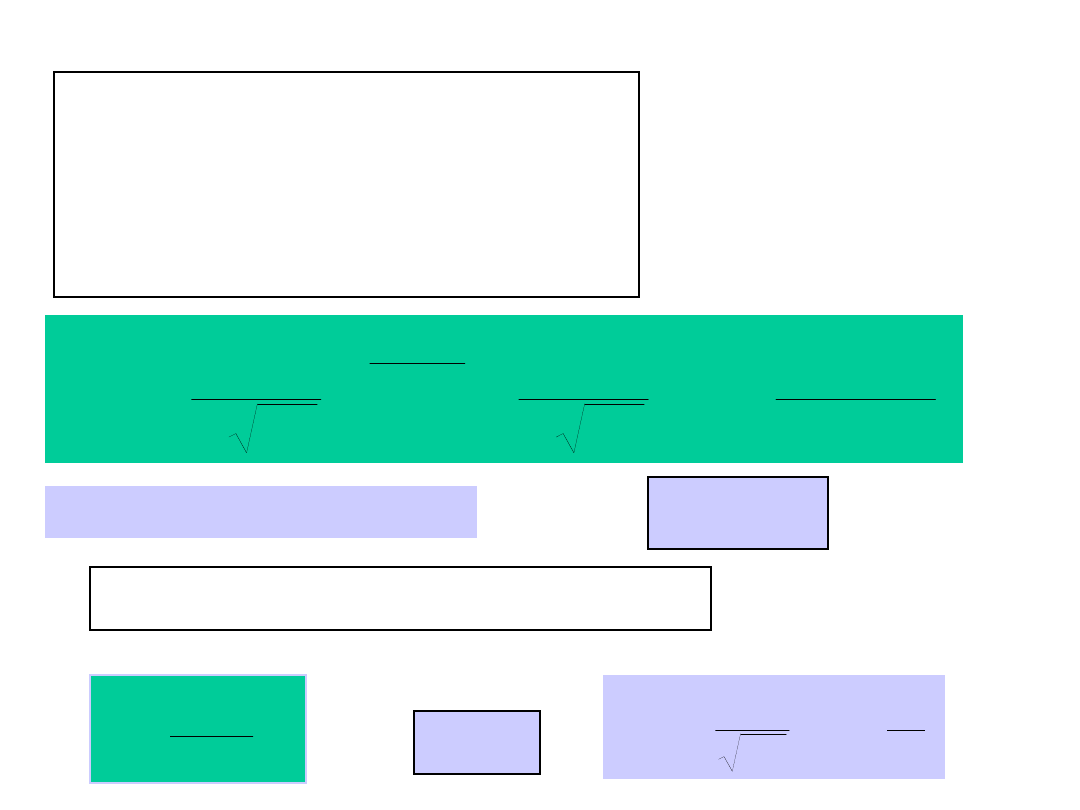
Podstawowe rozkłady ciągłe
Rozkład gamma Rozkład beta
Rozkład t-Studenta
Rozkład χ
2
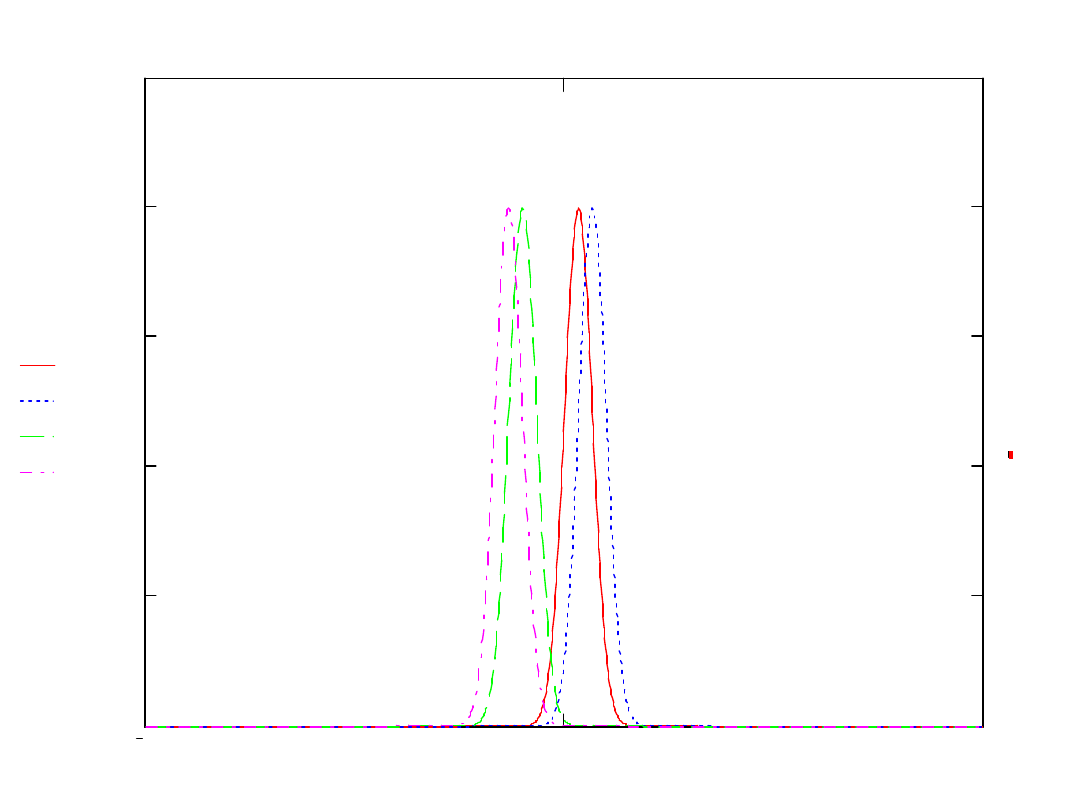
Rozkład normalny ( rozkład Gaussa)
)
2
)
(
exp(
2
1
2
1
)
(
2
2
2
)
(
2
2
m
x
e
x
f
m
x
)
2
exp(
2
1
)
(
2
x
x
f
2
2
X
D
m
EX
N(m,
)
N(0,1
)
m
X
U
Unormowany rozkład Gaussa

Centralne twierdzenie
graniczne
30
0
30
0
0.1
0.2
0.3
0.4
0.5
0
dnormx 1
1
(
)
dnormx 2
1
(
)
dnormx 3
1
(
)
dnormx 4
1
(
)
30
30
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.2
0
pnormx 0
1
(
)
pnormx 2
1
(
)
pnormx 3
1
(
)
pnormx 4
1
(
)
10
10
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
pnormx 2
1
(
)
pnormx 0
3
(
)
pnormx 2
0.4
(
)
pnormx 3
0.8
(
)
x x
x
x
10
8
6
4
2
0
2
4
6
8
10
0
0.2
0.4
0.6
0.8
1
1
0
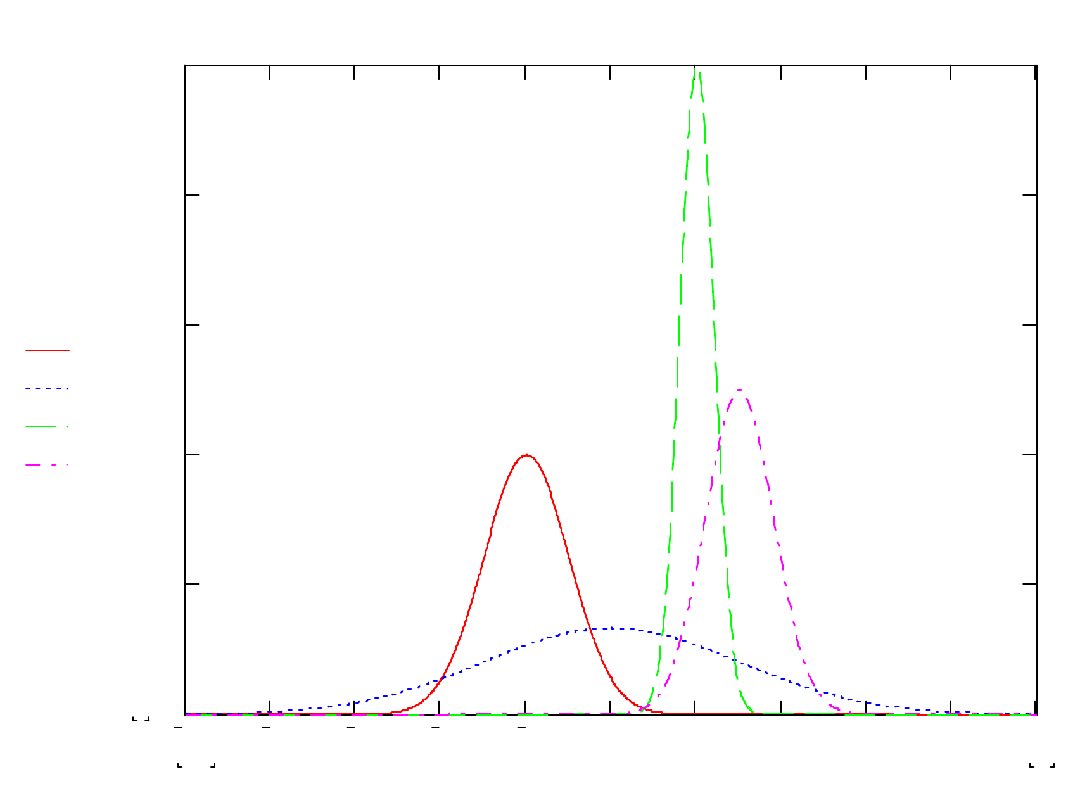
dnormx 2
1
(
)
dnormx 0
3
(
)
dnormx 2
0.4
(
)
dnormx 3
0.8
(
)
10
10
x x
x
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
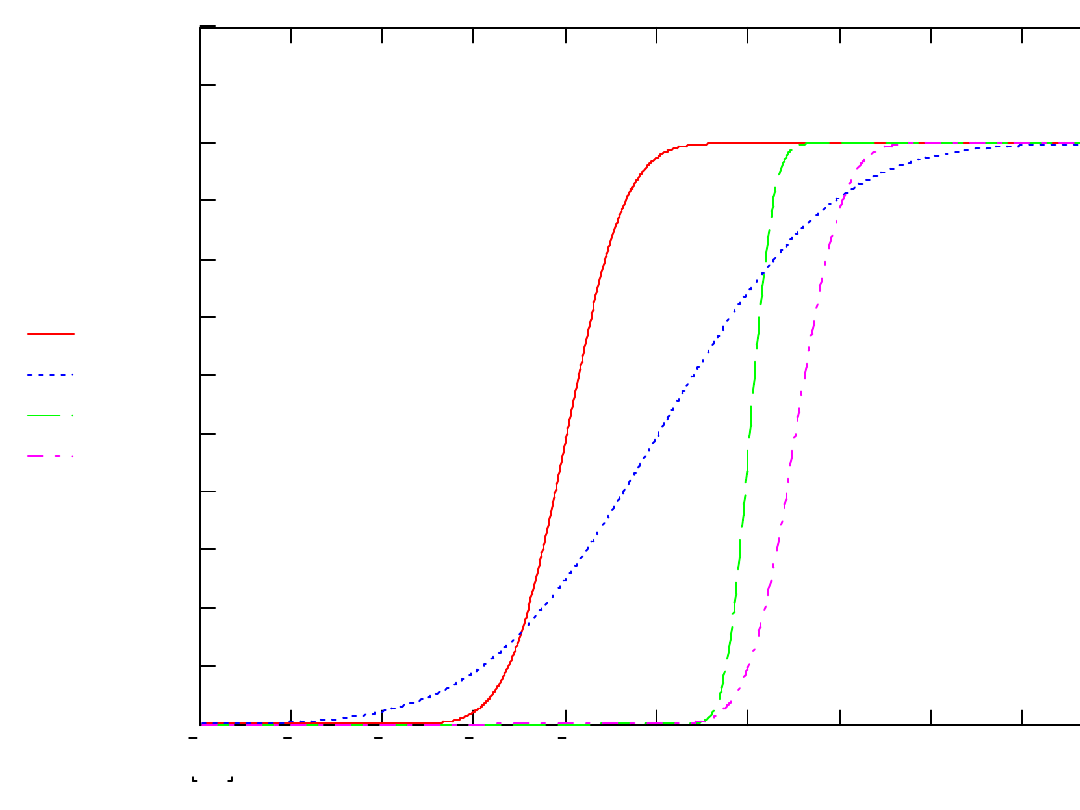
pnormx 0
1
(
)
pnormx 2
1
(
)
pnormx 3
1
(
)
pnormx 4
1
(
)
x
10
8
6
4
2
0
2
4
6
8
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.2
0
pnormx 2
1
(
)
pnormx 0
3
(
)
pnormx 2
0.4
(
)
pnormx 3
0.8
(
)
10
10
x x
x
x
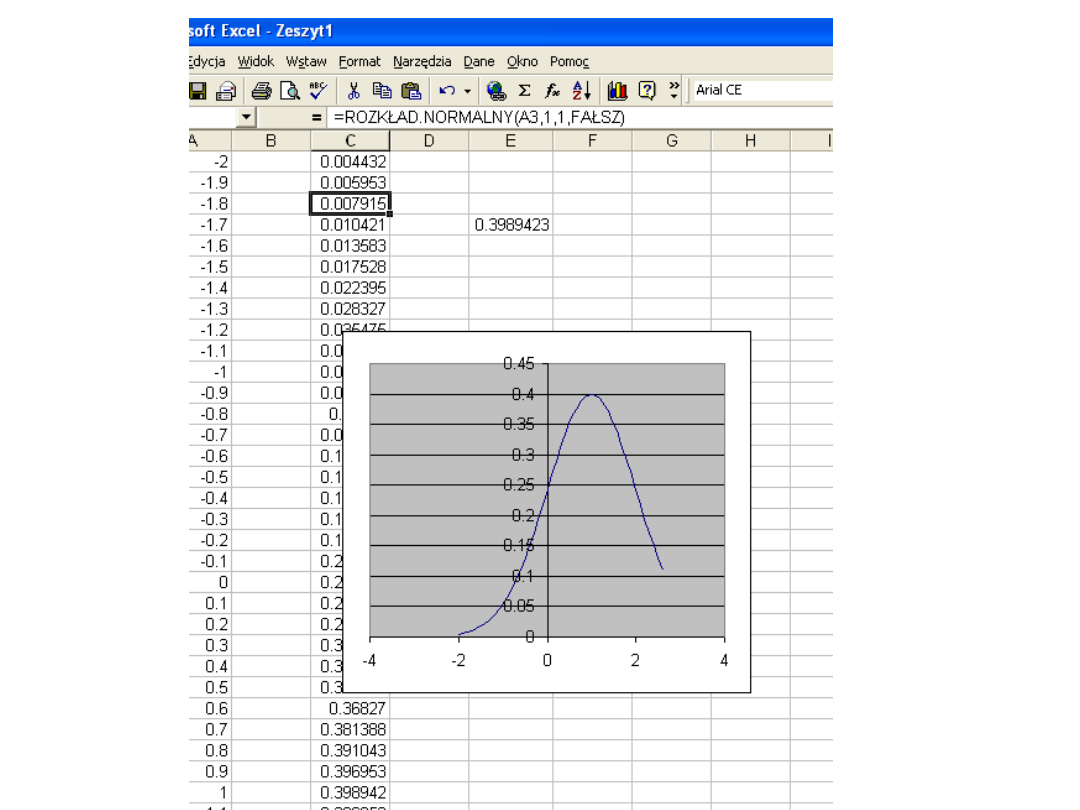

ROZKŁAD.NORMALNY
Daje w wyniku normalny rozkład łączny dla danej średniej i
normalnego odchylenia. Funkcja ta ma bardzo szeroki zakres
zastosowań w statystyce, łącznie z badaniem hipotez.
Składnia
X jest to wartość, dla której chcemy mieć rozkład.
Średnia jest to średnia arytmetyczna rozkładu.
Odchylenie_std jest to standardowe odchylenie rozkładu.
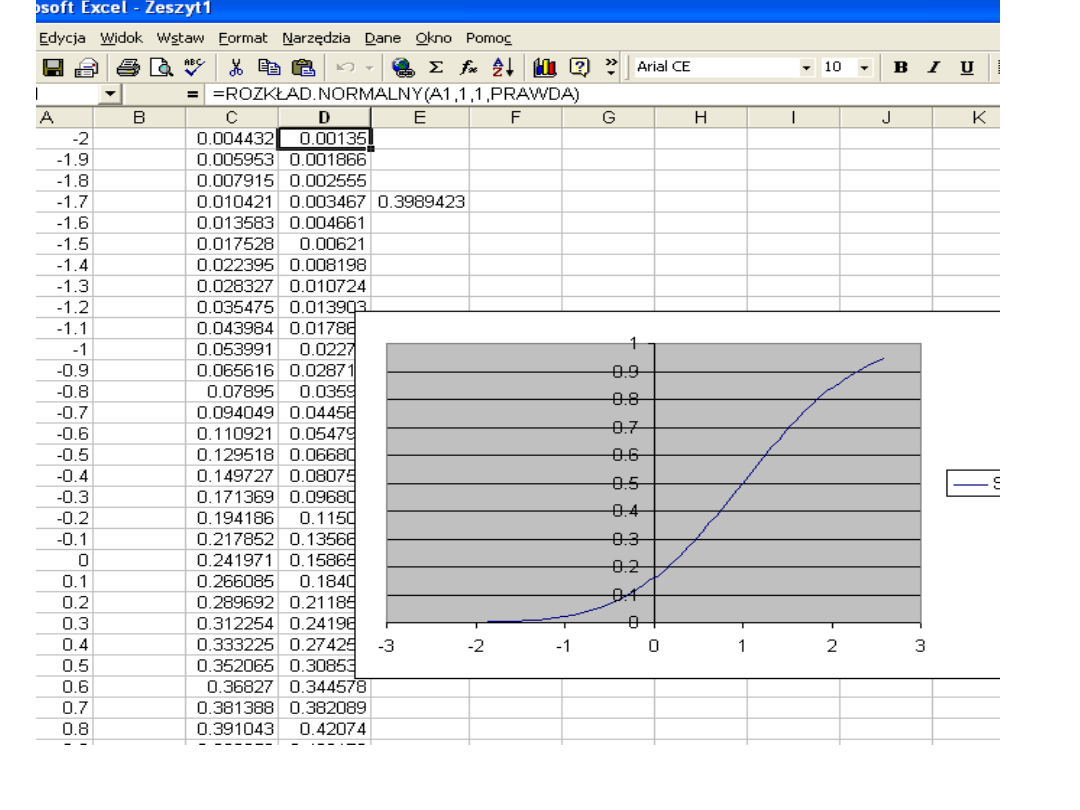
Skumulowany jest to wartość logiczna, która określa rodzaj funkcji.
Jeżeli skumulowany ma wartość PRAWDA, wówczas funkcja
ROZKŁAD.NORMALNY daje w wyniku łączną funkcję rozkładu, a jeśli
FAŁSZ, wówczas funkcja ta daje w wyniku funkcję gęstości
prawdopodobieństwa.
ROZKŁAD.NORMALNY(x;średnia;odchylenie_std;skumulowany)

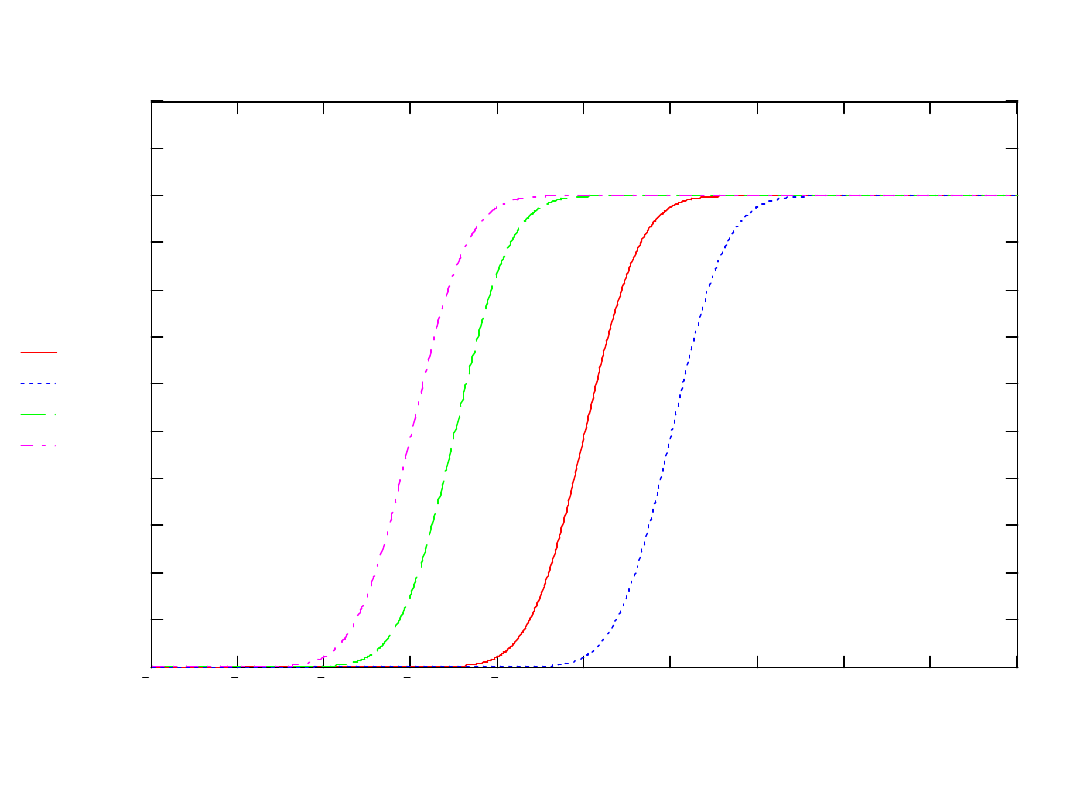
ROZKŁAD.NORMALNY.S
Oblicza standardowy skumulowany rozkład
(dystrybuantę) normalny o zadanych
parametrach. Rozkład ten ma średnią zero i
odchylenie standardowe równe jeden. Funkcję tę
należy stosować zamiast tabeli obszarów
standardowych krzywych normalnych.
Składnia
Z jest to wartość, dla której chcemy określić
rozkład.
ROZKŁAD.NORMALNY.S(z)

ROZKŁAD.NORMALNY.ODW
Oblicza wartość funkcji odwrotnej
skumulowanego rozkładu normalnego.
Składnia.
ROZKŁAD.NORMALNY.S.ODW(prawdopodobie
ństwo)
Prawdopodobieństwo jest to
prawdopodobieństwo odpowiadające
rozkładowi normalnemu.
Średnia jest to średnia arytmetyczna
rozkładu.
Odchylenie_std jest to standardowe
odchylenie rozkładu
ROZKŁAD.NORMALNY.ODW(prawdopodobieństwo;średnia;odchyleni
e_std)

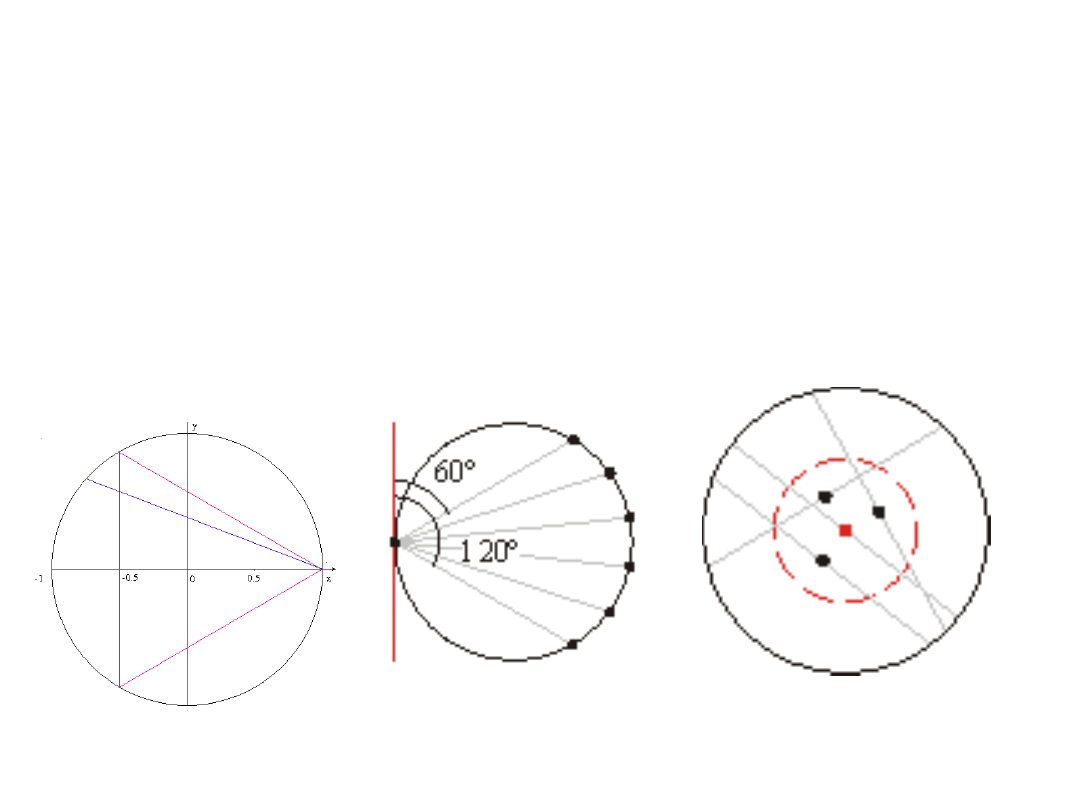
a) 1/2
b)
1/3
c) 1/4
Paradoks Bertranda
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
Wyszukiwarka
Podobne podstrony:
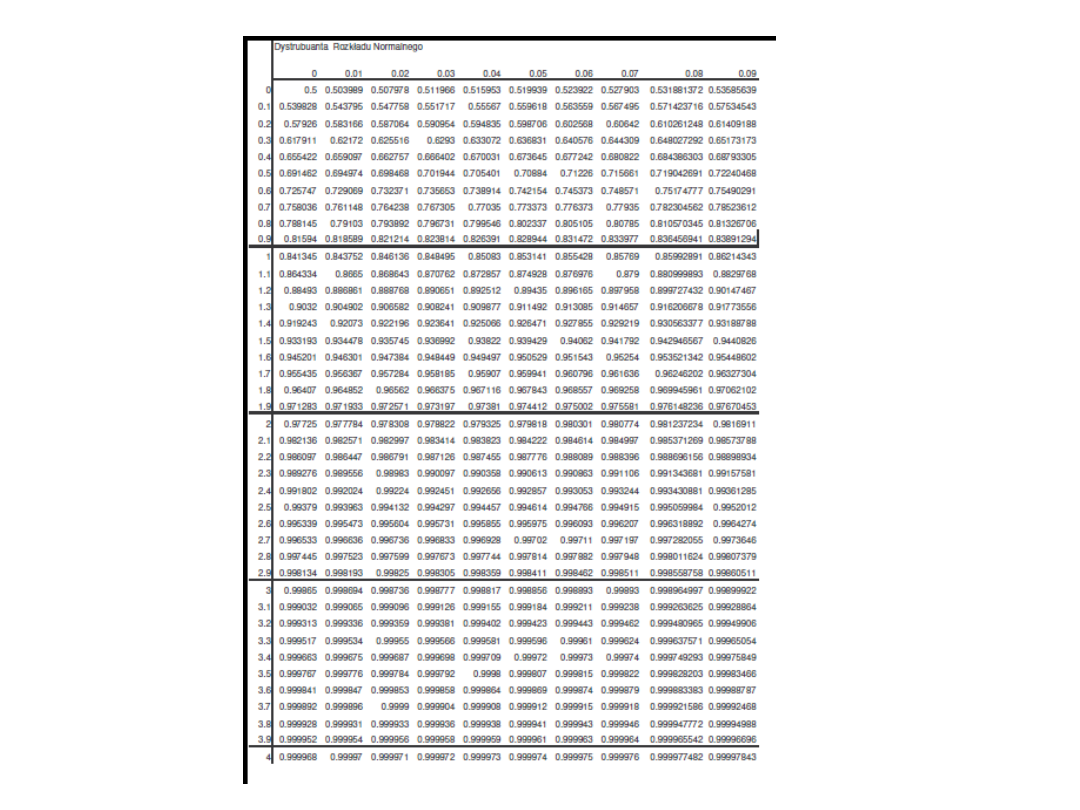
Tablica standaryzowanego rozkładu normalnego o wartości oczekiwanej równej zeru i wariancji równej j
T3 Rozkład normalny
sad-materialy-pomocnicze, Rozkład Normalny N, Rozkład Normalny N(0,1)
Prawdopodobieństwo Rozkład dwumianowy Rozkład normalny
Rozkład normalny, sql
rozklad normalny
statystyka wykłady, Wyklad5-6, Rozkład normalny
6 Statystyka w badaniach Rozkład normalny
tablice statystyczne wartosci krytyczne rozkladu normalnego
03 Tablica standardowego rozkladu normalnego
dystrybuanta-rozkladu-normalnego-standaryzowanego
Psychologia społeczna Zachowania społeczne Cielecki wykład 3 Normalizacja i konformizm ppt
09 normalizacjaid 8089 ppt
rozklad normalny, centyle
Wykład3 rozkład normalny
3408 rozklad normalny
1 Rozkład normalny
02 ROZKŁAD NORMALNY, JEDNOSTANJY i DWUMIANOWY
więcej podobnych podstron