ZASTOSOWANIA ROZKŁADU NORMALNEGO. dr Rumiana Górska

RACHUNEK DYSTRYBUANT

Rozkład normalny - funkcja gęstości rozkładu normalnego ma postać:

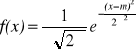
m,
- parametry rozkładu, zapisujemy X~N(m;
).

Standaryzacja rozkładu normalnego. Jeśli zmienna losowa X ma rozkład normalny z parametrami (m;
), to zmienna losowa
ma standardowy rozkład normalny.

Czyli: X~N(m;
)

~N(0; 1).

Zadania:

1. Jeśli zmienna losowa X ma standardowy rozkład normalny X~N(0;1) sporządzić wykres funkcji gęstości oraz obliczyć: P(X<0),
.

2. Zmienna losowa X ma rozkład normalny o parametrach: m=100, σ=20.

a) Sporządzić wykres funkcji gęstości oraz zaznaczyć P(X=80), P(X
80), P(X<80), P(80<X<110), P(X>130).

b) Obliczyć wartość prawdopodobieństwa: P(X<80); P(80<X<110); P(X>130).

W Excelu funkcja:

=ROZKŁAD.NORMALNY.S(1,5) podaje wartość Ф(1,5)

Odp. Ф(-1)= 0,1587; Ф(0,5)-Ф(-1)= 0,6915- 0,1587=0,5328;

1- Ф(1,5)=1-0,9332=0,0668

3. Wiadomo, że rozkład masy mężczyzny należącego do klubu „Smakosze boczku” jest rozkładem normalnym z wartością oczekiwaną 100 kg i odchyleniem standardowym 10 kg. Jakie jest prawdopodobieństwo, że losowo wybrany mężczyzna z klubu będzie ważył:

a) nie więcej niż 110 kg, b) powyżej 105 kg, c) między 90 a 100 kg?

4. Czas oczekiwania w kolejce w Banku ma rozkład normalny N(m; 3) w minutach. Wiadomo, że co 20 osoba czeka powyżej 10 min.

a) Jaka jest wartość oczekiwana rozkładu?

b)Jakie jest prawdopodobieństwo, że losowo wybrana osoba będzie czekać w kolejce mniej niż 5 min?

5. Waga pewnego tropikalnego owocu ma rozkład normalny ze średnią 100 g i wariancje 25 g².

a) Jaka w przybliżeniu jest część owoców, której waga nie różni się od średniej o więcej niż jedno odchylenie standardowe?

b) Jaka w przybliżeniu jest część owoców, której waga nie różni się od średniej o więcej niż dwa odchylenia standardowe?

c) Jaka część owoców ma wagę, która rózni się od średniej o więcej niż trzy odchylenie standardowe?

d) Jakie byłyby odpowiedzi z pkt a) b) c) jeśli rozkład wagi owocu jest N(110, 7)?

6.Dla zmiennej losowej N(50, 30) znajdź taką wartość, żeby prawdopodobieństwo przekroczenia tej wartości przez zmienną losową było równe 25%.

7. Niech X jest zmienną losową o rozkładzie N (100; 15). Znajdź takie x, żeby P(108<X<x)=0,05.

---