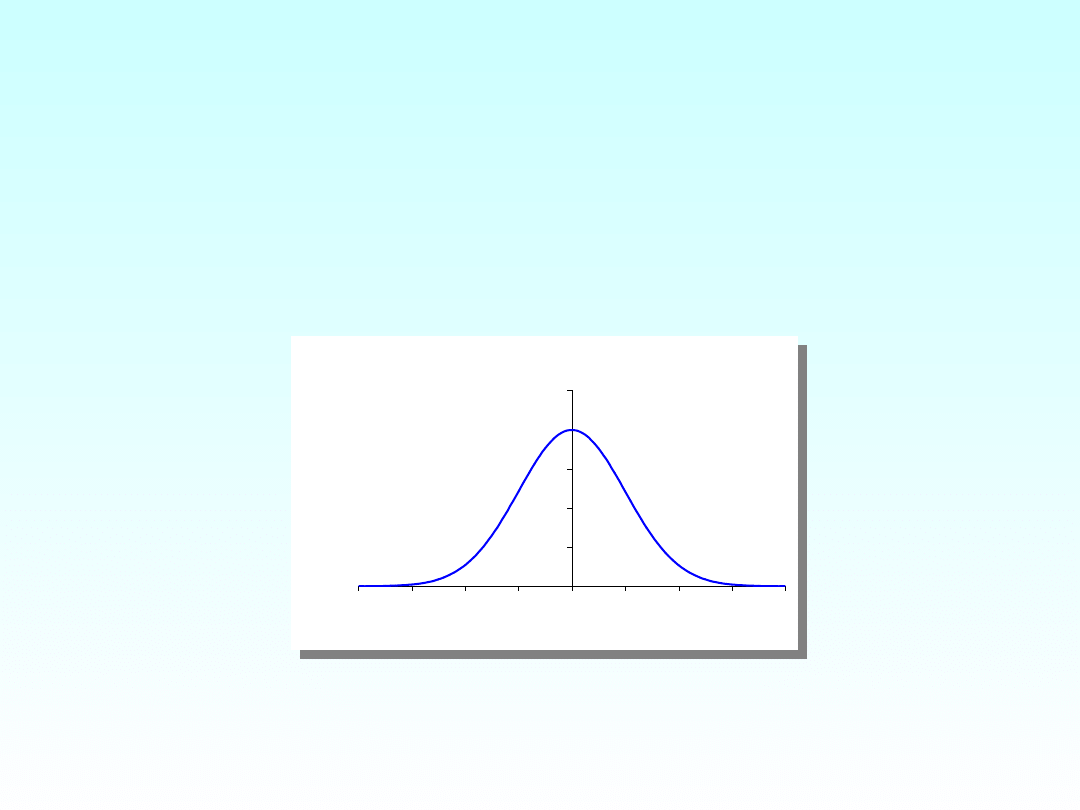
ROZKŁAD NORMALNY

ROZKŁAD NORMALNY

Rozkład normalny standardowy

0,00

0,10

0,20

0,30

0,40

0,50

-4

-3

-2

-1

0

1

2

3

4

z [-]

G

[

-]

Rozkład normalny standardowy

0,00

0,10

0,20

0,30

0,40

0,50

-4

-3

-2

-1

0

1

2

3

4

z [-]

G

[

-]

Z rozkładem normalnym

Z rozkładem normalnym

(Gaussa) zmiennej

(Gaussa) zmiennej

mierzalnej mamy do

mierzalnej mamy do

czynienia wtedy, gdy na

czynienia wtedy, gdy na

wartość tej zmiennej

wartość tej zmiennej

wpływa nieskończenie

wpływa nieskończenie

wiele (w praktyce

wiele (w praktyce

wystarczy samo „wiele”)

wystarczy samo „wiele”)

niezależnych

niezależnych

czynników

czynników

Odległość rzutu piłką

Odległość rzutu piłką

palantową

palantową

• skład włókien mięśniowych,
• zdolności koordynacyjne,
• wysokość ciała,

• stopień wytrenowania ruchu,
• stan zdrowia,
• motywacja,

• kierunek i prędkość wiatru,
• temperatura powietrza.

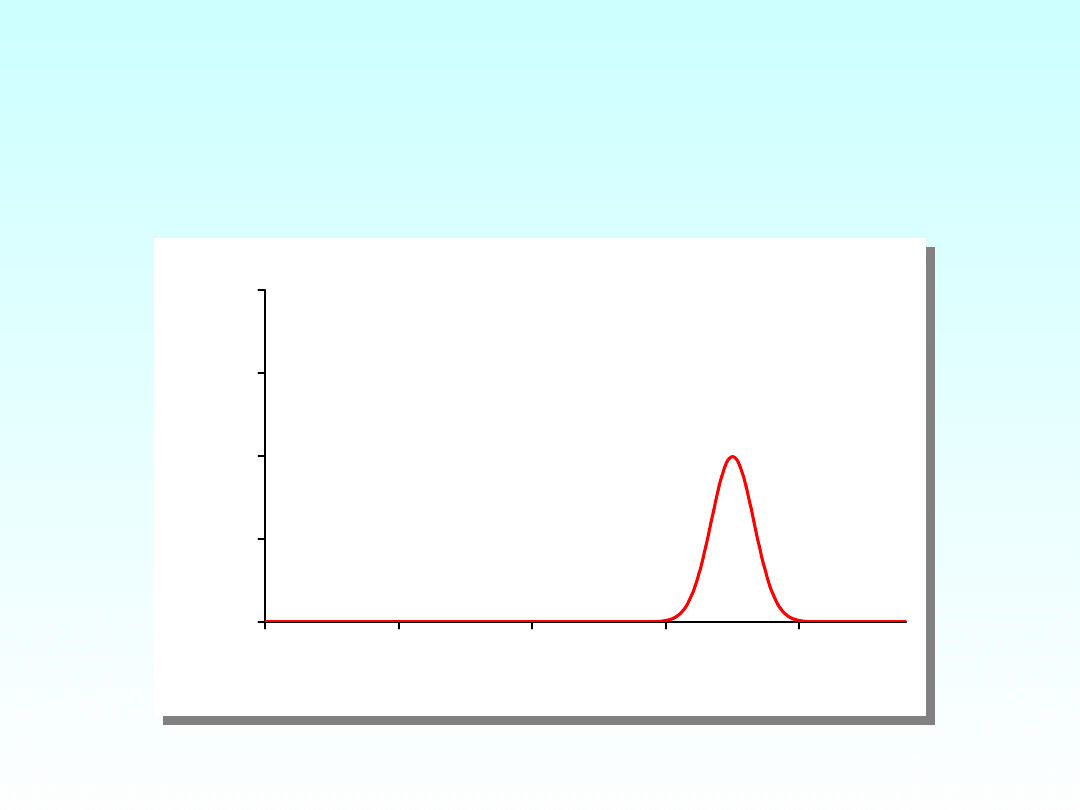
Rozkład wysokości ciała w

Rozkład wysokości ciała w

populacji mężczyzn

populacji mężczyzn

0,000

0,025

0,050

0,075

0,100

0

50

100

150

200

wysokość ciała [cm]

G

[

1

/c

m

]

0,000

0,025

0,050

0,075

0,100

0

50

100

150

200

wysokość ciała [cm]

G

[

1

/c

m

]

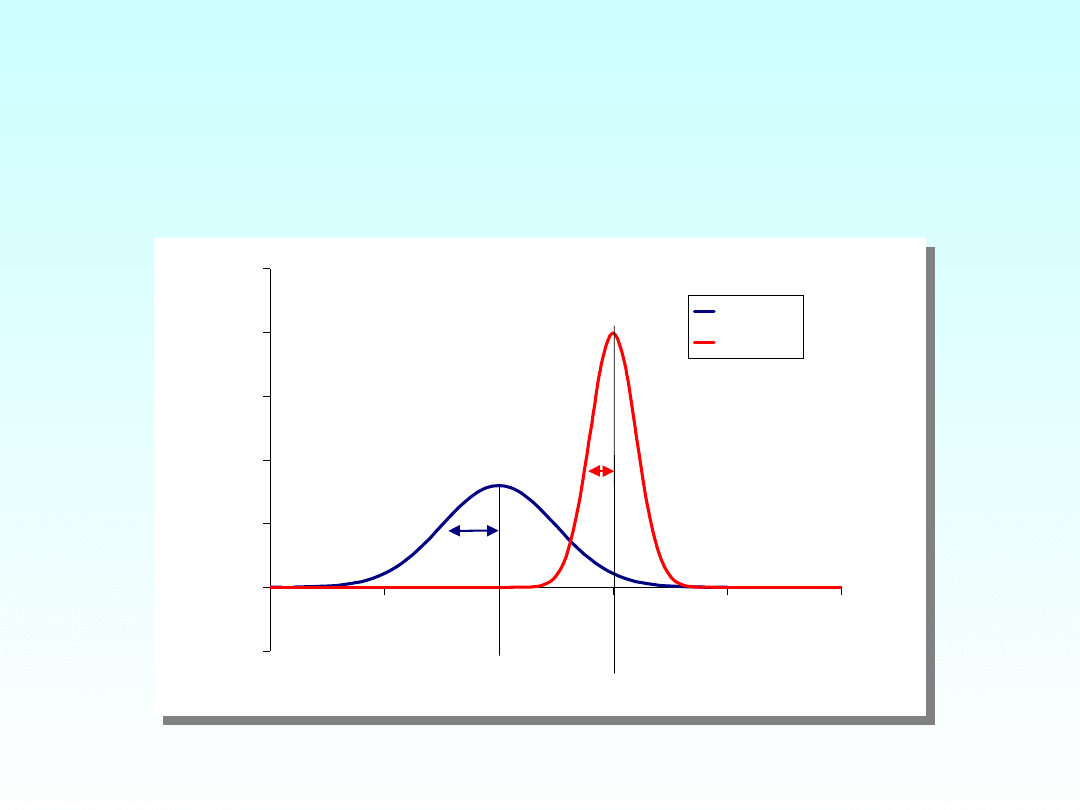
Kształt krzywej w zależności

Kształt krzywej w zależności

od średniej i odchylenia

od średniej i odchylenia

standardowego

standardowego

-0,05

0

0,05

0,1

0,15

0,2

0,25

0

10

20

30

40

50

wartość cechy

G

ę

st

o

ść

r

o

zk

ła

d

u

N(20,5)
N(30,3)

5

2

-0,05

0

0,05

0,1

0,15

0,2

0,25

0

10

20

30

40

50

wartość cechy

G

ę

st

o

ść

r

o

zk

ła

d

u

N(20,5)
N(30,3)

5

2

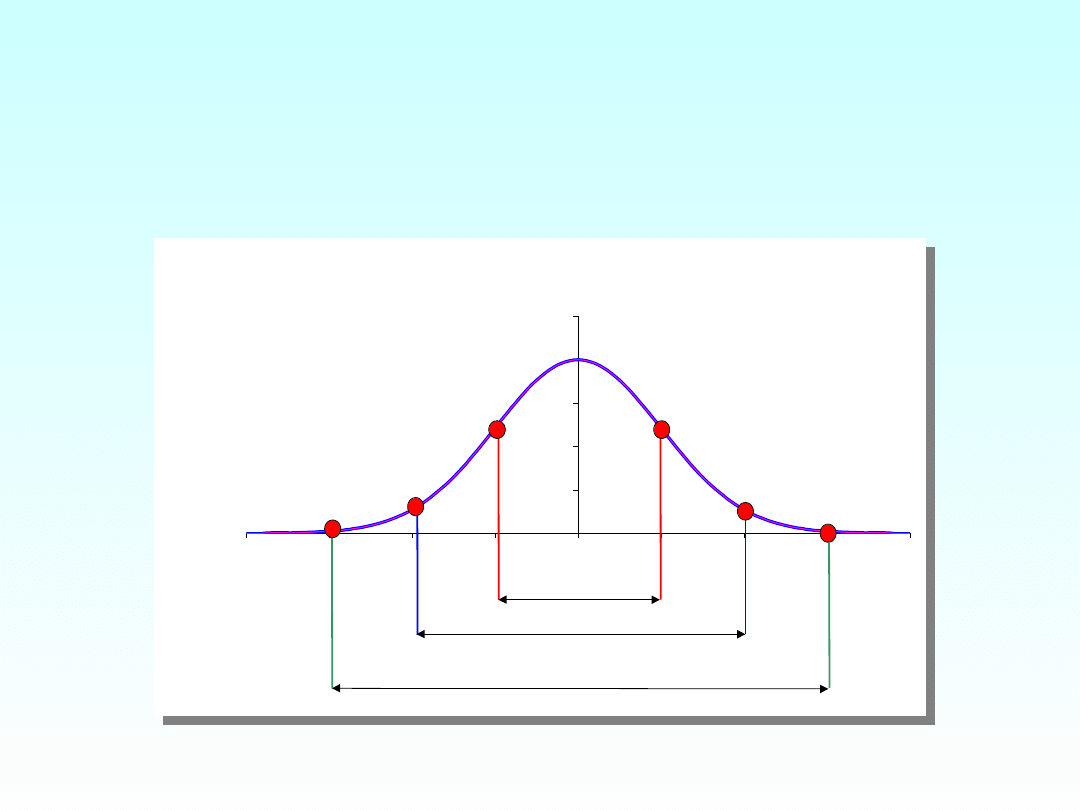
Rozkład normalny

Rozkład normalny

standardowy

standardowy

średnia z

śr

=0,

odchylenie standardowe =1

0,00

0,10

0,20

0,30

0,40

0,50

-4

-3

-2

-1

0

1

2

3

4

z [-]

G

[

-]

68%
95%

99,9%

średnia z

śr

=0,

odchylenie standardowe =1

0,00

0,10

0,20

0,30

0,40

0,50

-4

-3

-2

-1

0

1

2

3

4

z [-]

G

[

-]

68%

95%

99,9%

Zasada trzech odchyleń

Zasada trzech odchyleń

standardowych

standardowych

• Jeżeli wartość zmiennej dla danego

przypadku oddalona jest

o więcej niż

3 odchylenia standardowe od
średniej

zachodzi uzasadnione

podejrzenie, że mamy do czynienia z
tzw.

błędem grubym

wynikającym z

pomyłki w zapisie danych. Przypadek
taki należy zweryfikować, a wobec
braku sensownego potwierdzenia po
prostu usunąć.

Zmienna unormowana

Zmienna unormowana

Jeżeli przez



oznaczymy wartość średnią, a

przez



odchylenie standardowe dla

populacji, to obliczenia wartości
unormowanej

x

*

i

dokonuje się dla każdej

wartości

x

i

według wzoru:

x*

i

=(x

i

-)/.

W praktyce zwykle nie znamy



i



dla

populacji, posługujemy się więc wzorem:

x*

i

=(x

i

-x

śr

)/s.

Ocena wartości zmiennej na

Ocena wartości zmiennej na

podstawie wartości

podstawie wartości

unormowanej

unormowanej

Jeżeli w populacji mężczyzn
średnia wysokości ciała
wynosi

175±8,1

cm to

wartość unormowana dla
mężczyzny o wysokości 198
wynosi:

h

*

=(198-175)/8,1= 2,84,

a dla mężczyzny o wysokości
165:

h

*

=(165-175)/8,1=-1,23.

Skala T - alternatywny

Skala T - alternatywny

sposób przedstawienia

sposób przedstawienia

wartości unormowanej

wartości unormowanej

T=50+10x

*

,

dla x

*

=2,84 T=78,

dla x

*

=0,00 T=50,

dla x

*

=-1,23 T=38.

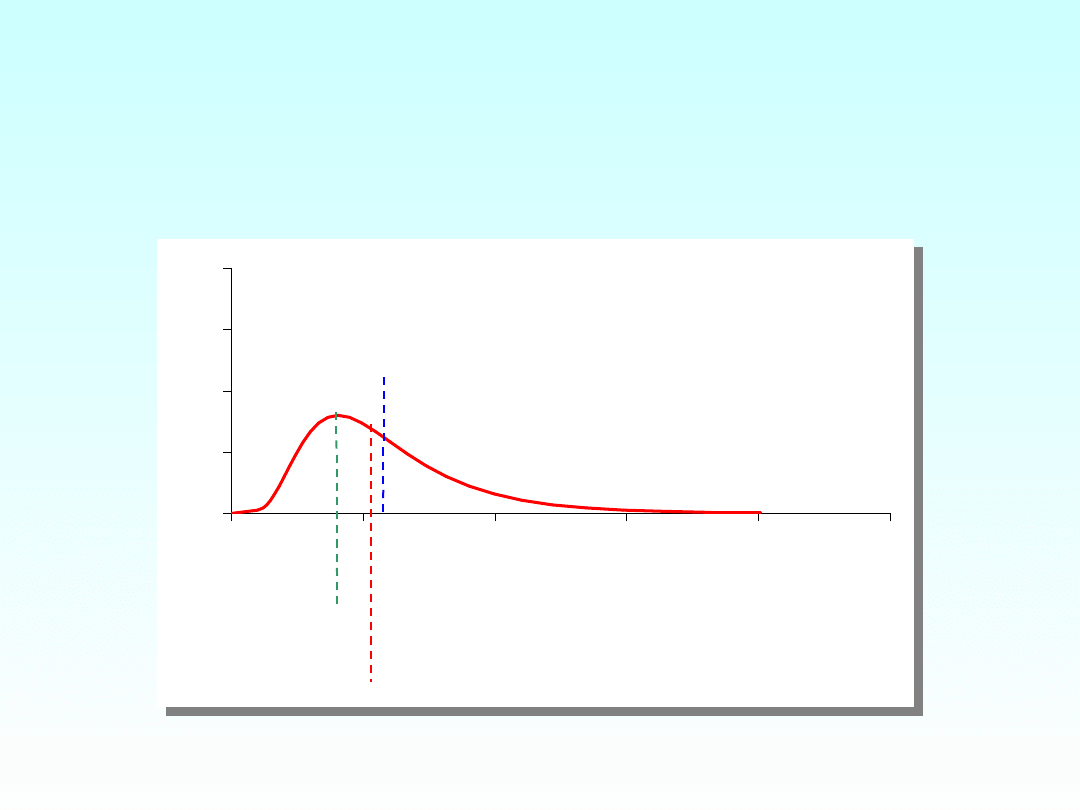
Rozkład prawoskośny

Rozkład prawoskośny

0,00

0,05

0,10

0,15

0,20

0

5

10

15

20

25

Wartość cechy

Gęstość rozkładu

MODA

MEDIANA

ŚREDNIA

0,00

0,05

0,10

0,15

0,20

0

5

10

15

20

25

Wartość cechy

Gęstość rozkładu

MODA

MEDIANA

ŚREDNIA

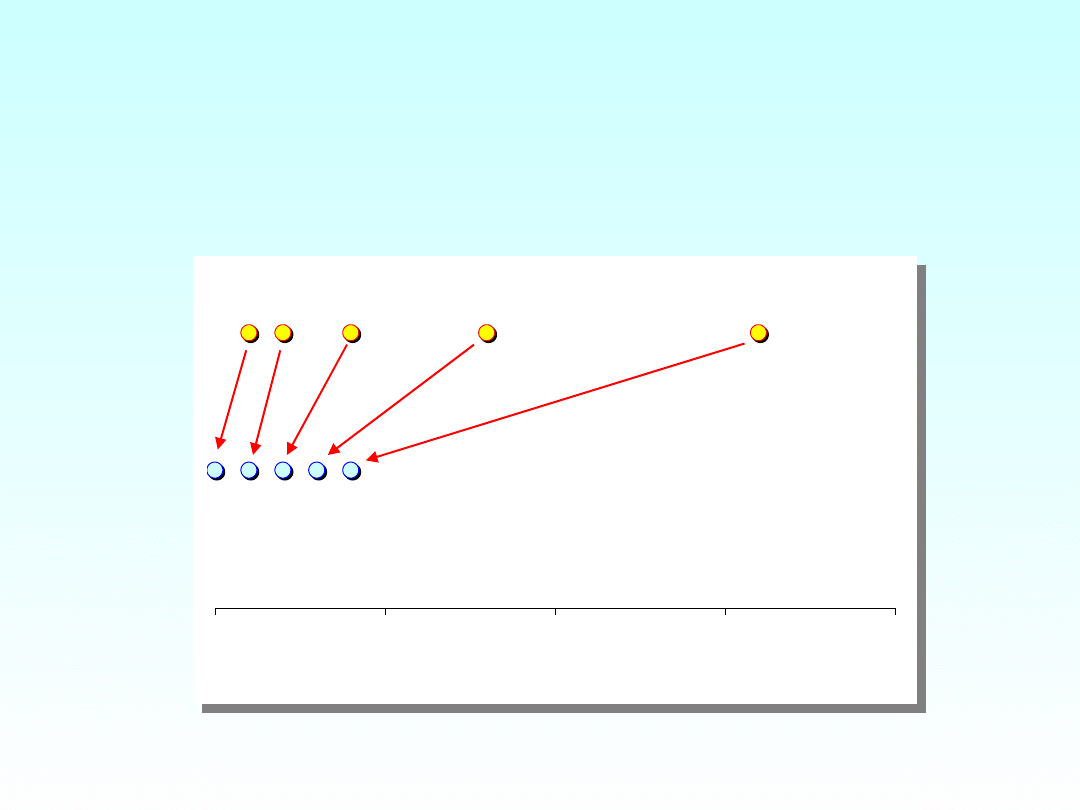
Transformacja logarytmiczna

Transformacja logarytmiczna

z=log(x)

z=log(x)

0

5

10

15

20

x

z = log

2

(x);

x=1, 2, 4, 8, 16
z=0, 1, 2, 3, 4

0

5

10

15

20

x

z = log

2

(x);

x=1, 2, 4, 8, 16
z=0, 1, 2, 3, 4

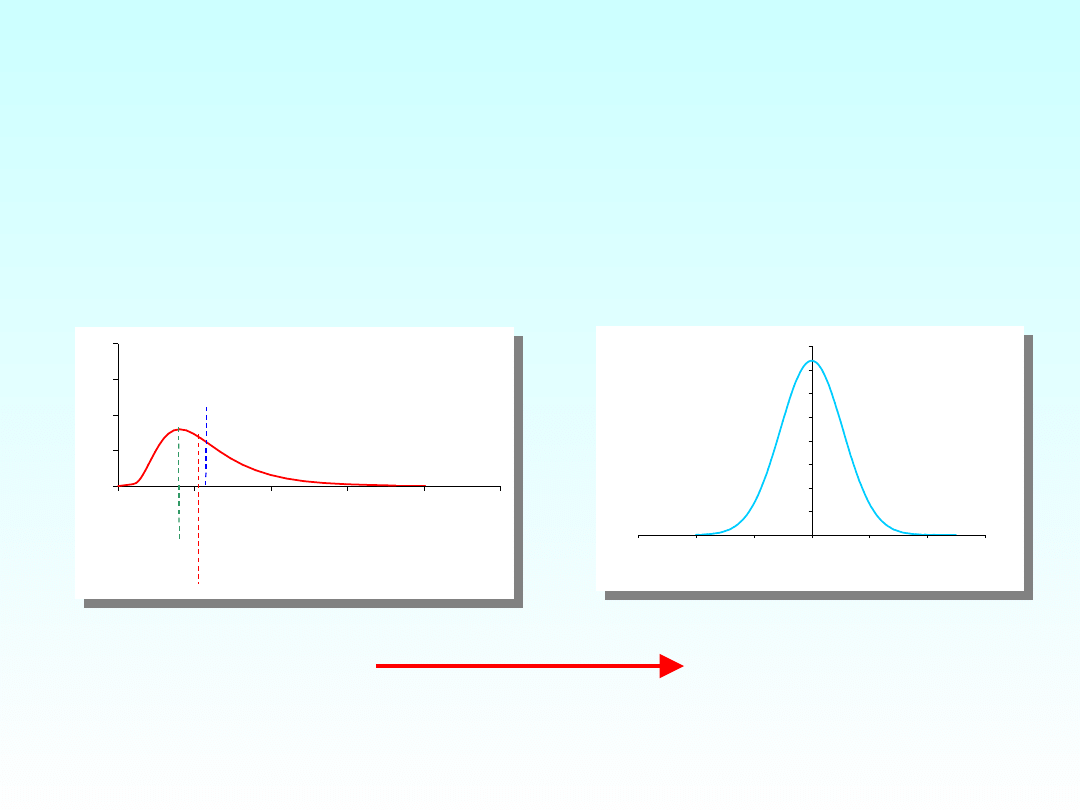
Efekt transformacji z=ln(x)

Efekt transformacji z=ln(x)

0,00

0,05

0,10

0,15

0,20

0

5

10

15

20

25

Wartość cechy

Gęstość rozkładu

MODA

MEDIANA

ŚREDNIA

0,00

0,05

0,10

0,15

0,20

0

5

10

15

20

25

Wartość cechy

Gęstość rozkładu

MODA

MEDIANA

ŚREDNIA

0

5

10

15

20

25

30

35

40

-0,06

-0,04

-0,02

0

0,02

0,04

0,06

Gęstość rozkładu

Wartość cechy

0

5

10

15

20

25

30

35

40

-0,06

-0,04

-0,02

0

0,02

0,04

0,06

Gęstość rozkładu

Wartość cechy

Dlaczego tak nam zależy na

Dlaczego tak nam zależy na

normalności rozkładu

normalności rozkładu

danych?

danych?

• Większość testów statystycznych dotyczących

oceny parametrów zmiennych mierzalnych i
zależności między tymi zmiennymi wymaga
normalności rozkładu danych.

• Tablice dystrybuanty standardowego

rozkładu normalnego mogą służyć do
obliczania frakcji przypadających na zadane
przedziały zmiennych.

Ocena normalności rozkładu

- testy normalności

• Test Shapiro-Wilka - małe liczebności (10-50);
• test Lilieforsa - duże liczebności (50+);
• test Kołmogorowa-Smirnowa - duże liczebności.