Rozkład normalny

Rozkład normalny

(wykładowi towarzysza folie –

(wykładowi towarzysza folie –

kopie w powielarni)

kopie w powielarni)

Wykład 6b

Ćwiczenie

Ćwiczenie



Hrabina Zenobia de’Omlasek w teście
znajomości zasad savoir-vivre’u
otrzymała 20 punktów



(średnia w badanej grupie hrabin wyniosła
25, odchylenie standardowe 5).



Natomiast w teście teoretycznej wiedzy
o tańcach towarzyskich dostała 5
punkty (średnia w grupie wyniosla 3,
odchylenie standardowe 2)



Na czym hrabina zna się lepiej?

odpowiedź

odpowiedź



Widać, że
hrabinie lepiej
wychodziło
tańczenie niż
dobre obyczaje

1

2

3

5

...

tan

1

5

25

20

...



















z

z

savoir

SD

X

X

z

Założenia testów statystycznych

Założenia testów statystycznych



Większość testów (testy
parametryczne) ma założenia odnośnie
tego, jaki rozkład mają nasze dane



Jednym z najważniejszych rozkładów
jest



Rozkład normalny, krzywa Gaussa

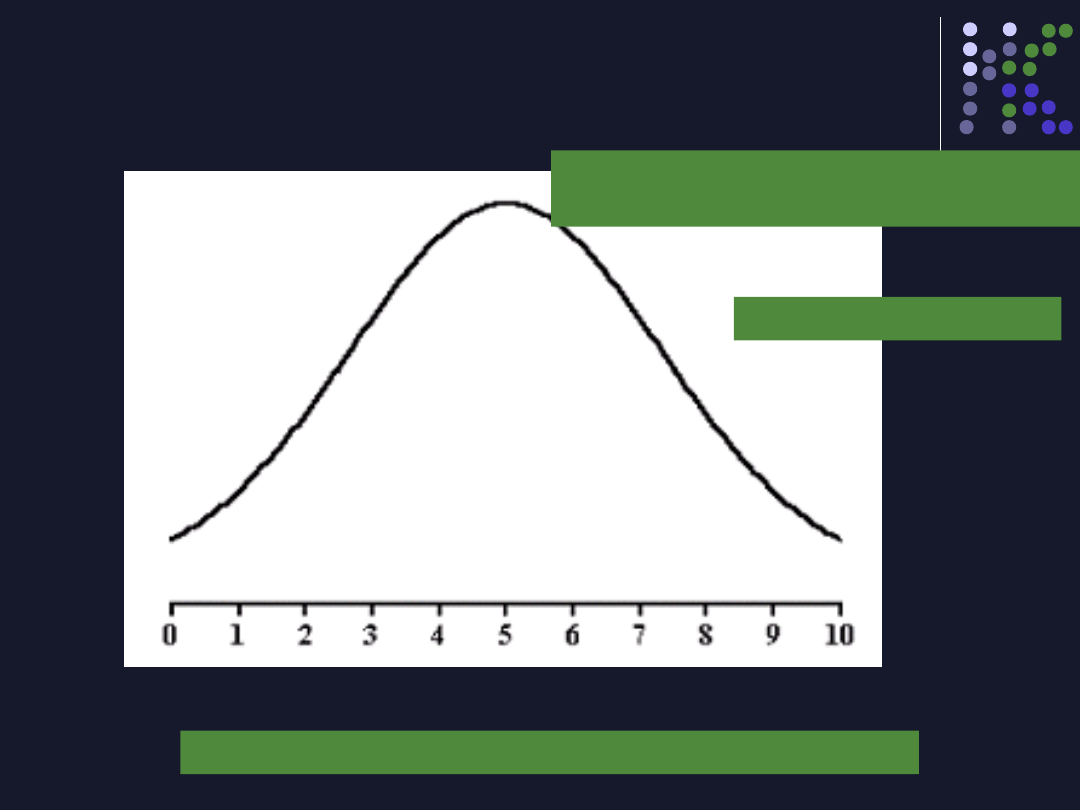
Rozkład nomalny

Rozkład nomalny

Na osi odciętych mamy możliwe wartośći zmiennej X

Na osi rzędnych widzimy gęstość –
częstość występowania danych wartości

Rozkład jednomodalny

Odrobina historii

Odrobina historii



Początkowo zajmował się rozkładem normalnym

DeMoivre (1667-1754) – do celów hazardu



Zdefiniowany przez Pierra Laplace i

doprowadzony do dzisiejszej formy przez Carl

Friedrich Gaussa(1777-1855),



matematyk niemiecki, jeden z najwybitniejszych

matematyków w dziejach świata, zajmował się

ponadto fizyką teoretyczną, geodezją i astronomią

sferyczną, od 1807 do śmierci był profesorem

matematyki w 

Getyndze

i dyrektorem tamtejszego

obserwatorium astronomicznego

.



Współcześni nazywali go “księciem matematyków”



Obaj panowie interesowali się rozkładem błedów

w obserwacjach astronomicznych

Rozkład Normalny

Rozkład Normalny



Kształt rozkładu wielu zmiennych, które mierzą

psychologowie ma kształt mniej więcej symetryczny,

przypominający dzwon.



Popularny w przyrodzie



Waga, wzrost, rozmiar butów, ......, inteligencja



Zmienność wyrażana przez odchylenie standardowe

została wykorzystana przez Karola Darwina w

"Pochodzeniu gatunków" jako ważny dowód w teorii

ewolucji.



Darwin założył, że średnia i odchylenie standardowe były

wrodzonymi cechami każdego gatunku.



Jeżeli zbadamy bowiem pewną grupę psów - np. labradorów pod

względem ich wzrostu i wzrost ten naniesiemy na oś poziomą a

częstość jej występowania na oś pionową to zauważymy, że

rozkład ten przybierze charakterystyczny kształt dzwonu,

zwanego rozkładem Gaussa lub rozkładem normalnym. Tak samo

się stanie jeżeli zbadany inne zwierzęta czy nawet ludzi.

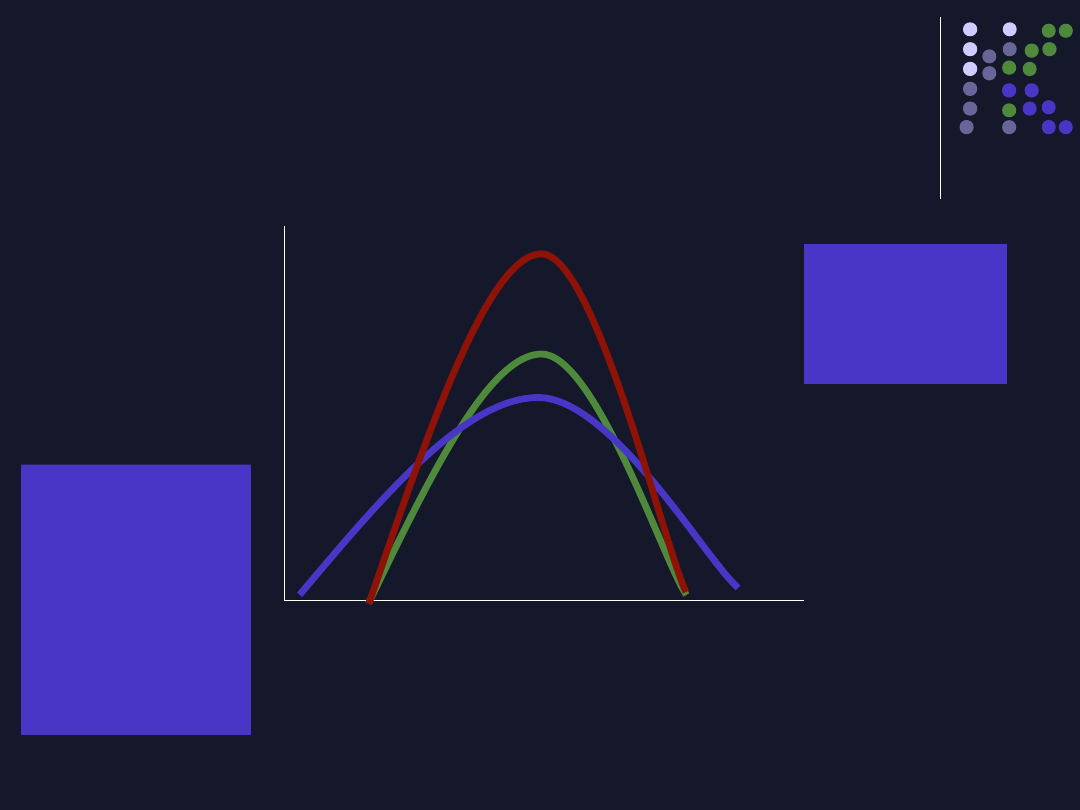
Powinien być symetryczny wokół średniej

Powinien być symetryczny wokół średniej

(lepty i plato)

(lepty i plato)

Średnia,
mediana i
modalna są
sobie równe

Wszystkie są
normalne,
chociaż, nie są
takie same,
różnią się
rozproszeniem
wyników,
spiczatością

Charakterystyki rozkładu normalnego

Charakterystyki rozkładu normalnego



Krańce rozkładu normalnego stykają się
z osią x w nieskończoności



Ma kształt dzwonu



Jest funkcją średniej i odchylenia
standardowego



Znając średnią i odchylenie standardowe
możemy wyznaczyć krzywą rozkładu
normalnego

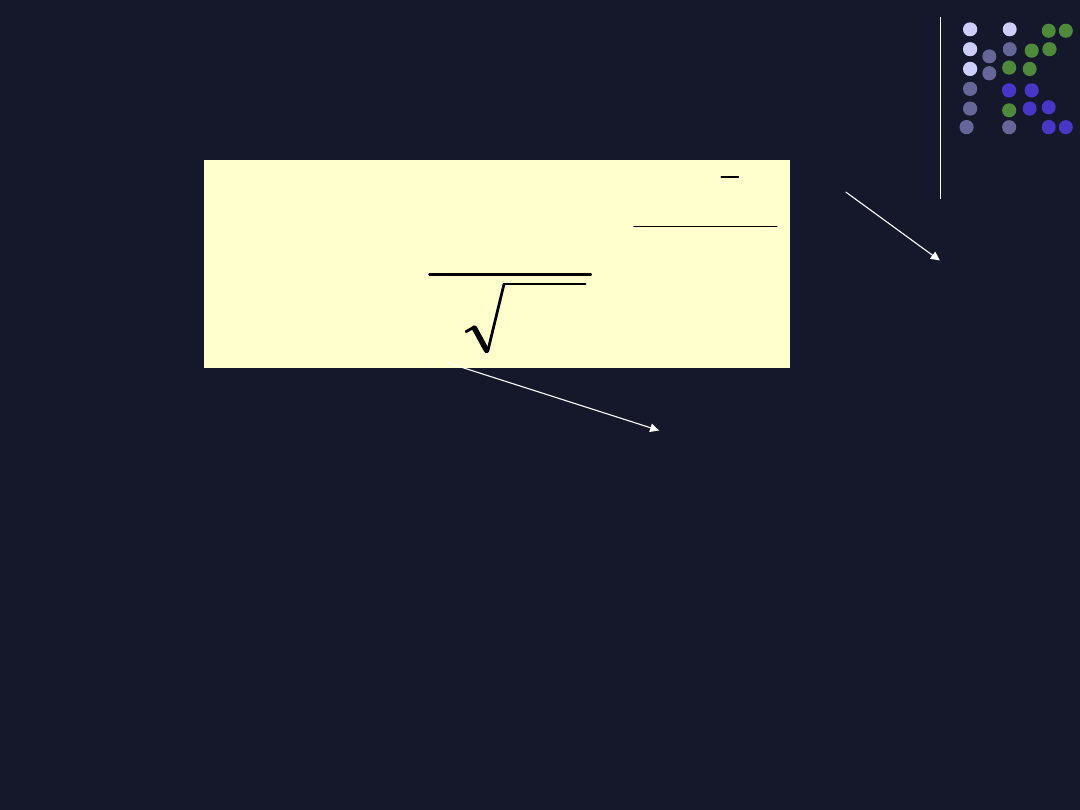
Wzór na rozkład normalny

Wzór na rozkład normalny



X warotść na osi odciętych



Y wysokość krzywej w zależności od X



=3,1416

i e=2,7183 to stałe

2

2

2

)

(

2

1

)

(

s

x

x

e

s

X

f









Odchylenie standardowe

średnia

Standaryzowany rozkład normalny

Standaryzowany rozkład normalny



Rozkłady zależą od wartości średniej i

odchylenia standardowego, wygodnie jest

więc wystandaryzować nasz rozkład, aby

móc, np powiedzieć jaki procent obserwacji

leży poniżej lub powyżej pewnego wyniku



Można to odczytać z tabel dla wystandaryzowanego

rozkładu normalnego



Zamieniamy wszystkie wartości X na watrości

standaryzowane z



tak, aby średnia wynosiła 0, a odchylenie

standardowe równało się 1



Powierzchnia pod krzywą jest równa 1

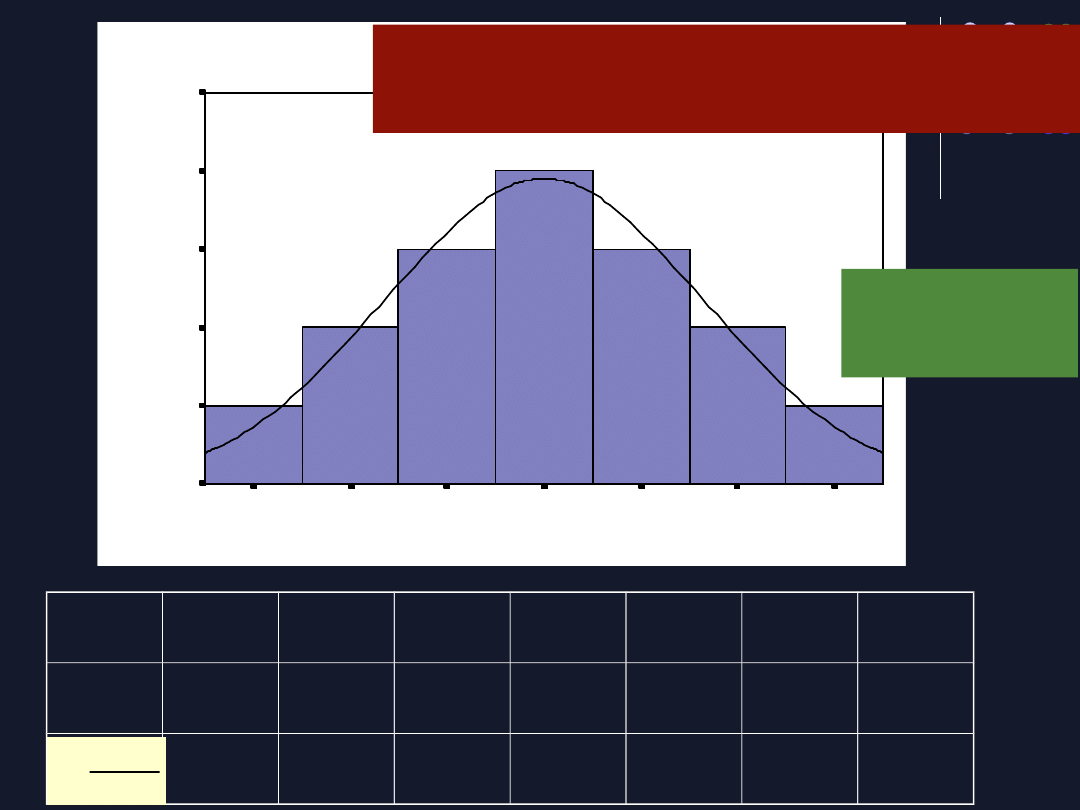
x

20

30

40

50

60

70

80

x-M -30

-20

-10

0

10

20

30

z=

-3

-2

-1

0

1

2

3

POLITYKA

80,0

70,0

60,0

50,0

40,0

30,0

20,0

POLITYKA

C

zę

st

oś

ć

5

4

3

2

1

0

Średnia M =50
SD=10
Wariancja =100

SD

x

z

M





Dokonując transfomacji na wartości z nie zmieniamy
Kształtu rozkładu, więc jeśli rozkład nie był normalny
wcześniej, nie będzie normalny po przekształceniu

Sposób na rozkład normalny

Sposób na rozkład normalny



Im bardziej zwiększamy naszę próbkę,
dodajemy obserwacje, tym bardziej
zbliża się on do normalnego



http://surfstat.newcastle.edu.au/surfstat

Tabele wartości

Tabele wartości

z

z



Korzystamy z tabel, aby znaleźć obszar pod krzywą

normalną, w tabeli są tylko pozytywne wartości z

(ale skoro rozkład jest symetryczny to to samo

odnosi się do wartości ujemnych z)

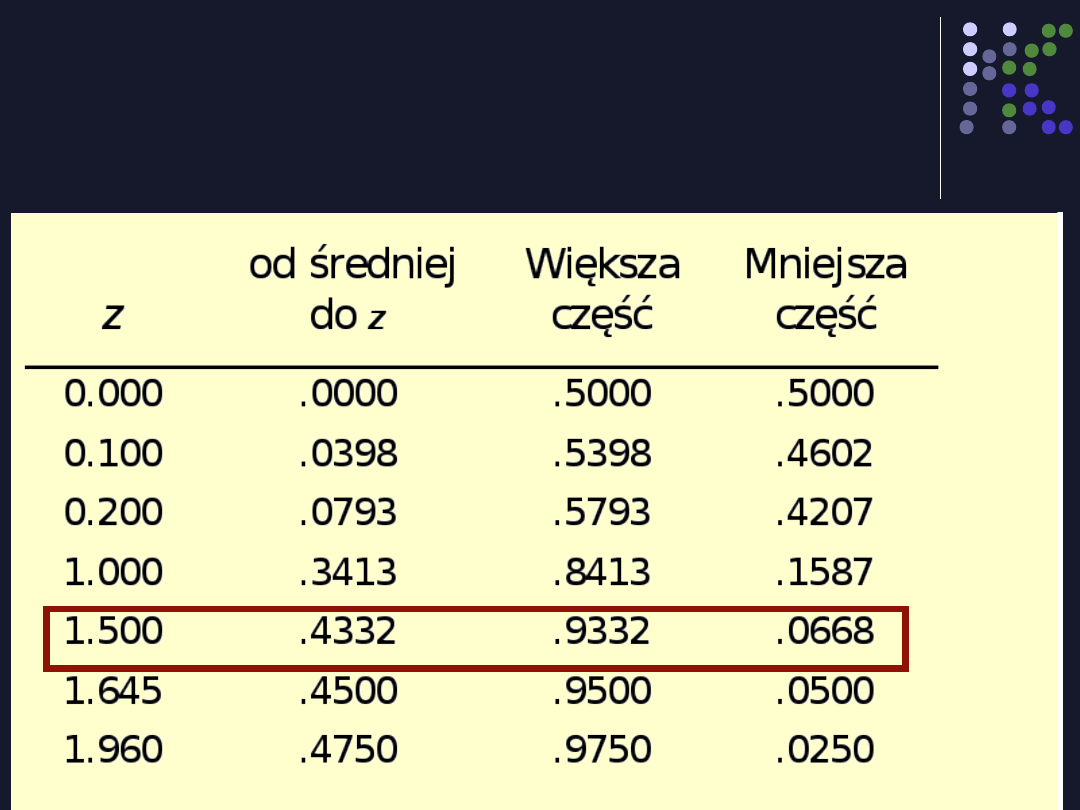
Tabela wartości

Tabela wartości

z

z



Na podstawie tabel można łatwo znaleźć

procent przypadków odpowiadający danej

wartości z, a także wartość z odpowiadającą

danemu procentowi przypadków.

0,0668

Mniejsza

część

0,4332

od średniej

do wartości

z

Większa część

pod krzywą

normalną

0,9332

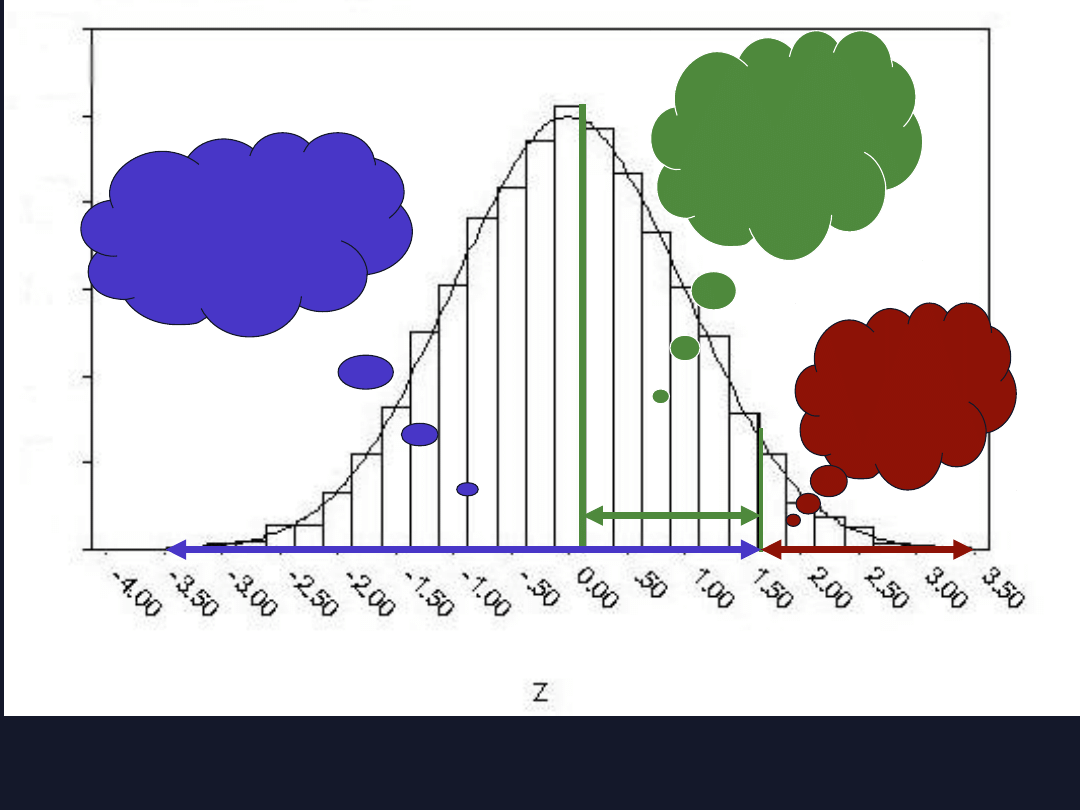
Patrząc na Tabele wartości

Patrząc na Tabele wartości

z

z



Możemy obliczyć dokładnie



Jaki procent obserwacji będzie mieścił się w przedziale

między dowolnymi dwoma punktami na krzywej

normalnej wyrażonymi w wartościach z



Np procent między z= +1,5 a z=-1.0



Powierzchnia między średnią a z=+1,5 =

0.4332



Powierzchnia między średnią a z=-1.0 =

0.3413



Dodajemy obszary 0.7745



Widzimy, że około 77% obserwacji będzie mieściło się w

przedziale między z = -1.0 and z = +1.5

Przykład 2, procent przypadków



Jaki procent obserwacji znajduje się
między z = 0,70 i z = -1.70



Od M do z=0,70 jest 0,2580 czyli 25,80%



Od M do z=-1,70 jest 0,4554 czyli 45,54%,



A ponieważ są po różnych stronach
rozkładu dodajemy procenty i wychodzi
71,34%



Dokładnie 71,34% przypadków znajduje
się między z = 0,70 i z = -1.70

Wracając do surowych wyników x

Wracając do surowych wyników x



Załóżmy że M= 50
and SD = 10



77% of the
distribution is
expected to lie
between 40 and 65

65

10

5

,

1

50

40

10

0

,

1

50



























x

x

SD

z

M

x

M

SD

x

z

Przedziały

Przedziały



W ostatnim przykładzie M=50, SD=10



Chcemy odciąć skrajne 2,5% obserwacji
z każdego krańca rozkładu



Sprawdzamy w tabeli wartości z



z = + 1.96

4

,

30

10

96

.

1

50

6

,

69

10

96

.

1

50

















x

x

SD

z

M

x







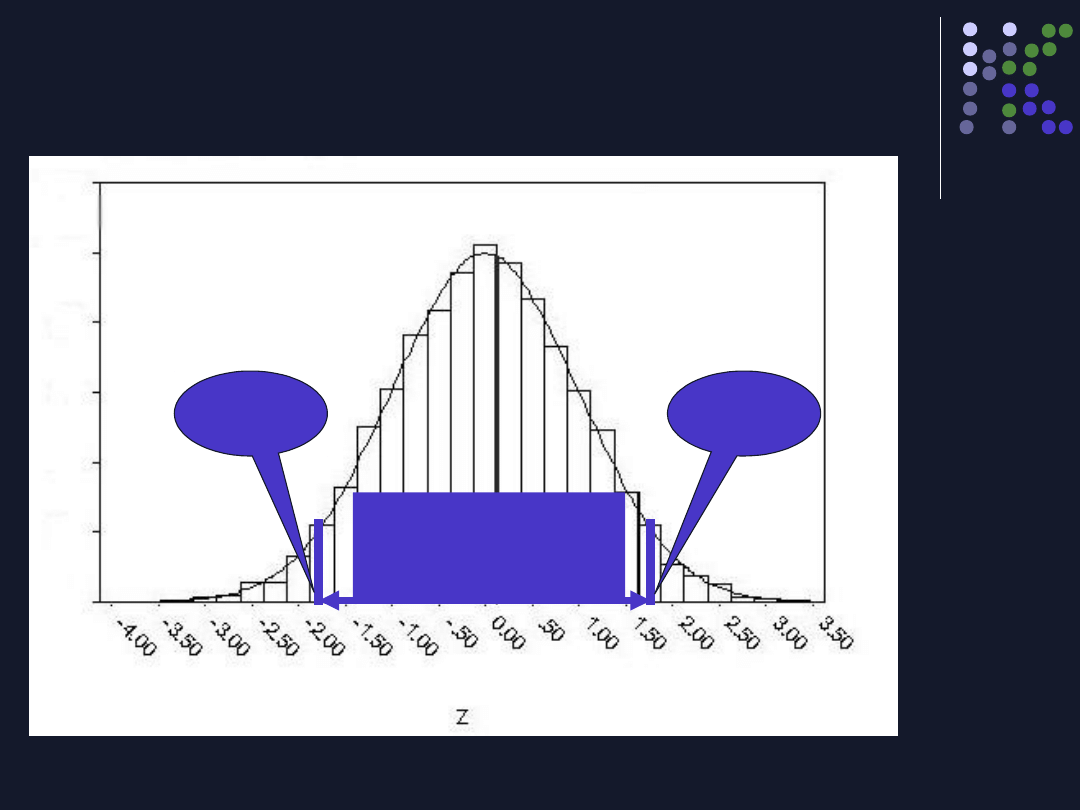
Procent wyników w danym przedziale

Procent wyników w danym przedziale



Szukamy przedziału w którym będzie
mieściło sie 95% wyników.



W naszym przykładzie 95% wyników
będzie się mieścić w przedziale (20,2 ;
39,8)



Stąd w 95% przypadków wynik losowo
wybranej z populacji osoby będzie się
mieścić w tym przedziale

95% wyników
mieści się w tym
przedziale

z=1,9

6

z=-

1,96

Jak znaleźć procent

Jak znaleźć procent

przypadków znajdujący

przypadków znajdujący

się poniżej lub powyżej

się poniżej lub powyżej

danego wyniku

danego wyniku

W oparciu o wyniki surowe i

tabelę wartości z

Kolejne kroki – procent osób poniżej

Kolejne kroki – procent osób poniżej

danego wyniku

danego wyniku



Aby obliczyć procent przypadków

znajdujących się poniżej danego wyniku:



Zamieniamy wynik surowy na wartość z



w tabeli dla danej wartości z znajdujemy jej

odległość od średniej



Jeśli nasze z jest dodatnie wtedy dodajemy

odczytany % do 50%



jeśli z jest ujemne, odejmujemy odczytany %

od 50



Zawsze dobrze jest sobie narysować

rozkład i umiejscowić naszą watrość z

Kolejne kroki – procent powyżej

Kolejne kroki – procent powyżej



Aby obliczyć procent przypadków
znajdujących się powyżej danego wyniku



Zamieniamy wyniki surowe na wartości z.



w tabeli dla danej wartości z znajdujemy jej
odległość od średniej



Jeśli nasze z jest dodatnie wtedy,
odejmujemy odczytany procent od 50,



a jeśli jest ujemne, dodajemy ten wynik do
50.

Test Coopera – test 12 minut

Test Coopera – test 12 minut



Jest to test stosowany przez

amerykańskich kosmonautów dla

sprawdzenia kondycji fizycznej,

wydolności



Opracowany przez Kennetha Coopera,

polega na przemierzeniu jak największego

dystansu w ciągu 12 minut



Zakładamy, że zmienna ta ma rozkład

normalny

Kondycja Jasia

Kondycja Jasia



W wieku 20-29
średnia= 2400 metrów,
SD=300 metrów



Jaś przebiegł 3000, jaki
procent panów biega
szybciej od Jasia



z=2, w przedziale od
średniej do z mieści się
47,72%,



Czyli 50 – 47,72=2,28%



Od Jasia szybciej biega
jedynie 2,28%

2

300

2400

3000











z

M

SD

x

z

A wolniej biega 97,72%

50+47,72=97,72

Kondycja Zbyszka

Kondycja Zbyszka



W wieku 20-29 średnia=

2400 metrów, SD=300

metrów



Zbyszek przebiegł 2100,

jaki procent panów biega

szybciej od Zbyszka, jaki

% jest poniżej wyniku

Zbyszka



z=-1, w przedziale od

średniej do z=-1 mieści się

34,13%,



Czyli 50 + 34,13=84,13%



84,13% biega szybciej



84,13% osób znajduje się

powyżej wyniku Zbyszka

1

300

2400

2100













z

M

SD

x

z

A wolniej biega 15,87%

50-34,13=15,87%

Ile metrów trzeba przbiec w ciągu 12

Ile metrów trzeba przbiec w ciągu 12

minut, żeby..

minut, żeby..



Znaleźć się w grupie 5% najlepszych biegaczy?



średnia=2400, SD=300



Odległość między wynikiem odcinającym górne 5% a
średnią wynosi 45%, odczytujemy z tabeli wartość z
dla odległości najbardziej zbliżonej =44,95%,



wartość z dla tej odległości wynosi 1,64



i podstawiamy dane do wzoru

2892

300

64

,

1

2400















x

SD

z

M

x

Żeby zmieścić się w 5% najlepszych biegaczy
trzeba przebiec co najmniej 2892

Ile metrów trzeba biegać, żeby..

Ile metrów trzeba biegać, żeby..



Znaleźć się w grupie 2% najgorszych biegaczy?



średnia=2400, SD=300



Odległość między wynikiem odcinającym dolne 2% a
średnią wynosi 48%, odczytujemy z tabeli wartość z
dla odległości najbardziej zbliżonej =47,98%,



wartość z dla tej odległości wynosi 2,05, ale wynik jest
poniżej średniej więc z=-2,05



i podstawiamy dane do wzoru

1785

300

05

,

2

2400















x

SD

z

M

x

Żeby zmieścić się w 2% biegaczy z najsłabszą
kondycją nie można przebiec więcej niż 1785
metrów

Do zapamiętania

Do zapamiętania



Przekszałcanie wyników surowych na
wartości z



Jak korzystać z tabel dla rozkładu
normalnego?



Jak określić procent przypadków
leżących pomiędzy dwiema wartościami
z?



Jak okreslić procent osób leżących
poniżej lub powyżej danej wartości?