Analiza

wariancji, czyli

co wymyślił sir

R. Fisher

Wykład 1

zaawansowa

ny

sir R. Fisher

Matematyk i statystyk,
Metodolog wykonujący badania
biologiczne, rolnicze, ewolucyjne

Fairly large print is a real antidote to stiff reading

Duża

czcionka

jest

prawdziwym

lekarstwem na nudne teksty

To consult the statistician after an experiment is finished
is often merely to ask him to conduct a post mortem
examination. He can perhaps say what the experiment
died of.”

Konsultacja ze statystykiem po wykonaniu
eksperymentu jest bardzo często prośbą o
zrobienie sekcji zwłok. Statystyk w takiej
sytuacji może tylko powiedzieć na co umarł
pacjent (ale nie może już mu pomóc)

Geniusz ale także zwolennik eugeniki

Pomysł prosty, ale nowy

Ocena zdolności dziecka przez nauczycieli –
czy jest trafna?

Jeśli jest 100% trafna to:
Dzieci mało zdolne Dzieci bardzo
zdolne
Średnia ocena dla:

dzieci mało zdolnych = 1 dzieci bardzo
zdolnych=6

Jakie wyniki mają pojedyncze dzieci?

Dzieci mało zdolne 1, 1, 1, Dzieci bardzo zdolne 6,
6, 6
wariancja wewnątrzgrupowa=0
Potraktujmy średnie grupowe jak zwykłe wyniki i
policzmy dla nich wariancję – wynosi ona 12,5 – to
jest wariancja międzygrupowa

Statystyki opisowe

12,500

SREDNIA

Wariancja

Co robi analiza wariancji?

Analiza wariancji porównuje:
wariancję międzygrupową (czyli tę, która określa
wielkość zróżnicowania średnich)
wariancją wewnątrzgrupową (nazywaną wariancją
błędu)
Statystyka F=war_my/war_wewn
Jaka jest wartość tej statystyki jeśli obie wariancje są
identyczne?

Czy wartość statystyki F może być ujemna?

F=1

Nie!

Analogia

Różnicę między średnimi w grupach
możemy przyrównać do interesującego nas
sygnału, zaś wariancję wewnątrz grup do
szumu. Dopóki sygnał nie będzie silniejszy
od szumu, nie usłyszymy go. Podobnie
dopiero gdy wariancja międzygrupowa
będzie odpowiednio duża, będzie się
wyróżniać na tle wariancji
wewnątrzgrupowej i będziemy mogli
stwierdzić istnienie istotnego efektu.

Analiza wariancji – podstawowe

informacje

Porównujemy więcej niż dwie grupy
Zmienna niezależna zwana tutaj czynnikiem jest
jakościowa
Zmienna zależna jest ilościowa

Pełna nazwa takiej analizy:
Jednoczynnikowa analiza wariancji w schemacie
międzygrupowym (bo porównujemy grupy
niezależne)

Ta analiza jest rozszerzeniem test T-Studenta dla
prób niezależnych

Hipoteza zerowa mówi – wszystkie średnie
grupowe są równe

Analiza wariancji – założenia

• Zbliżona liczebność w poszczególnych
podgrupach (testy nieparametryczne –Chi)

• Pomiary zmiennej zależnej powinny mieć
rozkłady normalne we wszystkich grupach.
(test Kołmogorowa – Smirnowa)

• Wariancje powinny być jednorodne w obrębie
wszystkich grup
(test Levene’a)

Test jednorodności wariancji

IQ1

6,370

2

21

,007

Test Levene'a

df1

df2

Istotność

Wydruk

 

 

Analiza wariancji

LICZBA DZIECI

466,889

2

233,445

100,014

,000

9371,513

4015

2,334

9838,402

4017

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

+

+

/

/

/

=

=

=

=

=

Suma kwadratów między dzielona przez df między daje średni
kwadrat między

To samo dla sumy kwadratów wewnątrz

Suma kwadratów między dodana do sumy kwadratów
wewnątrz daje sumę kwadratów ogółem

To samo dla stopni swobody

Oszacowanie

wariancji

Wydruk – stopnie swobody

Stopnie swobody międzygrupowe
df= liczba grup –1
Stopnie swobody wewnątrzgrupowe
df= liczba osób - liczba grup
Stopnie swobody ogółem
df= liczba osób – 1
Ile tutaj osób badanych? A ile grup?

Analiza wariancji

LICZBA DZIECI

466,889

2

233,445

100,014

,000

9371,513

4015

2,334

9838,402

4017

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Wydruk – zapis APA

F(2, 4015)=100,014; p<0,001

df między, df wewnątrz

Wniosek – grupy różnią się między sobą
Dlaczego warto robić analizę wariancji?

Analiza wariancji

LICZBA DZIECI

466,889

2

233,445

100,014

,000

9371,513

4015

2,334

9838,402

4017

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Przykład na danych – różnice między osobami o
głowie małej, przeciętnej i dużej w IQ.
Wzięto pod uwagę dwie skrajne grupy osób –
nie uzyskano istotnych statystycznie różnic

Test dla prób niezależnych

,012

,913

,612

14

,550

,612

13,998

,550

Założono równość
wariancji
Nie założono
równości wariancji

IQ

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Test t równości średnich

Statystyki dla grup

8 102,8750
8 102,2500

NTILES of GLOWA
1
3

IQ

N

Średnia

Jeśli weźmiemy pod uwagę

trzy

grupy

zobaczymy, że związek jest

krzywoliniowy i dlatego nie okazał

się istotny w teście T.

Jednoczynnikowa ANOVA

IQ

3285,083

2 1642,542

45,611

,000

756,250

21

36,012

4041,333

23

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

0

20

40

60

80

100

120

140

wielkość głowy

mała
przeciętna
duża

Statystyka T a statystyka F

F=T

2

Test dla prób niezależnych

,012

,913

,612

14

,550

,612

13,998

,550

Założono równość
wariancji
Nie założono
równości wariancji

IQ

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Test t równości średnich

Jednoczynnikowa ANOVA

IQ

1,563

1

1,563

,375

,550

58,375

14

4,170

59,938

15

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Testy post hoc – idea i

rodzaje

Podstawowa tabela analizy wariancji
mówi nam tylko, czy są różnice między
średnimi. Nie informuje nas o tym, które
średnie się różnią.
Jak to zrobić?
Wracamy do pomysłu zaczerpniętego z
testu T

Jednoczynnikowa ANOVA

IQ1

296,583

2

148,292

3,645

,044

854,375

21

40,685

1150,958

23

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

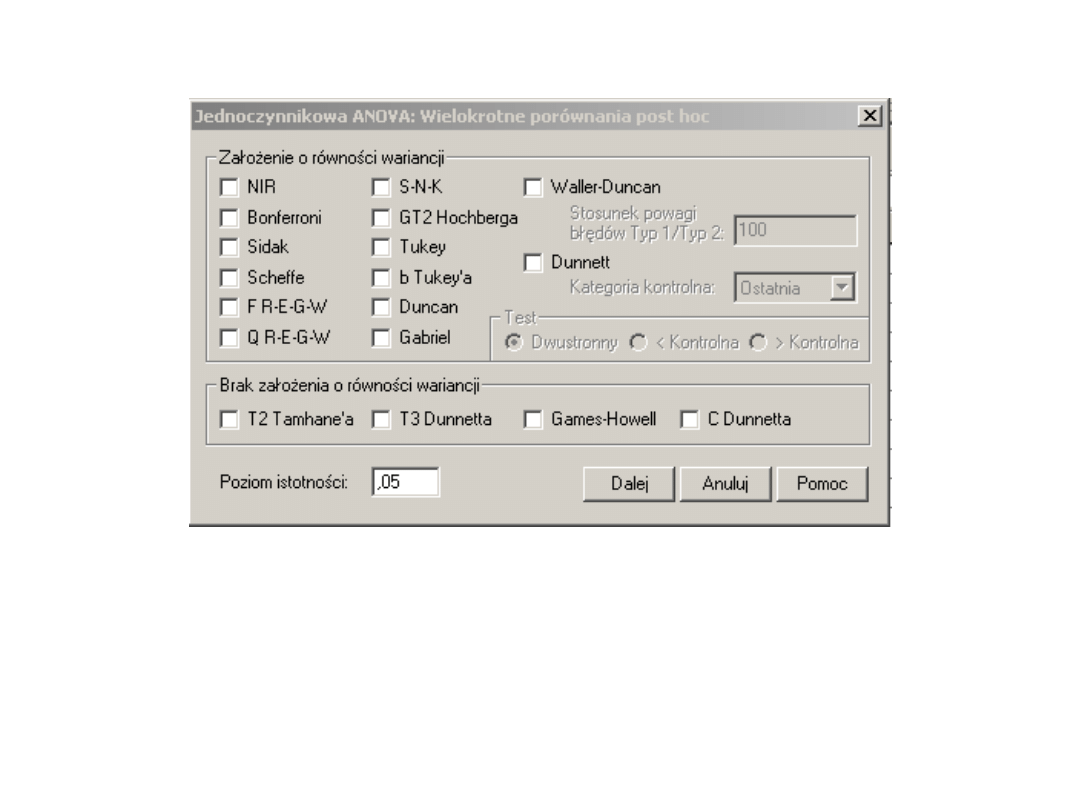
Testy post hoc - do wyboru do

koloru

SPSS oferuje wiele testów post hoc. Jak

wybrać?

Testy liberalne – NIR, SNK

Pośrednie – Duncan

Konserwatywne - Scheffe, Tukey

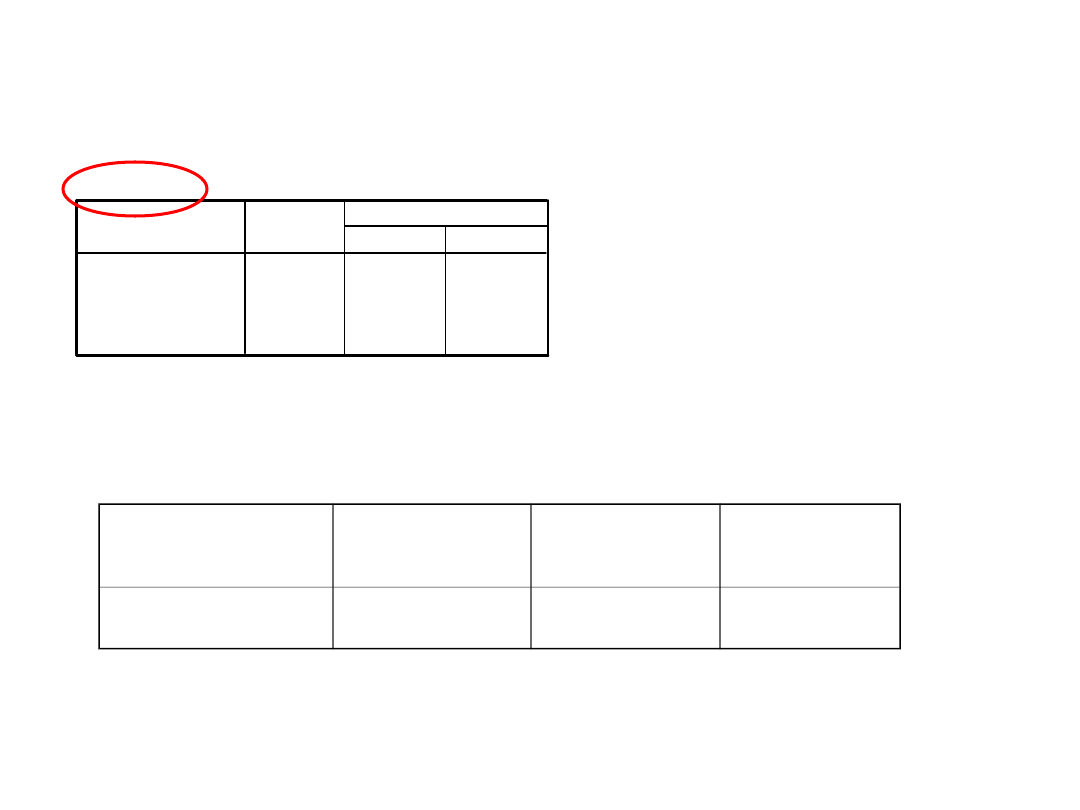
Testy post hoc - indeksy i

interpretacja

średnie, które się nie
różnią mają te same
indeksy
średnie, które się różnią
mają inne indeksy

IQ1

Test Duncana

a

8 102,2500
8 102,8750
8

110,0000

,847

1,000

NTILES of GLOWA
3
1
2
Istotność

N

1

2

Podzbiór dla alfa = .05

Wyświetlane są średnie dla grup jednorodnych.

Wykorzystywana jest średnia harmoniczna
wielkości próby = 8,000.

a.

Wielkość

głowy

mała

przeciętna

duża

Średni IQ 102,8

a

110

b

102,2

a

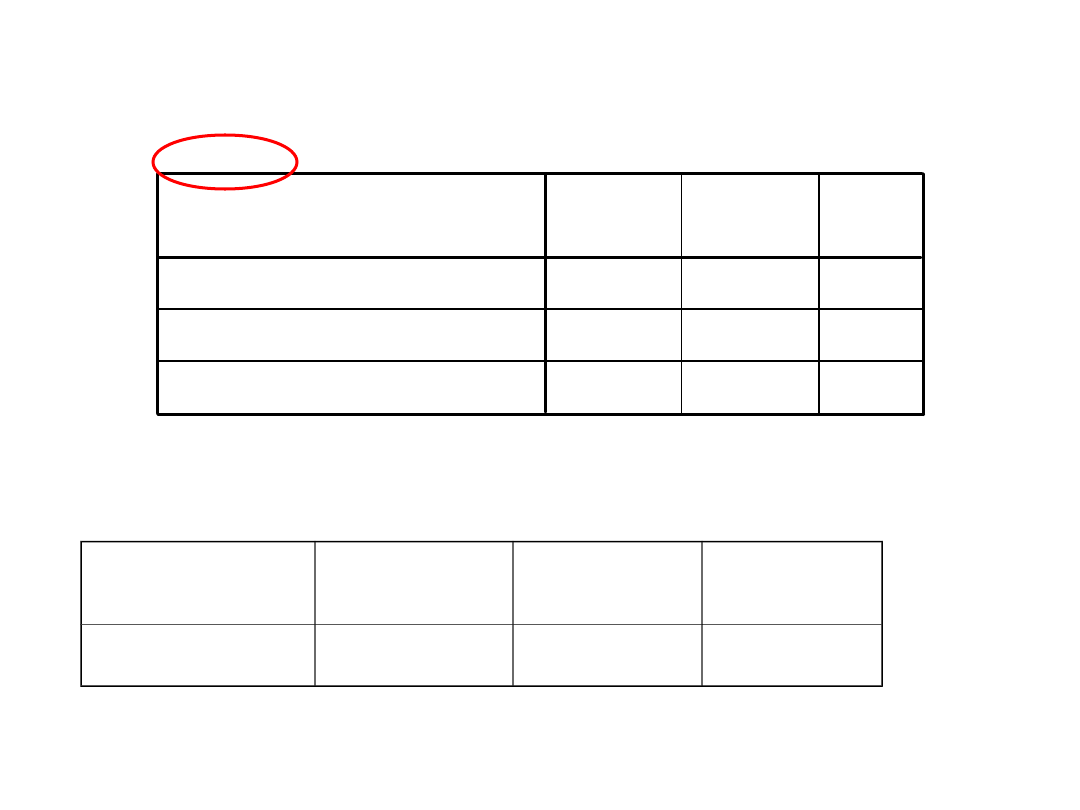
Porównania wielokrotne

Zmienna zależna: IQ1
Test Scheffe

-7,1250

3,18922

,107

,6250

3,18922

,981

7,1250

3,18922

,107

7,7500

3,18922

,074

-,6250

3,18922

,981

-7,7500

3,18922

,074

(J) NTILES of GLOWA
2
3
1
3
1
2

(I) NTILES of GLOWA
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

Wielkość

głowy

mała

przeciętna

duża

Średni IQ 102,8

110

102,2

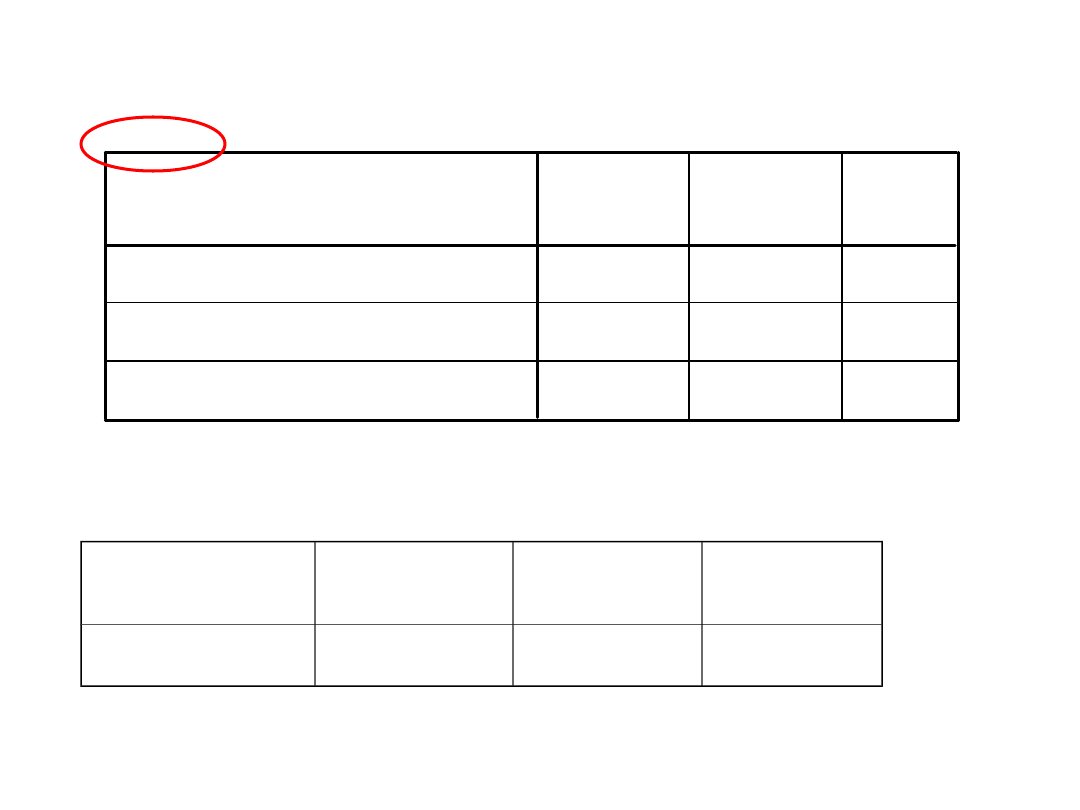
Porównania wielokrotne

Zmienna zależna: IQ1
Test NIR

-7,1250*

3,18922

,036

,6250

3,18922

,847

7,1250*

3,18922

,036

7,7500*

3,18922

,024

-,6250

3,18922

,847

-7,7500*

3,18922

,024

(J) NTILES of GLOWA
2
3
1
3
1
2

(I) NTILES of GLOWA
1

2

3

Różnica

średnich (I-J)

Błąd

standardowy

Istotność

Różnica średnich jest istotna na poziomie .05.

*.

Wielkość

głowy

mała

przeciętna

duża

Średni IQ 102,8

a

110

b

102,2

a

Testy post hoc - do wyboru do

koloru?

Konserwatywne testy post hoc - Scheffe,

Tukey – stosujemy wtedy, gdy ogólna

zależność jest silna i porównujemy dużą liczbę

grup a zależy nam na uchwyceniu wyrazistych

różnic

Testy liberalne – NIR, SNK – stosujemy wtedy,

gdy zależność jest bardzo słaba – na granicy

istotności statystycznej. Jest wtedy szansa, że

test post hoc w ogóle pokaże nam jakieś

różnice średnich.

Pośrednie – Duncan – to jest złoty środek

Istotność i jej związek z liczbą osób

badanych

Im więcej osób badanych tym mniejszy
poziom istotności. Tak więc sam poziom
istotności nie jest dobrą miarą porównań
badań robionych na różnych ilościach osób
badanych.

Aby porównywać wyniki pochodzące z
różnych badań potrzebna jest miara
niezależna od liczby osób

dane

R

2

– procent wyjaśnionej

wariancji

R

2

= SS między/ SS całkowita

R

2

=

Mając zatem standardowy zapis APA możemy
obliczyć ile wynosi R

2

, które informuje nas jaki

zakres zmienności zmiennej zależnej wyjaśnia
nasz czynnik - zależy nam oczywiście na tym,
żeby czynnik wyjaśniał jak najwięcej wariancji,
czyli 100%.
Przykład: F (2, 90)= 4; p<0,05

(F) (df
między)

(F) (df między) + df
wewnątrz

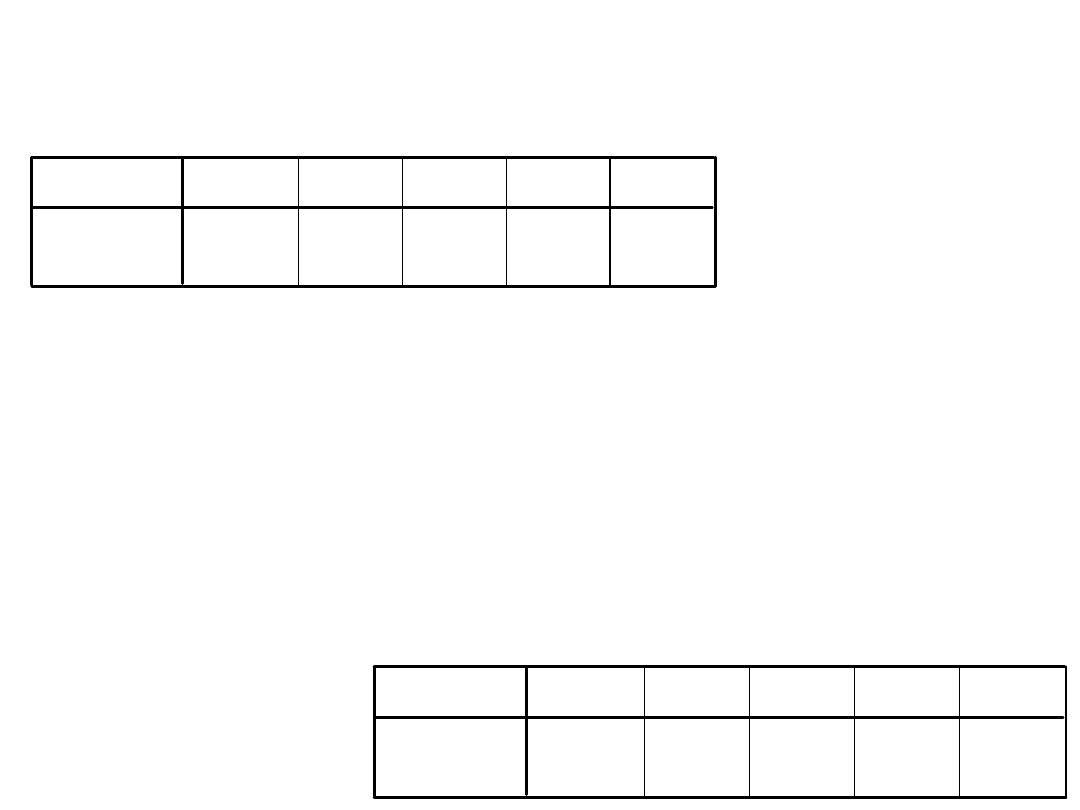
Istotność i jej związek z liczbą osób badanych-

wydruki

R

2

= SS my/ SS całkowita

Wydruk 1 - 24 osoby R

2

=296/1150=0,26

26%

Wydruk 2 – 71 osób R

2

=880/3443=0,26

26%

Jednoczynnikowa ANOVA

IQ1

296,583

2

148,292

3,645

,044

854,375

21

40,685

1150,958

23

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Jednoczynnikowa ANOVA

IQ1

880,433

2

440,217

11,679

,000

2563,060

68

37,692

3443,493

70

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Tabelka

Suma

kwadrató

w

D

F

Średni

kwadr

at

F

Poziom

istotno

ści

Między

grupami

Wewnątrz

grup

Ogółem

40
60

8

10

Suma

kwadrató

w

D

F

Średni

kwadr

at

F

Poziom

istotno

ści

Między

grupami

Wewnątrz

grup

Ogółem

80

40

20

0,66

7

Problem badawczy1

W badaniu nad związkiem temperamentu a
posiadaniem określonego rodzaju zwierzęcia
domowego przebadano łącznie 3400 hodowców
rybek, ptaszków i psów. Uzupełnij poniższą tabelę.

Suma

kwadrató

w

D

F

Średni

kwadr

at

F

Poziom

istotno

ści

Między

grupami

Wewnątrz

grup

Ogółem

250
6874

Przykład: jaki test zastosować?

1.

W jednej sali kinowej widzowie oglądali „Za wszelką
cenę”, a w drugiej „Meet the Fockers”. Po projekcji
zostali poproszeni o wypełnienie kwestionariusza
autorstwa Aarona Becka.

2.

Badacz chciał sprawdzić czy istnieją różnice
międzypłciowe w preferencjach dotyczących
kompozytorów muzyki filmowej. Osoby badane
deklarowały czy wolą muzykę Jana A. P. Kaczmarka czy
Zbigniewa Preisnera.

3.

Osoby badane miały zapamiętać ile Oscarów dostał
Martin Scorsese. Następnie obejrzały film Gangi
Nowego Jorku. Po projekcji zadano im pytanie „Na ile
Oscarów zasłużył Martin Scorsese?”. Czy istnieją
różnice między liczbą Oscarów zapamiętaną przed
obejrzeniem filmu a oszacowaniem po projekcji?

4.

Badacz chciał się dowiedzieć, czy pojawienie się Halle
Berry na rozdaniu „Malin” odniosło skutek reklamowy.
Po okresie 1 roku od rozdania „Malin” spytał osoby,
które uczestniczyły w tej uroczystości czy aktorka była
na gali.

Przykład: jaki test zastosować?

•

Chcemy sprawdzić czy istnieje związek między ilością
godzin spędzanych w kinie a reaktywnością emocjonalną.

•

Badacz chciał sprawdzić, czy Zdzisław Beksiński jest
bardziej popularny w Warszawie czy w Osace. W obydwu
miastach osoby badane odpowiadały czy wiedzą kim był
Zdzisław Beksiński.

•

Chcemy się dowiedzieć, czy średnia wieku wśród widowni
rzeczywiście wynosiła 14 lat, tak jak pisali w gazetach.

•

Chcemy sprawdzić, czy osoby o wysokiej wrażliwości
sensorycznej budzą się rzadziej (w ciągu nocy) od osób o
niskiej wrażliwości sensorycznej. W tym celu dzielimy
osoby badane wg proporcji 33:33:33.

•

Rozkład wyników jest silnie zaburzony, wariancje nie są
homogeniczne a test chi-kwadrat jest istotny statystycznie.
Czy w takim przypadku korzystamy z testu t?