Dwuczynnikowa analiza

wariancji – zaawansowane plany

eksperymentalne

Wyjaśnienie

Psychologowie mają wyższy poziom dominacji niż

ludzie innych zawodów.

• Dlaczego?
• Bo my chcemy wpływać na innych ludzi
• A zatem psychologia jako nauka próbuje

dostarczyć nam informacji o:

• Na kogo działają określone „sztuczki”
• Jak one działają (co zmienia w psychice odbiorcy

określona „sztuczka”?)

Rzeczywistość

Jednostka

Środowisk
o

Środowisk
o fizyczne

Środowisk
o
społeczne

Kto osiągnie sukces po miesięcznym treningu

jogi?

Cechy
fizyczne

Cechy
psychiczne

Osoba,

która dużo

ćwiczy -

wysiłek

Osoba, która

ma giętkie

ścięgna

Osoba,

która chce

być

atrakcyjna

Osoba, która spełnia wszystkie te warunki:

Ma giętkie ścięgna i (jednocześnie) dużo

ćwiczy i (jednocześnie) chce być atrakcyjna

Złożony plan eksperymentalny

• Dodając kolejną zmienną, z prostego

badania tworzymy badanie bardziej
złożone

• Plany złożone – wykorzystywane do

testowania wpływu dwóch lub więcej
zmiennych niezależnych w jednym
badaniu

• Każda zmienna może być badana w

ramach planu międzygrupowego lub w
planie powtarzanych pomiarów

Test dla prób niezależnych

76,142

,000

-1,644

58

,106

-1,644

35,154

,109

Założono równość
wariancji
Nie założono
równości wariancji

atywność poznawcza

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Test t równości średnich

Badanie 1 - chronotyp

• Chronopsychologia – czy „ranne ptaszki” inaczej

funkcjonują niż „sowy” (W. Ciarkowska)?

• Sprawdzamy jak rozwiązują dosyć trudne zadanie

poznawcze.

• Wynik:

Statystyki dla grup

4,9333

,69149

5,6000

2,11073

RAN_WIEC
ranne ptaszki
sowy

atywność poznawcza

Średnia

Odchylenie

standardowe

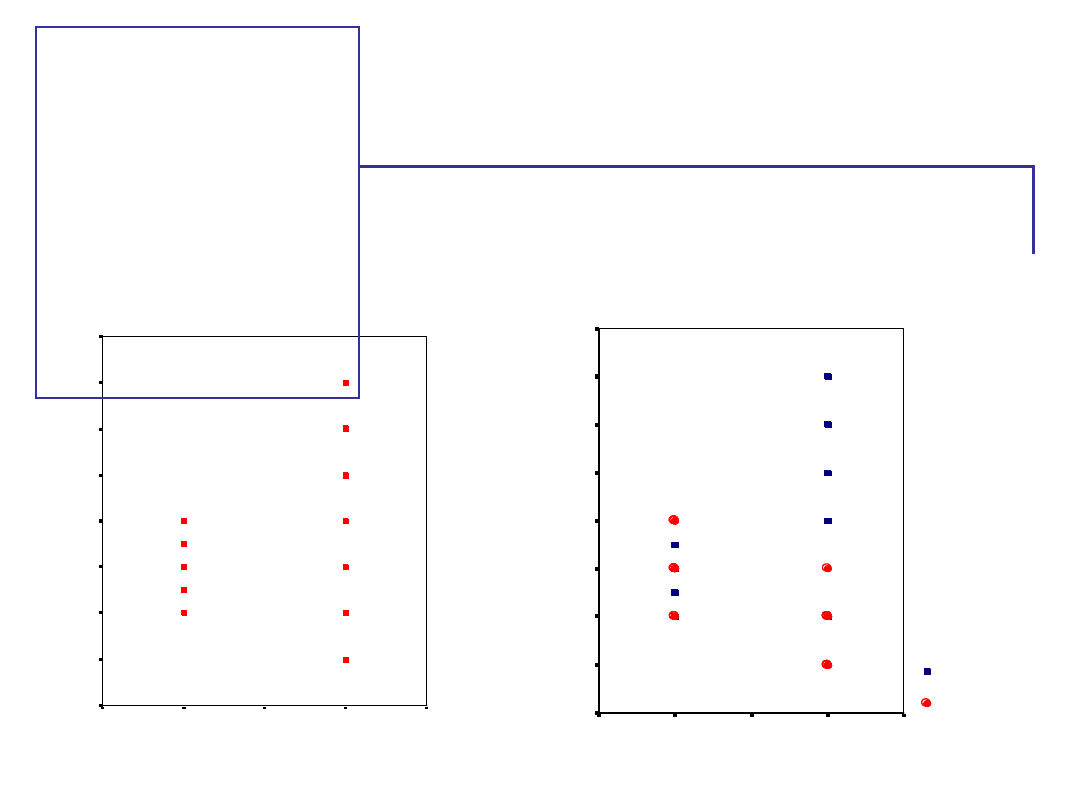
Zobaczmy ten wynik na

wykresie

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

Być może
pominęliśmy jakąś
ważną zmienną –
skoro badamy
funkcjonowanie
różnych
chronotypów, to
może warto wziąć
pod uwagę porę
dnia

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

PORA

wieczorem

rano

Statystyki dla grup

4,9333

,69149

5,6000

2,11073

RAN_WIEC
ranne ptaszki
sowy

atywność poznawcza

Średnia

Odchylenie

standardowe

Gdy uwzględnimy porę

dnia

Dzięki
uwzględnieniu
dodatkowego
czynnika – pory
dnia - wariancja
wewnątrzgrup się
wyrównuje

Statystyki opisowe

Zmienna zależna: atywność poznawcza

5,2000

,77460

3,6667

,61721

4,4333

1,04000

4,6667

,48795

7,5333

,91548

6,1000

1,62629

4,9333

,69149

5,6000

2,11073

5,2667

1,59306

RAN_WIEC
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem

PORA
rano

wieczorem

Ogółem

Średnia

Odchylenie

standardowe

Kombinacja czynników

• Zestawiamy każdy poziom jednej zmiennej

niezależnej (pierwszego czynnika) ze
wszystkimi poziomami drugiej zmiennej
niezależnej (drugiego czynnika), w naszym
przykładzie „typy ranne” były testowane
zarówno rano jak i wieczorem, tak samo „typy
wieczorne”

• Liczba warunków eksperymentalnych

opartych na planie złożonym jest równa
iloczynowi poziomów czynników, np. 2 x 2 =
4; 3 x 3=9 itd.

Złożony plan eksperymentalny

• W najprostszej postaci jest to schemat z

dwiema zmiennymi niezależnymi na
dwóch poziomach (2 x 2 – „dwa na dwa”)

• Do analizy takich schematów

wykorzystujemy dwuczynnikową analizę
wariancji – najprostszy przypadek
wieloczynnikowej analizy wariancji

W dwuczynnikowej analizie wariancji

mamy możliwość oszacowania:

• Osobno wpływu każdej zmiennej niezależnej na

zależną

dwa efekty główne

– Ogólny efekt pory dnia bez uwzględniania wpływu

chronotypu

– Ogólny efekt chronotypu bez uwzględniania wpływu

pory dnia

• Łączny efekt zmiennych niezależnych –

efekt interakcji

– Łączny wpływ obu zmiennych niezależnych na zmienną

zależną

Interakcje

• Pomagają ogarnąć złożoność

interesujących nas zjawisk

• Zamiast poprzestawać na pytaniach o to

– Czy występują różnice między typami rannymi

i wieczornymi w rozwiązywaniu zadań
umysłowych?

• Możemy pytać:

– Jak funkcjonują „ranne ptaszki” oraz „sowy” w

różnych porach dnia?

Możliwe scenariusze wyników

Efekt główny

pory dnia

Efekt główny

chronotypu

Interakcja

pory dnia i

chronotypu

-

-

-

+

-

-

-

+

-

-

-

+

+

+

-

+

-

+

-

+

+

+

+

+

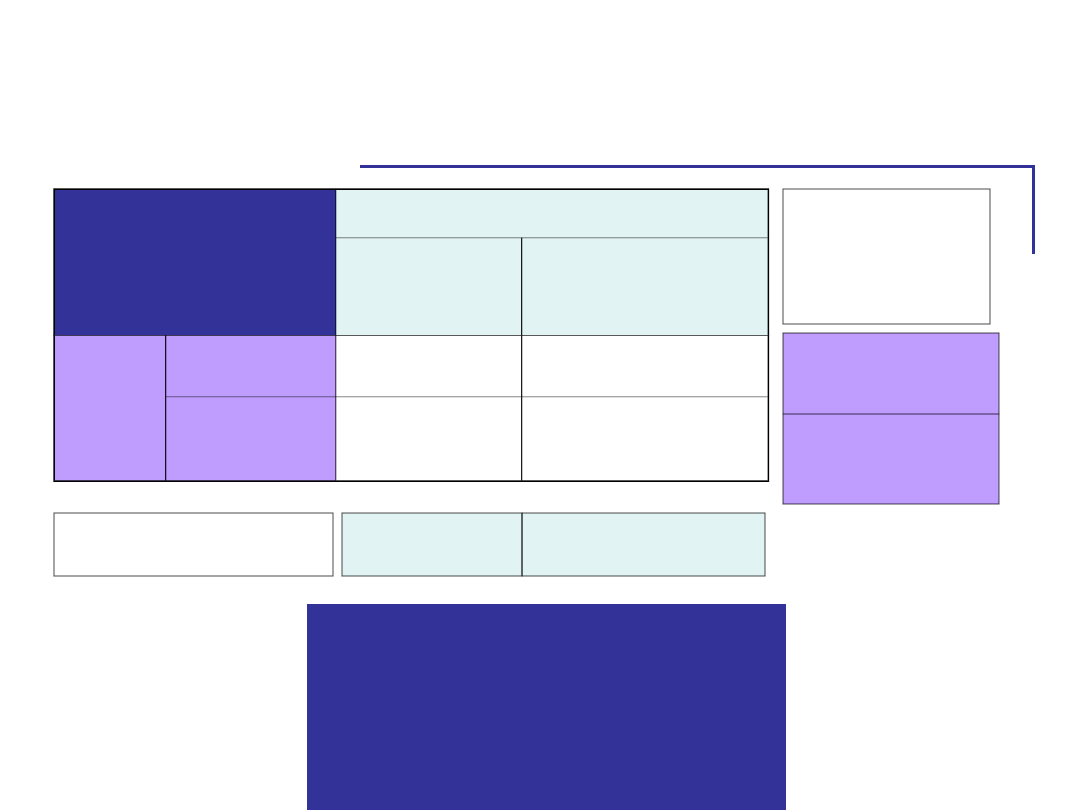
Przyglądamy się efektom głównym

Zmienne

niezależne

Chronotyp

RANNY

WIECZORNY

Pora

RANO

5,2

3,7

WIECZÓ

R

4,7

7,5

4,4

6,1

4,9

5,6

Średnie
wierszy

Średnie kolumn

Jeżeli średnie z wierszy
różnią się wskazuje to efekt
główny Pory.
Jeżeli różnią się średnie z
kolumn sugeruje to efekt
główny Chronotypu

Obliczanie średnich dla efektów

głównych

Średnie dla efektów głównych zostały obliczone na

podstawie średnich w poszczególnych celkach,

- dla efektu głównego zmiennej Chronotyp

uśredniliśmy wyniki w kolumnach,

- dla efektu głównego drugiej zmiennej średnia została

wyciągnięta z poszczególnych wierszy; np.

średnia dla

Chronotypu rannego została obliczona poprzez wyciągnięcie średniej

z wyników osiąganych przez te osoby rano i wieczorem (5,2 + 4,7)/2 =

4,9.

- Można w ten sposób obliczać średnie dla efektów

głównych tylko wtedy, gdy liczba osób w

poszczególnych kratkach jest taka sama, inaczej

trzeba stosować poprawkę na nierówną liczbę osób.

Kiedy interakcja?

• Mamy do czynienia z interakcją, gdy wpływ

pierwszej zmiennej niezależnej zmienia się,
kiedy przechodzimy na kolejne poziomy drugiej
zmiennej niezależnej - Zmiana musi być istotna
statystycznie.

• Tutaj przydają się porównania planowane

Metoda odejmowania do szukania

interakcji

•

Interpretacja efektu interakcyjnego polega na analizie
efektów prostych lub porównań analitycznych (gdy
zmienna niezależna posiada trzy lub więcej poziomów).

Efekt prosty (simple effect): wpływ jednej zmiennej

niezależnej, który zachodzi na określonym poziomie
drugiej zmiennej niezależnej

•

Parząc na średnie w tabelce o interakcji możemy
wnioskować na podstawie prostej metody
odejmowania.

Polega ona na porównywaniu między sobą różnic między

średnimi z każdego wiersza (lub kolumny).

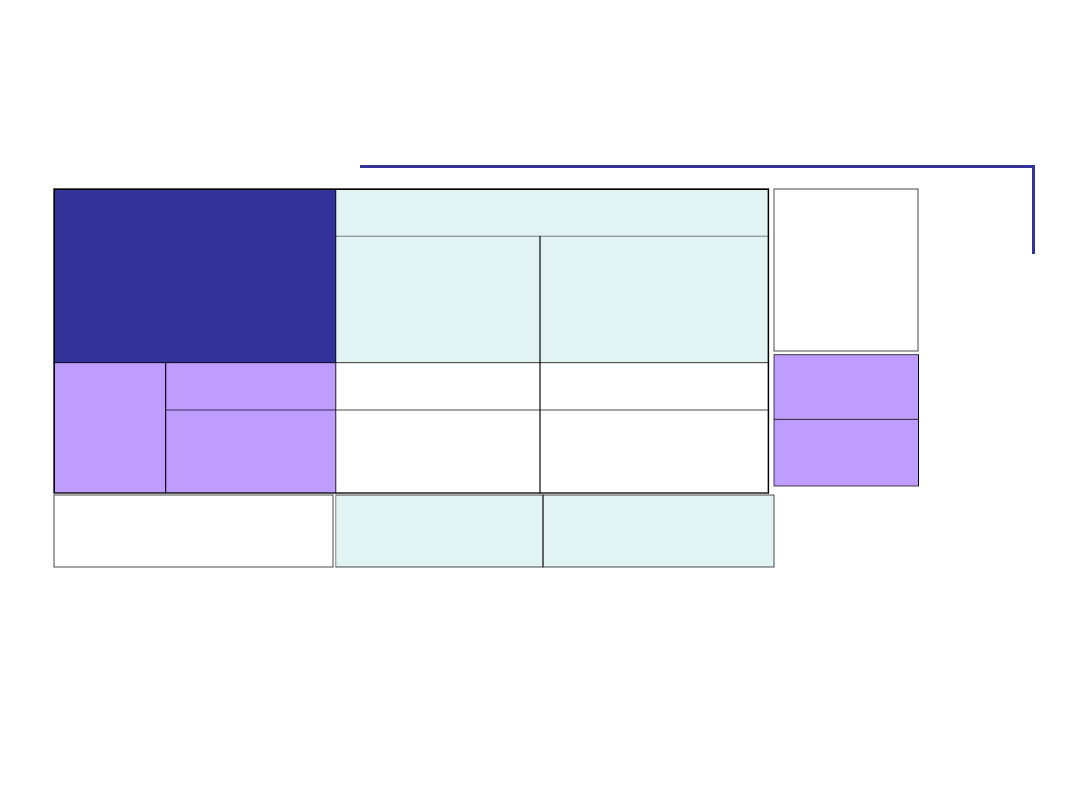
W naszym przykładzie

Zmienne

niezależne

Chronotyp

RANNY

WIECZORNY

Pora

RANO

5,2

3,7

WIECZÓ

R

4,7

7,5

1,5

-2,8

0,5

-3,8

Różnica

Różnica

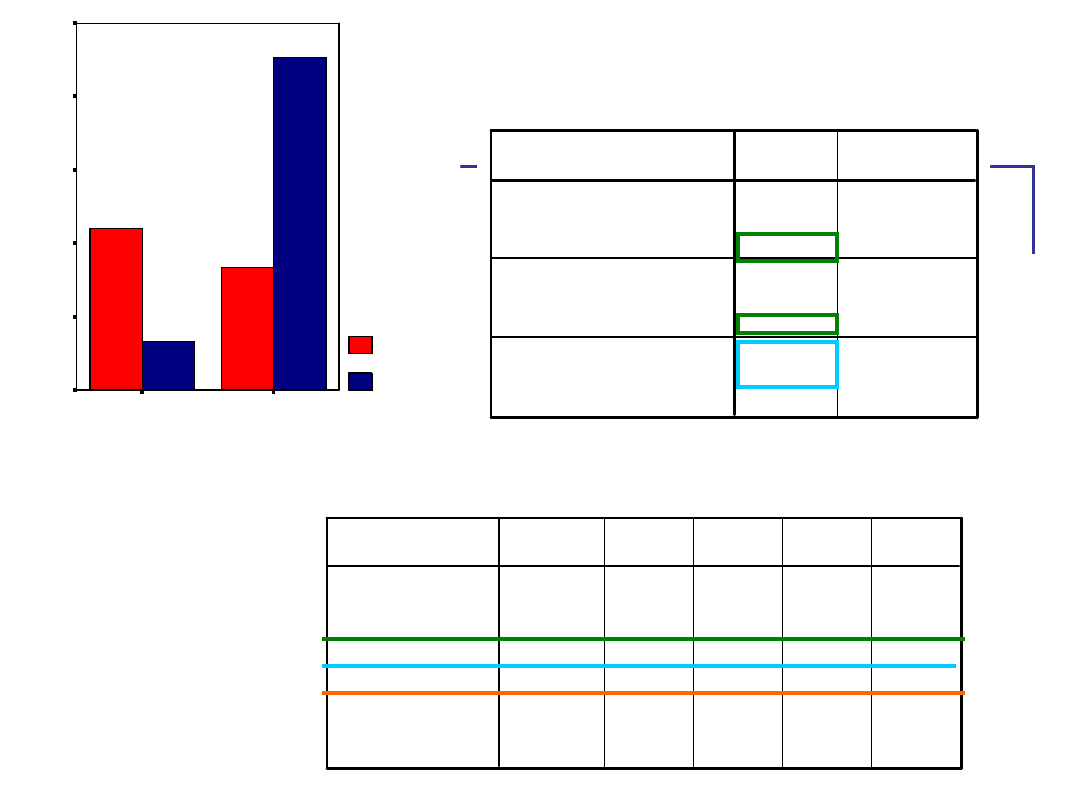
Testy efektów międzyobiektowych

Zmienna zależna: atywność poznawcza

120,933

a

3

40,311

78,383

,000

1664,267

1 1664,267 3236,074

,000

41,667

1

41,667

81,019

,000

6,667

1

6,667

12,963

,001

72,600

1

72,600

141,167

,000

28,800

56

,514

1814,000

60

149,733

59

Źródło zmienności
Model skorygowany
Stała
PORA
RAN_WIEC
PORA * RAN_WIEC
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,808 (Skorygowane R kwadrat = ,797)

a.

Statystyki opisowe

Zmienna zależna: atywność poznawcza

5,2000

,77460

3,6667

,61721

4,4333

1,04000

4,6667

,48795

7,5333

,91548

6,1000

1,62629

4,9333

,69149

5,6000

2,11073

5,2667

1,59306

RAN_WIEC
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem

PORA
rano

wieczorem

Ogółem

Średnia

Odchylenie

standardowe

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

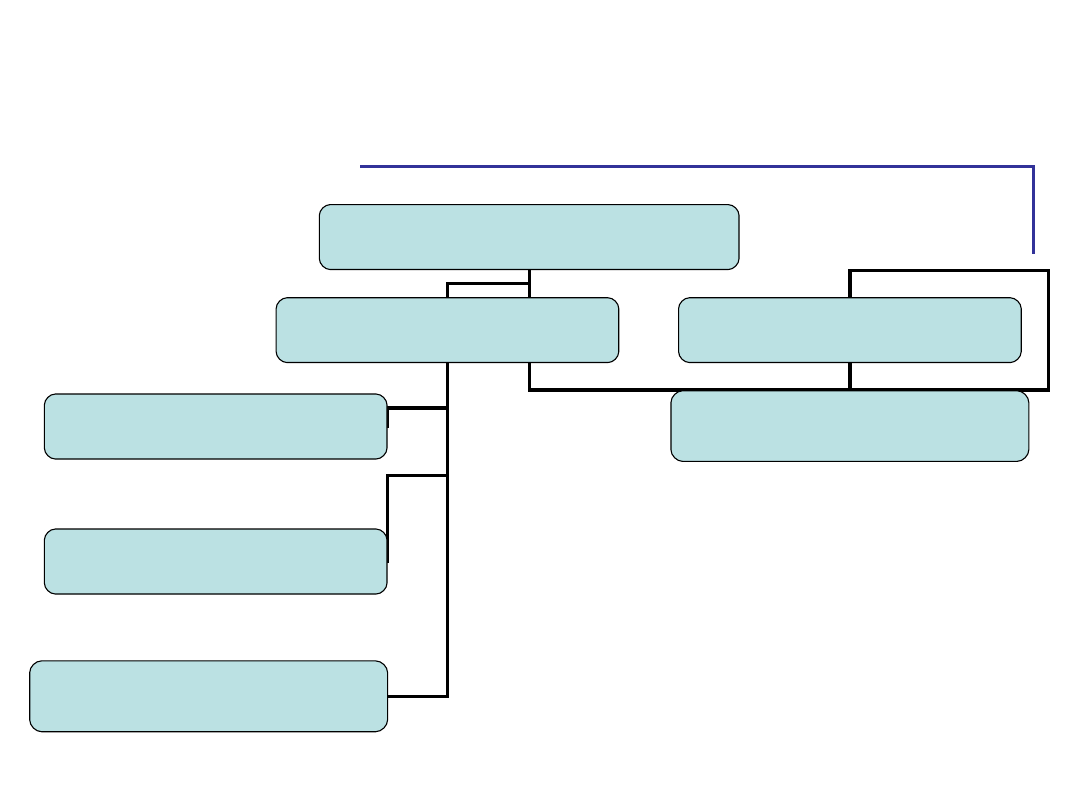
Podział wariancji

Całkowita wariancja

wyjaśniona

niewyjaśniona

Interakcja

błędu

1 zmienna

2 zmienna

Stopnie swobody

zmiennej

2

poziomów

liczba

-

zmiennej

1

poziomów

liczba

-

)

1

(

)

1

(

interakcji

efekt

1

1

glowne

efekty

2

1

2

1

12

2

2

1

1

k

k

k

k

df

k

df

k

f

















ZN

1

poziomow

liczba

-

celce

w

osób

liczba

-

badaniu

w

osób

liczba

-

1

)

1

(

1

2

1

2

1

k

n

N

N

df

ogolem

n

k

k

df

k

k

N

df

o

bledu

bledu













Badanie 2 - Zdolności językowe – efekty główne

Płeć

Presja czasu

TAK NIE

mężczyzna

5

2

kobieta

2

5

Średnie

3,5

3,5

• Osoby badane (kobiety i mężczyźni) zostały poproszone o

wymyślenie krótkich rymowanek tzw. Lepiejów i odwódek

Lepszy teść obleśny

piernik
Niźli z tej cukierni

sernik

Lepsze uszkodzenie
grdyki
Niż uczenie statystyki

Od wódki rozum krótki

Od Anovy bóle głowy

Badanie 2 - Zdolności werbalne – szukanie

interakcji

Na przykład porównujemy różnice średnich między wierszami:

• 5-2= 3
• 2-5 = -3

– Widać, że różnice średnich w obu rzędach są różne stąd możemy

wnioskować, że zapewne mamy do czynienia z interakcją.
• Przy liczeniu różnic ważne jest, aby zawsze odejmować w tę samą

stronę, ponieważ ważny jest znak różnicy.

Płeć

Presja czasu

TAK NIE

mężczyzna

5

2

kobieta

2

5

Badanie 3

Zdolności przestrzenne a płeć i

uszkodzenie półkul

przykład – oprac. dr.Izabela

Krejtz

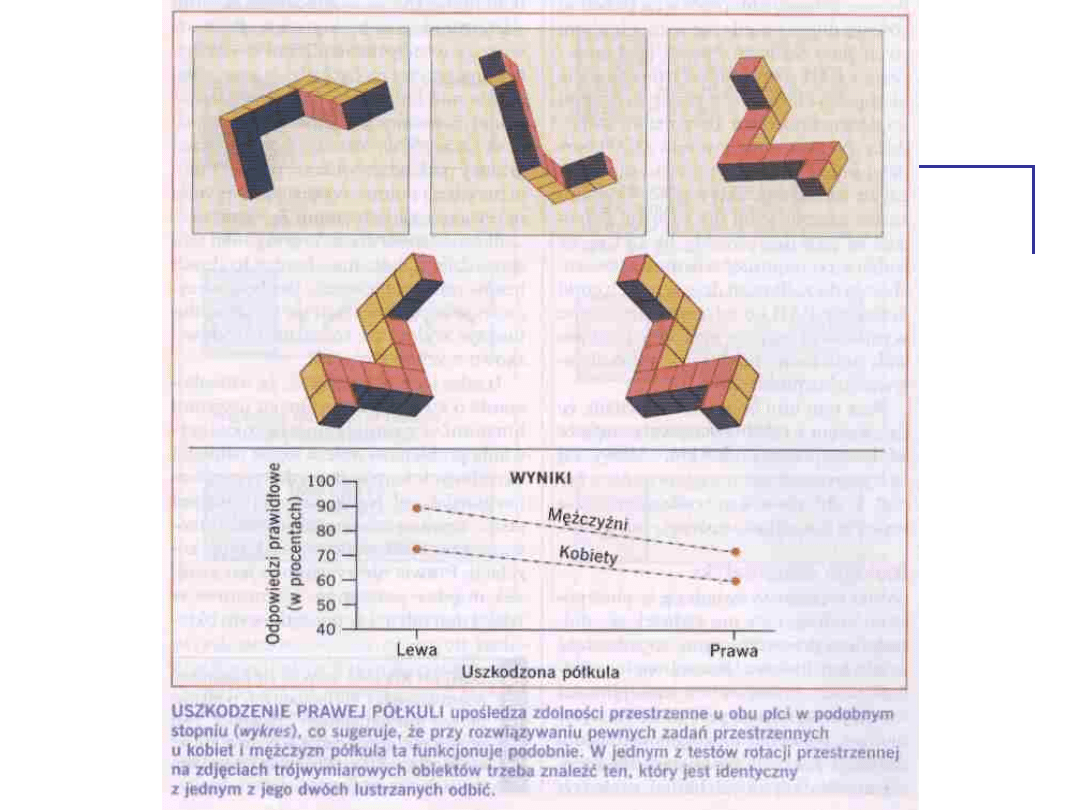
Przyglądamy się efektom

głównym

Zmienne

niezależne

USZKODZONA PÓŁKULA

LEWA

PRAWA

PŁEĆ

K

70

60

M

90

80

65
85

80

70

Średn

ie

wiers

zy

Średnie kolumn

Jeżeli średnie z wierszy różnią się wskazuje to efekt
główny Płci
Jeżeli różnią się średnie z kolumn sugeruje to efekt główny
Półkuli

Szukamy interakcji

Zmienne

niezależne

USZKODZONA PÓŁKULA

LEWA

PRAWA

PŁEĆ

K

70

60

M

90

80

70-60=

10
90-80=

10

70-90=-20

60-80=-20

Różnice
średnich

Różnice

średnich

Różnice średnich w wierszach są takie same
–
Brak interakcji

Badanie 4 – wpływ pobudzenia i trudności

zadania na jego wykonanie

Szukamy efektów głównych

Zmienne

niezależne

Pobudzenie

niskie

wysokie

zadani

e

Trud

ne

50

20

Łatw

e

30

40

35

35

40

30

Średnie

Średnie

Brak efektu głównego zadania
Efekt główny pobudzenia

Co mam mówią średnie brzegowe

• Jeśli spojrzymy na średnie brzegowe dla efektu

pobudzenia, widać, że są sobie równe, co

wskazuje na brak efektu głównego tej zmiennej.

• Brak efektu głównego zmiennej nie świadczy o

tym, że ta zmienna w ogóle nie działa.

• Możliwe, że pojawiła się interakcja między

poziomem pobudzenia a trudnością zadania.

– Jeśli nie ma interakcji między wpływem zmiennych

niezależnych wtedy efekty główne mogą być

analizowane tak jak w przypadku dwóch oddzielnych

eksperymentów z jedną zmienną niezależną.

Szukamy efektu

interakcyjnego

Zmienne

niezależne

Pobudzenie

niskie

wysokie

zadani

e

Trud

ne

50

20

Łatw

e

30

40

30

-10

20

-20

Różnica
średnich

Różnica

średnich

Różnice w kolumnach i wierszach są różne
więc jest efekt interakcyjny

Efekt interakcyjny

• Należy pamiętać że zależność interakcyjna

działa w obie strony oznacza to, że jeśli jedna

zmienna niezależna wchodzi w interakcję z

drugą zmienną niezależną, ta druga również

musi wchodzić w interakcję z pierwszą.

– Stąd można różnie sformułować konkluzję

płynącą z efektu interakcyjnego, zależnie od

tego, na którą zmienną chcemy położyć większy

nacisk komentując wyniki analiz; który aspekt

interakcji jest dla nas ważniejszy.

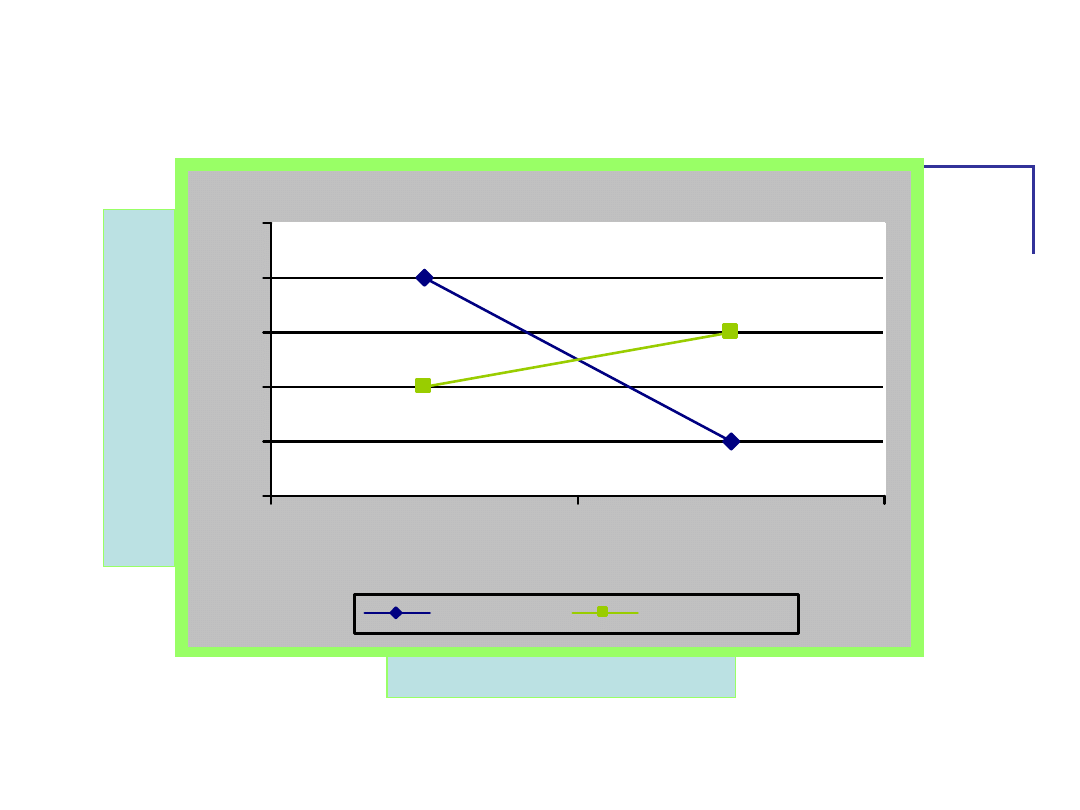
Jak te zależności widać na

wykresie?

Pobudzenie

Po

zi

o

m

w

y

ko

n

a

n

ia

za

d

a

n

ia

10

20

30

40

50

60

niskie

wysokie

zadanie łatwe

zadanie trudne

Wykresy

• Efekt interakcyjny jest dobrze

widoczny na wykresie.

– Kiedy linie na wykresie przecinają się lub

istnieje szansa, że kiedyś się przetną,
czyli nie są równoległe względem siebie,
wtedy możemy przypuszczać, że analiza
statystyczna wykaże istotną interakcję.

– Jeśli linie na wykresie są równoległe,

możemy liczyć tylko na efekty główne.

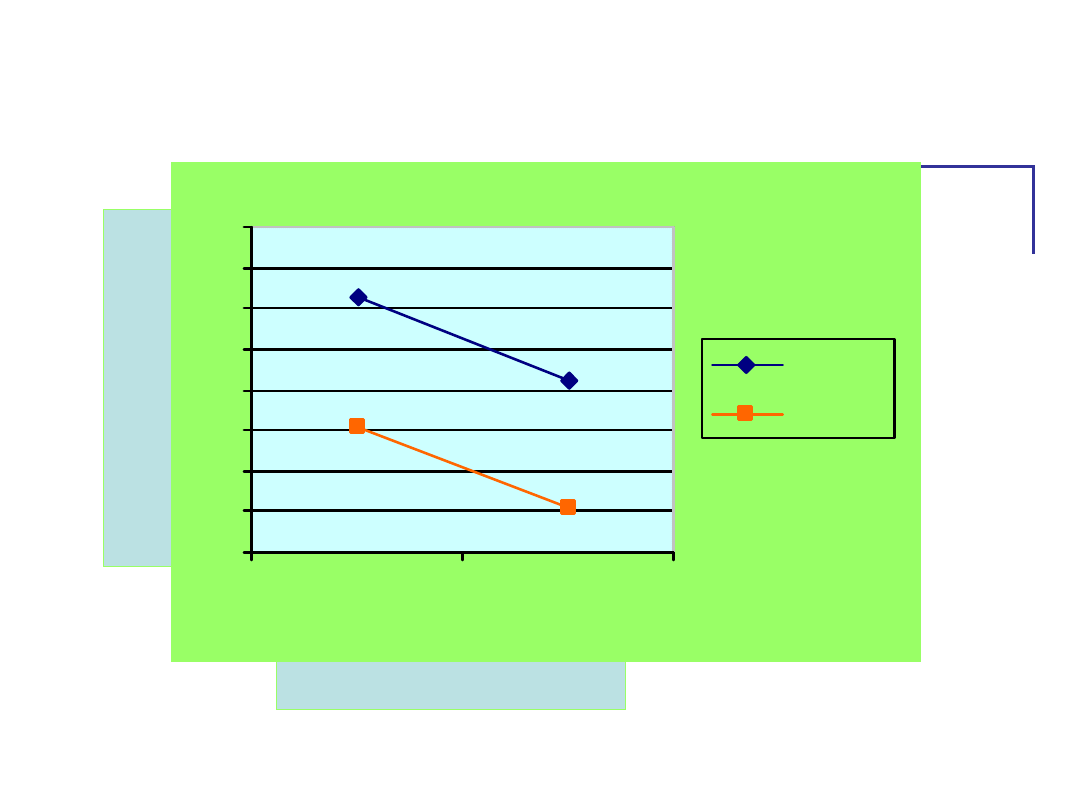
Jakie efekty widać na tym wykresie?

lęk

Po

zi

o

m

w

y

ko

n

a

n

ia

za

d

a

n

ia

0

1

2

3

4

5

6

7

8

niski

wysoki

łatwe
trudne

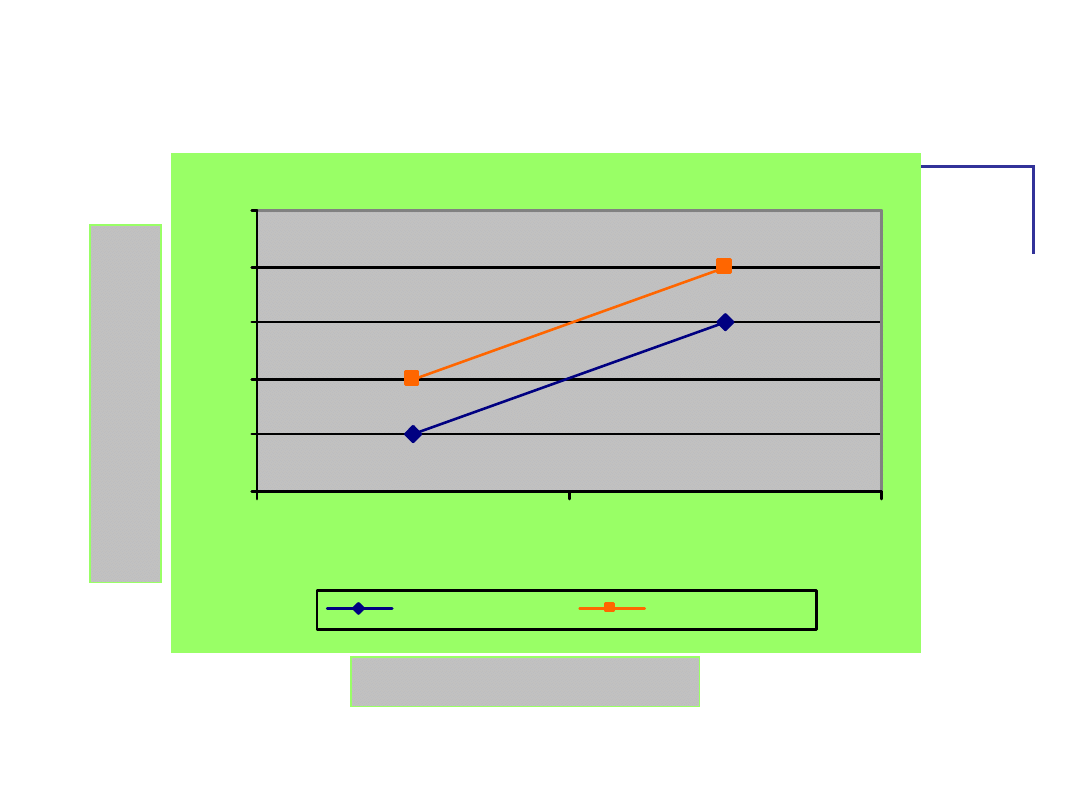
Średni czas reakcji na bodziec

właściwy.

Liczba dystraktorów

C

za

s

re

a

kc

ji

w

m

se

c.

400

500

600

700

800

900

mało

dużo

zadanie pojedyncze

zadanie podwójne

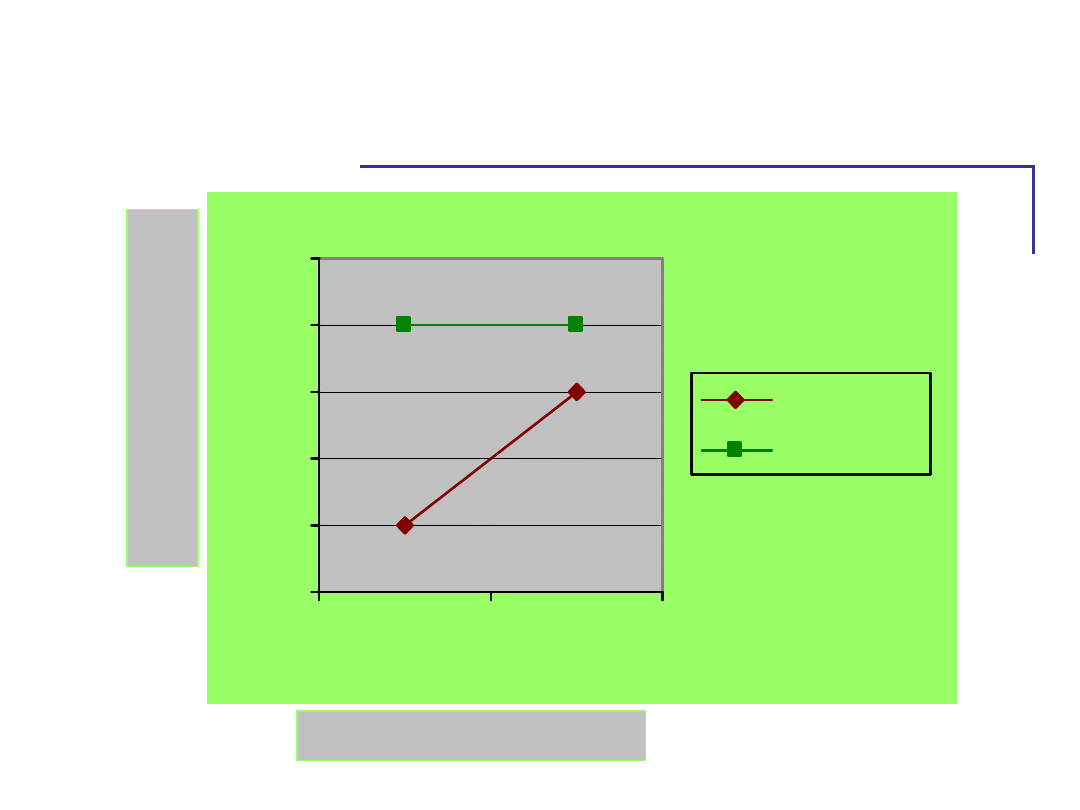
Średni czas reakcji na bodziec

właściwy.

Liczba dystraktorów

C

za

s

re

a

k

cj

i

w

m

se

c.

400

500

600

700

800

900

mało

dużo

pojedyn.
podwójne

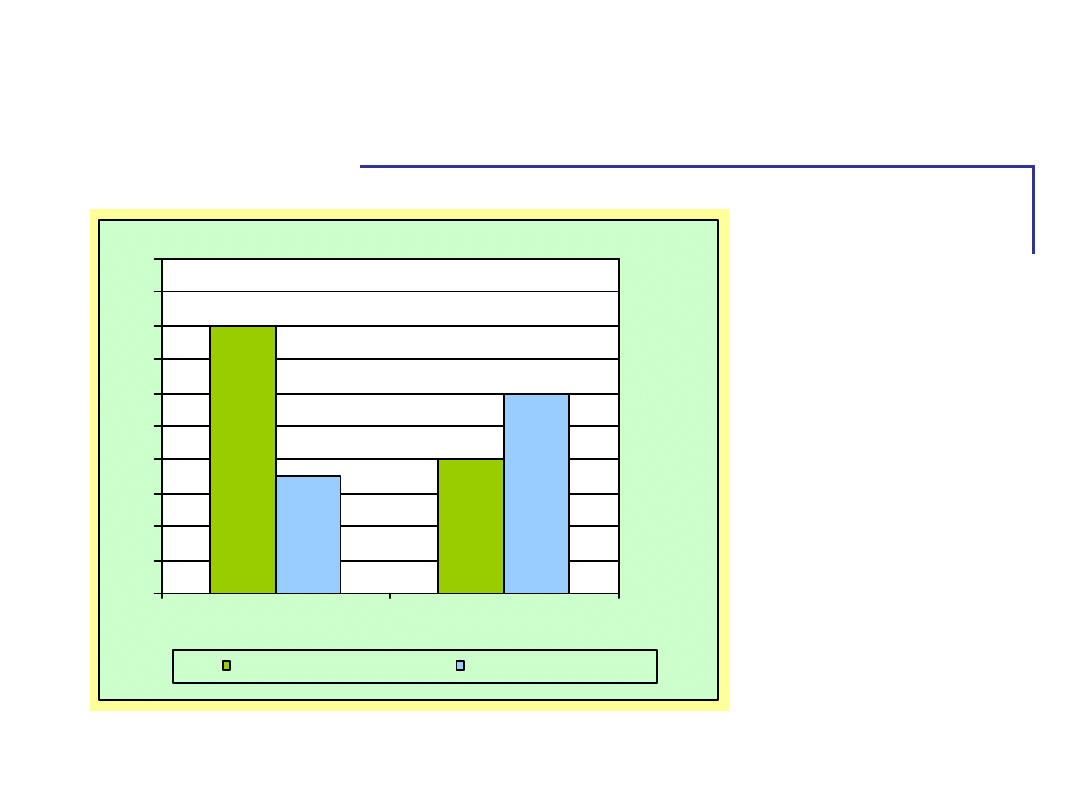
Średnia liczba zapamiętanych określeń jako

funkcja rodzaju cech i poziomu uprzedzeń

8

4

3,5

6

0

1

2

3

4

5

6

7

8

9

10

uprzedzone

nieuprzedzone

cechy stereotypowe

cechy niestereotypowe

Badanie 4 Zjawisko zagrożeniem

stereotypem

Osobami badanymi są członkowie grup co do których

istnieje powszechna, stereotypowa opinia, że są gorsi
w jakiejś dziedzinie np. policjantów o których mówi
się, że są głupi, kobiety rzekomo gorsze z matematyki.

Podczas rozwiązywania testu inteligencji przypomina się

policjantom stereotypową opinię – to obniża wynik
testu inteligencji, ale tylko tym policjantom dla
których bycie inteligentnym jest ważne. W sytuacji
neutralnej policjanci są tak samo inteligentni jak
grupa kontrolna

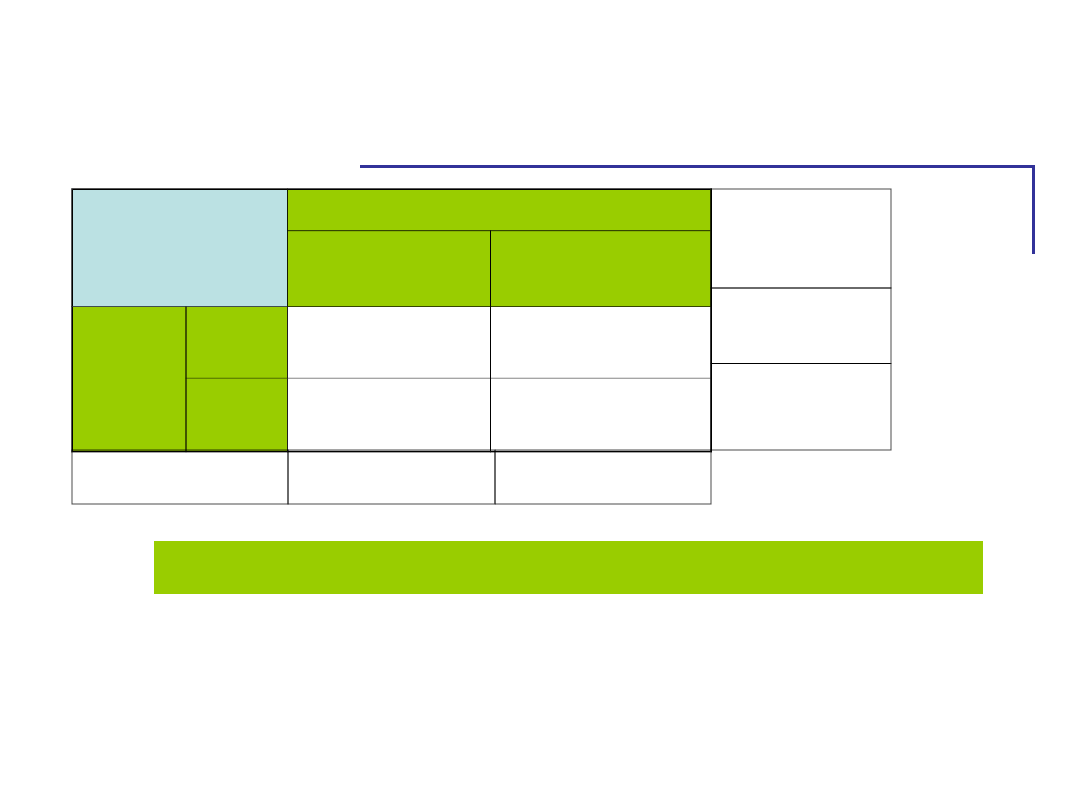
Szukamy efektów głównych

Zmienne

niezależne

Zagrożenie stereotypem

niskie

wysokie

płeć

K

50

20

M

50

50

30

50

50

35

Średnie

Średnie

Pojawiają się oba efekty główne

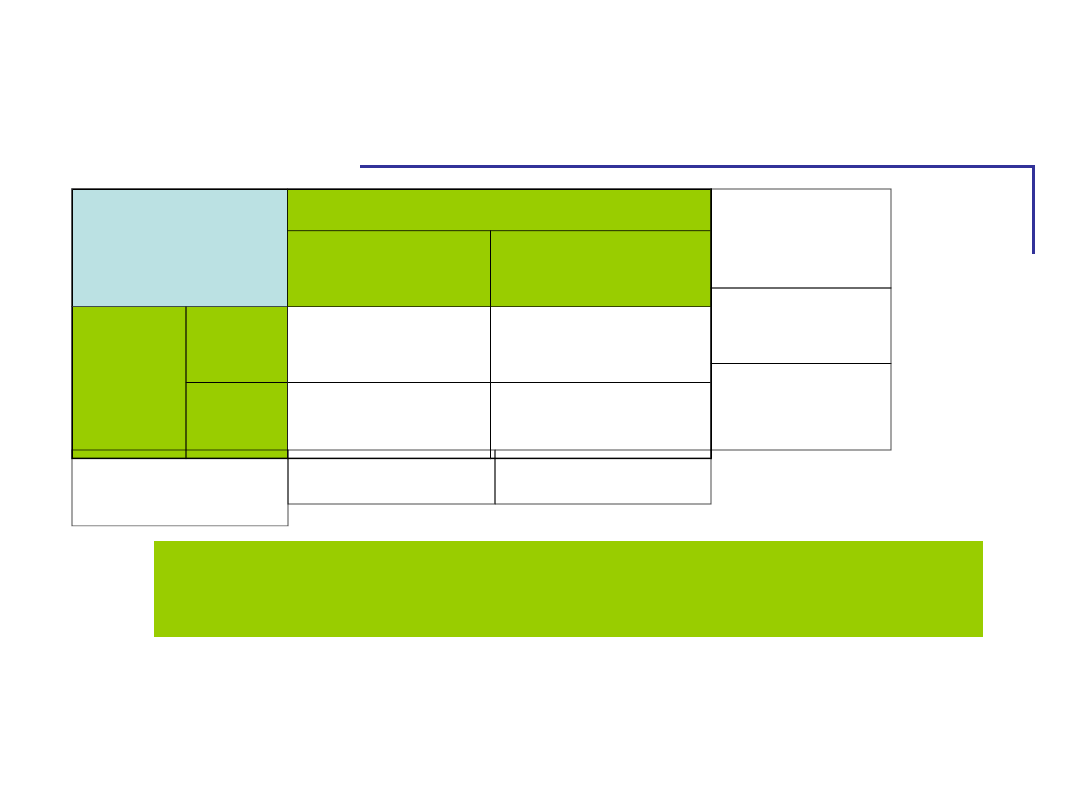
Szukamy efektu

interakcyjnego

Zmienne

niezależne

Pobudzenie

niskie

wysokie

zadani

e

Trud

ne

50

20

Łatw

e

50

50

20

0

0

-30

Różnica
średnich

Różnica

średnich

Różnice w kolumnach i wierszach są różne
więc jest efekt interakcyjny

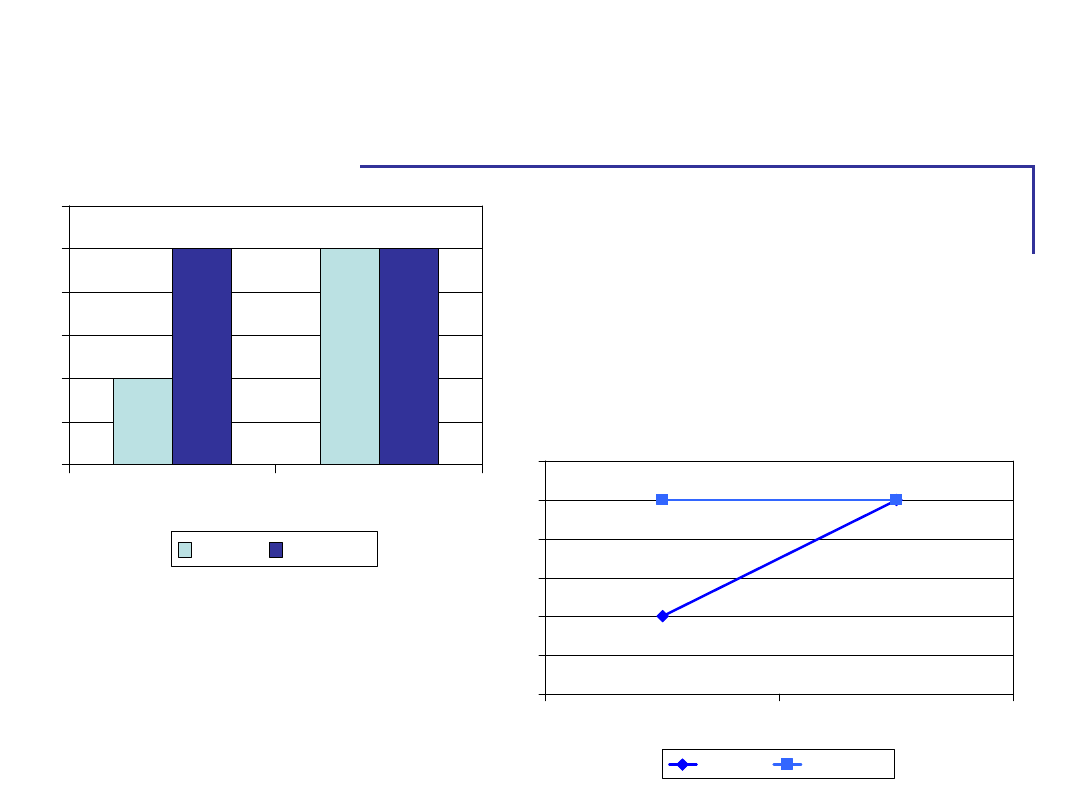
Wykresy

Są wszystkie

możliwe efekty

20

50

50

50

0

10

20

30

40

50

60

zagrożenie stereotypem sytuacja neutralna

kobiety mężczyźni

0

10

20

30

40

50

60

zagrożenie stereotypem

sytuacja neutralna

kobiety

mężczyźni

Rozstrzygnięcia ostateczne

• Oczywiście nigdy nie decydujemy na oko,

tylko robimy wydruk i patrzymy na
poziomy istotności.

• Jeśli mamy schemat 2x 2 i eekty główne są

istotne to patrzymy już tylko na średnie,
aby zinetrpretować efekt.

• Do efekty interakcyjnego musimy robić

testy post hoc albo kontrasty.

Zagrożenie stereotypem -

wydruk

Testy efektów międzyobiektowych

Zmienna zależna: ZADANIE

512,900

a

3

170,967

51,205

,000

11764,900

1 11764,900 3523,597

,000

176,400

1

176,400

52,832

,000

220,900

1

220,900

66,160

,000

115,600

1

115,600

34,622

,000

120,200

36

3,339

12398,000

40

633,100

39

Źródło zmienności
Model skorygowany
Stała
ZAGR
PLEC
ZAGR * PLEC
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,810 (Skorygowane R kwadrat = ,794)

a.

Wszystkie efekty istotne

Średnie grupowe

• Efekt główny zmiennej płeć

• Efekt główny zmiennej zagrożenie/brak

2. ZAGR

Zmienna zależna: ZADANIE

15,050
19,250

ZAGR
zagrożenie stereotypem
brak zagrożenia

Średnia

3. PLEC

Zmienna zależna: ZADANIE

14,800
19,500

PLEC
kobieta
mężczyzna

Średnia

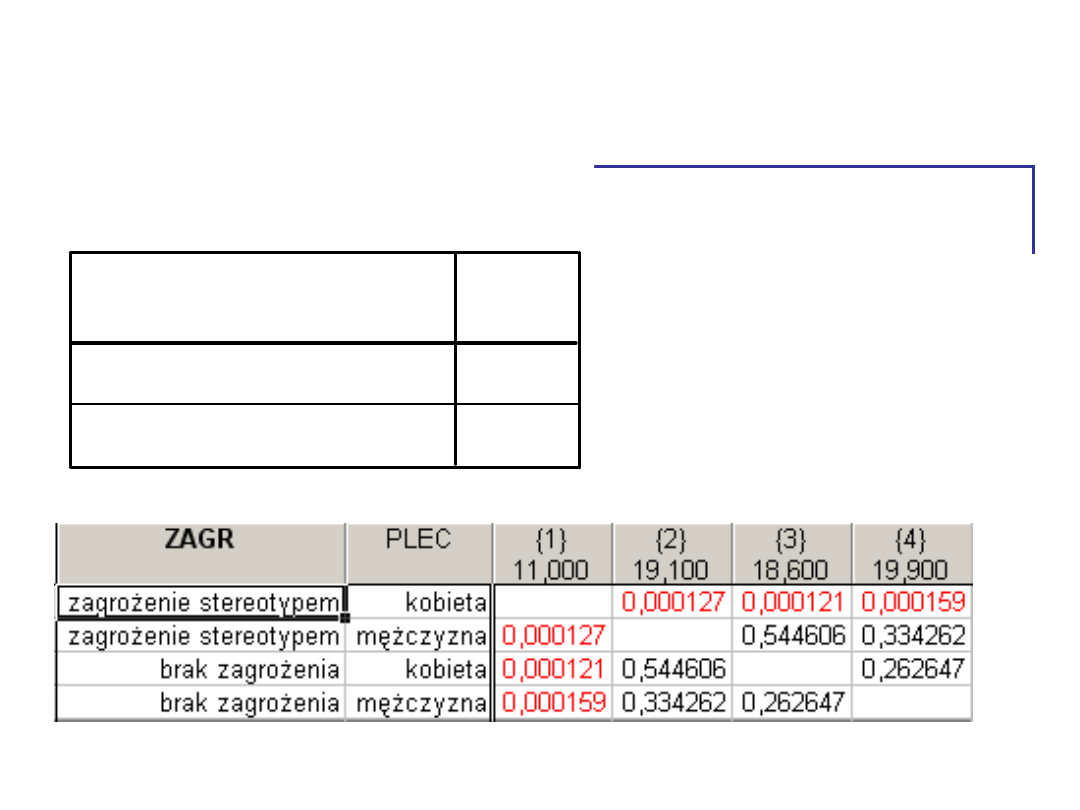
Efekt interakcyjny – test post

hoc

• Grupa kobiet w

sytuacji zagrożenia

stereotypem różni

się od reszty.

Pozostałe grupy

nie różnią się

między sobą

1. ZAGR * PLEC

Zmienna zależna: ZADANIE

11,000
19,100
18,600
19,900

PLEC
kobieta
mężczyzna
kobieta
mężczyzna

ZAGR
zagrożenie stereotypem

brak zagrożenia

Średnia

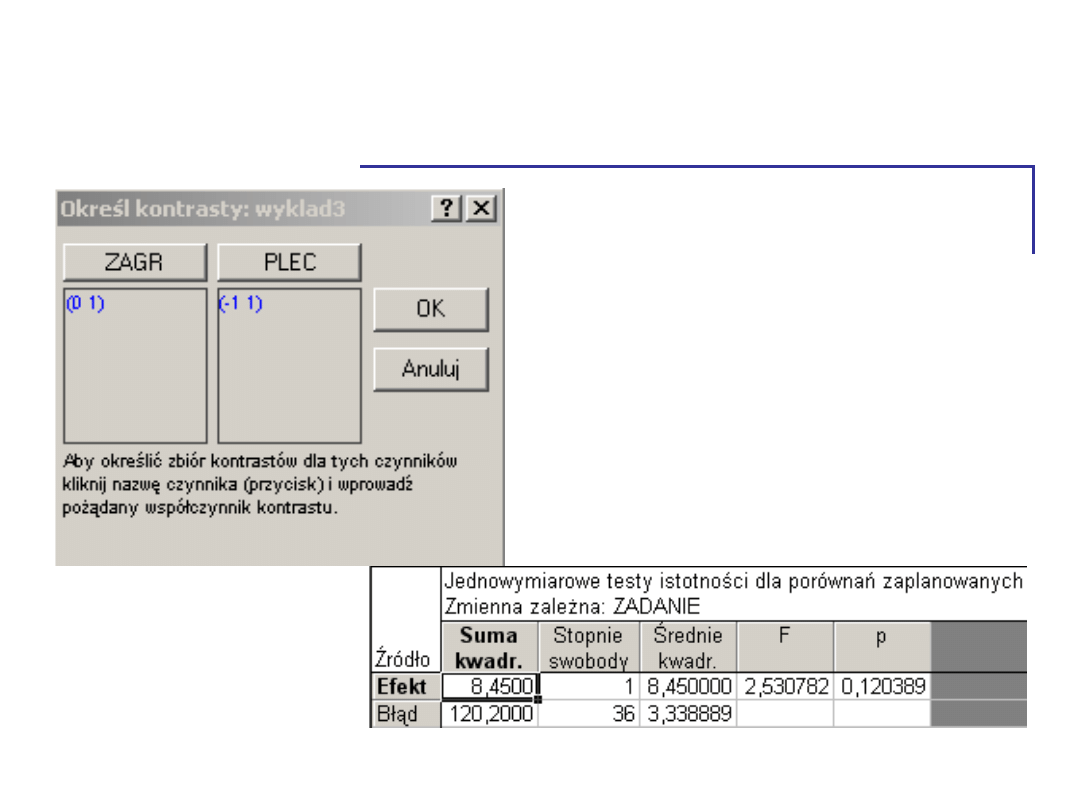
Efekt interakcyjny - kontrasty

• W sytuacji kontrolnej

brak różnic między
kobietami i
mężczyznami

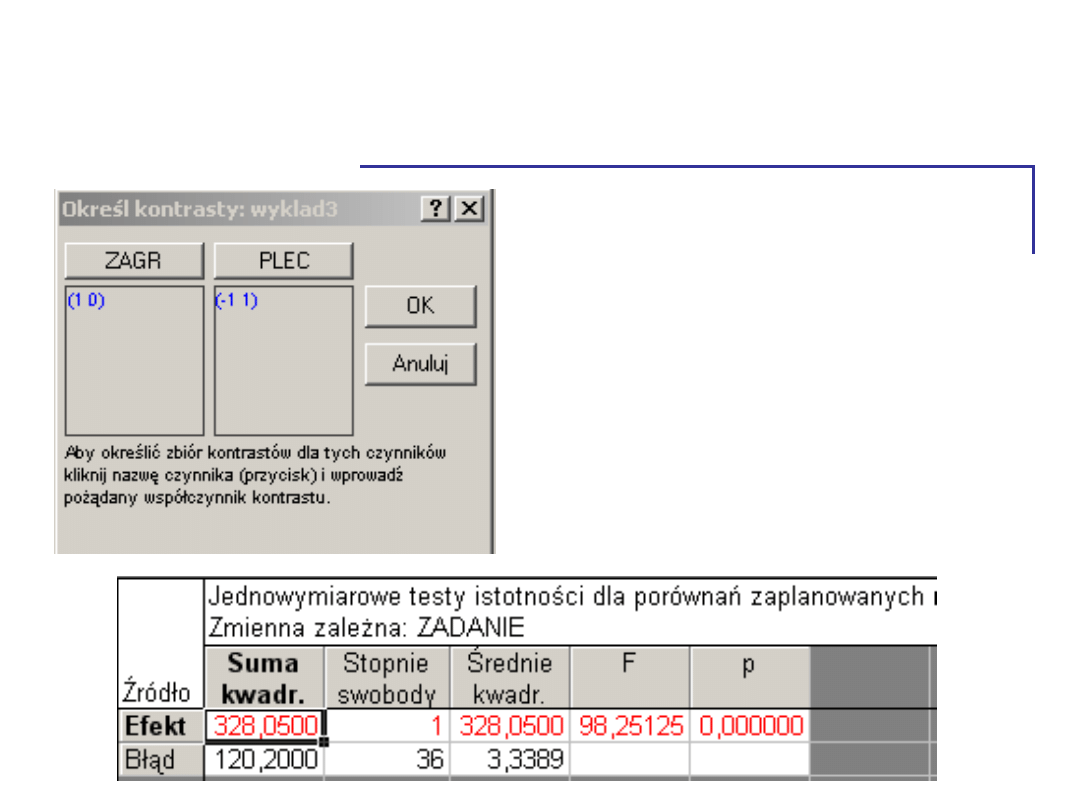
Efekt interakcyjny - kontrasty

• Najpierw porównujemy

kobiety i mężczyzn w
sytuacji zagrożenia
stereotypem