Dwuczynnikowa analiza

wariancji – zaawansowane plany

eksperymentalne

Jeszcze słowo o

wielomianach…

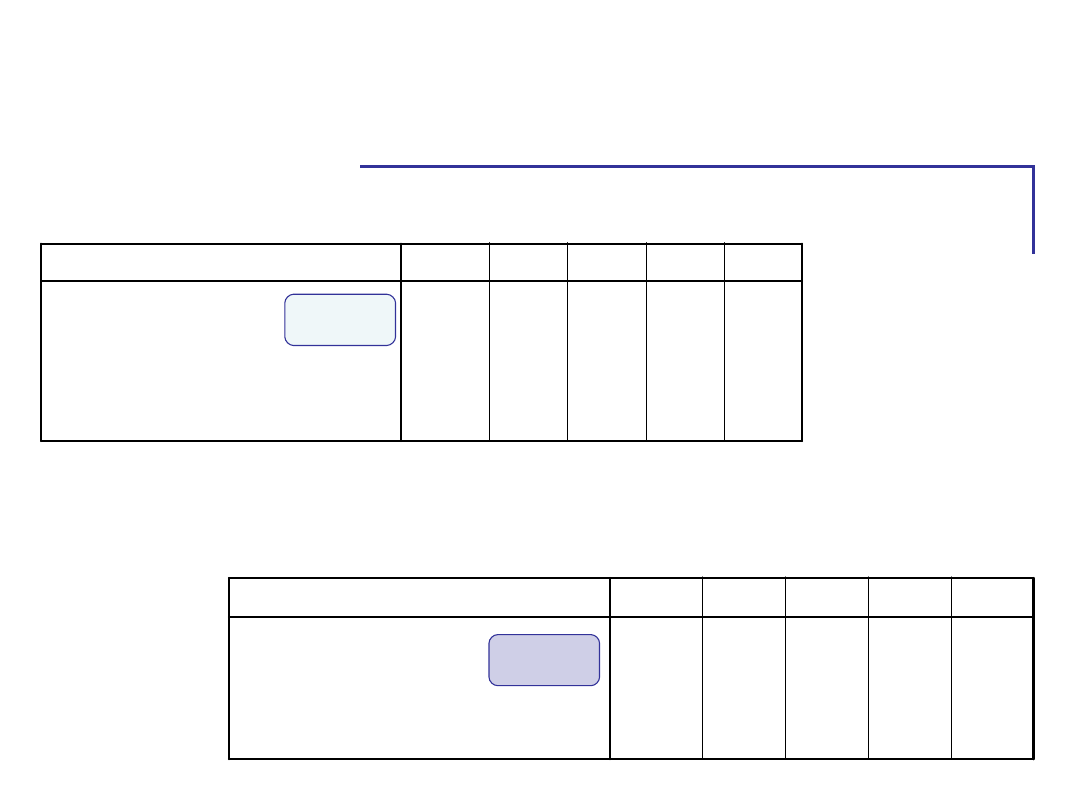
Analiza wariancji

poziom lęku

1954,451

2

977,226

19,619

,000

1877,778

1 1877,778

37,699

,000

1877,778

1 1877,778

37,699

,000

76,673

1

76,673

1,539

,221

76,673

1

76,673

1,539

,221

76,673

1

76,673

1,539

,221

2291,222

46

49,809

4245,673

48

(Połączone)

Nieważone
Ważone
Odchylenie

Składnik liniowy

Nieważone
Ważone

Składnik kwadratowy

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Analiza wariancji

wynik w teście pamięci

42,178

2

21,089

28,511

,000

36,300

1

36,300

49,075

,000

5,878

1

5,878

7,946

,007

5,878

1

5,878

7,946

,007

31,067

42

,740

73,244

44

(Połączone)

Kontrast
Odchylenie

Składnik liniowy

Kontrast

Składnik kwadratowy

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

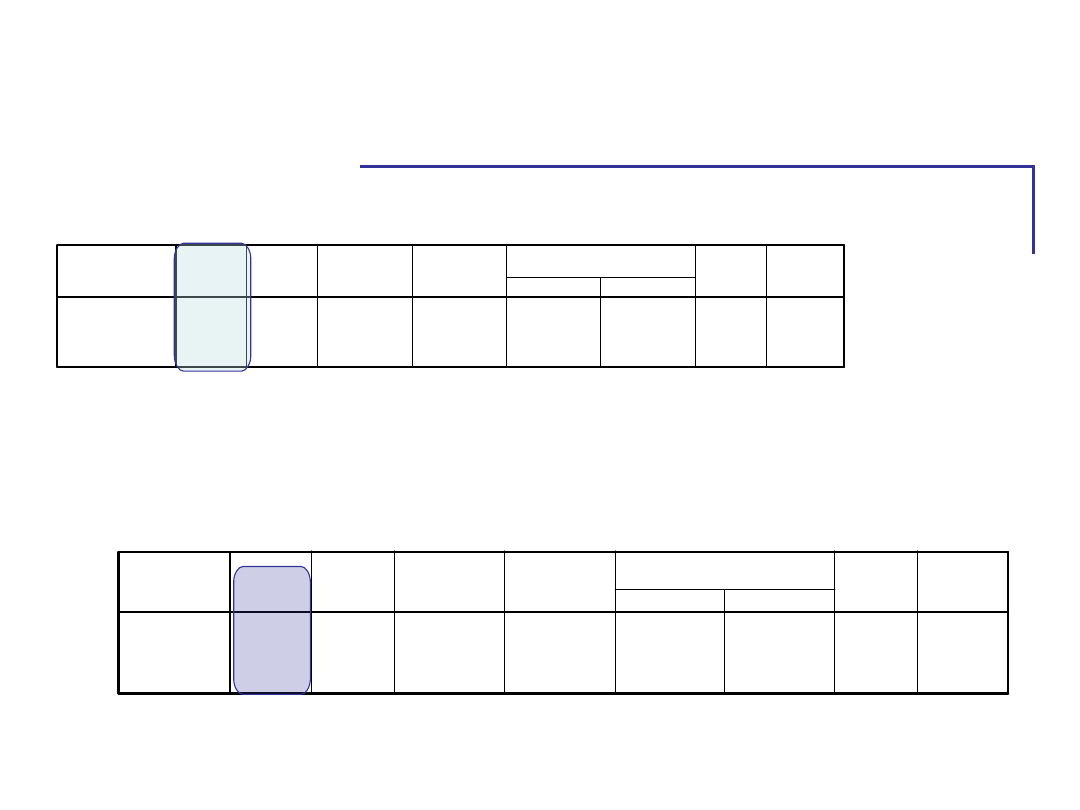
Statystyki opisowe

wynik w teście pamięci

15

8,1333

,9155

,2364

7,6264

8,6403

7,00

10,00

15

7,8000

,8619

,2225

7,3227

8,2773

6,00

9,00

15

5,9333

,7988

,2063

5,4910

6,3757

5,00

7,00

45

7,2889

1,2902

,1923

6,9013

7,6765

5,00

10,00

wysokie dawki
niskie dawki
placebo
Ogółem

N

Średnia

Odchylenie

standardowe

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności dla

średniej

Minimum Maksimum

Statystyki opisowe

poziom lęku

18

32,61

5,29

1,25

29,98

35,24

24

44

13

37,00

5,03

1,40

33,96

40,04

27

45

18

47,06

9,43

2,22

42,37

51,74

32

64

49

39,08

9,40

1,34

36,38

41,78

24

64

niedepresyjni
depresyjni
depresyjno_lękowi
Ogółem

N

Średnia

Odchylenie

standardowe

Błąd

standardowy Dolna granica Górna granica

95% przedział ufności dla

średniej

Minimum Maksimum

Warto poszukiwać czegoś

więcej…

• Chronopsychologia – czy „ranne

ptaszki” inaczej funkcjonują niż
„sowy”

(W. Ciarkowska)

?

• Sprawdzamy jak rozwiązują dosyć

trudne zadanie poznawcze.

• Wynik:

Independent Samples Test

76,142

,000 -1,644

58

,106

-,6667

,40552 -1,47840 ,14506

-1,644 35,154

,109

-,6667

,40552 -1,48978 ,15645

Equal variances
assumed
Equal variances
not assumed

AKTYWNOS
atywność poznawcza

F

Sig.

Levene's Test

for Equality of

Variances

t

df

Sig. (2-tailed)

Mean

Difference

Std. Error

Difference

Lower

Upper

95% Confidence

Interval of the

Difference

t-test for Equality of Means

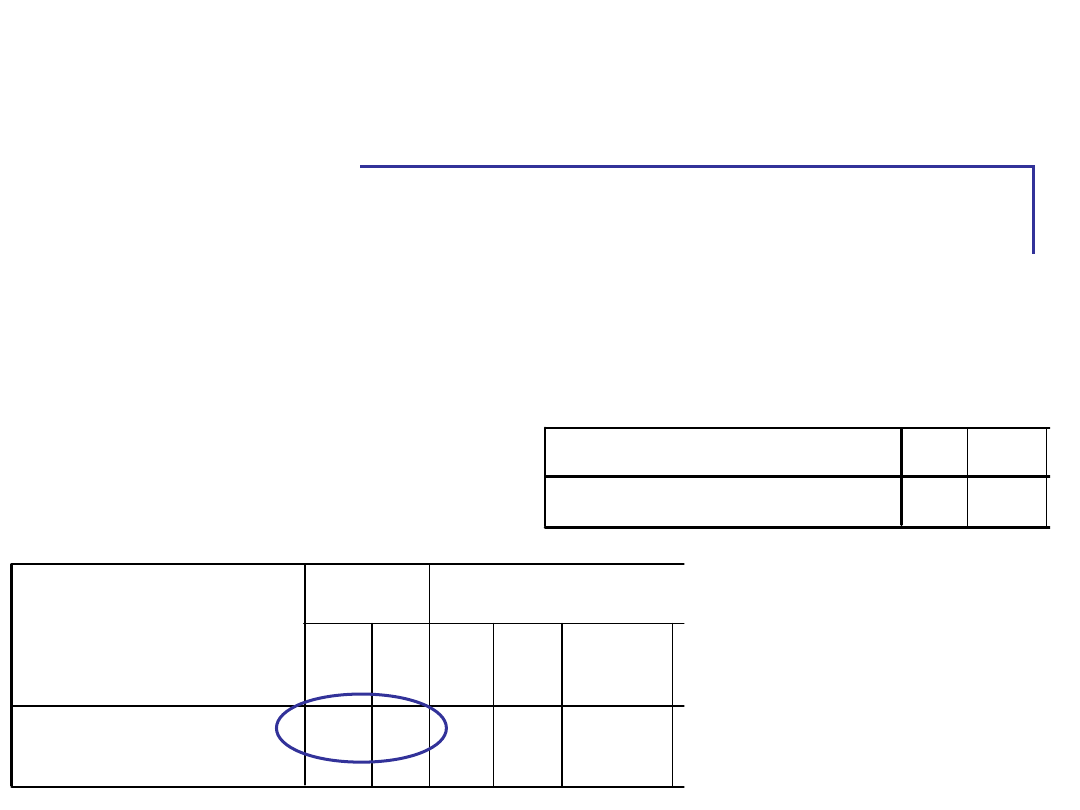
Group Statistics

30 4,9333

,69149

,12625

30 5,6000

2,11073

,38536

RAN_WIEC
1,00 ranne ptaszki
2,00 sowy

AKTYWNOS
atywność poznawcza

N

Mean

Std. Deviation

Std. Error

Mean

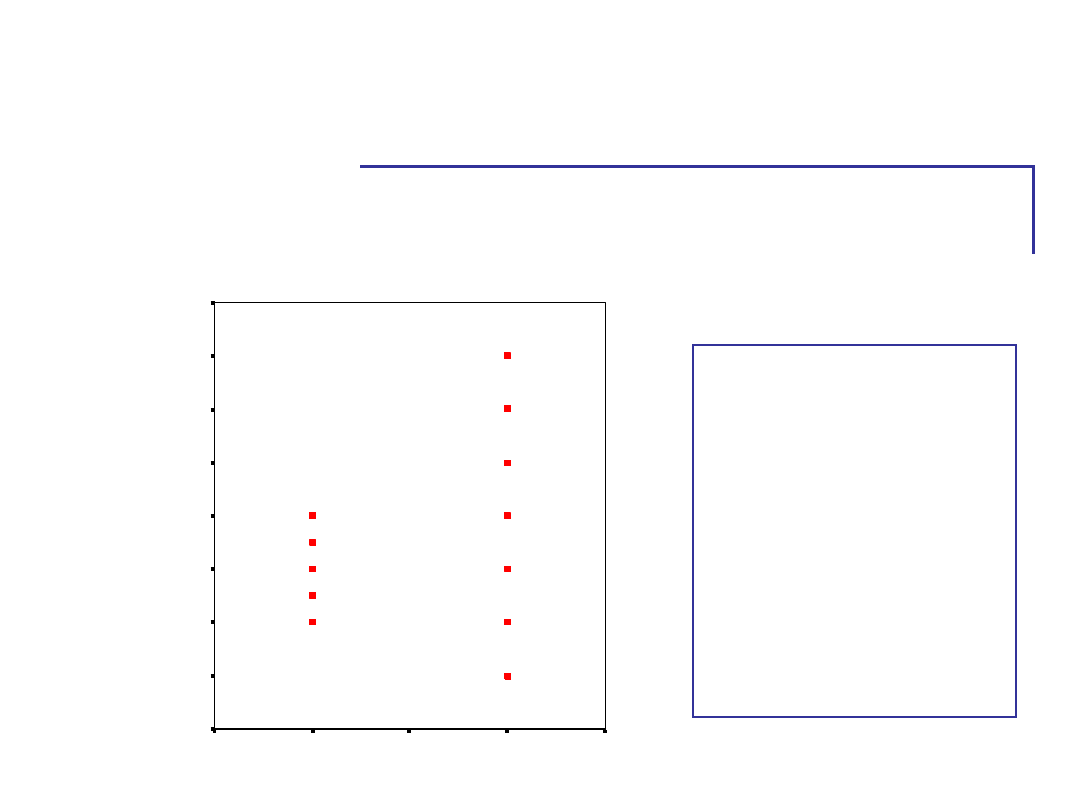
• Zobaczmy ten wynik na wykresie:

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

Być może
pominęliśmy jakąś
ważną zmienną –
skoro badamy
funkcjonowanie
różnych
chronotypów, to
może warto wziąć
pod uwagę porę
dnia

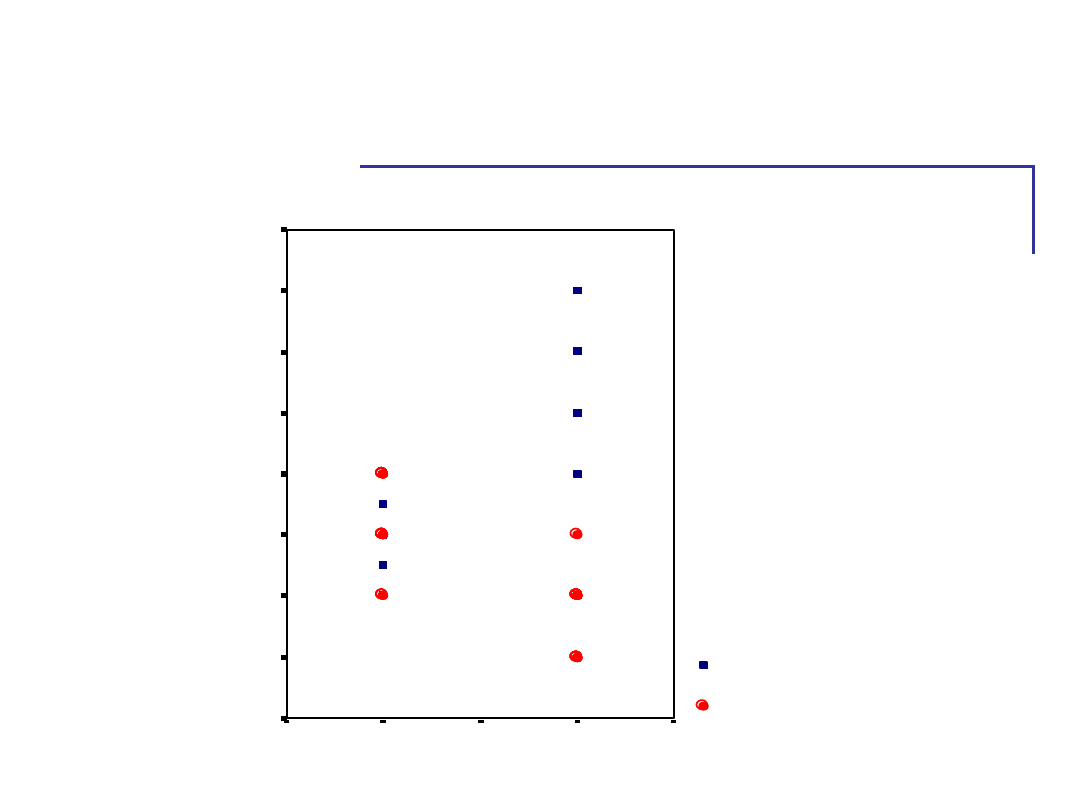
Gdy uwzględnimy porę dnia, to wykres
pokazuje:

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

PORA

wieczorem

rano

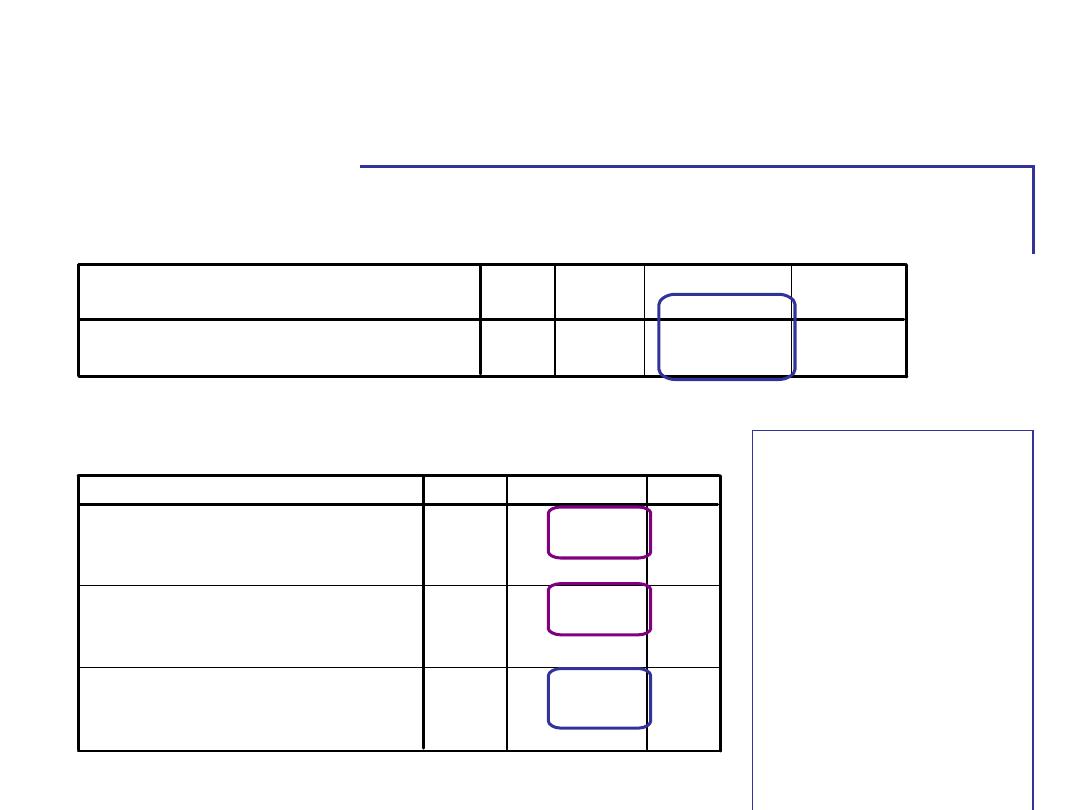
Gdy uwzględnimy porę dnia

Descriptive Statistics

Dependent Variable: AKTYWNOS atywność poznawcza

5,2000

,77460

15

3,6667

,61721

15

4,4333

1,04000

30

4,6667

,48795

15

7,5333

,91548

15

6,1000

1,62629

30

4,9333

,69149

30

5,6000

2,11073

30

5,2667

1,59306

60

RAN_WIEC
1,00 ranne ptaszki
2,00 sowy
Total
1,00 ranne ptaszki
2,00 sowy
Total
1,00 ranne ptaszki
2,00 sowy
Total

PORA
1,00 rano

2,00 wieczorem

Total

Mean

Std. Deviation

N

Group Statistics

30 4,9333

,69149

,12625

30 5,6000

2,11073

,38536

RAN_WIEC
1,00 ranne ptaszki
2,00 sowy

AKTYWNOS
atywność poznawcza

N

Mean

Std. Deviation

Std. Error

Mean

Mniejsza
wariancja w
grupach, po
uwzględnieniu
dodatkowej
zmiennej.

Lepsza kontrola
zmienności
zmiennej
zależnej

Złożony plan eksperymentalny

• Dodając kolejną zmienną, z prostego

eksperymentu tworzymy eksperyment
złożony

• Plany złożone – wykorzystywane do

testowania wpływu dwóch lub więcej
zmiennych niezależnych na zmienną
zależną w jednym eksperymencie

• Każda zmienna może być badana w

ramach planu międzygrupowego lub w
planie powtarzanych pomiarów

Kombinacja czynników

• Zestawiamy każdy poziom jednej zmiennej

niezależnej (pierwszego czynnika) ze
wszystkimi poziomami drugiej zmiennej
niezależnej (drugiego czynnika), w naszym
przykładzie „typy ranne” były testowane
zarówno rano jak i wieczorem, tak samo „typy
wieczorne”

• Liczba warunków eksperymentalnych

opartych na planie złożonym jest równa
iloczynowi poziomów czynników, np. 2 x 2 =
4; 3 x 3=9 itd.

Złożony plan eksperymentalny

• W najprostszej postaci jest to schemat z

dwiema zmiennymi niezależnymi na
dwóch poziomach (2 x 2 – „dwa na dwa”)

• Do analizy takich schematów

wykorzystujemy dwuczynnikową
analizę wariancji – najprostszy
przypadek czynnikowej analizy wariancji

• Możliwe różne schematy w

dwuczynnikowej analizie wariancji: 3 x 2;
5 x 2; 3 x 4 itd..

W dwuczynnikowej analizie wariancji mamy

możliwość oszacowania:

• Osobno wpływu każdej zmiennej

niezależnej na zależną - dwa efekty
główne

– Ogólny efekt jednej zmiennej niezależnej

bez uwzględniania wpływu drugiej
zmiennej niezależnej

• Łączny efekt zmiennych niezależnych

– jeden efekt interakcji

– Łączny wpływ obu zmiennych

niezależnych na zmienną zależną

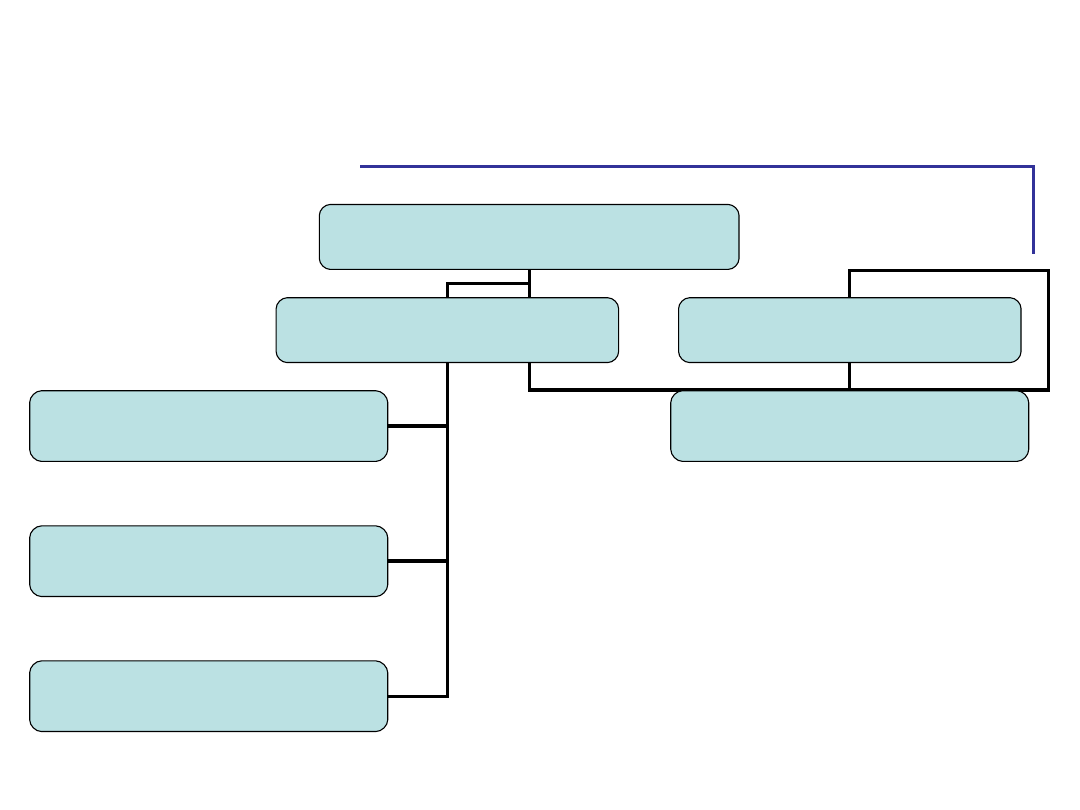
Logika analizy – źródła

wariancji

Całkowita wariancja

wyjaśniona

niewyjaśniona

MS

1ZN

MS 2ZN

MS Interakcji

MS błędu

Testy F w dwuczynnikowej

ANOVie

•

W dwuczynnikowej analizie wariancji mamy do czynienia

z trzema testami F:

– 1) dla efektu głównego pierwszego czynnika
– 2) dla efektu głównego drugiego czynnika
– 3) dla efektu interakcyjnego

•

W liczniku każdego z tych stosunków znajdzie się

wariancja międzygrupowa, która odnosi się do

porównań między średnimi dla danego efektu głównego

lub interakcyjnego

•

Natomiast wariancja wewnątrzgrupowa we wszystkich

trzech testach F będzie taka sama - jest to zawsze

średnia oszacowań wariancji w populacji utworzona z

wyników wewnątrz każdej z celek (wariancja błędu)

Logika analizy

• Pierwszy krok – istotność F

– Podobnie jak w jednoczynnikowej

analizie wariancji

• Interpretacja zależna od wystąpienia

bądź nie interakcji

• Do interpretacji niezbędne statystyki

opisowe, wykresy…

Jeśli nie ma interakcji

• Jeżeli brak interakcji analizujemy

efektu główne

• Jeśli zmienne niezależne na więcej

niż dwóch poziomach wykonujemy
porównania analityczne (porównania
par średnich)

Interakcje

• Pomagają ogarnąć złożoność

interesujących nas zjawisk

• Zamiast poprzestawać na pytaniach o to

– Czy występują różnice między typami

rannymi i wieczornymi w rozwiązywaniu
zadań umysłowych?

• Możemy pytać:

– Jak funkcjonują „ranne ptaszki” oraz „sowy”

w różnych porach dnia?

Kiedy interakcja?

• Mamy do czynienia z interakcją, gdy

wpływ pierwszej zmiennej
niezależnej zmienia się, kiedy
przechodzimy na kolejne poziomy
drugiej zmiennej niezależnej zmiana
musi być istotna statystycznie.

• Tutaj przydają się porównania

planowane

Interakcje

• Jeżeli interakcja istotna statystycznie, to
• Interpretujemy ją analizując efekty proste

– Efekt prosty (simple effect): wpływ jednej

zmiennej niezależnej, który zachodzi na
określonym poziomie drugiej zmiennej
niezależnej

• Najlepiej widać z jakimi efektami prostymi mamy do

czynienia na wykresie średnich

• Jeżeli czynnik ma więcej niż dwa poziomy

źródeł efektu prostego szukamy za pomocą
porównań analitycznych

Możliwe scenariusze wyników

Efekt główny

pory dnia

Efekt główny

chronotypu

Interakcja

pory dnia i

chronotypu

-

-

-

+

-

-

-

+

-

-

-

+

+

+

-

+

-

+

-

+

+

+

+

+

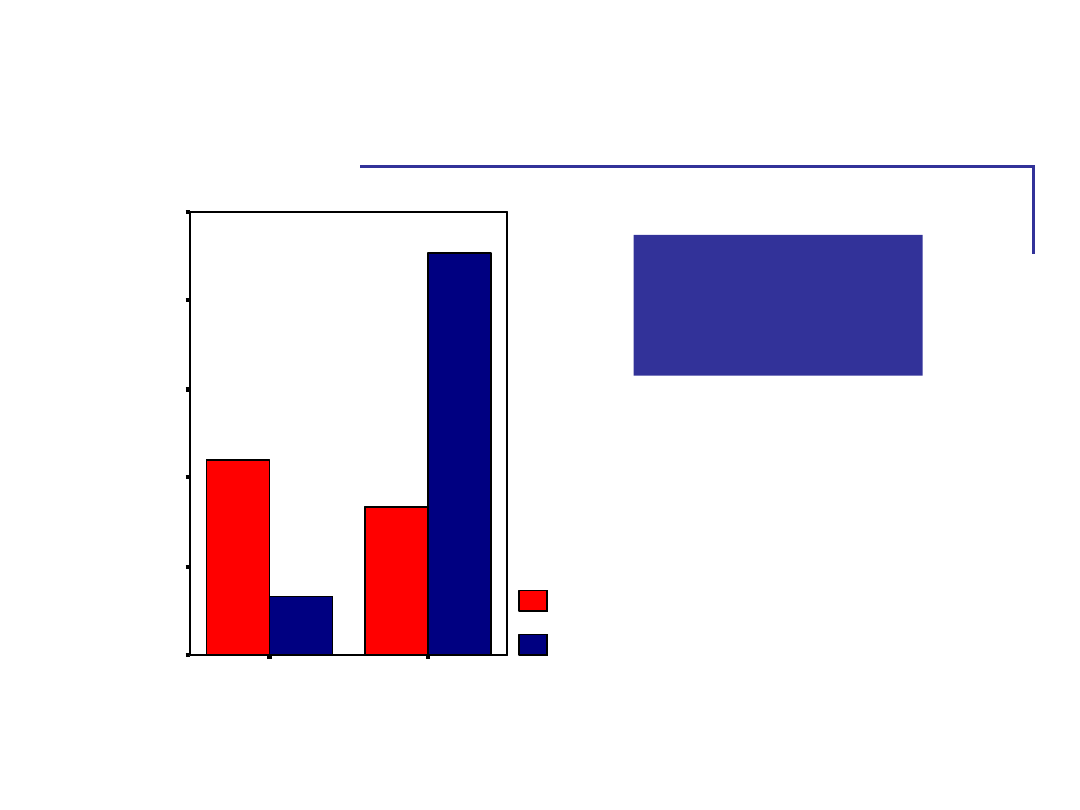
Wyniki badania nad

chronotypami

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

Wszystkie trzy
efekty
zauważalne

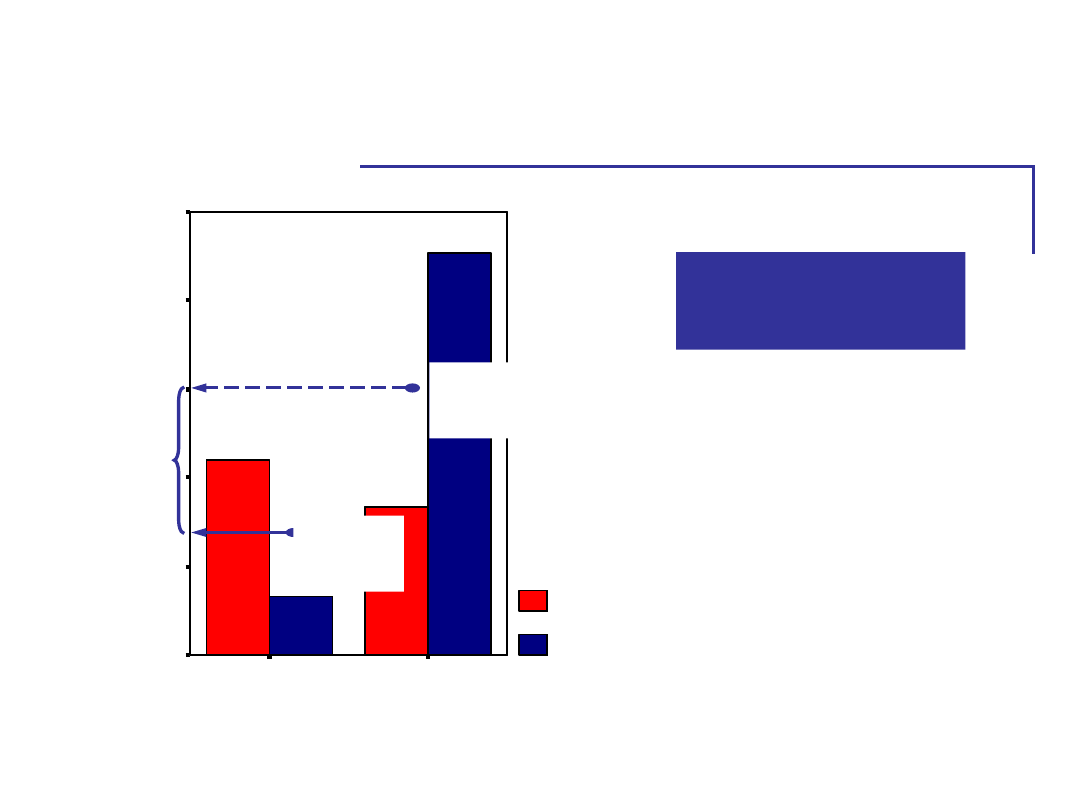
Wyniki badania nad

chronotypami

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

Efekt główny
pory badania

M
rano

M
wieczorem

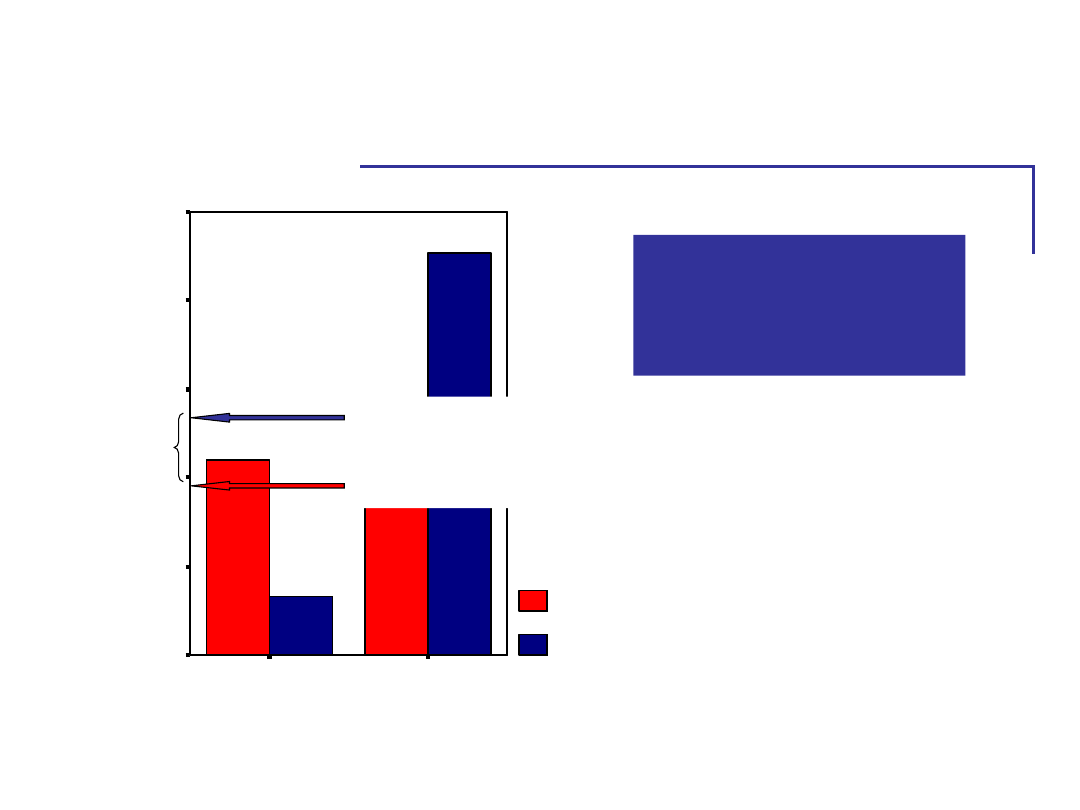
Wyniki badania nad

chronotypami

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

Efekt główny
rodzaju
chronotypu

M typów
wieczornych

M typów rannych

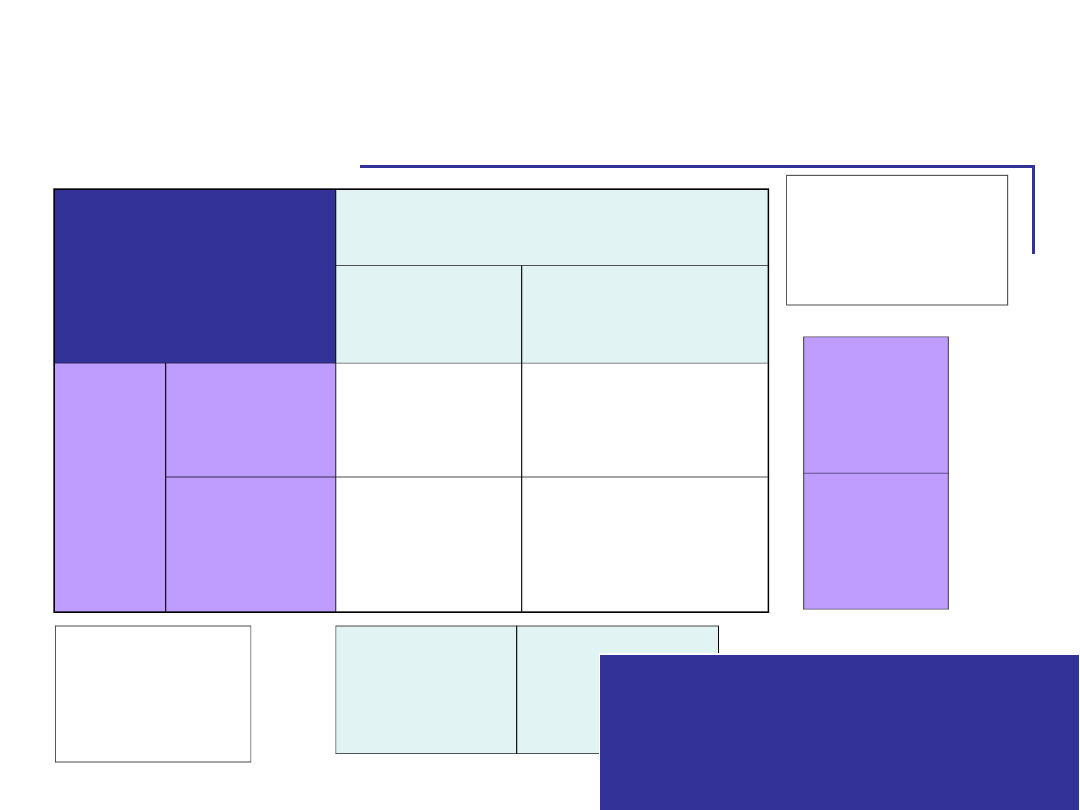
Przyglądamy się efektom

głównym

Zmienne

niezależne

Chronotyp

RANNY

WIECZORNY

Pora

RANO

5,2

3,7

WIECZÓ
R

4,7

7,5

4,4

6,1

4,9

5,6

Średnie
wierszy

Średnie
kolumn

Jeżeli średnie z wierszy
różnią się wskazuje to efekt
główny Pory.
Jeżeli różnią się średnie z
kolumn sugeruje to efekt
główny Chronotypu

Obliczanie średnich dla

efektów głównych

• Średnie dla efektów głównych zostały

obliczone na podstawie średnich w

poszczególnych celkach,

– dla efektu głównego zmiennej Chronotyp uśredniliśmy

wyniki w kolumnach,

– dla efektu głównego drugiej zmiennej średnia została

wyciągnięta z poszczególnych wierszy;

• np. średnia dla Chronotypu rannego została obliczona

poprzez wyciągnięcie średniej z wyników osiąganych przez

te osoby rano i wieczorem (5,2 + 4,7)/2 = 4,9.

– Można w ten sposób obliczać średnie dla efektów

głównych tylko wtedy, gdy liczba osób w

poszczególnych kratkach jest taka sama, inaczej

trzeba stosować poprawkę na nierówną liczbę osób.

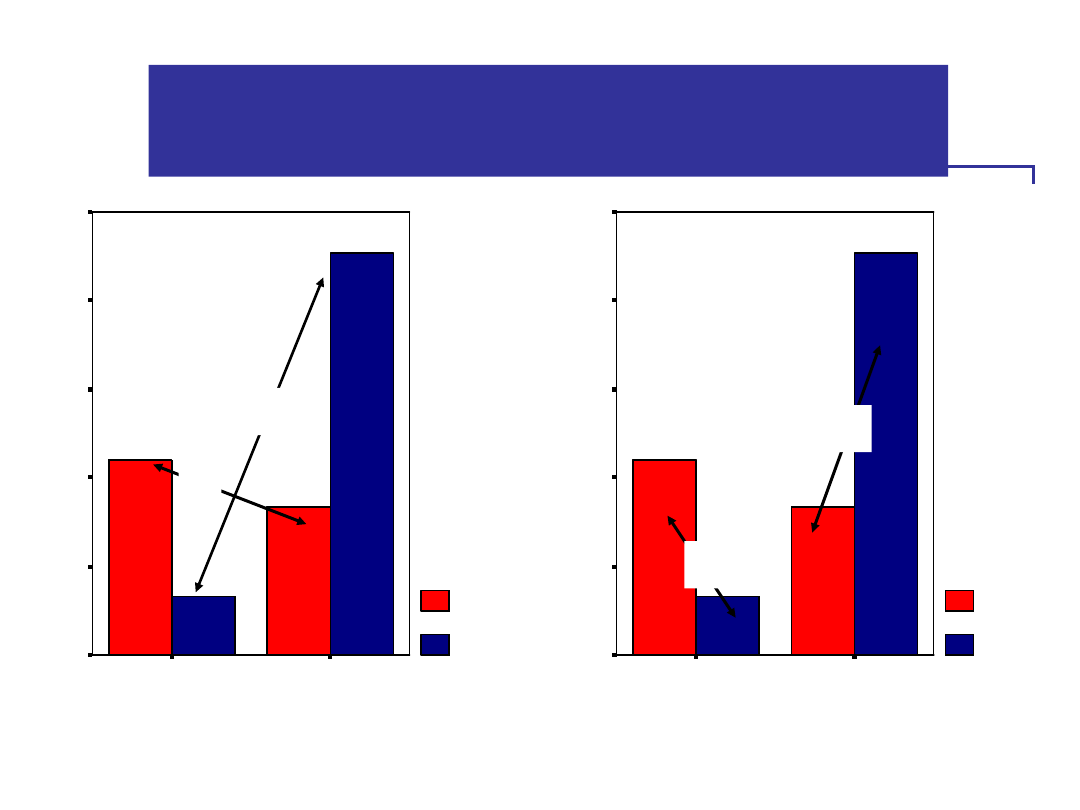
Efekt Interakcji. Szukanie efektów
prostych

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

1

2

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

3

4

Metoda odejmowania do

szukania interakcji

• Parząc na średnie w tabelce o interakcji

możemy wnioskować na podstawie

prostej metody odejmowania.

– Polega ona na porównywaniu między sobą

różnic między średnimi z każdego wiersza

(lub kolumny).

• Interpretacja efektu interakcyjnego

polega na analizie efektów prostych lub

porównań analitycznych (gdy zmienna

niezależna pozsiada trzy lub więcej

poziomów ).

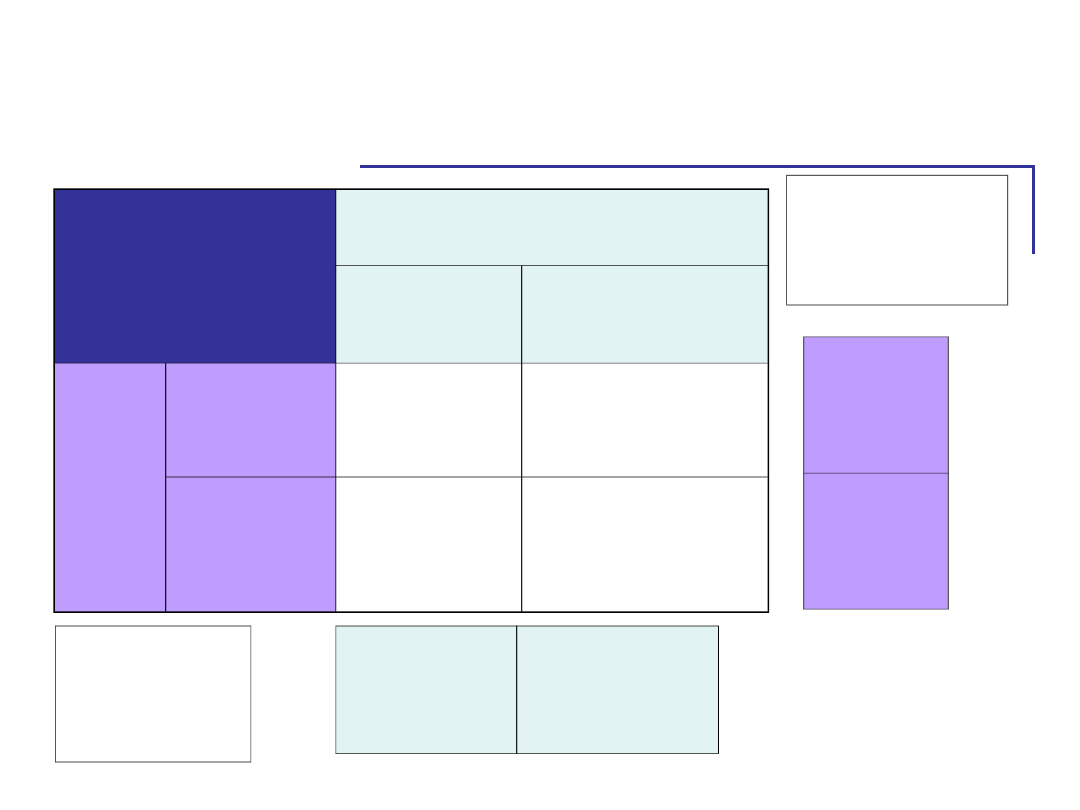
W naszym przykładzie

Zmienne

niezależne

Chronotyp

RANNY

WIECZORNY

Pora

RANO

5,2

3,7

WIECZÓ
R

4,7

7,5

1,5

-2,8

0,5

-3,8

Różnica

Średnie
kolumn

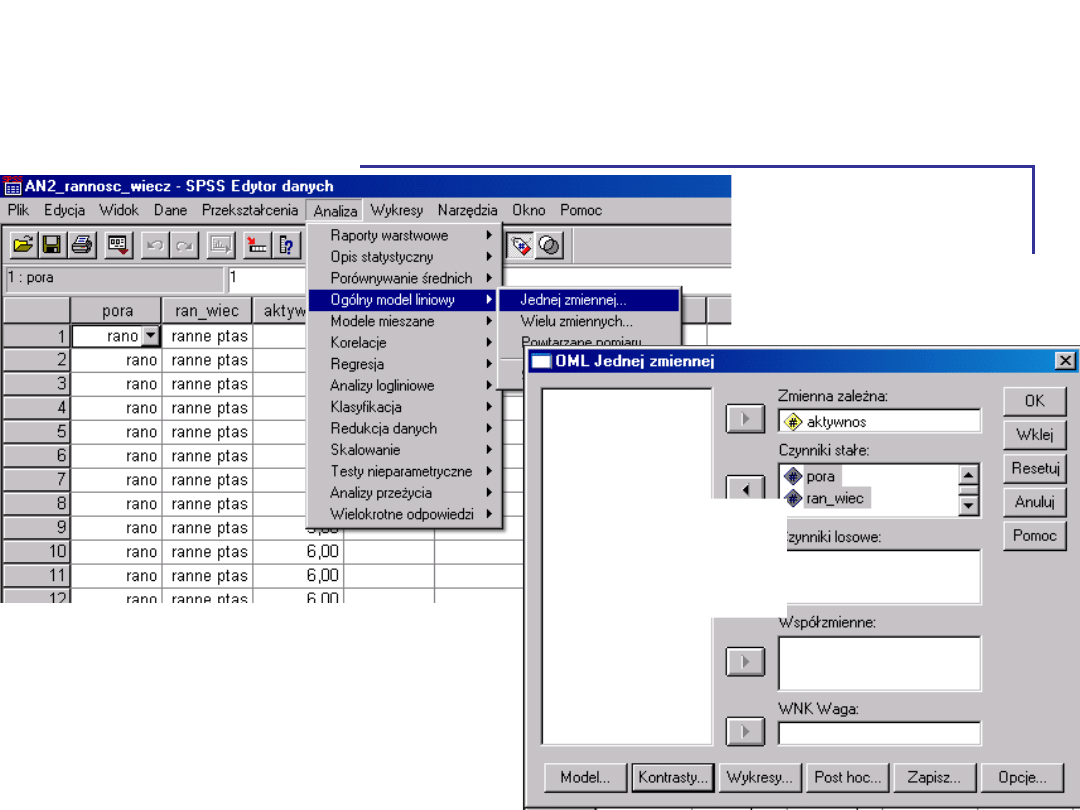
Jak to robi SPSS

Zmienne
niezależ
ne

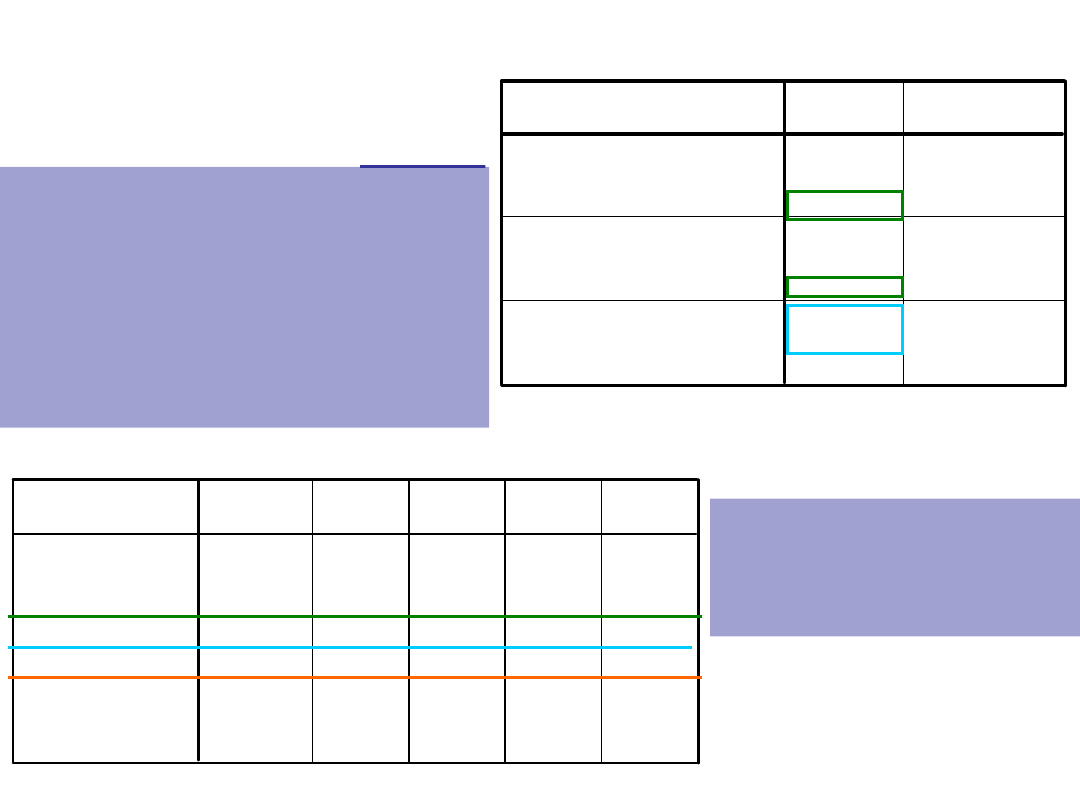
Statystyki opisowe

Zmienna zależna: atywność poznawcza

5,2000

,77460

3,6667

,61721

4,4333

1,04000

4,6667

,48795

7,5333

,91548

6,1000

1,62629

4,9333

,69149

5,6000

2,11073

5,2667

1,59306

RAN_WIEC
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem

PORA
rano

wieczorem

Ogółem

Średnia

Odchylenie

standardowe

Testy efektów międzyobiektowych

Zmienna zależna: atywność poznawcza

120,933

a

3

40,311

78,383

,000

1664,267

1 1664,267 3236,074

,000

41,667

1

41,667

81,019

,000

6,667

1

6,667

12,963

,001

72,600

1

72,600

141,167

,000

28,800

56

,514

1814,000

60

149,733

59

Źródło zmienności
Model skorygowany
Stała
PORA
RAN_WIEC
PORA * RAN_WIEC
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,808 (Skorygowane R kwadrat = ,797)

a.

Efekt główny pory badania:
F(1,56) = 81,02; p<0,001
(M

r

=4,43; M

w

=6,1)

Efekt główny typu: F(1,56) =
12,96; p<0,001 (M

s

=5,6;

M

p

=4,9)

Efekt interakcji:

F(1,56) = 141;
p<0,001

Stopnie swobody

• Dla efektów głównych:

– Stopnie swobody dla każdego z efektów głównych

( dla każdej wariancji międzygrupowej) to liczba
poziomów zmiennej minus 1

– Jeśli zmienna na dwóch poziomach to mamy 1

stopień swobody; jeśli na trzech to liczba stopni
swobody dla efektu głównego wynosi 2.

– Wyraża się to wzorem:

df

1

= k

1

– 1

df

2

= k

2

– 1

Gdzie k1 i k2 to liczba poziomów pierwszego i drugiego czynnika

Stopnie swobody

• Stopnie swobody dla wariancji

międzygrupowej przy efekcie

interakcyjnym to liczba wszystkich grup

minus stopnie swobody dla obu efektów

głównych, minus 1, czyli:

df

12

= N

grup

– df

1

– df

2

– 1

• Prościej możemy je policzyć jako iloczyn

stopni swobody dla efektów głównych.

• Ile stopni swobody dla schematu 3 x 4?
• Ile grup? 12

Stopnie swobody

• Stopnie swobody dla wariancji błędu -

suma stopni swobody dla wszystkich grup

• Dla każdej celki bierzemy liczbę

przypadków i odejmujemy 1 i następnie

dodajemy otrzymane wyniki do siebie

• Oznacza to, ze liczba stopni swobody dla

wariancji wewnątrzgrupowej to: liczba

osób minus liczba grup

• Ile df jeżeli 60 osób i schemat 3 x 3? 60-

9=51

Przykład: Zdolności językowe – efekty główne czy

interakcja?

Płeć

Presja czasu

TAK NIE

mężczyzna

5

2

kobieta

2

5

Średnie

3,5

3,5

• Osoby badane (kobiety i mężczyźni) zostały poproszone o

wymyślenie krótkich rymowanek tzw. Lepiejów i odwódek

Lepszy teść obleśny

piernik
Niźli z tej cukierni

sernik

Lepsze uszkodzenie
grdyki
Niż uczenie statystyki

Od wódki rozum krótki

Od Anovy bóle głowy

Różnice

średnic
h

3

-3

Przykład - zdolności

przestrzenne a płeć i

uszkodzenie półkul

Dzięki uprzejmości dr Izabeli

Krejtz

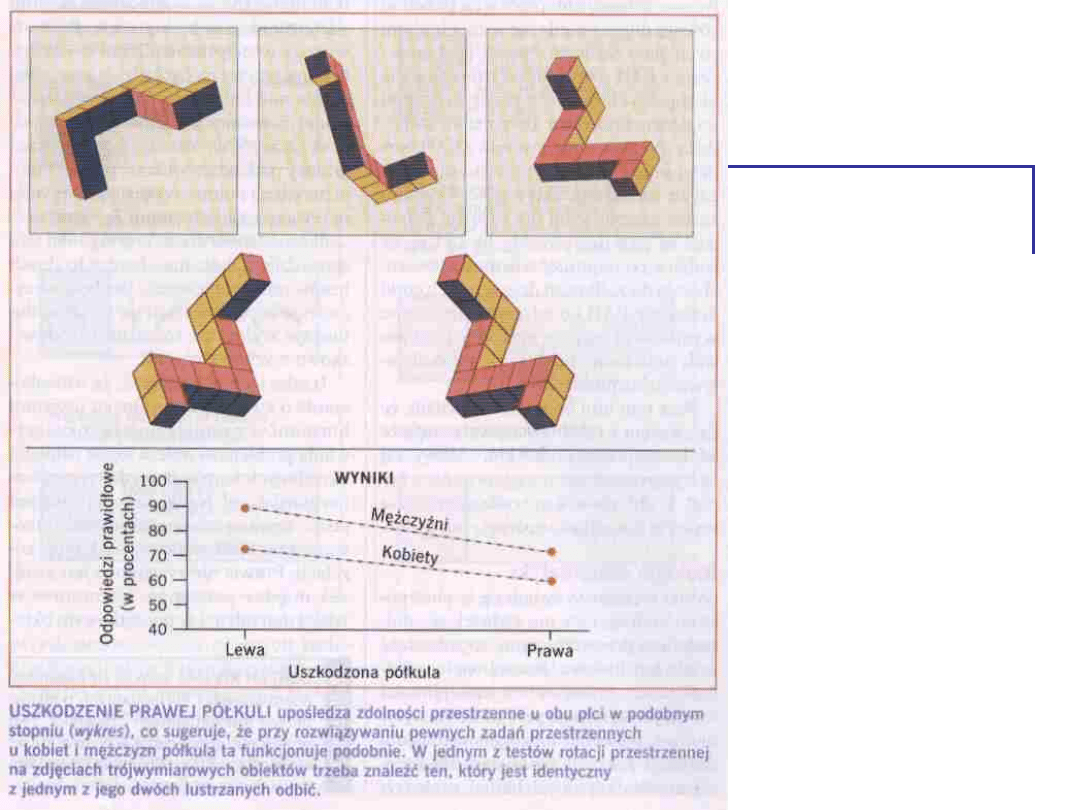
• Efekt Główny

Płci

• Efekt Główny

Półkuli

• Brak

Interakcji

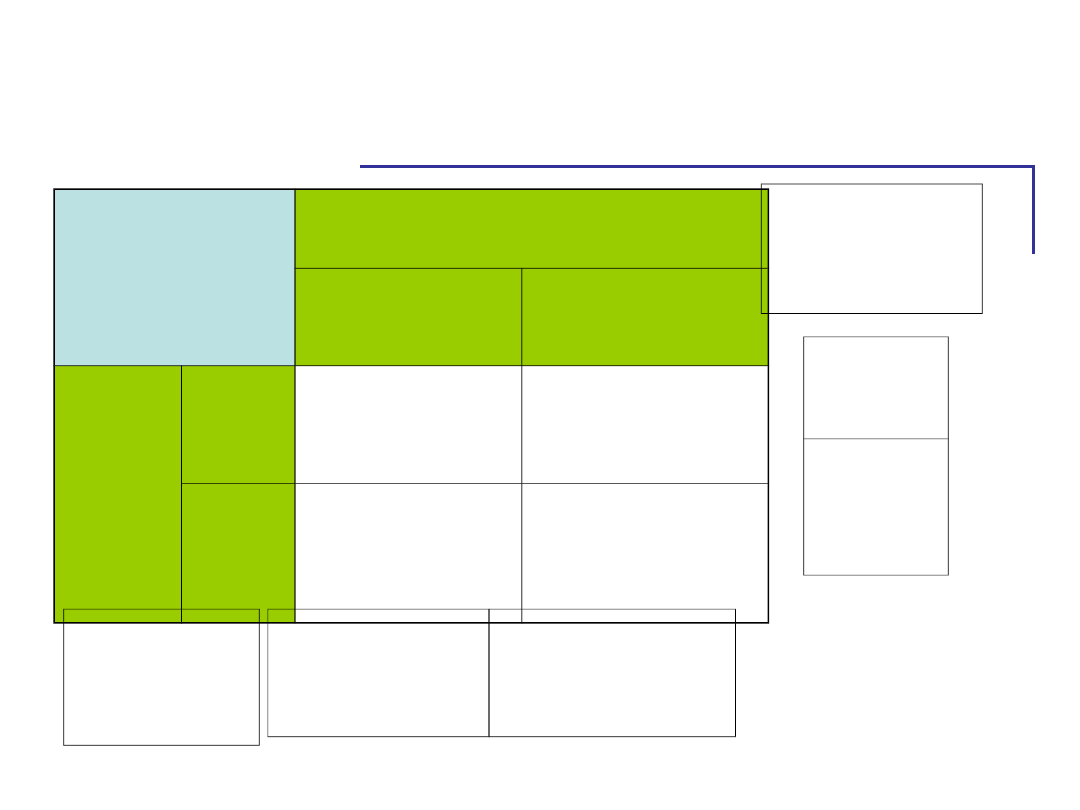
Przyglądamy się efektom

głównym

Zmienne

niezależne

USZKODZONA PÓŁKULA

LEWA

PRAWA

PŁEĆ

K

70

60

M

90

80

65

85

80

70

Średnie
wierszy

Średnie
kolumn

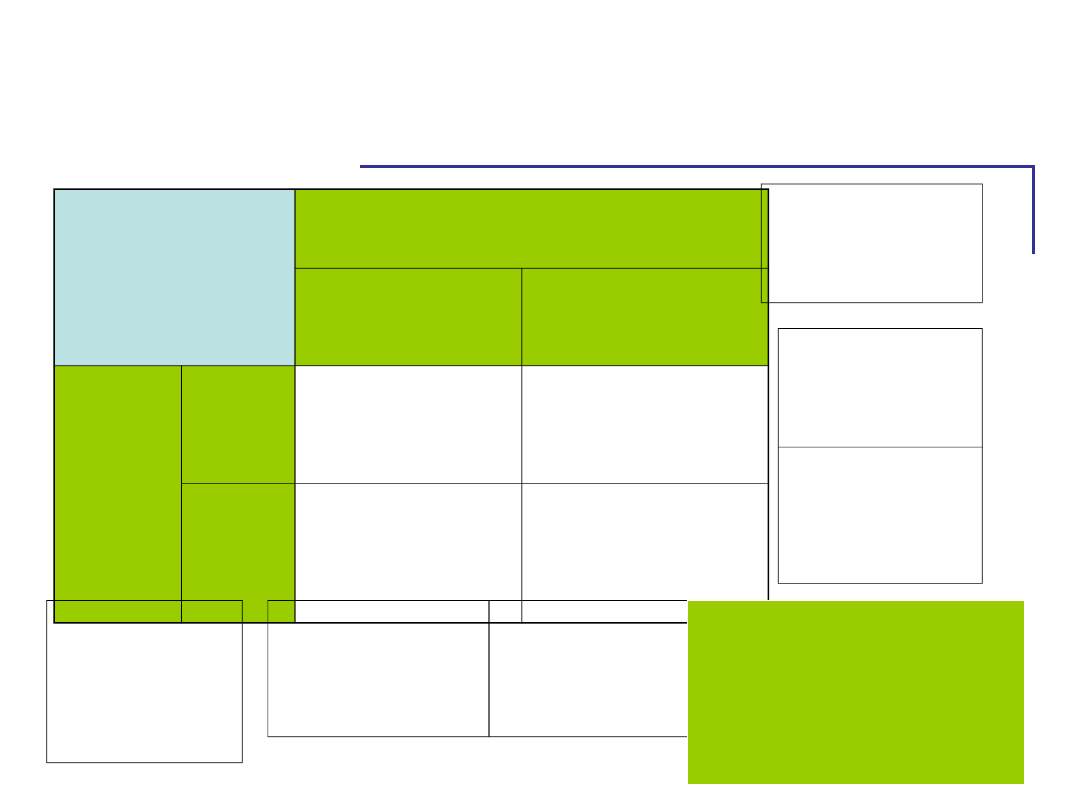
Szukamy interakcji

Zmienne

niezależne

USZKODZONA PÓŁKULA

LEWA

PRAWA

PŁEĆ

K

70

60

M

90

80

70-60=

10
90-80=

10

70-90=
-20

60-80=
-20

Różnice

średnich

Różnice

średnic

h

Różnice średnich
w wierszach
są takie same –
Brak interakcji

Przykład – wpływ pobudzenia i trudności

zadania na jego wykonanie

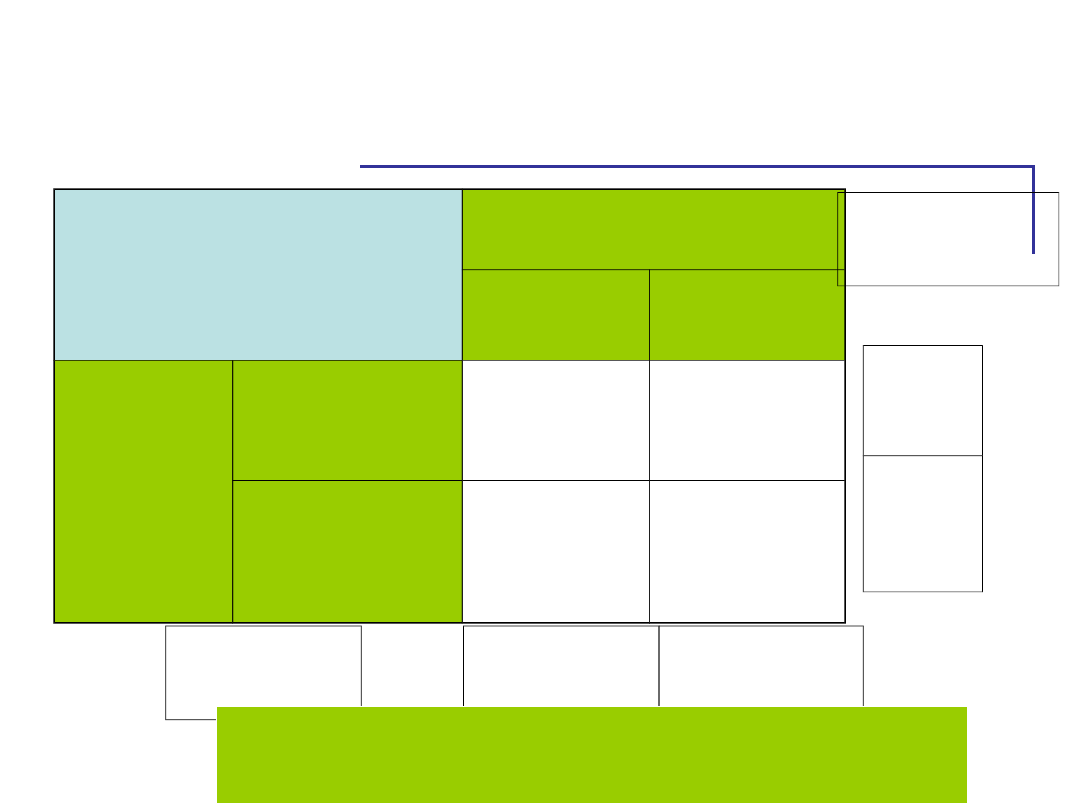
Szukamy EFEKTÓW

GŁÓWNYCH

Zmienne niezależne

POBUDZENIE

NISKIE

WYSOKIE

ZADANIE

ŁATWE

50

20

TRUDNE 30

40

35

35

40

30

Średnie

Średnie

Brak efektu głównego Zadania
Efekt główny Pobudzenia

Co mam mówią średnie

brzegowe

• Jeśli spojrzymy na średnie brzegowe dla efektu

pobudzenia, widać, że są sobie równe, co

wskazuje na brak efektu głównego tej

zmiennej.

• Brak efektu głównego zmiennej nie świadczy o

tym, że w ogóle nie działa.

• Możliwe, że pojawiła się interakcja między

poziomem pobudzenia a trudnością zadania.

– Jeśli nie ma interakcji między wpływem zmiennych

niezależnych wtedy efekty główne mogą być

analizowane tak jak w przypadku dwóch oddzielnych

eksperymentów z jedną zmienną niezależną.

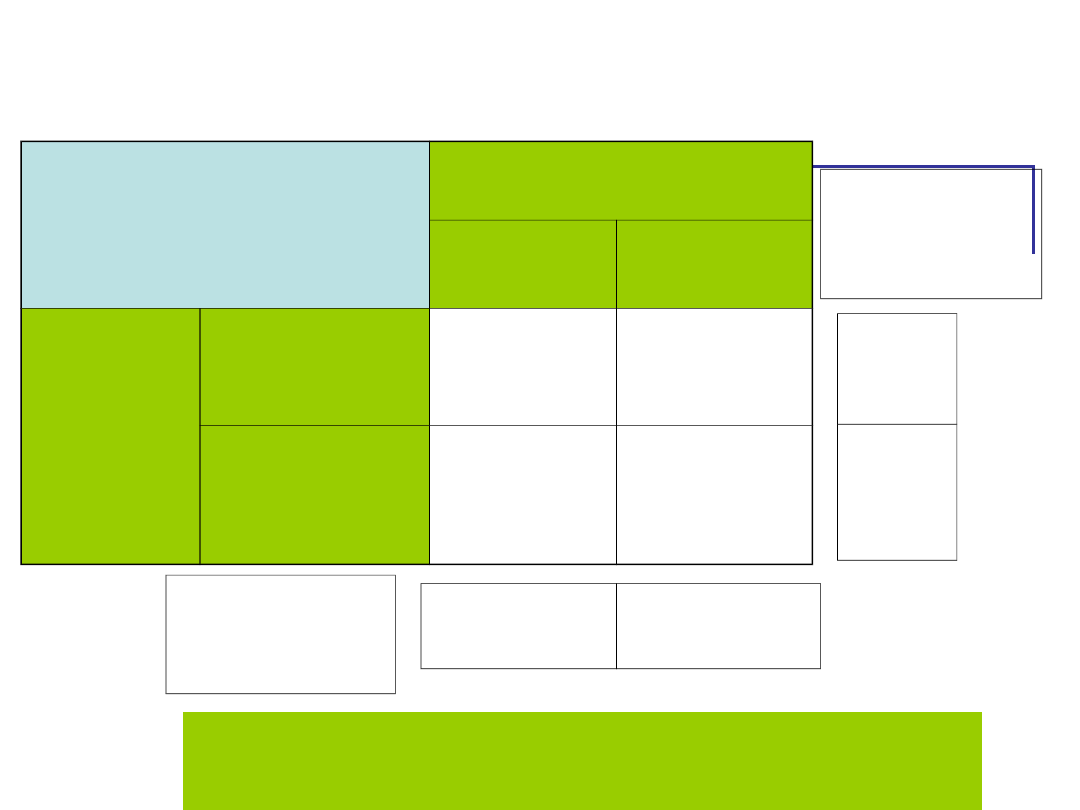
Szukamy interakcji

Zmienne niezależne

POBUDZENIE

NISKIE

WYSOKIE

ZADANIE

ŁATWE

50

20

TRUDNE 30

40

30

-10

20

-20

Różnica
Średnich

Różnica

Średnich

Różnice średnich w wierszach
(kolumnach)
mają przeciwne znali – Efekt interakcji

Efekt interakcyjny

• Należy pamiętać że zależność

interakcyjna działa w obie strony

oznacza to, że jeśli jedna zmienna

niezależna wchodzi w interakcję z drugą

zmienną niezależną, ta druga również

musi wchodzić w interakcję z pierwszą.

– Stąd można różnie sformułować konkluzję

płynącą z efektu interakcyjnego, zależnie od

tego, na którą zmienną chcemy położyć większy

nacisk komentując wyniki analiz; który aspekt

interakcji jest dla nas ważniejszy.

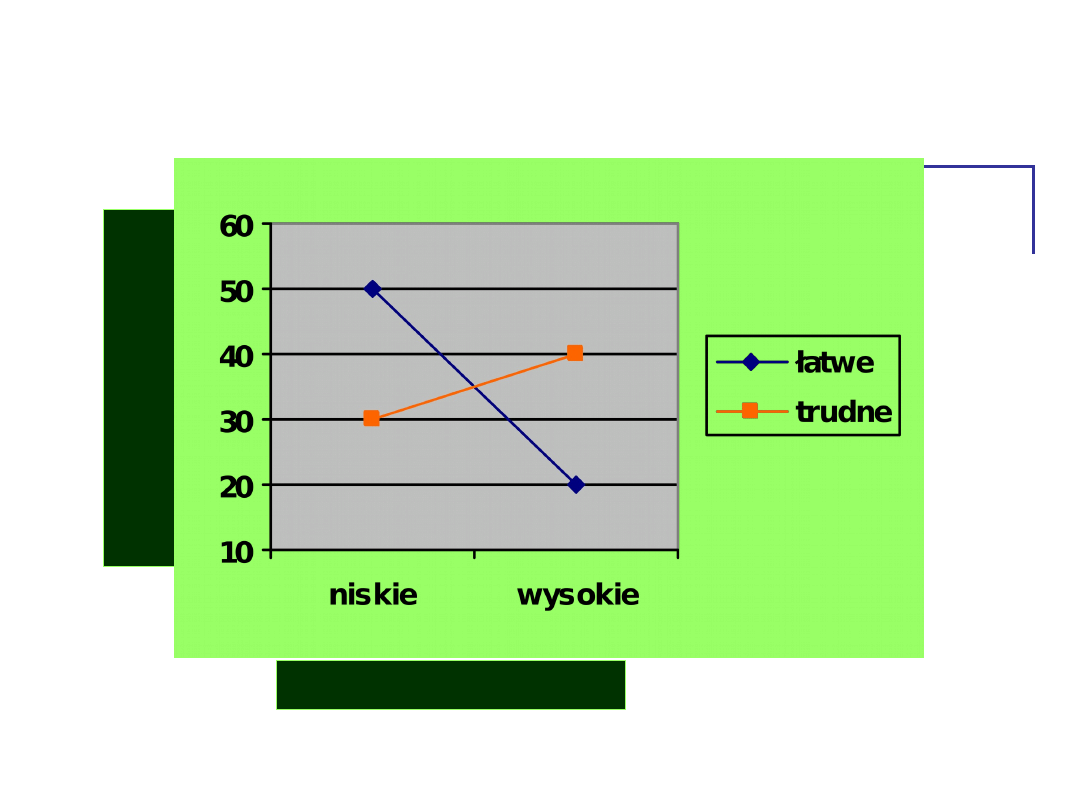
Jak te zależności widać na

wykresie?

Pobudzenie

Po

zi

o

m

w

y

ko

n

a

n

ia

za

d

a

n

ia

Poziom
Lęku

Poziom zadania

Łatwe Trudne

Niski

3

3

Wysoki 5

2

Znajdź interakcję

3-3 =0

5-2 =3

3-5=-2 3-2=1

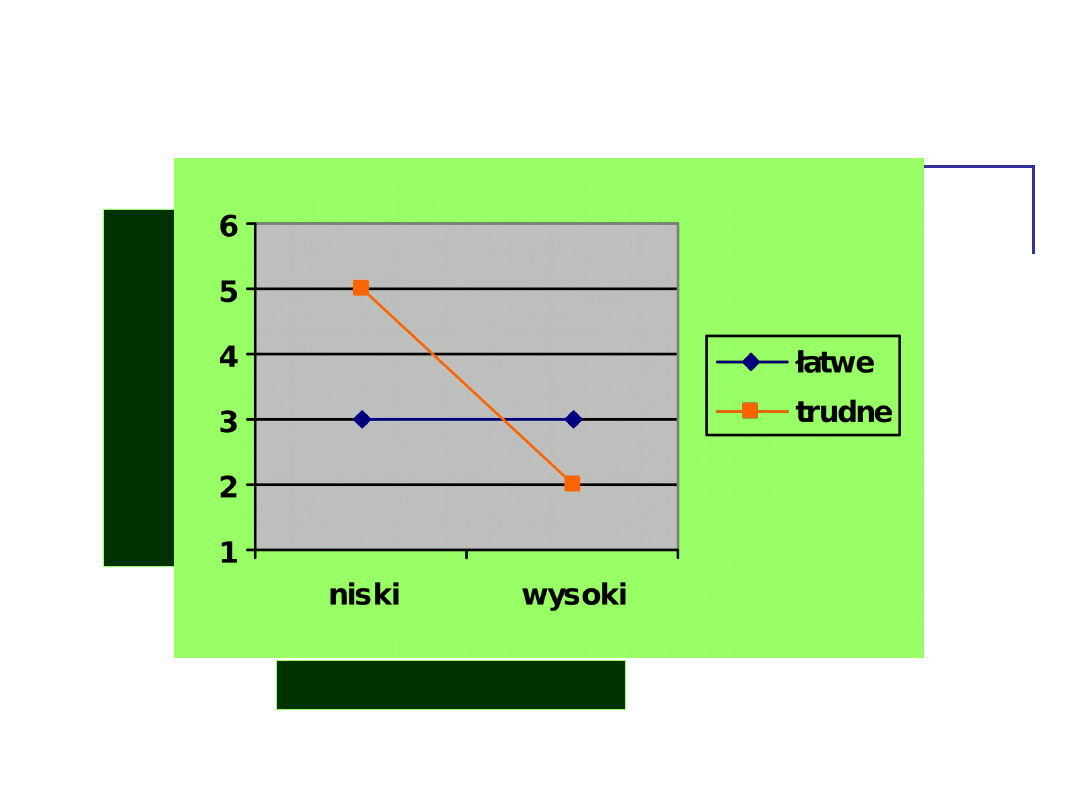
Jak te zależności widać na

wykresie?

LĘK

Po

zi

o

m

w

y

ko

n

a

n

ia

za

d

a

n

ia

Poziom
Lęku

Poziom zadania

Łatwe Trudne

Niski

6,25

3,10

Wysoki 4,25

1,10

6,25-3,10
=

3,15

4,25-1,10=

3,15

6,25-4,25

=

2

3,1-1,1 =

2

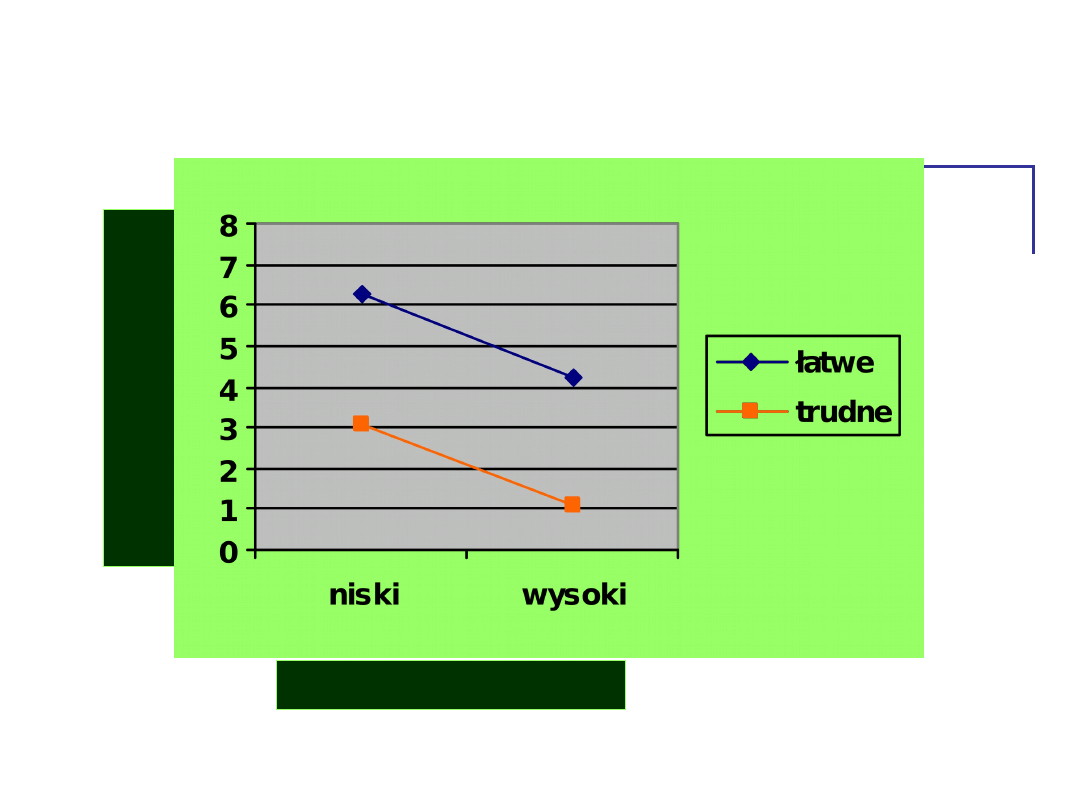
Jak te zależności widać na

wykresie?

lęk

Po

zi

o

m

w

y

ko

n

a

n

ia

za

d

a

n

ia

Wykresy

• Efekt interakcyjny jest dobrze

widoczny na wykresie.

– Kiedy linie na wykresie przecinają się lub

istnieje szansa, że kiedyś się przetną,
czyli nie są równoległe względem siebie,
wtedy możemy przypuszczać, że analiza
statystyczna wykaże istotną interakcję.

– Jeśli linie na wykresie są równoległe,

możemy liczyć tylko na efekty główne.

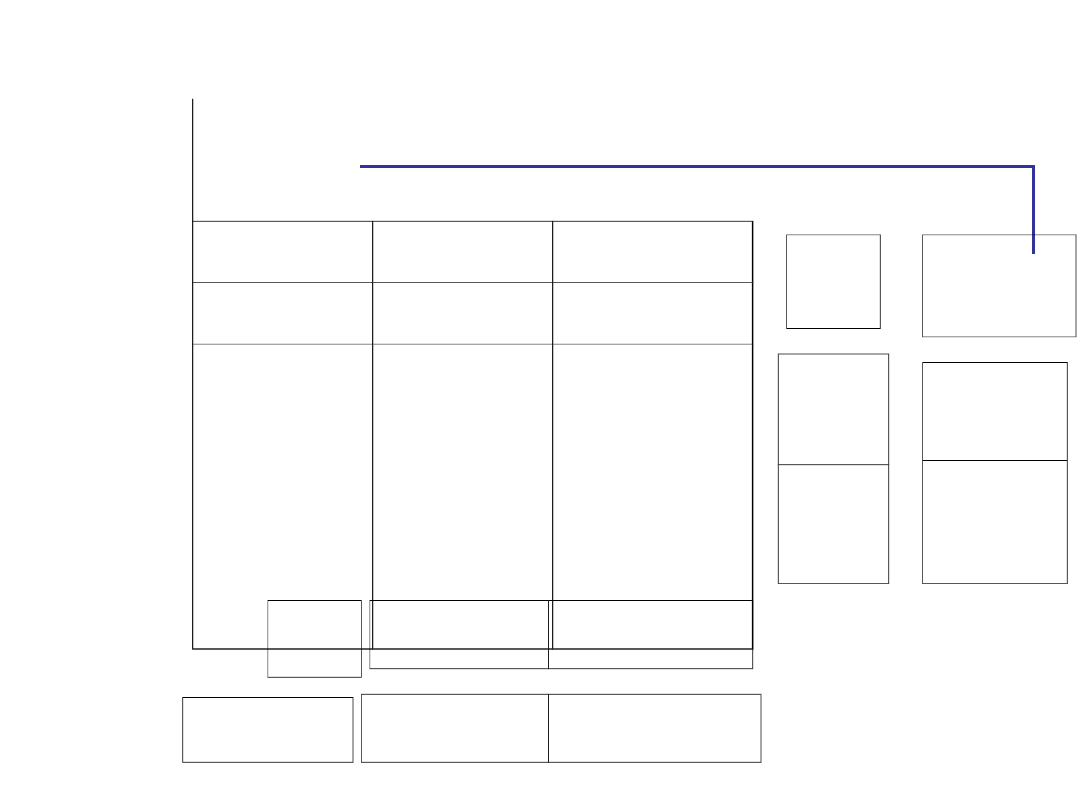
Dystr.

Zadanie

Pojed. Podwój.

Mało

500

800

Dużo

700

800

Jakich efektów możemy się

spodziewać?

650

750

600

800

-200

0

Śr.

R. Śr.

Śr.

R. Śr

-300

-100

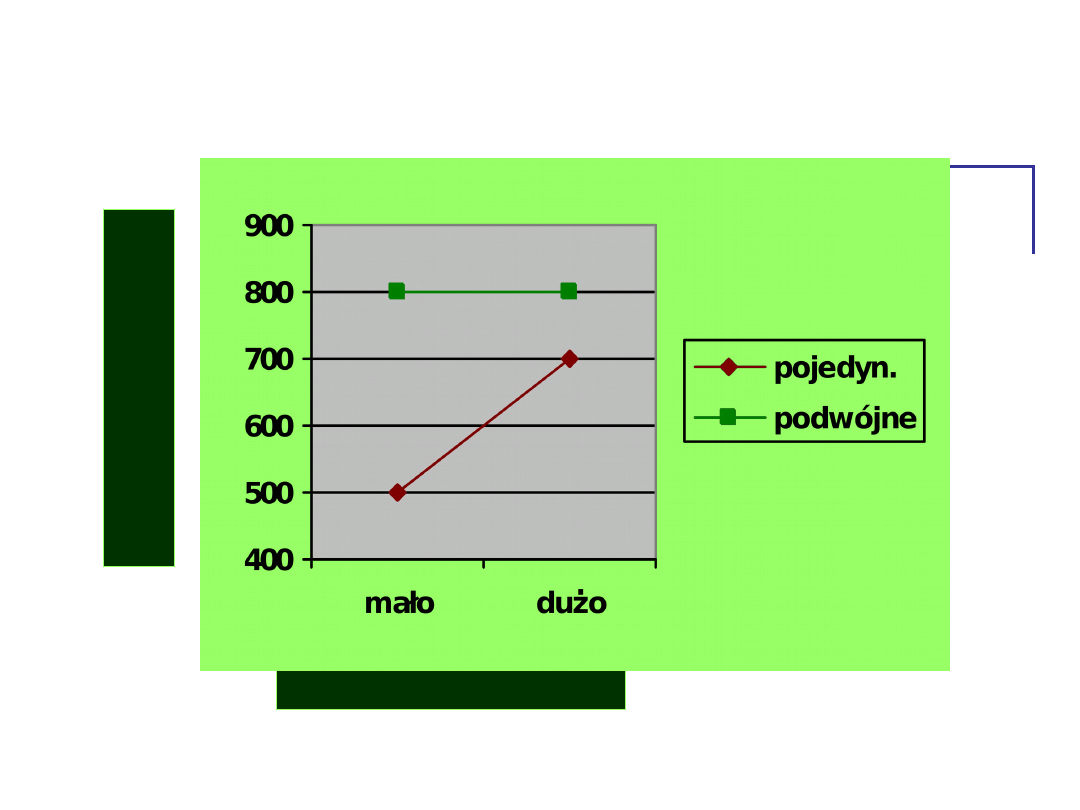
Średni czas reakcji na bodziec

właściwy.

Liczba dystraktorów

C

za

s

re

a

kc

ji

w

m

se

c.

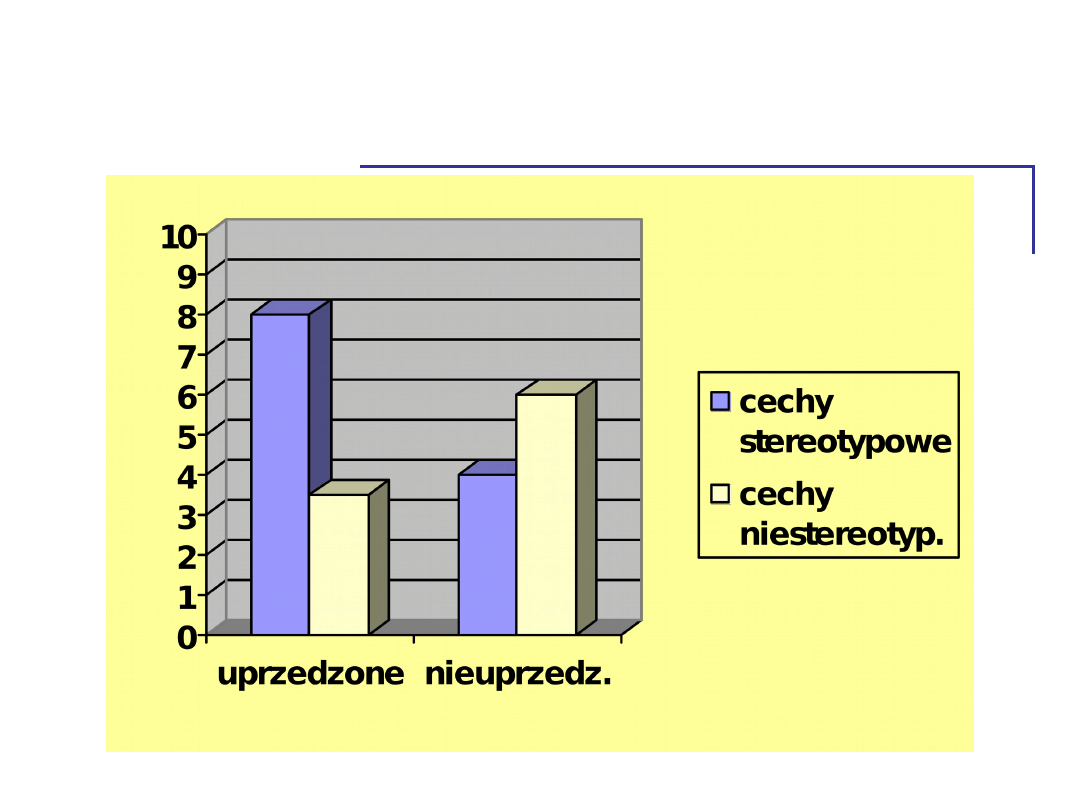
Średnia liczba zapamiętanych

określeń jako funkcja rodzaju cech i

posiadania stereotypu

Badanie 4 Zjawisko zagrożeniem

stereotypem

Osobami badanymi są członkowie grup co do których

istnieje powszechna, stereotypowa opinia, że są gorsi
w jakiejś dziedzinie np. policjantów o których mówi
się, że są głupi, kobiety rzekomo gorsze z matematyki.

Podczas rozwiązywania testu inteligencji przypomina się

policjantom stereotypową opinię – to obniża wynik
testu inteligencji, ale tylko tym policjantom dla
których bycie inteligentnym jest ważne. W sytuacji
neutralnej policjanci są tak samo inteligentni jak
grupa kontrolna

Szukamy efektów głównych

Zmienne

niezależne

Zagrożenie stereotypem

niskie

wysokie

płeć

K

50

20

M

50

50

30

50

50

35

Średnie

Średnie

Pojawiają się oba efekty główne

Szukamy efektu

interakcyjnego

Zmienne

niezależne

Pobudzenie

niskie

wysokie

zadani

e

Trud

ne

50

20

Łatw

e

50

50

20

0

0

-30

Różnica
średnich

Różnica

średnich

Różnice w kolumnach i wierszach są różne
więc jest efekt interakcyjny

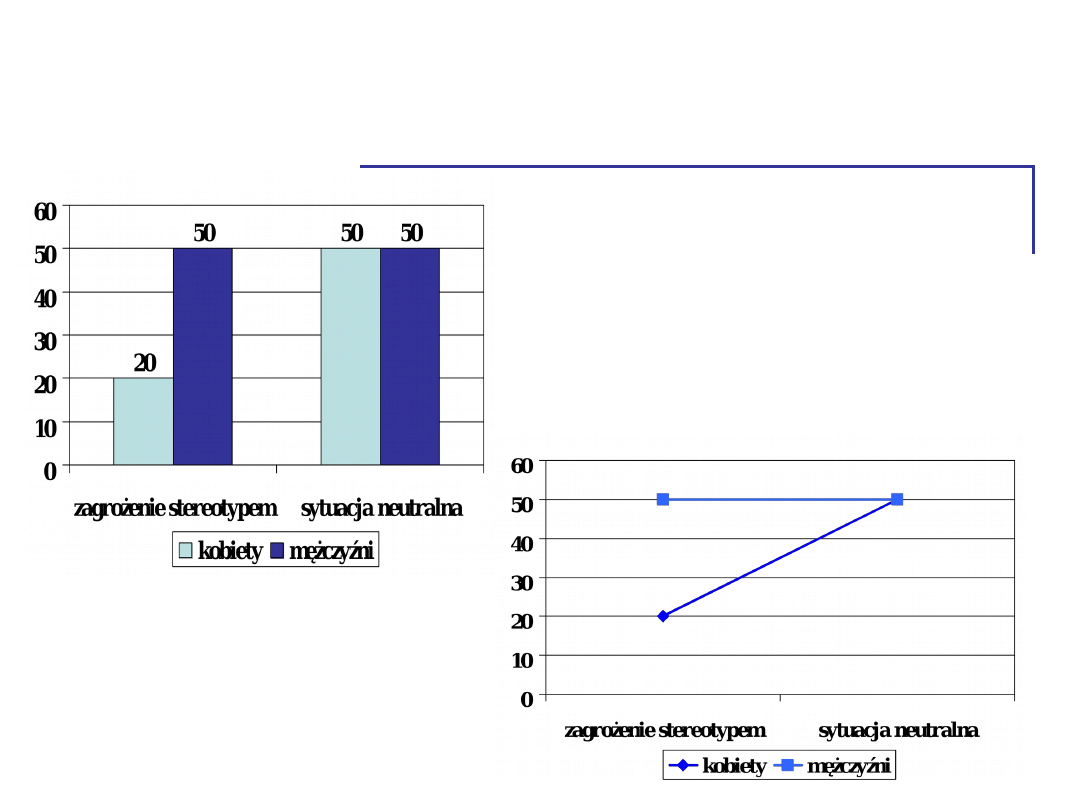
Wykresy

Są wszystkie

możliwe efekty

Rozstrzygnięcia ostateczne

• Oczywiście nigdy nie decydujemy na oko,

tylko robimy wydruk i patrzymy na
poziomy istotności.

• Jeśli mamy schemat 2x 2 i eekty główne są

istotne to patrzymy już tylko na średnie,
aby zinetrpretować efekt.

• Do efekty interakcyjnego musimy robić

testy post hoc albo kontrasty.

Zagrożenie stereotypem -

wydruk

Testy efektów międzyobiektowych

Zmienna zależna: ZADANIE

512,900

a

3

170,967

51,205

,000

11764,900

1 11764,900 3523,597

,000

176,400

1

176,400

52,832

,000

220,900

1

220,900

66,160

,000

115,600

1

115,600

34,622

,000

120,200

36

3,339

12398,000

40

633,100

39

Źródło zmienności
Model skorygowany
Stała
ZAGR
PLEC
ZAGR * PLEC
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,810 (Skorygowane R kwadrat = ,794)

a.

Wszystkie efekty istotne

Średnie grupowe

• Efekt główny zmiennej płeć

• Efekt główny zmiennej zagrożenie/brak

2. ZAGR

Zmienna zależna: ZADANIE

15,050
19,250

ZAGR
zagrożenie stereotypem
brak zagrożenia

Średnia

3. PLEC

Zmienna zależna: ZADANIE

14,800
19,500

PLEC
kobieta
mężczyzna

Średnia

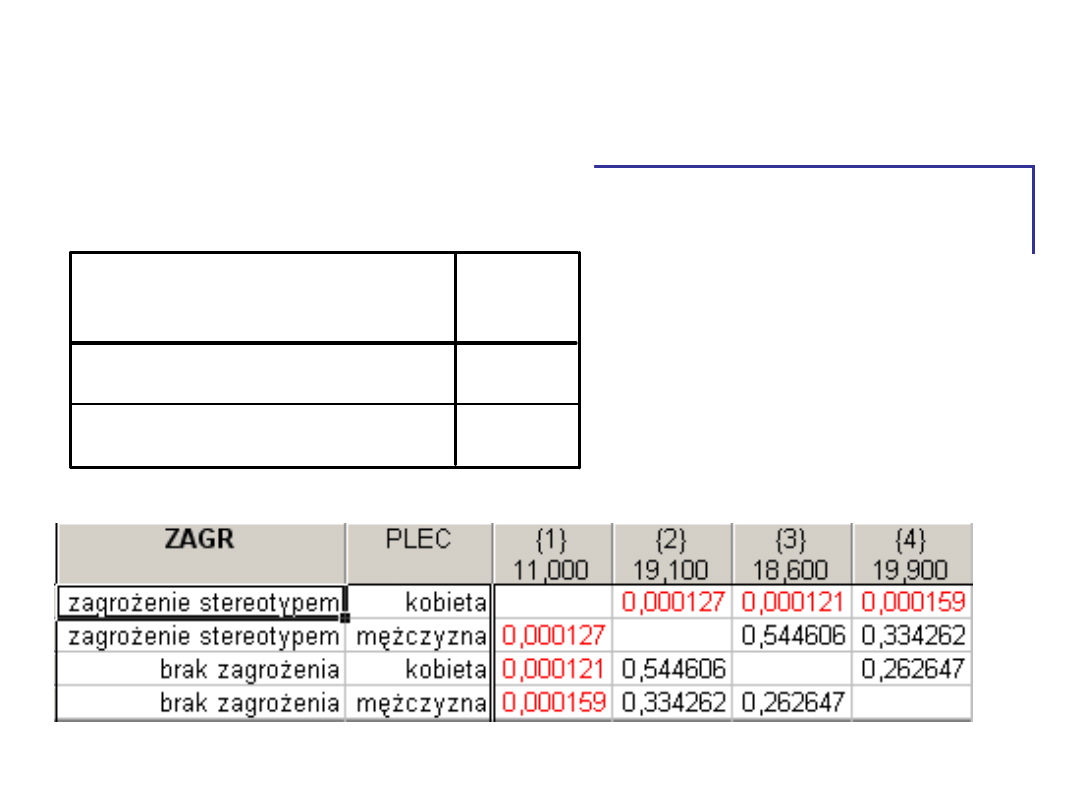
Efekt interakcyjny – test post

hoc

• Grupa kobiet w

sytuacji zagrożenia

stereotypem różni

się od reszty.

Pozostałe grupy

nie różnią się

między sobą

1. ZAGR * PLEC

Zmienna zależna: ZADANIE

11,000
19,100
18,600
19,900

PLEC
kobieta
mężczyzna
kobieta
mężczyzna

ZAGR
zagrożenie stereotypem

brak zagrożenia

Średnia

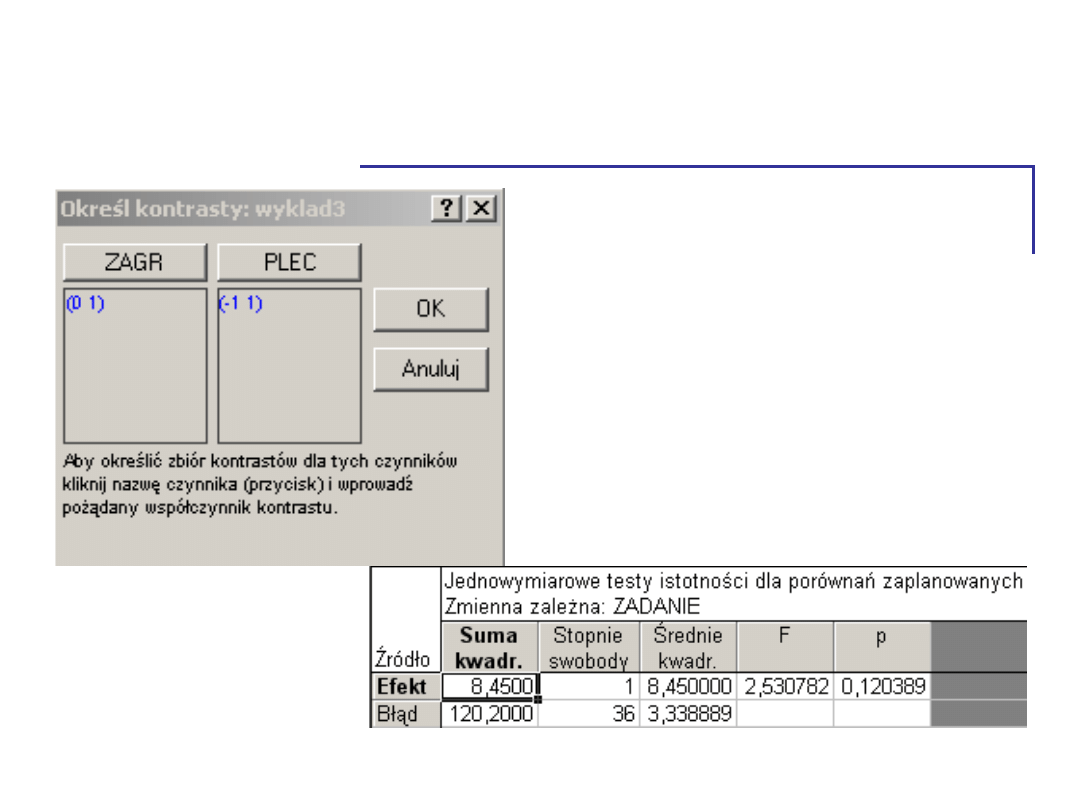
Efekt interakcyjny - kontrasty

• W sytuacji kontrolnej

brak różnic między
kobietami i
mężczyznami

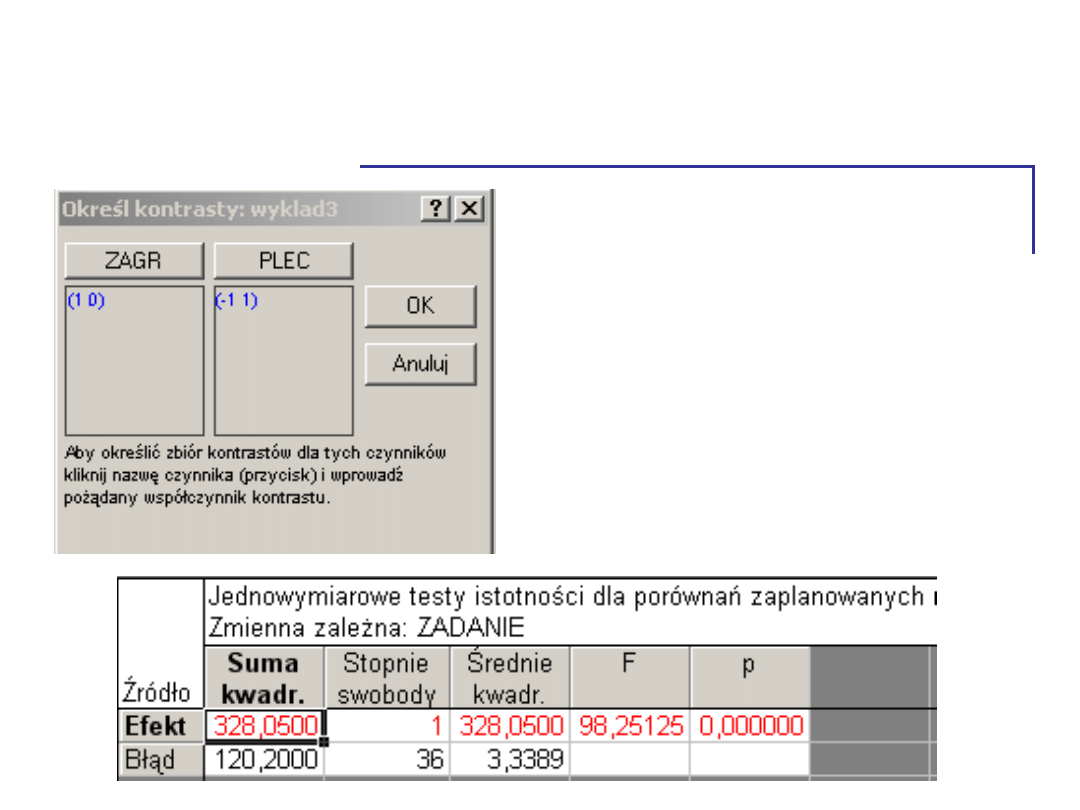
Efekt interakcyjny - kontrasty

• Najpierw porównujemy

kobiety i mężczyzn w
sytuacji zagrożenia
stereotypem