Testy T-Studenta

Już po raz ostatni

Rozwiązanie zagadki

Zagadka

5. Dziadek Staś uzyskał wynik w skali artretyzmu

20 punktów. Rozkład zmiennej artretyzm jest
normalny, mediana wynosi 10 a odchylenie
std. 4 punkty. Przelicz wynik dziadka Stasia
na jednostki standardowe.

Mediana = 10, średnia = 10

OS = 4

Z=20-10/4=2,5

Na czym skończyliśmy?

Test T-Studenta dla prób niezależnych

• Porównanie dwóch średnich
• Spełnianie założeń

– O równości wariancji (test Levena)
– O normalności rozkładu (test K-S)

• Stopnie swobody

– Test T dla jednej próby: N-1
– Test T dla dwóch prób niezależnych: N-2

Wartość statystyki T

• Im jest większa, tym łatwiej odrzucić

hipotezę zerową

– Wartość negatywna jest tak samo

ważna jak pozytywna

• W teście T-Studenta dla jednej próby mówi

o tym, czy wartość naszej średniej jest
większa czy mniejsza od wartości
testowanej

• W teście T-Studneta dla dwóch prób znak

zależy od tego, jak zakodowaliśmy nasze
grupy

Miara wielkości efektu - d

• Wielkość różnicy między średnimi wyrażona

w jednostkach odchylenia standardowego

• Umożliwia porównywanie wyników z

różnych badań, w których posługiwano się

różnymi jednostkami pomiarowymi

• Częste w metaanalizach
• Wzór na d Cohena



2

1

X

X

d





grupach

obu

w

std

odchylenie .





Wielkość efektu

• Mając do dyspozycji średnie,

odchylenia standardowe i wielkości

grup, możemy policzyć jak DUŻE są

uzyskane różnice (w jednostkach OS)

– d=0,20 mała wielkość efektu
– d=0,50 umiarkowana wielkość efektu
– d=0,80 duża wielkość efektu

• Czy możliwe d>1

Przykład

• Jeżeli w badaniach nad różnicami

płciowymi uzyskano:

– Dla zdolności werbalnych d=0,2
– Dla zdolności przestrzennych d=-0,8

(X

1

-kobiety, X

2

-mężczyźni)

To pod względem których zdolności

występują większe różnice i na czyją
korzyść?

Test T-Studenta dla dwóch prób zależnych -

założenia

• Plany dla dwóch grup zależnych
• Wyniki powiązane ze sobą

– Powtarzany pomiar, ale również
– Dwa różne zadania w tym samym

czasie, składowe zadania (np. serie)

– Badania bliźniąt, par małżeńskich itp.

• Normalność rozkładu w

analizowanych grupach

• Pomiar zmiennej zależnej na skali

ilościowej

• porównanie średniej wysokości zarobków absolwentów

SWPS w rok oraz w dwa lata po ukończeniu uczelni

• osoby badane zostają poddane badaniu tętna przed i po

wykonaniu 20 przysiadów; test t porównuje w tym

przypadku średnie tętno osób badanych z pomiaru przed

wysiłkiem ze średnim tętnem osób badanych po wysiłku i

weryfikuje hipotezę o równości tych średnich

• ważymy osoby badane na początku turnusu „dla grubasów”

i pod koniec tego pobytu; test t porównuje średnią wagę

uczestników turnusu z początku i z końca wyjazdu

• porównujemy średnią ilość wypalanych przez osoby badane

papierosów na początku roku akademickiego i średnią ilość

wypalanych papierosów w pierwszym tygodniu sesji

zimowej

Kiedy stosujemy?

• czy średnia długość urlopu, na jaki wyjeżdżali badani

jest taka sama jak średnia długość wymarzonego

przez nich urlopu

• czy średni wzrost babć osób badanych jest taki sam

jak średni wzrost mam osób badanych

• czy średnia z faktycznego dochodu osób badanych

jest taka sama jak średnia z tego, na co badani

swoim zdaniem zasługują

• czy średni wiek, w którym ojcowie respondentów

ożenili się jest taki sam jak średni wiek matek osób

badanych w chwili wychodzenia za mąż

• ale np. para zmiennych „liczba rodzeństwa’ oraz

„wzrost osoby badanej” nie nadaje się do tej analizy

- różnica „troje rodzeństwa – 170 cm” jest bez sensu.

Kiedy stosujemy?

Jak go wykonać?

• Hipoteza zerowa zakłada brak różnic między

porównywanymi średnimi

• Statystykę t dla prób zależnych wylicza się

bardzo podobnie, jak dla jednej próby,

• Zmienną testowaną jest w tym wypadku różnica

wartości uzyskanych przez osoby badane w

pierwszym i drugim pomiarze (zadaniu, itp.)

• Można to zapisać np. tak:

D

BS

D

t 

Średnia różnica między parami wyników

Błąd standardowy tej różnicy

Teraz przykład o jajach

Czy większe jaja dostarczają więcej
energii?

Jak go wykonać?-Poziom energii po zjedzeniu jaj Crane,a i Grouse’a

OSOB
A

Energia

RÓŻNIC
A

ODCHYL
ENIE

KWADRAT
ODCHYLE--
NIA

jaja

żurawia

jaja

pardwy

1

18

12

6

6-2=4

16

2

21

21

0

-2

4

3

19

16

3

1

1

4

21

16

5

3

9

5

17

19

-2

-4

16

6

20

19

1

-1

1

7

18

16

2

0

0

8

16

17

-1

-3

9

9

20

16

4

2

4

Σ:

170

152

18

0

60

Co musimy policzyć:
Dla różnicy wyników:
M (D)= 18/9 = 2.0.

S

2

= SS/df = 60/(9-1) = 7.5.

BS

2

= S

2

/N = 7.50/9 = .83.

BS = √ BS

2

= √.83 = .91.

wartość krytyczna testu t
ze stopniami swobody df
= 8, dla poziomu
istotności p<,01 i testu
dwustronnego = 2.897.

Dla analizowanej próby
wartość testu t=(M –
μ)/BS= (2.00 – 0)/.91 =
2.20.

Skoro grupy są powiązane…

• To wyniki mogą być skorelowane ze sobą
• SPSS oprócz wartości statystyki T,

podaje również wartość i istotność
statystyczną korelacji R-Pearsona

• Hipoteza zerowa R-Pearsona
H0:R=0
Czyli brak związku liniowego między

analizowanymi zmiennymi

Zastanówmy się
teraz nad
pewnym
hipotetycznym
badaniem, w
którym
sprawdzano jak
zachowują się
kocie brzuchy po
wypiciu mleka:

Rozważmy
możliwe
scenariusze.

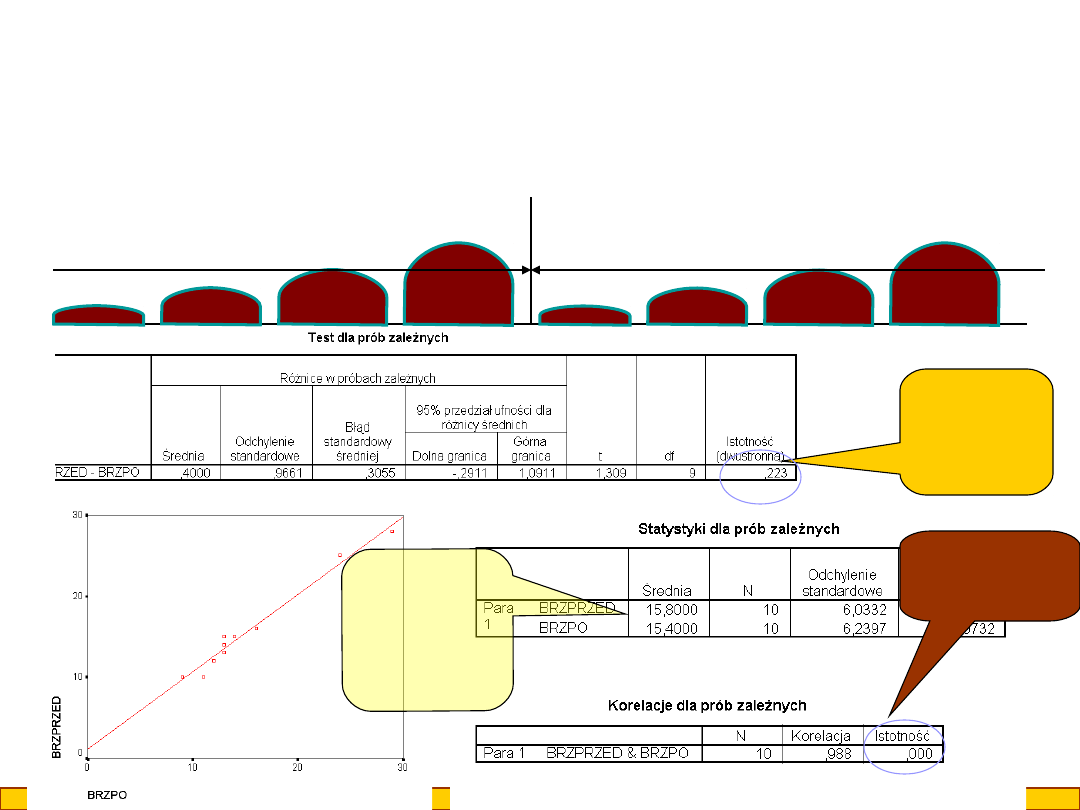
Test t

nieistotny

; p>0,05

Korelacja

istotna;

p<0,001

Kiedy otrzymujemy wyniki jak poniżej (test t dla prób zależnych
nieistotny, silna korelacja dodatnia) oznacza to, że po wypiciu mleka
kotki, które miały duże brzuchy nadal mają je duże, a te, które miały
małe nadal je maja małe, bez istotnych zmian

A średnie

przed i po

praktyczni

e się nie

różnią

PRZED

PO

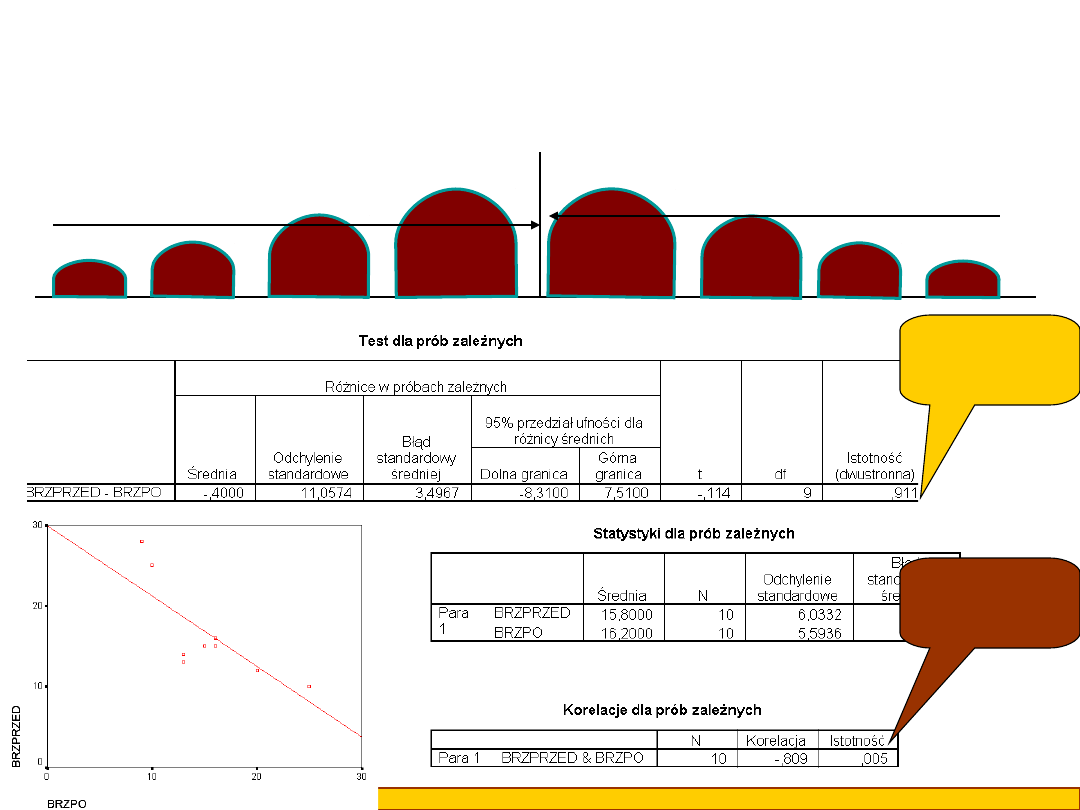
Kiedy wyniki układają się nam w następujący sposób (test t dla prób
zależnych nieistotny, silna korelacja ujemna) oznacza to, że po wypiciu mleka
kotki, które miały duże brzuchy teraz mają je małe, a te, które miały małe
teraz mają je duże, brak natomiast jest różnic w średnich grupowych

Korelacja

istotna;

p<0,001

Test t

nieistotny;

p>0,05

PRZED

PO

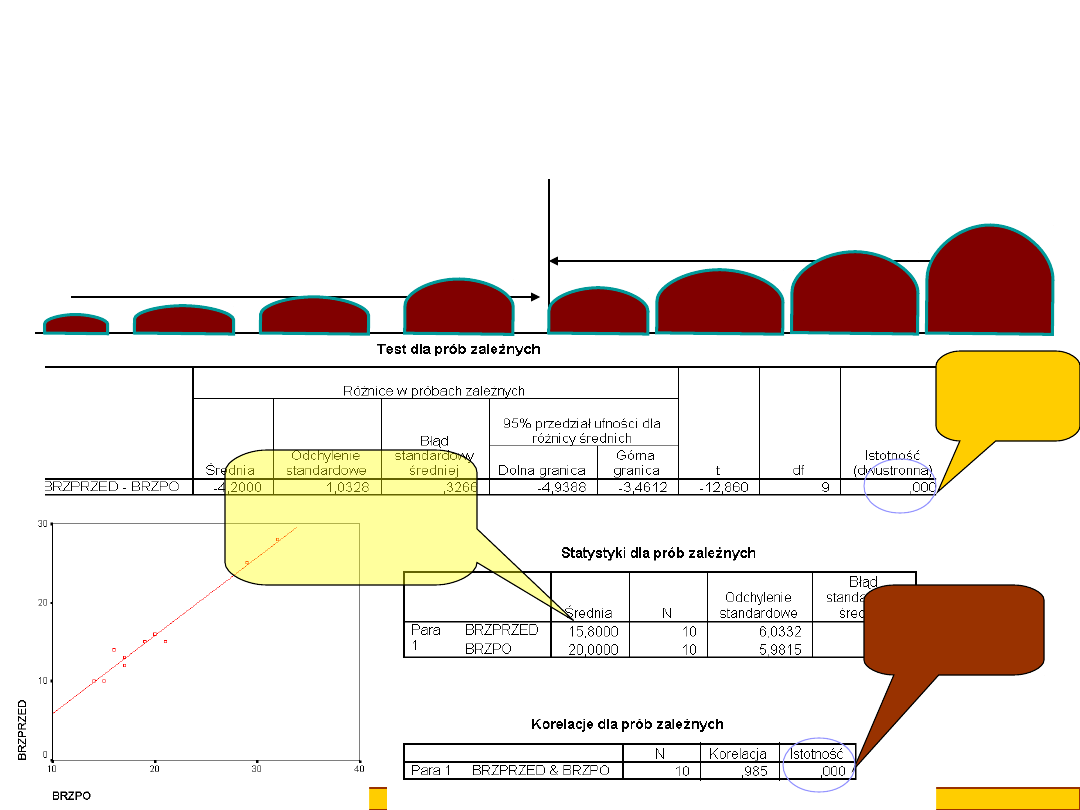
Kiedy otrzymujemy wyniki, w których zarówno test t jest istotny jak i
korelacja jest dodatnia i istotna oznacza to, że po wypiciu mleka kotki, które
miały duże brzuchy nadal mają je duże na tle grupy, a te, które miały małe
nadal je maja małe, i dodatkowo wszystkim brzuchom coś przybyło, lub ubyło
(w naszym przykładzie przybyło)

Korelacja

istotna;

p<0,001

Test t

istotny;

p<0,00

1

Widać również,

że średnia przed

jest niższa niż po

wypiciu mleka

PRZED

PO

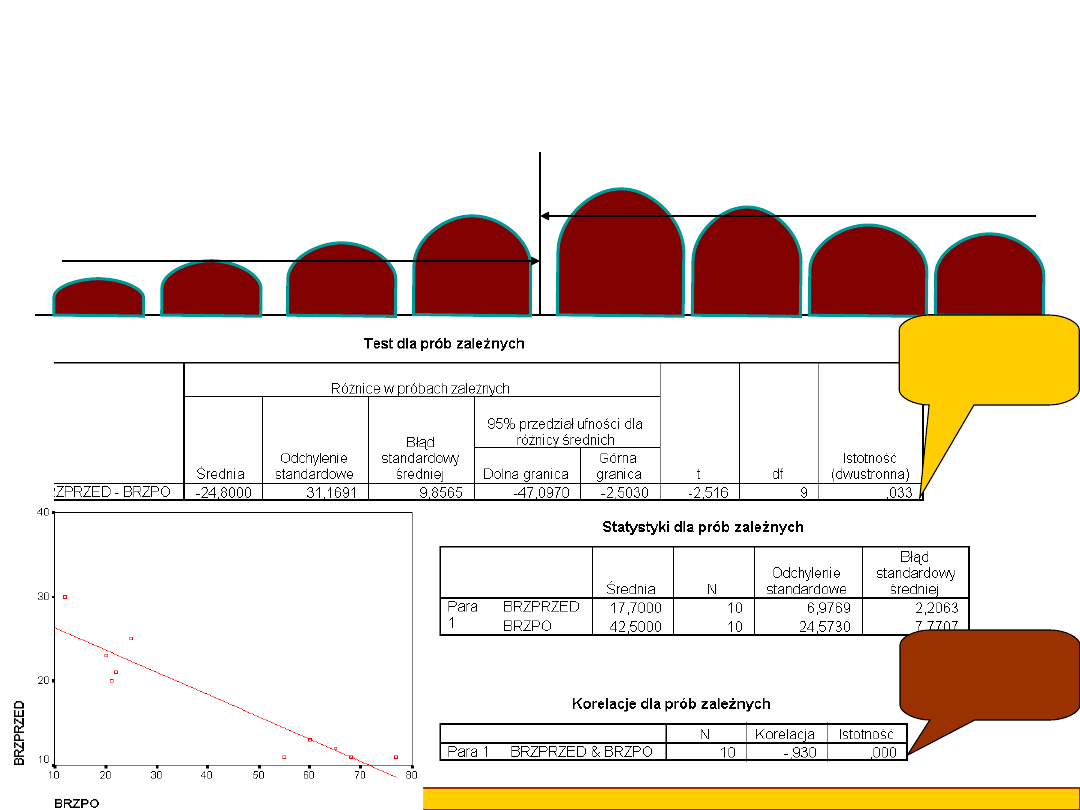
Kiedy otrzymujemy wyniki takie jak poniżej (test t istotny, silna korelacja
ujemna) oznacza to, że po wypiciu mleka kotki, które miały duże brzuchy
teraz mają je małe na tle grupy, a te, które miały małe teraz mają je duże, i
jednocześnie następuje ogólna zmiana w wielkości ich brzuchów - in plus lub
in minus.

PRZED

PO

Test t

istotny;

p<0,05

Korelacja

istotna;

p<0,001

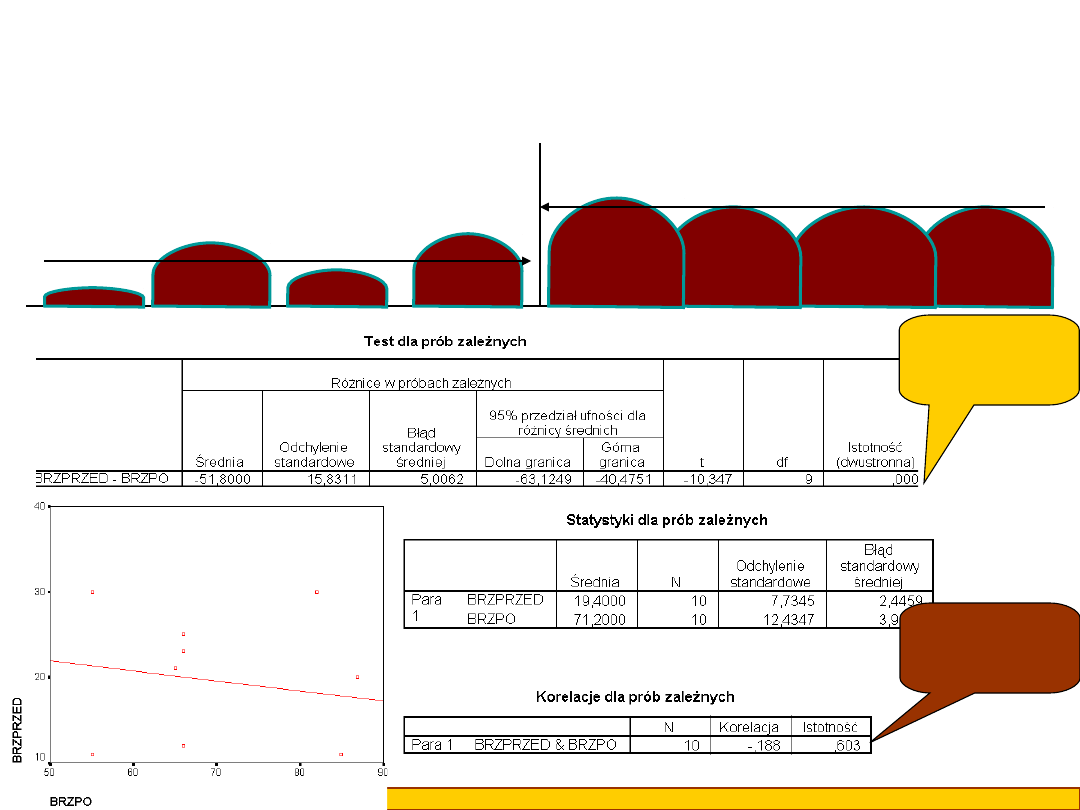
Możemy również mieć do czynienia z sytuacją, kiedy test t jest istotny,
natomiast korelacja nie. Dzieje się tak na przykład w przypadku, kiedy przed
wypiciem mleka brzuchy były różnej wielkości, a po wypiciu wszystkie stały
się ogromne

PRZED

PO

Test t

istotny;

p<0,001

Korelacja

nieistotna;

p>0,05

Główne elementy testu statystycznego

Para hipotez:

zerowa

alternatywna

statystyka testu,
stopnie swobody
poziom
istotności

odrzucenie
hipotezy
zerowej

i przyjęcie
alternatywnej

nie odrzucenie

hipotezy
zerowej

i nie przyjęcie
alternatywnej

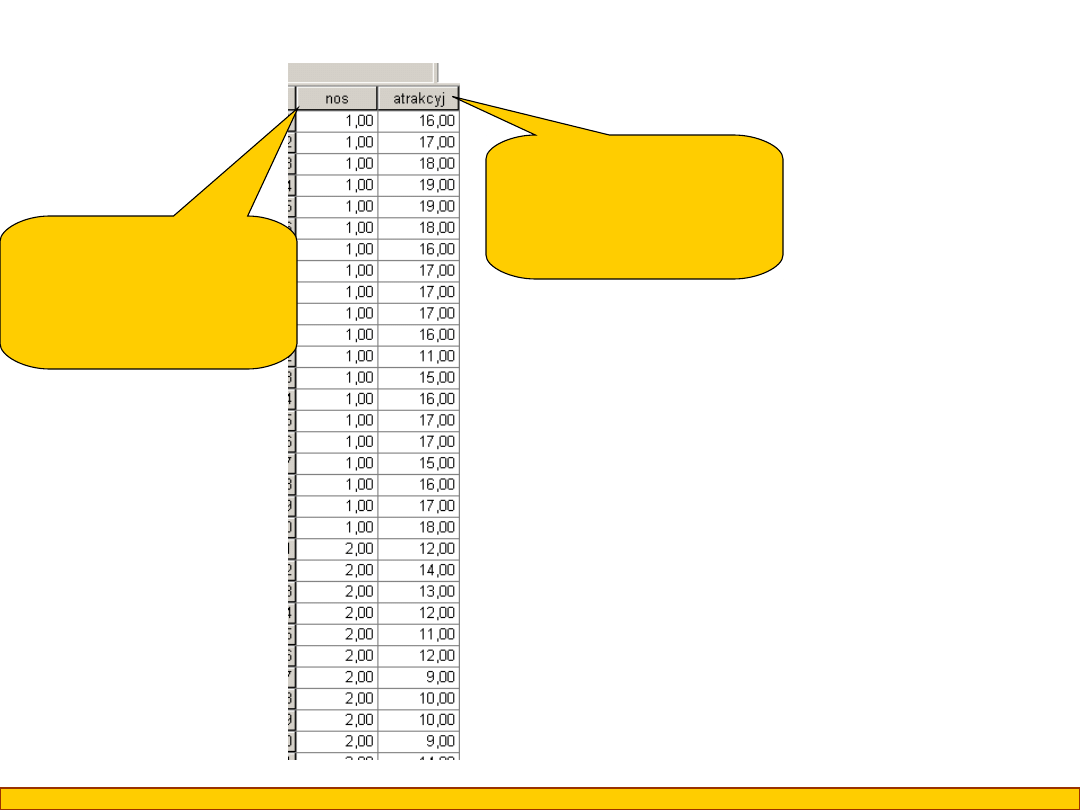
Test T-Studenta dla prób

niezależnych stosujemy
wtedy, gdy jedna
zmienna jest
jakościowa
dychotomiczna a druga
zmienna jest ilościowa

Zmienna

ilościowa -

atrakcyjność

Zmienna

jakościowa –

rodzaj nosa –

zadarty lub

prosty

Test T-Studenta dla dwóch prób niezależnych

Para hipotez:

zerowa: M

1

=M

2

alternatywna: M

1

#M

2

statystyka testu
T

stopnie swobody
N-2

poziom
istotności

odrzucenie
hipotezy
zerowej

i przyjęcie
alternatywnej

nie odrzucenie

hipotezy
zerowej

i nie przyjęcie
alternatywnej

Wydruk testu T-Studenta dla prób niezależnych

Statystyki dla grup

20

16,6000

1,72901

,38662

20

11,5500

1,63755

,36617

NOS
prosty
zadarty

atrakcyjnosc fizyczna

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla prób niezależnych

,221

,641

9,484

38

,000

5,0500

,53250

3,97202

6,12798

9,484

37,888

,000

5,0500

,53250

3,97191

6,12809

Założono równość
wariancji
Nie założono
równości wariancji

atrakcyjnosc fizyczna

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Różnica

średnich

Błąd

standardowy

różnicy

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Test t równości średnich

Założenie

testu T

Statystyki

testu T

Średni

e

Założenia testu T-Studenta dla prób niezależnych

• Jednorodność wariancji Test F Levene’a
• Równoliczność grup Test chi kwadrat
• Normalność rozkładu zmiennej zależnej we

wszystkich podgrupach Test Z Kołmogorowa
Smirnowa

Test Levene’a

zerowa: s

1

2

= s

2

2

alternatywna: s

1

2

# s

2

2

statystyka testu
F

poziom
istotności

Test chi kwadrat

zerowa: N

1

= N

2

alternatywna: N

1

# N

2

statystyka testu
χ

2

poziom
istotności

Test

Kołmogorowa

-Smirnowa

zerowa:

rozkład nie odbiega od normalnego

alternatywna:

rozkład odbiega od normalnego

statystyka testu
Z

poziom
istotności

Test T-Studenta dla dwóch prób zależnych

Para hipotez:

zerowa: M

1p

=M

2p

alternatywna: M

1p

#M

2p

statystyka testu
T

stopnie swobody
N-1

poziom
istotności

odrzucenie
hipotezy
zerowej

i przyjęcie
alternatywnej

nie odrzucenie

hipotezy
zerowej

i nie przyjęcie
alternatywnej

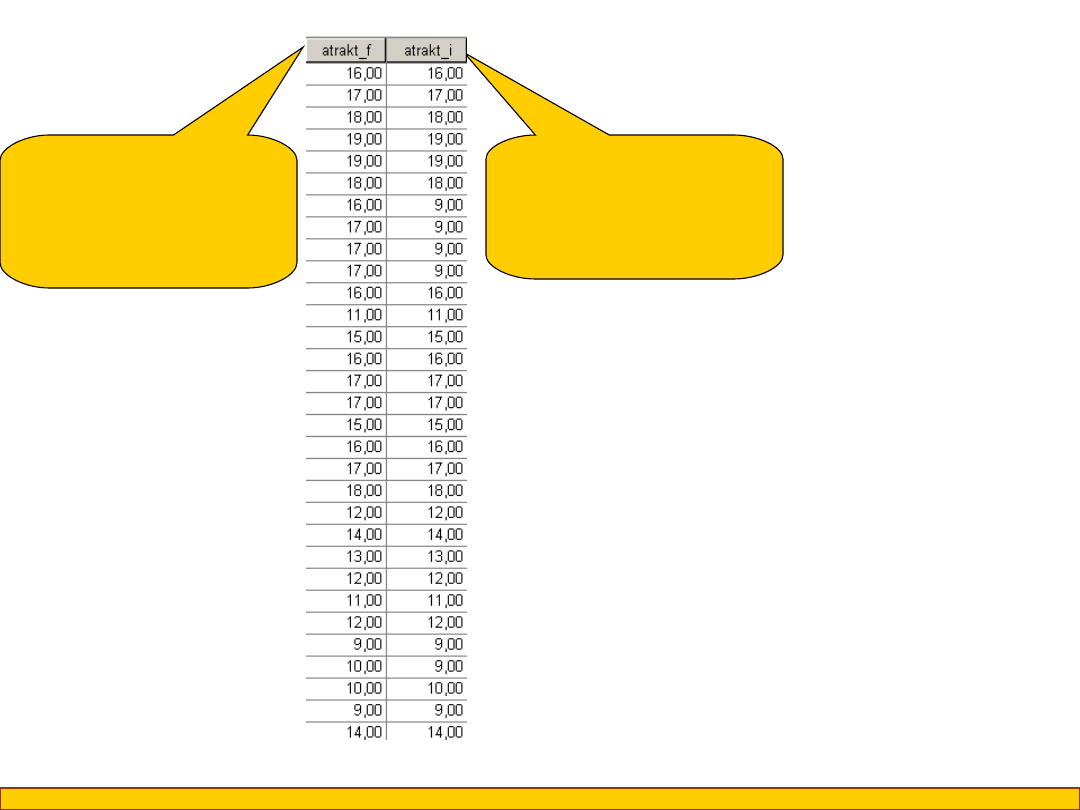
Test T-Studenta dla prób

zależnych stosujemy
wtedy, gdy obie
zmienne są ilościowe

Zmienna

ilościowa –

atrakcyjność

interpersonalna

Zmienna

ilościowa –

atrakcyjność

fizyczna

Statystyki dla prób zależnych

14,0750

40

3,04991

,48223

12,8750

40

3,59621

,56861

atrakcyjnosc fizyczna
atrakcyjnośc
interpersonalna

Para
1

Średnia

N

Odchylenie

standardowe

Błąd

standardowy

średniej

Wydruk testu T-Studenta dla prób zależnych

Korelacje dla prób zależnych

40

,707

,000

atrakcyjnosc fizyczna
& atrakcyjnośc
interpersonalna

Para
1

N

Korelacja

Istotność

Statystyki

testu T

Test dla prób zależnych

1,2000

2,59388

,41013

,3704

2,0296

2,926

39

,006

atrakcyjnosc fizyczna
- atrakcyjnośc
interpersonalna

Para
1

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Różnice w próbach zależnych

t

df

Istotność

(dwustronna)

Średni

e

Współczynn

ikkorelacji

R

Założenia testu T-Studenta dla prób zależnych

• Normalność rozkładu obu zmiennych - Test Z

Kołmogorowa Smirnowa

Test

Kołmogorowa

-Smirnowa

zerowa:

rozkład nie odbiega od normalnego

alternatywna:

rozkład odbiega od normalnego

statystyka testu
Z

poziom
istotności

Test T-Studenta dla jednej próby

Para hipotez:

zerowa: M=stała

alternatywna: M#stała

statystyka testu
T

stopnie swobody
N-1

poziom
istotności

odrzucenie
hipotezy
zerowej

i przyjęcie
alternatywnej

nie odrzucenie

hipotezy
zerowej

i nie przyjęcie
alternatywnej

Test T-Studenta dla jednej

próby wtedy, gdy
zmienna jest ilościowa

Zmienna

ilościowa –

iloraz

inteligencji

Stała = 100 punktów

Wydruk testu T-Studenta dla jednej próby

Statystyki

testu T

Statystyki dla jednej próby

29 123,1379

11,23999

2,08721

iloraz inteligencji

N

Średnia

Odchylenie

standardowe

Błąd

standardowy

średniej

Test dla jednej próby

11,086

28

,000

23,1379

18,8625

27,4134

iloraz inteligencji

t

df

Istotność

(dwustronna)

Różnica

średnich

Dolna granica Górna granica

95% przedział ufności dla

różnicy średnich

Wartość testowana = 100

Średni

a

Założenia testu T-Studenta dla jednej próby

• Normalność rozkładu obu zmiennych - Test Z

Kołmogorowa Smirnowa

Test

Kołmogorowa

-Smirnowa

zerowa:

rozkład nie odbiega od normalnego

alternatywna:

rozkład odbiega od normalnego

statystyka testu
Z

poziom
istotności

Przesądy – Widmo Brockenu
Badano dwie grupy osób – te które w

czasie wędrówek w górach zobaczyły

efekt oraz tymi, które tego efektu nie

widziały. Analizowano ilość

negatywnych wydarzeń w ich życiu.

Przebadano łącznie 60 osób. Jaki

test statystyczny zastosowano do

analizy tego problemu?

a. Test T-Studenta dla jednej próby
b. Test T-Studenta dla dwóch prób

niezależnych

c. Test T-Studenta dla dwóch prób

zależnych

d. Test Kołmogorowa-Smirnowa
Ile było stopni swobody w tym teście?
a.

60

b.

59

c.

58

d.

2

Jeśli poziom istotności testu był

p<0,05 to oznacza to, że:

a. Średnie w obu grupach się różnią
b. Średnie w obu grupach się nie różnią

Czy szczury lubią telewizję?

Badacz analizował, czy zmieniające się bodźce wizualne są dla

szczurów atrakcyjne. Sprawdzał ile czasu szczury spędzały w

części klatki, w której znajdował się „telewizor”. Najpierw

umieszczał szczura w klatce, w której były atrakcyjne dla

szczura korytarze i schody a następnie umieszczał szczura w

klatce z telewizorem. Zbadano 60 szczurów.

Jaki test statystyczny zastosowano do analizy tego problemu?
a. Test T-Studenta dla jednej próby
b. Test T-Studenta dla dwóch prób niezależnych
c. Test T-Studenta dla dwóch prób zależnych
d. Test Kołmogorowa-Smirnowa
Ile było stopni swobody w tym teście?
a.

60

b.

59

c.

58

d.

2

Jeśli poziom istotności testu był p>0,05 to oznacza to, że:
a. Średnie w obu pomiarach się różnią
b. Średnie w obu pomiarach się nie różnią

Badacz zajmujący się świadomością prawną postanowił sprawdzić,

czy młodzi ludzie wiedzą w jakim wieku mogą zwierać

małżeństwa. Przebadał więc 55 dziewcząt, zadając im pytanie

„W jakim wieku można zawierać związek małżeński?”.

Jaki test statystyczny zastosowano do analizy tego

problemu?

a. Test T-Studenta dla jednej próby
b. Test T-Studenta dla dwóch prób niezależnych
c. Test T-Studenta dla dwóch prób zależnych
d. Test Kołmogorowa-Smirnowa
Ile było stopni swobody w tym teście?
a.

54

b.

53

c.

55

d.

22,5

Jak brzmi hipoteza zerowa tego testu?
a.

Średnia w grupie różni się od 55

b.

Średnie w obu grupach nie różnią się

c.

Średnia w grupie nie różni się od 55

W teście Levene’a badacz uzyskał istotny

statystycznie wynik (p<0,05). Co to oznacza?

a. Wariancje są równe
b. Wariancje są nierówne
c. Średnie są równe
d. Średnie nie różnią się
W teście Kołmogorowa-Smirnowa uzyskano

istotność p<0,05. Jaki jest rozkład zmiennej?

a. Rozkład nie odbiega od normalnego
b. Rozkład odbiega od normalnego
c. Nie możemy nic powiedzieć o rozkładzie

zmiennej

Zadanie do przemyślenia w domu....

Badacz postanowił sprawdzić, czy kobiety i

mężczyźni różnią się poziomem wykształcenia.

Zbadał 25 kobiet i 30 mężczyzn zadając im

pytanie „Na jakim poziomie skończyłeś edukację

szkolną?”. Badani mogli wybrać: szkoła

podstawowa, zawodowa, średnia, technikum,

szkoła wyższa”.

Jaki test statystyczny zastosowano do analizy

tego problemu?

a. Test T-Studenta dla jednej próby
b. Test T-Studenta dla dwóch prób niezależnych
c. Test T-Studenta dla dwóch prób zależnych
d. Test Kołmogorowa-Smirnowa
e. Test Levene’a