Anova czyli 3 w 1

Hipoteza dotycząca różnic między więcej niż dwiema grupami

Wystąpią różnice w wydajności pracy w zależności od rodzaju

muzyki prezentowanej w czasie wykonywania zadania

Hipoteza

niekierunkowa:

Wystąpią różnice...

Wybór: analiza
wariancji

Hipoteza

kierunkowa:

Słuchający muzyki

klasycznej będą bardziej

wydajni

Testy post hoc

Porównania a

posteriori

Znany

kształt

zależnoś

ci

Nieznany

kształt

zależności

Wielomiany

rodzaj

kontrastów

Porównania

planowane –

kontrasty

Porównania a priori

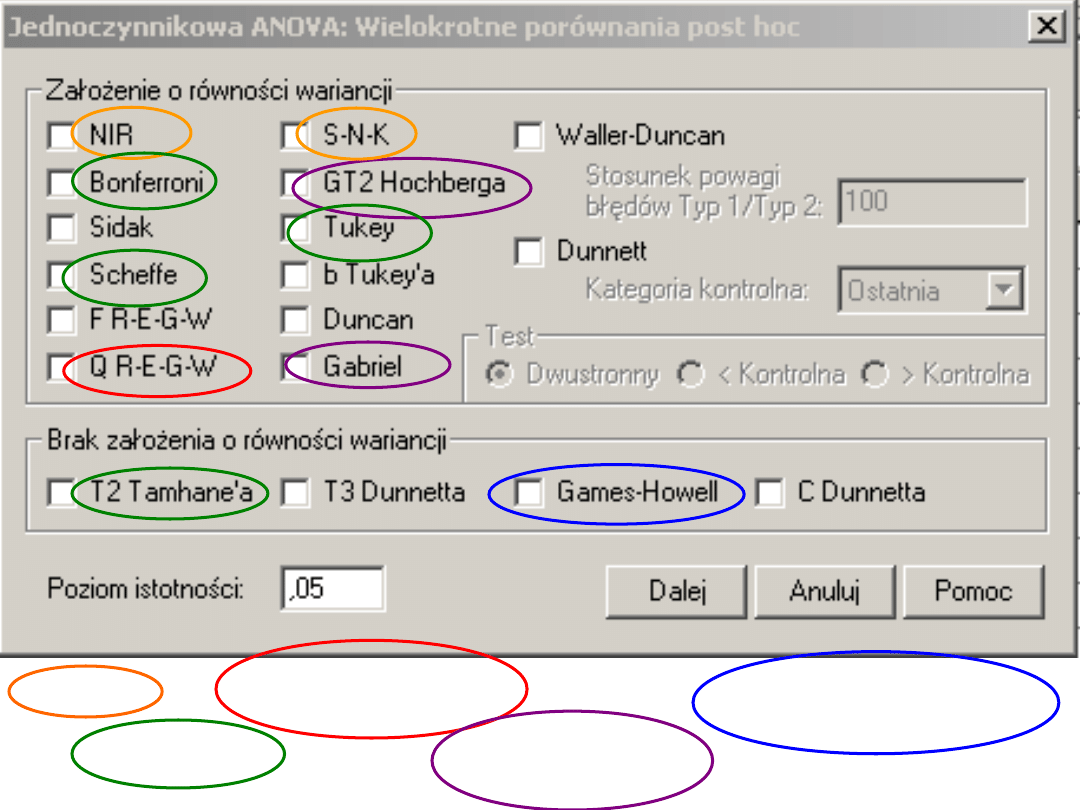
liberalne

konserwatywne

Polecany przy

rówolicznych grupach

Polecane przy

nierównych grupach

Przy nierównych grupach

i zaburzonej wariancji

Czynnik

Zmienna

zależna

Nie chodzi na

randki

Okazjonalnie

chodzi na

randki

Ma stałego

partnera

Oporność

skory

19

b

19,29

b

15,14

a

Chęć

spotkania

19,14

b

14,57

a

18,86

b

Postrzegana

atrakcyjno
ść

13,14

a

17

b

17

b

Przebadano 21 studentek, które oglądały różne

czasopisma zawierające zdjęcia atrakcyjnych
mężczyzn. Następnie mierzono poziom
pobudzenia psychofizjologicznego (oporność
skóry) jak również chęć spotkania się z danym
mężczyzną oraz jego atrakcyjność w opinii
studentek.

Które średnie się różnią?

Porównania post hoc a porównania

a’priori

• Porównania a posteriori są techniką

eksploracyjną, gdy okaże się, że są

różnice eksplorujemy je za pomocą

testów post hoc.

– O ich przeprowadzaniu badacz decyduje po

wstępnej analizie danych, która może mu

wskazać celowość takich porównań.

• Porównania a priori (zwane też

porównaniami planowanymi), planuje się

przed przeprowadzeniem eksperymentu.

– Bezpośrednio związane z teorią, na której

opiera się eksperyment.

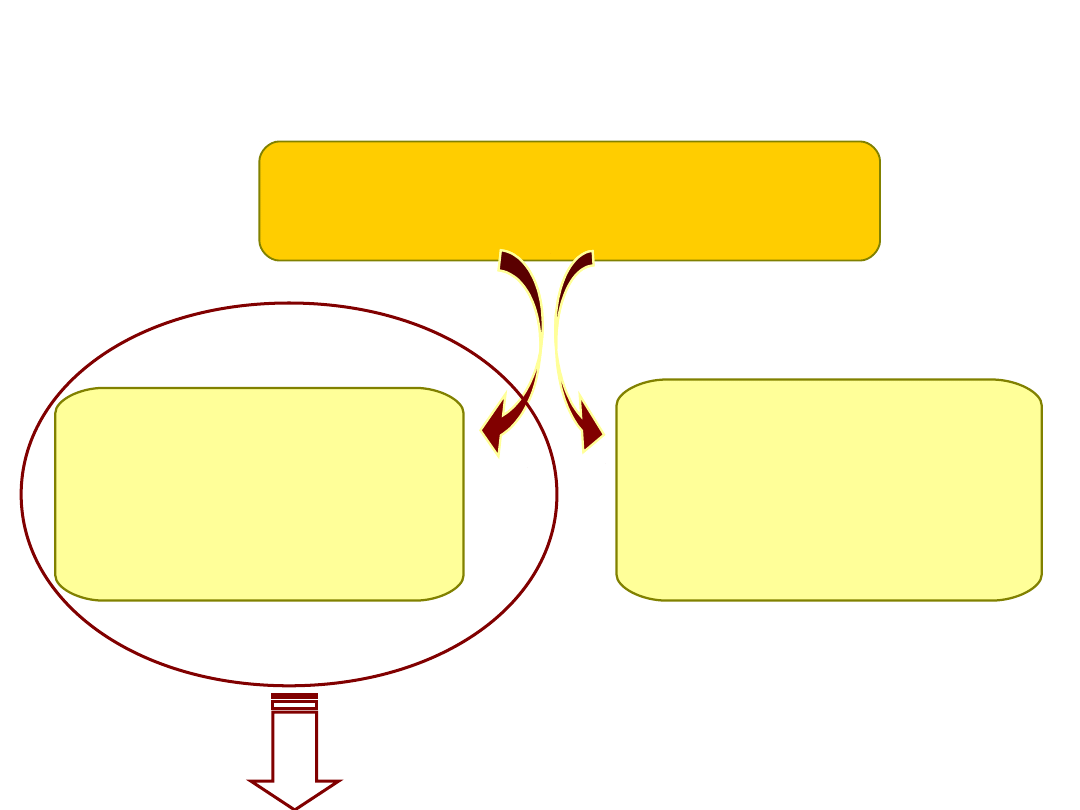
Całkowita wariancja naszych danych

Wariancja wyjaśniona

Wariancja międzygrupowa

Wariancja kontrolowana

Wariancja niewyjaśniona

Wariancja wewnątrzgrupowa

Wariancja błędu

Logika porównań planowanych

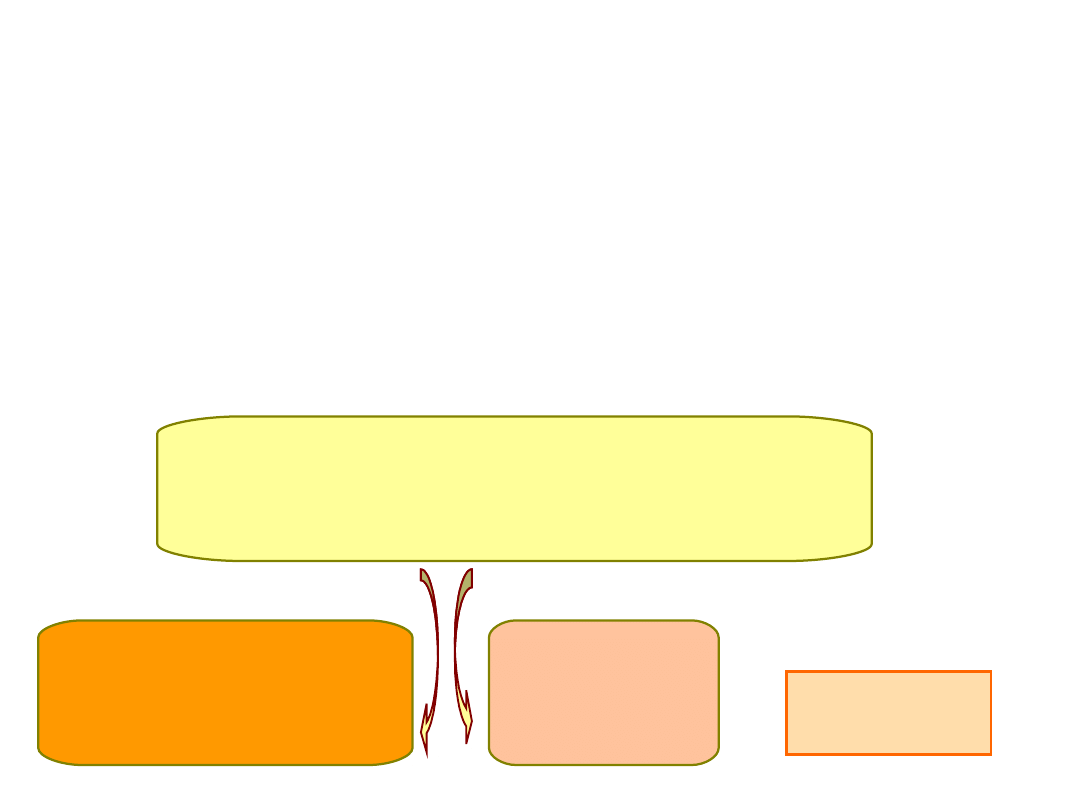
• Prawie w każdym eksperymencie mamy grupę

kontrolną, dlatego

– prawie zawsze wykonywanie kontrastów zaczynamy

od porównania grupy kontrolnej z
eksperymentalnymi (chyba, że mamy inne hipotezy)

Jak porównujemy?

Wariancja międzygrupowa

Trzy grupy: E1, E2 i K1

Wariancja wyjaśniona

przez E1, E2

Wariancja

wyjaśniona

przez K1

Porównani
e 1

Definiowanie kontrastów poprzez wagi –

cd.

W przykładowym eksperymencie mamy 3 grupy. Chcemy porównać

grupy 1 i 2 z trzecią. Chcemy udowodnić, że:

M1 + M2 = M3 (hipoteza alternatywna)

Hipoteza zerowa musi zakładać, że średnie są sobie równe.

Załóżmy, że hipoteza ta jest prawdziwa i średnie mają wartość

równą 10.

A zatem 10 + 10 = 10
To niestety nie jest prawda. Musimy zatem dodać wagi kontrastu.
1* 10 + 1*10 = 2 *10

Aby przetestować tę hipotezę możemy zastosować test T-Studenta

dla jednej próby i porównać interesujący nas układ średnich z

wartością 0.

Jak przekształcić ten układ, żeby był równy 0?

1

*10

+ 1

* 10

– 2

*10= 0

Definiowanie kontrastów poprzez

wagi

Wobec tego nadajemy każdej grupie odpowiednie wagi

posługując się następującymi zasadami:

1. Musimy skontrastować te grupy, które porównujemy

– nadajemy im wagi o przeciwnych znakach.

2. Suma wag w każdym porównaniu musi wynosić zero.
3. Grupy, które pomijamy otrzymują wagę równą zero.

Mamy pięć grup
Jak zdefiniować kontrast, gdy chcemy

porównać grupę drugą z trzecią i piątą?

0, 2, -1, 0, -1

0, 4, -2, 0, -2

0, -1, 0,5, 0, 0,5

0, -10, 5, 0, 5

Wariancja wyjaśniona przez eksperyment

Trzy grupy: E1, E2 i K1

Wariancja wyjaśniona

przez E1, E2

+

Wariancja

wyjaśniona przez K1

-

Wariancja

wyjaśniona

przez E1

Wariancja

wyjaśniona

przez E2

Porównani
e 1

Porównani
e 2

E1: +1 E2:
+1

K1: -2

(+1)+ (+1)+(-2)
= 0

E1: +1
E2: -1

K1: 0

+

-

(+1)+ (-1)+(0) =
0

Przykład

• W badaniu nad skutecznością pewnego środka

podnoszącego sprawność umysłową

przeprowadzono badanie, w którym porównywano

osoby przyjmujące niskie i wysokie dawki

specyfiku z grupą kontrolną oraz placebo

• Jakie wagi dla pierwszego kontrastu

porównującego obie grupy eksperymentalne z

dwiema kontrolnymi?

Grupa E1 Grupa E2

Wysokie dawki Niskie dawki

Grupa K1 Grupa K1

Nic Placebo

vs
.

+1 +1 -1 -1
kontrast 1

Jakie dalsze porównania

możliwe?

Grupa E1 Grupa E2

Wysokie dawki Niskie dawki

Grupa K1 Grupa K1

Nic Placebo

vs
.

+1 -1 0
0 kontrast 2

Grupa E2

Niskie dawki

Grupa E1

Wysokie dawki

vs
.

Grupa K1

Placebo

Grupa K1

Nic

vs
.

0 0 +1
-1 kontrast 3

Ortogonalność kontrastów

• Jak sprawdzić czy kolejne wykonywane

porównania są od siebie wzajemnie

niezależne, czyli ortogonalne

• Przemnażamy przez siebie współczynniki

kontrastu odpowiednio dla każdej grupy

• Suma iloczynów powinna wynosić zero –

jeśli nie, kontrasty nie są ortogonalne

Czy poniższe kontrasty są

niezależne?

Porównujemy średnie pochodzące z czterech

grup: osób lubiących jazz, muzykę klasyczną,
rock i pop pod względem ekstrawersji

Jeżeli pierwszy kontrast:
1, 1, 1, -3

(która grupa jest przeciwstawiana

którym?)

To pozostałe, które są ortogonalne:
1, 1, -2, 0
1, -1, 0, 0

Przykład 1

• 1, 1, 1, -1,5, -1,5

(trzy pierwsze z dwiema

ostatnimi)

• -1, 1, 0, 0, 0
-1 1 0 0 0 iloczyn
Suma iloczynów: 0

Przykład 2

• 2, 0, -1, -1
• 1, -1, 0, 0
2 0 0 0 iloczyn
Suma iloczynów: 2

Niezależn

e?

Niezależn

e?

Jeżeli będziemy w ten sposób

postępować (czyli wykonywać
porównania niezależne), to liczba
możliwych (niezależnych,
ortogonalnych) kontrastów wyniesie:

k-1

k oznacza liczbę grup

Podsumowanie

• Zawsze wybieramy sensowne porównania
tylko dwie „porcje” wariancji (gdy w „porcji” więcej

niż jedna grupa – porównujemy średnią z tych grup)

• Porównywane grupy mają

przeciwny znak

współczynnika

• Wartości współczynników dla średnich w tej samej

podgrupie muszą być

takie same

• Grupy, które są

wyłączone

z porównań mają

wagę

zero

• Suma współczynników

w danym kontraście zawsze

równa

zero

• Jeżeli wykonujemy więcej niż jeden kontrast –

porównania powinny być niezależne (ortogonalne)

Mnożenie / dodawanie

• Analiza kontrastów pozwala przemnażać

średnie przez pewne współczynniki, ale nie
ma możliwości dodawania niczego do
średnich.

• Możemy sprawdzać, czy dochód mężczyzn jest

2 razy większy niż dochód kobiet, ale nie
sprawdzamy (przy użyciu kontrastów), czy
mężczyźni zarabiają o 500 złotych więcej niż
kobiety.

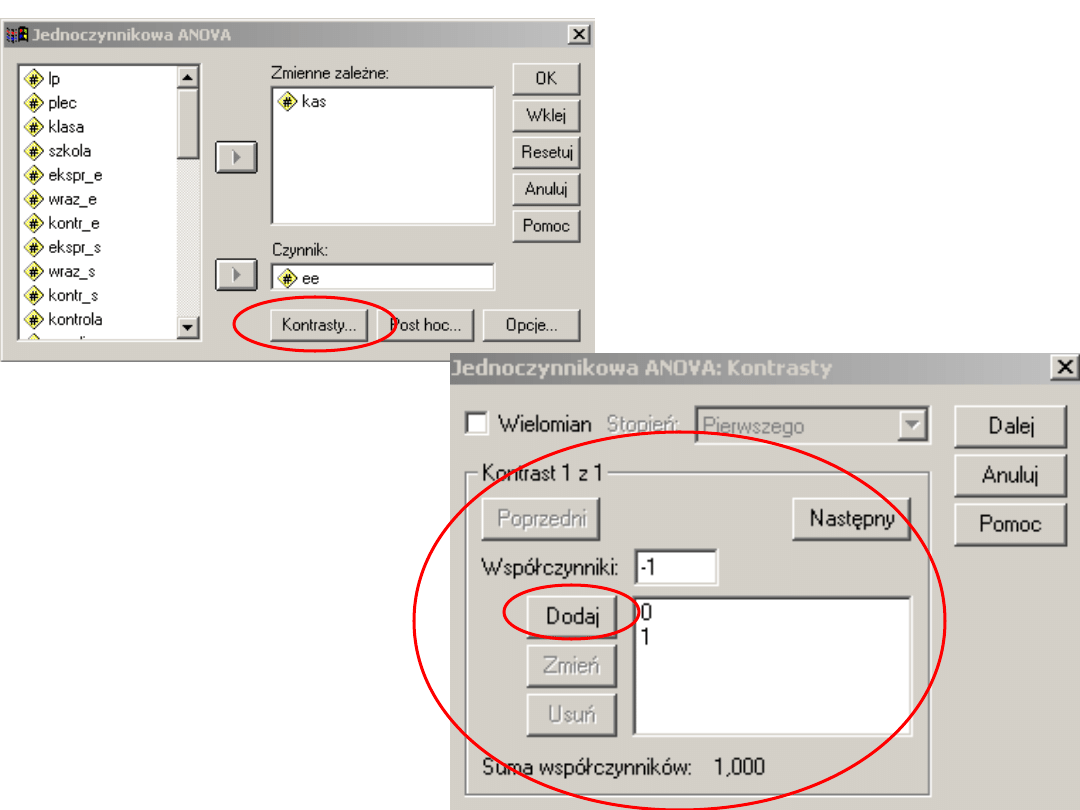
Jak definiować w SPSS?

Współczynniki
kontrastu
wprowadzamy
kolejno klikając
DODAJ

Wydruk

Współczynniki kontrastu

-1

0

1

Kontrast
1

niska

ekspresy

wnosc

przeciętna

ekspresyw

nosc

wysoka

ekspresy

wnosc

EE

Testy kontrastu

-2,8935

1,21084

-2,390

264

,018

-2,8935

1,24807

-2,318

123,797

,022

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

PASYWNY

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Test jednorodności wariancji

PASYWNY

,134

2

264

,875

Test Levene'a

df1

df2

Istotność

Test Levene’a wskazuje,
że wariancje są
homogeniczne, więc
wydruk odczytujemy z
górnego wiersza. Wynik
zapisujemy tak, jak
standardowy test T
Studenta T(264)=2,39;
p<0,05. Teraz jeszcze
informacja o średnich, by
zinterpretować wynik.

Statystyki opisowe

PASYWNY

29,6935

28,2286

26,8000
28,2210

niska ekspresywnosc
przeciętna
ekspresywnosc
wysoka ekspresywnosc
Ogółem

Średnia

Statystyki opisowe

KAS

24,9710

25,2500

26,3043
25,4371

niska ekspresywnosc
przeciętna
ekspresywnosc
wysoka ekspresywnosc
Ogółem

Średnia

• Analiza wariancji

nie pokazała
istotnych
wyników a
kontrast
porównujący dwie
skrajne grupy tak!

Współczynniki kontrastu

-1

0

1

Kontrast
1

niska

ekspresy

wnosc

przeciętna

ekspresyw

nosc

wysoka

ekspresy

wnosc

EE

Testy kontrastu

1,3333

,67801

1,967

283

,050

1,3333

,67100

1,987

136,000

,049

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

KAS

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Jednoczynnikowa ANOVA

KAS

72,066

2

36,033

2,272

,105

4488,301

283

15,860

4560,367

285

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Test jednorodności wariancji

KAS

,021

2

283

,979

Test Levene'a

df1

df2

Istotność

Analiza trendu

Analiza trendu jest wykorzystywana wtedy, gdy poszukujemy

specyficznego układu średnich. Najczęściej stosujemy ją

wtedy, gdy zmienna jest porządkowa, lub gdy mamy

teoretyczne przesłanki by określić, że jakieś średnie będą

wyższe a inne niższe.

Trendy są najbardziej poszukiwaną wartością - trendsetterzy
Trendy w języku – „jazzy”
Trendy w przemyśle – samochody dla kobiet mają okrągłe

linie nawiązując do cech „dziecięcości”

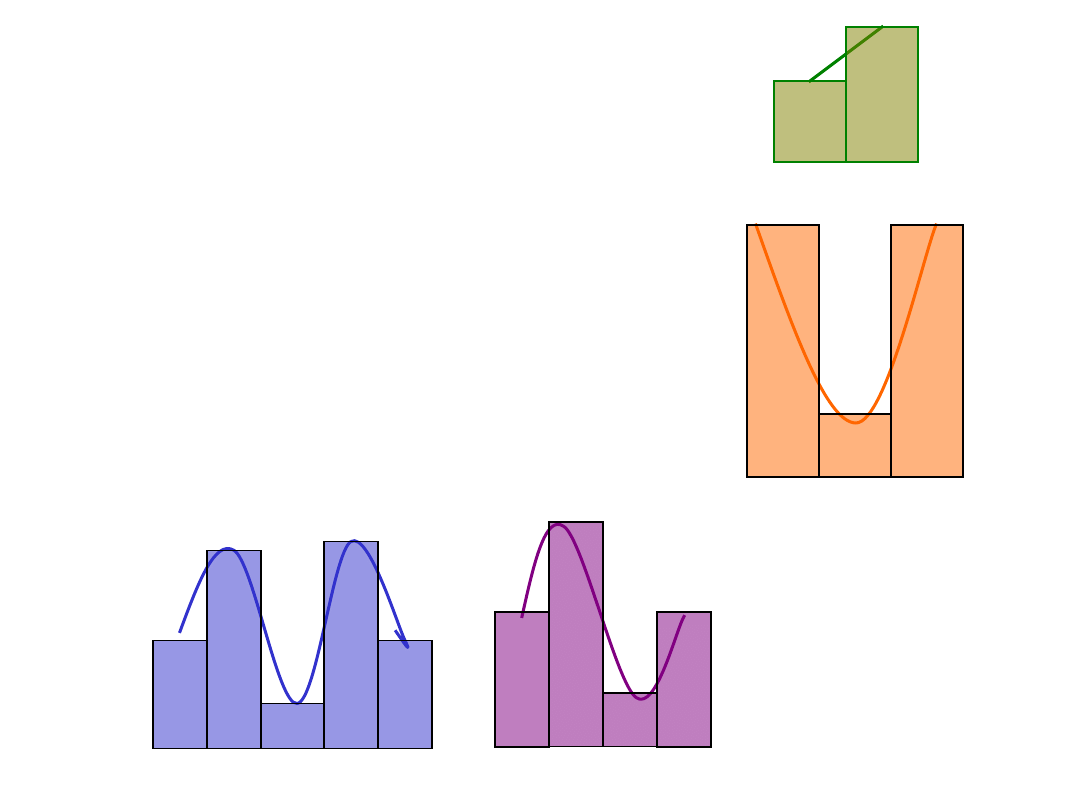
Analiza kontrastów – badanie

trendów

Poznane do tej pory metody –
R-Pearsona czy test T-Studenta pozwalały

nam badać jedynie zależności

prostoliniowe

• Analiza kontrastów pozwala poszukiwać

innych kształtów zależności niż

prostoliniowe.

• Obliczeniowo jest identyczna jak zestaw

ortogonalnych kontrastów. Jeśli szukamy

trendu to ogólna analiza wariancji nie

musi być istotna.

Wielomian czwartego

stopnia

Wielomian trzeciego

stopnia

Wielomian drugiego

stopnia

Wielomian pierwszego

stopnia

Współczynniki kontrastu dla trendu liniowego,

kwadratowego i sześciennego

Porównujemy 2

średnie

• Liniowy –1 1

Porównujemy 3

średnie

• Liniowy –1 0 1
• Kwadratowy 1 -2 1

Porównujemy 4 średnie
• Liniowy –3 –1 1 3
• Kwadratowy 1 –1 –1 1
• Sześcienny –1 3 -3 1

Porównujemy 5 średnich
• Liniowy –1 –1 0 1 2
• Kwadratowy 2 –1 –2 –1

2

• Sześcienny –1 2 0 –2 1

Aby poszukiwać złożonych kształtów zależności
(krzywoliniowych) potrzebujemy

odpowiedniej ilości

porównywanych grup,

np.. Gdy chcemy znaleźć zależność

kwadratową to musimy mieć przynajmniej 3 średnie.

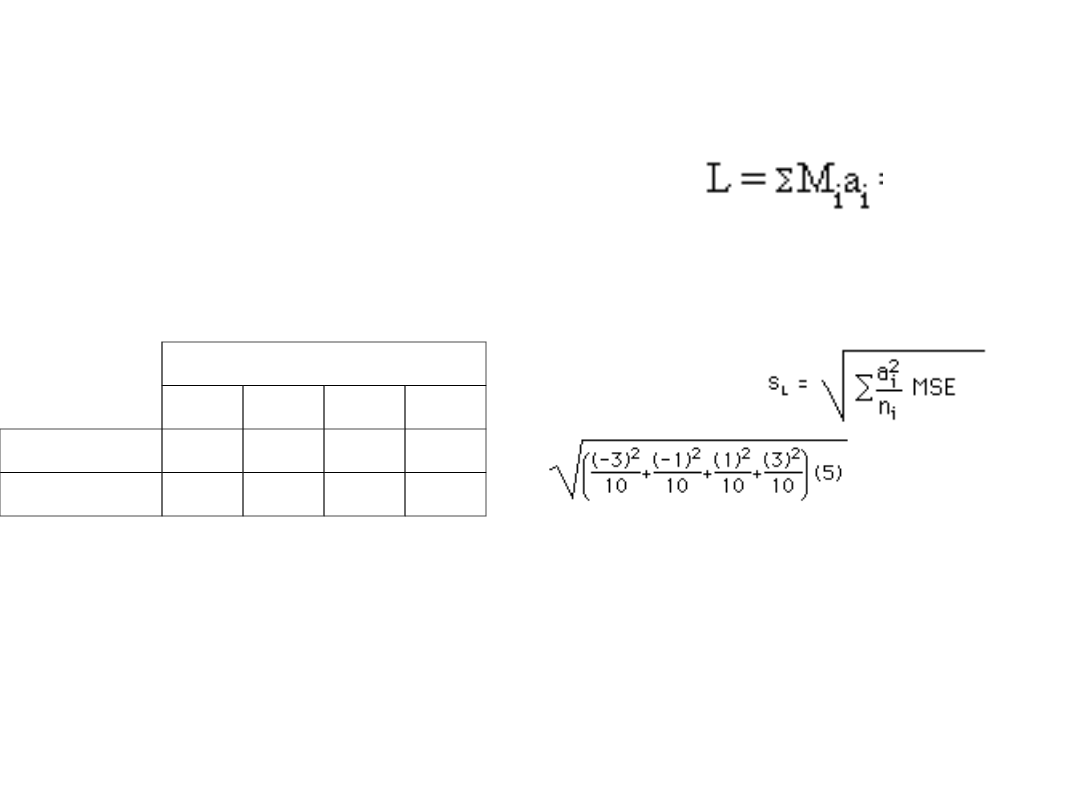
Obliczamy statystykę

T

Licznik:

10*(-3) + 6*(-1)+4*1+

3*3=-23

Mianownik

3,162

T=-23/3,162=

-7,27

Stopnie swobody tego

testu t są równe

stopniom swobody

błędu dla tej analizy

wariancji 40-4 = 36

Obliczanie trendu

kwadratowego

Wielkość nagrody a czas

przebiegania przez

labirynt (liczebność

szczurów w każdej grupie

10, wariancja błędu

MSE=5)

http://members.aol.com/johnp71/pdfs.html

Wielkość nagrody

2

4

6

8

szybkość

10

6

4

3

kontrast

-3

-1

1

3

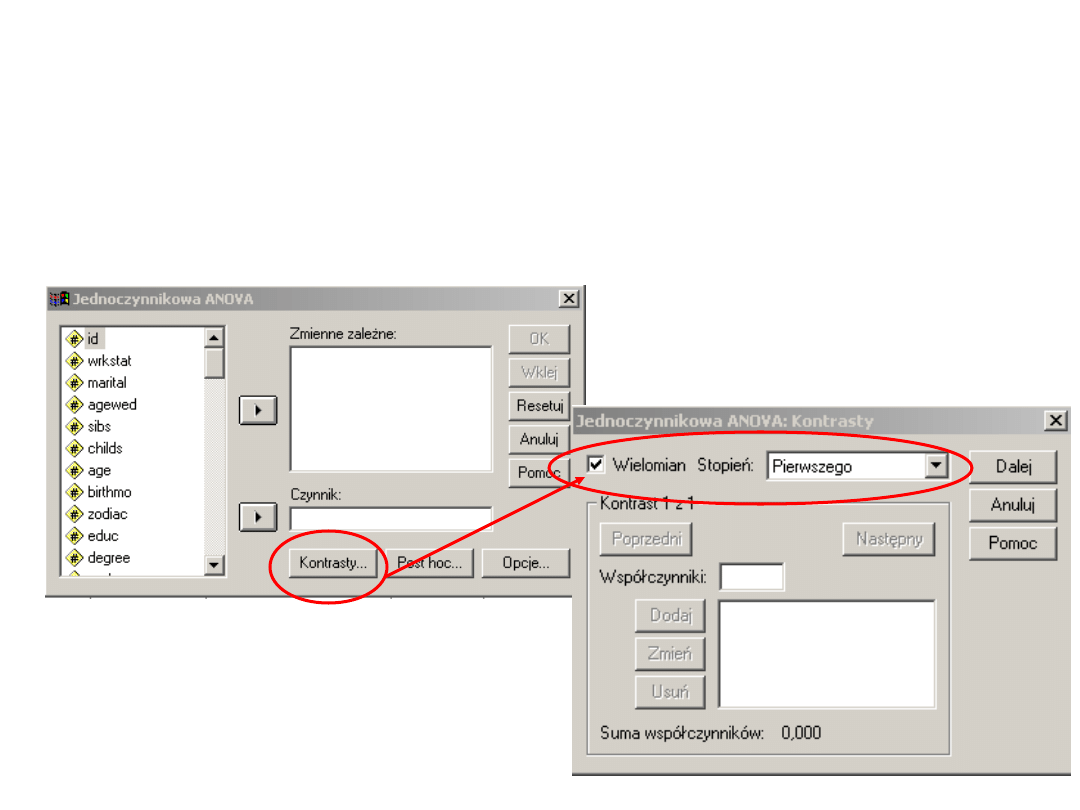
Wielomiany – jak w spss-ie?

Zależność wykształcenie i liczby dzieci przyjmuje
kształt prostoliniowy – osoby z wyższym
wykształceniem maja mniej dzieci niż te z
wykształceniem podstawowym i średnim.

Wydruk

Wniosek – średnie układają się w kształt

funkcji kwadratowej

Jednoczynnikowa ANOVA

Liczba dzieci

157,450

4

39,362

14,405

,000

92,601

1

92,601

33,887

,000

124,883

1

124,883

45,701

,000

32,566

3

10,855

3,973

,008

18,177

1

18,177

6,652

,010

30,795

1

30,795

11,269

,001

1,772

2

,886

,324

,723

,271

1

,271

,099

,753

,055

1

,055

,020

,887

1,716

1

1,716

,628

,428

1,716

1

1,716

,628

,428

1,716

1

1,716

,628

,428

4063,405

1487

2,733

4220,855

1491

(Połączone)

Nieważone
Ważone
Odchylenie

Składnik liniowy

Nieważone
Ważone
Odchylenie

Składnik
kwadratowy

Nieważone
Ważone
Odchylenie

Składnik
sześcienny

Nieważone
Ważone

Składnik czwartego
stopnia

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

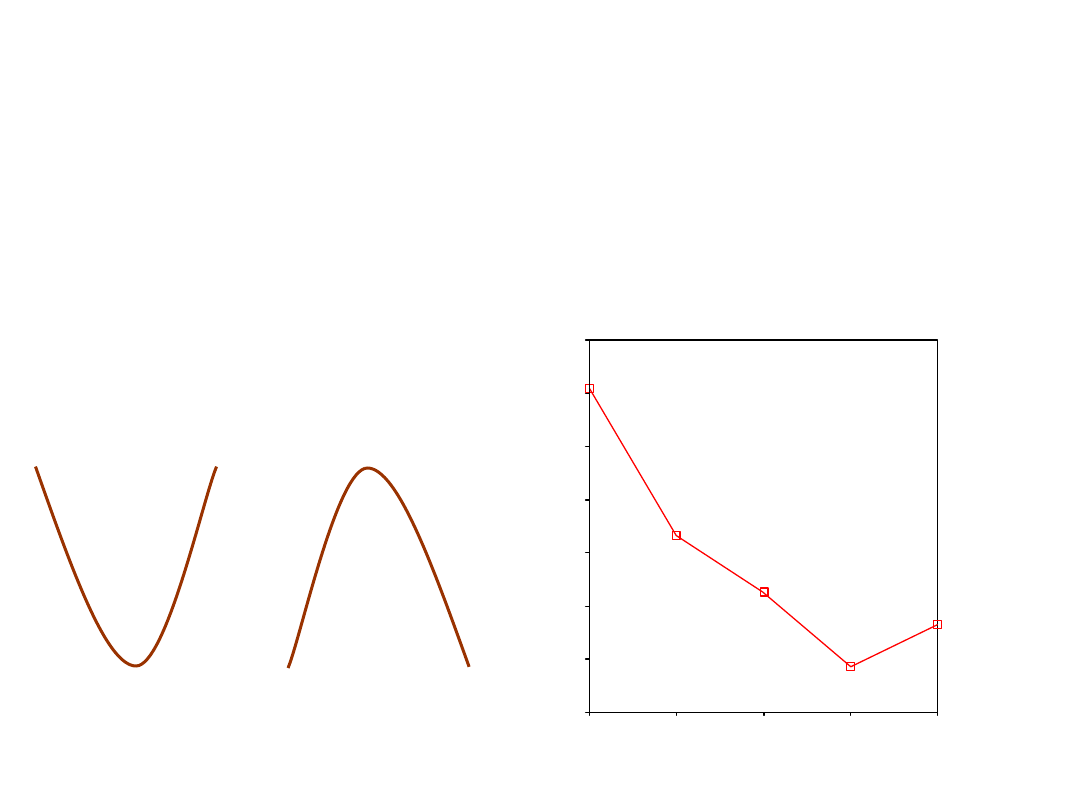
Interpretacja

• Wiemy już, że średnie układają się tworząc

wielomian drugiego stopnia, ale, żeby
zinterpretować go musimy obejrzeć wykres.
Wydruk nie pozwala nam bowiem stwierdzić,
który wariant układu mamy.

Poziom wykształcenia respondenta

Graduate

Bachelor

Junior college

High s chool

Mniej niż HS

Ś

re

d

n

ia

-

L

ic

zb

a

d

z

ie

ci

2,6

2,4

2,2

2,0

1,8

1,6

1,4

1,2

Humanistyczny charakter uczelni znajduje

odbicie w sympatii jej studentów do muzyki

bluegrass

Zależność ta okazała się prostoliniowa F(1, 1330)=9,334;

p<0,01– patrzymy na wykres, by ją zinterpretować

Jednoczynnikowa ANOVA

Bluegrass

12,645

4

3,161

3,067

,016

9,817

1

9,817

9,526

,002

9,619

1

9,619

9,334

,002

3,026

3

1,009

,979

,402

,017

1

,017

,016

,899

1,050

1

1,050

1,019

,313

1,975

2

,988

,958

,384

,629

1

,629

,610

,435

1,054

1

1,054

1,023

,312

,921

1

,921

,894

,345

,921

1

,921

,894

,345

,921

1

,921

,894

,345

1370,641

1330

1,031

1383,285

1334

(Połączone)

Nieważone
Ważone
Odchylenie

Składnik liniowy

Nieważone
Ważone
Odchylenie

Składnik
kwadratowy

Nieważone
Ważone
Odchylenie

Składnik
sześcienny

Nieważone
Ważone

Składnik czwartego
stopnia

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

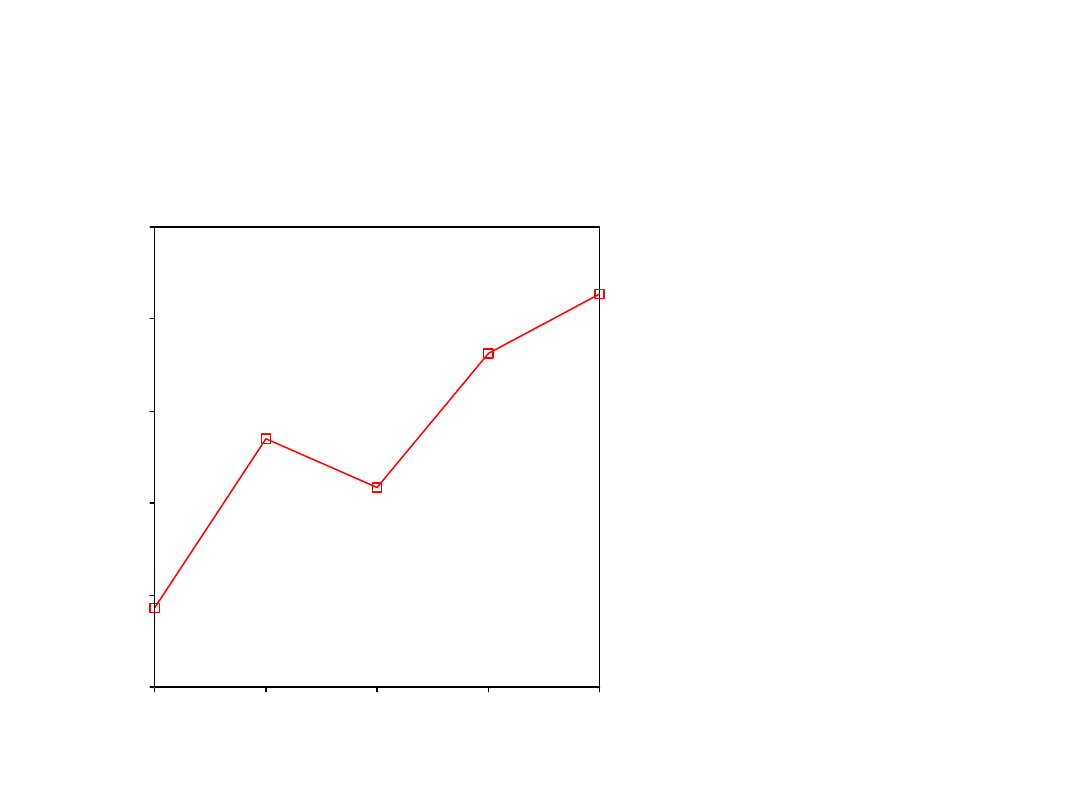
Wykres pokazuje, że nasza zależność jest

prawie prostoliniowa

szkoła wyższa

SWPS

UMK

UW

SGGW

SGH

Ś

re

d

n

ia

-

B

lu

e

g

ra

ss

2,9

2,8

2,7

2,6

2,5

2,4

Pytania sprawdzające

1. Jak brzmi hipoteza zerowa analizy wariancji
2. Jak brzmią założenia analizy wariancji
3. Dlaczego analiza wariancji jest lepsza niż wielokrotne

porównywanie testem T

4. Jak to jest, że wariancja jest używana do porównywania

średnich?

5. Gdyby policzyć skośność rozkładu T to rozkład ten byłby

dodatnioskośny, czy ujemnieskośny

6. Ile wynosi modalna rozkładu F?
7. Kiedy stosujemy porównania planowane?
8. Kiedy stosujemy testy post hoc
9. Kiedy stosujemy analizę trendu?
10. Jeśli mamy 6 średnich to ile ortogonalnych kontrastów

możemy policzyć?