Wykład integrujący

Jak się dobrać do jeża…

Chcemy odpowiedzieć na pytanie, czy wiek

w jakikolwiek sposób wiąże się z

subiektywnie odczuwanymi zmianami w

funkcjonowaniu poznawczym

W tym celu

∞Formułujemy hipotezę badawczą
∞Ustalamy poziom pomiaru zmiennych
∞Dobieramy odpowiedni test statystyczny
∞Wyciągamy wnioski

Możemy zrobić to na kilka sposobów…

Sposób pierwszy - najłatwiejszy

Hipoteza badawcza: osoby starsze częściej

niż młodsze będą oceniały swoje możliwości
umysłowe jako niezadowalające

Pytamy grupę osób starszych i grupę osób

młodszych czy są zadowolone ze swojej np.
pamięci

∞Osoby odpowiadają: TAK/ NIE

Zmienne? Na jakich skalach?

Zmienna niezależna: Wiek (starsi/ młodsi) – skala dychotomiczna

Zmienna zależna: zadowolenie z pamięci (tak/ nie) – skala
dychotomiczna

Sposób pierwszy - c.d.

 Skoro obie zmienne są na skali nominalnej, możemy

policzyć tylko częstość występowania różnych
kategorii. Jakiego testu możemy użyć aby
odpowiedzieć na pytanie badawcze?

Oczywiście testu chi-kwadrat dla dwóch zmiennych

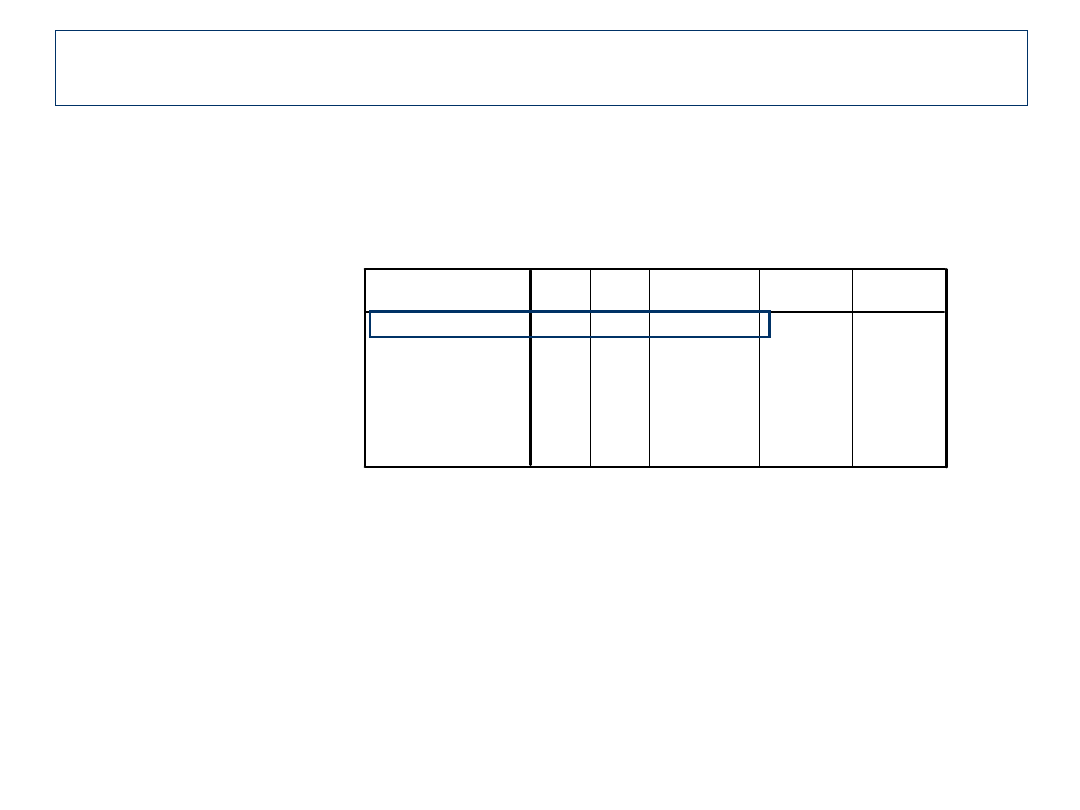
Chi-Square Tests

7,242

b

1

,007

5,436

1

,020

7,551

1

,006

,012

,009

7,008

1

,008

31

Pearson Chi-Square
Continuity Correction

a

Likelihood Ratio
Fisher's Exact Test
Linear-by-Linear
Association
N of Valid Cases

Value

df

Asymp. Sig.

(2-sided)

Exact Sig.

(2-sided)

Exact Sig.

(1-sided)

Computed only for a 2x2 table

a.

0 cells (,0%) have expected count less than 5. The minimum expected
count is 7,26.

b.

Sposób pierwszy - c.d.

Następnie formułujemy hipotezę zerową:

H0: E=O

i ją testujemy

Chi2(1, N=31) = 7,24; p<0,01
Przy takim wyniku odrzucamy H0

Co nam „wyszło”, odczytujemy z tabeli krzyżowej

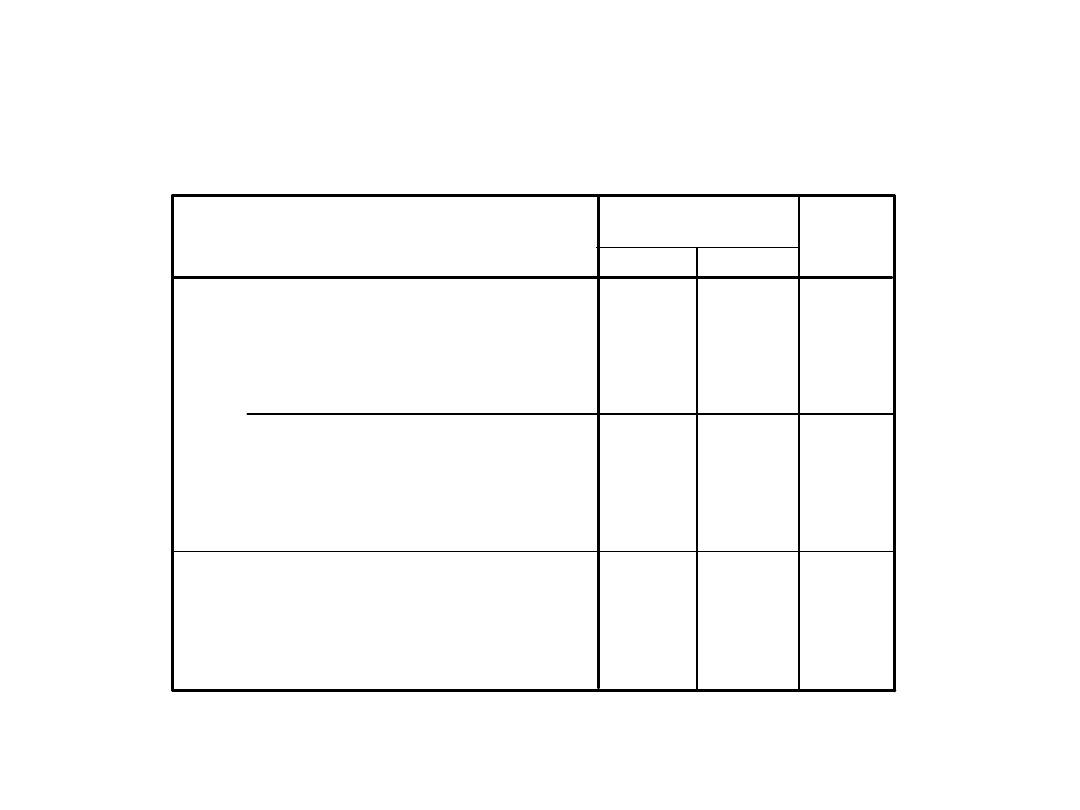
WIEK * ZADOWOLE zadowoleni Crosstabulation

4

11

15

7,7

7,3

15,0

26,7%

73,3% 100,0%

25,0%

73,3%

48,4%

12

4

16

8,3

7,7

16,0

75,0%

25,0% 100,0%

75,0%

26,7%

51,6%

16

15

31

16,0

15,0

31,0

51,6%

48,4% 100,0%

100,0%

100,0% 100,0%

Count
Expected Count
% within WIEK
% within ZADOWOLE
zadowoleni
Count
Expected Count
% within WIEK
% within ZADOWOLE
zadowoleni
Count
Expected Count
% within WIEK
% within ZADOWOLE
zadowoleni

1,00 starsi

2,00 młodsi

WIEK

Total

1,00 tak 2,00 nie

ZADOWOLE

zadowoleni

Total

A na wykresie wygląda to tak…

młodsi

starsi

lic

zb

a

od

po

w

ie

dz

i

14

12

10

8

6

4

2

zadowoleni?

tak

nie

Sposób drugi – badamy trochę dłużej…

Możemy również dokonywać dokładniejszego

pomiaru funkcjonowania poznawczego – np.
prosząc osoby badane o rozwiązanie testu
uwagi, pamięci, itp.

W takim przypadku hipoteza badawcza

będzie brzmiała: Osoby starsze uzyskają
gorsze wyniki w teście funkcji
intelektualnych w porównaniu do osób
młodszych.

Sposób drugi – badamy trochę dłużej…

W tym przypadku zmienna zależna

zmierzona jest na skali ilościowej,
porównujemy dwie grupy, czyli użyjemy
odpowiedniej wersji testu T-Studenta

Hipoteza zerowa brzmi: Nie ma różnic

między osobami starszymi i młodszymi w
rozwiązywaniu zastosowanego zadania

Sposób drugi – badamy trochę dłużej…

Sprawdzamy, czy zostały spełnione założenia

testu T-Studenta dla prób niezależnych

∞Równoliczność grup
∞Zmienna zależna zmierzona na skali ilościowej
∞Normalność rozkładu zmiennej zaleznej w

podgrupach

∞Równość wariancji

Jeśli tak, wykonujemy test

Sposób drugi – konkretny przykład

Chcemy sprawdzić, jak osoby starsze, w

porównaniu do osób młodszych wykonają
test przepisywania cyfr

Przebadaliśmy dwie grupy osób i…

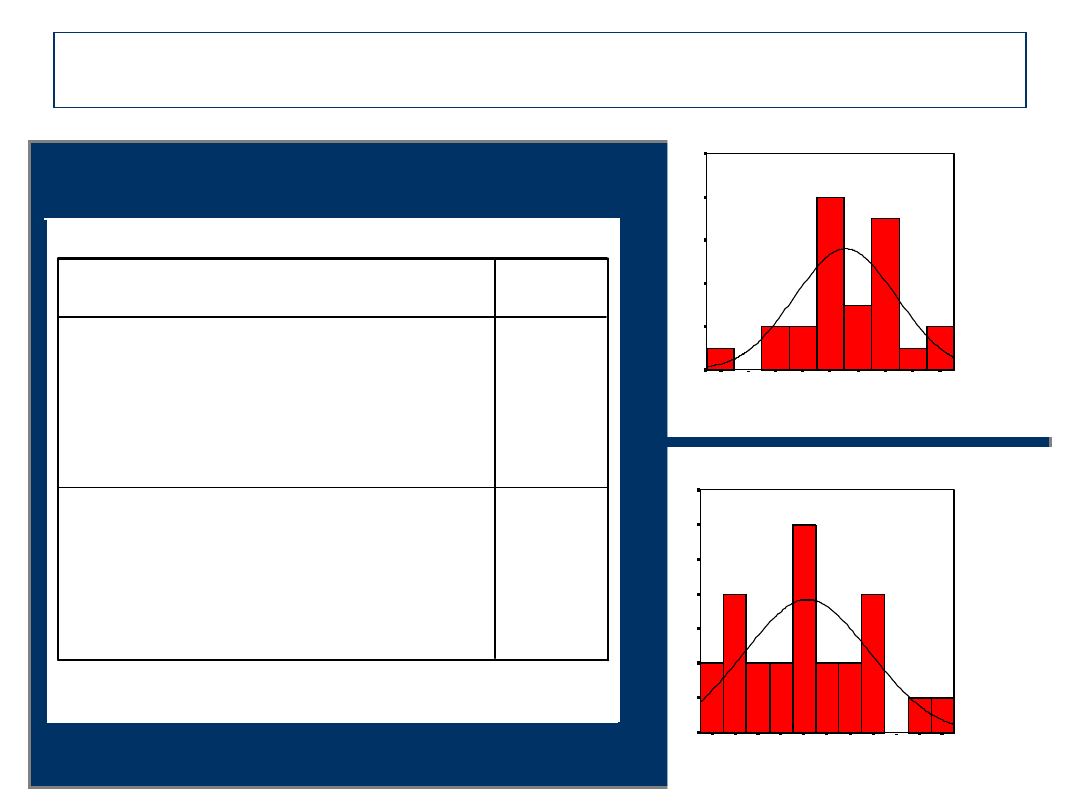
Sposób drugi – konkretny przykład

One-Sample Kolmogorov-Smirnov Test

26

37,7692
9,22738

,110
,101

-,110

,563
,910

26

55,3462
6,75244

,097
,097

-,069

,496
,966

N

Mean
Std. Deviation

Normal Parameters

a,b

Absolute
Positive
Negative

Most Extreme
Differences

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
N

Mean
Std. Deviation

Normal Parameters

a,b

Absolute
Positive
Negative

Most Extreme
Differences

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)

GRUPA
1,00 starzy

2,00 mlodzi

DD liczba

przepisanych

cyfr

Test distribution is Normal.

a.

Calculated from data.

b.

liczba przepisanych cyfr

55,0

50,0

45,0

40,0

35,0

30,0

25,0

20,0

15,0

GRUPA: 1,00 starzy

10

8

6

4

2

0

Odch.Std = 9,23
Średnia = 37,8
N = 26,00

liczba przepisanych cyfr

70,0

67,5

65,0

62,5

60,0

57,5

55,0

52,5

50,0

47,5

45,0

GRUPA: 2,00 mlodzi

7

6

5

4

3

2

1

0

Odch.Std = 6,75
Średnia = 55,3
N = 26,00

Założenia:

liczba przepisanych cyfr

55,0

50,0

45,0

40,0

35,0

30,0

25,0

20,0

15,0

GRUPA: 1,00 starzy

10

8

6

4

2

0

Odch.Std = 9,23
Średnia = 37,8
N = 26,00

liczba przepisanych cyfr

70,0

67,5

65,0

62,5

60,0

57,5

55,0

52,5

50,0

47,5

45,0

GRUPA: 2,00 mlodzi

7

6

5

4

3

2

1

0

Odch.Std = 6,75
Średnia = 55,3
N = 26,00

One-Sample Kolmogorov-Smirnov Test

26

37,7692
9,22738

,110
,101

-,110

,563
,910

26

55,3462
6,75244

,097
,097

-,069

,496
,966

N

Mean
Std. Deviation

Normal Parameters

a,b

Absolute
Positive
Negative

Most Extreme
Differences

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
N

Mean
Std. Deviation

Normal Parameters

a,b

Absolute
Positive
Negative

Most Extreme
Differences

Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)

GRUPA
1,00 starzy

2,00 mlodzi

DD liczba

przepisanych

cyfr

Test distribution is Normal.

a.

Calculated from data.

b.

Sposób drugi – konkretny przykład

Independent Samples Test

2,110

,153 -7,838

50

,000

-17,5769

2,24242 -22,08096 -13,07288

-7,838 45,808

,000

-17,5769

2,24242 -22,09120 -13,06265

Equal variances
assumed
Equal variances
not assumed

DD liczba
przepisanych cyfr

F

Sig.

Levene's Test

for Equality of

Variances

t

df

Sig. (2-tailed)

Mean

Difference

Std. Error

Difference

Lower

Upper

95% Confidence

Interval of the Difference

t-test for Equality of Means

Group Statistics

26 37,7692

9,22738

1,80964

26 55,3462

6,75244

1,32426

GRUPA
1,00 starzy
2,00 mlodzi

DD liczba
przepisanych cyfr

N

Mean

Std. Deviation

Std. Error

Mean

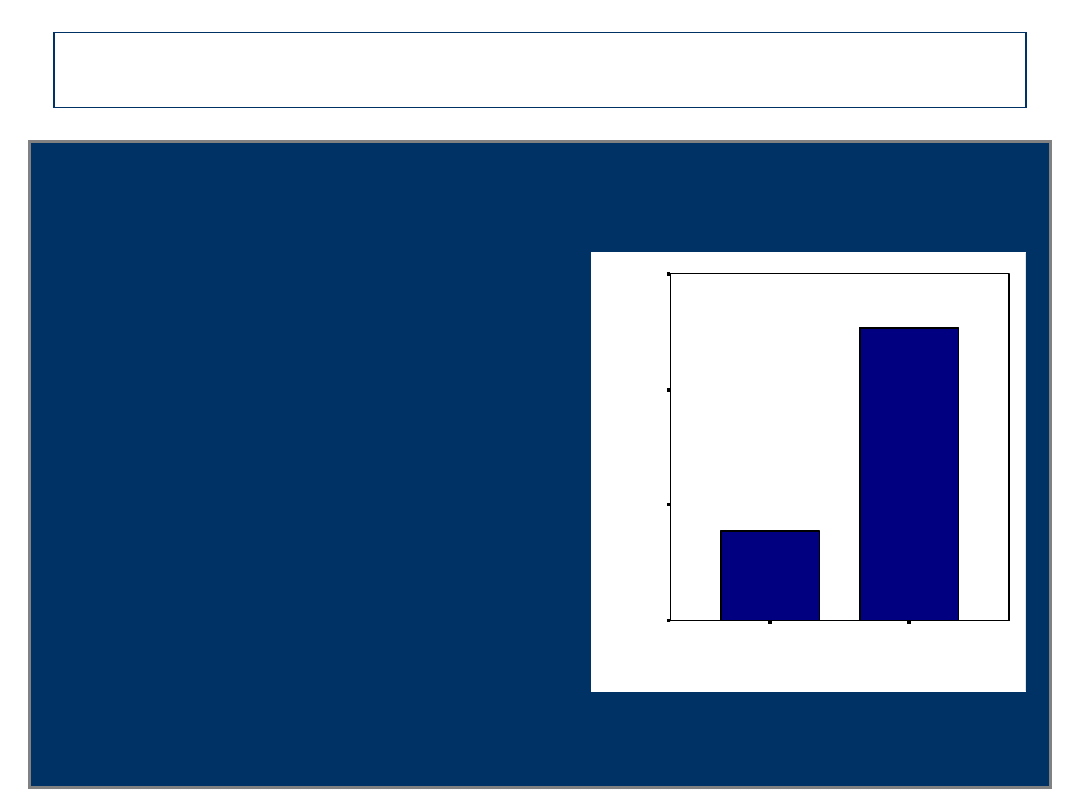
Sposób drugi – konkretny przykład

Jak zapisać? Jakie wnioski?
T(50)=7,84; p<0,001
 Ms=37,77; Mm=55,35

Wniosek:

∞Odrzucamy H0

Stwierdzamy, że
osoby starsze wolniej
przepisują cyferki

GRUPA

mlodzi

starzy

śr

ed

ni

a

lic

zb

a

pr

ze

pi

sa

ny

ch

c

yf

r

60

50

40

30

Jeszcze jeden sposób

Postawiony na początku problem możemy

potraktować jeszcze inaczej

∞Zamiast dzielić osoby na starsze i młodsze,

pytamy o ich wiek i sprawdzamy, czy im ktoś
starszy tym gorzej funkcjonuje intelektualnie,
czyli wykonujemy

∞Korelację R-Pearsona
∞Założenia? Pomiar zmiennych na skali ilościowej,

normalny rozkład

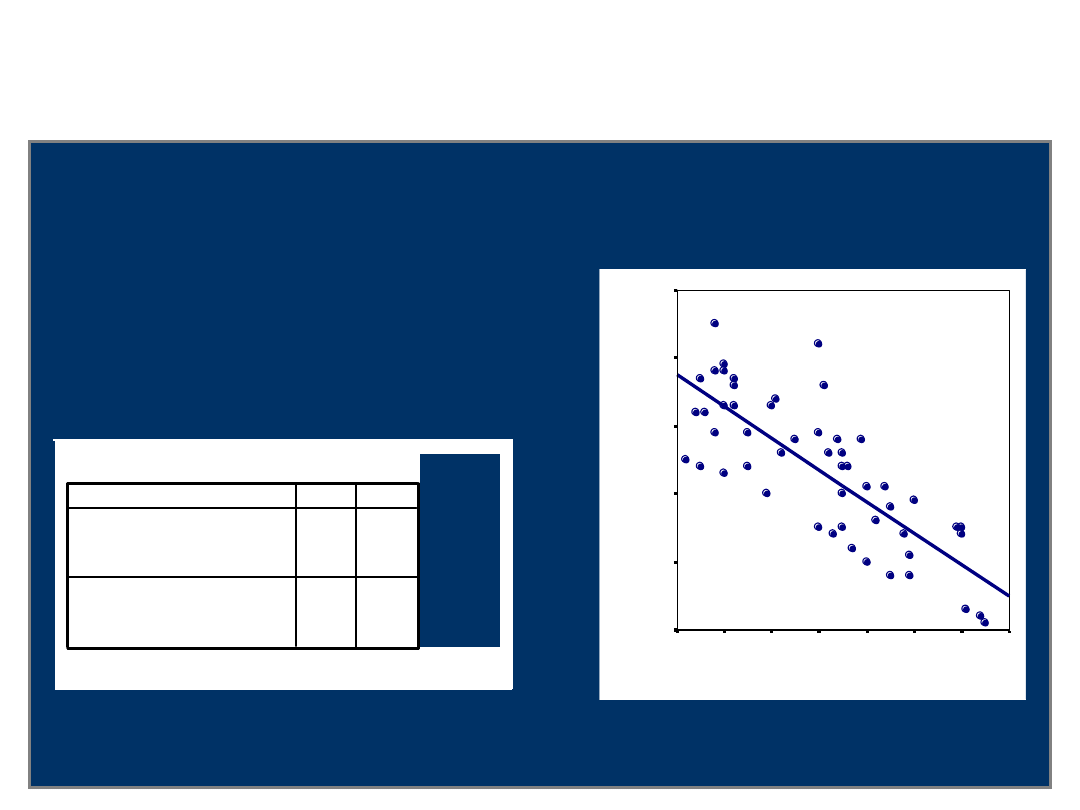
Okazuje się, że liczba przeżytych lat istotnie

koreluje z wynikami testu podstawiania
(podskala Wechslera)

R=-0,79; p<0,001

Correlations

1

-,787**

.

,000

52

52

-,787**

1

,000

.

52

52

Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N

LATA

DS

LATA

DS

Correlation is significant at the 0.01 level
(2-tailed).

**.

LATA

90

80

70

60

50

40

30

20

D

S

60

50

40

30

20

10

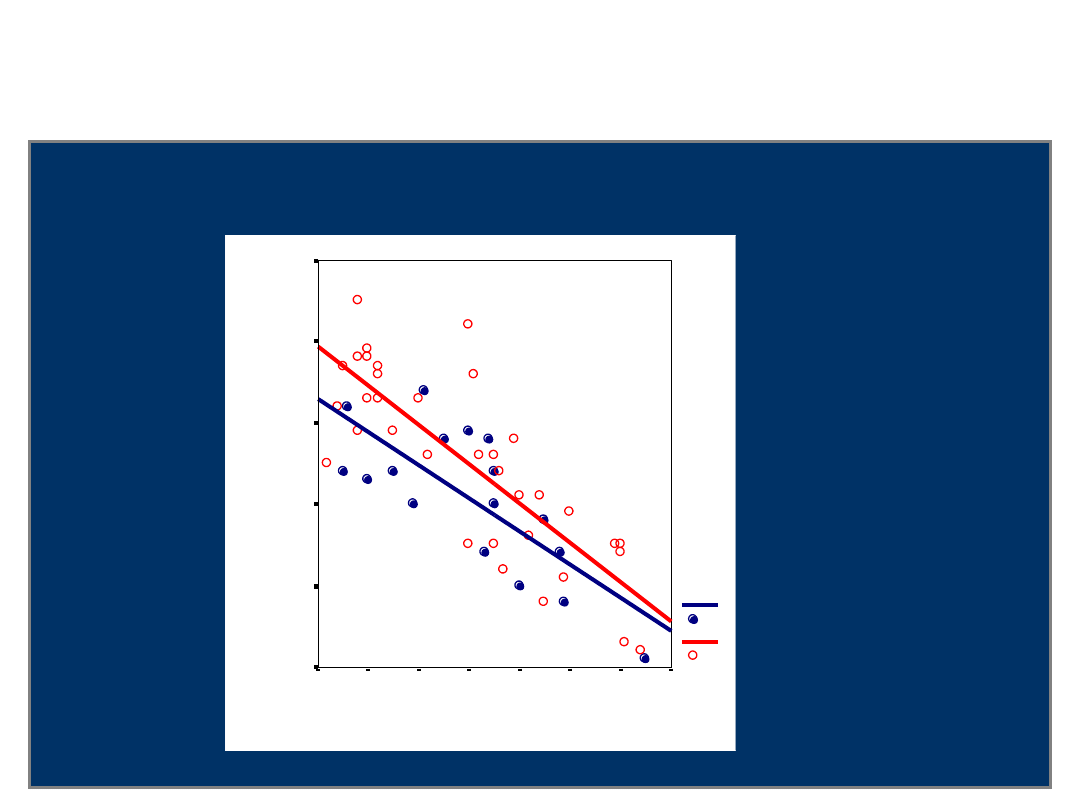
Osobno dla kobiet i mężczyzn

LATA

90

80

70

60

50

40

30

20

D

S

60

50

40

30

20

10

PLEC

m

k

Przystojny w średnim wieku szuka ciepłej humanistki

Autorki: Paulina Kannewiszer, Małgorzata Nodzak

  Zauważono, że mężczyźni najczęściej pragną

kobiet młodych i pięknych, o dużym potencjale
rozrodczym, podczas gdy kobietom zależy na
partnerach ambitnych i inteligentnych, o wysokim
statusie społecznym i materialnym (Buss 1996,
Wojciszke 1995)

 Badaczkami kierowała chęć znalezienia różnic

między kobietami i mężczyznami przy
poszukiwaniu partnera (brano pod uwagę wiek,
sytuację ekonomiczną i stan cywilny). Zwrócono
uwagę na istniejące różnice pomiędzy wyborem
związku krótko i długotrwałego.

Do przeprowadzenia badania posłużyło 300 ogłoszeń

pochodzących z trzech różnych źródeł. Biorąc pod uwagę
hipotezę badawczą: Istnieją różnice w doborze partnera
heteroseksualnego w zależności od rodzaju związku oraz
płci, wyodrębniono następujące zmienne:

 Zmienne niezależne: rodzaj związku: długo i krótkotrwały

oraz płeć poszukującego

 Zmienne zależne: waga, atrakcyjność fizyczna, stan

cywilny, wykształcenie, religia, stosunek do dzieci, seksu i
sponsoringu, nałogi, wiek, wzrost, waga, zainteresowania,
charakter, sytuacja finansowa, waga1(1 przy zmiennej
oznacza, że jest to cecha posiadana przez osobę
zamieszczającą ogłoszenie ), kolor oczu1, kolor włosów1,
długość włosów1, biust1, atrakcyjność fizyczna1,
zainteresowania1, wykształcenie1, sytuacja finansowa1,
charakter1, stosunek do seksu1, stosunek do sponsoringu1,
stan cywilny1, nałogi1.

Przystojny w średnim wieku szuka ciepłej humanistki

      

Uzyskano istotne różnice w częstości wyborów

opiekuńczości w zależności od rodzaju związku
preferowanego przez osoby szukające partnera za
pomocą ogłoszeń matrymonialnych chi

2

(1,

N=294)=17,97; p<0,001.

Testy Chi-kwadrat

17,969

b

1

,000

16,011

1

,000

25,240

1

,000

,000

,000

17,908

1

,000

294

Chi-kwadrat Pearsona
Poprawka na ciągłość

a

Iloraz wiarygodności
Dokładny test Fishera
Test związku liniowego
N Ważnych obserwacji

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

Istotność
dokładna

(dwustronna)

Istotność
dokładna

(jednostr

onna)

Obliczone wyłącznie dla tabeli 2x2.

a.

,0% komórek (0) ma liczebność oczekiwaną mniejszą niż 5. Minimalna liczebność
oczekiwana wynosi 8,92.

b.

Na podstawie tabeli można stwierdzić, że cecha ta jest

rzadko wspominana w ogłoszeniach matrymonialnych.
Jeśli jednak już występuje to nie jest w ogóle
wspominana w ogłoszeniach osób nastawionych na
związek krótkotrwały (liczebność 0) podczas, gdy w
przypadku związku długotrwałego 19 osób wybrało tę
cechę.

Tabela krzyżowa rodzaj związku * opiekuńcza\ opiekuńczy

137

19

156

145,9

10,1

156,0

138

0

138

129,1

8,9

138,0

275

19

294

275,0

19,0

294,0

Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana

długotrwały

krótkotrwały

rodzaj związku

Ogółem

niewystąpien

ie tej cechy

opiekuńcza\

opiekuńczy

opiekuńcza\ opiekuńczy

Ogółem

Uzyskano istotne różnice płciowe w częstości wyboru cech

związanych z sytuacja finansową poszukiwanego
partnera poszukiwanego za pomocą ogłoszeń
matrymonialnych chi

2

(2, N=294)=9,524; p<0,01.

Testy Chi-kwadrat

9,524

a

2

,009

10,310

2

,006

9,354

1

,002

294

Chi-kwadrat Pearsona
Iloraz wiarygodności
Test związku liniowego
N Ważnych obserwacji

Wartość

df

Istotność

asymptotyczn

a

(dwustronna)

33,3% komórek (2) ma liczebność oczekiwaną mniejszą
niż 5. Minimalna liczebność oczekiwana wynosi 4,47.

a.

Kobiety częściej niż mężczyźni

zamieszczały w ogłoszeniach
matrymonialnych informacje o
sytuacji finansowej poszukiwanego
partnera – 8 kobiet zamieściło w
swoim ogłoszeniu kilka informacji
dotyczących tej charakterystyki a
24 zamieściło jedną cechę
dotyczącą sytuacji finansowej
partnera

Tabela krzyżowa osoby * sytuacja finansowa

114

24

8

146

122,7

18,9

4,5

146,0

133

14

1

148

124,3

19,1

4,5

148,0

247

38

9

294

247,0

38,0

9,0

294,0

Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana
Liczebność
Liczebność oczekiwana

kobieta

mężczyzna

osoby

Ogółem

0

1 cecha

cechy

sytuacja finansowa

Ogółem

osoby

mężczyzna

kobieta

Li

cz

e

b

n

o

ść

30

20

10

0

sytuacja finansowa

1 cecha

cechy

Physical Fitness Training: Beneficial for Professional Psychologists? ,  By: John C.
Barrow, Thomas English, Rolffs S. Pinkerton, Professional Psychology: Research
and Practice, 1987, Vol. 18, Issue 1

 The importance of the psychotherapist's mood and adjustment to

psychotherapeutic outcome is reasonably well documented (

Bandura, Lipsher, & Miller, 1960

;

Gurman, 1972

;

Wogan, 1970

).

In summarizing the research on the therapist's mental health and

its relation to process and outcome in psychotherapy,

Parloff,

Waskow, and Wolfe (1978)

concluded that the higher the

therapists' adjustment levels are, the more useful they are likely to

be to their clients (p. 236). Thus a life-style that enables the

psychotherapist to live reasonably comfortably and to moderate

natural life stresses not only would have a positive personal

impact but would presumably also influence interactions with

others.

Folkins and Sime (1981)

,

Folkins and Amsterdam (1977)

,

and

Taylor et al. (1985)

attested to the positive influence of

physical fitness training on self-concept and mood states,

especially anxiety.

Dienstbier (1984)

, reviewing the effects of

running on personality, concluded that "the well-designed exercise

program holds the promise of other positive changes ... on the

psychological side, improved self-esteem and an enhanced sense

of mastery and internality" (p. 270).

 Of the 196 respondents, 140 (71. 43%) indicated that they did

engage in regular physical fitness training or other exercise
routine. Of the 140 exercisers, 56 (40%) had exercised for
seven years or more, 34 (24%) for four to six years, 33 (24%)
one to three years, and 14 (10%) less than one year. The
frequency of exercise in a week was two to four times for
most of the 140 respondents (72. 14%); 25% reported
exercising daily, and only 2. 86% reported exercising once per
week. The physical fitness activity listed most often as the
"primary" method used by the 127 respondents who
answered the item correctly (13 marked more than one
activity) was jogging (31. 5%), followed by walking (15. 75%)
and competitive individual sports (11. 81%). Tennis and
racquetball were the most frequently mentioned competitive
individual sports. Calisthenics, body-building, swimming, and
bicycling were each cited by 5%-10%, whereas yoga and
competitive team sports were each cited by less than 5%.

Who Exercises, How Often, and By What Methods?

Chi-square analyses of demographic variables with exercise pattern

variables revealed more experienced therapists to be somewhat less

likely to exercise than less experienced therapists, χ

2

(1,N = 196) = 3.

96, p < . 05 . Experience and age were highly related, χ

2

(2,N = 196) =

267, p < . 0001 ; however, the relation of age with likelihood of

exercising approached but did not reach significance. Several trends

also emerged in the kind of exercise favored by respondents: Those

using highly aerobic exercises such as jogging, swimming, bicycling, or

walking were likely to exercise more frequently than were those

in competitive and skeletal muscle development exercises, χ

2

(4,N = 129) = 9. 6 ; older respondents were more likely than younger

ones to use walking and less likely to use competitive sports or

demanding aerobic exercises, χ

2

(8,N = 132) = 16. 97 ; men were

more likely to have been exercising for a long time (seven or more

years) than were women, χ

2

(3,N = 139) = 7. 82 ; men were more likely

than women to be involved in competitive sports and jogging and less

likely to use walking, swimming, and yoga, χ

2

(10,N = 140) = 23. 81, p

< . 01 ; therapists with humanistic orientations were somewhat

less likely than those of other orientations to be involved in aerobic

exercise that is highly demanding of the cardiovascular system (e. g. ,

running) and more likely to use walking, whereas those favoring

behavioral and cognitive behavioral orientations were somewhat more

likely to be engaged in skeletal muscle strengthening activities, χ

2

(12,N = 132) = 25. 52 .

 The great majority of respondents (93. 57%)

indicated that they would recommend regular
exercise to other psychotherapists; 34. 29%
reported that they would recommend exercise "for
personal effect," and 59. 29% advocated it "for
personal and work-related effect. " Chi-square
analysis indicated that more men than women
would make the recommendation for both personal
and work-related effect, χ

2

(3,N = 138) = 9. 54, p <

. 05 ; this finding is perhaps related to the fact that
more men than women are long-time users. The
great majority of respondents (92. 86%) would
recommend exercise to their patients. Only 5%
indicated that they "never" made such a
recommendation, whereas 52. 86% did
"occasionally," 30% did "routinely" and 10% did "all
the time. "

Mój najlepszy przyjaciel

Individual Differences and Developmental Changes in Preschoolers' Friendships ,  By: Kathryn A.

Park, Keng-Ling Lay, Laura Ramsay, Developmental Psychology, 1993, Vol. 29, Issue 2

The design was longitudinal. Preschool friend pairs were observed

in two 1-hr play sessions spaced approximately 1 year apart (M
= 12. 8 months). Fifty pairs of best friends were observed at
the first visit. The final sample included 9 girl-girl pairs, 6 boy-
boy pairs, and 9 girl-boy pairs.

Kryteria doboru par

przyjaciół

 Najczęściej się bawią
 Dzieci często o sobie

wspominają

 Dzieci bardzo się lubią
 Najlepiej się bawią
 Chcą się ze sobą bawić

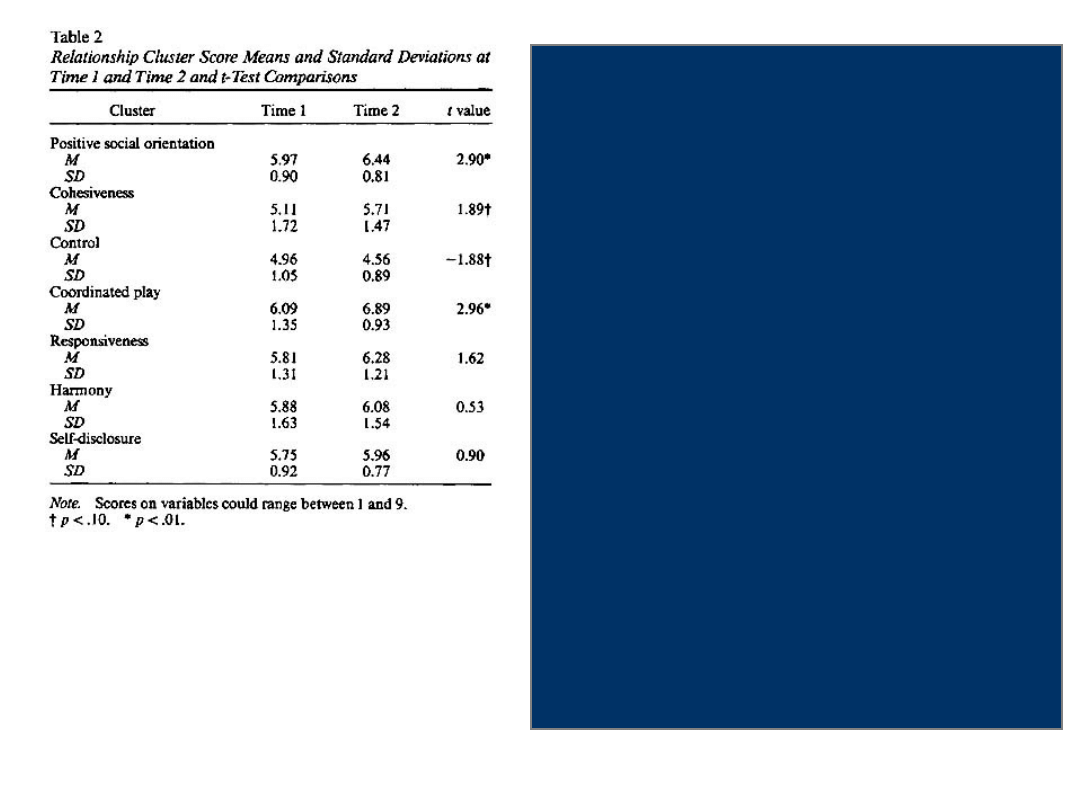
Test T-Studenta dla prób

zależnych pokazał, że związki

przyjacielskie zmieniają się na

wymiarach:

pozytywnej orientacji społecznej

(pozytywne emocje +

zachowania prospołeczne)

wspólnej zabawy (zabawa

ineraktywna).

Na poziomie tendencji

zaobserwowano także zmiany

w obrębie:

kontroli (hamowanie agresji i

chęć nawiązywania interakcji)

spójności (bliskość fizyczna,

koordynacja ruchów)

Table 2. At the second
time point, the
friends' play was
significantly more
coordinated and
positive (ps < . 01).

Uczenie się mimowolne - badania dr R. Balas

Czy jesteśmy w stanie uczyć się

mimowolnie?

Najpierw prezentowano osobom

sztuczny język uporządkowany zgodnie
z określonymi regułami. Zadaniem
osoby badanej było śledzenie słów
pojawiających się na ekranie w celu ich
późniejszego rozpoznania.

 Następnie sprawdza się, czy osoby badane

rozpoznają prezentowane wyrazy „sztucznej

gramatyki”

 A także (niespodzianka!) pyta się, czy nowe

wyrazy są zgodne z regułami sztucznego

języka.

 Osoba odpowiada TAK/ NIE więc ma 50% szans,

że zgadnie.

 Mając poprawność takich odpowiedzi można

stwierdzić, czy ludzie mimowolnie nauczyli się

reguł analizując tę zmienna testem T-Studenta

dla jednej próby. Jeśli poprawność jest zbliżona

do 50% to znaczy, że nie jesteśmy w stanie

uczyć się mimowolnie.

Wyniki

Wartością testowaną będzie 50%. Tak więc

jeśli w teście t-Student dla jednej próby
uzyskamy wynik T(24)=3,7; p<0,05 to
oznacza to, że poziom poprawności różni się
od 0,5. Jeśli jeszcze przeciętna poprawność
jest większa od 0,5 to możemy z cała
pewnością stwierdzić, że uczenie się
mimowolne istnieje 

Na koniec kilka podchwytliwych pytań

Jeżeli otrzymaliśmy wynik:

Chi

2

(3)=4,5; p<0,05

∞Jaka tabela krzyżowa była podstawą jego

otrzymania?

• 2x2
• 3x2
• 4x2
• 4x3

20 kobiet i 20 mężczyzn pytano jakie zwierzę

lubią najbardziej: kota, psa, chomika czy
świnkę morską

∞Jakiego testu użyć?
∞Ile stopni swobody?