Wprowadzenie

Wprowadzenie

do

do

wnioskowania

wnioskowania

statystycznego

statystycznego

Wykład 8

(dodatkowe folie w

powielarni)

Materiały do wykładu Izabela Krejtz

Proces analizy danych

Proces analizy danych



Statystyka opisowa – wstępny proces
analizy danych



Statystyka inferencyjna



pozwala na wyciąganie wniosków z danych



możemy na podstawie próby wnioskować o
populacji

Materiały do wykładu Izabela Krejtz

Statystyki i parametry

Statystyki i parametry

s

s

X

,

,

2







,

,

2

Statystyki na poziomie próby

Parametry w populacji

Statystyki w próbie są estymatorami odpowiednich parametrów w populacji

Materiały do wykładu Izabela Krejtz

Błąd próby

Błąd próby



Jeśli wylosujemy próbkę z
populacji:



Średnia w tej próbie może być
większa/mniejsza od średniej w
populacji



Właśnie to, w jakim stopniu
statystyka próby (np. średnia) różni
się od odpowiednigo parametru w
populacji (np. średniej w populacji)
określa się błędem próby.

Dlaczego ten błąd się

pojawia i jak go

zminimalizować????

Materiały do wykładu Izabela Krejtz

Dlaczego się pojawia?

Dlaczego się pojawia?



Ponieważ nie badamy całej populacji, wszystkich
np. osób depresyjnych, Świętych Mikołai



Za każdym razem decydując się na pobranie
próby, musimy pogodzić się z tym, że będzie ona
obciążona pewnym błędem



Np. chcemy zbadać przyrost wagi u noworodków w
ciągu pierwszych 3 tygodni ich życia – zbadamy
wszystkich?



Jeśli zważymy 20% noworodków – uzyskamy średni
przyrost wagi, który będzie dobrym oszacowaniem
średniego przyrostu wagi całej populacji noworodków,
ale niekoniecznie równy rzeczywistemu

Materiały do wykładu Izabela Krejtz

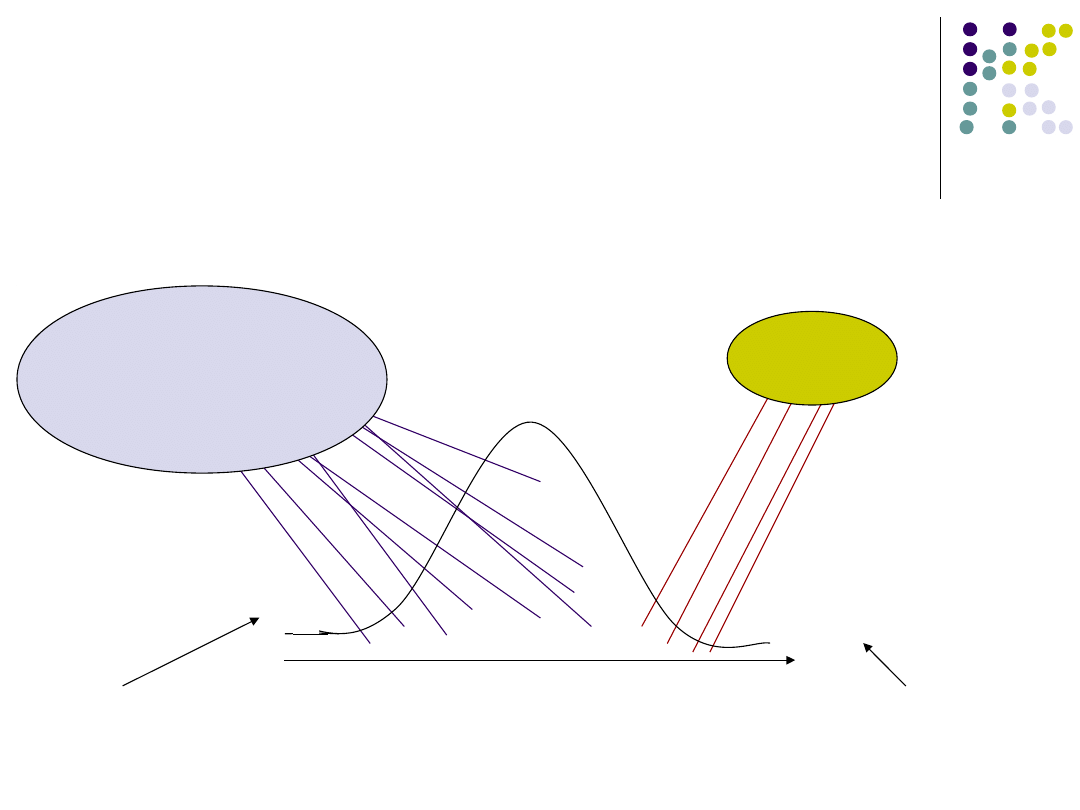
Zakładamy, że większość zmiennych

Zakładamy, że większość zmiennych

ma rozład normalny w populacji

ma rozład normalny w populacji

Dużo pieniędzy na badanie

Mało pieniędzy na badanie

Duża próba – lepsze
oszacowanie populacji,
mniejszy błąd, lepsza
reprezentacja populacji

Mała próbka, większe
prawdopodobieństwo błędu,
możemy uzyskać
wyniki z krańców

Średnia z tej próby – dobrze
Oszacowanie średniej w populacji

Średnia w tej próbie
byłaby większa od średniej
w populacji, duży błąd próby

Materiały do wykładu Izabela Krejtz

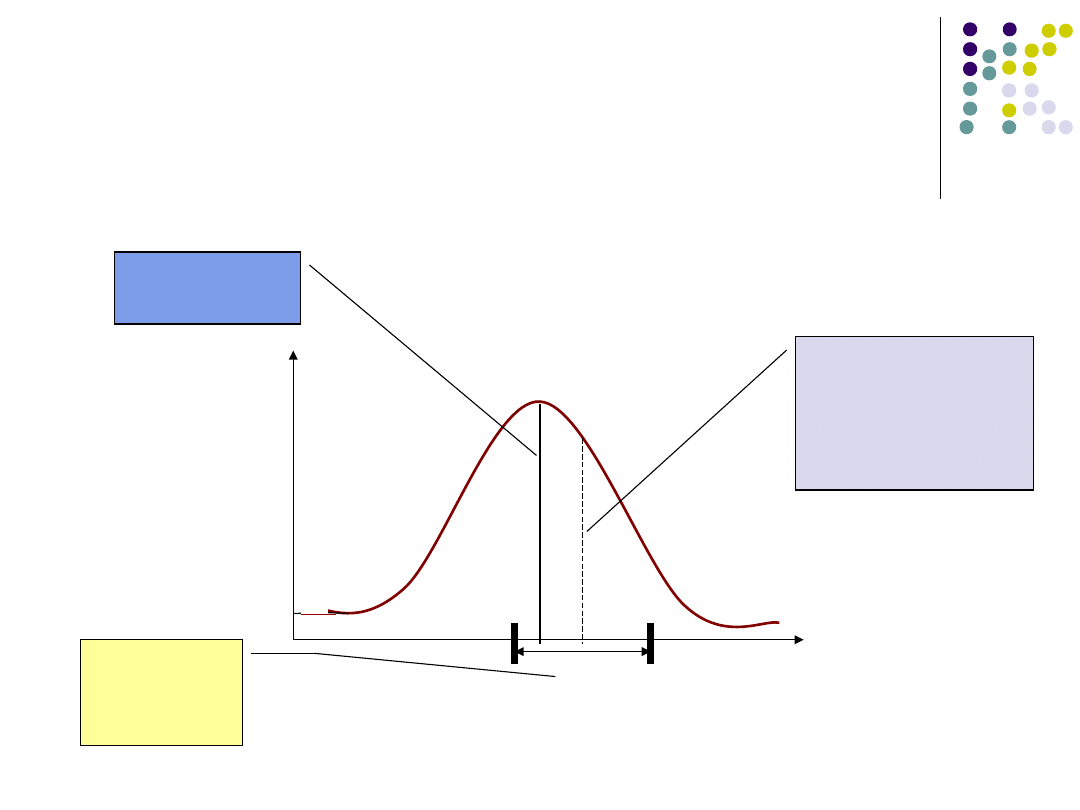
przedział ufności dla średniej - średnia

przedział ufności dla średniej - średnia

daje punktowe oszacowanie średniej w

daje punktowe oszacowanie średniej w

populacji, podajemy przedział ufności w

populacji, podajemy przedział ufności w

jaki znajdzie się rzeczywista średnia

jaki znajdzie się rzeczywista średnia

Nasza średnia

jako estymator

średniej w

populacji

Średnia w

populacji

Przedział

ufności

dla

średniej

Nadal trzeba określić jak pewni jesteśmy tego oszacowania

Materiały do wykładu Izabela Krejtz

Przedział ufności dla średniej

Przedział ufności dla średniej



Im mniejsze przedziały ustalamy tym
mniejsze prawdopodobieństwo, że
obejmą średnią w populacji



Tradycyjnie w psychologii przyjęło się
obierać 95% przedział ufności dla
średniej



Czyli taki, gdzie jesteśmy w 95% pewni, że
zawiera on średnią w populacji



Czasem przyjmuje się 99% przedział ufności

Materiały do wykładu Izabela Krejtz











z

M

Materiały do wykładu Izabela Krejtz

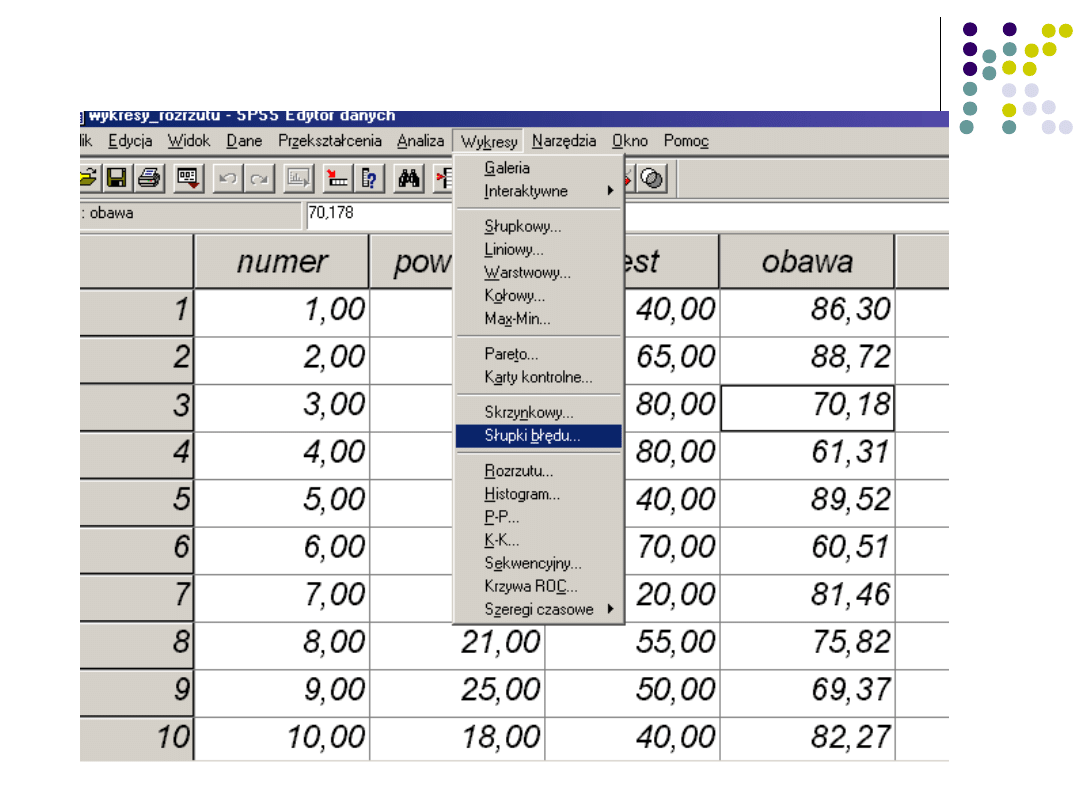
Przypomnienie wykresów słupków

Przypomnienie wykresów słupków

błędu

błędu

Materiały do wykładu Izabela Krejtz

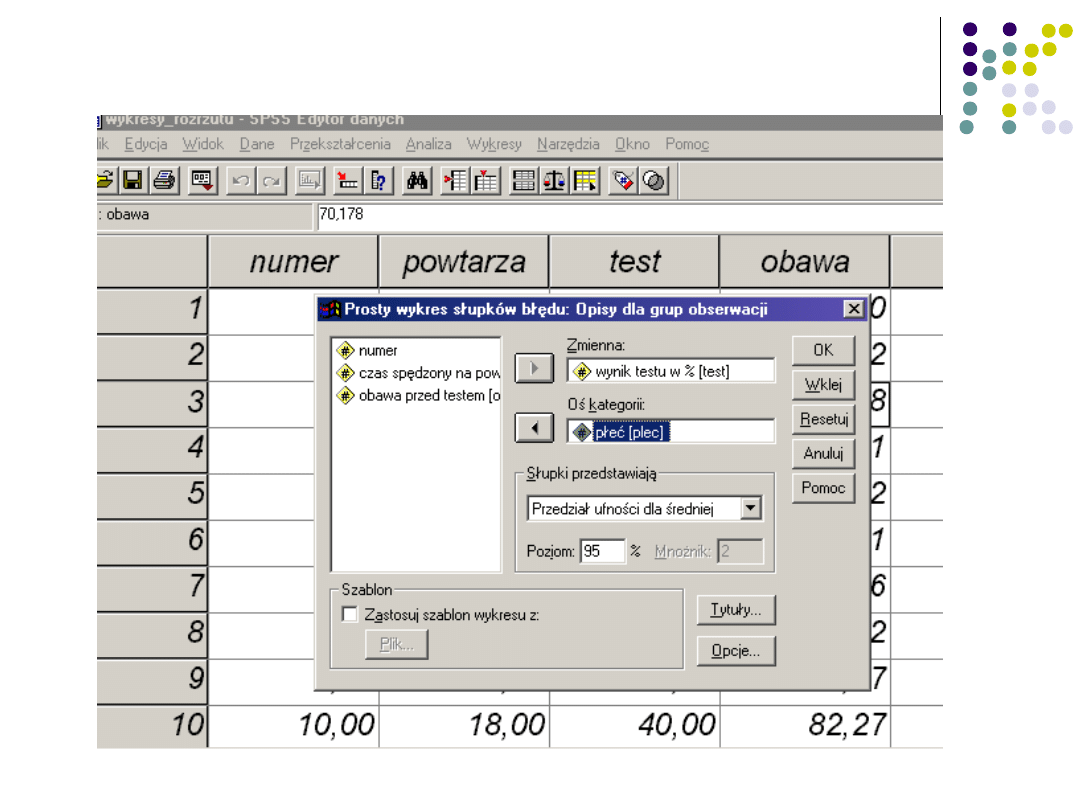
Definiowanie wykresu

Definiowanie wykresu

Materiały do wykładu Izabela Krejtz

51

52

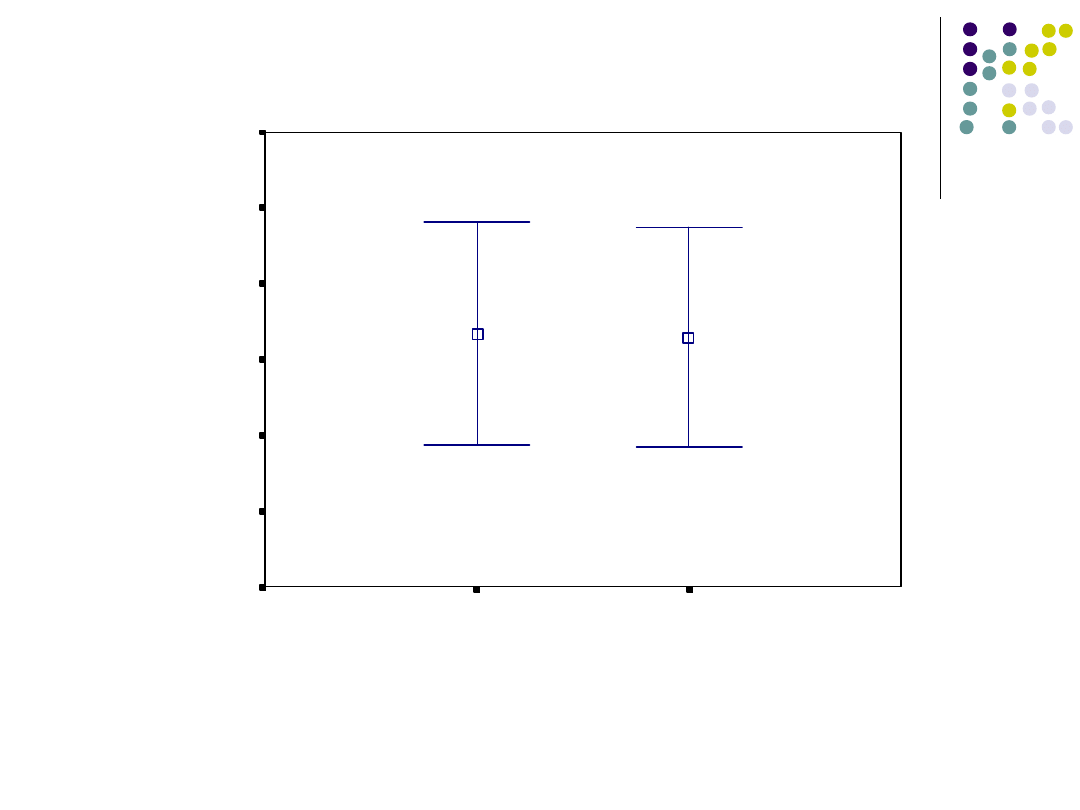
N =

płeć

kobieta

mężczyzna

95

%

P

U

w

yn

ik

t

es

tu

w

%

70

65

60

55

50

45

40

Materiały do wykładu Izabela Krejtz

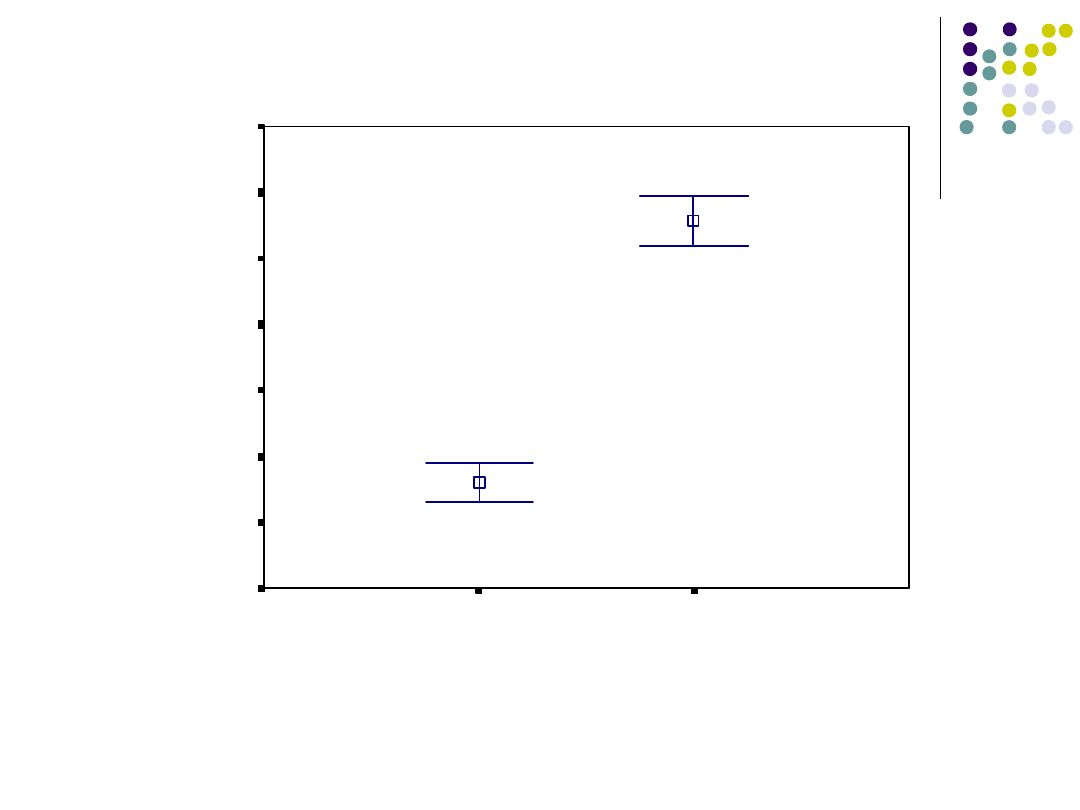
51

52

N =

płeć

kobieta

mężczyzna

95

%

P

U

o

ba

w

a

pr

ze

d

te

st

em

90

80

70

60

50

40

30
20

Materiały do wykładu Izabela Krejtz

Testowanie hipotez i istotność

Testowanie hipotez i istotność

statystyczna

statystyczna



Stawiamy hipotezy



o różnicy między warunkami eksperymentalnymi.



o związkach między zmiennymi.



Zbieramy dane na ich poparcie



Jakie jest prawdopodobieństwo, że uzyskany przez nas

związek między zmiennymi, czy różnica jest dziełem

przypadku, błędu próbkowania?



Im mniejsze to prawdopodobieństwo, tym bardziej pewni

jesteśmy, wniosku o występowaniu rzeczywistych różnic

na poziomie populacji

Materiały do wykładu Izabela Krejtz

Testowanie hipotez

Testowanie hipotez



Skąd wiemy, że zebrane dane dają
potwierdzenie naszych przewidywań?



Mamy dane



Określamy prawdopodobieństwo, że
uzyskane wyniki są dziełem przypadku
(korelacja, czy też różnica między
zmiennymi)



Jeśli odpowiednio małe jest to
prawdopodobieństwo – znaleźliśmy poparcie
dla naszej hipotezy

Materiały do wykładu Izabela Krejtz

Rozkład z próby średnich

Rozkład z próby średnich



Jeśli wylosowalibyśmy z populacji wiele próbek,
wtedy moglibyśmy zrobić rozkład średnich z tych
prób



Średnia z tych prób byłaby bliska rzeczywistej
średniej w populacji



Co więcej rozkład z tych prób jest bliski
normalnemu



Im więcej próbek wylosujemy tym rozkład z
próby będzie zbliżony do normalnego,
niezależnie od kształtu rozkładu populacji



Centralne twierdzenie graniczne

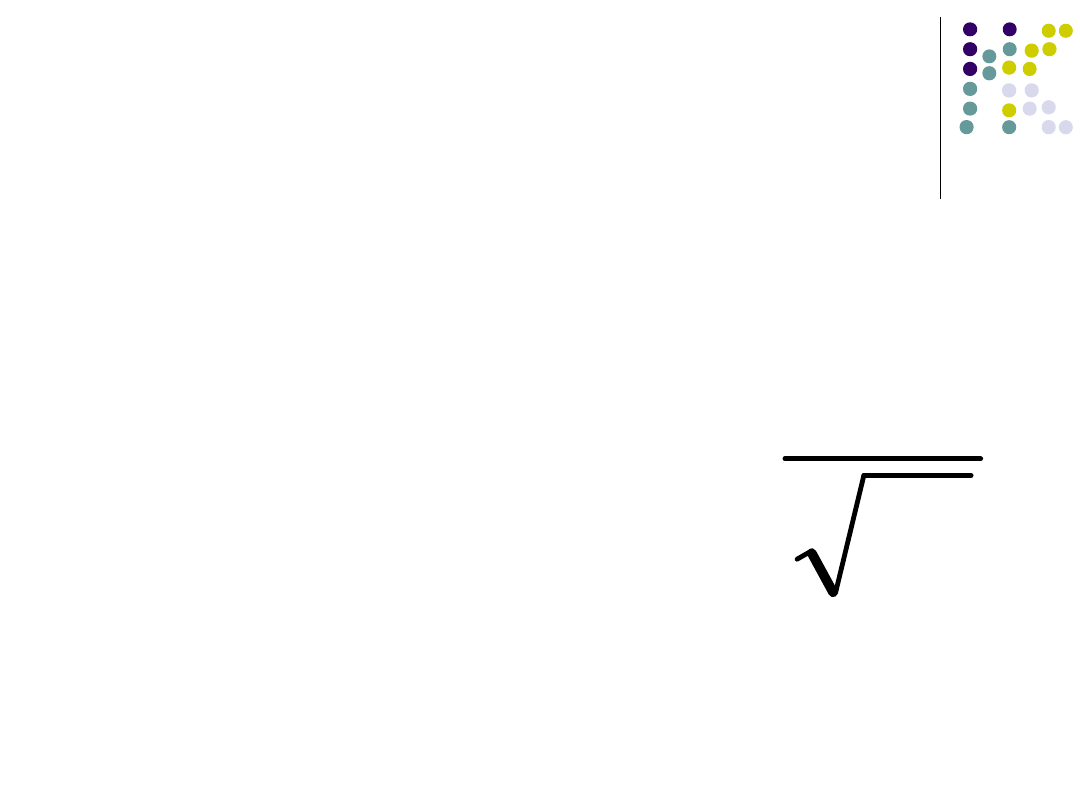
Materiały do wykładu Izabela Krejtz

Błąd standardowy średniej

Błąd standardowy średniej



Określa na ile średnie próbek

różnią się od średniej z tych

średnich (średniej z próby)



Błąd standardowy



N- wielkość próby – czyli im

większa próba tym mniejszy

błąd standardowy



Wykorzystywany do

określenia przedziału, w

jakim znajdować się może

średnia w populacji

(mając do

dyspozycji naszą średnią w

próbie badanych osób)

N

s





Materiały do wykładu Izabela Krejtz

Etapy testowania hipotez

Etapy testowania hipotez



Stawiamy hipotezę badawczą



Zbieramy dane



Stawiamy hipotezę zerową



Konstruujemy rozkład prawdopodobieństwa

otrzymania takiego wyniku przy założeniu, że

hipoteza zerowa jest prawdziwa



Porównujemy wynik uzyskany z rozkładem



Znajdujemy prawdopodobieństwo uzyskania

takiego wyniku



Podejmujemy decyzję o odrzuceniu bądź nie

hipotezy zerowej.

Materiały do wykładu Izabela Krejtz

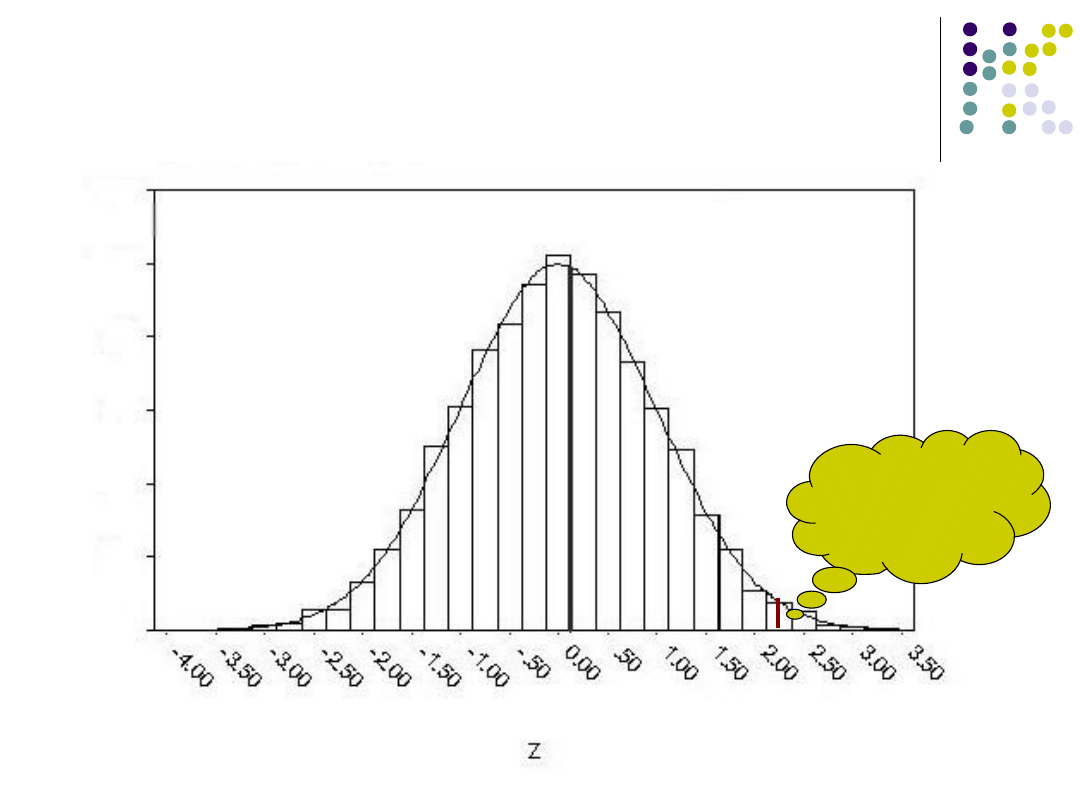
Obszar odrzucenia

Obszar odrzucenia

5%

Materiały do wykładu Izabela Krejtz

Błędy wnioskowania statystycznego

Błędy wnioskowania statystycznego



Błąd I rodzaju – α (alfa)



Odrzucenie hipotezy zerowej, gdy jest
prawdziwa



Równy poziomowi istotności



Błąd II rodzaju – β (beta)



Nie odrzucenie hipotezy zerowej mimo, że
jest fałszywa